Introduction

Motivations and State of the Art

Underactuated multibody and robotic systems are those where the number of independent control forces is smaller than the number of degrees of freedom (DOFs). Underactuation is caused by the presence of flexible links, passive joints, as well as in case of actuator failure. Accurate and precise trajectory tracking in underactuated systems relies on the presence of effective control schemes, with feedback and feedforward terms, and an optimized motion planning accounting for the presence of some unactuated coordinates and of the related vibrational dynamics [1, 2]. Both feedforward control and motion planning usually exploit the inversion of the dynamic model [3], that is not straightforward as in fully actuated systems because of the rectangular force distribution matrix. The algebraic solution of the inverse dynamic problem is possible if the system is differentially flat [4]. Unfortunately, flatness is a system property that is not straightforward to assess and finding a flat output definition is not trivial because it imposes a lot of algebraic manipulations [5] since no systematic approach exists. Additionally, the use of flatness in underactuated systems imposes very smooth reference trajectories, usually with four continuous derivatives, that are often not desiderable because of high values of the maximum and average speed and accelerations [6].

The difficulties in model inversion are exacerbated in the case of non-minimum phase systems that have also unstable internal dynamics. In the case of linear systems, this is related to the presence of zeros with positive real part: if the model is inverted these zeros become right half-plane poles, making the control actions divergent. Generally speaking, also with reference to nonlinear systems, inversion of the dynamic model, either for computing the feedforward forces or the commanded motion of the actuated coordinates, is usually solved through approximate or non-causal solutions. The literature proposes several approaches to model inversion in underactuated systems, and some papers also address the more challenging non-minimum phase occurrence. More attention is, however, paid to inverse dynamics for computing the control forces, while motion planning is less investigated.

In [7], an inversion-based approach to nonlinear output tracking control is proposed, together with a feedback term to stabilize the system along the desired trajectory; the solution is achieved by applying the Byrnes–Isidori regulator to a specific trajectory, leading to a non-causal solution that requires pre-actuation (i.e., the actuator should move before the desired motion of the controlled output starts).

Another interesting approach is the method of servo constraints, that has been proposed in [8] and in the related papers. It transforms the system model into a set of DAE where the reference to track is properly represented through algebraic constraints. The method, in its original formulation, does not formulate the internal dynamics and therefore is not suitable in those case of non-minimum phase systems where it should be properly stabilized to obtain non-diverging results. Such a method has been also applied to various systems, such as a crane with hoisting in [9], and in [10] for motion planning in a two-disk system.

Two further feedforward control techniques are proposed in [11]: in the first one, the model inversion is performed through the concept of nonlinear input–output normal form, which is achieved thanks to a coordinate transformation, while the second one exploits servo constraints, leading to solve a set of differential algebraic equations (DAEs). Both techniques are exploited in an optimization problem. An interesting comparison is presented in [12], considering two different strategies that are present in the literature: the standard stable inversion method, which is solved through the formulation of a two-point boundary value problem, and an alternative optimization problem formulation, which is defined without any boundary conditions. This comparison shows that both approaches can be formulated through DAEs and, additionally, numerical results are presented considering manipulators with passive and compliant joints.

Optimization-based formulations exploiting two-point boundary value problems have been also adopted, either for inverse dynamics [13,14,15,16] or motion planning [17]. In the usual formulation of two-point boundary value problems, no specifications are set on the path connecting the boundary points, while a function cost is minimized to accomplish secondary tasks, such as increasing robustness.

The techniques discussed so far are devoted to general underactuated systems. In the specific case of cranes, the most famous motion planning technique is the input shaping that has been mainly developed for two-DOF cranes (i.e., with just one vibrational mode) [18]. Basically, the reference trajectory is convolved with a baseline of impulses, computed on the basis of a simplified system model, to delete the residual vibration of the unactuated load. Input shaping in spatial crane has been mainly applied to rest-to-rest linear motions [19], although some papers [20, 21] also apply it to path and trajectory tracking. In motion planning and control of spatial cranes, a lot of attention has been paid to feedback control (see e.g., as some relevant examples, the schemes proposed in [22,23,24,25,26,27,28,29]), also including techniques proposed by some of the authors of this paper for performing closed-loop modifications of the reference trolley trajectory to ensure control of the load swing [30] or accurate path tracking [31].

Contributions of the Paper

In this paper, a stable model inversion technique suitable for non-minimum phase underactuated multibody systems is exploited for motion planning design in a 4-DOF spatial overhead crane. The goal is to compute the reference trajectories for the actuated coordinates, ensuring that the controlled output tracks the desired reference, in terms of both trajectory in time and spatial path. No feedback control on the load side is exploited, and hence, path and trajectory control, as well as load swing reduction, are just executed through an optimized motion planning of the trolley.

Firstly, the crane dynamic model is partitioned into two parts: an actuated subsystem and an unactuated one, that is useful to obtain the internal dynamics and to disregard the equations related to the actuated subsystem that would be of interest just for the computation of the control forces. Secondly, the desired output trajectory of the system is described as a nonlinear separable function of the actuated and unactuated coordinates, to allow for a simple formulation of the internal dynamics. Output redefinition is then exploited to stabilize and solve it, to compute the time history of the internal dynamics in the trajectory execution. Output redefinition is an established approach to transform a non-minimum phase system into a minimum phase one by defining a different output selection [32]. It is worth to notice that nonlinear output redefinition is here exploited, while several approaches proposed in the literature employ the so-called “linear output redefinition” [11], even if the input–output relation is nonlinear. Finally, the commanded trajectory for the actuated coordinates is computed through kinematic nonlinear inversion of the output equation. The algebraic model of the output equations is handled in this paper without any linear approximation; hence, the proposed method provides an improvement compared to the existing methods that adopt the linear approximation in solving this kind of problems.

The proposed method relies on the numerical integration of the obtained ordinary differential equations (ODE), without requiring optimization as many methods in the literature do (see e.g., [13,14,15,16,17] and the references therein), and with a reduced computational effort. The obtained solution is causal since it does not require pre-actuation. This is another advantage over several methods, such as [7], that lead to non-causal solution that cannot be exactly implemented.

The paper proposes the theory that is itself a new contribution in the literature thanks to the novel use of the nonlinear separable formulation of the output, the numerical validation and, finally, the experimental application through a laboratory setup, in the execution of several trajectories. Comparison with the well-known input shaping technique [21], that is often assumed as a benchmark in the field of motion planning of underactuated cranes, as well with the unshaped command is provided, to further demonstrate the effectiveness.

System Model and Method Description

System Dynamic Model

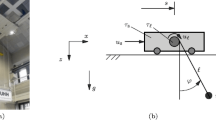
Let us consider the dynamic model of the 4-DOF overhead Cartesian crane under investigation sketched in Fig. 1. The independent coordinates include two absolute translations describing the planar motion of the platform (also denoted as the trolley) of the crane, that are the two actuated coordinates \({\mathbf{q}}_{{\mathbf{A}}} = \left[ {\begin{array}{*{20}c} {x_{P} } & {y_{P} } \\ \end{array} } \right]^{T}\)\(\in {\mathbb{R}}^{2}\), and two unactuated components of the swing angle \({\mathbf{q}}_{{\mathbf{U}}} = \left[ {\begin{array}{*{20}c} {\theta_{X} } & {\theta_{Y} } \\ \end{array} } \right]^{T}\)\(\in {\mathbb{R}}^{2}\). \(\theta_{X}\) is the swing angle projected on the \(XZ\) plane, while \(\theta_{Y}\) is the swing angle measured from the \(XZ\) plane. By assuming that the cable is taut with tensile stress and that hoisting is not allowed (i.e., the cable length \(h\) is constant), the following four nonlinear ordinary differential equations (ODEs) describe the system dynamic behavior:

$$\begin{gathered} \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\left( {M_{X} + m} \right)} \\ 0 \\ {m\,h\cos \left( {\theta_{X} } \right)\cos \left( {\theta_{Y} } \right)} \\ { - m\,h\sin \left( {\theta_{X} } \right)\sin \left( {\theta_{Y} } \right)} \\ \end{array} } & {\begin{array}{*{20}c} 0 \\ {\left( {M_{Y} + m} \right)} \\ 0 \\ {m\,h\cos \left( {\theta_{Y} } \right)} \\ \end{array} } & {\begin{array}{*{20}c} {m\,h\cos \left( {\theta_{X} } \right)\cos \left( {\theta_{Y} } \right)} \\ 0 \\ {m\,h^{2} \cos^{2} \left( {\theta_{Y} } \right)} \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} { - m\,h\sin \left( {\theta_{X} } \right)\sin \left( {\theta_{Y} } \right)} \\ {m\,h\cos \left( {\theta_{Y} } \right)} \\ 0 \\ {m\,h^{2} } \\ \end{array} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\ddot{x}_{P} } \\ {\ddot{y}_{P} } \\ {\ddot{\theta }_{X} } \\ {\ddot{\theta }_{Y} } \\ \end{array} } \right] + \hfill \\ + \left[ {\begin{array}{*{20}c} { - m\,h\,\dot{\theta }_{X}^{2} \sin \left( {\theta_{X} } \right)\cos \left( {\theta_{Y} } \right) - m\,h\,\dot{\theta }_{Y}^{2} \sin \left( {\theta_{X} } \right)\cos \left( {\theta_{Y} } \right) - 2\,m\,h\,\dot{\theta }_{X} \dot{\theta }_{Y} \cos \left( {\theta_{X} } \right)\sin \left( {\theta_{Y} } \right) + c_{X} \dot{x}} \\ { - m\,h\,\dot{\theta }_{Y}^{2} \sin \left( {\theta_{Y} } \right) + c_{Y} \dot{y}} \\ { - 2\,m\,h^{2} \,\dot{\theta }_{X} \dot{\theta }_{Y} \sin \left( {\theta_{Y} } \right)\cos \left( {\theta_{Y} } \right) + c_{\theta } \dot{\theta }_{X} } \\ {m\,h^{2} \,\dot{\theta }_{X}^{2} \sin \left( {\theta_{Y} } \right)\cos \left( {\theta_{Y} } \right) + c_{\theta } \dot{\theta }_{Y} } \\ \end{array} } \right] = \hfill \\ = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ { - m\,h\,g\sin \left( {\theta_{X} } \right)\cos \left( {\theta_{Y} } \right)} \\ { - m\,h\,g\cos \left( {\theta_{X} } \right)\sin \left( {\theta_{Y} } \right)} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 1 \\ 0 \\ 0 \\ 0 \\ \end{array} } & {\begin{array}{*{20}c} 0 \\ 1 \\ 0 \\ 0 \\ \end{array} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {u_{x} } \\ {u_{y} } \\ \end{array} } \right] \hfill \\ \end{gathered}$$
(1)
Fig. 1
figure 1

Simplified scheme of the underactuated overhead Cartesian crane

Full size image

The following definitions have been introduced in Eq. (1): \(u_{X}\), \(u_{Y}\) are the control forces that are applied to the platform along the \(X\) and \(Y\) directions; \(m\) is the lumped mass of the suspended load; \(c_{X}\), \(c_{Y}\), \(c_{\theta }\) are the viscous friction coefficients; \(M_{X}\), \(M_{Y}\) are the translational masses of the platform along the \(X\) and \(Y\) directions, respectively; \(g\) is the gravity acceleration.

Equation (1) can be written in a concise form as the typical model of a nonlinear multibody system, where \({\mathbf{M}}\left( {{\mathbf{q}}_{{\mathbf{U}}} } \right)\)\(\in {\mathbb{R}}^{4\times 4}\) is the position-dependent mass matrix, \({\mathbf{C}}\left( {{\mathbf{q}}_{{\mathbf{U}}} ,{\dot{\mathbf{q}}}_{{\mathbf{U}}} } \right)\) is the vector of the speed-dependent contributions (both inertial terms and viscous friction terms), \({\mathbf{F}}\left( {{\mathbf{q}}_{{\mathbf{U}}} } \right)\)\(\in {\mathbb{R}}^{4}\) is the vector of forces due to gravity acceleration, B \(\in {\mathbb{R}}^{4\times 2}\) is the control forces distribution matrix, and \({\mathbf{u}} = \left[ {\begin{array}{*{20}c} {u_{x} } & {u_{y} } \\ \end{array} } \right]^{T}\)\(\in {\mathbb{R}}^{2}\) collects the control forces.

$${\mathbf{M}}\left( {{\mathbf{q}}_{{\mathbf{U}}} } \right)\;\left[ {\begin{array}{*{20}c} {{\mathbf{q}}_{{\mathbf{A}}} } \\ {{\mathbf{q}}_{{\mathbf{U}}} } \\ \end{array} } \right] + {\mathbf{C}}\left( {{\mathbf{q}}_{{\mathbf{U}}} ,{\dot{\mathbf{q}}}_{{\mathbf{U}}} } \right) = {\mathbf{F}}\left( {{\mathbf{q}}_{{\mathbf{U}}} } \right) + {\mathbf{Bu}}$$
(2)

The goal of motion planning is to precisely make the suspended load track a desired path (both in in space and in time). Since just two control forces are applied, the motion of just two output coordinates is imposed. The output vector \({\mathbf{y}}\)\(\in {\mathbb{R}}^{2}\) is therefore defined as the following nonlinear algebraic function of the four independent coordinates, by exploiting trigonometric kinematic relations:

$${\mathbf{y}} = \left[ {\begin{array}{*{20}c} {x_{L} } \\ {y_{L} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {x_{P} + h\sin \theta_{X} \cos \theta_{Y} } \\ {y_{P} + h\sin \theta_{Y} } \\ \end{array} } \right]$$
(3)

Formulation and Stabilization of the Internal Dynamics

The dynamic model in Eqs. (1) and (2) can be partitioned into actuated and unactuated coordinates:

$$\left[ {\begin{array}{*{20}c} {{\mathbf{M}}_{{{\mathbf{AA}}}} } & {{\mathbf{M}}_{{{\mathbf{AU}}}} } \\ {{\mathbf{M}}_{{{\mathbf{AU}}}}^{T} } & {{\mathbf{M}}_{{{\mathbf{UU}}}} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\mathbf{\ddot{q}}}_{{\mathbf{A}}} } \\ {{\mathbf{\ddot{q}}}_{{\mathbf{U}}} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {{\mathbf{C}}_{{\mathbf{A}}} } \\ {{\mathbf{C}}_{{\mathbf{U}}} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\mathbf{F}}_{{\mathbf{A}}} } \\ {{\mathbf{F}}_{{\mathbf{U}}} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {{\mathbf{B}}_{{\mathbf{A}}} } \\ {\mathbf{0}} \\ \end{array} } \right]{\mathbf{u}}$$
(4)

By considering just the unactuated subsystem, the following set of two nonlinear ODEs is obtained:

$${\mathbf{M}}_{{{\mathbf{AU}}}}^{T} {\mathbf{\ddot{q}}}_{{\mathbf{A}}} + {\mathbf{M}}_{{{\mathbf{UU}}}} {\mathbf{\ddot{q}}}_{{\mathbf{U}}} + {\mathbf{C}}_{{\mathbf{U}}} = {\mathbf{F}}_{{\mathbf{U}}}$$
(5)

The trajectory design exploits the inversion of the equations of motion in Eq. (5): the input of the inverted equations will be the desired trajectory in time of the controlled output (\({\mathbf{y}}^{{{\mathbf{ref}}}} ,{\dot{\mathbf{y}}}^{{{\mathbf{ref}}}} ,{\mathbf{\ddot{y}}}^{{{\mathbf{ref}}}}\)), while the final output to be computed are the commanded values of the actuated variables, ensuring that y tracks such a reference.

In this work, the formulation of the desired output is exploited, and hence of the reference trajectory, as a nonlinear, separable function of \({\mathbf{q}}_{{\mathbf{A}}}\) and \({\mathbf{q}}_{{\mathbf{U}}}\). This is another novel contribution of the paper. Indeed, it can be easily recognized that the following form of Eq. (3) can be formulated, with \({\mathbf{g}}:\;{\mathbb{R}}^{2} \mapsto {\mathbb{R}}^{2}\), \({\mathbf{g}}\left( {{\mathbf{q}}_{{\mathbf{U}}} } \right) = h\left[ {\begin{array}{*{20}c} {\sin \theta_{X} \cos \theta_{Y} } \\ {\sin \theta_{Y} } \\ \end{array} } \right]\), as a nonlinear function:

$${\mathbf{y}} = \,{\mathbf{q}}_{{\mathbf{A}}} + \,{\mathbf{g}}\left( {{\mathbf{q}}_{{\mathbf{U}}} } \right)$$
(6)

The second derivative of the output is, in turn:

$$\begin{gathered} {\mathbf{\ddot{y}}} = \left[ {\begin{array}{*{20}c} {\ddot{x}_{P} } \\ {\ddot{y}_{P} } \\ \end{array} } \right] + h\left[ {\begin{array}{*{20}c} {\cos \theta_{X} \cos \theta_{Y} } & { - \sin \theta_{X} \sin \theta_{Y} } \\ 0 & {\cos \theta_{Y} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\ddot{\theta }_{X} } \\ {\ddot{\theta }_{Y} } \\ \end{array} } \right] + \\ h\left[ {\begin{array}{*{20}c} { - \sin \theta_{X} \cos \theta_{Y} \dot{\theta }_{X}^{2} - 2\cos \theta_{X} \sin \theta_{Y} \dot{\theta }_{X} \dot{\theta }_{Y} - \sin \theta_{X} \cos \theta_{Y} \dot{\theta }_{Y}^{2} } \\ { - \sin \theta_{Y} \dot{\theta }_{Y}^{2} } \\ \end{array} } \right] \\ \end{gathered}$$
(7)

Therefore, the desired output acceleration can be written in the following concise form,

$${\mathbf{\ddot{y}}}^{{{\mathbf{ref}}}} = \,{\mathbf{\ddot{q}}}_{{\mathbf{A}}} + \,{\mathbf{J}}_{{\mathbf{g}}} \left( {{\mathbf{q}}_{{\mathbf{U}}} } \right)\;{\mathbf{\ddot{q}}}_{{\mathbf{U}}} + {{\varvec{\upgamma}}}_{{\mathbf{g}}} \left( {{\mathbf{q}}_{{\mathbf{U}}} ,{\dot{\mathbf{q}}}_{{\mathbf{U}}} } \right)$$
(8)

where \({\mathbf{J}}_{{\mathbf{g}}}\)\(\in {\mathbb{R}}^{2\times 2}\) is the Jacobian matrix of \({\mathbf{g}}\), and \({{\varvec{\upgamma}}}_{{\mathbf{g}}}\)\(\in {\mathbb{R}}^{2}\) contains the centripetal terms. In writing Eq. (8), it is assumed that the trajectory \({\mathbf{y}}^{{{\mathbf{ref}}}} \left( t \right)\) is, at least, twice differentiable. This is an obvious requirement for any mechanical system, also in the case of fully actuated ones, where finite accelerations (and hence finite control forces) are required [33].

The formulation of the controlled output as a separable function is a more general formulation of the linearly combined output proposed by the authors in [34], as well as in [11, 35], for the solution of the inverse dynamic problem, and allows effectively handling larger elastic displacements than a linear representation.

Equation (8) enables writing the internal dynamics as just a function of \({\mathbf{q}}_{{\mathbf{U}}}\) (and its derivatives) and \({\mathbf{\ddot{y}}}^{{{\mathbf{ref}}}}\), by removing the dependence of Eq. (5) on \(\,{\mathbf{\ddot{q}}}_{{\mathbf{A}}}\), leading to the following nonlinear ODEs:

$$\left[ {{\mathbf{M}}_{{{\mathbf{UU}}}} - {\mathbf{M}}_{{{\mathbf{AU}}}}^{T} {\mathbf{J}}_{{\mathbf{g}}} } \right]{\mathbf{\ddot{q}}}_{{\mathbf{U}}} + \left[ {{\mathbf{C}}_{{\mathbf{U}}} - {\mathbf{M}}_{{{\mathbf{AU}}}}^{T} {{\varvec{\upgamma}}}_{{\mathbf{g}}} } \right] = {\mathbf{F}}_{{\mathbf{U}}} - {\mathbf{M}}_{{{\mathbf{AU}}}}^{T} {\mathbf{\ddot{y}}}^{{{\mathbf{ref}}}}$$
(9)

The stability of the internal dynamics can be effectively studied through the associated zero dynamics [35], i.e., the internal dynamics with the output constrained to be zero for all the time, that is computed by setting \({\mathbf{y}}^{{{\mathbf{ref}}}} = {\dot{\mathbf{y}}}^{{{\mathbf{ref}}}} = {\mathbf{\ddot{y}}}^{{{\mathbf{ref}}}} = {\mathbf{0}}\) in Eq. (9). In this way, the effect of the input reference trajectory is removed. Then, the local asymptotic stability of the equilibrium point \({\mathbf{q}}_{{\mathbf{U}}} = {\dot{\mathbf{q}}}_{{\mathbf{U}}} = {\mathbf{0}}\) of the nonlinear system is assessed: if some eigenvalues have positive real parts, the internal dynamics is locally unstable [11] and therefore divergent integration of Eq. (9) is obtained, leading to unbounded solutions and hence the impossibility to compute a feasible, exact and causal system inversion. These systems are said to be non-minimum phase.

This evaluation shows that the internal dynamics is unstable when y is defined as the load position, thus leading to divergent integration of the ODEs in Eq. (9). In this work, the concept of “output redefinition” within the internal dynamics is therefore exploited, i.e., a fictitious output \({\tilde{\mathbf{y}}}\) to be controlled, that is placed along the cable at a distance \(\tilde{h}\) from the attachment point of the cable, is assumed:

$${\tilde{\mathbf{y}}} = \left[ {\begin{array}{*{20}c} {x_{P} } \\ {y_{P} } \\ \end{array} } \right] + \tilde{h}\,\left[ {\begin{array}{*{20}c} {\sin \theta_{X} \cos \theta_{Y} } \\ {\sin \theta_{Y} } \\ \end{array} } \right]$$
(10)

\(\tilde{h}\) should be chosen to ensure stability of the internal dynamics and accurate model inversion.

By considering Eqs. (7) and (8), the desired output acceleration of the fictitious output can be written as follows:

$${\mathbf{\ddot{\tilde{y}}}}^{{{\mathbf{ref}}}} = \,{\mathbf{\ddot{q}}}_{{\mathbf{A}}} + \,\beta {\mathbf{J}}_{{\mathbf{g}}} \left( {{\mathbf{q}}_{{\mathbf{U}}} } \right)\;{\mathbf{\ddot{q}}}_{{\mathbf{U}}} + \beta {{\varvec{\upgamma}}}_{{\mathbf{g}}} \left( {{\mathbf{q}}_{{\mathbf{U}}} ,{\dot{\mathbf{q}}}_{{\mathbf{U}}} } \right)$$
(11)

where \(\beta = \frac{{\tilde{h}}}{h}\).

The stabilized internal dynamics, to be solved for computing the trajectory of the unactuated coordinates in tracking the desired reference, is therefore:

$$\left[ {{\mathbf{M}}_{{{\mathbf{UU}}}} - \beta {\mathbf{M}}_{{{\mathbf{AU}}}}^{T} {\mathbf{J}}_{{\mathbf{g}}} } \right]{\mathbf{\ddot{q}}}_{{\mathbf{U}}} + \left[ {{\mathbf{C}}_{{\mathbf{U}}} - \beta {\mathbf{M}}_{{{\mathbf{AU}}}}^{T} {{\varvec{\upgamma}}}_{{\mathbf{g}}} } \right] = {\mathbf{F}}_{{\mathbf{U}}} - {\mathbf{M}}_{{{\mathbf{AU}}}}^{T} {\mathbf{\ddot{\tilde{y}}}}^{{{\mathbf{ref}}}}$$
(12)

The eigenvalue analysis of the zero dynamics associated to Eq. (12) reveals that stability is achieved if and only if \(0 < \beta < 1\). The parameter \(\beta\) should be chosen as close as possible to the unitary value to ensure a good reconstruction of the desired output trajectory, thanks to a redefined output close to the actual one, while assuring stable integration. Indeed, it should be noted that the actual stability of Eq. (12) is affected by the numerical integration schemes adopted in the solution, that might cause numerical instability even if the theoretical eigenvalues have negative, though small, real parts. For example, conditionally stable and low-order algorithms such as Euler’s scheme might be unstable for values of \(\beta\) approaching 1, for large sample times and in the presence of roundoff errors. A relevant computational feature of the proposed approach is that it does not impose a specific integration scheme, and therefore, the ones leading to more accurate results can be chosen among those usually adopted in simulating multibody systems [36].

As far as \({\mathbf{\ddot{\tilde{y}}}}^{{{\mathbf{des}}}}\) is concerned, since \(\beta\) approaches 1, it can be reasonably set \({\mathbf{\ddot{\tilde{y}}}}^{{{\mathbf{ref}}}} \equiv {\mathbf{\ddot{y}}}^{{{\mathbf{ref}}}}\), i.e., no reference correction is necessary to compensate for the use of the redefined output in solving the internal dynamics.

Computation of the Command Values of the Actuated Coordinates

Once the internal dynamics is stable, \({\mathbf{q}}_{{\mathbf{U}}}^{{}}\), \({\dot{\mathbf{q}}}_{{\mathbf{U}}}^{{}}\) and \({\mathbf{\ddot{q}}}_{{\mathbf{U}}}^{{}}\) are computed by integrating the differential equations in Eq. (12) over the whole cycle time (and will be henceforth denoted as \({\mathbf{q}}_{{\mathbf{U}}}^{*}\), \({\dot{\mathbf{q}}}_{{\mathbf{U}}}^{*}\), \({\mathbf{\ddot{q}}}_{{\mathbf{U}}}^{*}\)). Then, the reference trajectory for the actuated coordinates (\({\mathbf{q}}_{{\mathbf{A}}}^{{{\mathbf{ref}}}}\), \({\dot{\mathbf{q}}}_{{\mathbf{A}}}^{{{\mathbf{ref}}}}\), \({\mathbf{\ddot{q}}}_{{\mathbf{A}}}^{{{\mathbf{ref}}}}\)) is obtained by exploiting the following equations, inferred from Eq. (8):

$$\begin{gathered} {\mathbf{q}}_{{\mathbf{A}}}^{{{\mathbf{ref}}}} \, = {\mathbf{y}}^{{{\mathbf{ref}}}} - \,{\mathbf{g}}\left( {{\mathbf{q}}_{{\mathbf{U}}}^{*} } \right) \hfill \\ {\dot{\mathbf{q}}}_{{\mathbf{A}}}^{{{\mathbf{ref}}}} = \,{\dot{\mathbf{y}}}^{{{\mathbf{ref}}}} - \,{\mathbf{J}}_{{\mathbf{g}}} \left( {{\mathbf{q}}_{{\mathbf{U}}}^{*} } \right)\;{\dot{\mathbf{q}}}_{{\mathbf{U}}} \hfill \\ {\mathbf{\ddot{q}}}_{{\mathbf{A}}}^{{{\mathbf{ref}}}} = \,{\mathbf{\ddot{y}}}^{{{\mathbf{ref}}}} - \,{\mathbf{J}}_{{\mathbf{g}}} \left( {{\mathbf{q}}_{{\mathbf{U}}}^{*} } \right)\;{\mathbf{\ddot{q}}}_{{\mathbf{U}}}^{*} - {{\varvec{\upgamma}}}_{{\mathbf{g}}} \left( {{\mathbf{q}}_{{\mathbf{U}}}^{*} ,{\dot{\mathbf{q}}}_{{\mathbf{U}}}^{*} } \right) \hfill \\ \end{gathered}$$
(13)

The computation of the forces necessary to execute such a motion for the trolley relies on the controller of the trolley, that can be based on any feedback or feedforward scheme ensuring precise tracking of \({\mathbf{q}}_{{\mathbf{A}}}^{{{\mathbf{ref}}}}\).

Some Comments on the Required Command Forces

Although it is not among the goals of the proposed paper, that is focused on trajectory planning, the developments proposed up to now can be also exploited to compute the command forces for the actuators driving the actuated coordinates, that can be adopted for feedforward control. By exploiting \({\mathbf{q}}_{{\mathbf{A}}}^{{{\mathbf{ref}}}}\), \({\dot{\mathbf{q}}}_{{\mathbf{A}}}^{{{\mathbf{ref}}}}\), \({\mathbf{\ddot{q}}}_{{\mathbf{A}}}^{{{\mathbf{ref}}}}\) computed in Eq. (13) and \({\mathbf{q}}_{{\mathbf{U}}}^{*}\), \({\dot{\mathbf{q}}}_{{\mathbf{U}}}^{*}\), \({\mathbf{\ddot{q}}}_{{\mathbf{U}}}^{*}\) computed in Eq. (12), such forces are obtained through the upper part of Eq. (4) that becomes an algebraic equation:

$${\mathbf{u}} = {\mathbf{B}}_{{\mathbf{A}}}^{ - 1} \left( {{\mathbf{M}}_{{{\mathbf{AA}}}} {\mathbf{\ddot{q}}}_{{\mathbf{A}}}^{{{\mathbf{ref}}}} + {\mathbf{M}}_{{{\mathbf{AU}}}} {\mathbf{\ddot{q}}}_{{\mathbf{U}}}^{*} + {\mathbf{C}}_{{\mathbf{A}}} \left( {{\mathbf{q}}_{{\mathbf{A}}}^{{{\mathbf{ref}}}} ,{\mathbf{q}}_{{\mathbf{U}}}^{*} ,{\dot{\mathbf{q}}}_{{\mathbf{A}}}^{{{\mathbf{ref}}}} ,{\dot{\mathbf{q}}}_{{\mathbf{U}}}^{*} } \right) - {\mathbf{F}}_{{\mathbf{A}}} \left( {{\mathbf{q}}_{{\mathbf{A}}}^{{{\mathbf{ref}}}} ,{\mathbf{q}}_{{\mathbf{U}}}^{*} } \right)} \right)$$
(14)

Experimental Application

Setup Description

The overhead crane is mimicked through the end-effector of an Adept Quattro s650 h parallel robot, whose planar Cartesian translations represent the motion of the actuated platform \({\mathbf{q}}_{{\mathbf{A}}} = \left[ {\begin{array}{*{20}c} {x_{P} } & {y_{P} } \\ \end{array} } \right]^{T}\). The values of the system parameters are summarized in Table 1.

Table 1 System parameters
Full size table

A picture of the manipulator is shown in Fig. 1. The robot is controlled by the proprietary Adept SmartController. The commanded trajectories, in terms of position \({\mathbf{q}}_{{\mathbf{A}}}^{{{\mathbf{ref}}}}\), are computed offline through a MATLAB code, and loaded through an array of points in time in the Adept SmartController that computes the command torques for the axis motor through its native controller. Offline computation has been performed, as usually done in motion planning whenever the reference is a-priori known; nonetheless, the small computational effort required by the proposed method also allows real-time implementation. Since such a control scheme is purely collocated and the inertia ratio approaches zero, the load oscillations are not visible to the platform side; therefore, no closed-loop control is made on the load motion. It should be noted that such a proprietary controller cannot be modified, and therefore, motion and vibration control in such a system must just rely on enhanced motion planning, as the method proposed in this paper. On the other hand, commanding the robot by means of the reference trajectory for its end-effector \({\mathbf{q}}_{{\mathbf{A}}}^{{{\mathbf{ref}}}}\), that is the output of the proposed method, does not require the knowledge of the dynamic model of the robot, as it would be required if a computed torque approach is used (by means of Eq. (14)).

The solution of the ODEs of the internal dynamics in Eq. (12) has been performed through the 4th order Runge–Kutta integrator, with a sampling time equal to 1 ms, and by setting \(\beta\) = 0.9999 since it provides stable and accurate solutions. Once the reference has been computed with such a sample time, that ensures reliable solution of the ODEs, decimation is performed to generate \({\mathbf{q}}_{{\mathbf{A}}}^{{{\mathbf{ref}}}}\) with the larger sample time of 16 ms, as required by the robot controller. As a result, the reference trajectory that is actually commanded to the robot is slightly perturbed, compared to the theoretical one, thus leading to slightly greater error than those expected (Fig. 2).

Fig. 2
figure 2

The experimental test bed: overview (a), the platform (b), the load with markers (c), a Vicon camera (d)

Full size image

The motion of the pendulum is measured through a Vicon motion capture system exploiting six high-speed cameras to reconstruct the position of some markers located on the robot end-effector and on the load. The nominal accuracy of the vision system, declared by the manufacturer, is 1.5 mm. In practice, the uncertainty band of the measures is higher, due to small errors that can occur in the positioning of the calibration wand and of the markers, as well as due to the environmental drift, i.e., the uncertainty due to the change of environmental factors after calibration such as temperature and unwanted light sources.

Three sample paths are shown in four tests, although the method can be applied to any path: a planar circle, with two different motion times, a planar rhombus and a planar spiral. Comparison is done with the input shaping zero vibration (henceforth denoted as ZV) approach [18], and by setting \({\mathbf{q}}_{{\mathbf{A}}}^{{{\mathbf{ref}}}} \left( t \right) = {\mathbf{y}}^{{{\mathbf{ref}}}} \left( t \right)\), i.e., by treating the system as if no vibrational dynamics affects its motion without any shaping to compensate for vibrations (henceforth denoted as “unshaped”). Since the oscillation frequency has been accurately identified, the use of the ZV is a proper choice, rather than using robust shapers (such as the ZVD, zero vibration derivative) that lead to remarkably higher accelerations and speeds.

In the analyses of the experimental results, the following variables are introduced and displayed: \(\left( {x_{P}^{{{\text{ref}}}} ,y_{P}^{{{\text{ref}}}} } \right)\) are the Cartesian reference values for the platform, while \(\left( {x_{P}^{\exp } ,y_{P}^{\exp } } \right)\) are the experimentally measured ones. The Cartesian reference values for the suspended load \({\mathbf{y}}^{{{\mathbf{ref}}}}\) are \(\left( {x_{L}^{{{\text{ref}}}} ,y_{L}^{{{\text{ref}}}} } \right)\), while \(\left( {x_{L}^{\exp } ,y_{L}^{\exp } } \right)\) are the experimentally measured ones. Performances are assessed by showing details on the tracking error on the load side \(\left( {e_{t,L}^{x} ,e_{t,L}^{y} } \right)\) and on the platform \(\left( {e_{t,P}^{x} ,e_{t,P}^{y} } \right)\) in both the X and Y directions. The contour error during motion, i.e., the actual difference in distance between the reference path and the actual path, is also evaluated through its root mean square (RMS) value, both for the load (\(e_{c,L}^{{}}\)) and for the platform (\(e_{c,P}^{{}}\)).

Test Case 1: Planar Circular Path with 8 s Motion Time

Numerical Results

In the first test, the suspended mass should track a 0.2 m radius circumference in 8 s, by assuming a 7th-degree polynomial motion law. The motion starts at 2 s. Numerical results are first briefly proposed, just for this test case, to prove how the proposed method is effective in inverting the model of a non-minimum phase system for accurate trajectory and path tracking.

Figure 3 shows the simulated and the reference load displacements in the Cartesian plane, as well as the commanded motion of the platform. The motion of the load is almost perfectly overlapped with the reference, with just some negligible errors. It is interesting to notice how the proposed method shapes the motion of the platform, i.e., of the actuated coordinates: centrifugal effects are compensated by a suitably smaller radius. Additionally, the load oscillations are weakly excited, leading to negligible residual vibrations as corroborated by the tracking errors shown in Fig. 4: the maximum value is 0.008 mm, at the end of the motion, and the RMS values are 0.004 mm along both the X and Y directions.

Fig. 3
figure 3

Test case 1, numerical results. Platform and load displacements in the Cartesian plane with the proposed method

Full size image
Fig. 4
figure 4

Test case 1, numerical results. Time history of the tracking errors

Full size image

These results confirm the correctness of the proposed approach, that is able to invert almost exactly the dynamic model despite its non-minimum phase nature.

Experimental Results

The platform reference motion computed in Sect. 3.2.1 is here fed to the robot controller to evaluate the experimental performances. Figure 5a, b show the time histories of the references and of the measured motions of both the platform and the load: the effectiveness of the proposed method is evident since the references and the actual measurements are, again, almost overlapped. A closer look is provided by the tracking errors in Fig. 5c, d. First, it can be observed that the tracking error of the robotic platform is not zero, as assumed in the numerical simulations of Sect. 3.2.1, thus distorting the optimal trajectory computed through the proposed method. This perturbation contributes to slightly bigger errors on the load side both in transient and after the end of the motion, if compared to the theoretical expectations. Additionally, some undesired parasitic motions increase the measured errors. For example, initial conditions are never exactly zero, as it can be observed in Fig. 5c, d, where oscillations are evident when t < 2 s (i.e., before the motion starts). Since the control scheme is purely collocated and the inertia ratio approaches zero, such oscillations sum up with the forced response and can be seen at the end of the motion as well (due to the negligible damping). Furthermore, the unbalance of the load mass introduces a spinning-like motion of the load itself about the cable. Nonetheless, the tracking errors are small, and tracking is accurate: RMS tracking errors for the load are 0.68 mm and 0.92 mm along the X and Y directions, respectively, while the maximum residual error at the motion completion is 0.80 mm in both the directions.

Fig. 5
figure 5

Test case 1. Time histories of the reference and experimental platform and load displacements in the Cartesian directions, (a, b), and the respective tracking errors, (c, d), with the proposed method

Full size image

Further evidence is provided by Fig. 6, that represents the results in the Cartesian plane. Again, the reference and the actual displacement of the loads are almost overlapped, with a maximum contour error for the load equal to 2.12 mm, and an RMS value equal to 0.93 mm. As for the robotic platform, it is also affected by contour error whose maximum and RMS values are 1.70 mm and 0.55 mm, respectively.

Fig. 6
figure 6

Test case 1. Reference and experimental platform and load displacements in the Cartesian plane, with the proposed method

Full size image

The effectiveness of the proposed method is further corroborated by comparison with the two benchmarks, i.e., the input shaping ZV method and the unshaped command. Figure 7 shows the results obtained by commanding the platform with the unshaped reference: as the motion begins, the load starts an almost-uncontrolled oscillation with an amplitude of more than 400 mm. Figure 8 shows the results sported by the ZV input shaping method: while oscillations are properly controlled, the trajectory of the load is remarkably perturbated. Indeed, the transfer function of the shaper creates harmonic distortion of the shaped references compared to the unshaped one, thus resulting in a smaller desired radius for the load path. As a matter of fact, the transfer function of the shaper resembles the one of a filter [37], and hence the ZV perturbs the path as more as its motion time decreases (and hence its spectrum becomes broader).

Fig. 7
figure 7

Test case 1. Reference and experimental load displacements in the Cartesian plane with the unshaped command

Full size image
Fig. 8
figure 8

Test case 1. Reference and experimental load displacements in the Cartesian plane with the ZV input shaping and the proposed method

Full size image

The lower the motion time, and the higher such a perturbation is. The tracking and contour errors sported by the input shaping are therefore remarkably larger than those achieved through the proposed method, as stated in Table 2, where the errors sported by the proposed method and the ZV are summarized.

Table 2 Test case 1
Full size table

Test Case 2: Planar Circular Path with 4 s Motion Time—Experimental Results

The second test consists of another planar circular path, to be executed with the remarkably smaller motion time of 4 s; the same radius as in Sect. 3.2 is commanded, and again, a 7th-degree polynomial motion law is employed. The goal of this test is to highlight the method effectiveness in a more severe trajectory: as the motion time halves, therefore accelerations quadruple and hence higher oscillations are excited.

Figure 9a, b show the time histories of the references and of the measured motion of both the robotic platform and the load: despite high accelerations and speed, the references and the actual measurements are almost overlapped. Clearly, slightly larger errors are obtained, both for the platform and consequently for the load. Indeed, reducing the motion time increases the harmonic contents of the motion law to be tracked by the robot and, therefore, larger harmonic distortion is obtained due to control bandwidth and interpolations. The robot platform motion has a maximum tracking error equal to 1.39 mm, that contributes to RMS values of the load tracking errors equal to 0.36 mm and 0.65 mm along the X and Y directions, respectively (it should be noted that such values are also affected by the initial oscillations that are not zero). Nonetheless, by considering the complexity of the test, the proposed method should be considered as very effective.

Fig. 9
figure 9

Test case 2. Time histories of the reference and experimental platform and load displacements in the Cartesian directions, (a, b), and the respective tracking errors, (c, d), with the proposed method

Full size image

The representation in the Cartesian plane in Fig. 10 corroborates the method effectiveness: the maximum contour error of the load is 5.21 mm, while its RMS value is 2.29 mm. In Fig. 10, it is interesting to observe that the motion of the robotic platform resembles a limaçon of Pascal.

Fig. 10
figure 10

Test case 2. Reference and experimental load displacements in the Cartesian plane, with the unshaped command

Full size image

Finally, comparison with the unshaped command (Fig. 11) and with the ZV input shaping (Fig. 12) is proposed for benchmarking: the errors sported by both these approaches are remarkably larger than those of the proposed method, and therefore, the motion of the load visibly does not approach the desired one.

Fig. 11
figure 11

Test case 2. Reference and experimental platform and load displacements in the Cartesian plane, with the proposed method

Full size image
Fig. 12
figure 12

Test case 2. Reference and experimental load displacements in the Cartesian plane with the ZV input shaping versus the proposed method

Full size image

Table 3 summarizes the errors obtained in this test. Once again, the deformation of the reference profile to be achieved is remarkable when using the input shaping: the RMS value of the load contour error is 41.21 mm which is about 18 times bigger than the RMS contour error obtained with the method proposed in this paper.

Table 3 Test case 2
Full size table

Test Case 3: Planar Rhombus Path—Experimental Results

The third test case considers the task of tracking a planar rhombus whose sides are equal to 0.3 m. The motion of each side is performed through a 7th-degree polynomial, rest-to-rest motion law, with an overall motion time equal to 6 s (the motion starts at t = 2 s). This test is assumed for further benchmarking with the ZV input shaping: indeed, this spatial path can be executed by input shapers without distortion (at least in ideal conditions), since it consists of a sequence of 4 rest-to-rest motions, to be shaped independently. Figure 13 shows the tracking in time, through the time histories along the X and Y directions (Fig. 13a, b), and their respective tracking errors (Fig. 13c, d). Although the tracking errors of the load are not zero, and some residual oscillations remain uncompensated after the motion end, the result is valuable: the RMS tracking errors are 1.49 mm and 1.88 mm along the x and y directions, respectively, while the maximum residual oscillation after the motion end is equal to 3.80 mm and 4.52 mm, respectively. The same figures show that the platform tracking error is not zero during motion, as well, because of the already mentioned distortion and presence of some parasitic motion. The representation in the Cartesian plane is shown in Fig. 14, which confirms the accuracy of path tracking: the maximum and RMS contour errors for the load are 4.11 mm and 2.11 mm, respectively (Table 4).

Fig. 13
figure 13

Test case 3. Reference and experimental platform and load displacements in the Cartesian directions, (a, b), and the respective trajectory tracking errors, (c, d), with the proposed method

Full size image
Fig. 14
figure 14

Test case 3. Reference and experimental platform and load displacements in the Cartesian plane, with the proposed method

Full size image
Table 4 Test case 3
Full size table

The effectiveness of the proposed approach is corroborated by the comparison with the two benchmarks in Fig. 15, that is provided through the representation in the Cartesian plane. If no shaping is performed, very large load oscillations are excited, leading to errors up to 800 mm. If the motion profiles are shaped through the ZV input shaping, visible errors are obtained. Figure 16 provides a closer look to the tracking errors sported by the ZV: the maximum residual error is 14.46 mm, i.e., 3.8 times bigger than the errors of the proposed method. This is caused by the unavoidable model uncertainty and by the distortion of the platform trajectory (that also affect the results of the proposed method). In addition, the non-negligible residual oscillations sported by the input shaping, evidenced through Fig. 16, arise because of the higher accelerations it requires to execute the motion in the prescribed time. Generally speaking, when the motion time decreases, and approaches the half-period of oscillation, remarkably high oscillations are imposed by the ZV [38], because of the convolution with the impulses of the shaper. This issue is even more relevant in the case of robust shapers, where more impulses are employed in the shaper. Such residual oscillations, that increase after each side of the rhombus, cause some motion components orthogonal to the desired path that create a visible difference between the commanded and the actual load path in Fig. 15b.

Fig. 15
figure 15

Test case 3. Reference and experimental load displacements in the Cartesian plane with different methods: unshaped command (a), ZV versus the proposed method (b)

Full size image
Fig. 16
figure 16

Test case 3. Experimental load tracking errors, (a, b): ZV versus the proposed method

Full size image

Test Case 4: Planar Spiral Path—Experimental Results

The fourth test consists of a planar spiral path formulated as an Archimedean spiral, where the radius is defined as a function of the rotating angle. The starting value of the radius is set equal to 0.2 m while the ending one is 0. The motion time is equal to 6 s (the motion starts at t = 2 s) and a 7th-degree polynomial motion law is assumed to execute 2 spatial revolutions.

The robot and payload time histories in the Cartesian directions x and y are shown in Fig. 17a, b. The platform motion is tracked with a good accuracy even if the complexity of the path yields to a non-negligible maximum tracking error which is equal to 3.49 mm as shown in Fig. 17c. As a consequence, the maximum tracking errors for the load are, respectively, equal to 5.26 mm and 5.08 mm along the X and Y directions, as evidenced by Fig. 17c, d. The RMS tracking errors are listed in Table 5. Figure 18 confirms the effectiveness of the proposed method in path tracking: the RMS contour error for the load is just equal to 3.38 mm. In contrast, the application of the unshaped command shown in Fig. 19.a leads to uncontrolled oscillations as the motion starts, whose amplitude is about 500 mm. If the ZV is adopted, the load oscillations are properly controlled; however, trajectory and path tracking are not satisfactory since the shapers remarkably modify the desired path leading to visible tracking and contour errors, as summarized also in Table 5: the RMS load contour error is equal to 37.98 mm, i.e., about 11 times bigger than the one obtained by the proposed method.

Fig. 17
figure 17

Test case 4. Reference and experimental platform and load displacements in the Cartesian directions, (a, b), and the respective trajectory tracking errors, (c, d), with the proposed method

Full size image
Table 5 Test case 4
Full size table
Fig. 18
figure 18

Test case 4. Reference and experimental platform and load displacements in the Cartesian plane, with the proposed method

Full size image
Fig. 19
figure 19

Test case 4. Reference and experimental load displacements in the Cartesian plane with different methods: unshaped command (a), ZV versus the proposed method (b)

Full size image

Conclusions

This paper proposes a novel technique to path and trajectory planning in an underactuated, non-minimum phase 4-DOF overhead crane. The method exploits stable inversion of the dynamic model governing the internal dynamics of the system, by leading to the commanded values of the actuated coordinates, ensuring that the controlled output tracks the desired reference.

The method relies on the following steps:

  • Partitioning of the model into actuated and unactuated coordinates.

  • Definition of the controlled output and its representation as a nonlinear separable function in the actuated and unactuated coordinates.

  • Formulation of the internal dynamics in terms of unactuated coordinates and desired output.

  • Stabilization of the internal dynamics through the concept of output redefinition.

  • Integration of the stabilized equation of motions of the internal dynamics for computing the time history of the unactuated coordinates.

  • Computation of the commanded values of the actuated coordinates through nonlinear kinematic inversion.

The computation of the commanded forces to be exerted by the actuators driving the actuated coordinates is then demanded to the control scheme of such actuators, thus allowing the implementation of the proposed technique in proprietary controllers (as those of industrial robots) where the control scheme cannot be modified.

The method formulation leads to a simple numerical solution of the motion planning problem, that is solved by adopting any scheme for solving ODEs, without requiring optimization problems. This is a relevant feature since low computational effort is required, thus making the proposed method suitable for real-time applications whenever the output reference trajectory is not a-priori completely known. The obtained commanded trajectory is, finally, causal since it does not require pre-actuation.

Numerical results show that almost exact model inversion is performed, with negligible transient and steady state errors, as corroborated by the negligible tracking and contour errors.

Experiments are performed through a laboratory setup composed by an Adept Quattro parallel robot that provides the platform motion, the suspended load to be moved. The experimental results, measured through a Vicon motion capture system, confirm the numerical expectation and hence corroborate the effectiveness of the proposed method: tracking and contour errors are, again, negligible in all the four tests, with different shapes and motion time. Just slightly greater errors are obtained, compared to the numerical simulations, because of the unavoidable model uncertainty and the distortion of the actual platform trajectory executed by the robot.

The comparison with the zero vibration input shaping, which is often assumed as a benchmark for motion planning in cranes, and with the unshaped trajectories further proves the benefits of using the proposed technique to achieve high performances in trajectory and path tracking in non-minimum phase underactuated mechanical system.