Introduction

Vibration control technology is indispensable to achieve mechanical systems that are lightweight and compact with a high performance. Various systems employ active vibration control due to its high vibration performance. Because many systems employ model-based control, the designed control system is susceptible to characteristic fluctuations and modeling errors as the controlled object ages. To tackle this problem, more accurate modeling and a more robust control theory in a model-based framework are useful. However, such efforts increase the burden on the control system designers.

Diverse fields have recently investigated designing a model-free control system without using a model of the controlled object [1, 2]. Applications are not limited to vibration control. For example, the method has been used for semi-active suspensions [3], automatic transmissions [4], hydroelectric power plants [5], and multi input multi output (MIMO) nonlinear systems [6].

A typical method to control vibrations in structures is fuzzy control [7]. The fuzzy logic approach is based on the if/then-type control law and consists of a fuzzy set that appropriately represents human knowledge, senses, and experience of the actual controlled object. Because fuzzy control does not necessarily need to use the model of the controlled object to design the controller, it can realize model-free control. Although fuzzy control has been applied to various systems, including vibration control [8,9,10,11,12,13,14], it may require trial and error to construct the control rules and adjust the membership functions. Therefore, a simpler design method is desirable.

Artificial intelligence such as neural networks and genetic algorithms has been actively applied to model-free control methods [15,16,17]. In vibration control, it has been used for active suspension [18], multiple launch rocket system [19], rotary crane systems [20], and flexible structures [21, 22]. However, these systems may require a large amount of data to be acquired for the learning process and the high computational load to achieve an appropriate control behavior.

As mentioned above, the design process of the control system using most of the conventional model-free methods is complicated and requires a lot of time and preparation. On the other hand, a new approach to realize model-free vibration control based on the idea of a virtual structure was proposed by Yonezawa et al. [23,24,25,26,27] This innovative method gives a model-free controller in a simpler manner without a complicated implementation process. The basic idea is to insert a properly designed single degree of freedom (SDOF) vibration model of a virtual structure between the proof-mass actuator and the actual controlled object. Then a state equation that consists of only the virtual structure and the actuator is derived. Since this state equation does not contain any parameters of the actual controlled object, model-free design is realized. In other words, the controller is designed by regarding the virtual structure as the controlled object instead of the actual controlled object.

The model-free controller can indirectly suppress the vibration of the actual controlled object. The transfer function from the actual vibration of the controlled object to the vibration of the virtual structure is considered. The parameters of the virtual structure are designed so that the gain of this transfer function in the vibration control band is approximately 0 dB with a phase delay of 0. Therefore, the vibrations of the virtual structure and the controlled object are equivalent in the vibration control band. The previous study also derived a simple design condition for this case [26]. The elegance of this control system is that a virtual structure can be designed without a mathematical model of the actual controlled objects. Because the virtual structure is a simple SDOF system, the number of design variables is small, and the computational load for controller design is also light.

The natural frequency of the proof-mass actuator in the previous study is on the lower frequency side compared to the natural frequency of the controlled object. The lower limit of the vibration control band where model-free control is possible must be higher than the natural frequency of the actuator. Moreover, the gain of the transfer function from the vibration of the controlled object to that of the virtual structure must be approximately 0 dB in the vibration control band. On the other hand, the gain characteristic does not become 0 dB because the resonance peak of the transfer function appears near the natural frequency of the actuator. Therefore, the vibration of the actual controlled object and that of the virtual structure are not equivalent, and the indirect model-free vibration suppression condition does not hold.

The aforementioned situation implies that an undesirable case may exist. Vibration modes that are too close to the natural frequency of the actuator degrade the robustness of the control system, even if the lower limit of the vibration control band is higher than the actuator natural frequency. The above negative effects are also apparent from the resonance of the actuator. However, the model-free controller designed in the previous study [26] does not ensure robustness for the vibration modes of the actual controlled objects that are too close to the natural frequency of the actuator.

This study clarifies the above undesired case, which was not explicitly considered in the previous paper [26], and presents a solution to improve the robustness of the model-free controller based on the virtual structure. The proposed method employs the idea of model-free control based on the virtual structure. The contributions of this research are as follows:

  1. 1.

    The adverse effect of the resonance of the proof-mass actuator used in the previous studies is clarified. Specifically, the case study demonstrates that the robustness of the model-free controller is not ensured when the vibration mode of the controlled object is too close to the natural frequency of the actuator.

  2. 2.

    The robustness of the model-free controller proposed by Yonezawa et al. [26] is improved. Specifically, a notch filter is introduced for the model-free \({H}_{\infty }\) controller, which was designed with a generalized plant consisting of the virtual structure and the actuator. The purpose of the notch filter is to improve the robustness of the controller by reducing the gain of the model-free controller near the natural frequency of the actuator while simultaneously damping the vibration modes of the actual controlled objects within the vibration control band.

First, the theory of the model-free vibration control with a virtual structure is explained. Second, the adverse effects of the natural frequency of the actuator on the control system, which were not considered explicitly in previous studies, are discussed. Third, the improvement of the previous method is inductively clarified through vibration control simulations using different controlled structures. In these cases, the closed-loop system with a model-free controller may become unstable when the low-order vibration mode of the controlled objects is too close to the natural frequency of the actuator. According to the time history responses, the major cause of this instability is the resonance of the actuator. Fourth, a new notch filter application is proposed to suppress the gain of the model-free controller around the natural frequency of the actuator. This method should avoid the control system instability due to the resonance of the actuator. The mechanism by which the proposed method can compensate for the effect of the natural frequency of the actuator is discussed based on the Bode diagram of the controller. Finally, the effectiveness of the proposed method is demonstrated via vibration control simulations. The proposed method enhances the robustness of the previous method [26].

Model-Free Control System Based on a Virtual Structure

Actuator

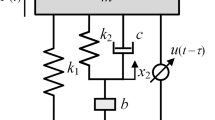
Here, a proof-mass actuator is used for vibration control by referring to the actuator used in the previous study (Fig. 1a). The effectiveness of the active vibration control using a proof-mass actuator has been well documented [28,29,30,31]. In this study, the actuator is modeled as a SDOF system (Fig. 1b). The principle behind the proof-mass actuator is that the reaction force in the perpendicular direction to the surface of the actual controlled object suppresses the vibration. The frequency response of the actuator from the control input to the displacement indicates that the natural frequency of the actuator is around 20 Hz (Fig. 2).

Fig. 1
figure 1

Proof-mass actuator a photograph and b SDOF model of the actuator

Full size image
Fig. 2
figure 2

Frequency response of the actuator (the ratio of the displacement to the input)

Full size image

Control System Design Using a Virtual Structure

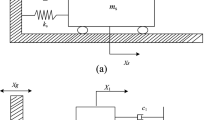
A virtual structure enables model-free vibration control of the actual controlled object. According to the previous studies [23,24,25,26,27], a two-degree-of-freedom (2-DOF) model in which a SDOF virtual structure is inserted between the actuator and the actual controlled object is considered (Fig. 3). Equations (1) and (2) express the equations of motion for the actuator and the virtual structure, respectively:

Fig. 3
figure 3

Model composed of the proof-mass actuator, virtual structure, and controlled object

Full size image
$${m}_{0}\ddot{{x}_{0}}+{\mathrm{c}}_{0}\left(\dot{{x}_{0}}-\dot{{x}_{v}}\right)+{k}_{0}\left({x}_{0}-{x}_{v}\right)=u,$$
(1)
$${m}_{v}\ddot{{x}_{v}}+{k}_{v}{(x}_{v}-{x}_{1})-{\mathrm{c}}_{0}\left(\dot{{x}_{0}}-\dot{{x}_{v}}\right)-{k}_{0}\left({x}_{0}-{x}_{v}\right)=-u,$$
(2)

where m, k, and c represent the mass, stiffness, and viscosity, respectively. The subscripts 0, v, and 1 indicate the parameters of the actuator, virtual structure, and controlled object, respectively. Via a Laplace transformation, the transfer function from the displacement of the controlled object to the displacement of the virtual structure can be written as

$${T}_{{x}_{v}{x}_{1}}=\frac{\left({m}_{0}{s}^{2}+{c}_{0}s+{k}_{0}\right){k}_{v}}{\left\{{m}_{v}{s}^{2}+{c}_{0}s+\left({k}_{v}+{k}_{0}\right)\right\}\left({m}_{0}{s}^{2}+{c}_{0}s+{k}_{0}\right)-{\left({c}_{0}s+{k}_{0}\right)}^{2}}=\frac{{m}_{0}{s}^{2}+{c}_{0}s+{k}_{0}}{\left\{{(m}_{v}/{k}_{v}){s}^{2}+({c}_{0}/{k}_{v})s+\left(1+{k}_{0}/{k}_{v}\right)\right\}\left({m}_{0}{s}^{2}+{c}_{0}s+{k}_{0}\right)-{\left({c}_{0}s+{k}_{0}\right)}^{2}/{k}_{v}}$$
(3)

The value of \({T}_{{x}_{v}{x}_{1}}\) converges to 1 when the limit operations \({m}_{v}\to 0\) and \({k}_{v}\to \infty\) are applied to \({T}_{{x}_{v}{x}_{1}}\). These limit operations cannot be realized because the controller is obtained by numerical calculations. Therefore, Eq. (4) can be approximated by setting \({m}_{v}\) to a sufficiently small finite value and \({k}_{v}\) to a sufficiently large finite value.

$${T}_{{x}_{v}{x}_{1}}\approx 1.$$
(4)

Equation (4) shows that the vibration suppression of the actual controlled object is equal to that of the virtual structure. Table 1 shows the parameters of the actuator and the virtual structure in this system.

Table 1 Parameters of the virtual structure and actuator
Full size table

Equations (5) and (6) give the state equation for this system as

$$\begin{gathered} \dot{x} = A_{v} x + B_{v1} w + B_{v2} u \hfill \\ y = C_{v} x + D_{v1} w + D_{v2} u \hfill \\ x = \left[ {\begin{array}{*{20}c} {x_{v} } & {x_{0} } \\ \end{array} \begin{array}{*{20}c} {\dot{x}_{v} } & {\dot{x}_{0} } \\ \end{array} } \right]^{T} , \hfill \\ \end{gathered}$$
(5)
$$\begin{gathered} A_{v} = \left[ {\begin{array}{*{20}c} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ { - \frac{{k_{0} + k_{v} }}{{m_{v} }}} & {\frac{{k_{0} }}{{m_{v} }}} & { - \frac{{c_{0} }}{{m_{v} }}} & {\frac{{c_{0} }}{{m_{v} }}} \\ {\frac{{k_{0} }}{{m_{0} }}} & { - \frac{{k_{0} }}{{m_{0} }}} & {\frac{{c_{0} }}{{m_{0} }}} & { - \frac{{c_{0} }}{{m_{0} }}} \\ \end{array} } \right] \hfill \\ B_{v1} = \left[ {\begin{array}{*{20}c} 0 & 0 & {\frac{1}{{m_{v} }}} & 0 \\ \end{array} } \right]^{T} ,B_{v2} = \left[ {\begin{array}{*{20}c} 0 & 0 & { - \frac{1}{{m_{v} }}} & {\frac{1}{{m_{0} }}} \\ \end{array} } \right]^{T} \hfill \\ C_{v} = \left[ {\begin{array}{*{20}c} { - \frac{{k_{0} + k_{v} }}{{m_{v} }}} & {\frac{{k_{0} }}{{m_{v} }}} & { - \frac{c_{0}}{m_{v} }} & {\frac{{c_{0} }}{{m_{v} }}} \\ \end{array} } \right] \hfill \\ D_{v1} = \left[ {\frac{1}{{m_{v} }}} \right], D_{v2} = \left[ {\begin{array}{*{20}c} { - \frac{1}{{m_{v} }}} \\ \end{array} } \right], \hfill \\ \end{gathered}$$
(6)

where the observed output \(y\) is the acceleration of the virtual structure, which is equivalent to that of the actual controlled object. The disturbance \(w\) is assumed as described below. This study assumes various kinds of disturbances involving low-frequency components, which make the control system based on a virtual structure prone to oscillations due to the resonance of the proof-mass actuator, as shown in "Vibration Control Simulation with K1".

$$w={k}_{v}{x}_{1}.$$
(7)

The state equation does not include the parameters of the actual controlled object. Hence, a controller designed to control this 2-DOF system can realize model-free control. Moreover, if Eq. (4) holds, the vibration of the virtual structure is equivalent to that of the actual controlled object. Therefore, the vibration of the actual controlled object can be indirectly suppressed. Thus, the introduction of the virtual structure into the vibration control based on a proof-mass actuator achieves indirect damping of the actual controlled object and realizes model-free control. Also, a simple structure composed of mass \({m}_{v}\) and spring \({k}_{v}\) reduces the burden on the controller designer.

It should be noted that the virtual structure does not actually exist. Therefore, the vibration of the controlled object, which is equivalent to that of the virtual structure, is used as the observed output based on Eq. (4) when constructing the feedback control system.

Controlled Frequency Band

Here, we consider the frequency range in which model-free control with a virtual structure can be established. As described in "Control System Design Using a Virtual Structure", \({m}_{v}\) and \({k}_{v}\) cannot be zero and infinite values. This numerical calculation constraint limits the frequency range in which Eq. (4) holds. In this study, the lower limit of the control frequency band is 25 Hz, and the upper limit is 3,000 Hz. The previous study[26] presents Eq. (8) as a design guideline for the parameters of the virtual structure when the lower and upper limits of the control frequency band are set to \({\Omega }_{1}^{\mathrm{cont}}\) and \({\Omega }_{2}^{\mathrm{cont}}\), respectively. Specifically, the parameters of the virtual structure are designed as follows:

  1. 1.

    Determine the lower and upper limits \({\Omega }_{k}^{\mathrm{cont}}(k=\mathrm{1,2})\) of the controlled frequency band.

  2. 2.

    Design the parameters of virtual structure so that the condition Eq. (8) is satisfied. \({m}_{v}\) and \({k}_{v}\) should be set to a sufficiently small finite value and a sufficiently large finite value, respectively.

  3. 3.

    Verify whether Eq. (4) is satisfied in the controlled frequency band.

Figure 4 shows the Bode plot of the transfer function expressed in Eq. (3) when the parameters are set to the values in Table 1, which satisfy this condition. The gain is almost 1, and the phase delay is negligibly small in the range of 25–10,000 Hz. This range includes the control band confirming that Eq. (4) is approximately established. Thus, the virtual structure and the actual controlled object have equal vibrations, and model-free vibration control can be realized in this controlled band.

Fig. 4
figure 4

Bode plot of \({T}_{{x}_{v}{x}_{1}}\)

Full size image
$$\left\{\left(\frac{{{\Omega }_{k}^{\mathrm{cont}}}^{2}}{{k}_{0}}-\frac{1}{{m}_{0}}\right){k}_{v}+{{\Omega }_{k}^{\mathrm{cont}}}^{2}\right\}\frac{1}{{m}_{v}}>\left(\frac{{{\Omega }_{k}^{\mathrm{cont}}}^{2}}{{k}_{0}}-\frac{1}{{m}_{0}}\right){{\Omega }_{k}^{\mathrm{cont}}}^{2}, \left(k=\mathrm{1,2}\right).$$
(8)

Effect of the Natural Frequency of the Proof-Mass Actuator

Next, we evaluated the adverse effect of the resonance of the proof-mass actuator on the control system.

Traditional Model-Free \({H}_{\infty }\) Controller Using a Virtual Structure

The previous study[26] designed an \({H}_{2}\)/\({H}_{\infty }\) controller based on a generalized plant in which the vibration control band and the parameters of the virtual structure were defined based on Eq. (8). Herein a similar \({H}_{\infty }\) controller (K1) was designed using the generalized plant G in Fig. 5a. The observed output \(y\) is the acceleration of the virtual structure which is equivalent to that of the controlled object. Pv represents a 2-DOF system consisting of actuators and a virtual structure described by Eqs. (5) and (6). The weights on the observed output and control input are \({W}_{y}=10\) and \({W}_{u}=\sqrt{8\times {10}^{10}}\), respectively. The controlled outputs \({z}_{1}\) and \({z}_{2}\) are the weighted control input and the weighted observed output, respectively. \({H}_{\infty }\) control minimizes the \({H}_{\infty }\) norm of the transfer function \({T}_{zw}\) from the disturbance \(w\) to the controlled output \(z( ={\left[{z}_{1},{z}_{2}\right]}^{T})\) in the closed-loop system consisting of G and K1:

Fig. 5
figure 5

Block diagram of control system. a Generalized plant G for K1. b Closed-loop system consisting of PFEM and K1. c Schematic of the closed-loop system in practice

Full size image
$$\mathrm{min}.{\Vert {T}_{zw}\Vert }_{\infty }.$$
(9)

Figure 5b shows a block diagram of the control system used in the vibration control simulations in "Vibration Control Simulation with K1". PFEM is the finite element (FE) model described below. It should be noted that the controlled object in the controller design is not PFEM but Pv. In other words, the proposed method achieves model-free control without a mathematical model of the controlled object. The generalized plant and the \({H}_{\infty }\) controller are designed using MATLAB’s Robust Control Toolbox.

Figure 5c shows a schematic of the closed-loop system in practice. The proof-mass actuator generates the damping force by feedbacking the acceleration of the controlled object equivalent to that of the virtual structure after the shaker disturbs the controlled object. It should be noted that the accelerometer is mounted directly under the proof-mass actuator to observe the same acceleration at the location where the actuator suppresses.

Controlled Objects

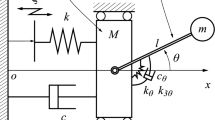
This study employed three types of FE models for the actual controlled objects: two types of cantilever plates (Structures A and B), which consist of a flat plate and weights shown in Fig. 6, and a beam supported at both ends (Structure C). The plant models of these beams are derived using modal analysis. Finite element analysis software ANSYS (2021 R2) was used to construct the FE models. Table 2 shows the dimensions and the number of weights in each beam. The numbers of modes employed were 6, 8, and 6 for Structures A, B, and C, respectively. All modal damping ratios were set to 0.5%. All adopted modes were in the control band. Table 3 shows the natural frequencies of each object. Table 4 shows the physical properties of the plates and weights.

Fig. 6
figure 6

FE models of controlled objects for (a) Structure A, (b) Structure B, and (c) Structure C, Images used courtesy of ANSYS, Inc

Full size image
Table 2 Dimensions of the controlled objects
Full size table
Table 3 Natural frequencies of the controlled objects calculated via FEM (Hz)
Full size table
Table 4 Physical properties of the plate and weight in the FE model
Full size table

Here, Eqs. (10) and (11) give the equations of motion for the proof-mass actuator and FE model, respectively[32].

$${m}_{0}\ddot{{x}_{0}}+{c}_{0}\left(\dot{{x}_{0}}-{b}_{u}^{T}\dot{{x}_{c}}\right)+{k}_{0}\left({x}_{0}-{b}_{u}^{T}{x}_{c}\right)=u,$$
(10)
$${M}_{c}\ddot{{x}_{c}}+{C}_{c}\dot{{x}_{c}}+{K}_{c}{x}_{c}={b}_{w}w+{b}_{u}\left\{-u+{c}_{0}\left(\dot{{x}_{0}}-{b}_{u}^{T}\dot{{x}_{c}}\right)+{k}_{0}\left({x}_{0}-{b}_{u}^{T}{x}_{c}\right)\right\}.$$
(11)

\({x}_{c}\) is the displacement vector of all nodes of the FE model. \({b}_{u}\) and \({b}_{w}\) are the coefficient vectors that determine the position of the input and disturbance, respectively. \({M}_{c}\) and \({K}_{c}\) are the mass and stiffness matrices of the FE model. It is assumed \({C}_{c}\) is the proportional viscous damping matrix. \(\Phi\) is the modal matrix, \(\xi\) is the modal coordinate, \({b}_{y}\) is the coefficient vector that determines the position of the observed output. \({x}_{c}\) = \(\Phi \xi\) transforms the physical coordinate system to the modal coordinate system. It should be noted that the higher-order vibration modes are omitted. The state and output equations are expressed as Eqs. (12)–(15).

$$\begin{gathered} \dot{q} = A_{FE} q + B_{FE1} w + B_{FE2} u \hfill \\ q = \left[ {\begin{array}{*{20}c} {x_{0} } & {\dot{x}_{0} } & \xi^{T} & {\dot{\xi^{T}}} \\ \end{array} } \right]^{T} , \hfill \\ \end{gathered}$$
(12)
$$\begin{gathered} A_{FE} = \left[ {\begin{array}{*{20}c} 0 & 1 & {0_{1 \times r} } & {0_{1 \times r} } \\ { - \frac{{k_{0} }}{{m_{0} }}} & { - \frac{{c_{0} }}{{m_{0} }}} & {\frac{{k_{0} }}{{m_{0} }}b_{u}^{T} \Phi } & {\frac{{c_{0} }}{{m_{0} }}b_{u}^{T} \Phi } \\ {0_{r \times 1} } & {0_{r \times 1} } & {0_{r \times r} } & {I_{r \times r} } \\ {k_{0} \Phi^{T} b_{u} } & {c_{0} \Phi^{T} b_{u} } & {\begin{array}{*{20}c} { - \left( {\Lambda + k_{0} \Phi^{T} b_{u} b_{u}^{T} \Phi } \right)} \\ \end{array} } & {\begin{array}{*{20}c} { - \left( {\Phi^{T} C_{c} \Phi + c_{0} \Phi^{T} b_{u} b_{u}^{T} \Phi } \right)} \\ \end{array} } \\ \end{array} } \right] \hfill \\ B_{FE1} = \left[ {\begin{array}{*{20}c} 0 & 0 & {0_{1 \times r} } & {b_{w}^{T} \Phi } \\ \end{array} } \right]^{T} { },{ }B_{FE2} = \left[ {\begin{array}{*{20}c} 0 & {\frac{1}{{m_{0} }}} & {0_{1 \times r} } & { - b_{u}^{T} \Phi } \\ \end{array} } \right]^{T}, \end{gathered}$$
(13)
$$y = C_{FE} q + D_{FE1} w + D_{FE2} u,$$
(14)
$$\begin{gathered} C_{FE} = \left[ {\begin{array}{*{20}c} {b_{y}^{T} \Phi \left[ {k_{0} \Phi^{T} b_{u} { }c_{0} \Phi^{T} b_{u} { }\begin{array}{*{20}c} { - \left( {\Lambda + k_{0} \Phi^{T} b_{u} b_{u}^{T} \Phi } \right)} \\ \end{array} { }\begin{array}{*{20}c} { - \left( {\Phi^{T} C_{c} \Phi + c_{0} \Phi^{T} b_{u} b_{u}^{T} \Phi } \right)} \\ \end{array} } \right]} \\ \end{array} } \right] \hfill \\ D_{FE1} = \left[b_{y}^{T} \Phi \Phi^{T} b_{w}\right] , D_{FE2} = \left[\begin{array}{*{20}c} { - b_{y}^{T} \Phi \Phi^{T} b_{u} } \\ \end{array}\right] . \hfill \\ \end{gathered}$$
(15)

r is the number of adopted modes, and Λ is the eigenvalue matrix expressed as

$$\Lambda =\mathrm{diag}\left[{\Omega }_{1},{\Omega }_{2},\cdots ,{\Omega }_{r}\right].$$
(16)

The observed output is the acceleration in the z-axis direction at the same position as the actuator on the opposite plane. For example, in Structure A, the nodal coordinates to which the control input in the z-axis direction is applied are (200, 45, 15), and the nodal coordinates used as the observation output are (200, 45, − 30). Figure 7 shows the positions of the control inputs and disturbances as magenta and red points, respectively, for each controlled object.

Fig. 7
figure 7

Positions of the disturbance and control input: a Structure A, b Structure B, and c Structure C

Full size image

Vibration Control Simulation with K1

We then examined an undesirable case where the model-free vibration control is unstable when lower-order modes of the controlled objects are too close to the natural frequency of the actuator. We assumed two situations for the controlled objects described in "Controlled Objects": one is the case of a nominal controlled object, and the other is a case where the vibration mode of the controlled object moves to the negative side (natural frequency becomes smaller). That is, a negative perturbation is added to each \({\Omega }_{i}\) included in \({\Phi }^{T}{C}_{c}\Phi\) and \(\Lambda\) in Eqs. (12)-(15).

The simulation conditions are as follows: the lower and upper limits of the control band were set to 25 Hz and 3000 Hz, respectively. The parameters of the virtual structure in Table 1 were selected to satisfy the design guideline of Eq. (8). The sampling frequencies for the discretization of the controlled object and the controller were 20,000 Hz, and the discretization method was the bi-quadratic transform. The disturbance was a linear sweep sinusoidal signal of 1–3000 Hz. Figure 5b shows the block diagram of the control system.

Here, vibration control simulations were performed as a typical example. We considered two cases. In the first one, Structure A has a nominal structure. In the second, all vibration modes of Structure A are subjected to a 75% negative fluctuation.

Figure 8a, b show the frequency response function (FRF) from the disturbance \(w\) to the observed output \(y\) for the nominal and fluctuating natural frequencies, respectively. The broken line and solid line denote the frequency response of the open-loop and the closed-loop with K1, respectively.

Fig. 8
figure 8

FRF of the closed-loop system (Structure A) with a the nominal model and b perturbed model

Full size image

Figure 9a, b show the time response of the observation output and its enlarged view when the vibration modes of the controlled object move to the negative side. The broken and solid lines show the time response of the observed output of the open-loop and the closed-loop system with K1, respectively. When Structure A is nominal, the low-order vibration modes such as the first and second modes are damped. However, the control system becomes unstable when the low-order modes of the controlled object are too close to the natural frequency of the actuator. Figure 9b shows that the control system tends to diverge due to the mode around 20 Hz, which is extremely close to the natural frequency of the proof-mass actuator. Structures B and C exhibit the same tendencies. The negative variations of all vibration modes in Structures B and C were set to 11% and 81%, respectively. The instabilities are due to the adverse interference between the resonance of the actuator and the low-order vibration mode of the actual controlled object.

Fig. 9
figure 9

Time response of the closed-loop system for a the perturbed model of Structure A and b enlarged view

Full size image

Stability Improvement of the Model-Free Controller

Application of a Notch Filter to Design a Model-Free Control System

This study proposes an improved model-free \({H}_{\infty }\) controller with an enhanced robustness by introducing a notch filter as a countermeasure to the instability, which was verified in Chapter 3. A notch filter has been used to suppress the resonance of mechanical systems [33,34,35,36,37]. Since the natural frequency of the actuator is around 20 Hz (see Fig. 2), a second-order notch filter was designed as described in Eq. (17) with \({\zeta }_{1}=0.1, {\zeta }_{2}=0.01, \omega =2\pi {f}_{n}, {\mathrm{and} f}_{n}=21\). The coefficients \({\zeta }_{1}\) and \({\zeta }_{2}\) are the parameters to define the depth and width around the natural frequency \(\omega\) of the notch filter [36, 37]. In this study, these parameters are designed so that the adverse effect of the resonance is blocked sufficiently without affecting the damping performance of the controller.

$${W}_{n}\left(s\right)=\frac{{s}^{2}+2{\zeta }_{2}\omega s+{\omega }^{2}}{{s}^{2}+2{\zeta }_{1}\omega s+{\omega }^{2}}.$$
(17)

Figure 10 shows the Bode plot of the notch filter. The notch filter described in Eq. (17) is included after Pv in the generalized plant G′ as shown in Fig. 11a. Furthermore, the \({H}_{\infty }\) controller designed based on G′ was multiplied by the notch filter in the control system as shown in Fig. 11b. This is because the original open-loop system does not include the notch filter. The controller designed in this way is denoted as K2. Previous studies [23,24,25,26,27] did not include a filter which focuses on the natural frequency of the proof-mass actuator in their model-free control system design. This combination of the notch filter and the model-free controller based on virtual structure is the technical novelty in this paper.

Fig. 10
figure 10

Bode plot of the notch filter

Full size image
Fig. 11
figure 11

Block diagram of proposed control system. a Generalized plant G′ for K′. b Closed-loop system consisting of PFEM and K2

Full size image

The solid and dashed lines in Fig. 12 denote the Bode plot of discretized K1 and K2, respectively. The discretized K2 with a notch filter effectively reduces the gain only around the natural frequency of the actuator compared to discretized K1. This frequency shaping indicates that K2 can ensure robustness for the undesired case where the actuator diverges due to the resonance.

Fig. 12
figure 12

Bode plot of discretized K1 and K2

Full size image

Vibration Control Simulation with K2 and Discussion

Finally, we validate whether the proposed method (K2), which introduces a notch filter, improves the robustness. Specifically, vibration control simulations were performed for three types of nominal controlled objects and those where the vibration modes fluctuate on the low-frequency side. The simulation conditions are the same as those in "Vibration Control Simulation with K1" except for the controller.

Figures 13, 14 and 15 show the results of the vibration control simulations as the FRF from the disturbance to the observed output, where (a) shows the simulation results of each nominal controlled object and (b) shows the simulation results when the vibration mode of each structure moves to the low-frequency side. The broken, solid, and dashed lines denote the results without control, the control result by K1, and the control result by K2, respectively. K2 has the same damping effect as K1 for the nominal controlled objects. Moreover, the closed-loop system with K2 is stable for perturbed models whereas the closed-loop system with K1 is unstable. Tables 5 and 6 show the vibration reduction amount with the model-free controllers (K1, K2) at the major peaks of the nominal controlled objects and the perturbed controlled objects, respectively. Table 7 shows the approximate minimum amount of fluctuation given to the natural frequency of each controlled object, which caused the control system composed of K1 or K2 to become unstable..

Fig. 13
figure 13

FRF of the improved system (Structure A) for a the nominal model and b perturbed model

Full size image
Fig. 14
figure 14

FRF of the improved system (Structure B) for a the nominal model and b perturbed model

Full size image
Fig. 15
figure 15

FRF of the improved system (Structure C) for a the nominal model and b perturbed model

Full size image
Table 5 Vibration reduction amount with the model-free controllers at the major peaks of each nominal model
Full size table
Table 6 Vibration reduction amount with the model-free controllers at the major peaks of each perturbed model
Full size table
Table 7 Approximate minimum amount of fluctuation given to the natural frequency when the control system composed of K1 or K2 becomes unstable
Full size table

Another vibration control simulation for nominal structure A was conducted to show the effectiveness of the proposed method from the viewpoint of the control input characteristics as the resolution of the frequency domain increased. The disturbance was set to a linear sweep sinusoidal signal 1–1000 Hz. Figure 16 represents the FRF from the disturbance to the control input at 0–30 Hz. The solid line and dashed line denote the FRF of K1 and K2. The control input of K2 is smaller than that of K1 at the natural frequency of the actuator, indicating that K2 suppresses the input near the natural frequency of the actuator more intensely than K1. The same tendencies were also confirmed for Structures B and C.

Fig. 16
figure 16

FRF with the nominal model of Structure A (the ratio of the control input to the disturbance)

Full size image

These results indicate that K2 can reduce the adverse effects of the actuator resonance, which destabilize the closed-loop system when the vibration modes of the controlled object shift to the low-frequency side. Thus, introducing a notch filter to the model-free vibration control system based on the virtual structure improves the stability of the closed-loop system at low frequencies.

Conclusion

This study investigates the adverse effects of a proof-mass actuator resonance in the model-free vibration control based on the virtual structure via vibration control simulations, which were not clarified in previous studies.

A virtual structure modeled as a SDOF system is inserted between the proof-mass actuator and the actual controlled object. This configuration achieves indirect damping of the actual controlled object by properly selecting the parameters for the virtual structure, realizing model-free vibration control.

The adverse interference between the proof-mass actuator and the low-order mode of the actual controlled object affects the stability of the model-free control system even if the mode is within the controlled frequency band. In fact, the closed-loop system with the previous model-free \({H}_{\infty }\) controller (K1) becomes unstable due to the resonance of the proof-mass actuator when the lower vibration mode of the controlled objects is too close to the natural frequency of the actuator.

To overcome this instability, a notch filter is introduced into the model-free \({H}_{\infty }\) controller design approach based on the virtual structure. The proposed method reduces the gain of the controller near the natural frequency of the actuator without affecting the damping performance. The robustness of the virtual-structure-based model-free \({H}_{\infty }\) controller against the disturbance involving the low-frequency components, which make the control system prone to oscillations because of the adverse interference between the resonance of the actuator and the low-order modes of the actual controlled object, is improved. Thus, the practicality and range of applications should be enhanced, which will greatly contribute to the vibration control of various mechanical systems.

In the future, we will confirm whether the notch filter compensation can effectively improve the robustness not only for the \({H}_{\infty }\) control but also for other model-free controllers based on a virtual structure.