Introduction

This paper experimentally investigates the fluid–structure interaction mechanics of a vibrating rigid circular cylinder, which is a kind of long slender structures. A long slender structure vibrates when placed in a fluid flow. This vibration phenomenon has attracted scientific and technological attention, because it involves interesting fluid–structure interaction processes and is closely related to fatigue accumulation in the structure. Long slender parts are used in large structures, such as bridges, chimneys, and underwater flexible pipes. By studying the vibrations of these objects in fluid flows, we can clarify the underlying fluid–structure interaction mechanics and develop ways of suppressing the vibrations, thereby establishing a design policy for implementing such structures. Another prospect is natural energy-harnessing technologies that convert the kinetic energy of fluid flows around the body to electric energy. Amplifying the vibrations could increase the magnitudes of the available energy.

When subjected to fluid flows, an isolated circular cylinder vibrates with an amplitude that sensitively depends on the speed of the flow. In extensive investigations, the mechanical cause of this vibration has been identified as vortex-induced vibration (VIV) (e.g., [1,2,3,4,5,6,7]). Multiple cylinders arranged in close proximity in a fluid flow mechanically influence each other through the surrounding fluid. The flow patterns and vortex structures appearing around two circular cylinders are described in [8].

The fluid-mediated dynamic interactions between two flexible circular cylinders arranged in tandem were experimentally investigated in [9]. Typical patterns of the flow fields around two tandemly fixed circular cylinders were presented in [10]. In side-by-side configurations of two cylinders, the formation of vortex sheets and flow induction between the cylinders (gap flows) depends on the spacings between the two cylinders in the inline and transverse directions (called the inline and transverse spacings, respectively) [11]. Vibrations of three circular cylinders have been investigated in a numerical simulation [12].

In many previous studies of two circular cylinders, one cylinder was fixed at an upstream point and the other cylinder was elastically supported at a downstream point [e.g., 13,14,15,16,17,18]. One exceptional study [19] examined an upstream movable cylinder and a downstream fixed one. In these arrangements, the vibrations of a circular cylinder placed near another cylinder are sustained even at reduced velocities exceeding 10. Such vibrations are referred to as wake-induced vibrations (WIVs) or wake-induced galloping.

VIVs and WIVs share a common mechanism of exciting vibrations but the mechanical details of VIVs differ from those of WIVs. The excitation of VIVs is described in terms of pressures around a vibrating cylinder (e.g., [20]). The viscosity of the flowing fluid impedes the downstream transport of the fluid kinetic energy along one side of the cylinder’s surface; consequently, a separated shear layer alternately forms on the two sides of the cylinder. The pressure difference between the upper and lower sides of the cylindrical surface induces a dynamic fluid force in the transverse direction, which directly acts on the cylinder. The excitation of WIVs is also explained by the pressure difference, but, differently from that of VIV, the pressure difference is influenced by wakes formed behind other cylinders.

These prior findings imply that if we intentionally change the flow field near a moving body, we can enhance the vibration amplitude and the amount of energy harnessed from the fluid flow. In this process, the gap flow plays a significant role as reported in previous studies (e.g., [17,18,19]). For a successful regulation of the gap flow, this study considers a downstream movable circular cylinder and two fixed circular cylinders. When deciding this arrangement, it was presumed that alternative formations of gap flows near both ends of a vibratory trajectory can efficiently enhance the vibration. If successful, this simple method of placing only two additional cylinders near the cylinder of interest can enhance the energy-harvesting ability of the system to practical levels.

The present study experimentally observes the vibratory responses of a circular cylinder placed in water flows near two fixed circular cylinders. From the measured responses, the effects of the fixed cylinders on the vibration of the unfixed cylinder are clarified and the related fluid–structure interaction mechanics are discussed.

Experimental Methods

Experimental Setup

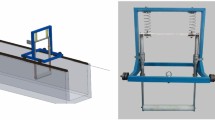
The movable cylinder was an acrylic circular cylinder of length 0.260 m and diameter 0.0300 m (Fig. 1). The upper end of the cylinder was connected to an acrylic bar (labeled “power transmission B” in Fig. 1 (a)), which rotated around a main shaft. In this configuration, the power of the motion was transferred from the movable cylinder to the main shaft. Another acrylic bar (labeled “power transmission A”) was rotated to transmit the power of the motion from the main shaft to springs. Vibrational motion of the movable cylinder was ensured by the elastic supports provided by the springs (Figs. 1a and 2a).

Fig. 1
figure 1

a Schematic of the circular cylinders and power transmission system installed on the observation window of the circulating water channel; b photograph of the observation window and moving cylinder

Full size image

The setup of cylinders, bars, and springs was installed in a circulating water channel (West Japan Fluid Engineering Laboratory Co., Ltd.). The channel was installed with 0.940-m-long transparent windows (labeled “Observation window” in Fig. 1) for observing the water flows and body motions. The channel was 0.465 m wide and the water depth was 0.220 m. The speed of the water flow through the channel was controlled by regulating the revolutions-per-minute of an impellor equipped in the channel. The bottom end of the movable cylinder was positioned at 0.080 m above the water-channel floor. To prevent interference of the channel floor on the cylinder motions, a circular plate was attached to the bottom surface of the cylinder.

A pair of acrylic circular cylinders of length 0.260 m and diameter 0.0300 m (labeled as “fixed cylinders” in Fig. 1a) were positioned upstream of the movable cylinder. Their top ends were fixed to a frame of the observation window.

Measurement Method

Through converting the rotational motions of power transmission A into translational motions, the amplitudes of the movable cylinder were observed as the lengths of linear motions. This transformation was performed with a Rapson slide (Figs. 2 and 3). The translational motions of the slide were driven by the rotation of power transmission A (“shaft link” in Fig. 3). The moving Rapson slide was sandwiched by a pair of bars (“slide guide” in Fig. 3). As the movable cylinder vibrated, the displacements of the back-and-forth rectilinear motions of the slide were detected by a laser displacement sensor (IL-600, Keyence Co. Ltd.). Analog time-series data of the displacements were transformed into digital data through a data-logger (NR-500, Keyence Co., Ltd.) and recorded in a storage medium. The data were analyzed with a Fast Fourier Transform program to determine the dominant amplitude and frequency in the temporal displacement record.

Fig. 2
figure 2

a Top view and b back view of the experimental setup

Full size image
Fig. 3
figure 3

Schematic of the Rapson slide and displacement sensor

Full size image

Experimental Conditions

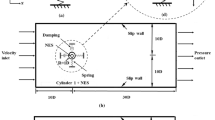
The inline spacing x was defined as the distance between the line segment connecting the centers of the cross sections of the fixed cylinders and the vertical line passing through the center of the cross section of the movable cylinder (between the two vertical dashed lines in Fig. 4a). Meanwhile, the transverse spacing y was defined as the length of the segment between the centers of the cross sections of the two fixed cylinders (between the two horizontal dashed lines in Fig. 4a). The x and y spacings were changed from 0.0500 to 0.160 m in 1.00-cm intervals. Forty-six combinations of x and y were tested as shown in Fig. 4b.

Fig. 4
figure 4

a Definitions of inline spacing x and transverse spacing y; b all combinations of x and y conditioned in the experiment. The upper and right axes in b represent the dimensionless spacings x′ ≡ x/d and y′ ≡ y/d

Full size image

In each configuration of x and y, the reduced velocity Vr, defined as

$$V_{{\text{r}}} \equiv \frac{V}{{f_{{\text{n}}} d}},$$

was ranged from 4.00 to 13.0 in 1.00-unit intervals (ten water speeds in total), where d [m] denotes the diameter of the movable cylinder, fn is the natural frequency of the vibratory system (involving the masses of the movable cylinder and power transmission bars, and the rigidities of the springs), and V [m/s] is the dimensional speed of the water flow. The natural frequency was determined in free damping tests without water flow: the movable cylinder was forcibly displaced from its resting position and then released. After obtaining the time histories of the resulting decaying vibrations five times and averaging the dominant frequencies, fn was determined as 1.66 Hz.

Results and Discussion

Hereafter, amplitudes are shown in texts and figures as dimensionless values obtained as the measured amplitudes divided by the diameter of the movable cylinder. Frequencies are shown as dimensionless values computed by dividing the dimensional frequencies by the natural frequencies. The experimental condition with spacing x and spacing y is denoted by “(x, y)”. In some parts of the subsequent texts and in Fig. 4, the spacings x and y are shown as the dimensionless ones defined as x′ ≡ x/d and y′ ≡ y/d, respectively.

Amplitudes and Frequencies of the Movable Cylinder

When the movable cylinder was installed in isolation (without the fixed cylinders), its responses resembled typical responses of a single circular cylinder in flow (Fig. 5). A reduced velocity of 4.0 produced few vibrations. As the reduced velocity increased from 4.0 to 8.0, the amplitudes grew to reach 0.38 at Vr = 8.0. At reduced velocities above 8.0, the amplitudes decreased and reached 0.02 at Vr = 13.0.

Fig. 5
figure 5

Dimensionless amplitudes (a, b, c, g, h, and i) and dimensionless frequencies (d, e, f, j, k, and l) as functions of reduced velocity. Inclined dashed lines show the dimensionless vortex-shedding frequency at a Strouhal number of 0.20 versus the reduced velocity

Full size image

Let us compare the responses of the isolated moving cylinder with those of the moving cylinder near two fixed cylinders. The case (5, 5) produced few responses at most of the reduced velocities. The case (6, 6) (Fig. 5a) yielded a distinct amplitude around 0.20 at Vr = 5.0 and smaller amplitudes at Vr = 4.0–9.0. Amplitudes around 0.10 appeared at Vr = 9.0 and were maintained at Vr over 10.0 (Fig. 5a). Two peaks dominated the amplitude response curve: the narrow peak around Vr = 5.0 and a wide peak in the Vr = 8.0–13.0 range. This two-peak pattern in the Vr profiles appeared in most of the cases with inline spacing x ≤ 8.0 cm (x′ ≤ 2.67) (Fig. 5b).

When the inline spacing x exceeded 9.0 cm (x′  > 3.00), the amplitude responses differed from those of the smaller x cases. In cases (9, 9) and (10, 10) (Fig. 5c), no peaks appeared at Vr = 5.0 and single peaks were observed at Vr = 8.0–9.0. The dimensionless amplitudes remained around 0.3 even when Vr exceeded 10.0. Very similar peak distributions were observed in the cases (11, 11) and (12, 12).

In the cases (5, 5) and (6, 6), the amplitudes were remarkably large, and the frequencies were close to the natural frequency (Fig. 5d, e). The frequencies in the cases (9, 9) and (10, 10) increased monotonically with increasing reduced velocity (Fig. 5f).

When the inline spacing x was 13.0 cm (x′ > 4.33) or longer, the amplitude responses exhibited a single peak that tended to shift to smaller Vr with increasing x; specifically, the peak appeared at Vr = 8.0, 8.0, and 7.0 in the cases (12, 12), (13, 13), and (15, 15), respectively (Fig. 5g–i). The amplitudes at greater Vr than the peak-amplitude Vr tended to decrease more sharply with Vr than in the smaller x cases. The emergence of these single peaks resembled that in the isolated movable cylinder case. The frequencies monotonically increased with reduced velocities (Fig. 5j–l), similar to those in cases (9, 9) and (10, 10) (Fig. 5f).

To more comprehensively see the dependencies of the amplitudes on x and y, the dimensionless amplitudes were plotted on the x–y plane at each reduced velocity (Fig. 6: in this figure, blue (red) circles represent greater (smaller) amplitudes in the cases with the fixed cylinders placed than the amplitudes in the isolated cylinder case). At Vr = 5.0, increasing the inline spacing x from 6.0 (x′ = 2.00) to 8.0 cm (x′ = 2.67) enhanced the amplitude response from that of the isolated movable cylinder, particularly in cases (7, 6) and (7, 7). At Vr = 6.0, the amplitudes were smaller and larger than those of the isolated cylinder at short and long inline spacings, respectively (Fig. 6b). The number of smaller amplitude cases (red circles in Fig. 6) was maximized at Vr = 7.0, because the amplitude response of the isolated movable cylinder peaked at Vr = 7.0 (Fig. 6c). The greater reduced velocities at Vr > 8.0 were responsible for the enlarged amplitudes in most of the (x, y) combinations (Fig. 6d–i). The diameters of the blue circles were largest around (8, 9) at Vr = 9.0 and 10.0 and were located around x = 7.0 cm (x′ = 2.33) in the Vr = 11.0–13.0 range.

Fig. 6
figure 6

x–y diagrams of the dimensionless amplitudes at each reduced velocity. The circle diameters represent the dimensionless amplitudes. Blue (red) colors indicate larger (smaller) amplitudes than those of the isolated cylinder. The numbers in the lower right corners of each panel are the maximal values of the dimensionless amplitudes at each reduced velocity

Full size image

Discussions on the Fluid–Structure Interaction Mechanics

When the twin cylinders were fixed upstream at inline spacings of x = 6.0–8.0 cm (dimensionless inline spacings x′ = 2.00–2.67), the vibrations were remarkably large at Vr = 5.0 (Fig. 6a). At the Reynolds numbers in this experiment (1.64 \(\times\) 105 to 1.07 \(\times\) 106), the Strouhal number (≡ fv*d/V, where fv denotes the frequency of vortex-shedding behind a fixed circular cylinder) was approximately 0.20 or higher (e.g., [20]). The fv computed at a Strouhal number of 0.20 matched the natural frequency of the movable cylinder (the intersection point of the horizontal dashed line at 1.0 and the inclined dashed line in Fig. 5d–f, j–l). As the inline spacing x ranged from 6.0 to 8.0 cm, the vibration frequencies at Vr = 5.0 remained quite close to the natural frequency. The left-side amplitude peaks at Vr = 5.0 were thus, probably excited by vortices generated on the twin fixed cylinders, whereas the isolated cylinder hardly showed vibrations at Vr = 5.0 (Fig. 6a), suggesting that those peaks are different from one seen in typical VIVs. Karman vortices were shed from the lower side of the upper fixed cylinder in Fig. 4a, and those shed from the upper side of the lower fixed cylinder in Fig. 4a regularly approached and interfered with the movable cylinder, thereby sustaining the vibrations. In this regime of vibration excitation, the moving cylinder was supplied with the kinetic energy from the outer system. It follows that these vibrations were forced ones.

Amplitude peaks around Vr = 9.0 or 10.0 were observed in the x = 8.0–10.0 cm (x′ = 2.67–3.33) and were sustained over a wide range of reduced velocities (Figs. 5b, c, and 6e, f), whereas the vibration amplitudes of the isolated movable cylinder monotonically decreased as the reduced velocity ranged from 9.0 to 10.0. The frequencies of the responses were closer to the natural frequency at x = 8.0–10.0 cm (x′ = 2.67–3.33) than in the isolated case (Fig. 5e, f), indicating an excitation process that differs from that of VIV.

A discussion is made here on a fluid-dynamic mechanism of the excitation of the observed vibrations. As the moving cylinder approached one of the fixed cylinders (Fig. 7a), the gap between these two cylinders was narrowed and the flow through the gap was accelerated. It is inferred from Bernoulli’s law (e.g., [20]) that the growth of gap flows triggered the distribution of a low-pressure region around the cylinder. The resulting increased pressure difference exerted a fluid-dynamic force in the transverse direction. One half-cycle after this instance, the moving cylinder was located near the other fixed cylinder (Fig. 7b) and the dynamic force on the moving cylinder switched direction. These fluid-dynamic forces alternated to induce the distinctive vibrations.

Fig. 7
figure 7

Schematics showing the interferences between the moving and fixed cylinders. In (a) and (b), the moving cylinder is positioned near the upper and lower fixed cylinder, respectively. The dashed lines indicate the center of the motion trajectory

Full size image

Can this mechanism be supported by similar fluid–structure interactions between gap flows and moving bodies reported in previous studies (e.g., [11, 18])? Can it certainly underlie the sustained vibrations at reduced velocities over 9.0 (Fig. 5b, c)? In these cases, the interference regions of the upstream cylinders probably reached the moving cylinder. The presence of such a region was reported in [8, 11]. In a previous study [13] on one movable circular cylinder and one fixed upstream cylinder, four categories of amplitude response curves were proposed involving two mechanical processes of vibration excitation: vortex resonance and galloping. The former and latter of these processes are the well-recognized VIV and WIV, respectively [13]. The category of an observed response depends on the inline and transverse spacings. The first category is pure vortex resonance (VIV) occurring at low reduced velocities; the second category is pure galloping, in which the vibration amplitudes grow monotonically with increasing reduced velocity. The third and fourth categories are mixtures of VIV and WIV. The amplitude peaks of VIV and WIV merge when the spacings x and y are very small (in category 3), or are separated when x and y are large (category 4). The responses of our experiment (Fig. 5b, c) fit into the third category, although two upstream cylinders were installed in our experiment differently from the experiment by [13] using a single upstream cylinder.

The arrangement of the cylinders in our study permitted gap flows to form at the two regions near the both ends of a vibratory trajectory and consequently to make the periodic fluid-dynamic forces bi-directional. For empowering an energy-harvesting system with fluid flows, this mechanism may serve as a vibration-amplifier.

When the inline spacing exceeded 9.0 cm (x′ > 3.00), the two peaks were not clearly separated and a distinct single peak dominated the amplitude response (Fig. 5c, g, h, i). Beyond the peak amplitude, the amplitudes declined monotonically with reduced velocity but exceeded those of the isolated movable cylinder (Fig. 6e–i). These responses were interpreted as VIV. In such vibrations, the moving cylinder is supplied kinetic energy through vortex-induced forces. Because the vortices are themselves stimulated by the cylinder’s motion, motion in the VIV regime is self-excited and scarcely affected by the fixed cylinders. Enlarging x and y allowed the vortices originating from the upstream cylinders to move downward with little interference on the moving cylinder.

Our experiment was limited by three technical difficulties. First, the flow vectors were not determined and the dynamics of the vortices behind the cylinders could not be captured. To make the above discussions on the gap flow clearer, the vorticity dynamics will be explored using particle image velocimetry in a follow-up study. Second, the earlier discussion on the fluid-dynamic force had to be qualitative based only on the indirect information; measurements of the forces acting on the cylinder as well as the displacements may provide data that supports the bi-directional excitation mechanism discussed by this study. The third problem is disturbances of the water surface in the channel. When the vibratory frequencies agreed with the natural frequency of the water in the channel, transverse standing waves were generated in the observation section of the channel. The resulting deformation of the water surface should be suppressed as it might affect the observed magnitudes of the vibrations.

Summary and conclusion

This study experimentally examined the fluid–structure interaction mechanics underlying the vibratory response of a circular cylinder subjected to fluid flows and placed in the proximity of twin fixed circular cylinders.

In this experiment, the two cylinders were fixed upstream of the movable cylinder. The vibrations of the movable one were measured for different inline and transverse spacings over a range of reduced velocities (4.0–13.0).

When the inline spacings were small, two amplitude peaks were generally observed: one around a reduced velocity of 5.0, the other around reduced velocities over 8.0. The first peak was understood as a growth of vibration forced by Karman vortex streets emerging from the upstream fixed cylinder. The second peak resulted from interferences of the wake behind the upstream cylinder with the downstream moving cylinder. As the inline spacing lengthened, these two peaks disappeared and were replaced by a single amplitude peak around a reduced velocity of 8.0. This peak corresponded to VIVs produced through the self-excitation process. This result explains why the response curves in the cases with long inline spacings resembled the response curve of an isolated circular cylinder.