An Exact Solution for Whirling Speeds and Mode Shapes of Multi-span Rotating Shafts with Each Span Carrying a Number of Rigid Disks

Abstract

Background

In the existing literature, the dynamic characteristics of the spinning shaft-disk systems are usually evaluated using the transfer matrix method (TMM), the finite element method (FEM) or the differential quadrature method (DQM).

Purpose

The results of the above-mentioned TMM, FEM or DQM are the approximate solutions and the exact solution concerned is rare. For this reason, this paper aims at presenting an analytical method to yield the exact whirling speeds and mode shapes of a “multi-span” continuous shaft mounted by arbitrary rigid disks.

Method

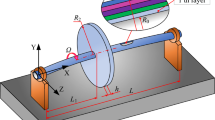
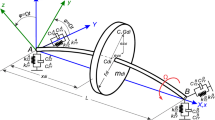
In theory, the whirling motion of a rotating shaft-disk system is three-dimensional (3-D), however, if the transverse displacement in the vertical principal xy-plane and that in the horizontal principal xz-plane for the cross-section of the rotating shaft located at axial coordinate x are combined using a complex number, and the effects of each rigid disk i mounted on the shaft are replaced by a lumped mass together with a frequency-dependent “equivalent” mass moment of inertia, then the whirling motion of a rotating shaft-disk system will be similar to the two-dimensional (2-D) transverse free vibration of a stationary beam. After the foregoing manipulations, the techniques for the free vibrations of a stationary beam carrying various concentrated elements (including the intermediate supports) will be available for the whirling motions of a rotating “multi-span” shaft mounted by arbitrary rigid disks.

Results and Conclusions

To confirm the reliability of presented theory and developed computer programs, most results obtained from the presented method are compared with the available literature or the results of FEM and good agreements are achieved. The presented method has the following merits: (a) The complicated 3-D whirling motions of a rotating shaft can be solved with the approaches for the simple 2-D free vibrations of a stationary beam, so that much computer time can be saved. (b) The damping matrix is eliminated so that the computer programming is easier. (c) The obtained results are the “exact” solutions and may be the benchmark for evaluating the accuracy of the other approximate methods.

Appendix: Non-zero coefficients for the matrix \([H]_{{\overline{n} \times \overline{n}}}\) appearing in Eq. (42)

If the two ends of the shafting system shown in Fig. 1 is supported by ball bearings [with the pinned–pinned (P-P) BC’s], then the non-zero coefficients for the matrix $[H]_{{\overline{n} \times \overline{n}}}$ appearing in Eq. (42) may be obtained from Eqs. (36a, b), (24a, b) and (25a, b), (30a, b) and (31a, b) or Eq. (32), and (37a, b), respectively, as follows:

For the Left Pinned End at Node 0

From Eq. (36a, b) one obtains,

$$ H_{1,1} = 0,\,H_{1,2} = 1,\,H_{1,3} = 0,\,H_{1,4} = 1, $$

(45)

$$ H_{2,1} = 0,\,H_{2,2} = 1,\,H_{2,3} = 0,\,H_{2,4} = - 1. $$

(46)

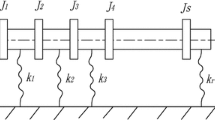
For the Intermediate Node i (with Total Number of Shaft Segments $n \ge 2$ )

If the intermediate node i is occupied by a disk, then from Eqs. (24a, b) and (25a, b) one obtains,

$$ \begin{aligned} H_{4i - 1,4i - 3} & = \sinh \beta_{i} x_{i} ,\;H_{4i - 1,4i - 2} = \cosh \beta_{i} x_{i} ,\;H_{4i - 1,4i - 1} = \sin \beta_{i} x_{i} ,\;H_{4i - 1,4i} = \cos \beta_{i} x_{i} , \\ H_{4i - 1,4i + 1} & = - \sinh \beta_{i + 1} x_{i} ,\;H_{4i - 1,4i + 2} = - \cosh \beta_{i + 1} x_{i} ,\;H_{4i - 1,4i + 3} = - \sin \beta_{i + 1} x_{i} , \\ H_{4i - 1,4i + 4} & = - \cos \beta_{i + 1} x_{i} , \\ \end{aligned} $$

(47)

$$ \begin{aligned} H_{4i,4i - 3} & = \beta_{i} \cosh \beta_{i} x_{i} ,\;H_{4i,4i - 2} = \beta_{i} \sinh \beta_{i} x_{i} ,\;H_{4i,4i - 1} = \beta_{i} \cos \beta_{i} x_{i} ,\;H_{4i,4i} = - \beta_{i} \sin \beta_{i} x_{i} , \\ H_{4i,4i + 1} & = - \beta_{i + 1} \cosh \beta_{i + 1} x_{i} ,\;H_{4i,4i + 2} = - \beta_{i + 1} \sinh \beta_{i + 1} x_{i} ,\;H_{4i,4i + 3} = - \beta_{i + 1} \cos \beta_{i + 1} x_{i} , \\ H_{4i,4i + 4} & = \beta_{i + 1} \sin \beta_{i + 1} x_{i} , \\ \end{aligned} $$

(48)

$$ \begin{aligned} H_{4i + 1,4i - 3} & = \cosh \beta {}_{i}x{}_{i} + Q_{i} \sinh \beta {}_{i}x_{i} ,\;H_{4i + 1,4i - 2} = \sinh \beta {}_{i}x{}_{i} + Q_{i} \cosh \beta {}_{i}x_{i} , \\ H_{4i + 1,4i - 1} & = - (\cos \beta {}_{i}x{}_{i} - Q_{i} \sin \beta {}_{i}x_{i} ),\;H_{4i + 1,4i} = \sin \beta {}_{i}x{}_{i} + Q_{i} \cos \beta {}_{i}x_{i} , \\ H_{4i + 1,4i + 1} & = - P{}_{i + 1}\cosh \beta {}_{i + 1}x{}_{i},\;H_{4i + 1,4i + 2} = - P{}_{i + 1}\sinh \beta_{i + 1} x_{i} , \\ H_{4i + 1,4i + 3} & = P{}_{i + 1}\cos \beta_{i + 1} x_{i} ,\;H_{4i + 1,4i + 4} = - P{}_{i + 1}\sin \beta_{i + 1} x_{i} , \\ \end{aligned} $$

(49)

$$ \begin{aligned} H_{4i + 2,4i - 3} & = \sinh \beta_{i} x{}_{i} - S_{i} \cosh \beta_{i} x_{i} ,\;H_{4i + 2,4i - 2} = \cosh \beta_{i} x{}_{i} - S_{i} \sinh \beta_{i} x_{i} , \\ H_{4i + 2,4i - 1} & = - (\sin \beta_{i} x{}_{i} + S_{i} \cos \beta_{i} x_{i} ),\;H_{4i + 2,4i} = - (\cos \beta_{i} x{}_{i} - S_{i} \sin \beta_{i} x_{i} ), \\ H_{4i + 2,4i + 1} & = - R{}_{i + 1}\sinh \beta_{i + 1} x_{i} ,\;H_{4i + 2,4i + 2} = - R_{i + 1} \cosh \beta_{i + 1} x_{i} , \\ H_{4i + 2,4i + 3} & = R_{i + 1} \sin \beta_{i + 1} x_{i} ,\;H_{4i + 2,4i + 4} = R_{i + 1} \cos \beta_{i + 1} x_{i} . \\ \end{aligned} $$

(50)

However, if the intermediate node i is occupied by a rigid pinned support, then from Eqs. (30a, b) and (31a, b) or Eq. (32) one obtains

$$ \begin{aligned} H_{4i - 1,4i - 3} & = sh\theta_{i} .\;H_{4i - 1,4i - 2} = ch\theta_{i} ,\;H_{4i - 1,4i - 1} = s\theta_{i} ,\;H_{4i - 1,4i} = c\theta_{i} , \\ H_{4i - 1,4i + 1} & = H_{4i - 1,4i + 2} = H_{4i - 1,4i + 3} = H_{4i - 1,4i + 4} = 0, \\ \end{aligned} $$

(51)

$$ \begin{aligned} H_{4i,4i - 3} & = H_{4i,4i - 2} = H_{4i,4i - 1} = H_{4i,4i} = 0, \\ H_{4i,4i + 1} & = sh\theta_{i} ,\;H_{4i,4i + 2} = ch\theta_{i} ,\;H_{4i,4i + 3} = s\theta_{i} ,\;H_{4i,4i + 4} = c\theta_{i} , \\ \end{aligned} $$

(52)

$$ \begin{aligned} H_{4i + 1,4i - 3} & = ch\theta {}_{i},\;H_{4i + 1,4i - 2} = sh\theta {}_{i},\;H_{4i + 1,4i - 1} = c\theta {}_{i},\;H_{4i + 1,4i} = - s\theta {}_{i}, \\ H_{4i + 1,4i + 1} & = - ch\theta {}_{i},\;H_{4i + 1,4i + 2} = - sh\theta {}_{i},\;H_{4i + 1,4i + 3} = - c\theta {}_{i},\;H_{4i + 1,4i + 4} = s\theta {}_{i}. \\ \end{aligned} $$

(53)

$$ \begin{aligned} H_{4i + 2,4i - 3} & = sh\theta {}_{i},\,H_{4i + 2,4i - 2} = ch\theta {}_{i},\,H_{4i + 2,4i - 1} = - s\theta {}_{i},\,H_{4i + 2,4i} = - c\theta {}_{i}, \\ H_{4i + 2,4i + 1} & = - sh\theta {}_{i},\,H_{4i + 2,4i + 2} = - ch\theta {}_{i},\,H_{4i + 2,4i + 3} = s\theta {}_{i},\,H_{4i + 2,4i + 4} = c\theta {}_{i}. \\ \end{aligned} $$

(54)

For the Right Pinned End at Node n

From Eqs. (37a, b) one obtains

$$ \begin{aligned} H_{4n - 1,4n - 3} & = \sinh \beta_{n} L,\,H_{4n - 1,4n - 2} = \cosh \beta_{n} L, \\ H_{4n - 1,4n - 1} & = \sin \beta_{n} L,\,H_{4n - 1,4n} = \cos \beta_{n} L, \\ \end{aligned} $$

(55)

$$ \begin{aligned} H_{4n,4n - 3} & = \sinh \beta_{n} L,\,H_{4n,4n - 2} = \cosh \beta_{n} L, \\ H_{4n,4n - 1} & = - \sin \beta_{n} L,\,H_{4n,4n} = - \cos \beta_{n} L. \\ \end{aligned} $$

(56)