Introduction

Studies on the flow-induced vibration (FIV) of a bluff body are conducted in three stages. The first is the suppression of the FIV, which has a relatively long research history and has been addressed in many previous studies (e.g., [1,2,3,4]). It is motivated by the significance of designing long and slender structures installed against the wind. The second involves the evaluation of FIV occurrences in offshore structures such as floating platforms and riser pipes. The third one, the enhancement of FIV, has drawn attention because it deals with the conversion of energy from fluid flow to the vibratory motion of a body driving electrical energy generators (e.g., [5,6,7,8,9]).

To date, several methods for amplifying FIV have been proposed. For example, positioning two cylinders in proximity was proved to increase the energy conversion efficiency by widening the flow-speed range of the water within which the FIV prominently occurred, resulting from the hydrodynamic interference of vortices generated behind one cylinder with the other one [9, 10]. A rotating arm with two cylinders at each of its extremities attained more significant vibration than a single cylinder [11] because the cylinder vibration in this arrangement was excited by both drag and lift forces acting on them.

Cylinders experiencing FIV are typically mounted using one or more springs to exert elastic forces and restore the cylinders to the position of rest. In many experiments and theoretical models on the FIV of a cylinder (e.g., [12, 13]), the line of action of the elastic force is assumed to be parallel to the vibratory motion trajectory, allowing the consideration of the spring as a linear spring, which exerts restoring forces in proportion to the displacement from the position of rest. In contrast, the linear spring assumption is no longer valid if the line of action of the elastic force deviates from the vibratory motion trajectory. The nonlinear effect emerges in the restoring force and induces a body-motion response that is peculiar to nonlinear vibration (geometric nonlinearity [14]), that is, even when the frequency of a body’s vibration in a nonlinear supporting system differs significantly from the natural frequency, the body can exhibit prominent responses. This contrasts the linear vibration, in which the response of the body is only significant for frequencies that are close to the natural frequency. An analytical study [15] was conducted to evaluate the stiffness of a mooring system, which is expected to involve nonlinear restoring forces and moments.

This study focuses on the nonlinearity of a spring supporting a moving circular cylinder. The mechanical essence of FIV lies in the interaction between viscous fluid mechanics and body motion, resulting in a nonlinear motion response, that is, the synchronization (lock-in) of frequency with natural frequency for a specific flow-speed range [12, 16, 17]. Accordingly, this study deals with two types of nonlinearity, i.e., nonlinearities originating from the geometry of the spring, and from the fluid–structure interaction. The reinforcement of the body-motion response obtained by combining these nonlinearities may yield a potential method for increasing the power harnessed by the fluid flow. This hypothesis will be verified by developing an experimental setup involving cylinders subjected to fluid flow and a spring arrangement with geometric nonlinearity, and examining the responses of the cylinders. In addition, this study constructed a theoretical model to express the nonlinear restoring force and interpret the measured vibrations.

Experimental Method

Experimental Setup

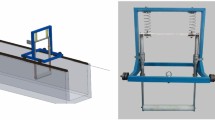
A circular acrylic cylinder was vertically deployed for use in flowing water (Fig. 1a). The submerged length of the cylinder was 0.134 m, and its weight was 0.106 kg. The cylinder was connected at its top end by an arm (cylinder connector), which rotated about a vertical bar (main shaft, point O), through which the rotation was transmitted to the rotation of another arm (spring connector). With the cylinder connector and main shaft, the cylinder was movable rotationally about the main shaft (Fig. 1b).

Fig. 1
figure 1

a Schematic of the experimental setup on the circulating water channel. Location of points O, L, MA, and MB are defined in the text and Table 1. b Top view of the experimental setup. c Photograph of the water circulating channel and deployed circular cylinder

Full size image

The principal parameters and geometric points of the experimental setup are listed in Table 1. The rotation of the spring connector was supported elastically by springs A and B (Figs. 1b, 2). One ends of the springs were connected to the spring connecter at point L, which was defined as the spring connection point in the resting state. The opposite ends of the springs were connected to a fixed plate at points \(M_{{\text{A}}}\) and \(M_{{\text{B}}}\). The motion of the cylinder was elastically supported by the motion transmission system comprising the cylinder connector, main shaft, and spring connector.

Table 1 Principal parameters and geometric points of the experimental setup
Full size table
Fig. 2
figure 2

Schematic of spring arrangement: a spring connector in the resting state (\(\lambda = 0^\circ\)). Angle \(\theta\) is defined as \(\angle {\text{OLM}}_{{\text{B}}}\), which equals \(\angle {\text{OLM}}_{{\text{A}}}\) in the resting state; b the spring connector is rotated at angle \(\lambda\); c photograph of the main shaft, springs A and B, and spring connector

Full size image

In the dynamic state, the point \(L\) in the resting state moved to a different point \(L^{\prime}\) about the main shaft (Fig. 2). The trajectory from \(L\) to \(L^{\prime}\) was part of the circumference of a circle with center O and a radius of OL (the distance between points O and L); the velocity vector was always perpendicular to the longitudinal axis of the spring connecter.

By changing the positions of points \(M_{{\text{A}}}\) and \(M_{{\text{B}}}\), the longitudinal axes of springs A and B were oriented in a direction different from the tangential vector on the \(LL^{\prime}\) trajectory.

For all cases that exhibited measurable vibrations, the lengths of the springs at the position of rest (\({\text{LM}}_{{\text{A}}}\) and \({\text{LM}}_{{\text{B}}}\)) and in the dynamic state were always longer than their equilibrium length \({\text{LM}}_{0}\) (pre-tension had been applied in the resting state).

The experimental setup was placed on a circulating water channel (Fig. 1a, c) with a length, width, and depth of 0.94 m, 0.465 m, and 0.22 m, respectively. The water flowed in the channel at a constant speed driven by impeller rotation, whose revolutions per minute were regulated by an electric controller.

Measurement

The displacements of the moving cylinder were recorded by a high-speed camera (Memrecam MX-5, Nac Image Technology Inc.) with a pixel resolution of \(1920 \times 1080\). The camera head (Fig. 1) was placed below the water channel floor, and optically captured the bottom surface of the cylinder through a transparent window in the water channel floor. A circular marker with two quadrant parts painted black and the remaining two painted white, was laminated using a transparent sheet and pasted onto the bottom surface of the cylinder to accurately trace the motion of the cylinder. The displacement data were consecutively generated by tracking the marker in the images taken by the camera, and recorded through a data logger (NR-500, Keyence Corp.) at a frame rate of 0.01 s. To determine the prevailing vibration motion amplitude and frequency, temporal series data of the displacements were processed by a fast Fourier transform (FFT) program.

The effect of the spring arrangement on the FIV response was evaluated by obtaining measurements using two varying quantities: the angle, \(\angle {\text{OLM}}\), denoted by \(\theta\) (Fig. 2), where M means either MA or MB hereinafter, and the length \({\text{OL}}\). At \(\theta = 90^\circ\), the line segment LM was parallel to the tangential direction of the trajectory of point \(L^{\prime}\) when \(L^{\prime}\) passed through point \(L\), minimizing the geometric nonlinear effect.

In the present experiment, the length OL was set as 20, 40, and 80 mm. The natural frequencies of the cylinder supported by the springs were measured for each measurement condition with length OL and angle \(\theta\), and used to specify the dimensionless speed of flow, which is referred to as reduced velocity \(V_{{\text{r}}}\) and defined as:

$$V_{{\text{r}}} = \frac{V}{{f_{{\text{n}}} d}},$$
(1)

where \(f_{{\text{n}}}\) is the natural frequency, V the flow speed, and d the diameter of the cylinder. The natural frequencies were obtained by determining the prevailing frequency of the decaying motions of the cylinder under the no-flow condition (free damping test). The damping ratios were calculated by determining logarithmic decrements from the decaying displacement time series.

Theoretical Model

This section presents a theoretical model for describing the vibratory mechanics in the experimental apparatus. In this model, an equation of the spring connector’s rotation motion is derived based on the geometry depicted in Fig. 2.

Let the elastic forces of springs A and B be denoted by \(F_{{\text{A}}}\) and \(F_{{\text{B}}}\), respectively. These two springs have the same equilibrium lengths \({\text{LM}}_{0}\) and rigidity constants \(k\).

At an instant in the dynamic state, the spring connector comprised a rotation angle \(\lambda\) (positive counter-clockwise), and the spring-ends, which had been positioned at point L in the resting state, were positioned at point \(L^{\prime}\) (Fig. 2b). The angles, \(\angle {\text{L}}^{\prime}{\text{OM}}_{{\text{A}}}\), \(\angle {\text{LOM}}_{{\text{A}}}\), \(\angle {\text{L}}^{\prime}{\text{OM}}_{{\text{B}}}\), \(\angle {\text{LOM}}_{{\text{B}}}\), and \(\lambda\), are related as follows:

$$\angle {\text{L}}^{\prime}{\text{OM}}_{{\text{A}}} = \angle {\text{LOM}}_{{\text{A}}} - \lambda ,$$
(2)
$$\angle {\text{L}}^{\prime}{\text{OM}}_{{\text{B}}} = \angle {\text{LOM}}_{{\text{B}}} + \lambda .$$
(3)

Using the law of cosines for triangles OLMA and \({\text{OL}}^{\prime}{\text{M}}_{{\text{A}}}\), the line segment length \({\text{L}}^{\prime}{\text{M}}_{{\text{A}}}\) is expressed as:

$${\text{L}}^{\prime}{\text{M}}_{{\text{A}}} = \left[ {2{\text{OL}}^{2} + {\text{LM}}_{{\text{A}}}^{2} - 2{\text{OL}} \cdot {\text{LM}}_{{\text{A}}} \cos \theta - 2{\text{OL}}\left\{ {\left( {{\text{OL}} - {\text{LM}}_{{\text{A}}} \cos \theta } \right)\cos \lambda + {\text{LM}}_{{\text{A}}} \sin \theta \sin \lambda } \right\}} \right]^{\frac{1}{2}} .$$
(4)

The elastic force exerted by spring A is expressed as:

$$F_{{\text{A}}} = k\left( {{\text{L}}^{\prime}{\text{M}}_{{\text{A}}} - {\text{LM}}_{{0}} } \right).$$
(5)

Using Eqs. (4) and (5), the elastic force of spring A can be expressed in terms of OL, LMA, \(\lambda\), and \(\theta\).

The elastic force exerted by spring B is written as:

$$F_{{\text{B}}} = k\left( {{\text{L}}^{\prime}{\text{M}}_{{\text{B}}} - {\text{LM}}_{{0}} } \right),$$
(6)
$${\text{L}}^{\prime}{\text{M}}_{B} = \left[ {2{\text{OL}}^{2} + {\text{LM}}_{B}^{2} - 2{\text{OL}} \cdot {\text{LM}}_{B} \cos \theta - 2{\text{OL}}\left\{ {\left( {{\text{OL}} - {\text{LM}}_{B} \cos \theta } \right)\cos \lambda - {\text{LM}}_{B} \sin \theta \sin \lambda } \right\}} \right]^{\frac{1}{2}} .$$
(7)

The elastic forces \(F_{{\text{A}}}\) and \(F_{{\text{B}}}\) have directional components, \(F_{{{\text{A}}\lambda }}\) and \(F_{{{\text{B}}\lambda }}\), respectively, in alignment with the tangential of the trajectory of point \(L^{\prime}\). These are expressed as:

$$F_{\lambda } = F_{{{\text{A}}\lambda }} + F_{{{\text{B}}\lambda }} ,$$
(8)
$$F_{{{\text{A}}\lambda }} = k\left( {{\text{L}}^{\prime}{\text{M}}_{{\text{A}}} - {\text{LM}}_{0} } \right)\sin\angle {\text{OL}}^{\prime}{\text{M}}_{{\text{A}}}$$
(9)
$$F_{{{\text{B}}\lambda }} = - k\left( {{\text{L}}^{\prime}{\text{M}}_{{\text{B}}} - {\text{LM}}_{0} } \right)\sin\angle {\text{OL}}^{\prime}{\text{M}}_{{\text{B}}} ,$$
(10)

where applying the law of cosines to triangles \({\text{OL}}^{\prime}{\text{M}}_{{\text{A}}}\) and \({\text{OL}}^{\prime}{\text{M}}_{{\text{B}}}\), \({\text{sin}}\angle {\text{OL}}^{\prime}{\text{M}}_{{\text{A}}}\), and \({\text{sin}}\angle {\text{OL}}^{\prime}{\text{M}}_{{\text{B}}}\) are related to the line segment lengths as:

$$\sin \angle {\text{OL}}^{\prime } {\text{M}}_{{\text{A}}} = \sqrt {1 - \left( {\frac{{{\text{OL}}^{2} + {\text{L}}^{\prime } {\text{M}}_{{\text{A}}}^{2} - {\text{OM}}_{{\text{A}}}^{2} }}{{2{\text{OL}} \times {\text{L}}^{\prime } {\text{M}}_{{\text{A}}} }}} \right)^{2} }$$
(11)
$$\sin\angle {\text{OL}}^{\prime}{\text{M}}_{{\text{B}}} = \sqrt {1 - \left( {\frac{{{\text{OL}}^{2} + {\text{L}}^{\prime}{\text{M}}_{{\text{B}}}^{2} - {\text{OM}}_{{\text{B}}}^{2} }}{{2{\text{OL}} \times {\text{L}}^{\prime}{\text{M}}_{{\text{B}}} }}} \right)^{2} } ,$$
(12)

\(F_{\lambda }\) can be computed by applying Eqs. (4), (7), (9), (10), (11), and (12).

In the present experiment, the maximal absolute values of \(\lambda\) were estimated as smaller than 0.29 rad, allowing the assumption that the terms with higher orders of \(\lambda\) than the second order were negligible. Expanding the functions of \(\lambda\) in Eqs. (9) and (10), and retaining the terms with the first order of \(\lambda\), the tangential component of the restoring force is reduced as follows:

$$F_{\lambda } \simeq - 2k\left\{ {\left( {{\text{OL}} - {\text{LM}}\cos\theta } \right) - \frac{{{\text{LM}}_{0} }}{{{\text{LM}}}}\left( {{\text{OL}}\cos^{2} \theta - {\text{LM}}\cos\theta } \right)} \right\}\lambda ,$$
(13)

where \({\text{LM}} = {\text{LM}}_{{\text{A}}} = {\text{LM}}_{{\text{B}}}\).

The equation of rotation motion of the spring connector has a linearized form as follows:

$$I\frac{{{\text{d}}^{2} \lambda }}{{{\text{d}}t^{2} }} = - 2k \cdot {\text{OL}} \cdot \left\{ {\left( {{\text{OL}} - {\text{LM}}\cos\theta } \right) - \frac{{{\text{LM}}_{0} }}{{{\text{LM}}}}\left( {{\text{OL}}\cos^{2} \theta - {\text{LM}}\cos\theta } \right)} \right\}\lambda ,$$
(14)

where t denotes time, and I denotes the moment of inertia of the mechanical system. The natural frequency of the rotational system can be calculated by applying Eq. (14).

To simplify the mathematical expression of the equation of motion, the quantities in the equations are transformed into their dimensionless forms. Defining dimensionless time \(t^{*} \equiv \sqrt {\frac{{k \times {\text{LM}}_{0} }}{I}} t\), and segment length ratios \(\beta \equiv \frac{{{\text{OL}}}}{{{\text{LM}}_{0} }}\) and \(\gamma \equiv \frac{{{\text{LM}}}}{{{\text{LM}}_{0} }}\), the above equation of motion is recast into the following dimensionless equation of motion:

$$\frac{{{\text{d}}^{2} \lambda }}{{{\text{d}}t^{{*2}} }} = - 2\beta ^{2} \left\{ {1 - \frac{1}{\gamma }\cos ^{2} \theta + \frac{1}{\beta }(1 - \gamma )\cos \theta } \right\}\lambda .$$
(15)

Equation (15) expresses that the coefficient of the elastic moment must meet the following inequality to ensure that it serves as the restoring moment:

$$2\beta ^{2} \left\{ {1 - \frac{1}{\gamma }\cos ^{2} \theta + \frac{1}{\beta }(1 - \gamma )\cos \theta } \right\} \ge 0,$$
(16)

which bounds the range of \(\cos\theta\) as:

$$\frac{1}{2}\left( {\frac{\gamma }{\beta }(1 - \gamma ) - \sqrt {\frac{{\gamma^{2} }}{{\beta^{2} }}(1 - \gamma )^{2} + 4\gamma } } \right) < \cos\theta < \frac{1}{2}\left( {\frac{\gamma }{\beta }(1 - \gamma ) + \sqrt {\frac{{\gamma^{2} }}{{\beta^{2} }}(1 - \gamma )^{2} + 4\gamma } } \right).$$
(17)

For the values of \(\beta\) and \(\gamma\) in this experiment, the inequality on the left in Eq. (17) was always satisfied, whereas the one on the right determined the minimum of \(\theta\).

The dimensionless forms of \(F_{\lambda }\), \(F_{{{\text{A}}\lambda }}\), and \(F_{{{\text{B}}\lambda }}\) are defined, respectively, as:

$$F_{\lambda }^{*} = F_{{{\text{A}}\lambda }}^{*} + F_{{{\text{B}}\lambda }}^{*}$$
(18)
$$F_{{{\text{A}}\lambda }}^{*} \equiv \frac{{F_{{{\text{A}}\lambda }} }}{{k\,{\text{LM}}_{0} }} = \left( {1 - \frac{1}{{\sqrt {\gamma^{2} - 2\beta \gamma \sin\theta } }}} \right)\sqrt {\gamma^{2} \sin^{2} \theta - 2\gamma \sin\theta (\beta - \gamma \cos\theta )\lambda }$$
(19)
$$F_{{{\text{B}}\lambda }}^{*} \equiv \frac{{F_{{{\text{B}}\lambda }} }}{{k\,{\text{LM}}_{0} }} = \left( {1 - \frac{1}{{\sqrt {\gamma^{2} + 2\beta \gamma \sin\theta } }}} \right)\sqrt {\gamma^{2} \sin^{2} \theta + 2\gamma \sin\theta (\beta - \gamma \cos\theta )\lambda } .$$
(20)

The first-order approximation of \(F_{\lambda }^{*}\) is written as:

$$F_{\lambda }^{*} \simeq - 2\beta \left\{ {1 - \frac{1}{\gamma }\cos^{2} \theta + \frac{1}{\beta }(1 - \gamma )\cos\theta } \right\}\lambda .$$
(21)

Results and Discussion

Natural Frequency and Damping Ratio

The natural frequencies were measured by conducting free damping tests for each angle \(\theta\) and length OL. They had almost increasing trends against \(\theta\) within the tested range (\(160^\circ \le \theta \le 1120^\circ\)) (circle plots in Fig. 3) for all the three OL lengths in this experiment. The natural frequencies calculated by the linearized theoretical model (solid lines in Fig. 3) also increased within the same \(\theta\) range, and were consistent with the measured ones.

Fig. 3
figure 3

Relationship between natural frequency and \(\theta\): a OL = 20 mm; b OL = 40 mm; and c OL = 80 mm. Closed circles represents experimental results, and solid lines represent theoretical results

Full size image

The mass-damping parameters [18] were estimated using the natural frequencies and damping ratios (Table 2). In this estimation, the moment of inertia of the experimental setup was divided by that of the fluid displaced by the cylinder (inertia ratio), the result was then multiplied by the damping ratio to determine the mass-damping parameter. The moment of inertia of the displaced fluid was the mass of the displaced fluid multiplied by the squared radius of gyration, where the radius of gyration was assumed to be equivalent to the distance from the centerline of the cylinder to the center of rotation (point O). The mass-damping parameters reduced to 28.4% of the values listed in Table 2 when the ratio of the cylinder’s mass to the displaced water mass (mass ratio [18]) was used. Further, the mass-damping parameters listed in Table 2 multiplied by 0.515 are employed when only the submerged portion of the cylinder is considered.

Table 2 Damping ratios and natural frequencies
Full size table

The theoretical minima of \(\theta\) expressed by Eq. (17) corresponds to the intercepts of the solid lines (Fig. 3) with the \(\theta\)-axes (horizontal axes). Although the model accurately represented the actual natural frequencies in the experiment, the experimental minima of \(\theta\) were greater than the theoretical ones. In the free damping tests, some values of \(\theta\) that were greater than the theoretical minima generated few vibratory responses (Table 2), making it difficult to detect the natural frequencies and damping ratios. These weaker responses are caused by fluid drag and mechanical friction involved in the experimental setup.

The mass-damping parameters ranged from 0.159 to 1.011, which were included in the low mass-damping regime following the regime definition made by [18].

Response Amplitudes and Frequencies

The magnitudes of the vibratory responses changed sensitively in response to the reduced velocity. In Figs. 4, 5 and 6, temporal series of cylinder displacements are shown as examples of remarkable responses. At \(\left( {{\text{OL}}, \theta , V_{r} } \right) = \left( 20\,{\text{mm}},120^\circ,9.0 \right)\) (Fig. 4), the displacement varied periodically and its frequency spectra had a single distinct peak at a frequency that was higher than the natural frequency by 20%. At \(\left( {{\text{OL}}, \theta , V_{{\text{r}}} } \right) = \left( 140\,{\text{mm}},120^\circ,8.0 \right)\) (Fig. 5) and at \(\left( {{\text{OL}}, \theta ,V_{{\text{r}}} } \right) = \left( 180\,{\text{mm}},70^\circ,8.5 \right)\) (Fig. 6), the periodic temporal variations occurred in a similar manner to the preceding case (Fig. 4), and frequency spectral peaks emerged at frequencies higher than the natural frequencies by 2%.

Fig. 4
figure 4

Displacement of cylinder for OL = 20 mm and \(\theta = 120^\circ\): a time series and b frequency spectrum

Full size image
Fig. 5
figure 5

Displacement of cylinder for OL = 40 mm and \(\theta =120^\circ\): a time series and b frequency spectrum

Full size image
Fig. 6
figure 6

Displacement of cylinder for OL = 80 mm and \(\theta = 70^\circ\): a time series and b frequency spectrum

Full size image

To observe the dependency of the responses on the reduced velocity, the prevailing frequencies and amplitudes determined by the FFT were plotted against the reduced velocity. The frequency exhibited a gradually increasing trend for OL = 20 mm and \(\theta = 100^\circ\), (Fig. 7a). This was also the case for \(\theta = 110^\circ\) and \(\theta = 120^\circ\). The displacement amplitudes for \(\theta = 100^\circ\) (Fig. 7b) were significantly large when the reduced velocity was greater than 8.0, but approximately zero otherwise. For \(\theta = 110^\circ\) and \(\theta = 120^\circ\), large amplitudes occurred if the reduced velocity exceeded 6.5 and 7.0, respectively.

Fig. 7
figure 7

Response curves against reduced velocity for OL = 20 mm: a frequency for \(\theta = 100^\circ\), \(110^\circ\), and \(120^\circ\). Dashed lines correspond to a Strouhal number of 0.2; b displacement amplitude (normalized by the cylinder diameter). c Velocity amplitude (normalized by the multiplication of the cylinder diameter and natural frequency)

Full size image

In the case of OL = 20 mm, measurements could not be made for the smaller \(\theta\) owing to the negligible restoring moments noted earlier.

For OL = 40 mm, the frequency response curves were quite similar for the different \(\theta\) s (Fig. 8a, b). These gradually increased as the reduced velocity increased, in the same manner as the frequency response curve for OL = 20 mm (Fig. 7a). The displacement amplitudes at \(\theta = 80^\circ\) were significantly large when the reduced velocity was greater than 7.5, whereas few responses were observed otherwise (Fig. 8c). In contrast, the displacement for \(\theta = 90^\circ\) exhibited a gradually rising slope at approximately \(V_{{\text{r}}} = 6.0\). Similar rising slopes also occurred for \(\theta = 100^\circ\) to \(120^\circ\) (Fig. 8d).

Fig. 8
figure 8

Response curves against reduced velocity for OL = 40 mm. Frequency for a \(\theta = 80^\circ\) and \(90^\circ\), and b for \(\theta = 90^\circ\), \(100^\circ\), \(110^\circ\), and \(120^\circ\). Dashed lines correspond to a Strouhal number of 0.2. Displacement amplitude (normalized by the cylinder diameter) for c \(\theta = 80^\circ\) and \(90^\circ\), and d for \(\theta = 90^\circ\), \(100^\circ\), \(110^\circ\), and \(120^\circ\). Velocity amplitude (normalized by the multiplication of the cylinder diameter and natural frequency) for e \(\theta = 80^\circ\) and \(90^\circ\), and f for \(\theta = 90^\circ\), \(100^\circ\), \(110^\circ\), and \(120^\circ\)

Full size image

The response curves of frequency (Fig. 9a, b) and displacement amplitude (Fig. 9c, d) for OL = 80 mm were generally similar to those in the case of OL = 40 mm (Fig. 8). Closer observation of the displacement amplitude revealed that the slopes of the response curve gradually rose at approximately \(V_{{\text{r}}} = 6.0\) for \(\theta\) smaller than \(90^\circ\) (Fig. 9c). The gradually rising slope became clearer for the larger \(\theta\) (Fig. 9d).

Fig. 9
figure 9

Response curves against reduced velocity for OL = 80 mm. Frequency for a \(\theta = 80^\circ\) and \(90^\circ\), and b for \(\theta = 90^\circ\), \(100^\circ\), \(110^\circ\), and \(120^\circ\). Dashed lines correspond to a Strouhal number of 0.2. Displacement amplitude (normalized by the cylinder diameter) for c \(\theta = 80^\circ\) and \(90^\circ\), and d for \(\theta = 90^\circ\), \(100^\circ\), \(110^\circ\), and \(120^\circ\). Velocity amplitude (normalized by the multiplication of the cylinder diameter and natural frequency) for e \(\theta = 80^\circ\) and \(90^\circ\), and f for \(\theta = 90^\circ\), \(100^\circ\), \(110^\circ\), and \(120^\circ\)

Full size image

Mechanical Interpretation

To theoretically understand the mechanics of the observed phenomena, the experimental results were interpreted from a vibratory mechanics perspective.

The frequency response curves for OL = 20, 40, and 80 mm in Figs. 7, 8, and 9 differed in their inclinations against the reduced velocity. Among the three curves, that of OL = 20 mm had the largest inclination and accordingly was the closest to the line of Strouhal number of 0.2. The positive inclination in the frequency response curve was reported in previous studies as one of the characteristics of frequency synchronization on the FIV of a circular cylinder (e.g., [2, 3, 10]). The displacement amplitude response curves had almost similar magnitudes; the maxima were approximately 0.6 for all the three OL lengths. It follows that the frequency synchronization, and consequently the FIV, certainly occurred in the cases with those OL lengths. Attention should be paid to the result that the extent to which a vibration frequency was entrained into the natural frequency varied against OL (the lever of restoring moment).

The steep rising slopes in the displacement amplitudes were different in configuration from the slopes in the initial branch, which are often observed in typical vortex-induced vibration (VIV) response curves (e.g., [3]). An initial branch includes small amplitudes at \(V_{{\text{r}}} = 4.0\) to \(5.0\), and gradually-growing amplitudes alongside an increase in \(V_{{\text{r}}}\). The appearance of the steeply rising slope, rather than the initial branch (Figs. 7b, 8c, 9c), suggests a more prominent nonlinear effect than the effect on the typical VIV [18]. In the cited paper, the VIV of circular cylinders with high and low mass-damping parameters provided quite different vibration amplitudes; the former exhibited initial and lower branches, whereas the latter exhibited initial, lower, and upper branches. The mass-damping parameters in the present study (Table 2) were considered as the lower ones. According to [18], the initial branch emerges irrespective of the magnitudes of the mass-damping parameters. Some of the experimental results of this study did not indicate an initial branch, thus it is necessary to discuss them from a novel perspective.

A plausible explanation for the expression of the steep rising slope is geometric nonlinearity, which is caused by the deviation of the spring’s longitudinal axis from the body’s trajectory. The present experiment imposed the deviation by setting angle \(\theta\) at the various values except \(90^\circ\). To quantify the magnitude of the geometric nonlinearity, the restoring forces were computed against varying \(\lambda\) using Eq. (18). The linearized restoring forces were also computed by Eq. (21). Representative examples of the computed restoring forces are plotted in Fig. 10. At OL = 80 mm and \(\theta = 120^\circ\), the two computations of the forces showed few differences. This was also the case for the shorter lever (OL = 20 and 40 mm), demonstrating that the vibratory system in this experiment was approximated mostly by the linear theory.

Fig. 10
figure 10

Relationships of restoring force at \(\theta = 120^\circ\) (Eq. 18, closed circles) and linearized restoring force (Eq. 21, solid lines) with the spring connector’s rotation angle \(\lambda\). a OL = 80 mm and b OL = 240 mm

Full size image

A longer lever of OL = 240 mm with \(\theta = 120^\circ\) achieves more distinct nonlinear effects (Fig. 10b). The absolute values of the nonlinear restoring forces were smaller than those of their linear counterparts, indicating that the inclined arrangement of springs A and B functioned as a soft spring, which is a type of nonlinear spring that might cause jumps in the responses. In the nonlinear vibration system governed by the Duffing equation, the soft and hard springs produce a bent response curve that permits the amplitude to have multiple values at a single-vibration frequency (e.g., [14, 16]). Lengthening the lever beyond 80 mm was difficult because of limitation in the structural design of the experimental setup. Improving this aspect enables evaluation of a longer lever.

It is worth exploring the FIV system addressed in this study as a method for harnessing natural energy from flowing fluid surrounding a vibrating body. Energy conversion efficiencies from the fluid to vibration, and from vibration to electricity typically depend on the magnitude of the vibration velocity [5], which can be calculated as the product of the displacement amplitude and frequency. The measured velocity amplitudes are shown in Figs. 7c, 8e, f, and 9e, f. Some conditions with the inclined springs (OL = 80 mm and \(\theta\) smaller than \(90^\circ\)) generated greater velocity amplitudes than the condition of \(\theta = 90^\circ\) (the linear spring condition). These results show that the synchronization of the vortex-shedding frequency and geometric nonlinearity produced by the inclined spring arrangement are combined and are consequently able to provide a greater velocity amplitude. Therefore, it is vital to further examine the applicability of the combined synchronization and geometric nonlinearity effect on energy harvesting using FIV, particularly the effect of longer levers.

In the present experimental setup, the radius of the cylinder’s rotation was kept constant (Table 1). Previous studies on FIV have reported the significance of two-dimensionality of the motion comprising the cross-flow and in-line components (e.g., [19, 20]). The rotational motion generally involves both components; therefore, a radius of the cylinder’s rotation that gives rise to a two-dimensional FIV to the maximum extent, may enable an increase in the available energy.

Summary and Concluding Remarks

The FIV of a circular cylinder was experimentally evaluated to reveal the influence of spring arrangements on the FIV. In the experimental setup, the vibratory motion of the circular cylinder was transmitted to the vibratory rotation of another body (spring connector), which was elastically supported by two springs. The two springs were arranged so that their longitudinal axes deviated from the motion trajectory of the spring connector. The experiment was performed for three moment lever lengths (distance from the rotation center to the action point of the elastic force).

A theoretical model was developed to represent the nonlinearity of the restoring force exerted by the inclined spring arrangement. The model was linearized to determine the theoretical natural frequencies. Comparisons between the experimental and theoretical natural frequencies showed reasonably good agreement.

The occurrence of a distinct vibration depended sensitively on the reduced velocity, similar to the typical VIVs of a circular cylinder, whereas the responses in the experiment differed from those observed for typical VIVs. In some conditions, zero responses occurred at reduced velocities smaller than the threshold, while maximum responses were observed at reduced velocities over the threshold. Other conditions yielded gradual increases in the displacement amplitude, similar to that of the initial branch frequently observed in VIVs. The disappearance of the initial branch suggested the influence of the inclined spring arrangement. This can be deduced from the nonlinear relationship of the restoring force and rotation angle determined by the theoretical model. Nonetheless, the very steep response curves observed in the experiment could not be quantitatively supported by the applied theory. Providing a solution to this issue necessitates further experiments employing longer moment levers than those employed in this study.