1 Introduction

Rocket engines typically utilize the propellants that can be categorized into solid, gel, and liquid types. Liquid rocket engines are well-known to have advantages over their solid or gelled counterparts: they have a higher specific impulse and increased throttling, restarting, and shutdown capabilities [1]. Therefore, given the present rocket market’s demand for reducing launch costs, high reusability, and high efficiency, liquid rocket engines emerge as the most suitable type [2].

Liquid rocket propellants include hypergolic propellants, which burn when the oxidizer and fuel come into contact, and non-hypergolic propellants, which require a separate ignition source. It is generally understood that non-hypergolic propellants are employed in 1st and 2nd stage engines [2]. The conventional impinging and swirl type injectors supply oxidizer and propellant to the combustion chamber for atomization and mixing. Various injectors, such as shear-type injectors, have also been applied. However, these injectors have a problem in that several must be used, and it is difficult to achieve uniform injection. Therefore, in engines under current development, pintle injectors are being utilized instead of multiple injectors, thereby reducing costs [2,3,4].

Research has been conducted recently on the spray characteristics of pintle injectors, focusing on their geometrical parameters. These various geometrical parameters, which include the blockage factor (BF) ratio, number of rows, and aspect ratio, are able to have an influence on the radial flow. The gap distance of the annular jet can affect the axial flow. Pintle injectors can be classified into two types, continuous pintles (slot type) and hole-type (slit type) pintles, depending on the spray type of the radial flow. Hole-type pintles can be designed in one or two rows [5,6,7,8,9], and Chang et al. confirmed that the heat load in the recirculation area is reduced in a discontinuous two-row pintle injector [5,6,7,8,9]. Meanwhile, the BF, which indicates how much the radial flow blocks the axial flow in the hole-type pintle injector, is known to be an important variable. Kim et al. confirmed that a pintle injector using hypergolic propellant has a short ignition delay time at a specific BF, and it is known that a value between 0.3 and 0.7 is generally used [10, 11]. Hwang et al. reported that the mixing ratio near the pintle tip changes according to the aspect ratio of each hole; accordingly, it can be confirmed that soot or melting of the pintle tip occurs [12]. Lee et al. analyzed the spray characteristics of the annular jet according to the change in its spray area [13]. They found that, an increase in the spray area under constant flow rate conditions resulted in decreased momentum of the spray, increased spray angle, and larger droplet size.

In general, it is known that flow passage plays an important role in the injector design process. Jung et al. analyzed the spray characteristics of sharp- and round-edged orifices. As the jet turbulence strength increased in the sharp-edged orifice, and the impact force also increased. It was also confirmed that the increased impact force attenuated the breakup length and changed the wavelength [14]. It is also known that the breakup characteristics vary depending on the shape of the flow passage (tangential entry, diameter of the swirl chamber, and open-closed-type swirl chamber) in the swirl injector. Chung conducted a study on the dynamic disruption characteristics in an open-closed-type swirl injector and confirmed that the closed-type injector showed stable characteristics against disturbance. He also confirmed that the amplitude decreased as the diameter of the swirl chamber increased, the length of the swirl chamber decreased, and the flow rate increased [15]. A separate flow passage was added to prevent the pintle injector from melting in the combustion environment when the internal flow passage of the pintle injector was applied [16, 17]. In addition, according to Lee et. al., the combustion efficiency of a pintle injector is maintained even if the insert nozzle is installed [18]. However, as in the swirl- and impinging-type injectors, research on the breakup characteristics according to the flow passage change is limited.

An experimental and numerical investigation was carried out on the spray characteristics of a double-slit-type pintle injector to understand the influence of the area ratio of the internal passage on the spray characteristics. First, to compare the spray characteristics, the flow conditions and total momentum ratio (TMR) were fixed, and the experiment was performed. The area ratio of the internal passage was tested for five cases based on the design of Kang [17]. For analysis on characteristics, an instantaneous image was acquired using the backlight imaging method, and the spray angle was determined from the image. The Sauter mean diameter (SMD) was also measured to analyze the actual spray characteristics. In addition, a numerical analysis was conducted to understand the internal flow characteristics and cooling performance.

2 Experimental Setup

2.1 Injector Design and Test Conditions

A schematic of the pintle injector is used to determine its injection characteristics according to the change in the area of the internal passage as shown in Figs. 1 and 2. To provide a uniform supply for the radial flow and annular jet flow manifold, the supply line was designed symmetrically, and an experiment was conducted. To prevent the pintle tip from melting during combustion, an insert structure was added at the top of the pintle, so that the fluid supplied into post could be separated in to two flow to form a forced flow. The fluid supplied through the pintle center flow passage and pintle outer flow passage is merged immediately before the pintle slit.

$$ {\text{BF }} = { }\frac{{n_{1} \cdot w_{1} { } + { }n_{2} \cdot w_{2} }}{{\pi \cdot D_{{\text{P}}} }}{ } \times { }100{ }\left[ {\text{\% }} \right] $$
(1)
$$ A_{{{\text{p.o}}}} = \pi \left( {\left( {D_{{{\text{p.o}}}} } \right)^{2} - \left( {D_{{{\text{p.w}}}} } \right)^{2} } \right),{ } A_{{{\text{p.c}}}} = \pi \left( {D_{{{\text{p.c}}}} } \right)^{2} $$
(2)
$$ {\text{TMR}}_{{{\text{target}}}} { } = { }\frac{{\dot{m}_{{\text{P}}} \cdot V_{{{\text{Radial}}}} }}{{\dot{m}_{{\text{A}}} \cdot V_{{{\text{Annular}}}} }} $$
(3)
$$ {\text{AR}}_{{{\text{up.slit }}}} \left( { = \frac{{{\text{Area}}_{{{\text{1st row.slit}}}} }}{{{\text{Area}}_{{{1 }{\text{.slit}}}} + {\text{Area}}_{{{2}{\text{.slit}}}} }}{ } \times { }100} \right) $$
(4)
$$ {\text{AR}}_{{{\text{ins}}}} \left( { = \frac{{{\text{Area}}_{{{\text{center.insert}}}} }}{{{\text{Area}}_{{{\text{center.insert}}}} + {\text{Area}}_{{{\text{outer.insert}}}} }} \times { }100} \right). $$
(5)
Fig. 1
figure 1

Schematics of a liquid–liquid hole-type pintle injector

Full size image
Fig. 2
figure 2

Design of the pintle post and internal flow passage

Full size image

Slit-type pintle injectors can be classified into single row and double row types, double row-type pintle injectors were selected in accordance with the recent trend in pintle injector in this study [16, 19]. The blockage factor (BF) was designed to be 0.58, which shows the best combustion performance, and the number of slits was determined to be 18 when considering manufacturability [16]. The skip distance (Ls/Dp) was designed to be fixed at 0.93. In addition, various studies have been conducted on the aspect ratio of pintle slits; however, the configuration that showed the best combustion performance was selected [12, 16, 17]. As specified in Table 1, three types of post configurations were investigated to understand the spray characteristics in accordance with the change in the upper and lower slit area ratio. Four inserts were designed to compare the internal and external flow characteristics. The central flow area (Ap.c) to the total flow area (Ap.c + Ap.o), which is expressed by Eq. 2, was area ratio of insert varied from 17 to 67% under constant total flow area. In addition, the pintle without the insert case was investigated to compare the effect of the insert. Meanwhile, the annular jet orifice is designed, so that TMRtarget expressed by Eq. 3 can be 1 when the mass flow rate of the radial and annular jet flow is 198 g/s and 90/s, respectively.

Table 1 Geometric parameters of pintle post and insert configuration [16, 19]
Full size table

2.2 Schematics of the Experimental Setup

To understand the spray characteristics, the backlight imaging method was used as shown in Fig. 3. The backlight imaging method obtains a general spray pattern by placing a pintle injector between a light source and a camera [20, 21]. Images were acquired using a high-resolution digital camera (Canon EOS 6D, 6240 × 4160 pixels) and lens (Canon EF 180 mm f/3.5L). Because it is difficult to capture the instantaneous spray shape using only a general digital camera, a stroboscope (Sugawara, MS-230A) was used as a light source. The stroboscope emitted light for 6 μs, and the experiment was performed by fixing the shutter speed of the stroboscope and camera to 20 Hz and 1/20 s, respectively, to synchronize with one another.

Fig. 3
figure 3

Schematics of the experimental setup for the backlight imaging technique

Full size image

To investigate atomization performance, droplet size was analyzed using a particle master system (LaVision). The particle master technique is a type of shadowgraphy method. Instead of a commonly used light source, a 527 nm wavelength laser irradiated with a point light source was used, passing through a diffuser with rhodamine-6G dye. A CMOS camera (Photron FASTCAM SA5) was used, and a programmable timing unit (LaVision PTU X) was used to synchronize the camera and laser.

2.3 Image Processing Procedure

Image processing was performed to understand the spray patterns and angle characteristics as shown in Fig. 4. First, over 100 images were acquired from the shadowgraphy technique for angle analysis. The acquired images were converted to grayscale, and the converted images were averaged. After binarizing the average image using Otsu’s method, the maximum intensity gradient point was defined according to the height to measure the spray angle, and the gradient was calculated using the x- and y-pixel information of each point. The spray angle was defined using the corresponding slope.

Fig. 4
figure 4

Image processing method for spray angle detection and calculation

Full size image

A particle master program was used to investigate droplet size and distribution. Because droplet size and distribution are known to play an important role in combustion efficiency and ignition stability, these parameters must be investigated [22, 23]. In this study, the resolution was secured using a calibration plate to increase the accuracy of the data. The interrogation spot was set to approximately 7 × 7 mm, so that the atomized droplet could be detected properly. In addition, it is inappropriate to measure the droplet size in the area, where the spray is maintaining the ligament or film, so the location, where the spray is completely atomized for all test conditions, is needed to be selected. Therefore, the spatial distribution of the droplet size was investigated by measuring SMD at intervals of 10° from a position 60 mm away from the pintle tip, as shown in Fig. 5.

Fig. 5
figure 5

Droplet size measuring location and calibration plate

Full size image

2.4 Numerical Analysis Conditions

In this study, FLUENT 2022 was used to analyze the spray and thermal analysis characteristics. First, the existing 3D shaped model was divided into 1/9, allowing for a more detailed analysis with the same number of meshes as shown in Fig. 6a. To determine the optimal number of meshes, a grid dependency test was conducted for three conditions (coarse, medium, and fine). The number of meshes for each condition was about 3, 5, and 7 million cells, respectively. The test was performed with 1000 iterations in each mesh conditions, and the outlet flow rate compared to the inlet flow rate was 99.197%, 99.966%, and 99.995%, respectively. The convergence criterion for this study was defined as conditions that the ratio of outlet to inlet flow rate exceeded 99.9%. In medium or fine meshes, the outlet flow rate compared to the inlet flow rate was 99.9% or higher, and the spray also showed almost the same patterns. Thus, the analysis was performed using the medium condition. Meanwhile, because thermal analysis must be conducted in a narrow region (30 cm3), 7 million meshes were applied and analyzed to secure higher accuracy rather than efficiency.

Fig. 6
figure 6

Numerical modeling for flow and heat transfer analysis

Full size image

As boundary conditions, the mass flow inlet and pressure outlet conditions were applied. The flow rate condition was 1/9 of the flow rate under full-scale conditions (21.4 g/s and 10 g/s for the radial and annular jet flows, respectively). The Reynolds stress–BSL model was used as a turbulence model, which is well-matched with the actual flow characteristics [24]. The adopted numerical scheme includes simple for transient, coupled for steady, and second-order upwind scheme for spatial discretization. To investigate cooling performance and internal flow, LOx and nickel–copper were applied as the oxidizer (coolant) and material, respectively. However, the analysis was performed by defining the ambient temperature as 3500 K and applying the temperature of LOx as 200 K without adding a separate combustion model [16, 25]. In addition, as shown in Fig. 6b, the ambient temperature condition was applied only to the area corresponding to the actual combustion chamber. The time scale condition was analyzed under transient conditions.

3 Results and Discussion

3.1 Spray Angle Patterns and Angle Variations

Most of studies related to the pintle injector have focused on the post configuration. However, Kang et al., reported that the pintle injector has a limitation regarding heat concentration, and the possibility of the insert having a cooling effect has been confirmed [16, 18]. The improved cooling performance implies that the flow rate of the fluid passing through the surface of the post increases. Thus, the flow rate of the fluid increases in the same area, so that we can predict that the insert affects the spray patterns. Therefore, an insert structure was designed to produce forced flow in the internal region of the pintle post, and the spray patterns influenced by the insert were quantitatively analyzed in this study.

Figure 7 shows the spray patterns according to the various configurations of the post and insert. Under the same post configuration, the spray angle increases as the increase of insert area ratio. It can be inferred that the spray angle is affected by forced flow due to the insert structure in the pintle post. However, the spray angle is relatively smaller than the original case (ARup.slit = 82.5%) when the post ARup.slit decreases. Thus, the post ARup.slit helps to control the spray angle characteristics. In addition, as ARins increases, drizzle (large drops) was observed beneath the pintle post. These characteristics are observed when ARins increases in the second-row slit-type pintle injector, regardless of the shape of the post.

Fig. 7
figure 7

Spray patterns with various insert and post area ratios (ARins and ARup.slit)

Full size image

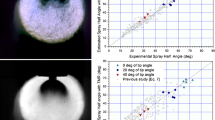
The consistency between the experimental and CFD analysis results is validated in Fig. 8. To display the iso-surface of the spray angle, the liquid volume fraction was set to 0.4, which shows an appropriate spray pattern. Figure 8 illustrates that the experimental and numerical spray angle analysis results are well-matched under each condition. Moreover, the spray angle diverges in two directions in areas with an ARins of 33% or more. This phenomenon is a result of the forced flow triggered by ARins, influencing the characteristics of the flow injected from the first and second rows of the pintle post.

Fig. 8
figure 8

Experiment and numerical simulation results at ARup.slit = 82.5%

Full size image

The characteristics mentioned previously were quantitatively analyzed by extracting data through image processing technique described in Sect. 2.3, with the results presented in Fig. 9. The spray angle increases with the area ratio of the insert, regardless of the post configuration (ARup.slit). Interestingly, the central area ratio of the insert remained almost constant up to 33%, but the angle increased sharply over 52%. To analyze these characteristics, streamline and velocity vectors are displayed in Fig. 10 using CFD.

Fig. 9
figure 9

Spray angle with various insert and post configurations

Full size image
Fig. 10
figure 10

Effect of the insert on streamline and vector when ARup.slit = 82.5%

Full size image

The flow was injected downward without local acceleration and upward without the insert structure as previously mentioned. However, the fluid supplied through the central flow passage was not fully injected through the second slit, and this affects the streamline of the first slit. The fluid supplied through the central flow passage increases in velocity when it passes through the insert and enters the narrow outer passage. The spray angle increases owing to the influence of the flow in the central flow passage.

For quantitative analysis of the characteristics, the velocity components at the post surface when ARins is equal to 0, 33, and 67% are shown in Fig. 11. The velocity of the fluid can be divided into two regions according to the ARins: the relatively low-velocity region where sub-stream region and the mainstream region. The sub-stream region can be referred to as a recirculation zone, as shown in Fig. 10. This recirculation zone occurs through interaction with an annular jet flow and radial jet flow, while the slit is not filled. When ARins is 33%, it shows almost the same velocity profile as when ARins is 0%, and the recirculation zone is observed in a higher position of the slit (Y/h1 = 0.95). When ARins is equal to 67%, the recirculation zone is observed in a lower region of the slit, where Y/h1 is 0.15.

Fig. 11
figure 11

Upper slit velocity profile and measuring location when ARup.slit = 82.5%

Full size image

On the other hand, the mainstream region shows a higher velocity than the recirculation zone. In this region, a single local maximum point was observed without an insert structure, while two local maximum points were detected with an insert structure. The lower maximum point is induced by the flow from the central passage, and the higher maximum point occurs due to the flow from the outer flow passage. When ARins is less than 33%, all of the maximum point is detected below the center of the slit. Conversely, all of the point is observed above the center of the slit when ARins is above 67%. This phenomenon is derived from the accelerated upward flow. The upper maximum point was lower than the lower maximum point in the mainstream region owing to the effect of the insert structure.

Another problem caused by the insert configuration is the drizzle that occurs beneath the pintle post. This drizzle results from an annular jet caused by a lack of sufficient mixing of the radial jet flow, as shown in Fig. 12. As previously mentioned, the injection velocity was relatively low under low ARins conditions, and the low injection velocity generated a relatively low local momentum ratio (LMR) in the first- and second-row slits. Relatively lower LMRs were accompanied by slower upward flow, which increased the effective area. Thus, the possible region in which the recirculation zone can occur is reduced. In this case, the jet deformation (\(\Delta \)) becomes larger because of the smaller LMR induced by the slower radial velocity. As a result, the amount of downward annular jet flow increases. Meanwhile, a higher momentum occurs owing to the higher velocity of the radial flow under a higher ARins, and the size of the jet deformation (\(\Delta \)) decreases. Therefore, the downward flow from the annular jet increases, while the annular jet flow and radial jet flow are not sufficiently mixed at the slits. In addition, the size of the effective area decreases owing to the higher velocity and upward flow, and a recirculation zone occurs in the rest of the slit region. Accordingly, the flow from the unmixed annular jet flow and recirculation zone is gathered at the pintle tip and dropped. This drizzle generated by such an unmixed flow may eventually negatively affect combustion efficiency.

Fig. 12
figure 12

Schematics of drizzle below the pintle tip with an effective area (blue region)

Full size image

3.2 Droplet Size Distribution

Figure 13 illustrates the spatial distribution of droplet distribution, with the droplet size distribution varying depending on ARup.slit and ARins. When ARup.slit is 82.5%, the position in which the maximum SMD appears below ARins = 52% is in two areas between 70 and 40 degrees, and this characteristic is induced by a structural characteristic of the double slit. Moreover, when ARins exceeds 52%, the maximum point shifts to between 30 and 0 degrees. This shift is due to an upward flow in a small region. The relative decrease in SMD for an ARup.slit of 52% occurs as the spray angle moves towards the injector head, causing the maximum SMD point to appear above the measurable area.

Fig. 13
figure 13

Droplet size distribution for various post and insert configuration (a–e) ARup.slit = 82.5%, e, f ARup.slit = 50.0%

Full size image

Moreover, the droplet size becomes larger in the post configuration when ARup.slit is equal to 50%, which shows unique characteristics compared to other ARup.slit cases. This characteristic is affected by the presence of large droplets in the bottom region of the tip, a phenomenon referred to as drizzle. In addition, a large droplet size is observed at 0 degree, because this location is near the spray surface.

Figure 14 illustrates the average droplet size for each condition. The ARup.slit is 82.5 and 17.5% conditions showed nearly identical trend in droplet sizes, but the average droplet size was smaller, when ARup.slit is 17.5%. When the double slit pintle injector operates under conditions in which TMR is 1, it can be expected that ARup.slit is 17.5% is more efficient. Moreover, the average droplet size decreases until ARins is 52% and then increases. As noted in the previous section, injection velocity increases as ARins increases, and the average droplet size decreases as the injection velocity increases. However, when the injection velocity of the radial flow becomes excessively large, the LMR increases significantly, and the downstream velocity decreases due to insufficient mixing of the annular jet and radial jet flow. Consequently, this poor atomization performance leads to the larger droplet size.

Fig. 14
figure 14

Average droplet size for all cases

Full size image

Distinct characteristics are observed under ARup.slit = 50%, compared to when ARins is 82.5% and 17.5%. With an increase in the central area of the insert, both the injection velocity and droplet size also increase. This characteristic occurs when the area ratio of the slit is 50%. Thus, the area ratio of the upper and lower slits leads to an increase in amount of downward flow, which causes a larger droplet size.

3.3 Effect of Insert on Cooling Characteristics

The insert structure in the pintle post is designed to prevent the post from damage. Consequently, this section is supposed to investigate the cooling performance in accordance with the configuration of the post structure and insert. First, to understand cooling performance according to the insert structure, a transient analysis was conducted until the surface temperature was sufficiently stabilized, as shown in Fig. 15. After stabilization, the data were obtained when the analysis was reliably completed. In addition, the area-averaged temperature of the bottom surface at the pintle post was used to confirm the generalized surface temperature.

Fig. 15
figure 15

Area weighted temperature at the bottom of the pintle post surface

Full size image

Cooling was hardly performed when there was no insert, except at the outlet surface of the pintle post, as illustrated in Figs. 15 and 16. However, when there was an insert, cooling was clearly observed. In addition, the surface temperature is the lowest at the slit surface of the injector, regardless of the presence or absence of an insert. These characteristics show that a higher velocity is formed at the slit surface with the radial flow, and as the velocity increases, the surface temperature decreases in an inversely proportional manner. The effective area and position of the outlet of the read flow changed, and the point, where the post was cooled also changed as mentioned in the 3.1. Therefore, to secure appropriate cooling performance, it is important to have a sufficiently large effective area.

Fig. 16
figure 16

Temperature contours at the pintle post surface when ARup.slit = 82.5%

Full size image

To analyze why cooling performance improves when ARins is 33% compared to 67%, the vector field in the bottom region of the pintle post was examined, as shown in Fig. 17. When there is no insert structure, the velocity component at the bottom surface appears close to zero. In general, it is well-known that the flow rate or mass flow rate of a fluid passing through a corresponding surface must be higher than lower mass flow rate to increase cooling performance. Therefore, when ARins is equal to 0%, the heated surface cannot be sufficiently cooled down due to the low velocity passing through the bottom surface.

Fig. 17
figure 17

Velocity vector field at the post with a lower slit

Full size image

However, a forced flow occurs inside the pintle post owing to the insert structure, and a relatively higher flow rate occurs at the bottom surface than when there is no insert owing to this forced flow. When ARins is less than 33%, the volume suddenly expands at the end of the insert, and a recirculation zone occurs at the bottom of the insert. Because of the recirculation zone, the fluid supplied from the central passage can be anchored to the bottom of the pintle and flow to the outlet. Therefore, cooling performance is improved as the fluid is supplied at a high velocity in the central passage, and the recirculation zone generated at the end of the insert increases.

When ARins is 52% or more, a separate recirculation zone does not occur, because the central passage is larger than the space at the bottom of the post and the space of the outer passage. Accordingly, the velocity component of the central flow at the bottom surface is not maintained continuously, resulting in a relatively lower velocity than when ARins is 33%. However, as the flow moves to a small outer passage area near the exit, the local velocity increases in the exit direction. As a result, a local increase in velocity only affects the spray angle, not cooling performance.

The area-weighted temperature of the bottom surface is plotted in Fig. 18. The surface temperature is almost the same when ARins is 0%, so it could be inferred that there is little difference in cooling performance in various ARup.slit conditions without the insert. However, a slight difference in cooling performance is observed when the insert structure is installed. In this case, the temperature value varies with different ARup.slit conditions, but the overall tendency is almost the same. When ARins is 17 and 33%, cooling performance is impacted in a similar way due to the recirculation zone generated at the end of the insert. In addition, when ARins is 52% or higher, the post is cooled down by the forced flow, but cooling performance is somewhat reduced, as mentioned previously. Moreover, when ARup.slit is equal to17.5%, there is relatively high cooling performance, which generates relatively low upward flow owing to the large injection area at the second-row slit, and most of the fluid is injected through this slit. When ARins is high, most of the fluid supplied through the central flow passage is injected through the second row. Accordingly, the fluid flow becomes active, and the flow at the bottom of the post becomes smooth. Thus, under the same flow rate and insert conditions, cooling performance can be improved with a smaller second-row slit area.

Fig. 18
figure 18

Effect of the insert area ratio on pintle post temperature

Full size image

4 Conclusion

In this study, an insert structure was suggested to produce forced flow, and the flow characteristics were investigated experimentally and numerically to mitigate the heating of the pintle post. Experiments were conducted to measure spray angle and droplet size while changing the internal flow passage and slit of the pintle injector. Furthermore, a numerical study was performed to understand the main cause of the change in spray characteristics and cooling performance.

First, we found that the spray angle increased when ARins was higher than 52%. This phenomenon occurs as the direction of the velocity increases and changes rapidly when the area ratio of the outer flow passage to the central flow passage decreases. Drizzle was observed downstream by an unmixed annular jet flow as the LMR increased. In addition, changing the area ratio of the first- and second-row slits can reduce the increase in spray angle caused by the insert configuration.

When the slit area ratios are 82.5 and 17.5%, the droplet size decreased less slowly than when the ratio was 52%, and the droplet size decreased further when the lower area was larger. However, when the slit area ratio was 50%, the droplet size increased as the mixing performance decreased, while the center area ratio increased.

When the insert structure was added, a forced flow was generated inside the pintle post, thereby enhancing cooling performance. With the insert structure, the temperature could be reduced by up to 31%. However, when the central area ratio of the insert was more than 52%, the temperature increased slightly, and this phenomenon occurs depending on the presence or absence of a recirculation zone inside the injector. The recirculation zone beneath the tip of the insert helps the flow to stick to the bottom surface of the pintle.

As a result, it is reasonable to add an insert to the pintle injector when considering spray angle, cooling performance, and droplet size. In addition, by operating the central area ratio of the insert at 52% and the upper and lower area ratios of the slit at 50% or more, we can expect to reduce heat load concentration occurring in the pintle rocket engine.