1 Introduction

1.1 GNSS in Aviation

The FAA Technical Standard Order TSO-C129 from December 12, 1992, allowed the use of GPS as a means for en route and approach navigation upon completion of its full operational capability. This full operational capability was announced by the US Air Force on July 17th, 1995. Since then, GPS navigation has evolved from being only a supplementary navigation device to the most often used singular means of point-to-point navigation. To provide a higher position accuracy and navigation integrity in a large geographic area, Space-Based Augmentation Systems (SBAS) were developed; the first such system was the Wide Area Augmentation System (WAAS), which went operational in July 2003. Initially thought as a means to remove Selective Availability from GPS, SBAS systems now provide a precision approach like capability without requiring any airport infrastructure (for an overview on SBAS use in aviation, see [3]). To achieve aircraft instrument approach down to category 3 autoland functionality using GNSS, Ground-Based Augmentation Systems (GBAS) were developed, which provide local differential corrections to aircraft within a service volume at an airport. With GBAS, the time to alarm in case of integrity failure can be held low [12, 14]. The first certified GBAS was operational in Bremen, Germany on February 9, 2012, providing category 1 approach services. GBAS is currently being certified to provide low visibility autoland service with expected system design approval (FAA) expected in 2019 [11]. A GBAS requires three to four reference antennas which must be installed at the airport according to [4]. The reference location of those antennas must be precisely known and determined by geodesic surveying techniques. This, of course, makes it impossible to use GBAS “out of the box”’ for mobile applications, where a quick deployment and minimal time to first use is needed.

Another possibility to obtain a similar accuracy and integrity without the need for a costly and length installation would be to use a GNSS receiver as a “beacon” and compute a relative 3D position between this beacon and an airborne receiver using a well-known technique called double-differencing that allows for spatially and temporally correlated errors to be removed. Using a relative position vector, the need for precisely measured reference antenna locations is eliminated. In this paper, we are using this technique to build an experimental Beacon Landing System (BLS) and evaluate its performance.

1.2 Double Differences

The GNSS double difference method is often used in surveying and real time kinematic applications to remove correlated errors and facilitate the carrier phase integer ambiguity resolution process (see, for example [2, 7], or [9]). This allows for precise positioning with sub-centimeter accuracy which is needed for geodetic surveying. As a first step in integer ambiguity resolution, the double difference carrier phase measurements and observation matrix are formed and the (biased) relative position is calculated. In this case double differencing refers to the formation of the difference between two single differences where single differences are obtained from taking the difference between the measurements from two receivers for the same satellite. In principle, it is enough to pick a reference satellite for the formation of the double differences as all other combinations would be linear dependent. With this technique all correlated errors are eliminated and we are left with receiver tracking loop noise and multipath. The latter can be reduced or even limited by careful antenna design and location. In the Beacon Landing System, we use the carrier-phase measurement to produce carrier smoothed code (for the smoothing algorithm, see [12]) and then apply the double difference technique to this new observable, just as we did in [15].

We assume that pseudorange between receiver k and satellite p can be modeled as follows:

$$\begin{aligned} \rho _{k}^{p}(t)=r_{k}^{p}+c(\delta ^{p}(t)-\delta _{k}(t))+Q_{k} +\gamma _{{\mathrm{iono}}}(t)+\gamma _{{\mathrm{tropo}}}(t), \nonumber \\ \end{aligned}$$
(1)

where \(r_{k}^{p}\) is the geometric range from receiver to satellite, \(\delta ^{p}\) and \(\delta _{k}\) are the satellite and receiver clock biases, \(Q_{k}\) is the receiver noise and multipath, \(\gamma _{{\mathrm{iono}}}\) the error introduced by propagation through the ionosphere and \(\gamma _{{\mathrm{tropo}}}\) is the error introduced by propagation through the troposphere. We now form the single difference (SD), between the measurements of receiver k and a second receiver m. Because of the proximity of the two receivers, we assume for the remainder of this section that the ionospheric and tropospheric delays between receiver k and m are the same and, hence, are removed in the differencing operation:

$$\begin{aligned} \text {SD}_{km}^{p}=\rho _{m}^{p}-\rho _{k}^{p}=r_{km}^{p}+Q_{km}+c(\delta _{k}-\delta _{m}). \end{aligned}$$
(2)

The SD corresponds to the difference of geometric ranges \(r_{km}^{p}=r_{k}^{p}-r_{m}^{p}\), a combined noise and multipath term \(Q_{km}\), and a term that contains the clock biases for both receivers. The satellite bias \(\delta ^{p}\) and the atmospheric errors are common to the two pseudoranges and are thus canceled by the difference operation. We can also express the SD as a function of the baseline (or relative position) between the two receivers by linking the baseline with the differential geometric ranges \(r_{km}^{p}\). We assume that the signal reaching the receiver k is equal to the signal reaching the receiver m plus an additional component related to the differential geometric ranges \(r_{km}^{p}\). Now let us define \(\vec {b}\) as the unknown three-dimensional baseline vector between the two receivers. Since GPS satellites are in a 20,000 km orbit with a 12 h period, we can assume that the propagation paths between the satellite and the two antennas are quasi parallel. We also know the line-of-sight vector \(\vec {e}^p\) to the satellite as derived from the satellite position and an estimate of the receiver positions. Hence, the single difference can easily be expressed as the projection of the relative position vector onto the line of sight vector to the satellite p. The differential geometric ranges \(r_{km}^{p}\) can thus be expressed as the dot product between the unit vector \(\vec {e^{p}}\) and the baseline \(\vec {b}\):

$$\begin{aligned} r_{km}^{p}=\vec {e}^{p}\cdot \vec {b}. \end{aligned}$$
(3)

Substituting Eq. 3 into Eq. 2 yields the following expression for the single difference:

$$\begin{aligned} \text {SD}_{km}^{p}=\vec {e}^{\vec {p}}\cdot \vec {b}+Q_{km}+c(\delta _{k}-\delta _{m}). \end{aligned}$$
(4)

We still have the error due to the receiver’s clock bias in this equation. To remove this term, we form another single-difference with respect to another satellite q:

$$\begin{aligned} \text {SD}_{km}^{q}=\vec {e}^{q}\cdot \vec {b}+Q_{km}+c(\delta _{k}-\delta _{m}). \end{aligned}$$
(5)

Next, we subtract the two SDs resulting in the double difference:

$$\begin{aligned} \text {DD}_{km}^{pq}= & {} \text {SD}_{km}^{p}-\text {SD}_{km}^{q}=(\rho _{m}^{p}-\rho _{k}^{p})-(\rho _{m}^{q}-\rho _{k}^{q}) \nonumber \\= & {} (\vec {e}^{\vec {p}}-\vec {e}^{\vec {q}})\cdot \vec {b}+Q_{km}^{pq} \end{aligned}$$
(6)

with \(Q_{km}^{pq}=(Q_{k}^{p}-Q_{m}^{p})-(Q_{k}^{q}-Q_{m}^{q})\) corresponding to the uncorrelated noise and the multipath of all the receivers. Dropping the vector notations and ignoring the noise term, the double difference becomes

$$\begin{aligned} \text {DD}_{km}^{pq}=(\vec {e}^{p}-\vec {e}^{q})\cdot \vec {b}, \end{aligned}$$
(7)

which can be solved using standard least squares methods. Using matrix notation yields the following equation:

$$\begin{aligned} \text {DD}={H}\vec {b}. \end{aligned}$$
(8)

Note that the geometry matrix H contains the difference between unit vectors to different satellites for all possible satellite combinations. The baseline \(\vec {b}\) can then be obtained using S, the pseudo-inverse of the geometry matrix H:

$$\begin{aligned} \vec {b}=({H}^{{\mathrm{T}}}{H})^{-1}{H}^{{\mathrm{T}}}\cdot \text {DD}. \end{aligned}$$
(9)

1.3 Weighted Least Squares

Obviously, since we form linear combinations between individual measurements to form single- and double differences, they are no longer independent and we must compute the covariance matrix C of the double differences. Its inverse \(W=C^{-1}\) can then be used as weights for the least squares algorithm to remove any correlation. When writing a single difference in matrix notation, we get

$$\begin{aligned} \begin{bmatrix} \text {SD}_{km}^{p} \\ \text {SD}_{km}^{q} \\ \vdots \\ \end{bmatrix} =\underbrace{ \begin{bmatrix} 1 &{} -1 &{} 0 &{} 0 &{} \ldots \\ 0 &{} 0 &{} 1 &{} -1 &{} \ldots \\ \vdots &{}\vdots &{}\vdots &{} \vdots &{}\ddots \\ \end{bmatrix} }_{=K} \begin{bmatrix} \rho _k^p \\ \rho _m^p\\ \rho _k^q \\ \rho _m^q\\ \vdots \end{bmatrix}. \end{aligned}$$
(10)

Therefore, the covariance matrix becomes

$$\begin{aligned} \varSigma _{{\mathrm{SD}}}=K\varSigma _{\rho }K^{\mathrm{T}}, \end{aligned}$$

where

$$\begin{aligned} \varSigma _{\rho }= \begin{bmatrix} {\sigma ^2}^p &{} 0 &{} \ldots \\ 0 &{} {\sigma ^2}^q &{} \ldots \\ \vdots &{} 0 &{} \ddots \end{bmatrix} \end{aligned}$$

is the diagonal covariance matrix of the pseudorange measurements, which are presumed independent and depending on the satellite elevation angle. Similarly, the double differences are formed from the single differences using the following relationship:

$$\begin{aligned} \begin{bmatrix} \text {DD}_{km}^{pq} \\ \text {DD}_{km}^{rq} \\ \vdots \\ \end{bmatrix} = \underbrace{ \begin{bmatrix} 1 &{} -1 &{} 0 &{} \hdots \\ 0 &{} -1 &{} 1 &{} \ldots \\ \vdots &{}\vdots &{} \vdots &{}\ddots \\ \end{bmatrix} }_{=M} \begin{bmatrix} \text {SD}_{km}^{p} \\ \text {SD}_{km}^{q} \\ \text {SD}_{km}^{r} \\ \vdots \end{bmatrix} \end{aligned}$$
(11)

and hence

$$\begin{aligned} \varSigma _{{\mathrm{DD}}}=M\varSigma _{{\mathrm{SD}}}M^{\mathrm{T}}. \end{aligned}$$
(12)

We can use the inverse of this covariance of the double differences as weights \(W=\varSigma _{{\mathrm{DD}}}^{-1}\) in Eq. (9) to obtain a uncorrelated and thus better estimate for the baseline:

$$\begin{aligned} \vec {b}=({H}^{{\mathrm{T}}}W{H})^{-1}{H}^{{\mathrm{T}}}W\cdot \text {DD}. \end{aligned}$$
(13)

The covariance of the ad hoc relative position (or baseline) error will be the first term of the general least squares expression (13)

$$\begin{aligned} \varSigma _{{\mathrm{Baseline}},{\mathrm{ad}}\text {-}{\mathrm{hoc}}}=({H}^{{\mathrm{T}}}W{H})^{-1}. \end{aligned}$$
(14)

It can be used to obtain a three-dimensional error ellipsoid to visualize uncertainty bounds of the three-dimensional relative position.

2 Concept of a Beacon Landing System

When installing GBAS, several reference antennas are placed at fixed location on the airport and their positions surveyed using geodesic techniques and expressed in the international terrestrial reference frame [1]. This is a lengthy process and requires dual frequency measurements from all reference antenna positions [4], even though GBAS is single frequency system only. Moreover, a GBAS ground station incorporates a processing computer and a backup unit to generate the correction data and integrity information. The certification of this unit is the most complex and costly part of the GBAS approval since it is such a vital part of the system.

Fig. 1
figure 1

Concept of the Beacon Landing System

Full size image
Fig. 2
figure 2

Computing deviations

Full size image

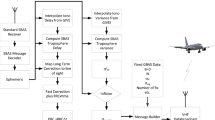
The Beacon Landing System (BLS) uses double difference pseudorange measurements from a quickly deployable GNSS receiver that acts as a beacon. It transmits its raw measurements of pseudorange (and optionally carrier phase) to a user on approach. The airborne receiver uses the double difference technique as described in Sect. 1.2 to compute the three-dimensional relative position vector between his ownship and the master antenna position as illustrated in Fig. 1. With some knowledge of the landing direction and the approach reference points (with respect to the beacon), the airborne processor can compute angular deviations from this selected landing direction and a glide path angle selected by the pilot (Fig. 2). We can then show these deviations on a course deviation indicator in the same manner as the pilot would view ILS or a GLS deviation for approach guidance. If we also require measurement integrity, we could include additional beacon receivers for measurement consistency checks at the cost of additional data volume to be broadcast. When the beacon receiver is not placed at the landing threshold we can add this offset to the relative position computed in the aircraft. Additionally, when using two beacon receivers, they could serve as runway alignment markers when placed at opposing sides of the runway. Overall, a BLS can be quickly deployed, uses a simple algorithm and uses the protected frequencies in the aeronautical band. We now assess the performance parameters of the BLS, such as accuracy of the double difference relative position, datalink capacity and integrity guarantees (Fig. 3).

Fig. 3
figure 3

Distribution of VDB messages

Full size image
Fig. 4
figure 4

Baseline error collected during 5 days at 2 Hz

Full size image
Fig. 5
figure 5

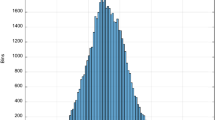
Histogram of the data presented in Fig. 4. The standard deviations are 0.2155, 0.2729 and 0.4692 m in east, north and up directions, respectively

Full size image
Fig. 6
figure 6

Variance of the glide path angle at 200 ft above the landing point into the northeast direction (\(45^{\circ }\)) using the data from Fig. 4. The spikes of high variance correspond to the larger errors of the baseline when the satellite geometry was sub-optimal

Full size image

3 Relative Positioning Using Double Differences

To assess the performance of the code-based double difference relative position, we placed two antennas of the roof of the DLR Institute of Flight Guidance separated by a distance of (8.602, \(-1.105\), 0.000) m in east, north and up direction (abbreviated E, N, Up), respectively. The antennas were a Novatel Pinwheel and a Leica AR20 GNSS reference antenna. They were connected to a Topcon NetG3 and a Javad Quattro receiver, respectively. Using our own live processing code, we collected baseline data for about six days to compare with the real relative position. Moreover, we recorded the relative position covariance matrix \(\varSigma _{{\mathrm{Baseline}},{\mathrm{ad}}\text {-}{\mathrm{hoc}}}\) for each epoch to estimate the angular error that would influence the pilot display as shown in Fig. 2. As input variances \(\varSigma _{\rho }\) for the individual pseudorange measurements we used the pseudorange uncertainties stipulated by [17] and applied a standard carrier phase smoothing algorithm with a time constant of 100 s to the pseudorange data [8]. Figure 4 shows the resulting time-series of the baseline error. We can observe that the error is, in general, below the one meter-level and the vertical error is larger than the errors in east and north direction. A statistical analysis shows the error to be quasi zero-mean with a covariance matrix of

$$\begin{aligned} \varSigma _{{\mathrm{baseline}}, {\mathrm{timeseries}}}= \begin{bmatrix} 0.0464 &{} -0.0014 &{} 0.0122\\ -0.0014 &{} 0.0745 &{} 0.0385\\ 0.0122 &{} 0.0385 &{} 0.2202 \end{bmatrix} \end{aligned}$$
(15)

in \(\hbox {m}^2\). Since the errors are spatially correlated due to the double difference technique, the cross-correlation is unsurprising. Histograms in Fig. 5 show the data to be normally distributed which we confirmed with the MATLAB built-in Kolmogorov–Smirnov test (\(\alpha =0.05\), [10]). From the recorded ad-hoc covariances we computed the angular deviation error at the standard minimum descent altitude of 200 ft above ground level on a three degree glide path. This altitude translates to a distance of 1163.2 m from the landing threshold. Using the Monte-Carlo method, we computed the angle \(\alpha =a\tan (\frac{Up+\epsilon _U}{\sqrt{(E+\epsilon _E)^2+(N+\epsilon _N)^2}})\) and a random error \(\epsilon \) generated from the ad hoc covariance matrix with 1 million samples. We always used the direction in which the error was largest, i.e. the direction of largest eigenvalue/eigenvector combination and subtracted the desired glide path angel of \(3^{\circ }\). The results are shown in Fig. 6 with the average error over the time series being 0.115\(^{\circ }\). The spikes of high variance correspond to the larger errors of the baseline in Fig. 4 when the satellite geometry was sub-optimal. The allowed tolerance for a category 1 ILS at this location is 8 ft vertically [16], corresponding to 0.12\(^{\circ }\). The results of the BLS are thus comparable to the ILS.

4 Data Transmission Alongside GBAS

The GNSS pseudoranges and carrier-phase measurements used by the BLS must be transmitted using a data link to the airborne user. Since GBAS already uses a VHF data broadcast (VDB), a compatible message that contains the necessary data has been defined. Details on the actual link structure and already defined messages can be found in [13]. A standard GBAS message consists of a total of 1776 usable bits. Its time length adds up to 62.5 ms for one VDB slot. There are 8 slots in total, A through H, which are equally distributed over 500 ms in one Time Division Multiple Access (TDMA) frame. To prohibit interference with other broadcasting stations, the TDMA pattern must be strictly obeyed. Only the assigned time slots can be used by one specific broadcasting station. Compliance with the TDMA structure allows for the use of the same frequency by multiple broadcasting stations. Up to 256 different message types (MT) can be defined and three are already in use for a standard GBAS approach service type C (MT1, MT2, MT4). MT1 contains differential corrections and must be broadcast once per frame for each measurement type, i.e. C/A code on L1, C/A code on L5. Currently, only C/A code on L1 is used for GBAS, but there is ongoing research into multi frequency, multi constellation GBAS. MT2 contains GBAS station and environment related information such as reference coordinates, ionosphere parameters and atmospheric refractivity. It must be broadcast at least once per 20 consecutive frames. MT4 contains Final Approach Segment (FAS) data and all FAS blocks must be sent once per 20 consecutive frames. Timestamp, PRN and pseudorange measurements (and carrier-phase measurements) between a satellite and a master station are required by the rover or airborne user to form the double difference for the determination of the baseline. Additionally, distance and direction between the reference receiver and the threshold must be included allowing the user to calculate direct course to the runway rather than towards the receiver. We define two additional messages that can be broadcast via the GBAS VDB: essential and complementary data, with their definitions as shown in Tables 1 and 2. If transmission occurs within two TDMA time slots, BLS data for up to 18 satellites in view can be transmitted alongside GBAS. In the case that three slots are available, we can increase the data to cover 33 satellites (Fig. 3). One of the major aims when a BLS is implemented utilizing a GBAS station and a GBAS-based data link is that the operation of GBAS can be conducted simultaneously. This requires sufficient data capacity so that both modes of operation can be served. A BLS requires different data to be submitted than when GBAS is operated. For this reason, data which are intended to serve GBAS cannot be applied for the operation of a BLS. Therefore, newly developed message types must be transmitted.

Table 1 Format of a VDB message block representing the complete structure of the message which includes essential data for the operation of a BLS
Full size table
Table 2 Format of a VDB message block representing the complete structure of the message which includes additional data for an advanced usability of a BLS
Full size table
Fig. 7
figure 7

(Top) ILS glide path and GNSS antenna location on the A320 D-ATRA. (Bottom) Runway and GNSS receiver location for the flight testing

Full size image

5 Flight Test

To evaluate the BLS in real-life conditions, we tested the BLS algorithms flying approaches into Braunschweig-Wolfsburg airport in Germany. On the ground, we installed a Septentrio PolaRx3 dual frequency GNSS receiver running at 2 Hz connected to a Leica AR20 antenna at DLRs institute of flight guidance (see Fig. 7, bottom), located south of runway 26. The flight test was conducted using DLR’s Airbus A320 on 13th of April 2016. The aircraft is equipped with a dual frequency GNSS antenna and a Septentrio PolaRx3 GNSS receiver. To have a meaningful comparison for the pilot during the flight trials, we computed angular deviation with respect to the existing ILS at EDVE airport. It consists of two radio transmitters in the very and ultrahigh-frequency band, which provide deviations from a desired straight path by translating the ILS difference in depth of modulations (DDM) to an angular deviation. Further details on the ILS technology can be found in [6].

Fig. 8
figure 8

Localizer and glide slope deviations of the BLS compared to the ILS. The data from the first approach are depicted in panels a and b, data from the second approach in panels c and d

Full size image
Fig. 9
figure 9

Localizer and glide slope deviations in pilot presentation. a The deviations with the axis limits corresponding to the pilots primary flight display. b Magnified version

Full size image

To accomplish this transformation, we added a three-dimensional offset vector from the AR20 position to the coordinates of the localizer (\(\varDelta \text {East}=1772.9~\text {m}, \varDelta \text {North}= -359.3220,\varDelta \text {Up}=-0.256~\text {m}\)) and glide path transmitter (\(\varDelta \text {East}=-523.1915, \varDelta \text {North}=-690.0403,\varDelta \text {Up}=11.22~\text {m}\)) antennas before computing deviations from the runway center-line course of 264.85\(^{\circ }\) true track and ILS glide path of 3\(^{\circ }\). The geometry is illustrated schematically in Fig. 7, bottom. At the aircraft, we account for the fact, that the GNSS antenna and the localizer antenna are located at different places along the longitudinal axis along the aircraft’s flight path (see Fig. 7, top). We flew two approaches to runway 26 descending from 2000 ft above means sea level to the runway threshold at 300 ft mean sea level using the BLS technology. At the same time, we recorded localizer and glides slope deviations from the instrument landing system installed at the airport.

The results are shown in Fig. 8. Each row shows the data recorded during one approach, the left hand column depicts the lateral localizer guidance and the right hand column is the vertical glide slope deviation. A value of zero means that the aircraft is exactly on the desired and designed path. We can immediately notice that the BLS signal is much smoother than the ILS one, and that the ILS localizer is much noisier than the glide path signal. The BLS deviations do not show significant differences in signal quality. This is to be expected since they originate from the same source, where as the ILS operates two separate hardware transmitters. We determined the root-mean-square (RMS) values of the difference between the two signals. With RMS values of 0.012 and 0.011 the BLS glide slope signal is actually a better match to the ILS than the localizer with RMS values of 0.018 and 0.020.

Figure 9a shows the information available to the pilots when flying a precision approach. The course deviation indicator scales from \(\pm 2.5^{\circ }\) laterally and \(\pm 0.75^{\circ }\) vertically. The pilot adjusts the aircraft’s path such that the deviation becomes nearly zero. Due to the angular nature of the guidance, the absolute path tracking becomes more precise when the aircraft gets closer to the ground. As in Fig. 8 we can already discern that the BLS guidance is much smoother that the ILS beam. Panel (b) shows a magnified view of (a).

To analyze the data like we did here, we need the precise position of the ground-based receiver so that we can add the offsets to ILS localizer and glide path transmitter. In the regular use case, one can place the GNSS beacon near the end of the runway as a threshold marker. The approaching aircraft can choose whatever approach course and glide angle it desires complete the landing. If desired, an additional GNSS beacon can be used as runway direction indicator.

6 Conclusions

We demonstrated that GNSS double differences can be used as underlying technique for a aircraft landing system. When cost effectiveness and rapid deployment is key, such a Beacon Landing System can be installed quickly at any airstrip and provides an accuracy as good as GBAS. The existing data transmission infrastructure of GBAS can be used to transmit the necessary additional information. Then, already existing receivers onboard the rover would only need a software update containing the BLS algorithms. The quality of guidance is comparable to the one reported by [5] for GBAS. The double differencing technique removes any correlated errors between base and rover receiver without the need of additional modeling of atmosphere effects and monitoring of satellite orbits. For the sake of availability and continuity, hardware should be built redundantly to eliminate a single source of failure. At a minimum this means doubling the GNSS receiver and the processing unit at the base station. Using one receiver only is a threat to continuity of service and system availability, but this configuration could be considered for applications involving unmanned aerial vehicles. When trying to land an aircraft on a moving platform, for example a shipboard landing of a rescue helicopter, the beacon landing system is better suited than a GBAS. On a moving vehicle, it is naturally not possible to geodetically survey the antenna location. Therefore, a relative navigation solution will provide a more robust and accurate guidance. Additionally, combined with multiple antennas on the ship, an attitude receiver can provide landing pad attitude to the approaching aircraft’s flight guidance computer to conduct automatic landings.