Introduction

The making of connections is included to a greater or lesser extent as an essential element in the construction of mathematical knowledge in some relevant theoretical frameworks (e.g. Dubinsky & McDonald, 2001; Duval, 2006; Godino et al., 2019; Lakoff & Núñez, 2000; Von Glaserfeld, 1995) and has also been stressed as an important dimension of mathematics teacher knowledge (Rowland et al., 2009).

This consensus on the importance of connections in the profound understanding of mathematics is also recognised by many curricular documents that emphasize the importance of the making of mathematical connections in the classroom (e.g. Department of Education U. K., 2013; National Council of Teachers of Mathematics, 2000). In particular, the connection standard (NCTM 2000) refers to connections between mathematics and other contexts and/or connections between mathematical ideas that include broad connections, such as the connection between rational numbers, proportionality and linear relationships, and more specific connections such as the connection between two specific representations of the same concept.

However, the incorporation of relevant mathematical connections to classroom practice is not a clear and direct process and plays a dual role. On the one hand, there is research that confirms the relation between the establishment of connections and profound mathematical knowledge (Adu-Gyamfi et al., 2017; Askew et al., 1997; Barmby et al., 2009; Caviedes et al., 2021; Cobb, 1991; Rittle-Johnson et al., 2009). For instance, Fyfe et al. (2017) report on the benefits of including explicit connections between representations for a deep understanding of algebra. On the other hand, other research indicates that when connections are made many students experience difficulties. For instance, the results of Fyfe et al. (2017) show that the inclusion of connections is also related to difficulties in the understanding of specific solution methods. Other studies report that connections may be related to an excessive cognitive load (Gick & Holyoak, 1980; Rittle-Johnson et al., 2009; Sweller et al., 1998). In addition, the lack of precision regarding what it means to establish a relevant mathematical connection and the lack of specific models of how to take them to the classroom generate difficulties in the teachers when explicitly incorporating connections into their classroom practice (Frykholm & Glasson, 2005). A gap between theory-based recommendations about connections and school reality, caused by the situated nature of teachers’ practice, is also reported by Leikin and Levav-Waynberg (2007).

The lack of a common definition of the notion of connection in mathematics education, the potential difficulties associated with connections in classroom practice and the scarce empirical evidence of the specificities of connections in a classroom context lead us to focus on the context of classroom practice. Some preliminary results of this research project (De Gamboa & Figueiras, 2014) revealed that, in a classroom context, connections may emerge as a result of a complex network of interactions between the teacher and the students, and that connections can be understood as a network of simpler relations. Therefore, investigating the preliminary ideas in greater depth, our research questions are (1) what is the specific nature of connections in a classroom context? and (2) What are the structural characteristics of such connections? With the aim of responding to these questions, we carry out an inductive analysis to propose a definition and a classification of connections that emerge from the data gathered in the context of classroom practice. In the “Discussion” section, we compare our results with those of other recent studies that have also proposed definitions and classifications for mathematical connections in different contexts. This study is particularly relevant for those researchers interested in the conceptualization of mathematical connections. Some factors that determine complexity are also discussed as a consequence of the results.

Theoretical Framework

Some Relevant Types of Connections

The growing interest in the notion of mathematical connections has led to the appearance of a line of research which seeks to study and characterise the connections in processes of teaching and learning mathematics and, to do so, several authors have developed theoretical models. Nonetheless, despite the consensus on the importance of making connections for the learning of mathematics, the meaning of the notion of connection is too broad and may vary depending on the context where it is used. The term connection can refer, among other meanings, to an epistemological characteristic of mathematics (Evitts, 2004); to a mental process performed by a person who makes mathematics (Dolores-Flores & García-García, 2017); or to a characteristic of teacher’s knowledge to promote students’ comprehension (Rowland et al., 2009). Therefore, the classifications proposed in different research studies depend on the context of the study and on the data analysed.

Although there are many empirically based classifications of connections, some types of connections reported in those classifications are particularly relevant in the context of mathematics teaching and learning. First, connections between mathematics and other contexts or disciplines are highlighted by curricular guidelines (e.g. NCTM, 2000). They are also at the heart of mathematical modelling at school and play an important role in STEM education when mathematics is brought into play. Moreover, they have been subject to study in some research studies about mathematical connections (e.g. Dolores-Flores & Garcia-Garcia, 2017; Evitts, 2004). Second, connections between representations are the kind of mathematical connection that appears in most theoretical models for connections from any perspective. One of the most relevant characterisations of connections between representations is the one proposed by Duval (2006), who introduces the idea of conversion when the connection involves a change of register of semiotic representation (a register of semiotic representation is a semiotic system that permits transformations of representations), and treatment when the register is maintained. The identification of this kind of connection is consistent in other relevant characterisations of connections (e.g. Adu-Gyamfi et al., 2017; Businskas, 2008; Dolores-Flores & Garcia-Garcia, 2017; Dreher et al., 2016; Rodríguez-Nieto, 2021) and in some of our previous results (De Gamboa & Figueiras, 2014). Third and finally, procedural connections are also a type of connection identified consistently in several studies. They were introduced by Businskas (2008), and refer to the use of rules, algorithms or formulas. This last kind of connections is also identified by Dolores-Flores & Garcia-Garcia (2017) and Eli et al. (2011).

Apart from the previous three kinds of connections, several studies have identified other types of connections that inform about relevant specificities of connections. Businskas (2008) analysed the notions of connections that emerged from conversations and interviews with teachers and reported on five categories of connections: different representations; procedural; implication, that refers to reasoning of the if–then type; part–whole, that refers to relations of inclusion; and the instruction-oriented connection, that refers to connections with previous knowledge. Eli et al. (2011) analysed the mathematical connections that emerged when prospective middle-grade teachers engaged in card sorting activities and propose, among others, two more relevant types of connections: categorical that refers to connections based on the use of surface features; and characteristic/property that refers to the use of common characteristics or properties. Dolores-Flores and García-García (2017) applied Businskas’ model to identify the intra-mathematical and extra-mathematical connections made by students when solving calculus problems. On the one hand, the five categories of connections proposed by Businskas were observed, and considering the limitations found in these categories when analysing the data, they proposed an extension, incorporating two categories: reversibility that refers to the use of inverse relations in mathematics; and meaning that refers to connecting different meanings of the same concept. In Rodríguez-Nieto (2021), the previous works are developed and an extended classification of mathematical connections is presented. In particular, the author proposes considering metaphorical connections as a new type of connection.

This research piece coincides with those of Dolores-Flores and García-García (2017) and Rodríguez-Nieto (2021) in the context of classroom practice. However, while they use Businskas’ (2008) classification and propose extensions of it, we have conducted an inductive study, and we did not explicitly adhere to a particular framework from the beginning. In the “Discussion” section, we compare our findings with those of other researchers.

Our View on the Mathematical Practices That Occur in the Classroom

We understand that the mathematical activity has the purpose of solving problems by performing mathematical practices, in the sense of the Onto-Semiotic Approach (OSA; Godino et al., 2019). A mathematical practice is conceived in this theory as a sequence of actions (Font et al., 2013). For the realization of these mathematical practices and for the interpretation of their results as satisfactory, it is necessary, in addition to the problem, to put into operation other mathematical objects. According to Font et al. (2013), the ‘object’ is used in a broad sense to refer to any entity which is, in some way, involved in mathematical practice and can be identified as a unit. Consequently, mathematical practices activate a conglomerate of primary objects formed by situations–problems, languages, definitions, propositions, procedures and arguments, articulated in what is called a configuration of primary objects (Godino et al., 2019). An essential example to distinguish practices from primary objects is when considering the mathematical activity involved in solving the task: Calculate the derivative of the function \(g(x)=({x}^{3}-2{x}^{2}+4)(5x-1)\). For resolution, the student performs a sequence of actions (practice), such as reading the statement and calculating the derivative using the rule for the derivative of the product of functions: \(g{\prime} (x)=(3{x}^{2}-4x)(5x-1)+5({x}^{3}-2{x}^{2}+4)\), which is a procedure (primary object). A key notion for connecting primary objects activated in mathematical practices is the notion of semiotic function (Godino et al., 2019), that is conceived, in a metaphorical way, as a correspondence between sets that brings into play three components: a plane of expression (initial object), a plane of content (final object), and a criterion or rule of correspondence (Godino et al., 2007). Semiotic functions are not usually established in isolation. They are usually part of chains or sets of semitic functions, which, in turn, can be considered globally as semiotic function.

In the particular context of classroom activity, mathematical practices can be understood, among others, from a cognitive, discursive and social perspective (Godino et al., 2019; Franke et al., 2007; Planas et al., 2021). We believe teachers’ and students’ discourse is a prominent part of their practice, and the analysis of discursive interactions can provide explicit evidence of connection making. Our discursive perspective focuses on Duval’s (2006) classification of registers of semiotic representation that includes natural language, iconic representations, geometric representations, symbolic systems, diagrams and graphs, and auxiliary gestures. In this study, we will not delve into the discussion of whether gestures are (or not) a register of representation different from others. We limit ourselves to considering that gestures can be considered, above all, as auxiliary metaphorical expressions that affect the way of understanding a representation. For example, the number line that represents Z can be considered statically as a set of points or dynamically by making hand gestures that suggest movement along the line (in this case a student may think of the point as lying on the line rather than a part of the line, and the line as a path through which the points travel, since the gestures suggest the conceptual metaphor: the line is a path).

Considering the broadness of the notion of connection reported above and using the relational and pragmatic perspective proposed by the OSA, we focus on discursive interactions between the teacher and the students. Therefore, we understand mathematical connections in the context of classroom practice as an explicit relation between two objects (Fig. 1).

Fig. 1
figure 1

Our preliminary definition of a mathematical connection

Full size image
$${O}_{1}\stackrel{relation}{\to }{O}_{2}$$

All these three elements (\({O}_{1}\), \({O}_{2}\) and relation) are identified from explicit utterances of the teacher and the students. The objects are understood in the sense of OSA. The relation between the two objects is established by the explicit description or justification of how \({O}_{1}\) and \({O}_{2}\) are related. For instance, a connection can be made between the symbolical representation \(-3\) (\({O}_{1}\)) and its representation as a point on the number line (\({O}_{2}\)), if there is an explicit utterance related to the equivalence between the two representations.

Method

The research framing the analysis of connections proposed in this article consists of the in-depth analysis of a class group (12–13 years old), in a public school in a centric neighbourhood in Barcelona, during a limited period of time defined by the teaching unit on integers. The class was composed of 10 girls and 13 boys. The teacher was a mathematics graduate, with more than five years of experience in teaching in secondary schools and previous experience teaching mathematics in the university. The teacher had also recently passed a public examination to become a permanent secondary school teacher.

Classroom practices included mostly whole-class discussions (Lamberg, 2012) on tasks previously solved individually by the students in the classroom. Since the data are determined by the interaction between teacher and students, and since we are interested in conducting a more in-depth analysis, we opted for a qualitative and interpretative approach. The methodological design is a case study (Bryman, 2004; Yin, 2014). According to Yin (2014), a case study is the in-depth empirical analysis of a phenomenon in its context. In this study, the case is the emergence of mathematical connections in the classroom and can be characterised, according to the classification by Yin (2014), as a common type or, in Bryman proposal (2004), as an exemplifying case. Parents gave informed consent of students’ participation.

The data used to perform the analysis are video and audio recordings of eight regular class sessions of 60 min and their corresponding transcriptions. The eight sessions covered topics such as basic properties of natural numbers (g.c.d and l.c.m), the introduction of negative numbers, the basic properties of the operations with integers, combined operations with integers, powers, roots, and some word problems. To collect the information, non-participant observation was used (Caldwell & Atwal, 2005; Cohen et al., 2007). Therefore, the class group was observed, listened to and video-recorded and notes were taken, without intervening in the design of the sessions, the activities proposed or the development of the sessions. The data were processed in two phases: the first was aimed at identifying connections and establishing episodes, and the second was aimed at characterising and classifying the connections identified in the first phase.

First Phase of Analysis

The first data-processing consists of viewing all eight class sessions from the teaching unit on integers. The only theoretical construct used in the analysis was the idea of object in the sense of the OSA. The aim of this first viewing is to identify and define episodes in which connections appear. Each session was viewed at least twice by two researchers that took notes of relevant moments in the videos in which potential connections may emerge. A connection is identified when there is an explicit utterance, in either teacher’s or students’ discourse, to the relation between \({O}_{1}\) and \({O}_{2}\) (Fig. 1). This requisite of explicitness is highly relevant because our analysis is focused on explicit evidence from the teacher’s or students’ discourse. When a possible connection is identified, the fragment in which it appears is viewed repeatedly, with the aim of identifying the first and last utterance from the teacher and/or students which is related with the connection. The fragment of the video comprised between the first and the last utterances is called episode and makes up the units analysed in the subsequent stages of analysis. Once a connection has been identified during the viewing of the classroom sessions, and having outlined the episodes, these are transcribed. The average duration of the episodes was 5 min and 55 s.

Second Phase of Analysis

To characterise and classify the connections identified in the first phase, we follow 4 stages that allow us to progressively refine the analysis of connections and their structure. The categories were developed and refined inductively as grounded in the data.

In stage 1, when the three elements that determine each connection defined in Fig. 1 are identified (\({O}_{1}\), \({O}_{2}\) and relation), the analysis revealed that, in some cases, the utterance that defined the connection may trigger (in the context of a classroom dialogue) other utterances that were related to the relation that defined the connection. These utterances created new relations between objects that enriched the original connection. These relations are called links. Each link can be a reformulation of the relation between O1 and O2, or a relation between either O1 or O2 and another object. Therefore, connections revealed as networks that can be made of one or more links. When a connection has only one link (i.e. it is defined by a single relation defined by a single utterance), the link coincides with the connection. When a connection is made of more than one link, the relation is defined by the coordination between the links involved in the network. The identification of this internal structure of connections motivated two parallel analyses of each connection in stages 2, 3 and 4 (Table 1): one global analysis focused on the role of each connection in the classroom context where it was made, and a specific analysis focused on the nature of each of the links that made up each connection.

Table 1 Description of the coding stages and their outcomes
Full size table

The categorisation process was first performed by two researchers (stages 1, 2 and 3). All the partial results were then discussed with a third researcher. All the categories and subcategories of mathematical connections and links were triangulated in stage 4 (Aguilar and Barroso, 2015) with an expert on mathematical connections that had already published some pieces of research on the definition and classification of mathematical connections. The expert used the emergent themes and matched them with the codes used in stage 2. This led to a refinement of the themes. Finally, content validity was used through expert judgement to search for the reliability and applicability of the characterisation of the emerging connections and links in the previous refinement. Expert judgement occurred in the context of a workshop on mathematical connections, with the participation of 10 researchers in mathematics education from Colombia, Mexico, Chile, Brazil and Spain, who had experience in the line of research on mathematical connections. Prior to the seminar, they were provided with the list of types of connections and types of links with fragments of the analysis so that they could assess whether the classification of the emerging connections and links was pertinent, based on the following four criteria taken from Vásquez et al. (2020): (a) sufficiency (if they allow to identify types of relationships); (b) clarity (if they are understood syntactically and semantically); (c) coherence (if they are logically related to the dimension they measure); and (d) relevance (if they are essential and should be included). The comparison between classifications of connections led to a more refined identification of coincidences and differences of our proposed categories of links with the classifications proposed in other research studies (Businskas 2008; Rodríguez-Nieto 2021) which led, in turn, to the introduction of new terms for naming categories of links, such as the term metaphorical projection.

Results

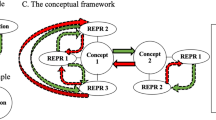
The analysis of the eight classroom sessions resulted in the identification of 34 connections. Stage 1 of the analysis revealed that in a classroom context a connection can be a network of relations called links. Therefore, connections can be understood as semiotic functions that many times appear as chains or sets of other semiotic functions (the links). Each of the links is sustained by a relation between objects, such as the equivalence between representations or procedures, the application of procedures, justifications, generalisations, implications, the emphasis on a particular case or the existence of a common feature. Figure 2 shows the general structure of connections in the classroom. The numbering of the links is defined by their chronological appearance. The maximum \(n\) that we have identified is 6. Connections can be made up of one single link or many coordinated links.

Fig. 2
figure 2

Elementary structure of connections as a network of links

Full size image

Classification of Connections

The results of the analysis led to the characterisation of the connections and the links that shaped their internal structure. Figure 3 shows the four categories of connections that were identified: intra-mathematical conceptual connections with treatment (IMCT) and with conversion (IMCC), intra-mathematical connections related to processes (IMCRP) and extra-mathematical connections (EMC). The connections have been numbered following their chronological order of appearance.

Fig. 3
figure 3

Classification of connections

Full size image

Intra-mathematical conceptual connections are relations established between representations, definitions, operations, properties, procedures, justifications, and models associated with a concept. These connections are in turn differentiated into two categories, those that involve conversions and those that only entail that a treatment appears, in the sense proposed by Duval (2006).

The intra-mathematical conceptual connections with treatment make up most of the connections identified in the classroom. They are connections that are made between objects related to the same concept, without changing registers (Duval, 2006). During the analysis, 22 conceptual intra-mathematical connections with treatment were identified. Although the 22 connections entail a transformation between representations in the same register, there are some connections that emphasize the characteristics of the representations used; connections that emphasize definitions; connections that emphasize procedures; and connections that emphasize patterns and properties. These different emphases result in four sub-categories of intra-mathematical conceptual connections with treatment. In Table 2, the different sub-categories of IMCT are described, and the connections belonging to each sub-category are listed.

Table 2 Description of the sub-categories of intra-mathematical conceptual connections with treatment
Full size table

Although all connections are made explicit through particular representations, their classification depends on what the connection emphasises. For instance, in C21 (Table 3; Fig. 4), the difference between \(\frac{{a}^{p}}{{a}^{q}}\) when \(p\ge q\) and when \(p<q\) is discussed and the relation between representations is emphasised. Iván’s utterance (l1) what if p is smaller than q? connects the representations of the previous case (\(p\ge q\)) with a new possible representation without the previous restriction. Next, his own inference (would it be negative?) along with the teacher’s answer (l2) introduces a link between powers with natural exponents and powers with integer exponent. In C22, on the contrary, the equivalence of procedures for calculating \(\frac{-{a}^{b}}{-{a}^{b}}\) is discussed focusing on their suitability for performing the calculation, and the emphasis is placed on why the two procedures are equivalent.

Table 3 Excerpts of the transcription that define the links for connection C21
Full size table
Fig. 4
figure 4

Internal structure of the connection C21

Full size image

One single intra-mathematical conceptual connection with conversion was identified, C15 (Table 4), which seeks to coordinate (l4) powers with integer bases with a real model (going to the basement –2 of a building). In this case, the logic of the model does not determine the interpretation of the operations (l3), since it does not seek to use a metaphor of the power in a real context, but the model is used to introduce a change in register which helps to show the difference between the order in which the two operations should be applied in each case (l1 and l2). Thus, it is not an extra-mathematical connection, but an intra-mathematical connection with conversion.

Table 4 Excerpts of the transcription that define the links for connection C15
Full size table

Intra-mathematical connections related to processes are relations established between a mathematical concept and a mathematical process that transverses the mathematical activity. More specifically, they are considered connections that establish relations with reasoning and justification, with the communication of mathematical information and with the heuristics related to problem-solving.

For example, connection C1 (Table 5; Fig. 5) emerges when solving an activity on the greatest common divisor and the lowest common multiple of a pair of numbers. A student observes that there is regularity when one of the numbers is a multiple of the other and intervenes in class to mention it. A connection is established between the calculation procedure of the l.c.m. and the g.c.d., and a property related to the l.c.m. and the g.c.d. of pairs of numbers, where one is the multiple of another. The establishment of this relation further explores the concepts of l.c.m. and g.c.d., since both the multiples and the denominators of both numbers are analysed exhaustively. The first link (l1) produced is between the general calculation method and the particular case in which one number is the multiple of the other (Table 5, Fig. 5). Below, the utterances of the students and the teacher highlight the property observed in the previous particular case, generalising for any pair of numbers in which one is a multiple of the other (l2). Based on the previous generalisation, the teacher establishes another generalisation formulating the previous property in a more elaborated way (l3). By demonstrating in a detailed and rigorous manner, the previous generalisation is further explored (l4). Lastly, through the final assessment of what it means to demonstrate, the teacher justifies the importance of the justification method that she has just shown (l5).

Table 5 Excerpts of the transcription that define the links for connection C1
Full size table
Fig. 5
figure 5

Internal structure of the connection C1

Full size image

The establishment of this connection may help students to understand that to be sure that a mathematical property is fulfilled, a rigorous justification must be performed in all cases, and we must not limit ourselves to accepting an inductive result, which is fulfilled in some particular cases, meaning it is a connection related with processes.

To identify this category of connections, it is necessary to identify an explicit element which serves to interpret that the connection goes beyond considering a specific concept and focuses on a more general process in mathematics which is applied to a wide variety of concepts. For instance, in the previous example, the explicit utterance of the teacher that defines l5 is what represents the move from a specific situation (the proof that the pattern can be generalised) to a process (the difference between inductive and deductive reasoning).

Eight intra-mathematical connections related with processes were identified, among which three blocks are differentiated: those related with explanation, justification and demonstration, as in the previous case (C1, C5, C7, C17 and C27); those related with accuracy in the use of mathematical language (C33); and those related to the ability to decide based on why and when to use a procedure or a property (C20, C29).

Extra-mathematical connections are established between an extra-mathematical reference and a mathematical content. Two main types of extra-mathematical connections are defined. First, the connections in which extra-mathematical references are used to improve comprehension of the mathematical concepts, such as the basic metaphors (grounding) described by Lakoff and Núñez (2000). Second, the connections that show applications of mathematics in extra-mathematical situations, such as the knowledge of aspects of real life both in everyday terms and in other curricular disciplines such as visual art, social science, experimental science, economics, technology and music. Although we did not identify any connection of this second type, as there was no application of mathematics to any other context, it is relevant to mention them as they have been widely studied in mathematics education.

Connection C4 is an example of a connection in which extra-mathematical references are used to improve comprehension of the mathematical concepts. The connection is created between the addition and subtraction of integers and a model of movement which helps to interpret them. While the students solve \((-8)-(-4)\), a connection is established between {Z, +} and a model of movement in which there is a positive direction (whether to the right or up) and a negative direction (the opposite to the previous one, respectively). Below, Table 6 displays the explicit utterances that define each link of connection C4 and Fig. 6 shows its structure.

Table 6 Excerpts of the transcription that define the links for connection C4
Full size table
Fig. 6
figure 6

Internal structure of the connection C4

Full size image

During the analysis, 3 extra-mathematical connections were identified (C4, C13, C31). Two of them refer to connections the teacher made between mathematical language and computer language (C13), and between mathematical language and musical language (C31). In both cases, characteristics of non-mathematical language were used to show the importance of understanding and using mathematical language correctly.

The previous characterisation of connections was obtained through a global analysis of connections that considered the role that each connection played in the construction of mathematical knowledge, in the classroom context where it was made. However, since most of the connections (27 out of 34) were formed by more than one link, it is necessary to consider how the links that form the connection are coordinated and how these links inform of the nature of mathematical connections.

Classification of the Links That Make Up the Internal Structure of the Connections

Throughout the analysis, we identified 12 types (themes) of links that can be grouped in 4 categories: representational, based on common feature, procedural and argumentative (Fig. 7). Below, we present a detailed description of each category and provide examples of each type. The numbers in parentheses stand for the number of the link in the internal structure of the connection that precedes the parentheses. For instance, C12(2) stands for the link 2 in C12.

Fig. 7
figure 7

Classification of links at stage 3 and stage 4 of the analysis

Full size image

Representational: The link is established between two representations of the same mathematical object (\({R}_{1}\to {R}_{2}\)). The link can relate equivalent representations (ER), when both representations belong to the same register (e.g. in C12(2) the teacher links \(-{2}^{5}\) and \(-{\left(+2\right)}^{5}\)) to emphasize the base of the power) or alternate representations (AR), when there is a change in the register (e.g. representing numbers geometrically).

Based on common features: The link is established between two objects \({O}_{1}\to {O}_{2}\) that share a common feature, without being equivalent. These links are triggered by erroneous and ambiguous interpretations of mathematical objects by the students. The common features that sustain the link can be related to their definition (CFD), for instance in C18(2) when a student makes the mistake \({\left(-1\right)}^{36}=-1\cdot 36\) and refers to the power as a multiplication. The student identifies that the notion of multiplication is used in both operations and assigns an erroneous meaning to \({\left(-1\right)}^{36}\). This category of links may also be related to commonalities in the representation (CFR), for instance in C15(1,2,3,4) (Fig. 4) or in C34(1), when a student explicitly refers to \(\frac{8}{32}\) and \(\frac{32}{8}\) as being equivalent. In this case, the student uses the numbers represented in the fraction \(\frac{8}{32}\) and searches for a way to obtain an integer result, assigning an erroneous meaning to \(\frac{8}{32}\). Finally, they can be related to some metaphorical projections (MP) in which the metaphor is used in a literal way. For instance, in C4(2), when a student interprets \(-4-(-8)\) as a metaphor of being in basement 8 and going up 4 floors.

Procedural: This category refers to two different types of links. The first is called procedure link (P) and refers to links between a concept and a procedure (\(C\to P\)) that can be used when dealing with the concept. For instance, in C4(1), the teacher suggests that using the rules for operating with integers to obtain a notation without double symbols is a good resource to make the calculation. The second one is called equivalent procedures link (EP) and refers to links (\({P}_{1}\to {P}_{2}\)) between two procedures that are useful for solving the same task. For instance, in C22(1,2,3,4,5,6), students propose four different procedures for solving \(\frac{{\left(-5\right)}^{7}}{{\left(-5\right)}^{7}}\) and the teacher conducts a discussion on their equivalence.

Argumentative: The link is established between two propositions (\({PR}_{1}\to {PR}_{2}\)), where \({PR}_{1}\) stands for a premise and \({PR}_{2}\) stands for a conclusion. This category of links includes reasoning of several kinds. First, it refers to justifications (JU) of practices in mathematics. For instance, in C1(5) (Table5; Fig. 5), the teacher discusses the difference between inductive reasoning and deductive reasoning emphasizing the meaning of a mathematical proof; in C27(1), the teacher discusses the difference between \(\sqrt{a+b}\) and \(\sqrt{a}+\sqrt{b}\) providing numerical examples; or in C21(2), the teacher justifies the use of the representation \({a}^{-k}, k\in N\). Second, it refers to arguments built upon a principle of transitivity (TR). For instance, in C16(2), a student asserts that two operations are the same because they have the same results and the teacher answers providing counterexamples of different operations that have the same result, explicitly emphasising that having the same result does not mean that the operations are the same. Third, it refers to implications (IM) or if–then arguments. For instance, in C14(3), when discussing the difference between \(-{2}^{5}\) and \({\left(-2\right)}^{5}\) the teacher shows three different representations of \({2}^{5}\)(\({2}^{5};2\cdot 2\cdot 2\cdot 2\cdot 2;\) and \(32\)) and argues that if we change the sign of all three of them, then they would also represent the same operation. Fourth, it can refer to the application of a property to a particular case (PC). For instance, in C7(1), the teacher examines a particular case of a procedure previously proposed by a student for solving \(-4-(-8)\). Finally, it can refer to generalisations (GE) of a property to a broader set, as in C21(1), when a student proposes a generalization of \(\frac{{a}^{p}}{{a}^{q}}\) when \(p\ge q\) to the case when \(p<q\).

Table 7 shows the relation between the categories of connections and the categories of links that were identified during the analysis of the eight sessions. The reduced amount of extra-mathematical connections and intra-mathematical conceptual connections with conversion that were identified in the analysis makes it difficult to observe a relation between them and specific types of links. However, in the case of intra-mathematical connections related with processes, they are mostly related to argumentative links. In the case of intra-mathematical conceptual connection with treatment, all the types of links were identified, which signals the diversity of such a kind of connections. Other implications of the coordination between the global and specific analyses (Table 7) are discussed in the next section.

Table 7 Types of links that made up each category of connection
Full size table

Discussion

The fact that the definition and the characterisation of connections stem from the analysis of classroom practice helps to identify determining aspects to understand the nature of mathematical connections in the classroom and their underlying structure. In the context of classroom mathematical activity, connections may emerge as a result of multiple interactions between teacher and students. This led to a conceptualization of connections as networks of links, which coincides with that proposed by Eli et al. (2011). This conceptualization entailed two complementary levels of analysis: global and specific. The coordination between these two levels enabled us to harmonise, from a classroom practice perspective, the broad idea of connection fostered by curricular guidelines (NCTM 2000; Department of Education U. K., 2013) with several classifications of specific connections provided by the research (Businskas, 2008; Dolores-Flores & García-García, 2017; Eli et al., 2011; Rodríguez-Nieto, 2021).

The four categories of connections characterised in the global analysis are closely related to the definition of connection provided by the connection standard (NCTM, 2000), as extra-mathematical connections and intra-mathematical conceptual connections with conversion can be identified in the descriptions of connections provided by the connection standard (NCTM, 2000). Intra-mathematical connections related to processes and intra-mathematical conceptual connections with treatment are relevant examples of important types of connections fostered by the connection standard, the formulation of which may be diffuse. Intra-mathematical connections related to processes provide explicit examples of what it means to understand how mathematical ideas interconnect and build on one another to produce a coherent whole, as they emphasize transversal processes that help to comprehend the coherent whole (NCTM, 2000). This category of connection occurs when the teacher uses a discussion on a particular activity to highlight the role of proof in mathematics (C1, C5, C7, C27), or the importance of rugosity in communication (C33), finding patterns (C17, C29), and finding alternative procedures (C20). The fact of connecting particular activities with general processes suggests that intra-mathematical connections related to processes may reinforce a bidirectional movement between an algorithmic context and another more abstract or general one. The explicit establishment of intra-mathematical conceptual connections with treatment is associated with discussions about the understanding of the objects that intervene in the practices that appear when operating with integers (representations, definitions or properties), which can promote the construction of a greater ability among students to relate objects and practices through semiotic functions. In the case of extra-mathematical connections, despite only three of this kind of connections being identified, it is important to study in greater depth the way extra-mathematical connections are built upon intra-mathematical connections, as reported by De Gamboa et al. (2020).

The specific analysis allows us to identify how the different categories and themes of links described in other research studies determine the role of each connection in the classroom context where it is made. Table 7 shows a trend in some links to appear as part of particular categories of connections. Equivalent representation links (e.g. Adu-Gyamfi et al., 2017; Businskas, 2008; Dolores-Flores & Garcia-Garcia, 2017), and the common feature of representation and common feature of definition links (Eli et al., 2011), tend to be part of intra-mathematical connections with treatment that are made at moments when the mathematical activity has an exploratory nature and the students must identify equivalent representations and use them to perform procedures that have been explained previously. Common features of representation and common features of definition links were related with moments at which the utterances of the students revealed ideas and questions related to misconceptions. The reasoning associated with the appearance of these links tends to be rather unsophisticated. Metaphorical projections (Rodríguez-Nieto, 2021) links tend to appear as part of extra-mathematical connections in which extra-mathematical references are used to improve comprehension of the mathematical concepts. Procedural links (Dolores-Flores & Garcia-Garcia, 2017) tend to be part of intra-mathematical conceptual connections with treatment made at moments when the interactions between students and the teacher included the use of the properties of integers and the operations with them at a descriptive level. Generalization, implication (Businskas, 2008), and particular case links (Businskas, 2008; Dolores-Flores & Garcia-Garcia, 2017) tend to appear as part of intra-mathematical connections related to processes and intra-mathematical conceptual connections with treatment made at moments related to the justification of new properties and some fundamental practices in mathematics, such as making a hypothesis, generalising or discussing the suitability of some practices in mathematics.

However, not all the identified links can be found in other research studies. In the case of the link equivalent procedure, situations that do not correspond to the procedure type proposed in the reviewed literature are observed, since two procedures appear simultaneously and the utterances determining the connection are aimed at justifying their equivalence, while in the case of the procedure type only one procedure is considered at a time. The identification of equivalent procedure links is relevant because they tend to be part of intra-mathematical conceptual connections made in classroom discussions about the differences and similarities between procedures that can be used to solve the same task. Identifying and justifying the equivalence of different procedures for a particular task may be a way of recognizing and using connections among mathematical ideas (NCTM, 2000). The link justification cannot be compared to the implication type proposed by Businskas (2008) and Rodríguez-Nieto (2021) since it is not limited to if–then reasonings, but rather refers to justifications in a broader sense that may include the justification of the correction of a procedure, the relevance of the application of a procedure in a specific context or the importance of demonstration in mathematics. The identification of justification links is relevant because this broad sense of justification may help students to use various types of reasoning that are not restricted to if–then reasonings, such as constructing viable arguments to validate the use of procedures.

Moreover, the coordination between the two levels of analysis allows us to describe factors that determine the complexity of connections. Results show that one same type of connection can be made at different levels of complexity depending on the role that links play (representational, regulatory, explanatory or justifying, in terms of the OSA). For instance, Table 7 shows that intra-mathematical connections that emphasise representations can be made at a descriptive level (C12), using representational and common feature links, or at a more complex level using argumentative links (C21; Table 3; Fig. 4) that have a justifying role in terms of the OSA. Therefore, the types of links that make up the connections may help to understand the complexity of such connection. This factor of complexity is consistent with the notion of quality introduced by Mhlolo et al. (2012). The combination of this factor, together with the complexity related to the appearance of conversions (Adu-Gyamfi et al., 2017; Duval, 2006) and the interactive nature of classroom activity, may help to understand specific difficulties experienced by students when working with connections as excess cognitive load (Rittle-Johnson et al., 2009; Sweller et al., 1998), problems with coordinating different semantic fields (Gick & Holyoak, 1980), and barriers created by differences in language (Jackson et al., 2014).

Conclusion

In the context of classroom practice, connections appear as networks of links that are made explicit by the teacher’s or students’ utterances. The coordinations between the global and the specific analyses illustrate how links are coordinated to shape categories of connections that may help to understand how some connections described in the connection standard are brought into play (intra-mathematical connections related to processes and intra-mathematical conceptual connections with treatment). These results complement those of Presmeg (2006), adding some specificities of classroom practice. The identification of explicit factors that may determine the complexity of connections in the classroom shows how and why the different categories of connections can be made at different levels of complexity and may shed some light on understanding the difficulties students experience when working with connections. As the making of connections in the classroom can trigger learning opportunities for students (De Gamboa et al., 2020), understanding the complexity of such connections may help teachers to understand student’s construction of new mathematical entities, as the coordination of the different links that form connections may be understood as a dynamic nesting of epistemic actions in the sense of Hershkowitz et al. (2001). Gaining an in-depth understanding of how mathematical connections work in the classroom can help teachers to better understand students’ difficulties and misconceptions when making connections, to better interpret curricular guidelines regarding connections, to adapt class methodologies, to design activities, and to manage classroom discussion with the goal of helping students to understand complex connections and make the most of the learning opportunities triggered by them (De Gamboa et al., 2020). This signals the importance of investigating the relationship between teacher knowledge and the effective use of connections in the classroom as is the case of Dreher et al. (2016) or De Gamboa et al. (2020) and the need to better understand how theory-based recommendations can be brought into play in classroom practice (Leikin & Levav-Waynberg, 2007).

Even if the case was selected as being of a common type or an exemplifying case, the characteristics of the classroom organisation and the topic that was worked on during the sessions conditioned the emergence of different types of connections. The results of this research can be particularly useful to understand how mathematical connections appear in classroom environments where the interactions between the teacher and the students are fostered, and particularly when the topic worked on is related to the definition of concepts, operations and properties. However, more research should be conducted on other kinds of classroom organisation and topics, as little evidence has been provided on the categories extra-mathematical connections and intra-mathematical conceptual connections with conversion.