Introduction

Two aspects that motivated the realization of this work were, on the one hand, the relevance of the topic of probability distributions in statistics and probability, and on the other hand, the fact that several authors have suggested the use of technology in its teaching. Nevertheless, the complexity of teaching the normal distribution has been little researched, particularly at the high school level.

The concept of distribution is central in statistics and probability since it is a powerful mathematical tool to represent and operate with variation and uncertainty. Two kinds of distributions can be distinguished: empirical and theoretical. In statistical practice, the problem of how to properly relate empirical distributions (data) and theoretical distributions (models) is recurrently presented to make predictions and generalizations: “Theoretical distributions are models that generate variation, which is similar to that which can be observed in empirical distributions” (Biehler et al., 2018, p. 155).

In teaching, the treatment of both kinds of distributions is usually done separately. Empirical distributions are studied in the descriptive statistics topic and theoretical (probabilistic) distributions in the probability topic. Moreover, the sequence of concepts studied in probability follows a path completely unrelated to empirical distributions: the notion of probability, random variables, and probability distributions. This separation does not contribute to form a solid basis for statistics or probability, which needs to be open to applications beyond games of chance. Research on the concept of distribution has focused on finding out how students reason with empirical distributions (Biehler et al., 2018), and there is little research to explore alternative ways to develop reasoning with theoretical distributions, particularly concerning the normal distribution (Batanero et al., 2004).

The availability of educational software provides the possibility of imagining another route to approach theoretical probability distributions through simulation processes closer to empirical distributions; in fact, in the literature, they are often called the same way. Although various ways of using simulation to address and solve classical inference problems have been proposed in mathematics education research, for example, the “three Rs” process of randomizing, repeating, and rejecting to organize the discussion (Lee, 2018); studies focused on producing a statistical sense of theoretical probability distributions are lacking.

The concept of the theoretical probability distribution is based on the notions of probability model and random variable. According to the research literature, with the help of computational simulation and a frequentist approach to probability, as mentioned below, it is possible to approach important notions about distribution by avoiding certain formalisms related to the probability model and leaving implicit the notion of a random variable. In this article, we further analyze a previous research report (Salinas et al., 2018).

Thus, in this research, we are interested in fostering an intuitive approach to the notion of normal distribution in real-world problem solving on the part of high school students. It aims at gaining insight into how the planning and application of a teaching experiment, designed in the framework of the lesson study methodology (Murata, 2011), plays a relevant role in the integration of a digital resource (software) (Trouche et al., 2020), allowing the simulation and discussion of a probability problem to take place.

The article consists of six sections, including the “Introduction”, “The Background”, the “Research Problem”, the “Theoretical Framework”, the “Research Design”, and “Discussion of Results and Conclusions”.

The Background

So far, few papers have been found on teaching and learning the normal distribution with high school students. Likewise, few works have been found on this topic at the university level and in introductory statistics courses. Similarly, research on teacher training to teach probability is very scarce (Batanero et al., 2016).

The topic of probability distributions brings together concepts of statistics and probability and is a bridge to statistical inference, in which the notion of normal distribution plays a central role. However, this topic involves a great mathematical complexity, and its understanding requires deep prior knowledge of mathematical analysis and probability (Carpio et al., 2009). All this generates an important challenge for its teaching. In addition, its approach in high school assumes previous knowledge of probability, such as understanding the classical and frequentist approaches to probability, being able to differentiate the characteristics of these approaches, and having the ability to relate them (Batanero, 2005), a process in which, in turn, underlie the concepts of variability, randomness, and independence (Sánchez & Valdez, 2017).

Jones et al. (2007) point out that the concept of distribution is usually introduced in the statistics and probability curriculum at the baccalaureate level, where, in general, curricula emphasize the binomial distribution. Among the didactic studies on this topic, we highlight the following. At the basic level, Abrahamson (2009) explores a physical semiotic mediation device for students (11–12 years old) to design groupings of objects that prefigure a hypergeometric (almost binomial) distribution. At the basic middle level, Flores et al. (2014) conducted a study where students’ (13–14 years old) progress in notions of probability is promoted and observed by simulating binomial data on a computer. At the high school level, we locate the works of Van Dooren et al. (2003), who report a tendency to apply proportionality properties in binomial problems where they are not relevant, and Bill et al. (2009), who report a study where a binomial problem is examined using three different approaches: classical, Pascal’s triangle, and a frequentist approach using Fathom; the latter approach proved fruitful for students with lower mathematical skills, and, finally, García et al. (2014) report an activity in which binomial data are generated and students’ perception of the variability of the simulated data is assessed. Finally, at the university level, Maxara and Biehler (2006) report an investigation with prospective mathematics teachers who had participated in an introductory course on stochastics. In their results, they found that working with statistical software allowed students to perceive variability in binomial situations, sample size effects, and aspects of the law of large numbers.

Probability distributions show important connections between probability and statistics through the notion of relative frequencies. For this reason, the frequency approach is very beneficial in teaching (Godino et al., 1987). It has also been said that this approach has the advantage that technology makes it possible to apply this approach straightforwardly. For example, using simulation, an experiment can be repeated a large number of times, and convergence is observed (Maxara & Biehler, 2006); thus, “The difficulty of the law of large numbers is thus addressed, replacing it with an empirical and intuitive approximation of it” (Gea et al., 2017, p. 268).

The absence or lack of consolidation of prior knowledge related to the normal distribution is one of the main difficulties detected in the literature. In this regard, Batanero et al. (2004) analyzed the results of a teaching experiment carried out with 117 university students and found that the complexity of the normal distribution is since its understanding requires the integration and relationship of different statistical concepts and ideas that are equally complex: probability, density curve, dispersion, skewness, and histogram. Along the same lines, Carpio et al. (2009) analyzed the mismatch between the personal meanings of 45 university students and the institutional meanings of the concept of normal distribution.

From the literature review, it can be observed that the main difficulty of the students analyzed is in the knowledge of conceptual content. The results of these works foreshadow the possible difficulties that high school students may exhibit.

Research Problem

We consider that the emphasis on mathematical formalism should not be the central focus of research on the teaching and learning process of statistics and probability in high school. At this school level, it is convenient to study the intuitive basis of the concepts of the randomness of the mathematical formalism of that subject and the type of difficulties encountered in developing intuition. In this sense, a very important didactic resource is simulation. We think of simulation as the process of replacing a random experiment or situation with an equivalent one that represents it. In this way, simulation is a didactic resource that can help to distinguish between model and reality and, without using mathematical symbolism, improve intuitions about random aspects (Batanero, 2009).

Thus, our research problem is to try to identify the type of reasoning performed by students from a high school group when using the Fathom software to solve a probability problem related to the context of school life and, in this way, to observe the possible contribution of this resource for the intuitive support of the notion of normal distribution, which could provide a basis for its later formal understanding. The use of the software is integrated into the process of simulating a problem. In this process, it is essential for students to realize that for large values of the number of trials, it is possible to find an approximate solution to a binomial problem, which anticipates the representation of the normal distribution.

Theoretical Framework

We consider the documentational approach to didactics (DAD) (Trouche et al., 2020), whose perspective is to study the way teachers interact (design, use, adapt, and modify) with curriculum and other resources during their practice. This approach is mainly inspired by the instrumental approach (Rabardel & Bourmaud, 2003), which seeks to understand how artifacts are transformed into instruments, specifically in the field of technology. Trouche et al. (2020) thus point out that “The development of the instrumental approach corresponded to a period where teachers were facing the integration of new singular tools (a calculator, a computer algebra software, a dynamic geometry system…)” (p. 38).

In DAD, and following Adler’s (2000) proposition, the term resource is used as “the verb re-source, to source again or differently” (p. 207) on the one hand, to consider the broad spectrum of resources (physical or psychological) that have the potential to nurture and modify the teaching activity and that are cultural and social means provided by human activity (e.g., computers and language), produced for specific purposes (e. g. problem solving, Gueudet & Trouche, 2009), and, on the other hand, to broaden the set of elements available for teachers’ work and include interactions between teachers (e.g., for lesson design) and between teacher and student in classroom interaction (Gueudet et al., 2012).

In this way, resources (including digital resources such as computer software) are conceived not only from material objects but from all those involved in understanding and problem-solving. The interaction that the teacher carries out with material and non-material resources in his/her teaching practice is the driving force of the genesis — emergence or transformation of these into others, called documents — since it allows the teacher to transform these resources. The teacher’s documentation work with the resources leads to their “emergence or transformation” into documents; this dialectical and dynamic process is known as documentational genesis (Gueudet & Trouche, 2010).

In documentational genesis, documents are created from a process in which teachers construct schemes of usage for situations within a variety of contexts, a process exemplified by the equation: “document = resources + schemes of usage” (Gueudet & Trouche, 2009, p. 205). Thus, an important notion is that of scheme. The scheme makes it possible to analyze teachers’ thinking from observable actions. As mentioned by Vergnaud (2011), “the scheme not only organizes observable behavior, but also the underlying thinking activity” (p. 43). It is the way activity is organized for a variety of situations. As Trouche et al. (2019) state: “a situation is an issue faced by an agent in his/her regular activity (e.g., for a teacher: preparing a lesson)” (p. 54). Schemes (e.g., how to work with a software during a lesson) comprise rules of action and inferences, structured through uses, and operational invariants during activity. Uses correspond to the observable part of the scheme, which occurs during the teacher’s action. While the operational invariants correspond to the cognitive structure that guides the teacher’s action, they constitute the epistemic part of the scheme. Operational invariants are the cognitive elements that determine scheme activation. There are two types of (associated) operational invariants: theorems-in-act, which are the propositions considered true, and concepts-in-act, which are the concepts considered relevant (Trouche et al., 2020). Thus, schemes are only observable through the actions carried out by the subject when working with the resources (Gueudet & Trouche, 2009).

Thus, in the context of the use of digital resources, in particular the use of educational software, different researchers have argued that a simulation using repeated sampling can be an essential didactic approach to help students develop an understanding of abstract statistical concepts and conceptually develop statistical inference (Maxara & Biehler, 2006; Lee, 2018). However, understanding each part of a simulation and the relationships between the parts is conceptually complicated (Lee, 2018).

We adopted as a central working hypothesis that the simulation of the problem with the software allows us to establish, in an intuitive way, a bridge between the binomial distribution and the notion of normal distribution. Since the function of the software was to perform the simulation of a problem for its resolution without using mathematical formalism, the importance of analyzing the simulation process as a modelling tool in probability emerges (Batanero, 2009). Simulation — through the resource — is closely linked to the modelling processes that constitute a central aspect of scientific knowledge, particularly in the teaching of probability. Therefore, it has been strongly recommended to pay attention to the modelling process (Batanero, 2005; Henry, 1997).

According to Batanero (2005) and Henry (1997), we consider simulation as a pseudo-concrete model that offers the possibility of working without mathematical formalism when analyzing random situations. Simulation can then act as an intermediary between reality and the mathematical model. For which it is important to distinguish between model and reality.

We formulate the following research question:

In what way does the simulation of a problem related to normal distribution contribute to the development of students’ intuition about this notion?

Research Design

This research is qualitative in nature and is guided by a design research approach, with a prospective vision that subsequently seeks to provide elements to improve the teaching and learning process of the proposed topic (Lehrer, 2019). We use this approach to conduct scientific research as a design experiment, in which both “engineering” of forms of learning and the study of those forms of learning within the context defined by the means, or resources, to support them are implied.

Context of the Study

To answer the research question, a working group was formed following the collaborative approach of the lesson study (LS) methodology (Murata, 2011) with the purpose of conducting a teaching experiment (Steffe & Thompson, 2000) with an exploratory character to observe the ways and means of operating of students in the treatment of the normal distribution, while interacting with a software, and in which a research team collaborates with a professor, member of the research team to assume the responsibility of instruction.

Six high school mathematics professors participated, whom we refer to in the data analysis as P1, P2, …, P5 respectively; all of whom at the time had research training in mathematics education: two PhDs, two doctoral students, and two with master’s degrees. Two of these participants are authors of this paper, and a third was the one who conducted the teaching experiment, and we refer to him in this paper as the “professor-researcher” (PR). Regarding teaching experience, two professors were tenured, full-time professors at the institution, with seniority of 41 and 42 years, respectively. The other four were part-time lecturers, with a seniority ranging from 1.5 to 7 years. In addition, four participants were teaching the Statistics and Probability course at the time of the study.

Research Stages and Data Collection

First Stage (3 sessions): elaboration of the research lesson, which was assumed as a teaching experiment according to the characteristics established by Steffe and Thompson (2000). All sessions were video recorded. We discussed collegially how to articulate the use of the Fathom software in the design of the experiment, and, subsequently, to examine its role in the teaching and learning process, that is, to reflect on the use of symbols (graphics) integrated into the software and its intervention in the development of meaning. Thus, adopting as the main resource the use of the Fathom software that uses the interpretation of frequential probability, it was taken as a research hypothesis of this exploratory study (Steffe & Thompson, 2000) that the simulation with this software would contribute to developing the intuition to advance in understanding the notion of the normal distribution as an approximation of the binomial distribution. This hypothesis is a derivation of the idea pointed out by different authors about the importance of computation in simulating stochastic processes that contribute to the intuition of abstract concepts.

Second Stage (3 sessions of 90 min each): application of the teaching experiment. It was applied by the professor-researcher to his group of high school students in the Statistics and Probability II curricular course, sixth semester. Following the LS methodology, three of the other professor-members of the team participated as observers. All sessions were video recorded. The group of students consisted of 18 students (ten females and eight males between 17 and 18 years old). Student participation is denoted, in data analysis, as S1, S2, …, Sn, respectively. The students had knowledge of the subject acquired in a previous course, in which they had also started working with the Fathom software. Approximately half of the group had a mathematics subject pending approval, reflected in operational and conceptual difficulties. Likewise, most of them acknowledged having chosen Statistics and Probability because they considered them less complicated to pass than Calculus. Therefore, this group did not participate much due to the apathy they felt for the subject and/or the insecurity they had about their knowledge.

Digital Resource: Fathom Software

Fathom dynamic statistics is a software for learning statistics at the high school level. It allows students to explore and analyze data from a graph to visualize distributions and relationships between variables. Dragging variables makes it possible to visualize how dynamically changing data and parameters affect measurements and related representations in real-time. A crucial aspect is that this software allows the creation of simulations to investigate and test relationships in the data (Biehler et al., 2012).

Analysis Strategy

An authentic context problem is considered to calculate the probability of a situation represented by a binomial distribution. The simulation of repeated sampling processes is used so that the software facilitates the visualization of the behaviour of the pattern generated by increasing the sample size. Using the simulation, students should be able to observe that the binomial distribution tends to approach a bell-shaped distribution as the number of repetitions increases, that is, to observe that it is possible to approximate the calculation of the probability of a Binomial distribution through the area represented by the corresponding part of the histogram. This aspect intuitively suggests the approximation of the probability of the normal distribution to the probability of the binomial distribution.

The study uses an interpretative approach because the objective is to obtain information on how the computational resource affects the reasoning of the students, considering how it is shown in their actions and responses to the problems of situations posed by the notion of distribution.

In this way, we first identified the operational invariants that guided the application of the teaching experiment while using Fathom. Special attention was paid to the use of the Fathom software – as a resource — and to the effect that — through its appropriation and transformation —it had on the teacher’s practice when carrying out the application of the experiment. Subsequently, in the first session of the implementation stage, the type of reasoning that the students developed in the simulation process with the use of the software were analyzed since an important aspect of a teaching experiment is to be able to observe the achievement of particular learning.

In the following section of the discussion of the results, the operational invariants are pointed out, and their development in the management of the activities carried out by the professor-researcher is described.

Discussion of Results and Conclusions

This section presents the results of the study, the analysis of the first session of the implementation of the teaching experiment, and the conclusions. In the first stage of the study, the operational invariants inferred from the use of resources used by the teacher in his teaching practice were identified (Trouche et al., 2020).

Operational Invariants. From the professor’s actions that were inferred during the discussion in the first phase, the following operational invariants regarding the lesson and the use of Fathom can be highlighted:

  • IO1 (Theorem-in-Act): “Students engage best with a situation that is familiar to them, both experientially and conceptually”; this theorem-in-act is linked to an associated concept-in-act: “contextualized problems/exercises.”

  • IO2 (Theorem-in-Act): “They understand and remember a concept and procedure best when they arise as a necessity.”

  • IO3 (Concept-in-Act) “Simulation (the visual and dynamic aspect of the software) facilitates understanding of statistical ideas.”

  • IO4 (Theorem-in-Act) “The exercises strengthen the understanding achieved through simulation.”

After each implementation session, the professors held a meeting among to reflect on what had taken place. There were several discussions about the use of the software. Prior to implementation, there were those who were skeptical about using the software as the main resource for the lesson:

  1. 1.

    P1: It seems to me that it may be a situation that reduces the applicability of the strategy because it presupposes [...] a professor who is going to use the software, but in general, it is not used. So, I feel that approach could limit us in some sense.

This reservation is based on an authentic context. There are very few professors who know and use technology in their classes. A very limited institutional infrastructure makes it possible for only very few professors to use a computer room, which also does not have enough computer equipment. On the other hand, there were those who considered the use of this resource adequate:

  1. 2.

    P2: This part [referring to one of the simulations proposed for the lesson] is very illustrative and interesting because you modify the non-standardized distribution as you want and see that the standardized (curve) stays the same.

The statement at the end of [2], “you see that the standardized curve stays the same,” reflects an erroneous assumption that the perception of an image is sufficient for students to understand the underlying concept. Post-implementation, most professors saw the possibility of using the software as the main resource for the lesson. Although there were those who maintained their reservation:

  1. 3.

    P3: Maybe I do not use [the software] as much as him [the professor in charge of this experience] did. They [The students] do not know so much Fathom, and there are many [...], if they are running late, or any [technical problem], they get lost.

Regarding the application of the teaching experiment and the analysis of the learning identified, it is important to say that the operational invariants (OI) identified in the first stage of the study guided the management of student participation in this research. During the application of the teaching experiment, the professor-researcher promoted the students to formulate questions and propose answers in a group environment. From this situation, three interrelated aspects are highlighted below: the cognitive involvement of the students when participating in a collective conversation, the construction of shared meanings, and the process of reaching a consensus on mathematical meanings to advance in learning (Carrillo et al., 2008). Likewise, the simulation process is then reflected upon to identify its possible effect on the development of students’ intuition. All the above is related to the research question. According to the operational invariant IO1, the teaching experiment was started, in the first session, by asking the students to solve the following problem:

Maria has come to take a university entrance exam. The exam is multiple choice and consists of 200 questions. Each question has three answer options, only one of which is correct. The minimum number of correct questions to pass the exam and enter the university is 120. Maria answers 75 questions correctly and the remaining ones randomly because she does not know the answers. What is the probability that Maria will enter the university? Justify your answer.

Some students tried to calculate the probability using the binomial distribution, according to the IO2 expectation, since it was the topic they had just seen in class. They also tackled a similar problem, but with fewer cases (20 questions in total, of which eight were already correct and the remaining 12 were answered randomly), but they realized how impractical it was to use this way due to the number and complexity of calculations involved, as observed in the dialogue [4–14].

  1. 4.

    PR: Can anyone tell me how to calculate the probability they are being asked to calculate?

  2. 5.

    S1: I was trying with the binomial distribution.

  3. 6.

    PR: And what happened?

  4. 7.

    S1: I am just doing it.

  5. 8.

    PR: Did anyone else try to use the binomial distribution?

  6. 9.

    S2: Me with Bernoulli. [PR reminds students that a binomial distribution is the sum of Bernoulli random variables].

  7. 10.

    S2: Ah! So yes. Well, yes, as in the previous example [which involved fewer cases and was solved with the binomial distribution].

  8. 11.

    PR: What happened?

  9. 12.

    S2: Since there are more cases, they are already larger multiplications.

  10. 13.

    PR: You can use the binomial distribution, but what is the drawback?

  11. 14.

    S3: That there are many cases.

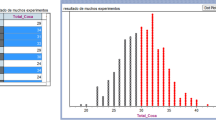
Due to the students’ experience with the software, as it was assumed (IO2), some of them directly considered using it. Then, in a co-responsible manner, and with the help of the professor-researcher, the whole group sought to solve the problem using this resource. The professor-researcher played a central role in the activity, both for skilfully manipulating the software and for guiding the students’ reflection on some important aspects of the simulation. It is important to mention that the simulation process was not accessible to the independent realization of the students themselves. From the simulation carried out by the professor-researcher (Fig. 1), an approximate answer was constructed, according to the IO3.

Fig. 1
figure 1

Simulation of the problem. It is represented from left to right: a the possible results of each question, b a possible result of answering 125 questions at random, c the number of correct answers obtained in each of 1000 samples of size 125, and d the histogram of the sampling distribution of the correct answers obtained in the 1000 samples

Full size image

It is important to notice that in Fig. 1d, the shaded area of the histogram (coloured in red) on the right side corresponds to the number of correct answers with which the exam is passed. Thus, by observing the simulation, the students interpret the solution to the problem:

  1. 15.

    PR: Looking at that simulation [...] Do you all think Maria will pass the exam? [Many students answer no]. Why?

  2. 16.

    S4: Because only 30 to 33% pass.

  3. 17.

    PR: How do you know it is between 30 and 33%?

  4. 18.

    S4: Because I selected the ones that got 45 hits forward (Fig. 1) and I get that it was 300 approximately.

Even though the concept of sampling distribution underlies the simulation and the students had not dealt with it in class, most of them were able to interpret the graph correctly and conclude that the probability of passing the exam was lower than the probability of failing [15, 16]. Concerning the research question, this situation shows that simulation helps students change their reasoning and move from calculating the probability of certain events to an inverse situation, i.e., given the observed results to infer the associated probabilities.

Thus, the simulation allows some students to conclude that the probability of passing the exam is low, as observed in the dialogue [16, 18]. This situation is neither spontaneous nor obvious; some students have difficulty recognizing that the proportion of cases in which 45 or more correct answers are obtained is the approximate probability that Mary will pass the exam. On the other hand, this difficulty shows the students’ lack of clarity about the relationship between the situation represented and the model, which underlies the simulation. That is, between the graph generated by the software and the problem at hand.

  1. 19.

    PR: What does that indicate? What is that? [some students point out that “it is a probability”, but it is not clear what they mean]. The probability of what?

  2. 20.

    S4: That 1,000 students in the same situation as Maria will get into university.

  3. 21.

    PR: No.

  4. 22.

    S2: The probability that María has [of passing the exam] [Nods the professor but clarifies that it is an approximate probability].

Even, as seen in the dialogue above [19–22], the students’ answers about the outcome of the simulation are uncertain. The ambiguity of their responses reflects confusion about which probability they are identifying. Something similar occurs with what Wilensky (1997) identified as epistemological anxiety: the feeling of confusion and indecision that learners experience when faced with various alternatives for answering a problem. Nevertheless, the solution of the problem through simulation with the software, the students are not able to justify the use of the simulation. This situation indicates that it is necessary to develop this intuition that favours simulation, which constitutes necessary support for later work with mathematical formalism.

Concerning the simulation process, three different states can be distinguished (Henry, 1997). The first is the concrete level in which students observe a real situation and describe it in their own words. This description already involves some abstraction and simplification of reality, insofar as it is necessary to choose what is relevant in the situation concerning the problem studied. Thus, one starts from this situation to represent such descriptions by a system of simple and structured relationships between idealized objects: this is the pseudo-concrete model level (Batanero, 2009). In this experience, their attention was assumed through the translation that the students made when considering the binomial distribution for its solution. The dialogue shown allows us to assume that the students identify the characteristics of the problem as the performance of repeated Bernoulli tests.

Following the above, and according to Henry (1997), the second modelling state in the simulation process is the formalization of the model, which presupposes the ability to represent the pseudo-concrete model in a symbolic system suitable for probabilistic computation. The probability theory then allows a solution to the problem posed. In our case, it is also observed that the students pretended to use the binomial distribution to solve the problem, but without success [4–14].

The third and final step highlights the importance of returning to the initial question and translating the mathematical results into terms of the pseudo-concrete model (model validation). However, in our case, since it was not possible to solve the problem directly using the mathematical model, we incorporated another step, not identified by Henry (1997), to perform the simulation with the software. Instead of using the idea of the random binomial distribution to estimate the probability of having “x” correct answers and to appreciate the relevance of this answer in the real situation, the software was used to solve the problem. Now the validation of the third step is given by translating the simulation results into terms of the pseudo-concrete model. As observed in [19–22], this situation is not immediate and requires a joint discussion with the students. The identification of this situation shows a difficulty manifested by the students related to being able to distinguish between reality and the model, that is, to differentiate between the practical situation of an experience and its graphical or symbolic representation that corresponds to the mathematical modelling through the software.

In the last activity of this episode, to motivate the introduction of the concept of normal distribution, the professor-researcher asked the students what they would do to solve the problem if they did not have the software. Moreover, based on the simulation of Fig. 1, he focused the students' attention on the graph in order to bring into play the concepts of density curve and normal distribution, and discuss the characteristics of the latter (symmetry, area under the curve equal to 1) and the properties of the normal curve (the shape is maintained when modifying the mean and/or standard deviation), when analyzing the shape that the distribution takes after a long series of repetitions. With the professor-researcher guidance, the density curve was plotted on the distribution graph (Fig. 2).

Fig. 2
figure 2

Approximation of the density curve to the histogram

Full size image

Regarding the characteristics of the normal curve, the students had difficulty recognizing that the area between the horizontal axis and the curve is equal to 1. Only one student was able to recognize that this property was fulfilled.

  1. 23.

    PI: This curve defines an area below it. Between this [horizontal] axis and the curve is an area. What do you think that area equals? [No student answers, but some murmur that it may be through the tools of integral calculus, a subject that some were taking at the same time in the semester]. Forget that there is the density curve. If I add the areas of each of these rectangles, what does the area equal?

  2. 24.

    S2: To one [Teacher nods].

  3. 25.

    PR: And if I am saying that this curve fits that data, what must the area under that curve be equal to?

  4. 26.

    S2: To one [student mumbles].

In general, students cannot interpret that there is a relationship between the binomial distribution and the normal distribution, which corresponds, in the simulation, to a transition from the discrete character of the former distribution to the continuous character of the latter. Although the graph represents discrete values of the variable, it also suggests the representation of a continuous variable when considering that the simulation can consider values as large as desired; hypothetically, when n → ∞. This result, related to the law of large numbers, does not appear spontaneously in an intuitive way, which leads us to conjecture that the professor should explicitly point out to the students’ awareness of this mathematical statement. Thus, adopting the law of large numbers will reinforce the students’ intuition that the binomial distribution tends to approach a bell-shaped distribution as the number of repetitions increases. Contrary to our hypothesis, the simulation with Fathom is insufficient to develop intuition and advance in understanding the notion of the normal distribution as an approximation of the binomial distribution. The fact that the teaching experiment was of very short duration suggests that further didactic work is required to improve the results.

Therefore, the support provided by the simulation to show that the density curve is a mathematical model of probability for a very large number of repetitions is not sufficient to understand this relationship. The fact that only the student who seemed to have an intuitive notion of limit related to calculus was the one who came partially close to understanding the relationship between the two types of distributions at stake, leads us to conjecture that this notion is a necessary condition to visualize the relationship between the two distributions. No other student made any proposal, indicating the great difficulty students have in visualizing that the density curve can be associated with a histogram with a very large number of cases. Going from the discrete to the continuous case is tough to understand, and it is not enough to visualize the graph, despite the simulation performed with the software.

In summary, the results of this research allow us to conclude that the use of the LS methodology with the theoretical framework (DAD), from the design of a lesson to its implementation, provided an important space for discussion to reflect collegially on the use of technology jointly with other resources (e.g., classroom management, pencil and paper, play videos) to intuitively introduce the notion of the Normal distribution. They allowed inferring the teachers’ knowledge (operational invariants) considering the observable part of the schemes and the usages of the technological resource, which contributed to focus the attention on the analysis of the management of the teaching experiment and see the relevant role played by the teacher-researcher in the implementation of the activity. Most of the professors saw well the possibility of using the software as the main resource of the lesson. However, there were those who maintained unconfident, considering the characteristics of their students, who did not know the software and technical problems observed in the implementation. Likewise, the teacher who applied the teaching experiment, and who was used to essentially using software to teach the subject of the normal distribution, also changed his vision and realized the need to incorporate other elements, such as activities with pencil and paper, history videos and applications to motivate the interest of students. In this way, it was observed that the collaborative work of planning, applying, and analysis of the teaching experiment contributed to improving the teachers’ knowledge about the conceptual content of the subject, as well as its didactic content (Ball et al., 2008; Carrillo-Yañez et al., 2018).

Likewise, the intuitive support provided by the software to the students through the simulation of the proposed problem was observed, as well as some difficulties that limited them to better understanding the activity. Evidence was found in favour of the fact that the software can support the intuition of stochastic concepts, in particular, that the simulation with the Fathom helped the students to change their reasoning from the calculation of the probability of certain events, as in a discrete distribution, to an inverse situation, in which, given the results observed in the simulation, they were able to infer the associated probabilities. In this way, the students’ tendency to perceive a data set as a collection of individual data was overcome (Hancock et al., 1992), and their attention was refocused on seeing the data set as a whole. This shift of attention is a significant step since, according to Bakker et al. (2003), students must see a data set as an aggregate, as a condition to develop the notion of distribution, intimately linked to the idea of shape, and to be able to interpret these shapes as symbols with meaning in terms of frequencies or density. From the simulation process, we could identify several difficulties the students manifested. Particularly, very important in the simulation process is to distinguish between reality and the model, that is, to differentiate between the practical situation of an experience and its graphical or symbolic representation corresponding to the mathematical modelling through the software. This situation indicates the need to pay more attention to the initial steps of a simulation process, which are related first to the analysis of the random situation of the problem and then to its simplified description, which allows passing to the model that represents it. In this teaching experiment, we moved immediately to this third step, the construction of the model. In addition, it is important to point out that there were difficulties on the part of the students in handling the software.

Regarding the working hypothesis, it was observed that the simulation with this software was insufficient to develop intuition and advance in understanding the notion of the normal distribution as an approximation of the binomial distribution. This result suggests the need to explicitly incorporate the law of large numbers as a prior idea to interpret the constructed graph as expected.

Finally, we consider that this research can contribute to the systematic study of the design, development, and evaluation of educational interventions as teaching–learning strategies and materials to advance knowledge about the characteristics of these interventions and the processes of designing and developing them.