Wave Breaking in Undular Bores with Shear Flows

Abstract

It is well known that weak hydraulic jumps and bores develop a growing number of surface oscillations behind the bore front. Defining the bore strength as the ratio of the head of the undular bore to the undisturbed depth, it was found in the classic work of Favre (Ondes de Translation. Dunod, Paris, 1935) that the regime of laminar flow is demarcated from the regime of partially turbulent flows by a sharply defined value 0.281. This critical bore strength is characterized by the eventual breaking of the leading wave of the bore front. Compared to the flow depth in the wave flume, the waves developing behind the bore front are long and of small amplitude, and it can be shown that the situation can be described approximately using the well known Kortweg–de Vries equation. In the present contribution, it is shown that if a shear flow is incorporated into the KdV equation, and a kinematic breaking criterion is used to test whether the waves are spilling, then the critical bore strength can be found theoretically within an error of less than ten percent.

1 Introduction

A river bore is an upriver-propagating transition between different flow depths which is generally caused by tidal forces. Similar flows can also be realized in controlled environments such as wave flumes, and a number of studies have been conducted to understand the main features of bores. In particular, in Favre’s work [21] a dedicated series of laboratory experiments and matching theory based on the shallow-water Saint-Venant equations is described. Favre’s experimental results have been examined theoretically from a number of angles. For example, the initial formation of the free-surface oscillations was explained from a physical perspective in [37, 43], the interaction of bores was considered in [9], and the breaking of the leading oscillations in the bore was considered in [10, 14, 22, 30]. Recent laboratory experiments revealing intricate properties of undular bores are detailed in [34, 35], and a numerical study of the flow structure is given in [8].

Of particular interest in the present article is the critical bore strength dividing the regime of laminar flow from the regime of partially turbulent flow. To explain the situation, assume without loss of generality that the downstream flow depth is the undisturbed depth in the wave flume, say $h_0$, and the incident depth is $a_0 + h_0$. Defining the bore strength by the ratio $a_0 / h_0$, it was found in [21] that there are three main bore types. If the bore strength is below 0.281, the flow is laminar, and since in this case, none of the waves are breaking, this case is termed the purely undular bore. If the ratio $\alpha = a_0/h_0$ exceeds 0.281, then the leading wave behind the transition front starts to break, and while the flow still features oscillations, there is some turbulence associated with the breaking waves. If the ratio exceeds 0.75, a fully turbulent bore appears.

The main purpose of the current paper is to demonstrate that the critical ratio found by Favre [21] can also be predicted using fairly simple nonlinear model equations such as the KdV equation in connection with a kinematic (or sometimes called convective) breaking criterion which defines the onset of breaking as the point when the horizontal component of the particle velocity exceeds the crest velocity. In effect, if we let the fluid particle velocity at the leading wavecrest of the bore be $U=U(x,\eta (x,t),t)$, and the local phase velocity of the wavecrest be C, then the wave starts spilling when $U/C > 1$. The kinematic wave breaking criterion is one of the simplest diagnostics for predicting the onset of wave breaking (see [28, 49] and the references therein), and has been shown to work well in a number of situations [25, 27, 29].

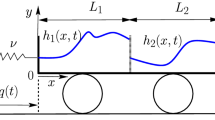
To study an undular bore in the context of the KdV equation, one needs to be able to pose a boundary-value problem where the incident-free surface level is imposed at, say, the left end of the domain, and the undisturbed level is imposed at the right end of the domain.¹ (see Fig. 1, left panel). Such a model has been developed for instance in [14, 42]. One can then evaluate the free surface numerically, and reconstruct the velocity field in the fluid column using the traditional asymptotic expansion of the velocity potential as an asymptotic Taylor series in powers of the vertical coordinate [51]. If the wave crest velocity is also evaluated numerically, then the convective criterion can be tested as an indication of whether the wave starts breaking or not.

Fig. 1

Left panel: definition sketch for undular bore. The bore front propagates at velocity C. The arrows indicate the vertical distribution of the horizontal velocity u(x, z, t) below the maximum surface displacement. Right panel: the critical amplitude $a_0$ dividing the purely undular case from the case where the leading wave features wave breaking graphed against the undisturbed depth $h_0$. The slope of the curves is the non-dimensional critical bore strength. The value $\alpha = 0.281$ was found in Favre’s experimental work [21]. The value $\alpha = 0.379$ was found in a previous work [10], the value $\alpha = 0.353$ was found in [14], and the value $\alpha = 0.307$ is found in the present work

Previous studies using this wave-breaking criterion in connection with a Boussinesq system and the KdV equation gave good qualitative results, but were not quantitatively convincing. In particular, the critical ratio was found to be $a_0 / h_0 \sim 0.379$ in [10] using a Boussinesq system, and $a_0 / h_0 \sim 0.353$ in the context of the KdV equation [14].

A possible improvement on these results may be obtained from the inclusion of vorticity into the description. Indeed, it is by now well known that vorticity can have a significant effect on the properties of surface waves (see for example [1, 30, 38, 41, 48] and references therein). One simple configuration is the case of a linear shear flow such as used in [48]. In particular in the case of long waves, this configuration is expected to capture many features of more general flows (see [17]), and it is our aim in the present work to determine whether the agreement with the experimental results of Favre may be improved by incorporating a constant shear flow into the governing equation. Indeed, the existence of vorticity in a similar situation was found in [26], and a mathematical inquiry into Favre’s results also suggested that vorticity might be present in such flows [30]. To get an idea of the strength of vorticity in Favre’s experiments, we derive a KdV equation in the presence of a linear shear flow. We then run a numerical simulation of an undular bore and try to match the wavelength of the oscillations of the numerical approximation of the KdV equation with the experimental wavelengths reported by Favre. This procedure leads to an estimate for the vorticity $\Gamma$ which is then used in simulations aimed at finding the critical bore ratio by testing the leading wave for incipient breaking. The approach outlined above yields a critical bore strength $a_0 / h_0 \sim 0.307$ which is within $9 \%$ of the experimental ratio of 0.281.

The plan of the paper is as follows. In the next section, the experiments of Favre are explained in some detail. Then in Sect. 3, the KdV equation with a shear flow is explained. Section 4 contains some comments about the numerical approach, and Sect. 5 describes the results of our numerical simulations. Finally, Sect. 6 contains a brief discussion which puts our findings into context with respect to some recent studies on breaking waves.

2 The Experiments of Favre

Favre (1935) conducted a series of experiments on undular bores in an open wave tank at the Hydraulic Laboratory of Ecole Polytechnique Fédérale of Zurich. The wave channel of rectangular cross section was 75.58 m long, 0.42 m wide and 0.40 m deep. Some experiments were performed with a horizontal tank and some were performed with a slightly inclined tank. Herein, we consider only experiments in the horizontal wave tank. The tank was supplied by a water tower of constant water level through a pipe $C_1$. The water tower was supplied by fixed reservoirs located in the laboratory attic through a pipe $C_2$. A third pipe $C_3$ was used to drain off the excess of water of the tower. The water level of the tower remained constant as long as the flow from $C_2$ was larger than that of $C_1$. The excess water was drained off via $C_3$ to a reservoir located in the laboratory basement, and then returned by pumps to the reservoirs located in the attic. The water flow from $C_1$ was adjusted by a valve operated by a servo-motor. The pipe $C_2$ included a device that allowed the determination of the flow from the water tower. At the end of the tank was a sluice gate that allowed control of the water discharge and full closing of the end of the tank. Beyond the sluice gate, the water was discharged in the same reservoir in the basement as mentioned above. With this setup, it was possible to tune the system so as to guarantee a constant inflow into the wave tank and adjust the inflow to create bores of varying strength. A schematic of the setup just described is shown in Fig. 2.

Fig. 2

Definition sketch for the experimental setup of Favre

Three measuring and recording devices were used: (1) six vertical scales located in the longitudinal axial plan of the tank and distributed along the tank every 12 m were used for measuring the water level at rest or in motion. The accuracy was on the order of one to two tenths of a millimeter. (2) To record the fluctuations of the free surface at the six locations Favre used pressure head (Pitot) tubes whose meniscus positions were recorded on sensitive paper exposed to light. An optical apparatus consisting of a prism, a lens, an electric lamp and a mirror was used to record the meniscus position. (3) The variations of the front of the undular bores were measured differently. The measurements were based on photos taken with exposure time of approximately 1/100 s.

Preliminary experiments were conducted to calibrate the devices. Undular bores were generated by a sudden variation of the flow at the upstream end of the tank. Favre performed a series of 30 experiments on undular bores on still water, grouped in three series corresponding to three different initial constant water depths (0.205 m, 0.155 m and 0.1075 m). A spillway plate was placed at the downstream end of the tank whose height was fixed to the desired depth, then the tank was filled through C1 until the water overflowed the spillway plate. Water filling was stopped and 20 min later the water level was stabilized at the height of the spillway plate.

The water flow was determined as a function of the valve displacement (see Figure 38 of Favre [21]). The water flowing into the tank generated an undular bore with a front consisting of a series of undulations whose number increased with the distance of propagation. To make the free surface easily visible, Favre sprinkled aluminum sawdust on the free surface and scattered confetti soaked with black ink. These measures made the free surface clearly visible on photographs. Favre photographed 21 fronts of undular bores: (1) 6 of the first series of experiments (nos. 2, 4, 6, 8, 10, 12; depth 0.205 m); (2) 6 of the third series of experiments (nos.  21, 22, 23, 24 , 26, 29; depth 0.1075 m); (3) 8 of the sixth series and one of the seventh series of experiments, which correspond to inclined tank. In the present work, we consider two cases of the third series of experiments, and the results of numerical simulations of experiments no. 22 and no. 23 are presented in Sect. 5.

The fronts of the undular bores were photographed when the crest of the first undulation was located at 64.78 m and 64.60 m from the upstream end of the tank for experiments no. 22 and no. 23, respectively. Recall that Favre introduced the bore strength parameter $a_0/h_0,$ where $a_0$ was the mean height of the head of the undular bore (see Figure 41 of Favre [21]) and $h_0$ was the initial water depth where the first crest of the undular bore was photographed. Bore strength values corresponding to experiments no. 22 and no.  23 are given in Sect. 5. Favre found that for weak values of bore strength the bore undulations were almost sinusoidal, whereas for high values they became cnoidal (experiments nos.  22, 23, 24).

In experiments no. 22 and no.  23, no wave breaking was observed. In experiment no.  24, the leading wave exhibited spilling breaking after traveling a considerable distance. Experiments no.  26 and no.  29 featured wave breaking after the front of the bore had traveled a shorter distance. Breaking and non-breaking cases can be clearly identified by observing the maximum height of the leading wave. Experimental results based on Favre’s data shown in Figure 49 of [21] are plotted in Fig. 3. It is apparent that the maximum height of the leading wave increases with increasing bore strength, up to a maximum of 2.06 times the incident depth $a_0$. That maximum occurs in experiment no.  24 which corresponds to $a_0/h_0=0.281$. As shown in these figures, experiments with higher bore strength feature earlier breaking and much lower wave heights for the leading wave.

As already stated above, the main purpose of the present work is to explore whether the critical bore strength can be found using fairly simple wave models such as the KdV equation. In the next section, the KdV equation will be derived in the presence of a shear flow, and then numerical simulations will be presented which suggest that the critical ratio can be found to within $9 \%$ error.

Fig. 3

Wave height $\mathrm {H}_1$ of the leading wave—normalized by $a_0$—as a function of the bore strength $a_0/h_0$. The experimental data are taken from Figure 49 in [21]. Legend: o - undisturbed depth $h_0 = 0.205$ m, $\Box$ - undisturbed depth $h_0 = 0.1075$ m

3 The KdV Equation in the Presence of Shear Flows

Consider a fluid contained in a long channel of unit width and depth $h_0$. The surface water-wave problem is generally described by the Euler equations with slip conditions at the bottom, and kinematic and dynamic boundary conditions at the free surface. We fix a coordinate system by aligning the x-axis with the undisturbed free surface, and suppose the fluid domain extends along the entire x-axis. It is assumed that the fluid is inviscid, incompressible and of unit density, the bottom of the channel is flat, and the wave motion transverse to the x-axis can be neglected.

With the assumption of irrotational flow and using the incompressibility of the fluid, the two-dimensional Euler equations can be written in terms of the Laplace equation for a velocity potential $\phi$, and the boundary conditions at the free surface are given in terms of $\phi$ and the surface excursion $\eta (x,t)$ by

$$\begin{aligned} \eta _t+\phi _x\eta _x-\phi _z&=0, \quad \text{ on } \ z=\eta (x,t)\,,\\ \phi _t + {\textstyle \frac{1}{2}} \big ( \phi ^2_x+\phi ^2_z \big ) + g\eta&=0, \quad \text{ on }\ z=\eta (x,t)\, , \end{aligned}$$

where g is the gravitational acceleration.

As is well known, this problem is difficult to treat both mathematically and numerically, and in practical situations, an asymptotic approximation of the Euler equations is often used. In the case at hand, we have long waves of small to moderate amplitude on a shallow fluid, and it appears that theses waves fall approximately into the Boussinesq scaling regime. Moreover, the waves travel only in one direction down the length of the wave flume, so that an appropriate asymptotic model to be used is the KdV equation, given in dimensional form by

$$\begin{aligned} \eta _t + c_0 \, \eta _x + {\textstyle \frac{3}{2}\frac{c_0}{h_0}} \, \eta \, \eta _x + {\textstyle \frac{1}{6}}c_0 h_0^2 \, \eta _{xxx} = 0. \end{aligned}$$

Here, $c_0 = \sqrt{g h_0}$ is the limiting long-wave speed, whereas already mentioned, where g is the gravitational acceleration and $h_0$ is the undisturbed depth.

The KdV equation features both nonlinearity and dispersion, and the balance of these two effects gives rise to both solitary-wave solutions and periodic traveling waves [31]. The equation is known to give a good description of the evolution of unidirectional surface water waves in the case when the waves are long compared to the undisturbed depth $h_0$ of the fluid, the average amplitude of the waves is small when compared to $h_0$ and transverse effects are negligible [12, 16, 32]. In the derivation of the KdV equation, the potential is written asymptotically as

$$\begin{aligned} \phi =f - { \textstyle \frac{z^2}{2}} f_{xx}, \end{aligned}$$

(1)

where f(x, t) represents an approximation to the velocity potential evaluated at the bottom. In addition, the assumption of wave propagation in the direction of increasing x values (to the right) leads to the relation

$$\begin{aligned} f_x = { \textstyle \frac{g}{c_0}} \left\{ \eta -{ \textstyle \frac{1}{4h_0}}\eta ^2 + { \textstyle \frac{h_0^2}{3}} \eta _{xx}\right\} \,. \end{aligned}$$

(2)

Using (1) and (2) shows that the horizontal velocity can be expressed to second order as

$$\begin{aligned} u(x,z,t) = \phi _{x}(x,z,t) = \frac{g}{c_0} \left\{ \eta - \frac{1}{4h_0} \eta ^2 + h_0^2\left( \frac{1}{3}- \frac{z^2}{2} \right) \eta _{xx}\right\} . \end{aligned}$$

That means if a solution $\eta$ of the KdV equation is given either in closed form or numerically, the horizontal particle velocity can always be found at any point in the fluid column. For more details, the reader may consult [2, 51]. In the case at hand, the velocity is evaluated at the free surface so that the breaking criterion can be tested. Using this approach, the authors of [14] found that the critical bore strength was $\alpha =0.353$, improving earlier work where a Boussinesq model was used [10]. In the present work, we will incorporate a background shear flow to further improve the comparison.

Fig. 4

Uniform shear flow with horizontal velocity $U=u-(z+h_0)\Gamma = \frac{\partial \phi }{\partial x}-(z+h_0)\Gamma$. In the figure, $\Gamma$ is negative

In the presence of background vorticity, the horizontal velocity field may be defined as $U(x,z,t)=u(x,z,t)-(z+h_0)\Gamma$ (see Fig. 4). Model equations of KdV and Boussinesq type for surface waves in the presence of background shear can be derived in a similar fashion as in the irrotational case. The reader may consult for example [15, 40, 46, 54]. Except for a minor modification, the equation to be used in the present study was derived in [40]. For background shear such as shown in Fig. 4, the appropriate KdV equation is

$$\begin{aligned} \eta _t + C_0^{+} \sqrt{gh_0}\eta _x + { \textstyle \frac{C_0^+(3+\tilde{\Gamma }^2)}{1+\left( C_0^+\right) ^2}} { \textstyle \frac{\sqrt{gh_0}}{h_0}} \eta \eta _x + { \textstyle \frac{C_0^{+} + \tilde{\Gamma }}{3\left( 1+\left( C_0^+\right) ^2\right) }}h_0^2\sqrt{gh_0}\eta _{xxx}=0. \end{aligned}$$

This equation is given in dimensional form, with the non-dimensional parameter $C_0^+={ \textstyle \frac{-\tilde{\Gamma } }{2}}+ \sqrt{{ \textstyle \frac{{\tilde{\Gamma }} ^2}{4}}+1}$ quantifying the strength of the background shear, and $\tilde{\Gamma }$ being the non-dimensional vorticity scaled with $\tilde{\Gamma }=\frac{\Gamma }{\sqrt{\frac{g}{h_0}}}$. The horizontal perturbation velocity field can be found in a similar way as for the irrotational case, and is given by

$$\begin{aligned} u= & {} { \textstyle \frac{\sqrt{gh_0}}{h_0}} \left\{ -C_0^-\eta + { \textstyle \frac{C_0^{-} + \tilde{\Gamma }}{2\left( 1+\left( C_0^+\right) ^2\right) }}{ \textstyle \frac{\eta ^2}{h_0}}+ { \textstyle \frac{C_0^{+} + \tilde{\Gamma }}{3\left( 1+\left( C_0^+\right) ^2\right) }}h_0^2 \eta _{xx}\right. \\&\left. - { \textstyle \frac{C_0^{-}}{6}}h_0^2\eta _{xx}+ { \textstyle \frac{C_0^{-}}{2}}h_0^2 \left( 1+{ \textstyle \frac{z}{h_0}} \right) ^2 \eta _{xx} \right\} , \end{aligned}$$

where we have used $C_0^-=\frac{-\tilde{\Gamma } }{2}- \sqrt{\frac{{\tilde{\Gamma }} ^2}{4}+1}$.

4 Non-Dimensionalization and Numerical Discretization

To prepare for the numerical discretization, it is convenient to scale the variables appearing in the equation above as follows: $x\rightarrow \frac{x}{h_0},\ z\rightarrow \frac{z}{h_0},\ t\rightarrow \frac{t}{\sqrt{\frac{h_0}{g}}},\ \eta \rightarrow \frac{\eta }{h_0},\ u\rightarrow \frac{u}{\sqrt{gh_0}},\ \Gamma \rightarrow \frac{\Gamma }{\sqrt{\frac{g}{h_0}}}.$ Using this scaling, the non-dimensional KdV equation can be expressed as

$$\begin{aligned} {\eta }_{{t}}+C_0^+{\eta }_{{x }}+ { \textstyle \frac{ {C_0^+}(3+{\Gamma ^2})}{1+\left( C_0^+\right) ^2}} {\eta }{\eta }_{{x}} +{ \textstyle \frac{C_0^++{\Gamma }}{3\left( 1+\left( C_0^+\right) ^2\right) }} {\eta }_{{x} {x}{x}} =0. \end{aligned}$$

(3)

The coefficients $C_0^+$ and $C_0^-$ are defined in the same way as in the last section. In the scaled variables, the horizontal velocity field appears as

$$\begin{aligned} U(x,z,t)&= - C_0^-\eta + { \textstyle \frac{C_0^-+\Gamma }{2\left( 1+\left( C_0^+\right) ^2\right) }}\eta ^2 + { \textstyle \frac{C_0^++\Gamma }{3\left( 1+\left( C_0^+\right) ^2\right) }}\eta _{xx} \\&\quad - { \textstyle \frac{C_0^-}{6}}\eta _{xx} + { \textstyle \frac{C_0^-}{2}}(1+z)^2\eta _{xx} - (z+1)\Gamma . \end{aligned}$$

It is well known that the KdV equation features exact solitary-wave solutions. If the coefficients of the KdV equation are defined such as in (3), the solitary wave has the form

$$\begin{aligned} \eta = \eta _0 {{\,\mathrm{sech}\,}}^2 \left( {\scriptstyle {\sqrt{{ \textstyle \frac{C_0^{+}(3 + \Gamma ^2 ){\eta _0}}{4\left( C_0^{+}+ \Gamma \right) }}}}} (x-x_0-ct) \right) , \end{aligned}$$

(4)

with the phase speed c given in terms of the amplitude $\eta _0$ by $c=C_0^{+} + \textstyle \frac{{C_0^{+}(3+{\Gamma ^2}) \eta _0}}{3(1+(C_0^{+})^2)}$. This exact solution will be used later to validate the implementation of the numerical algorithm.

The numerical approximation of the solutions $\eta (x,t)$ and $U(x,\eta (x),t)$ is based on a finite-difference method for the spatial derivatives and a hybrid Adam–Bashforth/Crank–Nicolson time integration scheme, such as previously used in [14, 42]. The local phase velocity C of the leading wavecrest is computed approximately by following the crest evolution and using a second-order central difference formula.

To define an appropriate numerical discretization, boundary conditions need to be imposed. In the far field upstream and downstream of the bore, the surface elevation $\eta$ approaches the stipulated values $\alpha$ and 0, respectively. These boundary conditions are exact up to machine precision as long as the spatial domain is large enough. In addition, a Neumann boundary condition needs to be specified in the far field downstream (see for example [13]). Using a homogeneous Neumann boundary condition and the Dirichlet conditions as indicated above yields the initial-boundary-value problem

$$\begin{aligned} \begin{aligned} {\eta }_{{t}}+ C_0^+{\eta }_{{x }}+ { \textstyle \frac{ {C_0^+}(3+{\Gamma ^2})}{1+\left( C_0^+\right) ^2}} {\eta }{\eta }_{{x}} + { \textstyle \frac{C_0^++{\Gamma }}{3\left( 1+(C_0^+)^2\right) }} {\eta }_{{x} {x}{x}} =&\ 0, \ x \in [-l,l], \ t \ge 0,\\ \eta (x,0) =&\ \eta _0 (x),\\ \eta (-l,t) =&\ \alpha ,\\ \eta (l,t) =&\ 0,\\ \eta _x(l,t) =&\ 0. \end{aligned} \end{aligned}$$

The initial data are given by $\eta _0 (x) = \frac{1}{2} a_0 \big [ 1 - \tanh (kx) \big ],$ where k is a model parameter denoting the steepness of the initial bore slope. In an idealized setting, one may take the limit as k approaches infinity, leading to the so-called dispersive shock problem [20, 23]. However in the present case, we take the finite value $k=1$.

It will be expedient to rewrite the problem to obtain homogeneous boundary conditions, and we define an auxiliary function $\zeta (x,t) \equiv \eta (x,t) - \eta _0(x).$ Using $\zeta$, the problem can be reformulated as an inhomogeneous equation with a forcing given in terms of $\zeta$ and $\eta _0$, but with homogeneous boundary and initial conditions. The equation for $\zeta$ can then be written as

$$\begin{aligned} \zeta _t + C_0^+ \zeta _x + { \textstyle \frac{ {C_0^+}(3+{\Gamma ^2})}{1+(C_0^+)^2}} \left( { \textstyle \frac{1}{2}}\zeta ^2+\eta _0 \zeta \right) _x + { \textstyle \frac{C_0^++{\Gamma }}{3(1+(C_0^+)^2)}} \zeta _{xxx} = \ -F, \ x \in [-l,l], \ t \ge 0, \end{aligned}$$

where

$$\begin{aligned} F \equiv C_0^+\eta _0' + { \textstyle \frac{ {C_0^+}(3+{\Gamma ^2})}{1+(C_0^+)^2}} \eta _0 \eta _0' + { \textstyle \frac{C_0^++{\Gamma }}{3(1+(C_0^+)^2)}} \eta _0''', \end{aligned}$$

and homogeneous boundary and initial conditions are imposed. We discretize the spatial domain $[-l,l]$ using a finite set of points, $\{x_j\}_{j = 0}^{N} \subset [-l,l]$, where $x_0 = -l$ and $x_N = l$, and $\delta x = 2l/N$ is the distance between two neighboring grid points. The time domain is also discretized uniformly by defining $t_n = n\delta t$, where $t_0$ is equal to zero. With this notation, the approximate function value at time $t_n$ and grid point $x_j$ is defined to be $v_j^n \approx \zeta (x_j,t_n)$.

Regarding the spatial discretization, the first and third derivatives at a point $x_j$ are approximated by the central difference formulas

$$\begin{aligned} \zeta _x(x_j,t) \approx \frac{v_{j+1} - v_{j-1}}{2\delta x} \end{aligned}$$

(5)

and

$$\begin{aligned} \zeta _{xxx}(x_j,t) \approx \frac{v_{j+2} - 2v_{j+1} + 2v_{j-1} - v_{j-2}}{2\delta x^3}. \end{aligned}$$

(6)

Since we impose the Dirichlet conditions $v_0 = 0$ and $v_N = 0$, the equation can be solved for the grid points $\{x_j\}_{j = 1}^{N - 1}$, and that leaves us with just two points for which the third derivative approximation is not valid. Given the Neumann condition and the central difference approximation, we have $(v_{N+1} - v_{N-1})/ 2\delta x = 0$ which implies $v_{N+1} = v_{N-1}$. This enables us to use the third derivative approximation at the grid point $x_{N-1}$ in the form

$$\begin{aligned} \zeta _{xxx}(x_{N-1},t) \approx \frac{ v_{N+1} - 2v_{N} + 2v_{N-2} - v_{N-3}}{2 \delta x^3} = \frac{v_{N-1} + 2v_{N-2} - v_{N-3}}{2\delta x^3}. \end{aligned}$$

(7)

As there is no Neumann condition on the left boundary, we employ a forward difference formula to approximate the third derivative at the grid point $x_1$ as follows:

$$\begin{aligned} \zeta _{xxx}(x_1,t) \approx \frac{-v_4 + 6v_3 - 12v_2 + 10v_1 - 3v_0}{2\delta x^3}. \end{aligned}$$

(8)

The difference formulas (5), (6), (7) and (8) applied at all grid points give rise to the discrete differentiation matrices $D_1$ and $D_3$ as follows:

$$\begin{aligned} D_1 = \frac{1}{2 \delta x} \begin{pmatrix} 0 &{} 1 &{} 0 &{} &{} &{} \cdots &{} 0 \\ -1 &{} 0 &{} 1 &{} 0 &{} &{} &{} \vdots \\ 0 &{} -1 &{} 0 &{} 1 &{} 0\\ \vdots &{} &{} &{}\ddots &{} \\ 0 &{} \cdots &{} &{} &{} &{} 0 &{} 1 \\ 0 &{} \cdots &{} &{} &{} &{} -1 &{} 0 \end{pmatrix}, \ \ \quad D_3 = \frac{1}{2 \delta x^3} \begin{pmatrix} 10 &{} -12 &{} 6 &{} -1 &{} 0 &{} \cdots &{} 0 \\ 2 &{} 0 &{} -2 &{} 1 &{} 0 &{} \cdots &{} 0 \\ -1 &{} 2 &{} 0 &{} -2 &{} 1 &{} 0 \\ 0 &{} -1 &{} 2 &{} &{} \ddots \\ \vdots &{} &{} &{} \ddots &{} &{} \ddots &{} 1 \\ &{} &{} &{} &{} \ddots &{} 0 &{} -2 \\ 0 &{} &{} \cdots &{} &{} -1 &{} 2 &{} 1 \end{pmatrix}. \end{aligned}$$

Applying a Crank–Nicolson method to the linear terms on the right-hand side of the equation, and an Adams–Bashforth method to the nonlinear terms, the difference equation for determining the vector $\mathbf {v}^{n+1}$ is given by

$$\begin{aligned} \begin{aligned} \frac{\mathbf {v}^{n+1} - \mathbf {v}^n}{\delta t} = -&\ { \textstyle \frac{ {C_0^+}(3+{\Gamma ^2})}{2(1+(C_0^+)^2)}} D_1 \bigg [ \ 3 \Big ( { \textstyle \frac{1}{2}} \big ( \mathbf {v}^n \big )^2 + \mathbf {v}^n \mathbf {\eta _0} \Big ) - \Big ( { \textstyle \frac{1}{2}} \big (\mathbf {v}^{n-1} \big )^2 + \mathbf {v}^{n-1} \mathbf {\eta _0} \Big ) \ \bigg ] \\ -&\ { \textstyle \frac{C_0^++{\Gamma }}{3(1+(C_0^+)^2)}} D_3 \Big ( \mathbf {v}^{n+1} + \mathbf {v}^n \Big ) \ - { \textstyle \frac{1}{2}} C_0^+ D_1 \Big ( \mathbf {v}^{n+1} + \mathbf {v}^n \Big ) - \mathbf {F}, \end{aligned} \end{aligned}$$

where $\mathbf {v}^n = (v_1^n, v_2^n, ..., v_{N-1}^n)^T$, $\mathbf {\eta _0} = (\eta _0(x_1),\eta _0(x_2), ...,\eta _0(x_{N-1}))^T$ and $\mathbf {F} = (F(x_1), F(x_2), ...,F(x_{N-1}))^T$. This $n\times n$-system of equations can easily be solved for $\mathbf {v}^{n+1}$, and then to advance the numerical approximation by one time step, only three multiplications by sparse matrices are required.

The implementation is verified by using the well-known exact solitary-wave solution of the KdV equation which is given in the form (4). In Tables 1 and 2, the equation is solved in the case $\Gamma = -0.2$ and with the amplitude $\eta _0 = 0.5$ on the time interval $t \in [0,1]$. It can be clearly seen that the second-order convergence is achieved in the spatial and the time discretization.

Table 1 Discretization errors and error ratios for numerical approximations of the time evolution of a solitary wave of the KdV equation (3) with $\Gamma =-0.2$ and $\eta _0 = 0.5$

Table 2 Discretization errors and error ratios for numerical approximations of the time evolution of a solitary wave of the KdV equation (3) with $\Gamma =-0.2$ and $\eta _0 = 0.5$

5 Simulations

To determine the critical bore ratio, the experiments of Favre are analyzed with regard to the strength of vorticity in the flow. We focus on Favre’s experiments no. 22, no. 23 and no. 24 with bore strengths of ${ \textstyle \frac{a_0}{h_0}}=0.1395$, ${ \textstyle \frac{a_0}{h_0}}=0.2307$ and ${ \textstyle \frac{a_0}{h_0}}=0.281$, respectively. A numerical domain $[-610,610]$ was used, and some experiments were double checked on a larger domain to make sure that there was no detrimental effect of numerical instabilities due to the treatment of the boundary conditions. A comparison of the first five waves is made at a propagation distance of about 600 depths, similar to the analysis in [30]. A plot of the surface elevation is shown in Fig. 5. Tables 3 and 4 show the wave heights and wavelengths of the five waves behind the bore front for several values of the vorticity $\Gamma$. The experiments were generally checked by making runs with smaller spatial and temporal grid sizes to make sure that numerical errors did not contribute to the results.

Fig. 5

Numerical approximation of the first five waves behind the borefront. The wave height and the wavelength of the leading wave are denoted by $H_1$ and $\lambda _1$, respectively. For the second wave, the wave height and wavelength are denoted by $H_2$ and $\lambda _2$, and so on

With the numerical measurements of wavelengths and wave heights of the five leading waves in hand, a comparison with the measurements from Favre’s experiment can be conducted. For each value of $\Gamma$ in Tables 3 and 4, an estimate of the relative error is calculated using the least-square method. The relative error for both the wavelength and the wave height are first calculated separately and then added together. In this way, for every value of $\Gamma$, the corresponding value of the relative error can be plotted as shown in Fig. 6. With polynomial curve fitting, the best approximate values of $\Gamma$ for the experiments no. 22 and no. 23 are found to be $\Gamma _{22}=-0.2749$ and $\Gamma _{23}=-0.2316$, respectively. An estimate of $\Gamma$ in Favre’s experiment no. 24 with bore strength ${ \textstyle \frac{a_0}{h_0}}=0.281$ was also made to obtain an overall better estimate of $\Gamma$ in the critical case. In Fig. 7, the strength of vorticity is given in terms of the bore strength from Favre’s experiments no. 22, no. 23 and no. 24. Using a straightforward regression analysis, an estimate of the strength of vorticity in Favre’s experiment with a bore strength of 0.281 is found to be $\Gamma =-0.2213$.

Table 3 Comparison of simulations with Favre’s experiment no. 22

Table 4 Comparison of simulations with Favre’s experiment no.  23

Fig. 6

Relative errors for different strengths of vorticity in Favre’s experiments no. 22 (left panel) and no. 23 (right panel)

Fig. 7

This figure shows the relation between the bore strength $a_0 / h_0$ and the strength of vorticity $\Gamma$. A straight line fit is made using data from experiments no. 22, no. 23 and no. 24

By implementing this value in the numerical scheme, together with a range of values of $a_0$ around the critical ratio, and letting the waves travel a distance close to 600 depths, we could observe whether the waves will break or not. In Fig. 8, the crest speed C and the horizontal velocity component at the free surface are plotted base on a computation with $\Gamma =-0.2213$ and $a_0=0.307$. The ratio between the crest speed and the horizontal particle velocity reaches $U/C\ge 1$ at about 600 depths, and this means that the leading wave is starting to spill which limits the further growth of the wave. Thus, with the inclusion of a background shear flow with constant vorticity the critical ratio is found to be 0.307.

Fig. 8

The solid curve represents the phase speed and the dashed curve represents the horizontal particle velocity. The constant vorticity is $\Gamma =-0.2213$ and the bore strength is 0.307

6 Discussion

As mentioned in the introduction, the kinematic wave breaking criterion is one of the most commonly used criteria for the prediction of the onset of wave breaking. The criterion has been shown to pinpoint the commencement of wave breaking in various situations. In particular, the criterion was shown to perform well in deep water in [29, 49], and in shallow water both on flat bathymetry [25] and on a sloping beach [27, 50]. In some situations where the kinematic breaking criterion performs poorly, the problem can be ascribed to the difficulty of accurately finding the phase velocity of the waves from measurements [45], and the directionality of the waves in three-dimensional situations [53].

Some authors have attempted to use the kinematic criterion in connection with numerical codes to determine whether to switch from a dispersive Boussinesq-type scheme to a shallow-water scheme with numerical dissipation to capture energy loss in breaking waves. It was suggested in [5] that this approach works best for wave shoaling if the criterion is tightened by introducing a positive constant $\kappa < 1$, and to define breaking onset as the first time that $U/C > \kappa$. However, this approach requires the determination of the constant $\kappa$. If an appropriate value for $\kappa$ can be found, then this breaking criterion can give excellent results [6, 11, 39].

Sharpening the kinematic criterion if used as a numerical switch makes sense as the numerical dissipation needs time to have an effect on the waves. In fact, tightening the kinematic criterion was already suggested earlier based on experimental evidence [45], and more recently based on studies of wave breaking in large and intermediate depth [7, 18]. In these works, a new parameter B based on crest speed and local energy flux and density was put forward as a diagnostic for the initiation of wave breaking. In particular, as shown in [7], using this parameter reduces to a sharpened convective criterion when evaluated at the free surface. In a nutshell, the sharpened criterion based on the parameter B predicts wave breaking when $B \sim 0.87$, though breaking may not commence until B is actually close to 1. As already alluded to, the new criterion based on the parameter B is based on a dynamic or energetic criterion based on evaluation of energy flux and density, such as put forward for example in [44].

To complete this brief review, one may add that geometric breaking criteria are popular in some quarters. Geometric criteria are based on the shape and in particular the steepness of the waves close to breaking, such as reviewed in [4]. Among them the most used is the limiting wave steepness parameter $s \approx ak_{\max },$ which can be transformed into the kinematic limit $u \approx c$. For a detailed review on geometric, kinematic and dynamic criteria for breaking onset one can refer to [3].

To further improve comparison with experiments using the simple kinematic criterion used in the current work, one might use fully nonlinear Boussinesq systems, such as the Serre or Green–Naghdi equations [19, 33] or higher-order KdV-type equations, such as the higher-order regularized long wave equation used in [55]. One possible obstacle with this approach is that the boundary-value problem must be shown to be stable to small perturbations.