Wave Emission From Bottom Vibrations in Subsurface Open-channel Shear Flow

Abstract

The linearized water-wave radiation problem for a 2D oscillating bottom source in an inviscid shear flow with a free surface is investigated analytically. The fluid depth is constant. The velocity of the basic flow varies linearly with depth (uniform vorticity), with zero surface velocity. The far-field surface waves radiated out from the 2D source are calculated, based on Euler’s equation of motion with the application of radiation conditions. There are always two waves, one emitted in the upstream direction and the other in the downstream direction. The energy fluxes of these two waves are calculated. The hydrostatic limit of zero wave number is related to the theory of undular bores.

1 Introduction

The submerged oscillatory source is recognized as an elementary solution for linearized water waves governed by Laplace’s equation. Oscillatory sources are Green functions that satisfy the linearized free-surface condition and radiation conditions at infinity. The first mathematical solutions were given by Kochin [12], summarized in [21]. These singular solutions are important building blocks for water waves interacting with submerged and floating bodies [9, 14].

We will derive a fundamental solution for two-dimensional (2D) bottom vibrations for a fluid layer with a free surface in the presence of a subsurface shear flow. This is a Green function formalism which considers one singular point of bottom oscillations, representing an oscillatory Dirac singularity for the normal velocity. The exact dispersive theory of linearized water waves is applied, while the conventional theories of open-channel hydraulics apply shallow-water approximations. Our assumption of 2D waves is representative also for 3D waves in open channels when the ratio of wavelength to channel width is of order one or greater.

The solution will be based on the Euler equation of motion for an incompressible inviscid fluid. The amplitudes of the radiated far-field waves will be calculated analytically. We will consider only the case of zero surface velocity where there are no Doppler effects. With zero surface velocity, there are always two waves emitted from the source. One upstream wave and one downstream wave.

The established research on fully dispersive water waves on shear flows [16] has focus on ocean wave drift and weakly nonlinear interactions. The possibilities of stopping a surface wave by generating a shear flow has been studied [4]. After a detailed discussion of the dispersion relation for linear waves [7], these results have been applied to study ship waves on a shear flow [6].

A 2D oscillatory line source submerged in a shear flow with a free surface has been investigated [8]. Constant depth was considered, where the subsurface shear flow has vanishing surface flow. In the present work, we will consider an oscillating bottom source, equivalent to a concentrated singular flux through the bottom. A bottom source represents a concentrated bottom vibration, according to linear theory.

The present model may be considered as the limit case of [8] where the submerged source comes in contact with the rigid bottom. However, only a submerged source can generate perturbation vorticity, since it may be surrounded by a closed material curve that may change in size and thereby change the local vorticity according to Lord Kelvin’s circulation theorem.

Solutions based on Laplace’s equation have been developed for the 2D radiation problem of submerged oscillatory line sources in shear flow. The cases without surface velocity [19] and with surface velocity [20] have been studied. A surface flow allows Doppler effects that may increase the number of waves and makes resonance possible. These strictly 2D problems seem mathematically convenient because the flow perturbation is assumed to obey Laplace’s equation, even though a vorticity is present. However, the application of Laplace’s equation is incorrect for a singular submerged source in the shear flow, generating perturbation vorticity. This was explained in [8] correcting earlier work [19] on the wave radiation problem of a 2D oscillating line source. A solution from first principles by the Euler equation of motion [8] revealed a critical-layer like perturbation vorticity inside the fluid, harmonically oscillating and convected with the basic flow. This downstream shear layer does not influence the dispersion relation of the regular waves, but it has a nonzero far-field amplitude, carrying a nonzero energy flux. Thereby it also modifies the other far-field wave amplitudes.

The physical inconsistencies inherent in [19] are met by the present work with a consistent analysis of oscillating boundary singularities in the presence of a shear flow. A wavy wake from a submerged oscillating source in a shear flow was identified in [8], and it was called the critical wave. In the present work there is no wake because the oscillating source is placed at the boundary. Our solution method is based on the Euler equation of motion, which is a robust first-principle approach that can be extended to three dimensions.

2 Mathematical Model

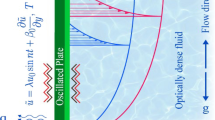
We consider an inviscid and incompressible fluid (liquid) in a steady shear flow, where the shear flow is aligned along a horizontal x axis. The fluid has constant depth H and a free surface subject to constant atmospheric pressure. Surface tension is neglected. Cartesian coordinates x, y, z are introduced, where the z axis is directed upwards in the gravity field and the x axis is aligned along the undisturbed free surface. The gravitational acceleration is g, and $\rho$ denotes the constant fluid density. The velocity perturbation vector is denoted by $({\hat{u}},{\hat{v}},{\hat{w}})$.

Fig. 1

Definition sketch of horizontal fluid layer with a subsurface shear flow U(z) and constant depth H, with a 2D bottom source q(t) generating waves with surface elevation $\zeta (x,t)$. The horizontal x-axis follows the undisturbed free surface, and the z-axis is vertical

The problem to be analyzed is sketched in Fig. 1. There is a 2D wave motion caused by a fixed oscillating line source (2D source), aligned in parallel with the z axis, going through the bottom point $(x,z) = (0,-H)$ delivering the area flux q(t). The angular frequency $\omega$ of this forced bottom source is given. The water wave problem will be linearized with respect to the surface elevation $\zeta (x, t)$ and the velocity perturbation.

There is a basic horizontal shear flow U(z) with uniform vorticity, aligned in the x direction. Its general profile is

$$\begin{aligned} U(z) = U_0 + S z,~~z <0, \end{aligned}$$

(1)

where $U_0$ a uniform surface velocity, but in the present work we will put $U_0 = 0$. The more complicated case with $U_0 \ne 0$ will be treated in a follow-up paper. It gives up to four emitted waves, and two of these waves will merge with resonance when the group velocity is zero. No resonances occur within the present model.

Euler’s equation of motion can be written

$$\begin{aligned} \mathbf {a} = - \frac{1}{\rho } \nabla P - g \mathbf {i}_3, \end{aligned}$$

(2)

where $\mathbf {a}$ is the acceleration vector and $\mathbf {i}_3$ is the vertical unit vector. The total pressure is denoted by P. The unit vector in the x direction is denoted by $\mathbf {i}_1$. The mass balance is given by the 2D continuity equation:

$$\begin{aligned} {\hat{u}}_x + {\hat{w}}_z = 0. \end{aligned}$$

(3)

The linearized kinematic free-surface condition is

$$\begin{aligned} \left. {\hat{w}} \right| _{z=0} = \zeta _t, \end{aligned}$$

(4)

with subscripts denoting partial derivatives. Surface tension is neglected, and the dynamic boundary condition is given by the tangential component of the Euler equation along the free surface. The tangent vector along the surface (not normalized) is $\mathbf {i}_1 + \zeta _x \mathbf {i}_3$. We take the scalar product of this tangent vector with the Euler equation, and evaluate the resulting expression at the free surface

$$\begin{aligned} (\mathbf {i}_1 + \zeta _x \mathbf {i}_3) \cdot \mathbf {a} = - g \zeta _x,~~\text{ at }~~z=\zeta (x,t) \end{aligned}$$

(5)

since the tangential derivative of the pressure is zero. Linearizing this condition gives

$$\begin{aligned} \mathbf {i}_1 \cdot \mathbf {a}\vert _{z=0} = ({\hat{u}}_t + S {\hat{w}})\vert _{z=0} = - g \zeta _x. \end{aligned}$$

(6)

We eliminate the horizontal velocity by the continuity equation to achieve the final dynamic condition

$$\begin{aligned} ({\hat{w}}_{zt} - S {\hat{w}}_{x})\vert _{z=0} = g \zeta _{xx}. \end{aligned}$$

(7)

The last boundary condition is the bottom condition with a singular oscillating bottom source located in the bottom point

$$\begin{aligned} {\hat{w}} = q_0 \delta (x) e^{-i \omega t},~~z=-H, \end{aligned}$$

(8)

where $q_0$ is the flux amplitude of the bottom source, given in 2D as area per time. We have already mentioned that this 2D bottom source does not generate perturbation vorticity, in contrast to a submerged source. The 2D bottom source emits volume flux over an angle of $\pi$, while a submerged source has flux emission over its full-circle periphery angle of $2\pi$. The Dirac delta function is denoted by $\delta (x)$, and i is the imaginary unit. We have introduced a complex time dependence with angular frequency $\omega$. The physical quantities are represented by the real parts of the complex variables.

The singular condition (8) represents the Green function for bottom vibrations, which is the building block for expressing an arbitrary distribution of monochromatic vibration along a finite portion of the bottom.

3 Fourier Transform of 2D Radiation Problem

We assume time-periodic flow with given angular frequency $\omega >0$, disregarding all transients. The flow is driven by a bottom source of harmonically pulsating strength

$$\begin{aligned} q(t) = q_0 \cos (\omega t). \end{aligned}$$

(9)

Since the source is 2D, we first assume waves in the 2D vertical x, z plane. The variables are Fourier transformed as follows:

$$\begin{aligned} ({\hat{u}},{\hat{w}},{\hat{p}}) = q_0 \frac{1}{2 \pi } \int _{-\infty }^{\infty } (u(z),w(z),p(z)) e^{i k x - i \omega t} \mathrm{d}k. \end{aligned}$$

(10)

Here ${\hat{p}}$ denotes the dynamic pressure. This Fourier integral consists of two different contributions: Waves propagating in the $+x$-direction, with positive wavenumber ($k>0$). Waves propagating in the $-x$-direction, with negative wavenumber ($k<0$).

The transformed components of the Euler equation are given by

$$\begin{aligned}&- i (\omega - k U) u + S w = - i k p/\rho , \end{aligned}$$

(11)

$$\begin{aligned}&- i (\omega - k U) w = - p'/\rho , \end{aligned}$$

(12)

where the derivative is taken with respect to z. The transformed continuity equation is

$$\begin{aligned} i k u + w' = 0. \end{aligned}$$

(13)

The surface elevation is Fourier transformed as follows:

$$\begin{aligned} \zeta (x,t) = q_0 \frac{1}{2 \pi } \int _{-\infty }^{\infty } B(\omega ,k) e^{i k x - i \omega t} \mathrm{d}k. \end{aligned}$$

(14)

From the transformed governing equations, we derive an equation for the vertical velocity alone

$$\begin{aligned} w'' - k^2 w = 0. \end{aligned}$$

(15)

The transformed version of the bottom condition (8) is

$$\begin{aligned} w = 1,~~z=-H. \end{aligned}$$

(16)

The solution of this second-order boundary value problem is

$$\begin{aligned} w(z) = \cosh k(z+H) + A \sinh k(z+H). \end{aligned}$$

(17)

Fourier transform (10) involves the whole spectrum of positive and negative wave numbers k. The transformed kinematic free-surface condition (4) is

$$\begin{aligned} w\vert _{z=0} = -i \omega B. \end{aligned}$$

(18)

By inserting the solution (17), we find the relationship

$$\begin{aligned} \cosh (k H) + A \sinh (k H) = -i \omega B. \end{aligned}$$

(19)

Similarly, the transformed dynamic free-surface condition (6) is

$$\begin{aligned} (-i \omega u + S w)\vert _{z=0} = \left. \left( \frac{\omega }{k} w' + S w\right) \right| _{z=0} = - i k g B, \end{aligned}$$

(20)

where we also insert the solution for w and find a second relationship between A and B

$$\begin{aligned} \omega \sinh (kH) + S \cosh (kH) + A (\omega \cosh (kH) + S \sinh (kH) ) = - i k g B. \end{aligned}$$

(21)

We can now eliminate A from these two relationships to solve for $B(\omega )$

$$\begin{aligned} B = i~\frac{\omega }{\sinh (kH)}~\frac{1}{\omega ^2 \coth (kH) + {\omega } S - g k}. \end{aligned}$$

(22)

4 The Radiated Waves

There are always two radiated waves in the 2D problem without surface flow: one upstream wave and one downstream wave. These are given by the 2D dispersion relation that will first be discussed.

4.1 The 2D Dispersion Relation

The conventional notion of the dispersion relation is the angular frequency $\omega$ as a function of the wavenumber k. However, in a radiation problem the emitted wavenumbers arise as functions of the angular frequency. Ellingsen and Tyvand [8] derived this dispersion relation for zero surface flow $(U_0 = 0)$, but with focus on infinite depth while the present work is based on constant depth. There are always two wavenumbers $k_\pm$ for $U_0 = 0$, given by the implicit formulas

$$\begin{aligned} g k_+ = \omega (\omega \coth k_+H + S),~~~~g \vert k_-\vert = \omega (\omega \coth \vert k_-H \vert - S), \end{aligned}$$

(23)

where $k_+ >0$ and $k_- <0$. We assume $S > 0$ so that $x<0$ is the downstream direction (subscript −) and $x>0$ is the upstream direction (subscript $+$), which are the conventions in [8].

The dispersion relation is implicit and must be evaluated numerically. For this purpose, we introduce the dimensionless versions of dispersion relation (23) valid for $U_0 = 0$

$$\begin{aligned} k_+ H= & {} \sqrt{\frac{H}{g}} \omega \left( \sqrt{\frac{H}{g}}\omega ~\coth (k_+H) + \sqrt{\frac{H}{g}} S \right) , \end{aligned}$$

(24)

$$\begin{aligned} \vert k_- H \vert= & {} \sqrt{\frac{H}{g}} \omega \left( \sqrt{\frac{H}{g}}\omega ~\coth \vert k_-H\vert - \sqrt{\frac{H}{g}} S \right) \end{aligned}$$

(25)

There are three dimensionless groups, based on the depth H as length unit, combined with a gravitational time unit $\sqrt{H/g}$. These are

$$\begin{aligned} \omega ^* = \sqrt{\frac{H}{g}} \omega ,~~~~S^* = \sqrt{\frac{H}{g}} S,~~~~k_\pm ^* = k_\pm H \end{aligned}$$

(26)

being the given dimensionless source frequency $\omega ^*$, the dimensionless vorticity $S^*$ and the source-induced upstream/downstream dimensionless wave numbers $k_\pm ^*$ of radiated waves, respectively. The dimensionless dispersion relation is thus given by the common equation for $k_\pm ^* (\omega ^*,S^*)$

$$\begin{aligned} k_\pm ^* - \omega ^* \left( \omega ^* ~\coth k_\pm ^* + S^* \right) = 0, \end{aligned}$$

(27)

which has one positive solution $k_+^*$ and one negative solution $k_-^*$. The phase velocity is defined as

$$\begin{aligned} c_f = \frac{\omega }{k} = c_f^* \sqrt{g H}, \end{aligned}$$

(28)

with the corresponding definition of the group velocity

$$\begin{aligned} c_g = \frac{d \omega }{d k} = c_g^* \sqrt{g H}, \end{aligned}$$

(29)

and thereby the dimensionless phase and group velocities $c_f^*$ and $c_g^*$ are also defined.

The dispersion relation (27) can be rewritten as

$$\begin{aligned} \omega ^* = \frac{\tanh k^*}{2} \left( - S^* \pm \sqrt{ (S^*)^2 + 4 k^* \coth k^*}\right) \end{aligned}$$

(30)

leading to the dimensionless phase velocity

$$\begin{aligned} c_f^* = \frac{\tanh k^*}{2 k^*} \left( - S^* \pm \sqrt{ (S^*)^2 + 4 k^* \coth k^*}\right) , \end{aligned}$$

(31)

and the dimensionless group velocity

$$\begin{aligned} c_g^* = \pm \frac{1 - 2 k^* ~\text{ csch }~ (2 k^*)}{\sqrt{ (S^*)^2 + 4 k^* \coth k^*}} + \frac{\text{ sech }^2 k^*}{2} \left( - S^* \pm \sqrt{ (S^*)^2 + 4 k^* \coth k^*}\right) . \end{aligned}$$

(32)

It is a trivial fact that the phase velocity is positive in the upstream direction $x>0$ and negative in the downstream direction $x<0$. It is important that the group velocity has the same sign as the phase velocity. We see from Eq. (32) that this is always the case, because $2 k^*~\text{ csch }~ (2 k^*) \le 1$ for any real value of $k^*$.

Table 1 Dimensionless wavenumbers $k_+^*>0$ (upstream) and $k_-^*<0$ (downstream) for combinations of angular frequency $\omega ^*$ and shear rate $S^*$ with zero surface velocity $(F = 0)$

Table 1 shows the upstream wave number $k_+$ (positive) and the downstream wave number $k_-$ (negative) as functions of $\omega ^*$ and $S^*$ (Figs. 2, 3).

Fig. 2

Illustration of the dispersion relation. The dimensionless wavenumber $k^*$ for the upstream waves ($k^*>0$) and downstream waves ($k^*<0$), as functions of the angular frequency $\omega ^*$, for three values for the shear rate $S^*$

Fig. 3

The dispersion relation represented by wave velocities. The dimensionless phase and group velocity are displayed as functions of the angular frequency $\omega ^*$, for three values of the shear rate $S^*$. In each case, the upper graph is the phase velocity $c_f^*$, and the lower graph is the group velocity $c_g^*$. a Upstream waves $(x>0)$. b Downstream waves $(x<0)$

4.2 Radiation from the 2D Bottom Source

We formulate the Fourier integral solution (14) for the surface elevation by inserting from Eq. (22)

$$\begin{aligned} \zeta (x,t) = \frac{i \omega q_0}{2 \pi } \int _{-\infty }^{\infty } \frac{e^{i k x - i \omega t} ~ dk}{\sinh (k H)~(\omega ^2 \coth kH + \omega S - g k)}. \end{aligned}$$

(33)

The radiated waves are determined by integration in the complex k plane, where $k = k_r + i k_i$.

First, we look at the downstream wave with negative wave number $k_-$, propagating to $x \rightarrow - \infty$. From residue calculus, we find the solution for the surface elevation as $x \rightarrow - \infty$

$$\begin{aligned} \zeta (x,t) = \omega q_0 \frac{e^{i k_- x - i \omega t}}{ \sinh (k_- H) }~\lim _{k \rightarrow k_-} \frac{ k - k_-}{\omega ^2 \coth (k H) + \omega S - g k}, \end{aligned}$$

(34)

and according to the radiation condition this integral must be closed in the lower half-plane where $k_i < 0$. The contour of integration is deformed slightly above the singularity at $k = k_-$. From L’Hôpital’s rule, we find

$$\begin{aligned} \zeta (x,t) = - \frac{q_0 ~\omega }{g}~ \frac{e^{i k_- x - i \omega t}}{\sinh (k_- H) + (h \omega ^2/g) ~\text{ csch }~ (k_- H)},~~x \rightarrow - \infty , \end{aligned}$$

(35)

where we recall that $k_- < 0$. There is no explicit dependence on S in this expression, but the vorticity influences the wave amplitude through the dispersion relation $k_- = k_-(\omega , S)$.

The upstream wave is also governed by Eq. (33), and in the far-field ($x \rightarrow \infty$) it is a sinusoidal wave with positive wavenumber $k_+$. From residue calculus, we find the solution for the surface elevation as $x \rightarrow \infty$

$$\begin{aligned} \zeta (x,t) = - \omega q_0 \frac{e^{i k_+ x - i \omega t}}{ \sinh (k_+ H) }~\lim _{k \rightarrow k_+} \frac{ k - k_+}{\omega ^2 \coth (k H) + \omega S - g k}, \end{aligned}$$

(36)

where this integral must be closed in the upper half-plane where $k_i > 0$. The contour of integration is deformed slightly below the singularity at $k = k_+$. From L’Hôpital’s rule, we find

$$\begin{aligned} \zeta (x,t) = \frac{q_0 ~\omega }{g}~ \frac{e^{i k_+ x - i \omega t}}{\sinh (k_+ H) + (H \omega ^2/g) ~ \text{ csch }~ (k_+ H)},~~x \rightarrow \infty , \end{aligned}$$

(37)

where we recall that $k_+ > 0$. Again there is no explicit dependence on S in this expression, but the vorticity influences the wave amplitude through the dispersion relation $k_+ = k_+(\omega , S)$.

We now introduce a common description for upstream and downstream far-field waves

$$\begin{aligned} \zeta (x,t) = \zeta _0 ~ e^{i k_\pm x - i \omega t},~~\vert x \vert \rightarrow \infty , \end{aligned}$$

(38)

with the elevation amplitude $\zeta _0$ given by

$$\begin{aligned} \frac{\zeta _0}{H} = \frac{q_0 \omega }{g H}~ \frac{1}{\sinh \vert k_\pm ^* \vert + {\omega ^*}^2 ~ \text{ csch } \vert {k_\pm ^* \vert }} = \frac{q_0^* ~\omega ^*}{\sinh \vert k_\pm ^* \vert + {\omega ^*}^2 ~ \text{ csch } \vert k_\pm ^* \vert }. \end{aligned}$$

(39)

Here we have introduced the dimensionless source strength $q_0^*$, defined as

$$\begin{aligned} q_0^* = \frac{q_0}{\sqrt{g H^3}}. \end{aligned}$$

(40)

Since the source is the cause of the radiated wave, it is obvious that the radiated amplitude is proportional to the source strength. An appropriate dimensionless version of the radiated wave amplitude is, therefore, $\zeta _0^*$, defined by

$$\begin{aligned} \zeta _0^* = \frac{\zeta _0}{ H q_0^*} = \frac{\zeta _0 \sqrt{g H}}{q_0} = \frac{\omega ^* }{\sinh \vert k_\pm ^* \vert + {\omega ^*}^2 ~ \text{ csch } \vert k_\pm ^* \vert }. \end{aligned}$$

(41)

Table 2 Dimensionless far-field wave amplitudes $\zeta _0^*$ for combinations of angular frequency $\omega ^*$ and shear rate $S^*$ with zero surface velocity

Table 2 shows the far-field wave amplitude $\zeta _0^*$ as a function of $\omega ^*$ and $S^*$ according to Eq. (41). We note that the amplitude does not go to zero as $\omega ^* \rightarrow 0$, so we need to explain this limit case, where the waves are non-dispersive. A simpler formula (45) will be derived for the non-dispersive waves with vanishing wavenumber, representing the first column in Table 2.

Fig. 4

The dimensionless far-field wave elevation $\zeta _0^*$ as function of the dimensionless frequency $\omega ^*$. Three values of $S^*$ are represented, with two graphs in each case. For each value of $S^*$ the lower graph represents upstream waves ($x>0$), while the upper graph represents downstream waves ($x<0$)

Figure 4 illustrates graphically the results in Table 2, by plotting the far-field elevations $\zeta _0^*$ according to Eq. (41). We see that there are two equal wave amplitudes in the limit of hydrostatic waves with zero wave numbers, which is not a trivial fact, because the waves are not identical since they have different propagation velocities. We also notice that a local maximum for the elevation of downstream waves emerges, at a value of $\omega$ which is a little bit greater than the value of S.

4.3 On the Zero-Frequency Limit and Bore Formation

The zero-frequency limit can be treated as an initial-value problem. This gives an interesting link to the theory of undular bores, which was pioneered by Benjamin and Lighthill [1] and Peregrine [15]. Imagine that a steady source $q_0$ is turned on and causes a uniform bore with elevation $\zeta _0$, corresponding to zero wave number. The bore expands simultaneously in both directions, with different upstream and downstream velocities. Mass balance then gives the simple relationship

$$\begin{aligned} q_0 \varDelta t = \zeta _0 (c_+ + c_-) \varDelta t, \end{aligned}$$

(42)

where $\varDelta t$ is the time interval since the source was turned on, and $c_\pm$ are the upstream and downstream velocities of non-dispersive hydrostatic waves (with zero wave number). From the dispersion relation, we have the limit velocities as $\vert k \vert \rightarrow 0$

$$\begin{aligned} c_\pm = H\left( \sqrt{\left( \frac{S}{2}\right) ^2 + \frac{g}{H}} \mp \frac{S}{2}\right) , \end{aligned}$$

(43)

representing non-dispersive hydrostatic waves. This formula is inserted in mass balance relationship (42) to obtain

$$\begin{aligned} \zeta _0\vert _{k=0} =\frac{q_0}{\sqrt{S^2 H^2 + 4 g H}}, \end{aligned}$$

(44)

which is rewritten in dimensionless version as

$$\begin{aligned} \zeta _0^*\vert _{k^*=0} =\frac{1}{\sqrt{S^{*2} + 4}}. \end{aligned}$$

(45)

The left-hand column in Table 2 is calculated by this formula, and these results agree with the elevation of the dispersive waves as the wavenumber tends to zero. Thereby we confirm a tacit but crucial assumption made in Eq. (42): the upstream and downstream elevations are equal in the hydrostatic zero-frequency limit.

Undular bores on subsurface shear flow have been investigated in two papers [11, 18]. Their results do not compare directly with our zero-frequency elevation (45). Our formula for small-amplitude bores (45) gives the limit $\zeta _0^*\vert _{k=0} \rightarrow 1/2$ as $S \rightarrow 0$, in agreement with [13]. Here an impulsively started source was taken as the cause for an undular bore, establishing a one-parameter family of bores represented by a Froude number. This type of modeling was introduced in [17] and gives a clearer causal approach than taking an already existing bore as a mathematical initial condition. The same approach was used in [2] for investigating interactions between undular bores. Experimentally, it is convenient to generate a steady bore level is by feeding a constant mass flux into an open channel. Similarly, undular bores may be generated by a moving weir in an open channel [10]. Borcia et al. [3] presented experiments on bores in a circular channel, providing mass flux by releasing a rectangular hump of fluid.

The dispersion relation prescribes a propagation velocity for the non-dispersive limit of zero wave number (43), which is rewritten in dimensionless form as

$$\begin{aligned} c^*_\pm = \sqrt{1 + \left( \frac{S^*}{2}\right) ^2} \mp \frac{S^*}{2}. \end{aligned}$$

(46)

This formula coincides with the linearized version of the propagation velocity for undular bores on a shear flow found by Kharif and Abid [11], their Eq. (30).

We will now discuss the small-shear limit of this formula (46) for non-dispersive propagation, expanded as

$$\begin{aligned} c^*_\pm = 1 \mp \frac{S^*}{2} + \frac{S^{*2}}{8} + O(S^{*4}). \end{aligned}$$

(47)

This is the asymptotic expansion when $S^* \ll 1$, for hydrostatic waves of vanishing frequency. This zero-frequency limit gives non-dispersive waves, and above we have used the linearized limit of a bore to derive the far-field elevation. Thus, we have now shown that the surface above the source rises like a piston by establishing a uniform steady elevation common to the bulk of the total bore in its simultaneous upstream and downstream propagation. The first-order shear contribution in (47) represents an added advection to the unit shallow-water propagation velocity. The added shear velocity $\vert S^* z^* \vert = S^*/2$ occurs at the average depth $z^*=-1/2$. The leading term confirms the simple intuitive picture of a hydrostatic wave that rides on the average velocity of the shear flow.

A complementary asymptotic expression for propagation velocity at a great shear rate $S^* \gg 1$ is

$$\begin{aligned} \frac{c^*_\pm }{S^*} = \frac{1}{2} \mp \frac{1}{2} + \frac{S^{*-2}}{8} + O(S^{*-4}). \end{aligned}$$

(48)

The downstream version of this formula is

$$\begin{aligned} c^*_- = S^* + \frac{S^{*-1}}{8} + O(S^{*-3}),~~x<0, \end{aligned}$$

(49)

showing that the propagation takes place with a velocity approximately equal to the maximal shear velocity at the bottom of the layer.

The upstream version of the same formula is

$$\begin{aligned} c^*_+ = \frac{S^{*-1}}{8} + O(S^{*-3}),~~x>0. \end{aligned}$$

(50)

We see that the upstream propagation in the presence of strong shear is effectively blocked [4] since the wave motion loses its contact with the bottom. We note the contrast between hydrostatic downstream waves and hydrostatic upstream waves at great shear rates $S^*$. The former waves propagate with an approximate velocity $S^*$, while the latter waves propagate with an approximate velocity $1/S^*$.

5 Energy Fluxes

The energy flux [5] is given by the formula:

$$\begin{aligned} \overline{\frac{\mathrm{d}E}{\mathrm{d}t}} = \frac{1}{2} \rho g \zeta _0^2 c_g, \end{aligned}$$

(51)

expressing the average rate of pressure work per unit of time and length in the y direction perpendicular to the 2D flow field. The dimensionless version of the upstream energy flux is

$$\begin{aligned} \begin{aligned}&\left( \frac{1}{2} \zeta _0^{*2} c_g^*\right) _+ = \frac{1}{2} \left( \frac{\omega ^* }{\sinh \vert k_+^* \vert + {\omega ^*}^2 ~ \text{ csch } \vert k_+^* \vert } \right) ^2 \\&\quad \left( \frac{1 - 2 k_+^* ~\text{ csch }~ (2 k_+^*)}{\sqrt{ (S^*)^2 + 4 k_+^* \coth k_+^*}} + \frac{\text{ sech }^2 k_+^*}{2} \left( - S^* + \sqrt{ (S^*)^2 + 4 k_+^* \coth k_+^*}\right) \right) . \end{aligned} \end{aligned}$$

(52)

The corresponding downstream energy flux is

$$\begin{aligned} \begin{aligned}&\left( \frac{1}{2} \zeta _0^{*2} c_g^*\right) _- = \frac{1}{2} \left( \frac{\omega ^* }{\sinh \vert k_-^* \vert + {\omega ^*}^2 ~ \text{ csch } \vert k_-^* \vert } \right) ^2 \\&\quad \left( \frac{- 1 + 2 k_-^* ~\text{ csch }~ (2 k_-^*)}{\sqrt{ (S^*)^2 + 4 k_-^* \coth k_-^*}} + \frac{\text{ sech }^2 k_-^*}{2} \left( S^* + \sqrt{ (S^*)^2 + 4 k_-^* \coth k_-^*}\right) \right) . \end{aligned} \end{aligned}$$

(53)

Fig. 5

The dimensionless energy flux as function of the dimensionless frequency $\omega ^*$. Three values of $S^*$ are represented, with two graphs in each case. For each value of $S^*$ the lower graph represents upstream waves ($x>0$), while the upper graph represents downstream waves ($x<0$)

Figure 5 shows the dimensionless energy flux for the three shear rates $S^* = 0$, $S^* = 1$, $S^* = 2$. The upstream and downstream energy fluxes are shown in each case, and one might also add up these two fluxes to get the total energy flux emitted by the oscillating source. We see from Fig. 5 that the individual energy fluxes in the upstream and downstream directions decrease monotonously with the frequency. Moreover, the total energy flux from the source will also decrease with increasing frequency.

For a low given frequency, the total energy flux decreases with increasing shear rate. This is shown in Fig. 6, displaying the total dimensionless energy flux as a function of dimensionless angular frequency, for the three shear rates $S^* = 0$, $S^* = 1$, $S^* = 2$. Figure 6 reveals a threshold value of $\omega ^*$, which is about unity in terms of the gravitational variables (26). For the high frequencies above this threshold value, the total energy flux increases with increasing shear rate.

Fig. 6

The total dimensionless energy flux as function of the dimensionless frequency $\omega ^*$. Three values of $S^*$ are represented. Each graph shows the sum of the upstream and downstream energy fluxes, which were displayed separately in Fig. 5

It is not surprising that the downstream energy flux is much greater than the upstream energy flux when the frequency is high since the subsurface current helps to transport highly oscillatory waves in the downstream direction. The downstream energy flux does not change much for small frequencies, but the dominating radiation spectrum is extended to higher frequencies. The upstream energy flux is effectively suppressed by the shear flow [4]; already for the moderate shear rate $S^* = 2$, we see that the upstream waves have an energy flux reduced by more than 80% compared with propagation on still water.

6 Discussion and Concluding Remarks

The present work is the first investigation of physical radiation of water waves in a shear flow, when the waves are caused by an oscillating structure. An oscillating element on a rigid bottom is convenient for studying wave radiation since there is no generation of perturbation vorticity. The elementary solution for radiated waves from a concentrated bottom source is a Green function from which a Green function integral can be constructed for an arbitrary amplitude distribution of monochromatic oscillations along the bottom.

Some previous work suffers from the dilemma that a submerged oscillating source produces an advected oscillating wake, so it cannot fully represent physical radiation in spite of its mathematical consistency [8]. A submerged oscillating source in a shear flow does not represent a physical radiation from a body, partly because it is coupled with a generation of perturbation vorticity that is convected downstream as a critical wave. The critical wave for a submerged source comes in addition to the two regular waves that are propagated in the upstream and downstream directions. Conservation of mass, momentum and energy for a submerged source are difficult principles to apply because they are all influenced by the critical wave: (i) mass conservation makes the source alternate between swallowing particles and eject them. (ii) The conservation of angular momentum for the particles going in and out from the source is troublesome since it generates perturbation vorticity. (iii) The energy flux from an oscillating source is complicated since it is not a pure radiation of wave energy, but also a convective transport of energy in the perturbation vorticity.

A concentrated source at a rigid bottom does not produce any perturbation vorticity, so there is no advected critical wave in our model. Therefore the interpretation of conservation of mass, momentum and energy is easier. There are always two waves in the absence of surface velocity, one upstream and one downstream wave. These waves are gravitational waves with dynamic behavior, in contrast to the critical wave of a submerged source [8], which is passively advected with the shear velocity at the depth of the source. The presence of critical waves [8] also affects the radiation of regular waves from a submerged source, and makes it irrelevant to compare directly wave radiation from a submerged source with our radiation problem for a rigid bottom with a concentrated bottom source.

The hydrostatic limit case without dispersion has been discussed separately, and it has interesting connections with the theory of undular bores. For small shear rates, the hydrostatic shear effect is easy to understand since an average shear velocity adds to (or is subtracted from) the standard hydrostatic propagation velocity $\sqrt{g H}$. For strong shear, the situation is different. The still water propagation with unit velocity will no longer contribute to the wave motion since it is dominated by the shear flow. A sufficiently strong shear flow blocks the pressure communication between the surface and the bottom, as far as the upstream waves are concerned [4]. The energy flux of hydrostatic upstream waves is very strongly reduced even for moderate shear rates.

The present model may seem too restrictive for applications due to the requirement of zero surface velocity, but a follow-up paper will treat the general case with a surface flow. The general case is complicated. Therefore, we find it important to expose separately the present problem where there is only one wave in each direction, and where there is no resonance.