1 Introduction

Intergranular corrosion is a very common local corrosion in duplex stainless steel, which has been widely studied for many years. The intergranular corrosion of duplex stainless steel is mainly caused by the formation of Cr-depleted zone along grain boundaries (GBs). During the solidification of duplex stainless steel, ferrite/austenite (α–γ) interface has a great influence on the microstructure and mechanical properties of the material. Carbide precipitation at the α–γ interface, especially the precipitation of chromium carbide, seriously affects the microstructure and structure of the steel, leading to the formation of Cr-depleted zone and intergranular corrosion [1, 2].

In duplex stainless steel, chromium carbide on the grain boundary leads to the formation of Cr-depleted zone, which is widely accepted. However, not all Cr-depleted zones are caused by precipitation of chromium carbide. According to the latest discovery, carbides are not the only factor leading to the formation of Cr-depleted zone [3]. B, C, P, Mo and Si are common and even unavoidable elements in duplex stainless steel. The impact of their segregation on material properties has been commonly researched [4,5,6,7,8,9,10]. The research shows that P in steel is an important element, and P segregation is mainly affected by the activity of alloying elements on carbides, which will weaken the bonding behavior on grain boundaries, reduce the cohesion of grain boundaries and increase the possibility of grain boundary fracture of materials [3, 6, 7]. Liu et al. [9] found that the added B can occupy the position of P segregation at the grain boundary, improving the cohesion of the grain boundary and preventing the occurrence of intergranular fracture. Suzuki et al. [11] found that the grain boundary segregation tendency of C is higher. C replaces the segregation position of P at the grain boundary, improves the cohesion of grain boundary and decreases the segregation degree of P element [11,12,13]. The ferrite formation element Mo not only promotes the precipitation of secondary phase, but also expands the range of passivation potential and reduces the self-corrosion current density [14]. Si not only forms oxide film on the surface, but also exists as Fe2SiO4 in the rust layer, which improves the formation of α-FeOOH phase, promotes the enrichment of Cr in the rust layer and improves the corrosion resistance of the material [15, 16].

Nonetheless, due to the limitation of experimental methods, people cannot judge which element promotes the formation of Cr-depleted zone and which element inhibits the formation of Cr-depleted zone by experimental means. The influence of their co-segregation with Cr on the formation of Cr-depleted zone is not evident. In this study, the influence of different co-segregation elements on the formation of Cr-depleted zone on α and γ interface is investigated by using three-dimensional atom-probe (3DAP) tomography and first-principles calculation, which provides a theoretical basis for enhancing the corrosion resistance of materials.

2 Experimental

2.1 Materials preparation

The chemical composition of the experimental steel is listed in Table 1. The sample is first heat treated at 1100 °C for 30 min followed by water cooling, and then heat treated at 550 °C for 30 min followed by air cooling. After electrolytic double spray with 10 vol.% perchloric acid + 90 vol.% anhydrous alcohol, the precipitation of secondary phase in the matrix was investigated by transmission electron microscopy (TEM, JEM-2100F) and Digital Micrograph software. After inlaying, polishing and cleaning the samples, corrosive solution is used to corrode for 1–3 min (1 g K2S2O5 + 15 mL HCl + 85 mL H2O). An energy dispersive X-ray spectrometer (EDS, le350 Penta FET X-3) is used to analyze the element segregation phenomenon, and double-loop electrochemical potentiokinetic reactivation (DL-EPR, CS 2350) corrosion test is conducted in 2.0 mol/L H2SO4 + 1.0 mol/L HCl solution at 25 °C. The corrosion of the samples was observed by field emission scanning electron microscopy (SEM, Nova 400 Nano SEM).

Table 1 Chemical composition of studied steel (mass%)
Full size table

2.2 Three-dimensional atom-probe analysis

Three-dimensional atom-probe tomography technology was applied to detect the local composition in the vicinity of the GBs at the atomic scale. Before 3DAP observation, we first found the interface between ferrite and austenite by TEM, and then made the needle tip sample containing ferrite and austenite interface by focused ion beam (FIB). Therefore, the interface observed by the 3DAP technique is the interface between ferrite and austenite. The samples were prepared and analyzed by the FIB system (FIB 600i, CAMECA LEAP-4000XHR) of Shanghai University, China, which uses a 532-nm green laser. To avoid sample fragmentation, the sample was analyzed in laser pulse mode with a frequency of 200 kHz and laser energy of 60 pJ. The temperature of the 3DAP sample was set to about 50 K. The manufacturing process of 3DAP analysis is demonstrated in Fig. 1 [17].

Fig. 1
figure 1

FIB manufacturing process. a Location of interested ferrite and austenite interface region; b sample welded to coupon of atom probe tomography; c shaping needle tip

Full size image

3 Results and discussion

3.1 Intergranular corrosion without carbide

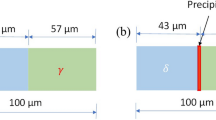
The behavior and mechanism of intergranular corrosion without carbide precipitation along GBs have not been fully studied, and it is still an important factor affecting the corrosion resistance of duplex stainless steel. Therefore, it is necessary and important to clarify the intergranular corrosion mechanism without GB carbide precipitation. Figure 2a and b shows that there is no precipitation of Cr, Ti and Nb carbides, inclusions and secondary phases on the ferrite and austenite grain boundaries. After electrochemical corrosion, it is observed by SEM that the interface between ferrite and austenite in Fig. 2c was corroded, which was consistent with the results observed by Takei et al. [3].

Fig. 2
figure 2

Characterization of ferrite and austenite interface. a Analysis of element distribution by EDS; b TEM image before corrosion test; c SEM image after corrosion

Full size image

3.2 Co-segregation of different elements and Cr distribution on ferrite and austenite interface

To further investigate Cr-depletion induced by co-segregation in the matrix, the local compositions of clusters of solute atoms were characterized by the method of 3DAP analysis. According to 3DAP detection and analysis (Fig. 3), the content of each component at the interface between ferrite and austenite has altered significantly. The interface range is about 23.5–27.0 nm. From Fig. 3a, it is discovered that there is Cr-depleted zone on the ferrite side, which will lead to intergranular corrosion. From Fig. 3b–f, the segregation of B, C, P, Mo and Si elements is discovered on the interface. The maximum content is 3.10%, 2.30%, 2.33%, 13.18% and 4.39%, and the average content is 1.41%, 0.92%, 0.87%, 6.11% and 2.13%, respectively. They all co-segregate with Cr atoms on the interface between ferrite and austenite.

Fig. 3
figure 3

Element distribution on α/γ interface. a Cr element; b B element; c P element; d C element; e Mo element; f Si element

Full size image

3.3 First-principles calculation

Through 3DAP tomography experiments, it has been found that the co-segregation of B, C, P, Mo, Si and Cr occurs at the interface between ferrite and austenite. In order to study the effect of these co-segregation elements on the formation of Cr-depleted zone, an interface between ferrite and austenite calculation models from Fe–B, Fe–C, Fe–P, Fe–Mo and Fe–Si binary system to Fe–B–Cr, Fe–C–Cr, Fe–P–Cr, Fe–Mo–Cr and Fe–Si–Cr ternary system was established. To establish the cell model, according to Dang et al. [18], the fundamental cell of austenite and ferrite and their surface model were established first, and then, the surface model of austenite and ferrite was expanded by 5 and 4 layers, respectively, so as to assure the interface matching of the two cell models. To achieve these goals, the widely accepted Kurdjumov–Sachs orientation relationship is used in this work ((011)α//(111)γ, [\(\overline{1}\overline{1}\)1]α//[\(\overline{1}\)01]γ) [19]. The (111) surface of austenite is established, and on this basis, it expands into 5 times of supercell along [\(\overline{1}\)01]γ direction. The (011) surface of ferrite is expanded into 4 times supercells along [\(\overline{1}\overline{1}\)1]α direction. Thus, the mismatch degree of austenite/ferrite interface is less than 3%. The building process of the interface supercell is shown in Fig. 4. The calculation model consists of five layers of austenite and five layers of ferrite. At the boundary of ferrite and austenite, the three layers closest to the interface between ferrite and austenite on the austenite side, from the interface between ferrite and austenite to the inside of austenite, are denoted as γ1, γ2 and γ3 layers, respectively. The three layers closest to the interface between ferrite and austenite on the ferrite side are denoted as α4, α5 and α6 layers, respectively (Fig. 5).

Fig. 4
figure 4

Composition of cell model of austenite (a–c) and ferrite (d–f). a, d Cell model; b, e surface model; c, f surface supercell model

Full size image
Fig. 5
figure 5

Interface calculation model of element segregation at different positions

Full size image

VASP package was used for the first-principles calculations. The Perdew–Burke–Emzerhof (PBE) form of the generalized gradient approximation (GGA) was used for the exchange–correlation with the cutoff energy of 300 eV and less than energy convergence of 2 × 10–6 eV [20, 21]. The convergence criterion of atomic force is 0.02 eV/Å. The Monkhorst–Pack method is used to sample the k-point grid in the Brillouin zone and test its convergence [22]. With a total number of 480 atoms, both ferrite and austenite are composed of 240 Fe atoms. Therefore, the selected k-points were 1 × 1 × 1 for the interface calculation.

The segregation energy can be calculated by the following formula [22]:

$${\Delta }E_{{{\text{seg}}}}^{i} = E_{{\text{b}}} \left( {GB + i} \right) - E_{{\text{b}}}^{{{\text{ref}}}} \left( {GB} \right)$$
(1)

where \(E_{{\text{b}}} \left( {GB + i} \right)\) is the binding energy of the supercell after inserting external elements; and \(E_{{\text{b}}}^{{{\text{ref}}}} \left( {GB} \right)\) is the binding energy of the original cell. The binding energy can be calculated by the following formula [23]:

$$E_{{\text{b}}} = \frac{1}{N}\left( {E_{{{\text{tot}}}} - \sum N_{i} \mu_{i} } \right)$$
(2)

where \(N\) is the number of atoms in the supercell; \(E_{{{\text{tot}}}}\) is the total energy of the cell; \(N_{i}\) is the number of atoms of each element in the cell; and \(\mu_{i}\) is the energy of a single atom.

Environment-sensitive embedding reflects the influence of the crystal unit inserted with external elements on the surrounding environment [23]:

$$E_{{{\text{ESE}}}} = \frac{1}{n}\left( {E^{{\text{A}}} - E^{{{\text{CL}}}} - E_{{\text{A}}}^{{\text{f}}} + nE_{{\text{f}}} } \right)$$
(3)

where \(E^{{\text{A}}}\) is the sum total energy of the supercell with external element; \(E^{{{\text{CL}}}}\) is the sum total energy excluding external element; \(E_{{\text{A}}}^{{\text{f}}}\) is the atomic energy in the isolated state of alloy atoms; \(E_{{\text{f}}}\) is the atomic energy in the isolated state of Fe atoms; and n is the number of external atoms.

Based on the first-principles of density functional theory (DFT), the influence of each element in the multicomponent system is calculated and separated. Firstly, the energy of single atoms of Fe, Cr, B, C, P, Mo and Si is calculated as − 3.404, − 4.441, − 0.287, − 1.301, − 1.890, − 4.598 and − 0.847 eV, respectively. According to the calculation method of Wang et al. [22, 23], Eb, \({\Delta }E_{{{\text{seg}}}}^{i}\) and EESE were calculated. The binding energy reflects the stability of the calculated cell, and the environment-sensitive mosaic energy reflects the impact of the calculated cell on the surrounding environment. The lower the binding energy and the environment sensitive mosaic energy, the smaller the impact of the cell on the surrounding environment and the more stable the cell structure. Among them, the segregation energy is the size of the segregation ability of each element at the corresponding position of the unit cell. The smaller the segregation energy, the stronger the segregation ability of the element here and the larger the segregation trend. Similar methods have proved that the theoretical calculation of Al, Mn, Ni and Si elements is consistent with the experimental segregation results [24, 25]. The results of these energies at different positions are displayed in Table 2.

Table 2 Calculated energies of interface for elements segregation at different positions
Full size table

According to Table 2, except for replacing Cr and C atoms on the austenite side, the replacement of atoms at other positions decreases the binding energy. Particularly for B, Mo and Si atoms, their binding energy is substantially lower than that of the original unit cell. For Cr atoms, the energy of ferrite side after replacing is significantly lower than that of austenite side and reaches the minimum value of − 3.874 eV at α4 position. That is to say, Cr atoms are more prone to ferrite side segregation, especially at α4 position. The energy change is the most evident for B. The segregation trend of C, P and Si is similar to that of Cr atoms. The energy of ferrite side segregation is lower than that of the austenite side segregation, but their energy at α5 position is the smallest, and the segregation trend here reaches the maximum. The segregation of Mo atom is different from that of C, P and Si. It prefers to segregate on austenite side, particularly on γ1 position of the austenite side interface between ferrite and austenite position. The binding energy of crystal cells is the smallest at that position, which is − 3.882 eV.

It can be seen from Table 2 that the influence trend of environment sensitive inlay energy of B, C and P is nearly the same, and the energy change trend of different replacing positions is very consistent. From the position of the austenite side of interface between ferrite and austenite (γ1) to ferrite internal position (α6), the energy first increases, then decreases, and eventually increases, and after replacement at α5 position, the energy reaches the minimum value. The energy trend of Cr atom replacement is similar to that of B, C and P, but it reaches the lowest value at α4 position. After the replacement of the remaining Mo and Si atoms, the influence of their replacement cell on the surrounding environment is greater than that of B, C and P atoms, and the environment sensitive mosaic energy reaches the minimum values of − 0.014 and − 0.009 eV at γ1 and α5 positions, respectively, whose position is consistent with the above binding energy results.

Table 2 illustrates the variation trend of segregation energy after replacement at different positions. The unit cell segregation energy after replacing Mo and Si atoms is the smallest, and the segregation ability is much higher than that of B, C and P atoms. The segregation trend is the most evident. Nonetheless, Mo atoms tend to be segregated on the austenite side, and the segregation energy gradually increases from the austenite side to the ferrite side. While Si atoms are just the opposite, the energy gradually reduces from the austenite side to the ferrite side and reaches the minimum value of − 2.064 eV at α5 position. However, the cell segregation energy of Mo atom after replacement at any position is lower than that of Si atom replacement, which is much lower than that of B, C and P atoms. That is to say, Mo atom has the strongest segregation ability, and the following is Si atom. The segregation energy of B, C, P and Cr atoms is smaller and considerably weaker than that of Mo and Si atoms. They reach the easiest segregation state at α5 and α4 positions. This is consistent with the above binding energy and environment-sensitive mosaic energy results.

It can be observed from the calculation results that the most secure segregation position of these elements in the crystal cell, the segregation position with the least impact on the surrounding environment and the simplest segregation position are consistent. In other words, when Cr is segregated in α4 layer and B, P, C and Ni are segregated in α5 layer, the segregation of Mo in γ1 layer is more conducive to the overall stability of the interface unit. The results are shown in Fig. 6.

Fig. 6
figure 6

Interface calculation model after element replacement in different positions

Full size image

In order to study the effect of segregation of different elements on the formation of Cr-depleted zone, these atoms were used to replace Fe atoms in the interface unit. The energy change of crystal cell is analyzed. The calculated energy is shown in Table 3. According to the calculation results, it can be seen that when compared with Cr segregation interface cell, EESE and Eb reduced substantially for Mo–Cr and Si–Cr co-segregation interface cell. When B–Cr, C–Cr and P–Cr are co-segregated on the interface between ferrite and austenite, the values of EESE and Eb decrease to a relatively small extent. The results indicate that Mo and Si elements strongly promote the segregation of Cr elements on the interface between ferrite and austenite, hence promoting the formation of Cr-depleted zone and aggravating the possibility of intergranular corrosion phenomenon. B, C and P elements also promote the segregation of Cr element on the interface between ferrite and austenite and the formation of Cr-depleted zone, but the effect is weaker than that of Mo and Si elements.

Table 3 Segregation energy and environment-sensitive embedding energy of interface structure with co-segregation of different elements
Full size table

4 Conclusions

  1. 1.

    The co-segregation of B, C, P, Mo, Si and Cr occurs on the interface between ferrite and austenite.

  2. 2.

    B, C, P, Si and Cr tend to segregate on the ferrite side of α/γ interface, and Mo tends to segregate on the austenite side of the interface.

  3. 3.

    Mo and Si strongly promote the segregation of Cr on the interface between ferrite and austenite, thus promoting the formation of Cr-depleted zone. B, C and P elements also promote the segregation of Cr element on the interface between ferrite and austenite and the formation of Cr-depleted zone, but their effect is weaker than that of Mo and Si elements.