1 Introduction

To satisfy the requirements of high-quality steel, secondary metallurgy is widely applied, which is often performed in a ladle furnace [1,2,3,4]. As a functional component of the ladle lining, the purging plug was used for stirring molten steel [5,6,7]. Thus, in service, the purging plug is periodically exposed to intense thermomechanical loads, which results from the collaborative impact of severe thermal shock due to blowing gas and molten steel, external mechanical constraints, and thermal expansion of its materials [8,9,10]. Accordingly, the extreme process conditions of the purging plug undertaken will generate the related thermomechanical behaviour inside the purging plug, which vary with location and operation time [11, 12]. Due to these thermomechanical loads, slow irreversible displacement, e.g. creep, will be triggered at a certain temperature owing to continuous thermomechanical loads [13]. The creep behaviour can cause the irreversible deformation of the purging plug body, resulting in cracks [14], damage [15], as well as failure of the purging plug, and is one of the crucial factors of the purging plug damage. For the reason mentioned above, the life span of the purging plug is shorter than that of the other parts of the ladle lining. Therefore, the shorter service life of the purging plug determines the higher maintenance frequency of the ladle, which has a consequential and negative impact on energy-saving and production efficiency. Thus, it is necessary to quantitatively investigate its creep deformation during service.

Moreover, the further accumulation of creep strain will inversely alter the microstructure of the refractory material. However, many previous researches of the creep were aimed at the material level [16], and few reports are available on the effect of creep deformation on the structural response under cyclical service conditions [17, 18]. As for the purging plug made from refractory, the ability to accurately describe its creep behaviour is significant in adjusting the chemical components of its material and optimizing its structural design, which can provide theoretical support for further prolongation of the life span of the purging plug.

Recently, the development of an efficient approach for predicting creep deformation of materials operating at high temperatures has been paid more attention. For instance, two advanced testing devices have been proposed to characterize the uniaxial behaviour of ordinary refractory ceramics at corresponding service loads [19,20,21,22], of which one is applied to measure the compressive creep at elevated loads and the other is dedicated to tensile creep measurement. With the test equipment, the creep curves of the refractory can be achieved in a reasonable time. According to the creep curve, many kinds of creep construction models usually can be deduced to account for creep strains. For integrating the material creep strain in terms of stress, time and temperature based on uniaxial stress, many suggestions were proposed, among which the Norton–Bailey creep law is widely employed. For instance, the time hardening formula was applied to describe the creep deformation of metallurgical components, in which the creep rate is a function of time [23,24,25]. Besides, Jin et al. [26] employed the Norton–Bailey strain hardening creep equation to evaluate the creep displacement of working lining, whose results indicate that the thermomechanical loads in the proposed lining concept remain within a reasonable range.

In this paper, based on the compressive creep tests, the creep parameters of the Norton–Bailey strain hardening rule were inversely identified by APDL code in ANSYS. Subsequently, the thermal-solid approach was employed to predict the creep behaviour of the purging plug during service, where the Norton–Bailey strain hardening law was taken into account. Moreover, the accumulation of creep strain was also calculated considering periodical service conditions. The numerical results were conducted to provide guidance for controlling creep deformation and optimizing the structural design of the purging plug.

2 Models and experiments

2.1 Geometry

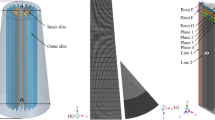
As shown in Fig. 1a, the purging plug with rectangular slits was employed for actual use. Moreover, the dimensions of the purging plug are given in Fig. 1b. With the commercial code ANSYS, a finite element model was created for conducting the numerical simulation, where one-tenth of the purging plug was considered due to the geometrical symmetry, as depicted in Fig. 1b. In this case, 9.5 × 105 hexahedron elements were assigned to the purging plug with rectangular slits, meeting the demands of grid independence.

Fig. 1
figure 1

3D representation of purging plugs with rectangular slits. a Cross-sectional view; b dimensions of one-tenth of purging plug

Full size image

2.2 Boundary conditions

Except for the preheating stage, the cyclic operations considered transporting, stirring, holding and idle time stages in simulation. The durations and defined working face temperature of each procedure are indicated in Table 1 and Fig. 2, respectively. In the first cycle, a simplified preheating process was assumed, and the working face was heated from room temperature to 1000 °C. Figure 3 shows the heat flux (Qf) of the cylindrical face and the heat convection of the bottom face in the load cycle. As depicted in Fig. 4, the heat convection of the slit wall was loaded during the stirring stage under cyclic service. For calibrating the above-mentioned boundary setting, the experimental device present in our previous research was designed [27].

Table 1 Duration for each process in a load cycle
Full size table
Fig. 2
figure 2

Temperature of working face in load cycle. T Temperature; t time

Full size image
Fig. 3
figure 3

Heat flux of cylindrical face and heat convection of bottom face in load cycle

Full size image
Fig. 4
figure 4

Heat convection of slit wall in load cycle

Full size image

2.3 Creep model

Generally speaking, a complete creep behaviour of corundum castable under constant load and temperature consists of three stages. As depicted in Fig. 5, the first stage, named primary creep, demonstrates a time-dependent strain rate that reduces with time. Subsequently, a constant creep strain rate was indicated in the secondary creep stage. As the minimum one of all three stages, it attributes an approximate equilibrium between hardening and softening processes. Finally, tertiary creep is characterized by an increasing strain rate until the failure of the material.

Fig. 5
figure 5

Creep curve with indications of three stages. εcr Creep strain

Full size image

In this study, the classical von Mises creep model, which is independent of hydrostatic pressure, was employed. Two terms of creep strain are usually used to model the creep deformation of materials, one of which is the creep strain \(\varepsilon_{ij}^{{{\text{cr}}}} (i,j = 1, 2, 3)\) in the respective stress direction and can be integrated by the corresponding creep rate (\(\dot{\varepsilon }_{ij}^{{{\text{cr}}}}\)) with respect to time as shown in Eq. (1).

$$\varepsilon_{ij}^{{{\text{cr}}}} = \smallint \dot{\varepsilon }_{ij}^{{{\text{cr}}}} {\text{d}}t$$
(1)

Another one can be represented as the equivalent creep (\(\overline{\varepsilon }^{{{\text{cr}}}}\)), which means an absolute and accumulative value of the global creep strain increment with respect to time. The equivalent creep strain follows Eq. (2).

$$\overline{\varepsilon }^{{{\text{cr}}}} = \smallint \dot{\overline{\varepsilon }}^{{{\text{cr}}}} {\text{d}}t = \int {\sqrt {\frac{2}{3}\dot{\varepsilon }_{ij}^{{{\text{cr}}}} :\dot{\varepsilon }_{ij}^{{{\text{cr}}}} } {\text{d}}t}$$
(2)

where \(\dot{\overline{\varepsilon }}^{{{\text{cr}}}}\) represents the equivalent creep strain rate.

As for the classical creep model, the creep strain rate matrix can be deduced according to Eq. (3).

$$\dot{\varepsilon }_{{{\text{cr}}}} = \dot{\overline{\varepsilon }}^{{{\text{cr}}}} \frac{\partial q}{{\partial \sigma }} = \frac{3}{2}\dot{\overline{\varepsilon }}^{{{\text{cr}}}} \frac{s}{q}$$
(3)

where s means the deviatoric stress; q can be expressed as \(\sqrt {\frac{1}{2}[\left( {\sigma_{1} - \sigma_{2} } \right)^{2} + \left( {\sigma_{2} - \sigma_{3} } \right)^{2} + \left( {\sigma_{1} - \sigma_{3} } \right)^{2} ]}\); and \(\sigma_{i}\) represents the principal stress; the subscripts 1, 2 and 3 refer to the three direction of the principal stress. After decomposition along the principal direction, the principal creep strain rates are further followed as Eq. (4).

$$\left( {\begin{array}{*{20}c} {\dot{\varepsilon }_{1}^{{{\text{cr}}}} } & {} & {} \\ {} & {\dot{\varepsilon }_{2}^{{{\text{cr}}}} } & {} \\ {} & {} & {\dot{\varepsilon }_{3}^{{{\text{cr}}}} } \\ \end{array} } \right) = \dot{\overline{\varepsilon }}^{{{\text{cr}}}} \left( {\begin{array}{*{20}c} {\frac{3}{2}\frac{{\sigma_{1} + p}}{q}} & {} & {} \\ {} & {\frac{3}{2}\frac{{\sigma_{2} + p}}{q}} & {} \\ {} & {} & {\frac{3}{2}\frac{{\sigma_{3} + p}}{q}} \\ \end{array} } \right)$$
(4)

where p is expressed as \(- (\sigma_{1} + \sigma_{2} + \sigma_{3} )/3\).

Creep strain intensity (\(\varepsilon_{\text{I}}^{{{\text{cr}}}}\)) is defined as the largest of the absolute values among \(\varepsilon_{1}^{{{\text{cr}}}} - \varepsilon_{2}^{{{\text{cr}}}}\), \(\varepsilon_{2}^{{{\text{cr}}}} - \varepsilon_{3}^{{{\text{cr}}}}\), and \(\varepsilon_{{3}}^{{{\text{cr}}}} - \varepsilon_{{1}}^{{{\text{cr}}}}\):

$$\varepsilon_{{\text{I}}}^{{{\text{cr}}}} = \max \left( {\left| {\varepsilon_{1}^{{{\text{cr}}}} - \varepsilon_{2}^{{{\text{cr}}}} } \right|,\left| {\varepsilon_{2}^{{{\text{cr}}}} - \varepsilon_{3}^{{{\text{cr}}}} } \right|,\left| {\varepsilon_{3}^{{{\text{cr}}}} - \varepsilon_{1}^{{{\text{cr}}}} } \right|} \right)$$
(5)

where \(\varepsilon_{1}^{{{\text{cr}}}}\), \(\varepsilon_{2}^{{{\text{cr}}}}\), and \(\varepsilon_{3}^{{{\text{cr}}}}\) are the principal creep strain. Thus, creep strain intensity is equal to the maximum shear creep strain (Ymax):

$$\varepsilon_{{\text{I}}}^{{{\text{cr}}}} = Y_{\max }$$
(6)

While a reversed uniaxial loading named a tension–compression cycle was employed, the absolute value of principal creep strain was decreased. This quantity represents the length change owing to creep in the respective direction. Furthermore, it demonstrated the significance of creep strain terms. Instead, the equivalent creep strain value exhibits that the creep effect is irreversible and additive. Indeed, the purging plug frequently experiences more complicated thermomechanical loads. Consequently, the term equivalent creep strain was applied in the present study and demonstrated the global creep response of the purging plug.

Therefore, the Norton–Bailey strain hardening/softening formulation was adopted to account for the creep behaviour of the purging plug material in the present study, of which the creep strain rate is a function of stress, creep strain and temperature:

$$\dot{\varepsilon }_{{{\text{cr}}}} = C_{1} \sigma^{{C_{2} }} \varepsilon_{{{\text{cr}}}}^{{C_{3} }} {\text{e}}^{{{\raise0.7ex\hbox{${ - C_{4} }$} \!\mathord{\left/ {\vphantom {{ - C_{4} } T}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$T$}}}}$$
(7)

where \({{C}}_{{1}}\) and \({C}_{4}\) are constant; and \({C}_{2}\) and \({C}_{3}\) are the stress and strain hardening exponents, respectively. These creep parameters are inversely identified in Sect. 2.4.2.

2.4 Material characterization

The density of the purging plug made of corundum castable is 2900 kg m−3. The Poisson’s ratio of 0.25 was assumed. In the literature, the thermal expansion coefficient, the thermal conductivity, and specific heat capacity, as well as the elastic modulus of the purging plug, were represented, which are measured in the laboratory [27, 28].

2.4.1 Creep test experiments

The compressive creep test was performed through the advanced spindle-driven testing device, which represents the creep deformation [29]. Specimens of sintered corundum castable were fabricated into the cylinder of ϕ35 mm × 70 mm. The detail of the creep test can refer to previous research [30, 31]. Figure 6 depicts the loaded compressive force of the specimen during creep tests.

Fig. 6
figure 6

Loaded compressive force of specimen during creep tests

Full size image

2.4.2 Creep evaluation procedure

The measured displacements comprise both the elastic and creep deformation. The total strain, that is, the sum of elastic strain and creep strain, was calculated to consider the initial extensometer legs distance (50 mm).

$${\varepsilon}_{\text{tot}} = {\varepsilon}_{{\text{cr}}} + \frac{\delta}{E}$$
(8)

where \({\delta}\) is the applied stress; \({\varepsilon}_{{{\text{tot}}}}\) represents the measured total strain; and E means Young’s modulus at the corresponding temperature.

Based on Eqs. (7) and (8), an approximation formula was deduced to identify the corundum castable parameters from compressive tests using the trapezoidal rule [19], which was expressed as:

$${\varepsilon}_{{{\text{cr}},i + 1}} = \left[ {{\varepsilon}_{{{\text{cr}},i}}^{{1 - C_{3} }} + \frac{{\left( {1 - C_{3} } \right) \cdot A \cdot \left( {\sigma_{i + 1}^{{C_{2} }} + \sigma_{i}^{{C_{2} }} } \right) \cdot \left( {t_{i + 1} - t_{i} } \right)}}{2}} \right]^{{\frac{1}{{1 - C_{3} }}}}$$
(9)
$$A = C_{1} {\text{e}}^{{{\raise0.7ex\hbox{${ - C_{4} }$} \!\mathord{\left/ {\vphantom {{ - C_{4} } T}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$T$}}}}$$
(10)

where the subscripts i and i + 1 of strain and stress mean the time step-index. To inversely identify the creep parameters, the sum of the squared differences of measured and simulated strains has been minimized by using the non-linear generalized reduced gradient method [19, 32, 33]. This procedure was realized in ANSYS with the APDL code. The identified creep parameters are displayed in Table 2.

Table 2 Norton–Bailey creep law parameters of castable corundum corresponding to different temperatures
Full size table

2.5 Experimental calibration

For calibrating the above-mentioned boundary setting, the experimental device and more details of the experimental procedure were present in our previous research [27]. In this apparatus, four thermocouples were installed at four measurement positions, respectively. Meanwhile, a thermal-solid coupling model was established to simulate the stirring process, in which the heat exchange between the slit and argon gas was validated compared with experimental results. The results indicated that some experimental points are aberrant and show more than 300 K in the opposite direction when the time approaches 8000 s. Several factors are attributed to the accuracy of the thermocouples. Firstly, the sealing between thermocouple, gas chamber, and measuring position is incomplete. Thus, the pressure of the air chamber declines, while the gas stops blowing, and the temperature of the measurement position is unstable. Moreover, the vibration of the air compressor during its operation also affects the measurement. Finally, the accuracy and sensitivity of thermocouples affect the measurement date. Therefore, the synergy of the mention-above factors has an impact on the accuracy of the thermocouples. However, the trend of experimental data with time is consistent with the simulation results, and the difference between numerical results and experimental results is less than 15%. Accordingly, the above-mentioned boundary setting was adopted to simulate the cyclic service process of the purging plug.

3 Results

3.1 Thermal results

The temperatures at points A, B and C (see Fig. 1) are plotted in Fig. 7, which display the temperature evolution of the purging plug with respect to the processing time. It shows that the temperature of the purging plug presents a periodic trend, starting from two service cycles. This attributes to the preheating temperature, which is lower than the temperature of molten steel. Thus, the purging plug cannot reach the thermal equilibrium state after the preheating process is applied to relieve thermal shock from liquid steel. Furthermore, there is a temperature drop at the beginning of the stirring stage, which is because of the heat transfer between argon and slit walls. Besides, due to the thermal shock from the pouring molten steel, the temperature rise occurs at the beginning of transporting process.

Fig. 7
figure 7

Temperature evolution of positions A, B and C with respect to processing time

Full size image

As discussed above, the temperature of the purging plug presents a periodic trend after one service cycle. Furthermore, Fig. 8 illustrates the temperature distribution of the purging plug at a specific time during the stirring stages at the 4th cycle. It indicates that the temperature gradient gradually rises with increasing time, so does the temperature gradient of the cylindrical surface. The phenomenon can be explained as follows: although the heat from liquid steel heats the working face of the purging plug, the injected argon cools down the slit wall of the purging plug. Meanwhile, the heat flux of the cylindrical face leads to the heat loss of the purging plug. The competition among three heat transfers would be reasonably balanced during the stirring process.

Fig. 8
figure 8

Temperature distribution in purging plug after stirring for 100 s (a), 300 s (b), and 600 s (c) during 4th cycle

Full size image

3.2 Thermomechanical results

Figure 9 depicts the axis stress evolution of positions A, B and C with respect to the processing time. It is evident that the thermomechanical behaviour did not present periodicity considering the periodic service process, in which the creep model was applied. Moreover, the accumulation creep displacement relieves the axial compressive stress inside the purging plug. Figure 10 shows the equivalent creep strain distribution of the purging plug at the end of each cycle. It indicates that the volume where the creep strain appeared increased with respect to the processing time. Furthermore, the region of creep of the purging plug is located near the working face. This attributes to the temperature gradient that also locates near the working face. Consequently, the creep behaviour occurs under the corresponding thermomechanical load. Besides, the accumulation of creep strain could increase with time until the creep failure appears, which may be a significant reason for spalling of the purging plug. After three service cycles, the increment of creep strain volume in the purging plug is imperceptible in Fig. 10.

Fig. 9
figure 9

Axis stress evolution of positions A, B and C with respect to processing time

Full size image
Fig. 10
figure 10

Equivalent creep strain distribution of purging plug at end of 1st cycle (a), 2nd cycle (b), 3rd cycle (c), 4th cycle (d), and 5th cycle (e)

Full size image

As shown in Fig. 11, the creep strain distribution of purging plugs for different cross sections at the end of the 3rd cycle, 4th cycle, and 5th cycle is displayed. It indicates that the creep strain in y-direction is concentrated around the slit. This may be a consequence of the axis stress concentrated around the slit. Owing to the heat convection between the slit and the injecting argon, the temperature gradient around the slit gradually rises. As a result, axis stress concentrating around the slit, which was reported in our previous study [27]. Furthermore, the closer the section is to the working face, the more pronounced the creep strain concentration is. This attributes to the competition of two kinds of heat transfer, of which one is heat transfer from molten steel and the other one is heat convection between the purging plug and argon.

Fig. 11
figure 11

Creep strain distribution of purging plugs for different cross sections at end of 3rd cycle, 4th cycle, and 5th cycle

Full size image

Figure 12b displays the creep strain intensity of the purging plug and relative creep deformation. By comparing with the original geometry (as shown in Fig. 12a), a relative deformation of the upper section of the purging plug was noticeable in the axis direction. Moreover, the creep strain intensity distributes in a layered form in the purging plug. When the creep damage caused by shear creep strain occurs, the purging plug end can experience gradual spalling. To reduce the possible gradual spalling, proper structural optimization and material selection are essential.

Fig. 12
figure 12

Creep strain intensity of purging plug and relative creep deformation before (a) and after (b) 5th cycle service (scale factor: 25)

Full size image

The geometrical deformation of the slits caused by thermal expansion and creep could also promote the infiltration of the liquid metal. As explained by Cheng and Zhu [34], when the molten steel contacts with the refractory surface, an adhesive force appears between melt and refractory, which prevents the molten steel from spreading along the refractory slit wall; a cohesive force of liquid metal will prevent the surface of liquid metal from tearing. Consequently, the molten steel in the slit can form a liquid film on the gas–liquid interface to withstand a certain amount of static pressure. Under limited static pressure, pressure equilibrium might be achieved with an optimized slit width. This equilibrium could be frequently broken when the slit width is cyclically changed caused by thermal expansion of materials or reduced further caused by the creep deformation of materials. As illustrated by Fig. 13b, the shrinkage of slit width could shear the liquid metal at the solid/liquid/gas interface. Accordingly, the clogging inside slits could appear with the penetration of liquid steel and molten slag. This will affect the performance of the purging plug during the stirring stage. Hence, oxygen burning and gas bottom injection need to clean the blockages of the purging plug and ensure the blow-off rate [35, 36]. On the other hand, the creep deformation of the purging plug could also be extreme enough to block the slits. Thus, the creep deformation may be a crucial reason for the clogged purging plug. Although the penetration of liquid steel and molten slag into the slit cannot be avoided in practice, it could be alleviated by choosing strong creep resistant materials or stable slit structure, e.g. circular shape.

Fig. 13
figure 13

Schematic illustration of molten steel penetration into slit at static process (a) [34] and dynamic process considering creep deformation (b)

Full size image

4 Conclusion

In the present study, the creep parameters of the Norton–Bailey strain hardening rule were inversely identified via the result of the creep test. Then, the thermal-solid approach was employed to predict the creep behaviour of the purging plug. The numerical results indicate that the temperature of the purging plug presents a periodic trend after the first service cycle due to the preheating temperature that is lower than the temperature of molten steel. The distribution of the creep strain intensity in a layered form is likely a crucial reason for the gradual spalling of the purging plug head in service. Moreover, the creep strain concentrated around the slit could contribute to the clogging of purging plugs. Therefore, due to alleviation of the stress concentration around the slit, optimizing the geometric structure of the slit for the purging plug will contribute to decreasing creep strain, which provides the orientation for the optimization of the service performance of the purging plug.