Abstract
A funnel-type mold is commonly used to provide necessary clearance for the submerged entry nozzle in the thin slab casting (TSC). The partially solidified shell is subjected to the mechanical deformations, which can lead to the defects formation and, as a results, to a breakout. Traditionally, the results of the flow simulation, performed by the finite volume method (FVM), are fed to the external package for the finite element analysis of stress and strain. A coupled model was assembled using “creeping solid” approach by blending the Norton-Hoff viscoplastic stress for the solidifying shell with the Newtonian viscous stress of the liquid melt. The FVM was used to combine both liquid and solid stress models within a single solver. The iterative procedure based on the improved both side diffusion method was introduced to treat the nonlinear relation between the viscoplastic stress and the strain rate. The modeled shell thickness was verified by previously published breakout measurements and the simulation results. Temperature distribution, obtained during the TSC simulation, dominantly corresponds to the viscoplastic range. Developed numerical approach is robust and has direct industrial application.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
During the solidification, the properties of the alloys, according to the pioneering work of Flemings [1], drastically vary at the two-phase region, also called the mushy zone. In the continuous casting (CC), the defects are formed and accumulated under the mechanical strain during the casting process and can result in a breakout due to the variation of the alloy properties. The course of the initial solidification in the CC mold, the interaction of the growing shell with the turbulent melt flow and its behavior during a withdrawal are one of the key features for the final product quality in the CC process [2,3,4,5,6].
The extended reviews on the methodology and practical applications of the numerical modeling of the continuous casting are presented throughout two decades starting from early two-thousands by Thomas [7] and Atkinson [8] and supplemented by recent works by many researchers [2, 4, 5, 9,10,11].
In early two-thousands, Thomas [7] stressed in his review that the enhanced heat flux at the exit of the mold could be an indication of the mold taper pressing to strongly against the shell. Additionally, the following factors, such as shell thickness at mold exit, the metallurgical length and the corresponding cooling practice are important, since the slab becomes susceptible to cracks due to the off-corner depression, reheating or non-uniform shell growth.
According to Ramirez Lopez et al. [5], the numerical modeling became a key tool to investigate the lubrication concepts in the continuous casting, giving insights into the heat transfer and solidification guided by the flow with an aim to predict defect formation, mentioned by Flemings [1] and Thomas [7]. It is promoted that by the oversimplification of the numerical models, the key issues can be missed. The numerical modeling achievements supplemented with the industrial observations should improve the knowledge and the conceptual point of view on modeling techniques.
Novel modeling techniques are applied nowadays to resolve the transient multiphase phenomena during CC, e.g., meshless approach employed by Vertnik et al. [12] to tackle the turbulent flow and solidification at the presence of the electromagnetic steering. Reduction in the problem dimensions allows to perform the investigation of the solidification during casting in shorter terms [13,14,15,16] or combine them with the industrial measurements to define proper casting strategy to avoid defects formation [17, 18]. Current authors suggested a novel single mesh approach to simulate the heat transfer during CC including convection in the liquid slag to predict the parasitic solidification in the submerged entry nozzle (SEN) region [19]. The scale adaptive modeling of the multiphase mold flow with application to the analysis of the opened eye formation was recently published elsewhere [20, 21].
As a funnel-type mold is used to provide necessary clearance in the narrow cavity region for the SEN, the (partially) solid shell of the thin slab casting is much stronger subjected to the mechanical deformations than that of conventional CC. Traditional approach for the funnel-type mold simulation, as presented in Vakhrushev et al. [22], provides steady-state distribution of the solid shell velocities. The full elasticity of the solid structure and neglecting its rheology variations due to the cooling are restrictive assumption. However, the steady-state approximation cannot tackle the transient phenomena that occur during continuous casting. The shell compression and tension are the provenance of the cracks and the hot tearing formation [23]. As recently revealed, the interaction of the highly conductive shell with the induced electric current during electromagnetic brake leads to the complex topology of the Lorentz force and to the complete alternation of the melt flow pattern [24,25,26].
The aim of the current work is to track the transient mechanical behavior of the solidifying shell during continuous casting in a funnel-type thin slab mold by employing a transient viscoplastic stress model. Traditionally, a decoupled one-way approach is employed in the computational fluid dynamics (CFD) community for complex full-size geometries. The flow simulation results are typically obtained with the finite volume method (FVM). Next, they are fed to an external package for the finite element analysis (FEA) [27,28,29]. Substantial contribution in this field was done in previous studies [30,31,32,33,34] by developing the arbitrary Lagrangian–Eulerian (ALE) formulation in the context of the alloy casting. The method includes a solution of the governing conservation laws for mass, momentum, and energy on the Eulerian mesh. The coupled solution is reflected via elasto-viscoplastic stress model to the corresponding mesh motion algorithm. To model the continuous casting, such an approach requires several steps: firstly, the thermomechanical analysis is performed by treating the mush as a non-Newtonian fluid; next, the initial and boundary conditions for the two-phase simulation are extracted from the first calculation by defining the point of the coherency of the two-phase core (> 65% of solid) and continuously crowing mesh in the frame of the ALE approach with the casting speed using special buffer zone as well.
Due to the complex cross-methodological (FVM/FEA or Lagrangian/Eulerian) coupling, such approaches are limited to 2D or axisymmetric geometries, reducing the studies mostly to the steady-state cases. The currently presented model is an attempt to overcome these limitations.
Additional motivation of the present study is to verify a single-phase volume-averaging approach for the application to model a viscoplastic stress in the two-phase region during alloy solidification. On the contrary to the previously applied multiphase Eulerian–Eulerian volume-averaging model for the equiaxed crystal sedimentation [35,36,37] and the twin-roll casting process [38,39,40], the so-called mixture model is very robust, numerically stable and fast in sense of the calculation time required. As an advantage of the presented work, a full 3D model is considered including an SEN, a funnel-type thin slab mold (879 mm in height) and strand part (4000 mm along casting direction including mold). The boundary layers were introduced to correctly predict near-wall flow and heat flux. A highly turbulent flow in the SEN (with maximum velocities of 3 m s−1) drastically limited the efficiency of the time marching algorithm to integration step of 10−4 s. Taking all arguments into account, the multiphase approach was found to be inappropriate for transient full-scale industrial simulation.
In the present study, a coupled model is assembled using viscoplastic approach in the frames of the “creeping solid” hypothesis. In this method, as the solid fraction increases specifically above a certain (coherency) limit, a considerable strain resistance of the solidifying alloy develops. The mush represents a columnar skeleton with liquid in the inter-dendritic mushy zone [41], which can sustain high stresses, while the solid and the liquid become strongly coupled. That is usually reflected in the viscoplasticity theory by an abrupt jump of the effective viscosity.
In current work, the viscoplastic Norton-Hoff type stress is applied to model a complex process of the thin slab continuous casting, and the first results are discussed. The blending of the stress tensor for the solidifying shell is done with the viscous liquid stress based on the solid fraction distribution. The advantage of the proposed approach is using finite-volume formulation within a single solver for both solid shell mechanical behavior and the strong melt flow. The latter is typically excluded in most studies on the mechanical stress calculations by simplifying to a plug-type flow. In the present study, the flow phenomenon is fully considered. The iterative procedure is introduced for the treatment of the nonlinear relation between the viscoplastic stress and the strain rate tensor.
The classical thermomechanical models were developed for the semi-solid state, providing the constitutive equations for porous metallic materials saturated with liquid. The difference between the cases lies in the solid-phase permeability and the material globular [41] as well as the dendritic morphology [42,43,44]. Some of the models are also restricted to the isothermal conditions only. The great endeavors were done by Fachinotti et al. [31, 45] by revising constitutive temperature and composition-dependent models and combining with the Lagrangian–Eulerian approach of Bellet and Fachinotti [30] to apply it to the actual casting processes.
According to the book of Rappaz et al. [46], the metal alloys perform as an elastic material till 1/3 of their absolute melting temperature. Then, the creeping occurs corresponding to the elasto-viscoplasticity of the material, and approximately, above 2/3 of the melting temperature, a fully viscoplastic behavior is observed. The viscoelasticity of an alloy represents rate-dependent unrecovered deformations of the material. Rate dependence in this context corresponds to the creeping of the solid according to the rate of load has been applied. Temperature distribution, obtained during the thin slab casting simulation, lies dominantly within the viscoplastic range slightly catching transition to the elastoplastic behavior.
The numerical results comparison showed good agreement with the previously obtained and experimentally verified ones. The detailed description of the numerical model and the simulation results are presented in the next sections; finally, the discussion and the conclusions are made.
2 Numerical model
Based on the previous experience of developing a numerical Eulerian–Eulerian model to simulate behavior of the packed bed of equiaxed crystals [35,36,37] and the macrosegregation during the twin roll casting [38,39,40], the viscoplastic stress model was applied to the thin slab casting by reducing it to the “mixture” formulation, which is more robust for the industrial scale simulations.
The following assumptions were made to model the viscoplastic behavior of the solidifying shell during its withdrawal:
-
(i)
An averaged “single”-phase approach is employed considering the simulated media to be a mixture of the liquid and solid.
-
(ii)
Main material properties such as density, specific heat and thermal conductivity are constant across both phases, and moreover, they are temperature-independent; thermo-solutal buoyancy is ignored.
-
(iii)
Temperature and pressure field equilibrium is assumed between liquid and solid phases.
-
(iv)
Total effective stress incorporates both the Newtonian and the viscoplastic one according to the phase fraction in the control element of the computational grid; thermomechanical stress is ignored.
2.1 General equations of motion
The continuity and momentum equations for the incompressible liquid become:
To perform the coupling between the solid and liquid phase, the total stress tensor is divided into deviatoric and hydrostatic parts, representing shear and volumetric forces correspondingly. Next, a volume averaging of all terms is considered:
Omitting the volume averaging notation hereinafter for all further derivations, the deviatoric part of the total stress tensor can be expressed as a blending of the viscoplastic stress for the solid and the Newtonian one for the liquid melt:
where the condition \(f_{{\text{s}}} + f_{\ell } \equiv 1\) is valid.
The deviatoric part of the liquid stress tensor is
where \(\dot{\user2{\varvec\varepsilon }}\) represents a symmetric part of \(\nabla {\varvec{u}}\):
To clarify the reformulation in right side of Eq. (5), one should revive the property of the \(\dot{\varvec{\varepsilon }}\) from Eq. (6) by recalling the continuity condition of incompressible fluid Eq. (1) and by simple manipulation. Consistently, it can be derived that
In other words, the strain rate is originally a deviatoric (or traceless) tensor for incompressible media. That will be later used in this work for the corresponding substitutions in further derivations, e.g., in the equivalent strain rate formulation. However, for the rheological models including the mush compressibility, such as reported by Fachinotti et al. [31], the non-hydrostatic terms will reflect the so-called bulk viscosity and the corresponding two-phase region compression. Here, the authors left this topic for the future detailed investigations.
As a concluding assumption of the presented approach, the pressure balance at the solid–liquid interface is taken, thereby leading to a single “pressure” field for both phases. To avoid confusion, the “pressure” is regarded as a spherical tensor of the volumetric forces defining compression–depression in the material regardless of its “liquid” or “solid” nature.
2.2 Norton-Hoff-type deformation model
2.2.1 General elasto-viscoplasticity at high temperatures
General solids show the elastic-viscoplastic behavior. The solid becomes purely viscoplastic close to the solidus temperature when the yield and hardening are negligible. Viscoplastic behavior is referred as the Ostwald-de-Waele law or more commonly the Norton-Hoff law [47].
With the rising temperatures, the strength properties of steel undergo significant weakening and become strain-rate-dependent, showing creeping behavior. At low strains, the solid stress can be split in two components by decoupling elastic and viscoplastic parts as formulated by Norton for the uniaxial stress [48]:

The difference \(\sigma^{{{\text{elvp}}}} - \sigma_{{{\text{stat}}}}\) is a so-called extra-stress. Below that threshold, the material acts as the elastic one. Above the limit, an irreversible portion of deformation happens, characterized by a \(\dot{\varepsilon }^{{{\text{vp}}}}\). The classical power law  in Eq. (8) was introduced by Norton [48] including two parameters
in Eq. (8) was introduced by Norton [48] including two parameters  and m. The von Mises equivalent stress is introduced as:
and m. The von Mises equivalent stress is introduced as:
where \({\text{dev}}\left( {{\varvec{\sigma}}^{{{\text{elvp}}}} } \right) = {\varvec{\sigma}}^{{{\text{elvp}}}} - \frac{1}{3}{\text{tr}}\left( {{\varvec{\sigma}}^{{{\text{elvp}}}} } \right){\varvec{I}}\). The von Mises equivalent strain rate for the incompressible media by recalling Eq. (7) is
The multiaxial analogue of Eq. (8) is obtained by generalizing it to the form of

Applying the overstress model and formalization of Perzyna [49, 50], the elasto-viscoplastic flow rule is obtained [46], where its viscoplastic part corresponds to
with \({\varvec{\xi}} = {\text{dev}}\left( {{\varvec{\sigma}}^{{{\text{elvp}}}} } \right)\) (see Eq. (9)) and the viscoplastic consistency \(K_{{{\text{vp}}}}\). By manipulating left- and right-hand side of Eq. (12) to extract the von Mises invariants according to Eqs. (10) and (9), one obtains:
After the nonlinear function \(\varLambda\) defined in Eq. (12) is plugged into Eq. (13), the extra-stress becomes
which allows to derive an expression for the consistency parameter in Eq. (11):

Combining the extra-stress from Eq. (14) with the Perzyna formulation (see Eq. (12)) gives a compact form of the elasto-viscoplastic flow rule by reducing it to
Summarizing, in this section, the rheological model reflecting the solidified alloys behavior at a high temperature range (above 1/3 of the liquidus) is described. Two model parameters, \(K_{{{\text{vp}}}}\) and m, are obtained experimentally and will be described later.
2.2.2 Pure viscoplasticity without static threshold
With continuously growing temperature at some critical point, the plasticity limit, \(\sigma_{{{\text{stat}}}}\), cannot be defined. In this regime, the unrecoverable deformations occur when the material undergoes even the weak loads. Such a rheological phenomenon is regarded as the pure viscoplasticity, which is valid, according to the book of Rappaz et al. [46], at temperature higher than 2/3 of their melting point.
The pure viscoplasticity law can be directly derived from the elasto-viscoplasticity formulation as presented in Eq. (8). The latter is reduced by excluding the static plastic threshold, assuming \(\sigma_{{{\text{stat}}}} \equiv 0\), to the pure power law. The flow rule Eq. (12) together with its compact form Eq. (16) can be inverted to the pure viscoplastic constitutive law, referred in the literature as the Norton-Hoff law:
where \({\varvec{\varSigma}}^{\text{vp}}\) is accepted to be a deviatoric part of the \({\varvec{\sigma}}^{{{\text{vp}}}}\).
2.2.3 Constitutive equation for viscoplastic stress and strain
As it was mentioned here previously, the viscoplastic model parameters are estimated experimentally. In the present study, a constructive equation model is used corresponding to the Model AI reported in Kozlowski et al. [51]. As reported by the authors, it is applicable for a wide range of low strain rates between 10–3 and 10–6 s−1 at high temperature range of 1223–1673 K when the carbon content is varied between significantly low (0.005 wt.%) and the high one (1.54 wt.%). The constitutive model of Kozlowski et al. [51] was constructed for the range where the employed experimental data from Wray [52] and Suzuki et al. [53] were the most consistent. Very recently, Koric and Abueidda [54] used Kozlowski model [51] for the 0.09 wt.% low carbon steel alloy for the neutral networks learning for the solidification predictions during CC. Moreover, Huespe et al. [55] could successfully apply this constitutive model for the billet casting of the 0.3 wt.% C alloy, and the results were approved experimentally. Fachinotti and Cardona [45] reviewed a wide range of the constitutive models, showing the whole variety of the applied approaches. As a conclusion, they stated that for the elevated temperature, the rate-dependent viscoplastic models (such as the Kozlowski model used in the present study) are the most appropriate.
It is worth reminding that a peritectic steel casting is considered with the 0.06 wt.% C alloy (the same as in the previous study [22]) which fits in the range of Kozlowski experimental work [51].
The original model includes constitutive equation, which expresses the \(\dot{\varepsilon }^{{{\text{vp}}}}\) as a function of the \(\sigma^{{{\text{vp}}}}\), temperature and the carbon content of the alloy [51]. The one-dimensional flow rule is expressed as an Arrhenius-type equation [45]:
where the relation between the \(Q\) and R is fixed to a value \(\frac{Q}{R} = 49 ,890\ {\text{K}}\). According to the accepted notation, the \(Q\) is defined as a variable parameter (which is generally a case); however, in the present study, it is included in the constant relation and does not vary. The material parameters are described based on \(T\) and c as follows [45]:
However, Eq. (18) is derived for the uniaxial stress and strain case. To extend it for the multidimensional deformations, its scalar analogue for the von Mises invariants are employed. Omitting the direct flow rule formulation, we switch to a reverted version derived in respect to the equivalent stress:
The elasto-viscoplastic extra-stress (see Eq. (14)) is rewritten for pure viscoplasticity without static plasticity threshold as:
Simple comparison of Eqs. (21) and (22) reveals that the strain rate sensitivity is expressed via the \(n\) as \(m = 1/n\), which results in
Finally, the viscoplastic stress law Eq. (22) and the inverted Kozlowski flow rule Eq. (23) are combined to derive the viscoplastic consistency parameter \(K_{{{\text{vp}}}}\) from the constitutive model in a form of
Thus, the parameter \(K_{{{\text{vp}}}}\) is now expressed as a function of temperature and the carbon content.
It is crucial to notice that since in Model IA in Kozlowski et al. [51] the stress is measured in MPa and the material constant C is taken in MPa−n s−1 [45, 51], thereby the \(K_{{{\text{vp}}}}\) (after some trivial manipulations) gets MPa s1/n or MPa sm as its units.
2.2.4 Viscoplastic model update algorithm
An important remark should be done for the one-phase formulation used in this study. The equality of the viscoplastic and liquid strain rate (\(\dot{\user2{\varvec\varepsilon }}^{{{\text{vp}}}} \equiv \dot{\user2{\varvec\varepsilon }}\)) is assumed since a single velocity field is used for both phases. Thereby, hereinafter, a notation of \(\dot{\user2{\varvec\varepsilon }}\) is used in the completed definition of the blended stress tensor deviator in Eq. (4). Moreover, in the von Mises invariant \(\dot{\varepsilon }_{{{\text{eq}}}}^{{{\text{vp}}}} ,\) the viscoplastic superscript is omitted as well as leading to its redefinition as \(\dot{\varepsilon }_{{{\text{eq}}}}^{{{\text{vp}}}} \equiv \dot{\varepsilon }_{{{\text{eq}}}}\).
Generalizing the viscoplastic stress formulation in Eq. (17), the “effective” or “apparent” \(\mu^{{{\text{vp}}}}\) is introduced as a nonlinear function of the equivalent strain rate \(\dot{\varepsilon }_{{{\text{eq}}}}\):
The strain rate characterizes the velocity gradient between the adjoin “layers” of the creeping material: the higher the strain rate is, the more velocity change is observed at the neighboring locations. The viscoplastic viscosity depends on this local characteristic of the motion which is referred as the rate-of-load. Since the strain rate is integrated into the “effective viscosity” calculation, a coupling procedure is applied to converge the nonlinear terms:
-
(i)
the strain rate is estimated using Eq. (6);
-
(ii)
according to Eqs. (10) and (25), the \(\dot{\varepsilon }_{{{\text{eq}}}}\) and the \(\mu^{{{\text{vp}}}}\) are updated;
-
(iii)
a new solution of the flow/heat transfer equation system is integrated based on the latest estimation of the blended stress distribution advancing to the next time step;
-
(iv)
repeat procedure by applying under-relaxation on pressure, velocity fields, released latent heat term as well as on the effective viscosity;
-
(v)
repeat above steps to reach a convergence criterion for the coupled solution;
-
(vi)
proceed to the next time step.
Additional coupling step was to overcome the solver stability issues. Since a strong nonlinear term in the Norton power law can cause the divergence of the solution, the enhanced numerical treatment was applied according to the improved both side diffusion method by Fernandes et al. [56] and more recently extended by Araújo et al. [57]. It employs the artificial diffusion term added to both sides of the momentum equation. The terms are treated separately in the implicit and explicit manner for the left- and the right-hand sides correspondingly. The method originates from the FEA and aims to tighten the velocity/stress coupling. It simultaneously helps avoiding the checkerboard pattern in solution. The improved algorithm is based on the larger computational stencil. Such a discretization is done due to the extended flexibility of the OpenFOAM CFD package.
2.3 Heat transfer and solidification model
As it was shown previously by the authors, the latent heat advection plays a dramatic role in build-up of the solid shell thickness and depends on the columnar phase velocities predicted by the model [22, 58]. However, in the coupled model for the flow and solidification, newly suggested here, which considers the viscoplasticity of the solidified shell, no information regarding the solid-phase velocities can be obtained due to the single-phase formulation. Assuming the constant \(\rho\) and \(\lambda\), the energy equation is taken in its general advection–diffusion form regarding the total enthalpy:
The total enthalpy for the mixture is estimated in the current approach by ignoring the temperature dependency of the \(C_{\it p}\) and the \({\mathcal{L}}\):
By inserting Eq. (27) into Eq. (26), the latent heat advection term is derived as follows:
The simulation results, using previously developed formulation [22, 58], are considered as a reference case. The corresponding latent heat advection term is:
The difference between two models, described in Eqs. (28) and (29), becomes obvious by simple comparison: in the current approach, the \({\varvec{u}}\) is used, whereas the \({\varvec{u}}_{{\text{s}}}\) is responsible for the latent heat advection within the frames of the previously used method. The details and outcomes are discussed later.
3 Modeling thin slab casting
According to the approach, presented in Sect. 2, the coupled numerical model was implemented by the authors as a standalone solver in the open-source CFD package OpenFOAM. The description of the numerical setup, the simulation results and their discussion come in the very next sections.
3.1 Viscoplastic model parameters
The basic parameters of the viscoplastic deformation model were selected here based on the Kozlowski constitutive Model IA (see Eqs. (19) and (20)), and the corresponding expression for the \(K_{{{\text{vp}}}}\) is derived here in Eq. (24).
Figure 1 shows that the temperature dependency of m and \(K_{{{\text{vp}}}}\) is presented and analyzed for the selected constitutive model used in this study. As it is observed, the m drops during cooling, which corresponds to faster response of the apparent viscoplastic viscosity to small strain rates, as shown in Fig. 2. Corresponding viscoplastic consistency grows during cooling, defining stronger viscoplastic stress magnitude in general. Additionally, the temperature range of the experimental work of Kozlowski et al. [51] is marked in Fig. 1 along with the liquidus and solidus temperatures of the alloy used for the thin slab casting simulation (see Table 1 for the details).
As shown in Fig. 1, the sensitivity parameter varies between 0.136 and 0.170 for the investigated alloy and in the pure viscoplastic temperatures, whereas the \(K_{{{\text{vp}}}}\) fits into the 5–115 MPa sm range. However, to simplify the analysis of the results, the presented studies were limited to the constant viscoplastic model parameters. The fixed strain rate sensitivity m* = 0.138 and the viscoplastic consistency \(K_{{{\text{vp}}}}^{*}\) = 44.62 MPa sm were selected corresponding to the reference temperature \(T^{*} \approx 1170.33{\text{ K}}\), which is referred to the transition between elasto- and pure viscoplastic rheology hypothesis according to the book of Rappaz et al. [46].
As shown in Fig. 2, with a decreasing parameter m, the apparent \({\mu }^{\text{vp}}\) dramatically grows in correspondence to Eq. (25) for the range of the \({\dot{\varepsilon }}_{\text{eq}}\) below 10–2 s−1, and thus the material strongly resists to the small velocity gradients namely the relative deformations in the material. On the contrary, its motion is allowed for significantly higher deformations since its resistance drops and the material starts to creep easier. For the sensitivity parameter m close to identity for the whole rate-of-strain range, the viscoplastic viscosity does not change dramatically, and more relative motion is allowed within the solid phase. However, based on previous studies and literature sources for the metal alloys, the casting range for the parameter m lies between values of 0.1 and 0.2, thereby in the region of rapid response to strain rates.
The strain rates range (expressed for the von Mises invariant \({\dot{\varepsilon }}_{\text{eq}}\)), which was used in the experimental work of Kozlowski et al. [51], is marked in Fig. 2 with a cyan stripe. Typical casting range for the strain rate sensitivity is marked in gray according to the literature and to the previously plotted temperature dependency in Fig. 1. The rheological curve of the apparent viscosity \({\mu }^{\text{vp}}={\mu }^{\text{vp}} (m, { K}_{\text{vp}, }^{*}{ \dot{\varepsilon }}_{\text{eq}})\) according to the m* is marked in red.
Current model uses, as shown in Fig. 3, the solid fraction/temperature correlation for the industrial alloy (see Table 1) determined by an engineering software IDS [59, 60], which is more complex than, for example, corresponding linear relation in Svensson et al. [27].
3.2 Numerical grid and model setup
The modeling domain sketch is shown in Fig. 4a; it includes the SEN, water-cooled mold cavity of the funnel type (879 mm in height) and the strand part (4000 mm along casting direction including mold) marked as the secondary cooling zone. The details of the dominantly hexahedral mesh are shown in Fig. 4b. The refined boundary layers are introduced to accurately resolve the extracted wall heat flux, which defines the growth of the solid shell. The melt flow/two-phase region interaction should also be carefully tracked along with the corresponding viscoplastic stress in the mush during the shell withdrawal. Thereby, the mesh refinement was extended toward the bulk region. Geometry dimensions for the 1726-mm-wide and 72-mm-thick funnel-type mold are shown in Fig. 4c. The corresponding applied heat flux profiles, adopted from the measured values in Camporredondo et al. [61], are gathered in Fig. 4d.
To simplify the analysis and the comparison of the results, the sub-grid unresolved turbulence flow effects are excluded in the present study. Instead, a laminar liquid stress model is employed by the authors on a very fine numerical grid (so-called “coarse DNS” approach).
The total grid size used in the study included around 10 million volume elements. The calculations are performed on the HPC cluster using two nodes each with 28 cores (Intel Xeon E5-2690v4 2.60 GHz) and 128 GB RAM. Time integration step in the simulation is 10−4 s to keep maximum Courant number below 1. For the time integration, the PIMPLE algorithm (a merge of PISO and SIMPLE) is utilized to stabilize the numerical procedure using under-relaxation to get the required convergence level.
4 Results and discussion
4.1 Simulation results
The developed model considering liquid flow, solidification and viscoplastic stress in the two-phase region was used to perform a simulation of the thin slab continuous casting process based on the process conditions and geometry shown in Fig. 4a and in Table 1, as well as it was reported previously by Vakhrushev et al. [22].
The flow and solidification simulation results are shown in Fig. 5, and the instantaneous velocity magnitude distribution in Fig. 5a is displayed along with temperature field and shown in Fig. 5b. As it is mentioned previously, the “coarse DNS” approach was applied on a numerical mesh with high cell resolution; as shown in Fig. 5a, the highly turbulent flow structures are obtained during simulation, which are further employed for solving coupled heat transfer problem.
Figure 5 shows the corresponding solution of the energy equation: the temperatures are scaled between the liquidus and the pouring temperature from Table 1 to provide better contrast and to distinguish the fresh and cold melt regions. The details of the temperature distribution in the vicinity of the narrow walls of the mold are analyzed in the zoomed Fig. 5c where the dark blue region corresponds to the growing solidified shell. The hot fresh melt jet, impinging and going along the mush in both vertical directions, is detected as well, damping the shell growth, as it was previously reported by Wu et al. [58].
4.2 Validity of viscoplastic regime in simulated domain
The viscoplastic deformation law was assigned in the presented study for the solidified shell description. However, a question arises, to which extending it reflects the real mechanical behavior of the cast steel without violating it. Thereby, the validity of the applied Norton-Hoff viscoplastic law is investigated next according to the criterion reported in Rappaz et al. [46]. As mentioned previously, the viscoplastic behavior is postulated to be valid for the alloys above two thirds of their absolute melting temperature. Applying for the presented study, this range corresponds to the temperature values above the \({T}_{\text{sol}}\times \frac{2}{3}\approx 1170.33\ \text{ K}\).
The surface temperature distribution is analyzed and shown in Fig. 6. The color scaling is performed in such a way that the critical viscoplastic regime temperature values (1170–1200 K) are reflected by the blue colors that allows to clearly detect them. As one observes, only limited part of the domain along the corners lies below the viscoplastic temperature range; it starts at 1710 mm below the mold exit (see Fig. 6).
The temperature evolution along centerline of the wide and narrow face of the mold and strand part of the slab is shown in Fig. 7. One can see that at the mold’s exit, the cooling curve reaches 1510 K at the wide and 1610 K at the narrow face. At the location of 4 m below meniscus, the surface temperature drops to 1460 K (wide side) and 1450 K (narrow side) correspondingly. Thus, the estimated centerline surface temperatures are significantly higher than a critical value for the pure viscoplastic law.
More significant slab surface temperature decrease is detected during performed numerical studies at the strand’s corner regions where it goes beyond the viscoplastic limit of 1170.33 K. As referred to the literature [46], the elastic behavior of the material is observed below one third of the melting temperature, which corresponds to 585.17 K in the present study. However, the minimum temperature observed for the simulation domain including 879-mm mold and the 3-m strand in the casting direction is higher than 1000 K. While insignificantly catching the transition from elasto-viscoplastic regime, the simulation results remain dominant in the frames of the pure viscoplasticity hypothesis, thus confirming the utilized stress model to be valid in the present study.
4.3 Solid shell thickness
The solid shell thickness was compared (see Fig. 8) between two cases: case I uses the precalculated solid velocities based on a fully elastic traditional approach disclosed elsewhere [22]; case II employs a viscoplastic model from this paper to treat the solid shell. It should be mentioned that the constant material properties are used in both cases. The validity of this assumption is discussed in the next section.
Solid shell thickness (95% solid) based on steady-state solid-phase velocities model (left pictures) and using current viscoplastic deformation model (right pictures). a, b Solid shell thickness along wide face of mold; c, d liquid-phase distribution at horizontal cross section at 2000 mm below meniscus level
Firstly, the comparison along the wide face of the slab is shown (see Fig. 8a, b). Corresponding numbers on the iso-lines show the shell thickness in millimeters. It is observed that only slight difference occurs in the casting (vertical) direction. However, it is more pronounced in the transversal direction: in the referenced Case I, the shell is thicker in the central part of the wide face, whereas for the results using new approach, it is thicker near the narrow side.
The deviation between the predicted shell thickness can be described by recalling Eq. (29), based on the previously derived formulations [22, 58], and the latent heat advection using the mixture velocity (as in Eq. (28)). Comparing these two formulations, the corresponding dference \({\Delta }S_{{\text{e}}}\) is obtained in the following form:
According to Eq. (30), \({\Delta }S_{{\text{e}}}\) is proportional to \({\varvec{u}}_{{\text{r}}}\). As a result, in the updated model formulation, used here, slightly more of the latent heat (released within the mushy zone during solidification) is advected along casting direction by the dendritic structure as compared to the case of the separately precalculated solid velocities. Thus, the growth of the solid shell is damped, and some deviation in shell thickness is observed, as shown in Fig. 8c, d for the slab’s horizontal cross section at 2000 mm below meniscus level. The shell thickness at the corresponding sections A–A in Fig. 8 is 20.5 mm for the model with predefined solid velocities (Fig. 8c) and 18.1 mm for the viscoplastic deformation model (Fig. 8d) with the 13.3% difference. For the narrow face distribution (section B–B), the thicknesses correspondingly are 14.8 and 13.6 mm been measured at the center of the slab’s narrow side, showing lower deviation of 8.8% between the models than at the wide side.
4.4 Model validation
The presented modeling results for the solidified shell thickness were verified against other simulation works [22, 62, 63] and the breakout measurements [61].
The solid shell thickness for the cases with the precalculated solid velocities using temperature-dependent properties (Fig. 9a, previous study [22]) and with the constant material data (Fig. 9b) is displayed against the industrial measurements [61] together with the presented viscoplastic model results (Fig. 9c). The mushy zone profiles are plotted along the vertical line located at 750 mm from the wide face center, where the shell thickness is least disturbed by the hot jets. It must be clarified that the proper consideration of the operation delay after the breakout and the partial solidification of the alloy, entrapped in the mush, during the drainage should be explained when comparing to the breakout shell [64].
Verification of modeled solid shell thickness (750 mm from wide face centerline) against breakout measurements [61], and cases with precalculated solid velocities using temperature-dependent properties [22] (a) and constant material properties (b), results for viscoplastic solid shell model with constant material properties (c)
Considering these uncertainties, the simulated shell thickness shows a good agreement with the measured one for the presented variety of the numerical setups (see Fig. 9). The experimental data lie between the iso-lines of solid fraction fs = 0.01 and fs = 0.30. As seen from the plots, the evolution of the shell can be well-tracked. The modeling results presented elsewhere [61,62,63] show the similar tendencies.
It is worth mentioning that a slight difference is observed between the case with temperature-dependent properties (Fig. 9a) and simulations with the constant ones (Fig. 9b, c). Moreover, there is a small deviation in the mushy zone distribution between the Case I in Fig. 9b and Case II in Fig. 9c due to the different withdrawal models, as discussed previously. However, all mismatches are minor. Thereby, the model verification is satisfying; the assumption of the constant material properties can be accepted. The material properties variation based on the temperature field, incorporation of the solid fraction in the constitutive model parameters, and appearance of the bulk viscosity due to the mush compressibility [31] are essential topics for the future studies.
As already shown, the verification data for the CC process mostly come after costly breakouts. However, in the future, we are looking for the experiments such as very recently published by Balogun, O’Malley and co-authors [65] combined with the withdrawal of the semi-solid shell.
4.5 Viscoplastic stress in solidified shell
Two viscoplastic stress components acting correspondingly along transversal and casting directions are investigated as shown in Fig. 10. The compression and tension zones in the solidified shell are indicated along the iso-surface of the 95% solid fraction by blue and red colors correspondingly. The iso-surface is enlarged 4 times in thickness direction for better resolution of the results. Strong tension/compression areas are detected especially along the curved funnel part of the mold cavity. It was found that the shell is under tension horizontally at the central and outer parts of the funnel (check for \({\varSigma}_{xx}^{\text{vp}}<0\) in Fig. 10) as well as vertically at the low part of the funnel, after it has been straightened in the parallel part of the mold (blue zone for \({\varSigma}_{yy}^{\text{vp}}\) in Fig. 10). The red zones correspond to the solid shell being under the compression especially at the vertical at horizontal transition zones from the curved funnel and the parallel mold plates.
As shown in Fig. 10, the critical tensile values in the simulation lie in the range of 250 kPa. The ultimate tensile stress (UTS) for the steel alloys is strongly temperature- and morphology (read composition)-dependent. As reported by Outinen and Mäkeläinen [66] and recently reviewed by Wang and Lui [67], the strength properties of the steel drop from the room temperature level of 500–1000 MPa to 5%–10% at the high temperatures above 1273 K. By extrapolating the experimental data [66, 67] up to 1723 K, the lowest range for the UTS becomes less than 0.5–1.0 MPa. That estimation makes the simulation values close to the critical limit. Thereby, at the upper part of the mold, the hot jet impingement and the local remelting of the solidifying skeleton can lead to the strength weakening till the rapture occurs.
However, it is not fully valid to compare the presented results with the real steel properties, since the constant viscoplastic model parameters were used for the apparent viscosity \({\mu}^{\text{vp}}\).
5 Conclusions
-
1.
A Norton-Hoff-type viscoplastic model was applied for the two-phase solidifying region to study the key phenomena in the curved mold during thin slab casting. A single FVM framework was used with the enhanced numerical treatment of the nonlinear viscoplastic stress tensor according to the improved both side diffusion method.
-
2.
A full 3D simulation of the industrial thin slab caster was performed including SEN region, the funnel-type mold, and the secondary cooling zone. The melt flow, heat transfer and viscoplastic stresses in the solidifying shell were calculated for the alloy with compositions of C 0.06, Ni 0.1, Mn 0.13, Si 0.1, Cu 0.08, Al 0.035, P 0.015 and S 0.012 within the typical casting range.
-
3.
The viscoplasticity was found dominantly valid in the calculation domain except small regions catching the elasto-viscoplastic transition. The tension and compression of the solid shell was detected along the mold’s funnel within the corresponding straightening and bending zones, where the local reheating or non-uniform solidification can cause the crack formation leading later to a breakout.
-
4.
The modeling results were verified against the breakout shell measurements and the numerical studies published elsewhere, showing a good agreement.
-
5
The described approach can be integrated with the free-surface tracking models, and include the magnetohydrodynamic effects, etc. The aim of the future development is to estimate the breakout risks using modern quality indices and defect detection techniques to be directly applied for the industrial process enhancement.
Change history
23 March 2022
A Correction to this paper has been published: https://doi.org/10.1007/s42243-022-00771-x
Abbreviations
- \(\nabla\) :
-
Gradient operator (m−1)
- \(\nabla ^{{\text{T}}}\) :
-
Transpose of gradient operator (m−1)
- \(\nabla { \cdot }\) :
-
Divergence operator (m−1)
- \(\nabla ^{2}\) :
-
Laplace operator (m−2)
- \(\user2{a} \otimes \user2{b}\) :
-
Outer product of two vectors
- \(\user2{A} : \user2{B}\) :
-
Double inner product of two tensors
- \({\text{dev}}\left( \user2{A} \right)\) :
-
Deviatoric part of a tensor
- \({\text{tr}}\left( \user2{A} \right)\) :
-
Trace of a tensor
- c :
-
Carbon content (wt.%)
- C :
-
Material constant (MPa−n s−1)
- \(C_{p}\) :
-
Specific heat capacity (J kg−1 K−1)
- \(C_{p}^{\ell }\) :
-
Specific heat capacity of liquid (J kg−1 K−1)
- \(C_{p}^{{\text{s}}}\) :
-
Specific heat capacity of solid (J kg−1 K−1)
- d :
-
Solid shell thickness (mm)
- \(f_{\ell }\) :
-
Liquid fraction
- \(f_{{\text{s}}}\) :
-
Solid fraction
- H :
-
Total enthalpy (J kg−1)
- \(\user2{I}\) :
-
Unit tensor
-
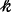 :
: -
Consistency parameter (Pa sm)
- \(K_{{{\text{vp}}}}\) :
-
Viscoplastic consistency (MPa sm)
- \(K_{{{\text{vp}}}}^{*}\) :
-
Viscoplastic consistency at elasto-viscoplastic transition (MPa sm)
- \({\mathcal{L}}\) :
-
Latent heat of fusion (J kg−1)
- m :
-
Strain rate sensitivity
- m * :
-
Strain rate sensitivity at elasto-viscoplastic transition
- n :
-
Net stress exponent
- p :
-
Pressure (Pa)
- Q :
-
Activation energy (J mol−1)
- R :
-
Universal gas constant (J K−1 mol−1)
- \(S_{{\text{e}}}^{{{\text{vp}}}}\) :
-
Latent heat release term in viscoplastic model (W m−3)
- \(S_{{\text{e}}}^{{{\text{ref}}}}\) :
-
Latent heat release term in reference model (W m−3)
- \({{\Delta }}~S_{{\text{e}}}\) :
-
Latent heat release difference between viscoplastic and reference models (W m−3)
- t :
-
Time (s)
- T :
-
Temperature (K)
- \(T_{{{\text{cast}}}}\) :
-
Casting temperature (K)
- \(T_{{{\text{liq}}}}\) :
-
Liquidus temperature (K)
- \(T_{{{\text{sol}}}}\) :
-
Solidus temperature (K)
- \(T^{*}\) :
-
Temperature of elasto-viscoplastic rheology transition (K)
- \(\user2{u},\user2{~}\left| \user2{u} \right|\) :
-
Velocity vector and magnitude (m s−1)
- \(u_{{{\text{pull}}}}\) :
-
Casting velocity (m min−1)
- \(\user2{u}_{{\text{r}}}\) :
-
Relative velocity (m s−1)
- \(\user2{u}_{{\text{s}}}\) :
-
Solid-phase velocity (m s−1)
- \(\dot{\varvec{\varepsilon}}\) :
-
Strain rate tensor (s−1)
- \(\dot{\varepsilon }^{{{\text{vp}}}}\) :
-
Viscoplastic strain rate (s−1)
- \(\dot{\varvec{\varepsilon}}^{\text{vp}}\) :
-
Viscoplastic strain rate tensor (s−1)
- \(\dot{\varepsilon }_{{{\text{eq}}}}^{{{\text{vp}}}} ,~\dot{\varepsilon }_{{{\text{eq}}}}\) :
-
Von Mises equivalent strain rate (s−1)
- \(\lambda\) :
-
Thermal conductivity (W m−1 K−1)
- \(\lambda _{\ell }\) :
-
Liquid thermal conductivity (W m−1 K−1)
- \(\lambda _{{\text{s}}}\) :
-
Solid thermal conductivity (W m−1 K−1)
- \(\varLambda\) :
-
Perzyna flow rule coefficient (Pa−1 s−1)
- \(\mu _{\ell }\) :
-
Dynamic viscosity of liquid (Pa s)
- \(\mu ^{{{\text{vp}}}}\) :
-
Apparent viscoplastic viscosity (Pa s)
- \(\varvec{\xi }\) :
-
Deviatoric part of viscoplastic stress (Pa)
- \(\rho\) :
-
Density (kg m−3)
- \(\rho _{\ell }\) :
-
Liquid density (kg m−3)
- \(\rho_{{\text{s}}}\) :
-
Solid density (kg m−3)
- \(\sigma ^{{{\text{elvp}}}}\) :
-
Elasto-viscoplastic stress (Pa)
- \({\varvec\sigma }^{{{\text{elvp}}}}\) :
-
Elasto-viscoplastic stress tensor (Pa)
- \(\sigma _{{{\text{stat}}}}\) :
-
Static plasticity threshold (“fluidity” limit of solid) (Pa)
- \({\sigma} ^{\text{vp}}\) :
-
Viscoplastic stress (Pa)
- \({\varvec\sigma} ^{{{\text{vp}}}}\) :
-
Viscoplastic stress tensor (Pa)
- \({\sigma }^{{{\text{vp}}}}_{\text{eq}}\) :
-
Von Mises equivalent stress for viscoplastic stress (Pa)
- \(\sigma _{{{\text{eq}}}}^{{{\text{elvp}}}}\) :
-
Von Mises equivalent stress for elasto-viscoplastic stress (Pa)
- \({\sigma }^{{{\text{tot}}}}\) :
-
Total stress tensor (Pa)
- \({{\varvec{\varSigma}} }^{{{\text{tot}}}}\) :
-
Deviatoric part of total stress (Pa)
- \({{\varvec{\varSigma}}}^{{{\text{liq}}}}\) :
-
Newtonian stress in liquid (Pa)
- \({{\varvec{\varSigma}} }^{{{\text{vp}}}}\) :
-
Viscoplastic stress in solid (Pa)
- \({{\varSigma } } _{xx}^{{{\text{vp}}}}\) :
-
Transversal component of viscoplastic stress tensor (MPa)
- \({{\varSigma } } _{yy}^{{{\text{vp}}}}\) :
-
Longitudinal component of viscoplastic stress tensor (MPa)
References
M.C. Flemings, Metall. Trans. A 22 (1991) 957–981.
P.D. Lee, P.E. Ramirez-Lopez, K.C. Mills, B. Santillana, Ironmak. Steelmak. 39 (2012) 244–253.
K.C. Mills, P.E. Ramirez-Lopez, P.D. Lee, High Temp. Mater. Proc. 31 (2012) 221–229.
K.C. Mills, P. Ramirez-Lopez, P.D. Lee, B. Santillana, B.G. Thomas, R. Morales, Ironmak. Steelmak. 41 (2014) 242–249.
P.E. Ramirez Lopez, P.N. Jalali, U. Sjöström, P.G. Jönsson, K.C. Mills, I. Sohn, ISIJ Int. 58 (2018) 201–210.
S.M. Cho, M. Liang, H. Olia, L. Das, B.G. Thomas, in: The Minerals, Metals & Materials Society (Ed.), TMS 2020 149th Annual Meeting & Exhibition Supplemental Proceedings, Springer, Cham, Switzerland, 2020, pp. 1161–1173.
B.G. Thomas, Metall. Mater. Trans. B 33 (2002) 795–812.
H.V. Atkinson, Prog. Mater. Sci. 50 (2005) 341–412.
P.H. Dauby, Rev. Metall. 109 (2012) 113–136.
B.G. Thomas, Steel Res. Int. 89 (2018) 1700312.
M. Vynnycky, Metals 8 (2018) 928.
R. Vertnik, K. Mramor, B. Šarler, Eng. Anal. Bound. Elem. 104 (2019) 347–363.
Y. Meng, B.G. Thomas, Metall. Mater. Trans. B 34 (2003) 685–705.
L.C. Hibbeler, M.M. Chin See, J. Iwasaki, K.E. Swartz, R.J. O’Malley, B.G. Thomas, Appl. Math. Model. 40 (2016) 8530–8551.
H. Zhang, W. Wang, Metall. Mater. Trans. B 48 (2017) 779–793.
S.L. Mitchell, M. Vynnycky, Appl. Math. Model. 48 (2017) 476–490.
M.L.S. Zappulla, S. Cho, B.G. Thomas, Steel Res. Int. 90 (2019) 1800540.
R.M. Pineda Huitron, P.E. Ramirez Lopez, E. Vuorinen, P. Nazem Jalali, M. Kärkkäinen, ISIJ Int. 61 (2021) 834–843.
A. Vakhrushev, A. Kharicha, M. Wu, A. Ludwig, Y. Tang, G. Hackl, G. Nitzl, J. Watzinger, J. Bohacek, Metals 11 (2021) 1375.
Z. Liu, A. Vakhrushev, M. Wu, A. Kharicha, A. Ludwig, B. Li, Metall. Mater. Trans. B 50 (2019) 543–554.
Z. Liu, B. Li, A. Vakhrushev, M. Wu, A. Ludwig, Steel Res. Int. 90 (2019) 1800117.
A. Vakhrushev, M. Wu, A. Ludwig, Y. Tang, G. Hackl, G. Nitzl, Metall. Mater. Trans. B 45 (2014) 1024–1037.
C. Olivier, C. Yvan, B. Michel, J. Eng. Mater. Technol. 130 (2008) 021018.
Z. Liu, A. Vakhrushev, M. Wu, E. Karimi-Sibaki, A. Kharicha, A. Ludwig, B. Li, Metals 8 (2018) 609.
A. Vakhrushev, A. Kharicha, Z. Liu, M. Wu, A. Ludwig, G. Nitzl, Y. Tang, G. Hackl, J. Watzinger, Metall. Mater. Trans. B 51 (2020) 2811–2828.
A. Vakhrushev, A. Kharicha, E. Karimi-Sibaki, M. Wu, A. Ludwig, G. Nitzl, Y. Tang, G. Hackl, J. Watzinger, S. Eckert, Metall. Mater. Trans. B 52 (2021) 3193–3207.
J. Svensson, P.E.R. López, P.N. Jalali, M. Cervantes, IOP Conf. Ser. Mater. Sci. Eng. 84 (2015) 012097.
M.L.S. Zappulla, S.M. Cho, S. Koric, H.J. Lee, S.H. Kim, B.G. Thomas, J. Mater. Process. Technol. 278 (2020) 116469.
H. Yang, P.E. Ramirez Lopez, D.M. Vasallo, Metall. Mater. Trans. B 52 (2021) 2760–2785.
M. Bellet, V.D. Fachinotti, Comput. Methods Appl. Mech. Eng. 193 (2004) 4355–4381.
V.D. Fachinotti, S. Le Corre, N. Triolet, M. Bobadilla, M. Bellet, Int. J. Numer. Meth. Eng. 67 (2006) 1341–1384.
M. Bellet, in: AIP Conference Proceedings, AIP, Porto, Portugal, 2007, pp. 1369–1374.
S. Zhang, G. Guillemot, C.A. Gandin, M. Bellet, Comput. Methods Appl. Mech. Eng. 356 (2019) 294–324.
S. Zhang, G. Guillemot, C.A. Gandin, M. Bellet, Metall. Mater. Trans. B 52 (2021) 978–995.
A. Ludwig, A. Vakhrushev, T. Holzmann, M. Wu, A. Kharicha, IOP Conf. Ser. Mater. Sci. Eng. 84 (2015) 012102.
A. Ludwig, A. Vakhrushev, M. Wu, T. Holzmann, A. Kharicha, Trans. Indian Inst. Met. 68 (2015) 1087–1094.
C.M.G. Rodrigues, A. Ludwig, M. Wu, A. Kharicha, A. Vakhrushev, IOP Conf. Ser. Mater. Sci. Eng. 861 (2020) 012042.
C.M.G. Rodrigues, A. Ludwig, A. Kharicha, M. Wu, Trans. Indian Inst. Met. 71 (2018) 2645–2649.
C.M.G. Rodrigues, A. Ludwig, M. Wu, A. Kharicha, A. Vakhrushev, Metall. Mater. Trans. B 50 (2019) 1334–1350.
C.M.G. Rodrigues, A. Ludwig, M. Wu, A. Kharicha, A. Vakhrushev, J. Mater. Process. Technol. 286 (2020) 116814.
T.G. Nguyen, D. Favier, M. Suery, Int. J. Plast. 10 (1994) 663–693.
C.L. Martin, D. Favier, M. Suéry, Int. J. Plast. 13 (1997) 215–235.
C.L. Martin, D. Favier, M. Suéry, Int. J. Plast. 13 (1997) 237–259.
C.L. Martin, D. Favier, M. Suéry, Int. J. Plast. 15 (1999) 981–1008.
V.D. Fachinotti, A. Cardona, J. Mater. Process. Technol. 135 (2003) 30–43.
M. Rappaz, M. Bellet, M. Deville, Numerical modeling in materials science and engineering, Springer Berlin Heidelberg, Berlin, Germany, 2003.
V. Favier, Comprehensive materials processing, Elsevier, 2014.
F.H. Norton, The creep of steel at high temperatures, McGraw-Hill Book, Inc., New York, USA, 1929.
P. Perzyna, Adv. Appl. Mech. 9 (1966) 243–377.
J.C. Simo, T.J.R. Hughes, Advances in applied mechanics, computational inelasticity, Corr. 2. print, Springer, New York, 1998.
P.F. Kozlowski, B.G. Thomas, J.A. Azzi, H. Wang, Metall. Trans. A 23 (1992) 903–918.
P.J. Wray, Metall. Trans. A 13 (1982) 125–134.
T. Suzuki, K.H. Tacke, K. Wunnenberg, K. Schwerdtfeger, Ironmak. Steelmak. 15 (1988) 90–100.
S. Koric, D.W. Abueidda, Metals 11 (2021) 494.
A.E. Huespe, A. Cardona, V. Fachinotti, Comput. Methods Appl. Mech. Eng. 182 (2000) 439–455.
C. Fernandes, M.S.B. Araujo, L.L. Ferrás, J. Miguel Nóbrega, J. Non-Newtonian Fluid Mech. 249 (2017) 63–78.
M.S.B. Araújo, C. Fernandes, L.L. Ferrás, Ž. Tuković, H. Jasak, J.M. Nóbrega, Comput. Fluids 172 (2018) 728–740.
M. Wu, A. Vakhrushev, A. Ludwig, A. Kharicha, IOP Conf. Ser. Mater. Sci. Eng. 117 (2016) 012045.
J. Miettinen, S. Louhenkilpi, H. Kytönen, J. Laine, Math. Comput. Simul. 80 (2010) 1536–1550.
J. Miettinen, S. Louhenkilpi, V.V. Visuri, T. Fabritius, IOP Conf. Ser. Mater. Sci. Eng. 529 (2019) 012063.
J.E. Camporredondo S., A.H. Castillejos E., F.A. Acosta G., E.P. Gutiérrez M., M.A. Herrera G., Metall. Mater. Trans. B 35 (2004) 541–560.
H. Liu, C. Yang, H. Zhang, Q. Zhai, Y. Gan, ISIJ Int. 51 (2011) 392–401.
C.J. Wang, Z.Q. Liu, B.K. Li, Metals 11 (2021) 948.
J. Iwasaki, B.G. Thomas, in: Supplemental Proceedings, Vol. 2: Materials Properties, Characterization, and Modeling, TMS, Wiley, Hoboken, USA, 2012, pp. 355–362.
D. Balogun, M. Roman, R.E. Gerald II, J. Huang, L. Bartlett, R. O’Malley, Steel Res. Int. 93 (2022) 2100455.
J. Outinen, P. Mäkeläinen, Fire Mater. 28 (2004) 237–251.
F. Wang, E.M. Lui, Int. J. Steel Struct. 2 (2017) 1000123.
Acknowledgements
The authors acknowledge the financial support by the Austrian Federal Ministry of Economy, Family and Youth and the National Foundation for Research, Technology and Development within the framework of the Christian Doppler Laboratory for Metallurgical Applications of Magnetohydrodynamics.
Author information
Authors and Affiliations
Corresponding author
Additional information
The original online version of this article was revised: assignment of affiliations was not correct.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Vakhrushev, A., Kharicha, A., Wu, M. et al. Norton-Hoff model for deformation of growing solid shell of thin slab casting in funnel-shape mold. J. Iron Steel Res. Int. 29, 88–102 (2022). https://doi.org/10.1007/s42243-021-00734-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s42243-021-00734-8















 :
: