Introduction

Artificial-membrane lungs (ML) are regularly used for extracorporeal gas exchange (oxygenation and decarboxylation) in case of acute respiratory failure or chronic lung disease. MLs are hollow fiber-membrane (HFM) devices in which blood flows around the fibers while oxygen flows through the inner lumen of the fibers. The exchange is enabled through diffusion of oxygen and carbon dioxide through the HFMs. Despite all the advances in material science, anticoagulation administration, and optimization of the flow design, long-term use of MLs is limited to days or weeks at most due to lack of hemocompatibility [1]. Thrombus formation in combination with protein adsorption is the most frequent clinical complication and can lead to decreased gas transfer performance of the ML, increased embolic risk to the patient, or even mechanical failure of the device that is essential to the patient’s survival [2, 3]. Thrombosis in MLs is typically associated with flow stagnation [4,5,6], unsteady cross-sectional changes [7], nonhomogeneous flow distribution and, especially, shut-off flow regimes such as corners [8]. These non-ideal flow scenarios, which lead to abnormal physiological blood reactions and clotting of the ALs, are the result of design limitations created by the manufacturing process—the so-called potting process.

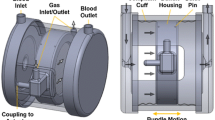
During manufacturing, HFM mats are arranged in their final position in the housing. Following arrangement, the housing is filled with the casting compound, which, once cured, forms the potting at the fiber ends and separates the gas and blood phases. However, an opposing force is required to overcome the capillary forces acting between those fibers that would otherwise drag the compound into the bundle. To this end, an acceleration field is typically artificially generated by rotation, causing a centrifugal force to overcome these capillary forces [9]. In the technical implementation, the unpotted module with potting caps on the fiber ends is positioned on a centrifuge and, during operation, biocompatible polyurethane or silicone is filled into the ML from the distant end. The potting material is pressed into the narrow fiber interstices and creates a gas- and liquid-tight cavity surrounded by the housing and potting [10]. The rotation of the centrifuge is maintained until the compound is thoroughly cured. As a result of the radial orientation of the centrifugal acceleration field, the cured potting material has a cylindrical surface depending on the centrifuge’s diameter (Fig. 1).

Fig. 1
figure 1

Schematic of centrifugal potting setup of a a circular-shaped ML [e.g., Nautilus (MC3, Dexter, USA) or the Mobybox device (Hemovent, Aachen, Germany)], b a hollow-cylindrical shape with curved end-faces [e.g., INSPIRE (LivaNova PLC, London, United Kingdom)], c a hollow-cylindrical ML (left) [e.g., Hilite 7000 (Xenios AG, Heilbronn, Germany) or Eurosets A.L.ONE ECMO (Eurosets, S.r.I., Medolla, Italy)] and a stacked, cuboidal-shaped ML (right) [e.g., iLA membrane ventilator (Xenios AG, Heilbronn, Germany) or Quadrox-i (Maquet GmbH, Rastatt, Germany)]. The MLs are spinning with a rotational speed n around the rotation axis. The diameter D describes the diameter of the resulting potting surface

Full size image

Depending on the ML design, commonly based on stacked or wound fiber mat configurations, the potting process is repeated for every side of the fiber bundle. There are between one, two or up to four potting steps necessary to achieve either a circular-shaped ML (Fig. 1a), a hollow-cylindrical shape with curved end-faces (Fig. 1b), a hollow-cylindrical ML (Fig. 1c, left), or a cuboidal shape (Fig. 1c, right) of the potting cavity [5, 7, 9]. For multiple potting steps, the device needs to be repositioned on the centrifuge after curing the potting material and potted again. After curing, potting caps are removed while the potting holds the HFMs in place. The potting is cut on the gas inlet and outlet sides so that the fibers are open for gas flow. The polycarbonate housing caps are then placed over the fiber ends, containing connections for the gas inlet and outlet.

Cuboidal MLs with a broad rectangular cross section always possess four corners between the potting surfaces and a large cross-sectional expansion at the inlet (see Fig. 2a). Clots are often found at the cross-sectional expansion in the inlet region [11,12,13]. Additionally, the corners have proven to be particularly prone to clotting due to an uneven flow distribution resulting in low flow regimes in the corners [8, 11]. The corners can be eliminated, for example by potting a stacked ML in a single step at the center of the centrifuge, forming a circular cross section for the blood flow (see Fig. 2a) [14, 15]. In light of previous observations indicating that the corners represent a hotspot for clotting [4, 6, 7, 16], the circular-shaped ML design shows promise to reduce clotting although there is no experimental prove yet. Still, the broad inflow expansion necessitated by the two-dimensional alignment of the potting remains a potential thrombotic hotspot. The design of a smooth transition from inlet housing to potting also remains a challenge. In hollow-cylindrical MLs, deflection points occur at the top and bottom surfaces of the cylinder, causing areas of stagnation in the corners between potting and housing (yellow circled area in Fig. 2b). In the case of hollow-cylindrical shapes with curved end-faces as a result of perpendicularly positioned and centrally potted wound MLs, such as INSPIRE (LivaNova PLC, London, United Kingdom) [17, 18], advantages in smooth blood transition have been reported [19, 20]. However, computed tomography (CT) scans reveal contact angles between potting and the inner cylinder of less than 90° at the flow deflection points at the fiber ends, presumably increasing the unfavorable stagnation volume (see Fig. 2c).

Fig. 2
figure 2

Stagnation hotspots on uniaxial potted MLs (potting, blue; housing, black) a stacked, cuboidal-shaped ML (Quadrox-i small adult, Getinge, Sweden), b hollow-cylindrical ML (Hilite 7000, Xenios AG, Heilbronn, Germany) and c hollow-cylindrical shape with curved end-faces (Inspire, LivaNova PLC, London, United Kingdom). Underlying housing contour according to CT scan. Red arrows indicate blood flow path. Marked areas (yellow circles) show disadvantageous corner between potting and housing for each ML

Full size image

Efficient and homogenous perfusion and shear rate distribution within the physiological range is essential to the design and improvement of MLs to avoid thrombosis and blood trauma [1, 4, 7, 21]. The improvement of blood flow inside of MLs is, however, limited to the contour results of the potting process. State-of-the-art potting techniques create corners, which are prone to blood trauma and thrombosis, limiting long-term use.

Here, we introduce 3D-potting, a novel potting technique based on the superposition of more than one acceleration field. This technique enables versatile, novel ML designs, facilitating the transition of blood flow into the fiber bundle and potting cavities with a smooth, flow-guiding shape. 3D-potting offers the previously unrealized potential of eliminating inefficient stagnation zones and creating more favorable blood flow conditions in MLs. This study focuses on potting designs achievable by the superposition of two acceleration fields generated by two perpendicular rotation axes with individual control of rotational speed.

Materials and methods

The arrangement in this study consists of two coupled axes. The first axis is the axis of the main centrifuge. The second axis is installed on the platform of the centrifuge and the module with the potting material is connected to this axis. The rotation axis of the main centrifuge is described by the y1-axis of the coordinate system (XYZ)1. The second rotating axis x2 of the coordinate system (XYZ)2 in the center of the module is collinear with x1. The overall acceleration field is then composed of (1) rotation around the first axis y1, (2) rotation around the second axis x2 and (3) gravity g. For the following mathematical description of the resulting acceleration field, the module’s coordinate system (XYZ)2 is considered the stationary reference frame. The outer coordinate system (XYZ)1 is assumed to rotate with the angular velocity \({-\omega }_{2}\) around the collinear axes x1 and x2, instead of the module’s rotation with the angular velocity \({\omega }_{2}\) around the x2-axis as illustrated in Fig. 3a.

Fig. 3
figure 3

Schematic of arrangement of axes for the multiaxial potting technique: a The coordinate system (XYZ)2 is the steady reference frame, while the first rotation axis \(\overrightarrow{{y}_{1}}\) spins with rotational speed \({n}_{2}\) in the y1z1-plane. Gravity always acts along rotation axis \(\overrightarrow{{y}_{1}}\). b Shortest distance \(\overrightarrow{{r}_{\mathrm{p}}}\) to arbitrary mass point \(\overrightarrow{P}\)(x, y, z) in the coordinate system (XYZ)2

Full size image

The first rotation axis y1 can then be described as dependent on the angular velocity \({\omega }_{2}\) around the second rotation axis x1:

$$\overrightarrow{{y}_{1}}=\lambda \left(\begin{array}{l}0\\ \mathrm{cos}({\omega }_{2}t)\\ \mathrm{sin}({\omega }_{2}t)\end{array}\right).$$
(1)

In Fig. 3a, the y1-axis is depicted at time point t0 = 0 s and after time span t. By then, the y1-axis has traversed an angle \({-\omega }_{2}\) t in the y1z1-plane. The parameter \(\lambda \) describes the position of point \(\overrightarrow{F}\) on \(\overrightarrow{{y}_{1}}\) with the smallest distance \(\overrightarrow{{r}_{p}}\) to an arbitrary mass point \(\overrightarrow{P}\) with the coordinates (x, y, z) in coordinate system (XYZ)2, as illustrated in Fig. 3b:

$$\overrightarrow{{r}_{p}}=\overrightarrow{P}-\overrightarrow{F}=\left(\begin{array}{l}x\\ y\\ z\end{array}\right)-\lambda \left(\begin{array}{l}0\\ \mathrm{cos}\left({\omega }_{2}t\right)\\ \mathrm{sin}\left({\omega }_{2}t\right)\end{array}\right).$$
(2)

Because of \(\overrightarrow{{r}_{p}}\perp \overrightarrow{{y}_{1}}\), the scalar product equals zero

$$\overrightarrow{{r}_{p}}\cdot \overrightarrow{{y}_{1}}= 0,$$
(3)

and allows the determination of \(\lambda \) in coordinate system (XYZ)2 as follows:

$$\lambda =y\cdot \mathrm{cos}\left({\omega }_{2}t\right)+z\cdot \mathrm{sin}\left({\omega }_{2}t\right),$$
(4)

thereby yielding the components of the primary acceleration as follows:

$$\overrightarrow{{a}_{1}}= \left(\begin{array}{l} {{\omega }_{1}}^{2}\cdot x\\ {{\omega }_{1}}^{2}\cdot \left(y-\left( y\cdot \mathrm{cos}\left({\omega }_{2}t\right)+z\cdot \mathrm{sin}\left({\omega }_{2}t\right)\right)\cdot \mathrm{cos}\left({\omega }_{2}t\right)\right)\\ {{\omega }_{1}}^{2}\cdot (z-\left( y\cdot \mathrm{cos}\left({\omega }_{2}t\right)+z\cdot \mathrm{sin}\left({\omega }_{2}t\right)\right)\cdot \mathrm{sin}\left({\omega }_{2}t\right))\end{array}\right).$$
(5)

The secondary acceleration field \(\overrightarrow{{a}_{2}}\) around the second rotation axis remains as follows:

$$\overrightarrow{{a}_{2}}=\left(\begin{array}{l}0\\ {{\omega }_{2}}^{2}\cdot y\\ {{\omega }_{2}}^{2}\cdot z\end{array}\right).$$
(6)

In combination, superposition of the two different rotational accelerations and gravity yields an overall acceleration \(\overrightarrow{{a}_{p}}\) on a mass point \(\overrightarrow{P}\) and is described as follows:

$$\overrightarrow{{a}_{p}}=\left(\begin{array}{l} {{\omega }_{1}}^{2}\cdot x\\ {{\omega }_{1}}^{2}\cdot \left(y-\left( y\cdot \mathrm{cos}\left({\omega }_{2}t\right)+z\cdot \mathrm{sin}\left({\omega }_{2}t\right)\right)\cdot \mathrm{cos}\left({\omega }_{2}t\right)\right)+{{\omega }_{2}}^{2}\cdot y+g \mathrm{cos}\left({\omega }_{2}t-\frac{\uppi }{2}\right) \\ {{\omega }_{1}}^{2}\cdot \left(z-\left( y\cdot \mathrm{cos}\left({\omega }_{2}t\right)+z\cdot \mathrm{sin}\left({\omega }_{2}t\right)\right)\cdot \mathrm{sin}\left({\omega }_{2}t\right)\right)+{{\omega }_{2}}^{2}\cdot z+ g \mathrm{sin}\left({\omega }_{2}t-\frac{\uppi }{2}\right)\end{array} \right).$$
(7)

In contrast to the gravity field, where the acceleration vectors are (close to) parallel, the acceleration field caused by rotation has a radial character determined by its axis of rotation. A mass point moving through two superposed, non-coaxial acceleration fields caused by rotation experiences transient acceleration depending on its position. In this specific case, the y- and the z-components of the field \(\overrightarrow{{a}_{1}}\) oscillate at double the frequency of \(\omega_{2} {/}(2\uppi )\). The potting material reacts by orienting perpendicularly to the acceleration field, resulting in circular oscillation of the potting surface. Rotational speed and dynamic viscosity of the potting material influence the height of the oscillation.

Instead of a cylindrical potting shape, as obtained from the common uniaxial potting approach, the biaxial potting technique yields an ellipsoid shape, depicted as dashed lines in Fig. 4, that can be altered in size and length by adjusting the rotational speeds and amount of potting material in the module. Any section of this ellipsoid can be taken as the concave shape for potting material. Both a cylindrical (D = 60 mm, H = 110 mm) and cuboidal module (90 mm × 90 mm × 25 mm) have been investigated. The incorporation of HFM has been omitted to facilitate accessibility for module measurements.

Fig. 4
figure 4

Arrangements investigated in this study: a centrally positioned, cylindrical section of an ellipsoid; b centrally positioned, tilted, cuboid ellipsoid section of an ellipsoid; c eccentrically arranged, cuboidal ellipsoid section of an ellipsoid (left) and eccentrically positioned, cylindrical ellipsoid section of an ellipsoid (right)

Full size image

When the cylindrical module is placed at the intersection of the two perpendicular rotation axes, both ends of the fiber bundle can be potted simultaneously, avoiding the creation of corners (Fig. 4a). Either the whole ellipsoidal cavity can be enclosed by the module or only a section of the cavity is used, depending on the volume fraction of potting material, as depicted in Fig. 4a. When applied to cuboidal-shaped MLs, the disadvantageous corners may be eliminated and the surface is given an additional curvature that offers presumably a smoother flow path (Fig. 4b). The module may be placed diagonally in the centrifuge’s center and tilted by angle \(\alpha \) within the center of the centrifuge, as shown in Fig. 4b, to achieve an oval shape. Using an eccentric position, the different ends can be a combination of differently shaped pottings (Fig. 4c, right) or a section of an ellipsoid with larger half axes can be produced (Fig. 4c, left). In this case, tilting angle \(\alpha \) may be used again depending on the desired transition from inlet to fiber bundle.

Numerical approach

Computational fluid dynamics (CFD) was used to identify parameter sets resulting in viable potting shapes. All operations for this numerical investigation, such as mesh generation (meshing), numerical modeling (CFX-Pre), solving (CFX-Solver) and post-processing (CFD-Post), were performed in Ansys Workbench 2020 R1 (Ansys, Inc., Canonsburg, USA). For both module geometries, the cylindrical and cuboidal fluid domains, a mesh was generated with 3.4 and 1.7 million elements, respectively. The fluid domains contained air and silicone with varying volume fractions depending on the potting design. Both the air and silicone were considered as continuous fluids under normal conditions. Silicone was described as a pure liquid substance with fluid-mechanical properties as provided in the manufacturer’s data sheet (ELASTOSIL RT 620, Wacker Chemie AG, Munich, Germany). No buoyancy was calculated. The turbulence behavior of both fluids was modeled using the shear stress transport model (SST). A surface tension coefficient of 0.02 N/m was assumed in a continuum surface force model, with silicone as the primary fluid. The interphase was modeled as a free surface. The acceleration field described by Eq. (7) was defined as the momentum source in the fluid domain.

Transient effects due to the superposition of two radial acceleration fields cause the potting material’s surface to oscillate. In practical applications, this oscillation may create a thin layer of potting material on the fibers within the oscillation amplitude. Consequently, this coated exchange surface may not contribute to the gas exchange. Although the HFM were not included in the simulations, the surface oscillations of the potting material were tracked. As a measure of the contaminated HFM surface, the local presence of silicone accumulated over time was normalized by the number of time steps. For this purpose, a volume fraction greater than 0.5 was set as the presence criterion for silicone. This volume was normalized by the final surface area of the potting as an approximation of the height of oscillation \({h}_{0}\). Consequently, the height in which the membrane fibers are covered with potting material is assumed to be \(\frac{{h}_{0}}{2}\). The rotational resolution is 5° per time step, resulting in 72 steps per revolution. After 2.5 turns, i.e., 180 time steps, the local presence of silicone was calculated over three revolutions around the x-axis.

Experimental setup

An experimental setup was developed to validate the final shape under consideration of the curing process and to test feasibility, as depicted in Fig. 5. To this end, an existing centrifuge was upgraded by adding a rotational axis perpendicular to the main axis. The centrifuge was conceptualized in the framework of an industrial batch centrifuge with a horizontal mounting plate of 1 m in diameter (GZ 1000, Carl Padberg Zentrifugenbau GmbH, Lahr, Germany) and operable at a rotational speed of up to 750 rev/min. The shaft of the secondary centrifuge was driven by a brushless 75 W DC-Motor (EC-i30, Maxon Motor AG, Sachselen, Switzerland) with a nominal speed of 6879 rev/min and a nominal torque of 107 mNm. The energy supply for the motors inside the batch centrifuge housing was provided by placing a rotary transmission (RX-RF-056B-QI1-04014S, B-COMMAND GmbH, Hamburg, Germany) in the center of the main centrifuge. The shaft was driven by a polyurethane MXL toothed belt (MISUMI Group Inc., Tokyo, Japan) with a transmission ratio of 3:1. Due to balance considerations, the secondary rotation axis was symmetrically mounted twice on the main centrifuge platform. Additionally, the shafts were rotated in opposite directions of rotation in relation to each other to prevent imbalance.

Fig. 5
figure 5

Experimental setup for validation of the numerical approach and feasibility test: the assembly of the secondary axis is located in duplicate on the rotary plate ① of the main centrifuge. The shaft ② of the secondary centrifuge is mounted in a deep groove ball bearing ③ and an angular contact ball bearing ④. Both bearings are mounted in housings, which are screwed onto the rotary plate. Using a toothed belt ⑤, the shaft is driven by a DC-motor ⑥. The motor is wired to a control box outside the centrifuge. Due to the rotation, the wires ⑦ are fed through a rotary transmission ⑧. The modules can be assembled on either end of the shaft, central ⑨ or eccentric ⑩ (here: cuboidal module)

Full size image

The modules can be placed either in central or eccentric position, where ‘central position’ is at the intersection of both rotation axes, as shown in Fig. 4a and 4b. ‘Eccentric position’ in turn means that the module is placed on an outer diameter to the main centrifuge axis, as illustrated in Fig. 4c. The silicone volume fraction is defined by the ratio of silicone volume by the total volume of the module. The rotational speed ratio parameter n2/n1 is defined as the ratio of the number of revolutions of the second to the first axis. For both the experimental and numerical approaches,, the design points (DPs) used for this study are summarized in Table 1.

Table 1 Design points for simulation and experiment
Full size table

Validation of potting shape

For qualitative comparison of the potting shape of the simulations after potting, an iso-surface was defined to represent the boundary surface between air and silicone. The iso-surface was determined by a time-averaged probability of silicone presence of 0.5. Additionally, characteristic measures were determined for quantitative comparison of the potting shape from simulations and experiments to measure curvatures for different designs in order to relate them to the rotational speed ratio. For the centrally potted cylinder, we compared the axial distance a between opposite curvatures and the gap width b between the opposite circular edges in simulation and experiment, as illustrated in Fig. 6a. For the centrally potted, diagonally tilted cuboids, the distances c′, c″, d′, and d″ at the outer section planes were used for the experimental validation (Fig. 6b). c′ and c″ as well as d′ and d″ were averaged to single values c and d, respectively. In the case of the eccentrically potted cylindrical module, the height at the central deepening e and at the circular edge f was measured, as depicted in Fig. 6c. The cuboidal module’s characteristic curvatures g and h were measured from the diagonal middle plane to the extrema of curvatures on both cutting planes (Fig. 6d).

Fig. 6
figure 6

Characteristic measures for different modules and configurations for validation purposes: a centrally potted, cylindrical module; b centrally potted, cuboidal module; c eccentrically potted, cylindrical module; and d eccentrically potted, cuboidal module. Dark blue: potting material in cutting plane; light blue: potting material visible behind cutting plane; white: air

Full size image

Results

Simulations and experiments were performed at the same DPs for the same module geometries. Figure 7a illustrates the results from simulations (top row) and experiments (bottom row) for the centrally potted, cuboidal module at three different DPs. The module intersects the ellipsoid diagonally and forms an oval cross section. The vertical half-axis grows with increasing rotational speed ratio n2/n1. Figure 7a shows the values for c and d over different speed ratios for both experiments and simulations. Notably, the length of the other half axis c only slightly changes compared to d. The highest deviation of the characteristic measures between simulations and experiments is 4.6% (absolute 3.17 mm) for c occurs at the lowest rotational speed ratio.

Fig. 7
figure 7

Direct comparison of resulting potting shape from simulations and experiments for a cuboidal-shaped module in central (a) and eccentric (b) positions. The images of the modules are shown slightly rotated for the simulation results so that the surfaces are clearly visible

Full size image

The potting in the eccentrically positioned cuboid forms a curved parabolic surface, as shown in Fig. 7b. Depending on the rotational speed ratio, the parabolic character increases. At the highest rotational speed ratio, the surface seems to twist. While the surface normal at the borders to the housing points away from the image plane, the surface normal at the minimum of the parabolic curvature points into the image plane (Fig. 7b). The difference in characteristic measures between experiments and simulations is the highest at n2/n1 = 2.0 with 13.2% (absolute 1.39 mm) for g. All other deviations for g for the remaining DPs are less than 6.6%. At the same rotational speed ratio, the deviation for h is the highest with 2.7% (absolute 0.7 mm).

Figure 8a compares the results from simulations and experiments for the centrally potted, cylindrical module. For the first DP (n2/n1 = 0.66), the potting mass separates into two portions of the same volume, each forming a dome. By increasing the rotational speed ratio, the domes seem to merge for the second (n2/n1 = 1.0) and third DPs (n2/n1 = 1.5). For the second DP, only a thin layer (100–200 µm) of potting material connects both domes. The simulations do not predict the same contact angle between potting and housing at higher DPs and, in consequence, the two separate portions do not merge even at the higher rotational speed ratios. However, the characteristic measures align between simulations and experiments with a maximum error of 3.6% for b (absolute 1.1 mm) at the lowest rotational speed ratio (Fig. 8a). The relative error for a is lower than 2.7% (absolute 2 mm).

Fig. 8
figure 8

Direct comparison of resulting potting shape from simulations and experiments for cylindrical-shaped module in central (a) and eccentric (b) positions

Full size image

Similarly, the results for the eccentric potting arrangement of the cylindrical module are presented in Fig. 8b. As already pointed out for the centrally potted, cylindrical module, the contact angle between housing and potting mass predicted by the simulation differs from the near tangential transition from potting to housing seen in the experiment. Still, the maximum error is 3.6% (absolute 1.38 mm) for f at the second DP (n2/n1 = 2.0). For e, the deviation is less than 2.8% (absolute 1.0 mm).

The transient effects caused by the superposition of two radial acceleration fields cause local oscillations. These local oscillations create an uncertainty in the resulting potting surface. Figure 9 illustrates the oscillation height for each potting configuration under investigation. The average amplitude of the surface oscillation is \(\frac{{h}_{0}}{2}\). Therefore, this value describes a range in which the membrane surface has come into contact with potting material during the process and is probably incapable of gas exchange. The values for \(\frac{{h}_{0}}{2}\) range from 0.51 to 0.911 mm, except for the centrally potted, cylindrical module. In this case, the oscillation height is between 0.97 and 1.36 mm. For both centrally potted modules the oscillation height decreases with the rotational speed ratio.

Fig. 9
figure 9

Oscillation height over rotational speed ratio for the investigated potting configurations

Full size image

Discussion

Thrombus formation in MLs prevents long-term use due to physiologically abnormal flow conditions. Corners, areas shut off from the flow, or stagnation zones particularly promote thrombus growth and are typically inefficient in terms of gas transfer performance due to lack of convection. However, with the contemporary potting process based on uniaxial centrifugation, the design of the current ML based on HFMs is very limited. Superposition of multiple acceleration fields results in new potting shapes for MLs. A multiaxial centrifugation process with two coupled rotations was evaluated in this study and simulations were performed to search for meaningful potting shapes. The biaxial model used was successfully implemented in a test setup, validating the numerical approach and proving the concept.

3D-potting allows new and improved flow path designs in MLs. In contemporary hollow-cylindrical MLs, blood enters the fiber bundle through the inner core on the bottom. This design causes blood to flow through most of the fiber bundle homogeneously except for the corners between potting and housing (Fig. 2b). When 3D-potting is applied to the bottom-end potting, these stagnation areas may be filled with potting material (Fig. 10a). Bartlett et al. [15] even proposed a perfectly round design for the prevention of thrombosis that reduces areas of recirculation and stagnation, thereby minimizing unsteady cross-sectional changes. To this end, cylindrical-central potting could be applied on a stacked membrane bundle where the inlet and outlet bores are positioned in each center of the opposing domes (Fig. 10b). Blood may enter through an inlet in the bottom dome where the cross section slowly expands. Near the top, the cross section converges, collecting the blood toward the outlet.

Fig. 10
figure 10

Conceptual flow path through 3D-potted MLs: a hollow-cylindrical, wound ML potted twice in an eccentric position, b stacked fiber arrangement potted in the centric position and c stacked fiber arrangement potted in the central position in a single step. Red arrows indicate blood flow path. The same representation style as in Fig. 2 was used to highlight the additional flow guidance within the potting margins in absence of disadvantageous corners between potting and housing

Full size image

The cuboidal central arrangement offers an interesting opportunity for cuboidal MLs with a rectangular cross section. The oval cross section would eliminate the corners. Further, with inlet and outlet at the opposing ends of the oval, the potting contours would guide the flow homogeneously through the fiber bundle (Fig. 10c). In addition, the oval cross-sectional area of the cuboidal-central arrangement may allow an alignment of the fibers along the short half axis to achieve a short fiber length suitable for high CO2 removal [22]. In addition, the design would still benefit from the advantages of a stacked AL with regard to a lower pressure drop. This design may also be achieved with the cuboid-eccentric arrangement in a two-step potting process. Instead of an oval shape, the result would be a lenticular cross-sectional area.

Despite the obvious potential and promise of 3D-potting, this study can only thus far provide a proof of concept. The obvious next steps will include flow simulations of the proposed designs and in vitro tests compared to the commercial MLs, as shown in Fig. 2, to quantify the advantages of 3D-potting.

A major challenge in the translation of the 3D-potting method to production of real MLs is the process of filling the compound into the ML without pre-wetting the HFMs meant for gas exchange. Currently, channels or tubing are implemented to connect the outside of the centrifuge with the potting area using slip rings to transport the potting material passively [18]. For the setup introduced in this study, two slip rings could be applied in series [23]. Other technical solutions could include a reservoir within the centrifuge connected to the ML, located inside the resulting ellipsoid, or releasing the compound using centrifugal force or active pumping [10]. The injection of the compound could either be done from outside the centrifuge via channels rotating with the centrifuge [18, 24,25,26] or by the use of reservoirs inside the centrifuge that release the potting compound through a controlled drive system.

In our tests thus far, the incorporation of HFMs was neglected in both the simulations and the experiments. This approach was justified by the accessibility of the modules to measurement in the experiments. Regarding the potting shape, no differences are expected, provided that the amount of potting material induced into the modules is adjusted by the volume fraction obstructed by HFMs. Otherwise, the lengths of the half axes will be considerably smaller. Furthermore, the forces acting on the fibers using 3D-potting are within the same range as in conventional potting. Also, the fiber bundles are typically packed densely in the housing before potting or held in place by additional means. Therefore, we do not expect that kinking of the fibers or local compacting of the fiber bundle would cause potential shunt flows later on. The oscillation height must, however, be reevaluated. Factors like friction between potting material and membrane surface, and capillary effects, may impact the transient oscillation height determined in the simulations and thus, surface smoothness. Furthermore, inertial forces, depending on density of the potting material, affect the tendency to follow the imposed acceleration. However, these viscous and inertia-dependent effects would dampen rather than enhance the oscillation height. Then again, the porosity of the fiber bundle, which relates the void volume and the volume obstructed by fibers, may potentially increase oscillation height depending on the local presence or absence of fibers within the oscillation height. Tests with real fiber mats in place are necessary to validate the impregnated fiber length due to the oscillation effect. In the simulations, the fluid domains could be transformed into porous domains with a porosity that describes the proportion of free volume to total volume.

The simulations have proven themselves a valuable tool in identifying parameters for the volume fraction of silicone and rotational speeds to determine a starting point for further development of meaningful designs applicable to artificial lungs. For the four cases presented in this study, the simulations are considered experimentally validated. The highest error in measurements is 13.2%. However, this error occurs in relation to a very low reference value and the absolute error is only 1.39 mm, which is in the range of the oscillation height. A major limitation of the simulations is the incorrect representation of the contact angle between the resulting potting surface and the housing wall for the centrally potted, cylindrical modules. Therefore, while the portions of potting mass merged in the experiment, this effect could not be observed in the simulations. Still, the complexity of the physics and the interaction of various parameters demand good spatial imagination. Nevertheless, the simulations should always be considered a simplified model of reality and thus undergo experimental validation.

Further combinations of more than two superposed rotational or even translational accelerations will be the subject of another study. These additional variants will generate even more diverse cavities that offer various design opportunities for artificial lungs and membrane modules of all kinds. However, not all combinations of rotations and translations may lead to a steady endpoint with an acceptable surface oscillation and therefore require a combined investigative approach of simulation and experiment.

Conclusions

A novel method for 3D-potting of membrane modules based on a multiaxial centrifugation process was introduced. This study provides numerical identification of feasible parameter sets for meaningful designs and experimental validation as proof of concept. Based on this new potting technique, a variety of novel designs with improved flow path and lower stagnation volumes may emerge to overcome the limitations of state-of-the-art potting processes and improve the long-term stability and efficiency of artificial lungs.