Precise robust motion control of cell puncture mechanism driven by piezoelectric actuators with fractional-order nonsingular terminal sliding mode control

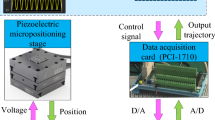
Abstract

A novel robust controller is proposed in this study to realize the precise motion control of a cell puncture mechanism (CPM) driven by piezoelectric ceramics (PEAs). The entire dynamic model of CPM is constructed based on the Bouc–Wen model, and the nonlinear part of the dynamic model is optimized locally to facilitate the construction of a robust controller. A model-based, nonlinear robust controller is constructed using time-delay estimation (TDE) and fractional-order nonsingular terminal sliding mode (FONTSM). The proposed controller does not require prior knowledge of unknown disturbances due to its real-time online estimation and compensation of unknown terms by using the TDE technology. The controller also has finite-time convergence and high-precision trajectory tracking capabilities due to FONTSM manifold and fast terminal sliding mode-type reaching law. The stability of the closed-loop system is proved by Lyapunov stability theory. Computer simulation and hardware-in-loop simulation experiments of CPM verify that the proposed controller outperforms traditional terminal sliding mode controllers, such as the integer-order or model-free controller. The proposed controller can also continuously output without chattering and has high control accuracy. Zebrafish embryo is used as a verification target to complete the cell puncture experiment. From the engineering application perspective, the proposed control strategy can be effectively applied in a PEA-driven CPM.

Appendix

Stability analysis

For TDE error $\Delta {\tilde{P}}$, a positive number $\varphi$ makes $\Delta {\tilde{P}}$ bounded, i.e., $| {\Delta {\tilde{P}}} |\le \varphi$. The boundedness certificate of $\Delta {\tilde{P}}$ can be referred to [35] and [36].

Definition 2

For the CPM described in Eqs. (1) and (2), if the FONTSM manifold represented by Eq. (16) and the fast-TSM-type reaching law represented by Eq. (17) are adopted, then the closed-loop system can achieve finite-time stability under the action of the proposed controller [Eq. (20)]. The system-state trajectory can converge to the following range:

$$\begin{aligned} {|s|\le \min \{{d_{1}, d_{2}}\}} \quad {d_{1} =\frac{\varphi }{k_{1}}} \quad {d_{2} =\left( {\frac{\varphi }{k_{2}}}\right) ^{1/\beta }} . \end{aligned}$$

(23)

The proof of Definition 2 and the stability of the closed-loop system are demonstrated by using Lyapunov theory.

Proof

A Lyapunov function is established as follows:

$$\begin{aligned} V=\frac{1}{2}s^{2}. \end{aligned}$$

(24)

The above function is differentiated with respect to time and then combined with FONTSM manifold (16) to obtain

$$\begin{aligned} {\dot{V}}=s({\ddot{e}+pD^{\lambda } \text {sig}(e)^{\alpha }}). \end{aligned}$$

(25)

Equation (21) is substituted in the above equation and yields

$$\begin{aligned} {\dot{V}}=-s({k_{1} s+k_{2} \text {sig} (s)^{\beta } -\Delta {\tilde{P}}}). \end{aligned}$$

(26)

Combined with boundary condition $| {\Delta {\tilde{P}}} |\le \varphi$, the above equation can be written as

Combined with boundary condition $| {\Delta {\tilde{P}}} |\le \varphi$, the above equations are transformed into inequality, as follows:

$$\begin{aligned} {\dot{V}}\le -s({k_{1} s+k_{2} \text {sig} (s)^{\beta } -\varphi }). \end{aligned}$$

The above inequality can be converted into the bellowing forms:

$$\begin{aligned} {\dot{V}}&\le -s \left[ {\left( {k_{1} -\frac{\varphi }{s}}\right) s+k_{2} \text {sig}(s)^{\beta }}\right] , \end{aligned}$$

(27)

$$\begin{aligned} {\dot{V}}&\le -s \left[ {k_{1} s+\left( {k_{2} -\frac{\varphi }{ \text {sig}(s)^{\beta }}}\right) \text {sig}(s)^{\beta }}\right] . \end{aligned}$$

(28)

For Eq. (27), if $| s |>\varphi /{k_{1}}$, then ${\dot{V}}<0$. Thus, Eq. (27) can be rewritten as follows:

$$\begin{aligned} {\dot{V}}\le -s({{\bar{k}}_{1} s+k_{2} \text {sig}(s)^{\beta }})=-{\bar{k}}_{1} s^{2}-sk_{2} \text {sig}(s)^{\beta }, \end{aligned}$$

(29)

where ${\bar{k}}_{1} =k_{1} -\dfrac{\varphi }{s}$.

Equation (29) is re-arranged as

$$\begin{aligned} {\dot{V}}+2{\bar{k}}_{1} V+2^{\frac{1+\beta }{2}}k_{2} V^{\frac{1+\beta }{2}}\le 0. \end{aligned}$$

(30)

According to Lemma 1, V converges to 0 in a finite time. The convergence time $T_{1}$ satisfies

$$\begin{aligned} T_{1} \le \frac{1}{{\bar{k}}_{1} (1-\beta )}\ln \left( \frac{2{\bar{k}}_{1} V_{1}^{\frac{1-\beta }{2}} (x_{0})}{2^{\frac{1+\beta }{2}}k_{2}} +1\right) . \end{aligned}$$

(31)

In finite time $T_{1}$, the system-state trajectory s converges to the following region:

$$\begin{aligned} | s |\le \frac{\varphi }{k_{1}} =d_{1}. \end{aligned}$$

(32)

Using similar analysis for Eq. (28), if $| s |^{\beta } >\varphi /{k_{2}}$, then ${\dot{V}}<0$. Thus, Eq. (28) can be rewritten as follows:

$$\begin{aligned} {\dot{V}}\le -s({k_{1} s+{\bar{k}}_{2} \text {sig}(s)^{\beta }})=-k_{1} s^{2}-s{\bar{k}}_{2} \text {sig}(s)^{\beta }, \end{aligned}$$

(33)

where ${\bar{k}}_{2} =k_{2} -\dfrac{\varphi }{\text {sig}(s)^{\beta }}$.

Equation (33) is re-arranged as follows:

$$\begin{aligned} {\dot{V}}+2k_{1} V+2^{\frac{1+\beta }{2}}{\bar{k}}_{2} V^{\frac{1+\beta }{2}}\le 0, \end{aligned}$$

(34)

According to Lemma 1, V converges to 0 in a finite time. The convergence time $T_{2}$ satisfies

$$\begin{aligned} T_{2} \le \frac{1}{k_{1} (1-\beta )}\ln \left( {\frac{2k_{1} V_{1}^{\frac{1-\beta }{2}} (x_{0})}{2^{\frac{1+\beta }{2}}{\bar{k}}_{2}} +1}\right) , \end{aligned}$$

(35)

In finite time $T_{2}$, the system-state trajectory s converges to the following region:

$$\begin{aligned} | s |\le \left( {\frac{\varphi }{{\bar{k}}_{2}}}\right) ^{\frac{1}{\beta }}=d_{2}, \end{aligned}$$

(36)

In sum, the system-state trajectory converges to the following range in finite time:

$$\begin{aligned} | s |\le \min \{{d_{1}, d_{2}}\}. \end{aligned}$$

Therefore, the stability of the closed-loop system is certain, and the proof of Definition 2 is completed. $\square$

Controller Adjustment

Six parameters, namely, $\alpha , \beta , k, k_{1}, k_{2}$, and $\lambda$, must be tuned in the proposed controller.

Remark 9

From Eqs. (31) and (35), a smaller $\beta$ corresponds to a shorter convergence time of the system-state trajectory and a higher accuracy of the control system.

Remark 10

From Eqs. (16), (17), and (20), when $\alpha \rightarrow 1,\beta \rightarrow 1$, , the sign function disappears, and the controller shows linear characteristics. When $\alpha \rightarrow 0,\beta \rightarrow 0$, the control law is discontinuous under the influence of the symbolic function. Therefore, $0<\alpha , \beta <1$ ensures that the controller exhibits not only the chattering-free characteristics of linear control but also the strong, robust characteristics of a discontinuous controller.

Remark 11

From Eq. (23), the $k_1$ and $k_2$ gains of the reaching law affect the convergence region of the state trajectory. Gains $k_1$ and $k_2$ must be satisfied as $\hbox {k}_{1} =k_{2} >|\Delta {\tilde{P}}|$ to make the state trajectory converge to a small region as soon as possible.

Remark 12

The FO term $D^{\lambda } ({\text {sig}(e)^{\alpha }})$ can enhance the sign function and show a large amplitude when the sign of displacement error changes. When $\lambda \rightarrow 1$, the amplitude increases. When $\lambda \rightarrow 0$, the effect of FO is weakened and reduced to IO. p is used to increase the variation amplitude of the FO term.

Three Controllers for Comparison

Three existing controllers are derived from the proposed controller as prototypes in the comparative experiments. These three controllers use the FONTSM manifold, the fast-TSM-type reaching law, and the TDE technology to build an FO controller without a model and apply the NTSM manifold, the fast-TSM-type reaching law, and the TDE technology to build an IO controller whether based on a model or not.

Control 1: Wang’s controller

The model of system dynamics (1) and (2) is simplified as

$$\begin{aligned} {\bar{m}}\ddot{x}+N (x, {\dot{x}}, \ddot{x}, k, d, h, \tau _{d}) =u, \end{aligned}$$

(37)

where $N (x, {\dot{x}}, \ddot{x}, k, d, h, \tau _{d}) =\bigg (\dfrac{m}{kd}-{\bar{m}}\bigg )\ddot{x}+\dfrac{1}{k}{\dot{x}}+\dfrac{1}{d}x +\dfrac{h}{d} -\dfrac{\tau _{d}}{kd}$. To simplify the expression, N(t) represents state of $N (x, {\dot{x}}, \ddot{x}, k, d, h, \tau _{d})$ at time t, and the simplified dynamic model is reformulated as

$$\begin{aligned} {\bar{m}}\ddot{x}+N (t)=u. \end{aligned}$$

(38)

Based on dynamic model (38), N(t) is estimated by TDE technology and is expressed as

$$\begin{aligned} N(t)\approx {\hat{N}}(t)=N({t-L})=u(t-L)-{\bar{m}}\ddot{x}(t-L). \end{aligned}$$

(39)

The FONTSM sliding surface and fast-TSM-type reaching law described in Eqs. (16) and (17) are used to construct a model-free, robust controller based on FONTSM and TDE. The designed control law imitates the following design ideas and methods of the control law provided in [44]:

$$\begin{aligned} u&={\bar{m}}({\ddot{x}_{u} +pD^{\lambda } ({\text {sig}(e)^{\alpha }})+k_{1} s+k_{2} \text {sig}(s)^{\beta }})\nonumber \\&\quad ~ +u_{(t-L)} -{\bar{m}}\ddot{x}_{(t-L)} . \end{aligned}$$

(40)

According to its proponent [44], this controller is called the Wang’s controller.

Control 2: MB-FNTSM controller

If $\lambda =0$, then the FO function in the controller is lost. The NTSM manifold is formulated as

$$\begin{aligned} s={\dot{e}}+p \text {sig}(e)^{\alpha }, \end{aligned}$$

(41)

By using the fast-TSM-type reaching law [Eq. (17)] and the dynamic model [Eq. (5)], the controller is constructed as

$$\begin{aligned}&u=\nonumber \\&\underbrace{\frac{1}{kd} \{{m [{\ddot{x}_{d} -p\alpha {\dot{e}} | e |^{\alpha -1}}]+b{\dot{x}}+kx-m({k_{1} s+k_{2} \text {sig}(s)^{\beta }})}\}}_{\text {FNTSM}}\nonumber \\&-\underbrace{\frac{m}{kd}\Delta {\hat{P}}}_{\text {TDE}}. \end{aligned}$$

(42)

NTSM manifold and fast-TSM-type reaching law are adopted in the sliding mode term of the proposed controller. This term is labeled FNTSM, and the model-based controller is abbreviated to MB-FNTSM for convenience.

Substituting the control law [Eq. (42)] into the dynamic model [Eq. (5)] leads to the following displacement error equation of the closed-loop system:

$$\begin{aligned} \ddot{e}+p\alpha {\dot{e}}\text {sig}(e)^{\alpha -1}+k_{1} s+k_{2} \text {sig}(s)^{\beta } =\Delta {\tilde{P}}, \end{aligned}$$

(43)

The difference between Eqs. (21) and (43) is called the FO term. A stability analysis of the MB-FNTSM controller can also be completed by referring to the analysis of the proposed controller.

Control 3: MF-FNTSM controller

Let $\lambda =0$. Then, the MB-FNTSM controller can be designed.

The unknown term is estimated by Eq. (39) using the dynamic model [Eq. (38)], NTSM manifold [Eq. (41)], and fast-TSM-type reaching law [Eq. (17)]. The control law can be designed by referring to the idea presented in [28] as shown below:

$$\begin{aligned} u&=\underbrace{{\bar{m}}({\ddot{x}_\mathrm{a} +p\alpha {\dot{e}} | e |^{\alpha -1}+k_{1} s+k_{2} \text {sig}(s)^{\beta }})}_{\text {FNTSM}}\nonumber \\&\quad ~ +\underbrace{u_{(t-L)} -{\bar{m}}\ddot{x}_{(t-L)}} _{\text {TDE}}. \end{aligned}$$

(44)

The controller is abbreviated as MF-FNTSM.

Remark 13

The complexity of the controller reflects the required amount of calculation and debugging. The four controllers are ranked as follows in a descending order according to their required amount of calculation: proposed controller>Wang’s controller>MB-FNTSM>MF-FNTSM. In engineering applications, the control accuracy and calculation amount of these controllers can be comprehensively balanced to determine the appropriate controller.