1 Introduction

The rapid development of vehicle-to-everything technologies provides more opportunities to promote vehicle intelligence, enabling multiple-source information exchange to improve vehicle safety, traffic mobility, and fuel economy [1]. To support these applications, the path following (PF) of autonomous vehicles is a crucial and non-negligible implementer, i.e., bridging the higher-level decision-making and lower-level vehicle dynamics. The prime target of PF is to effectively track the reference path as close as possible to the premise of vehicle stability. This is not a facile task since the control effects are sensitive to the vehicle dynamics, especially under extreme driving conditions [2]. The force features of tires under extreme cycles exhibit high nonlinearity, which potentially induces the risks of vehicle instability. This also leads to design difficulties in controller developments.

To prevent vehicle instability, the first question is how to evaluate the vehicle stability status. To this end, the phase plane portrait approach is widely adopted, which can intuitively yield the variants of vehicle motion phase trajectories by giving different initial states and driving conditions. In general, two types of phase planes are mostly studied in the last decade, i.e., sideslip angle-sideslip angle rate (\(\beta\)-\(\dot{\beta }\)), and sideslip angle-yaw rate (\(\beta\)-\(\gamma\)). In Refs. [3, 4], the \(\beta\)-\(\dot{\beta }\) phase plane was analyzed, and the diamond vehicle stability region is defined by two saddle points and two calibrated interactions of zero sideslip angle. In Refs. [5, 6], the two-lines method was developed to determine the stability region in \(\beta\)-\(\dot{\beta }\) phase planes. To avoid potential tire skids, the yaw rate limits of the maximum lateral acceleration are considered in \(\beta\)-\(\dot{\beta }\) phase planes, and a modified stability region based on the two-lines method was proposed in Ref. [7]. The above approaches are verified to be effective in assessing vehicle stability, but entailing enormous work burdens for vertices calibrations or polynomial fittings. Unlike \(\beta\)-\(\dot{\beta }\) phase plane portraits, the \(\beta\)-\(\gamma\) one is more accurate and easier to operate since the stable bounds can be directly expressed by the limits of yaw rate and tires’ sideslip angle. In Refs. [8, 9], the parallelogram envelope is proposed to define the vehicle stability region, which is derived from the maximum values of yaw rate and sideslip angle of rear tires. Based on the parallelogram envelope, Refs. [10, 11] concluded that the bounds regarding limited yaw rate, and front and rear tires’ sideslip angles, will meet at one saddle point. Hence, the steering angle envelope can be deduced for vehicle stability assessments. Further, Ref. [10] points out that the above parallelogram envelop will cause small overshoots of yaw rate when converging to the equivalent point during steady-state steering. To solve that, the limited front and rear tires’ sideslip angle, as well as yaw acceleration nullclines, are combined to develop the stable region by \(\beta\)-\(\gamma\) phase plane analysis. Although the above research is successful, there still exists a deficiency for PF issues under extreme conditions. That is their limited yaw rate bounds, derived from maximum lateral acceleration, are set up under the assumptions of zero lateral velocity differential. The zero-sideslip angle is generally pursued in stability control, making zero lateral velocity differential, but it is not always helpful for PF control under extreme conditions. For instance, during vehicle turning in high velocity and low tire-road friction, the reasonably increase/decrease of lateral velocity is beneficial to minimize PF errors, inducing the nonzero lateral velocity differentials. If the yaw rate is restricted by the bounds with zero lateral velocity differential, the vehicle steering capacity may be confined, entailing the deteriorations in PF effects.

After defining the vehicle stability regions, the outstanding PF controller should be developed. There are a series of PF control approaches proposed in the last decade [12, 13], e.g., fuzzy logic control [14], sliding mode control (SMC) [15], robust \({\mathcal{H}}_{\infty }\) control [16], and nonlinear Lyapunov control [17]. To avoid the disturbances on path curvature, a vision-based lane keep controller is developed by two proportional-integral nested loops [18]. In Ref. [19], an exponential-like-sliding-mode fuzzy type-2 neural network strategy was designed, which is verified to yield the desirable convergence and robustness. In Ref. [15], considering the system uncertainties, a sliding mode control (SMC)-based composite nonlinear feedback controller was proposed to reject the lumped disturbance. In Ref. [20], the Takagi–Sugeno fuzzy technique was adopted to consider the time-varying vehicle velocity in modeling, and output feedback gain-scheduled PF strategy was proposed that can improve the closed-loop transient performance by \(\mathcal{D}\)-stability concept. To handle the uncertainties of impaired driver behaviors, a linear-parameter-varying based robust \({\mathcal{H}}_{\infty }\) strategy was designed for PF of driver assistance control system [21]. For active steering and direct yaw moment control (DYC) issues, an integrated controller was developed by Lyapunov nonlinear method, which actualized the function-decoupling control and guarantees the closed-loop system stability [17].

However, the aforementioned research mainly focuses on transient performance or robustness but neglects constraint handling performance. There are various system constraints in real-world PF applications, such as limits of vehicle stability, actuator, and driving area. Often, they are ignored in the controller design phase and then introduced through post-process operations (like imposing saturation limits regarding inputs and/or control barrier function [22]), while this may deteriorate the control optimality. Therefore, it is significant to think about the constraints during controller development.

Alternatively, model predictive control (MPC) is an effective and appropriate choice. Unlike other methods, in MPC, the constraints can be easily considered by explicit expressions, and the system states in the predictive horizon can be optimized by algorithms, which guarantees control optimality [23, 24]. In Ref. [11], an MPC control strategy based on a linear single-track model was proposed for PF and vehicle stabilization. In Ref. [25], the linear-time-varying (LTV) MPC was developed for active steering control, while with poorer performance than nominal nonlinear MPC (NMPC). Indeed, considering the high nonlinearity of tires, the NMPC is preferable to linear MPC but suffers from huge calculation burdens. To this end, the explicit MPC was proposed in Ref. [26]. It is verified to show a similar control performance with nominal NMPC in the premise of a smaller grid, but leading to high memory requirements that limit its wider application. Benefited from the parallel process capacity of field-programmable gate array (FPGA) chip, the NMPC by particle swarm optimization algorithm is validated to be real-time applicable under hardware-in-the-loop test [27]. That said, it is hard to have a large-scale application due to the high expense of FPGA chips.

Except for the real-time capability, the closed-loop stability is also a crucial property of the control system. Because the control commands in MPC are determined by optimization, they are implicit in the system state, bringing huge difficulties in analyzing the closed-loop stability, in particular for nonlinear systems. The popular methods are to first linearize the system and then introduce the terminal constraints and the terminal cost [28]. However, as mentioned previously, the linearized MPC is hard to take the nonlinearities of vehicle dynamics into account, entailing poorer performance.

To fill the above gaps, this paper proposes a real-time NMPC strategy for desirable effects of PF and vehicle stability. The distributed drive electric vehicle (DDEV) is selected as the study object in this paper, which brings more control degrees of freedom (DOF) for improved effects but with greater complexities [29]. The main contributions are summarized:

  1. (1)

    For the expected PF effects and application requirements, an accurate but not too complicated model for controller design is indispensable, which is generally named a “control-oriented model”. In this paper, an accurately nonlinear control-oriented model combined with the Magic Formula tire model and the single-track vehicle model is established to feature the lateral dynamics of vehicles. Unlike lots of previous research [30] that apply front steering angle, the lateral force of front tires is adopted as the control variable, to reduce control complexity but reserve the front tires’ nonlinearity.

  2. (2)

    The lateral velocity differential is considered in the maximum lateral acceleration, and the phase plane analysis of lateral velocity and yaw rate are carried out. It is found that for constant steering angle and tire-road friction, the maximum lateral acceleration is varied with vehicle states and markedly different from the yaw rate bounds without considering lateral velocity differential. Moreover, there exists a steering angle under critical stability cases, and meanwhile, the yaw rate of the maximum lateral acceleration will converge to that without considering the lateral velocity differential. Given the phase plane analysis, the stable bounds of the steering angle are proposed and transformed as front tires’ lateral forces according to the vehicle model. The proposed bounds can effectively guarantee vehicle stability. Owing to the consideration of lateral velocity differential in the maximum lateral acceleration, it can also improve the vehicle steering capacity, which is very helpful for PF control under extreme conditions.

  3. (3)

    To guarantee the closed-loop stability in PF, the Lyapunov-based constraint is developed for the NMPC strategy. Its sufficient conditions for recursive feasibility and closed-loop stability are explicitly derived.

  4. (4)

    The C/GMRES algorithm is proposed for real-time optimization in the NMPC strategy. To handle the inequality constraints, the relaxation function method is adopted to transform the inequality constraints as the equivalent cost in the optimization objective. The proposed C/GMRES algorithm-based NMPC strategy is verified to implement superior control effects computationally.

The rest of this paper is organized as follows. Section 2 describes the control-oriented model. Section 3 introduces the control framework of the proposed strategy. Section 4 illustrates the C/GMRES algorithm-based NMPC controller. The inversive tire model’s application and torque allocation method are shown in Sect. 5. Section 6 gives the validations and analysis, followed by the conclusions in Sect. 7.

2 Control-Oriented Model Formulation

The studied vehicle is an autonomous DDEV with front-steering and four-wheel independently-driven functionalities. Before modeling, some assumptions are arranged: (1) the vehicle velocity \({v}_{x}\), the lateral velocity \({v}_{y}\), the yaw rate \(\gamma\), and the tire-road friction factor \(\mu\), can be accurately observed or estimated by advanced sensors/algorithms; (2) assuming that the rotational inertia of wheels is small, there is \({F}_{x}\approx T/{r}_{\mathrm{w}}\), where \({F}_{x}\) and \(T\) are the longitudinal force and the torque for one tire and related IWM, respectively, and \({r}_\text{w}\) is the tire effective radius.

The schematic of the PF issue is depicted in Fig. 1. Defining the lateral position error as \({y}_{\mathrm{e}}\) and heading error as \({\psi }_{\mathrm{e}}\) [31]:

$$\left\{\begin{aligned}&{\dot{y}}_{\mathrm{e}} ={v}_{y}{\psi }_{\mathrm{e}}+{v}_{x}\\\,&{\dot{\psi }}_{\mathrm{e}} =\dot{\psi }-{\dot{\psi }}_{\mathrm{r}}=\gamma -{\dot{\psi }}_{\mathrm{r}}\end{aligned}\right.$$
(1)

where \(\psi\) and \({\psi }_{\mathrm{r}}\) are the vehicle heading angle and its reference value, respectively. To determine the appropriate waypoints, a preview method in the previous research [32] is employed, which can violate the scene “take a shortcut” and contribute to the expected effects.

Fig. 1
figure 1

Path following schematic of autonomous vehicles

Full size image

The single-track vehicle model is applied to feature vehicle motions, as the schematic in Fig. 2:

$$\left\{\begin{array}{c}m{\dot{v}}_{y}={F}_{y\mathrm{f}}+{F}_{y\mathrm{r}}-m{v}_{x}\gamma \\ {I}_{z}\dot{\gamma }={l}_{\mathrm{a}}{F}_{y\mathrm{f}}-{l}_{\mathrm{b}}{F}_{y\mathrm{r}}+\Delta {M}_{z}\end{array}\right.$$
(2)

where \(m\) is the vehicle mass. \({l}_{\mathrm{a}}\) and \({l}_{\mathrm{b}}\) are the distances from front axle and rear axle to body center of gravity (CG), respectively. \({I}_{z}\) is the body yaw moment of inertia. \({F}_{y\mathrm{f}}\) and \({F}_{y\mathrm{r}}\) are the total lateral tire force of front and rear wheels, respectively, which can be represented by \(\left\{\begin{array}{c}{F}_{y\mathrm{f}}={F}_{y\mathrm{fl}}+{F}_{y\mathrm{fr}}\\ {F}_{y\mathrm{r}}={F}_{y\mathrm{rl}}+{F}_{y\mathrm{rr}}\end{array}\right.\). In this paper, the subscripts of “fl”, “fr”, “rl”, and “rr”, indicate that the corresponding variables are related to left front, right front, left rear, and right rear wheels, respectively. Unlike traditional powertrains, IWMs in DDEV can independently provide the traction torque at each wheel, so that the external yaw moment \(\Delta {M}_{z}\) is produced surrounding the vertical axle of vehicle CG to govern yaw motion, as shown in the second equation of Eq. (2).

Fig. 2
figure 2

Single-track vehicle model schematic

Full size image

The sideslip angles of front and rear tires, i.e., \({\alpha }_{\text{f}}\) and \({\alpha }_{\text{r}}\), are expressed:

$$\left\{\begin{array}{c}{\alpha }_{\mathrm{f}}=\delta -\left({v}_{y}+{l}_{\mathrm{a}}\gamma \right)/{v}_{x}\\ {\alpha }_{\mathrm{r}}=\left({l}_{\mathrm{b}}\gamma -{v}_{y}\right)/{v}_{x}\end{array}\right.$$
(3)

where \(\delta \) is the steering angle of the front wheels. To characterize the tire lateral forces, the Magic Formula model with similarity theory under pure-slip conditions [33] is employed:

$${F}_{y}={\psi }_{y}\left(\frac{{\mu }_{\mathrm{o}}}{\mu }{\alpha }_{\bullet },\mu ,{F}_{z\bullet }\right)={D}_{y}\mathrm{sin}\left\{{C}_{y}\mathrm{arctan}\left[{B}_{y}\frac{{\mu }_{\mathrm{o}}}{\mu }{\alpha }_{\bullet }-{E}_{y}\left({B}_{y}\frac{{\mu }_{\mathrm{o}}}{\mu }{\alpha }_{\bullet }-\mathrm{arctan}\left({B}_{y}\frac{{\mu }_{\mathrm{o}}}{\mu }{\alpha }_{\bullet }\right)\right)\right]\right\}$$
(4)

where \({F}_{z\bullet }\) is the vertical force of one wheel. \({B}_{y}\) is the stiffness factor, and \({D}_{y}\) is the peak factor. Here \({D}_{y}=\frac{\mu {F}_{z\bullet }}{{\mu }_{\mathrm{o}}}\), \({B}_{y}={C}_{yF\alpha }/\left({C}_{y}{D}_{y}\right)\), and \({C}_{y F {\alpha} }={B}_{y}{C}_{y}{D}_{y}={c}_{1} \mathrm{sin} \left(2 \mathrm{arctan} \left({F}_{z \bullet }/{c}_{2} \right) \right)\). \({C}_{y}\), \({E}_{y}\), \({c}_{1}\), and \({c}_{2}\) are the adjustment factors. \({\mu }_{\mathrm{o}}=1\) is the friction coefficient of tire measurement. By Eq. (4), the maximum \({\alpha }_{\bullet }\) of different tire-road frictions can be determined by \(\overline{{\alpha }_{\bullet }}=\frac{\mu }{{\mu }_{\mathrm{o}}}\overline{{\alpha }_{\mathrm{o}}}\), where \(\overline{{\alpha }_{\mathrm{o}}}\) is the maximum sideslip angle of tires under friction coefficient \({\mu }_\text{o}\). The symbols “\(\overline{\left(\right)}\)” and “\(\underline{\left(\right)}\)” indicate the allowable maximum and minimum for corresponding variables, respectively.

To sum up, the control-oriented model can be sorted as

$$\left\{ \begin{gathered} \dot{\user2{x}} = f\left( {{\varvec{x}},{\varvec{u}},d} \right) = \left[ {\begin{array}{*{20}c} {v_{y} + v_{x} \psi_{{\text{e}}} } \\ {\gamma - \dot{\psi }_{{\text{r}}} } \\ {\left( {F_{{y{\text{f}}}} + F_{{y{\text{r}}}} } \right)/m - v_{x} \gamma } \\ {\left( {l_{{\text{a}}} F_{{y{\text{f}}}} - l_{{\text{b}}} F_{{y{\text{r}}}} } \right)/I_{z} + \Delta M_{z} /I_{z} } \\ \end{array} } \right] \hfill \\ y = Cx \hfill \\ \end{gathered} \right.$$
(5)

where \({\varvec{x}}={\left[{y}_{\mathrm{e}},{\psi }_{\mathrm{e}},{v}_{y},\gamma \right]}^{\mathrm{T}}\) is the state variable, \({\varvec{u}}={\left[{F}_{y\mathrm{f}},\Delta {M}_{z}\right]}^{\mathrm{T}}\) is the control variable, and \(d={\dot{\psi }}_{\mathrm{r}}\) is the external disturbance. \({\varvec{y}}\) is the system output. \({\varvec{C}}\) is the output matrix and equals to \(\mathrm{diag}\left\{\left[1,1,0,0\right]\right\}\). In this paper, \({v}_{x}\) is fed back from the vehicle system.

Remark 1: Rather than \(\delta\) as the control variable for general models, \({F}_{y\mathrm{f}}\) is chosen, and \(\delta\) command can be acquired by the inversive tire model (as introduced in Sect. 5). In this manner, the high nonlinearity from couples between \({F}_{y\mathrm{f}}\) and \(\delta\) is wiped out, which lowers the model complexity and reduces the calculation loads in the controller.

Remark 2: Due to the study emphasis in this paper, the longitudinal motion is arranged as a constant velocity tracking issue. That is the velocity variant of each tire will not be greatly changed, resulting in a small tire slip rate. Hence, the Magic Formula model under pure-slip conditions can represent the tire lateral force with acceptable accuracy.

3 Control Framework

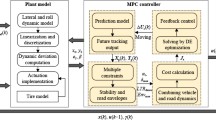
The control framework of the proposed strategy is illustrated in Fig. 3. It is assumed that there is a higher-level path planner that can generate the desirable path based on the road environment, and the path information is applicable. At each control instant, the path information, stable bounds of front tires’ lateral force, Lyapunov-based stability constraint, and feedback states, are provided to the NMPC controller. In the controller, the relaxation function is applied to transform the original problem into an unconstrained one for the inequality constraint handling. The optimization problem is solved by the C/GMRES algorithm in a computationally efficient way, which outputs the expected front tires’ lateral force and external yaw moment. With the target total front lateral force, the steering angle command is acquired by the inversive tire model and inputs into the vehicle plant. A torque allocation method based on Karush–Kuhn–Tucker (KKT) conditions is also employed to gain the expected IWMs’ torque commands, to minimize tire workload and satisfy virtual torques (i.e., total traction torque and external yaw moment). Here a proportional-integral controller is applied to output the total traction torque for longitudinal velocity tracking, which is widely used and verified to be effective [7].

Fig. 3
figure 3

Control framework schematic

Full size image

4 Real-time NMPC-based PF and DYC by C/GMRES Algorithm

4.1 Nonlinear Model Predictive Control Problem

The optimization objective is defined as

$$J={\int }_{0}^{{N}_{\mathrm{p}}-1}\left({{\varvec{y}}}^{\mathrm{T}}{\varvec{Q}}{\varvec{y}}+{{\varvec{u}}}^{\mathrm{T}}{\varvec{R}}{\varvec{u}}\right)\text{d}t$$
(6)

subject to Eqs. (14), (16), and (17), which are elaborated in Sect. 4.2. \({N}_{\mathrm{p}}\) is the predictive horizon length. \({\varvec{Q}}=\mathrm{diag}\left\{\left[{q}_{1},{q}_{2}\right]\right\}\) and \({\varvec{R}}=\mathrm{diag}\left\{\left[\frac{{r}_{1}}{{\mu }^{2}{{F}_{z\mathrm{f}}}^{2}},\frac{{r}_{2}}{{\overline{\Delta {M }_{z}}}^{2}}\right]\right\}\) are the weight matrixes of outputs and controls, respectively. For ease of weight parameters’ tuning, the quadratic cost item of \({\varvec{u}}\) in Eq. (6) is normalized via dividing \({r}_{1}\) and \({r}_{2}\) by \({\mu }^{2}{{F}_{z\mathrm{f}}}^{2}\) and \({\overline{\Delta {M }_{z}}}^{2}\), respectively. While for \({y}_{\mathrm{e}}\) and \({\psi }_{\mathrm{e}}\), the controller is considered to effectively track the target path, and the normalization is not imposed.

4.2 Constraints

4.2.1 Vehicle Stability Constraint of Front Tires’ Lateral Force

For vehicle stability, one popular parallelogram envelope is proposed by Stanford University’s laboratory [8, 34, 35]:

$$-\frac{\mu g}{{v}_{x}}=\underline{\gamma } \le \gamma \le \overline{\gamma }=\frac{\mu g}{{v}_{x}}$$
(7)
$${v}_{x}\mathrm{tan}\left(\frac{{l}_{\mathrm{b}}\gamma }{{v}_{x}}+\mathrm{tan}\underline{{\alpha }_{\mathrm{r}}}\right) \le {v}_{y} \le {v}_{x}\mathrm{tan}\left(\frac{{l}_{\mathrm{b}}\gamma }{{v}_{x}}+\mathrm{tan}\overline{{\alpha }_{\mathrm{r}}}\right)$$
(8)
$$\underline{{F}_{y\mathrm{f}}} \le {F}_{y\mathrm{f}} \le \overline{{F }_{y\mathrm{f}}}$$
(9)

where Eqs. (7), (8) and (9) are derived from the maximum lateral acceleration and maximum rear wheel sideslip angle, respectively. Equation (9) is to limit \({\alpha }_{\mathrm{f}}\) within a stable range since \({F}_{y\mathrm{f}}\) is positively related to \(\alpha_{{\text{f}}}\) when \(\underline{{\alpha_{{\text{f}}} }}\le {}\alpha_{{\text{f}}} \le{}\overline{{\alpha_{{\text{f}}} }}\). The envelope of Eqs. (7) to (9) can also be explained in the \({v}_{y}\)-\(\gamma\) phase plane portraits. The \({v}_{y}\)-\(\gamma\) phase plane profiles and the bounds of Eqs. (7) to (9) are shown in the upper subfigures of Fig. 4 (a) to (g). Here, the symbols of solid dark “○” and “◇”are stable and saddle points, respectively; the green solid and dotted lines are the maximum and minimum bounds regarding \(\underline{{\alpha }_{\text{f}}}\) and \(\overline{{\alpha }_{\text{f}}}\), respectively; the blue solid and dotted lines are the maximum and minimum bounds regarding \(\underline{{\alpha }_{\text{r}}}\) and \(\overline{{\alpha }_{\text{r}}}\), respectively; and the red solid and dotted lines are the maximum and minimum bounds for \(\gamma =\pm \mu g/{v}_{x}\), respectively. With the increasing \(\delta\), the stable points (i.e., the coordinate position \(\left[{{v}_{y}}^{*},{\gamma }^{*}\right]\)) move towards the minus \({v}_{y}\) direction. When \(\delta\) reaches 12 deg or -12 deg, the stable point disappears, and only a saddle point on one side of \(\gamma\)-axis exists. To determine the stability zones, the unstable portions are removed [8, 34, 35], as the regions outside blue lines by Eq. (8), red lines by Eq. (7), and green lines by Eq. (9). However, it should note that the maximum \(\gamma\) bounds in Eq. (7) are based on \({v}_{y}\approx 0\) since \(\left| {v_{x} \gamma + \dot{v}_{y} } \right| = \left| {a_{y} } \right|\le{}\mu g\). Hereinafter, we name the \(\gamma\) bounds of \(\overline{{\gamma }_\text{static}}=-\underline{{\gamma }_\text{static}}=\mu g/{v}_{x}\) as static bounds, and the \(\gamma\) bounds of \(\overline{{\gamma }_\text{dynamic}}=\left(\mu g-{\dot{v}}_{y}\right)/{v}_{x}\) and \(\underline{{\gamma }_\text{dynamic}}=-\left(\mu g+{\dot{v}}_{y}\right)/{v}_{x}\) dynamic bounds. Although the zero-sideslip angle is generally pursued in vehicle stability control, making \({\dot{v}}_{y}\approx 0\), it is not always beneficial for PF issues under extreme conditions. From Eq. (1), sometimes, the reasonably increasing/decreasing \({v}_{y}\) is good to simultaneously reduce \({y}_{\mathrm{e}}\) and \({\psi }_{\mathrm{e}}\), but bringing varying \({\dot{v}}_{y}\). This case is similar to that under drift cycles by professional race drivers when a relatively great \({v}_{y}\) is helpful for extreme turning. More intuitively, the bottom subfigures of Fig. 4a–g illustrate the phase plane trajectories of static and dynamic \(\gamma\) bounds, where the symbols of hollow “○” represent the convergence points for dynamic \(\gamma\) bounds. For constant \(\delta\), the dynamic \(\gamma\) bounds are varied with vehicle states and markedly different from static ones. Hence it is difficult to directly introduce the dynamic \(\gamma\) bounds into a stable region of vehicle by phase planes.

Fig. 4
figure 4figure 4

Phase plane profiles of vehicle lateral motion and dynamic maximum \({\varvec{\gamma}}\) under drive condition of \({{\varvec{v}}}_{{\varvec{x}}}\)=12 m/s and \({\varvec{\mu}}\)=0.85. red lines: static bounds of yaw rate; blue lines: bounds regarding absolute maximum sideslip angle of rear wheels; green lines: bounds regarding absolute maximum sideslip angle of front wheels; solid “○”: stable points of motion status; solid “◇”: saddle points of motion status; and hollow “○”: convergence points of dynamic yaw-rate bounds

Full size image

Herein, the stability bounds of front tires’ lateral force are proposed considering dynamic \(\gamma\) bounds, and the derivations are:

  1. (1)

    Figure 4 illustrates that with increasing/decreasing \(\delta\), the stable point moves towards the negative/positive saddle point, respectively, and the stable zones disappear after the overlapping of stable point and one saddle point. Under the critical situation to reserve self-stable zones, the bounds derived from \(\underline{{\alpha }_{\mathrm{f}}}\), \(\underline{{\alpha }_{\mathrm{r}}}\), and \(\underset{\_}{{\gamma }_{\mathrm{static}}}\), interact at the saddle point of positive \({v}_{y}\), and those derived from \(\overline{{\alpha }_{\mathrm{f}}}\), \(\overline{{\alpha }_{\mathrm{r}}}\), and \(\overline{{\gamma }_{\mathrm{static}}}\), are crossed over at the saddle point of minus \({v}_{y}\). Meanwhile, the lines of \(\overline{{\gamma }_{\mathrm{dynamic}}}\) and \(\underline{{\gamma }_{\mathrm{dynamic}}}\) are convergent to points of \(\left[{{v}_{y}}^{*},\overline{{\gamma }_{\mathrm{static}}}\right]\) and \(\left[{{v}_{y}}^{*},\underline{{\gamma }_{\mathrm{static}}}\right]\), respectively. This is because when \({v}_{y}={{v}_{y}}^{*}\), \({\dot{v}}_{y}=0\), and the maximum acceleration limits are \(\left| {v_{x} \gamma } \right| = \left| {a_{y} } \right| \le \mu g\) that is the static \(\gamma\) bounds. Therefore, the \(\overline{\delta }\) and \(\underline{\delta }\) for vehicle, stability can be gained by \(\overline{{\alpha }_{\mathrm{f}}}\), \(\overline{{\alpha }_{\mathrm{r}}}\), \(\overline{{\gamma }_{\mathrm{dynamic}}}\), and \(\underline{{\alpha }_{\mathrm{f}}}\), \(\underline{{\alpha }_{\mathrm{r}}}\),\(\underline{{\gamma }_{\mathrm{dynamic}}}\). Considering the angle relations for front and rear axles, there are

$$\left\{\begin{array}{c}\text{tan}\left(\overline{\delta }-\overline{{\alpha }_{\mathrm{f}}}\right)=\text{arctan}\left({v}_{y}/{v}_{x}\right)+{l}_{\mathrm{a}}\left(\mu g-{\dot{v}}_{y}\right)/{{v}_{x}}^{2}\\ \text{tan}\overline{{\alpha }_{\mathrm{r}}}={l}_{\mathrm{b}}\left(\mu g-{\dot{v}}_{y}\right)/{{v}_{x}}^{2}-\text{arctan}\left({v}_{y}/{v}_{x}\right)\end{array}\right.\Rightarrow \overline{\delta }=\mathrm{arctan}\left(\frac{\left({l}_{\mathrm{a}}+{l}_{\mathrm{b}}\right)\left(\mu g-{\dot{v}}_{y}\right)}{{{v}_{x}}^{2}}-\mathrm{tan}\overline{{\alpha }_{\mathrm{r}}}\right)+\overline{{\alpha }_{\mathrm{f}}}$$
(10)
$$\left\{\begin{array}{c}\text{tan}\left(\underline{\delta }-\underline{{\alpha }_{\mathrm{f}}}\right)=\text{arctan}\left({v}_{y}/{v}_{x}\right)-{l}_\text{a}\left(\mu g+{\dot{v}}_{y}\right)/{{v}_{x}}^{2}\\ \text{tan}\underline{{\alpha }_{\mathrm{r}}}=-{l}_{\mathrm{b}}\left(\mu g+{\dot{v}}_{y}\right)/{{v}_{x}}^{2}-\text{arctan}\left({v}_{y}/{v}_{x}\right)\end{array}\right.\Rightarrow \underline{\delta }=\mathrm{arctan}\left(-\frac{\left({l}_{\mathrm{a}}+{l}_{\mathrm{b}}\right)\left(\mu g+{\dot{v}}_{y}\right)}{{{v}_{x}}^{2}}-\mathrm{tan}\underline{{\alpha }_{\mathrm{r}}}\right)+\underline{{\alpha }_{\mathrm{f}}}$$
(11)

By introducing \({\dot{v}}_{y}\) in Eqs. (10) and (11), \(\overline{\delta }\) and \(\underline{\delta }\) can be adaptively adjusted by the vehicle states to improve the vehicle steering property for PF under extreme conditions. Moreover, Eqs. (10) and (11) are effective to stabilize vehicles since they are calculated for the limited steering of vehicle stability (see Fig. 4 (b), and (f)). If we adopt \(\overline{{\gamma }_{\mathrm{static}}}\) and \(\underline{{\gamma }_{\mathrm{static}}}\) to calculate \(\overline{\delta }\) and \(\underline{\delta }\),\({\dot{v}}_{y}=0\), and it is a special case of \({v}_{y}={{v}_{y}}^{*}\).

  1. (2)

    To reserve the benefits from \({F}_{y\mathrm{f}}\) control (see Remark 1), Eqs. (10) and (11) are changed to the bounds of \({\alpha }_\text{f}\):

$$\overline{{\alpha }_{\mathrm{fnew}}}=\overline{\delta }-\mathrm{arctan}\left(\mathrm{arctan}\left({v}_{y}/{v}_{x}\right)+{l}_{\mathrm{a}}\gamma /{v}_{x}\right)$$
(12)
$$\underline{{\alpha _{{{\text{fnew}}}} }} = \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\delta } - {\text{arctan}}\left( {{\text{arctan}}\left( {v_{y} /v_{x} } \right) + l_{{\text{a}}} \gamma /v_{x} } \right)$$
(13)

From Eq. (4), the stable bounds of \({F}_{y\mathrm{f}}\) can be gained:

$$\underline{{F_{{y{\text{fnew}}}} }} \le F_{{y{\text{f}}}} \le \overline{{F_{{y{\text{fnew}}}} }}$$
(14)
$$\overline{{F }_{y\mathrm{fnew}}}={\psi }_{y}\left(\overline{{\alpha }_{\mathrm{fnew}}},\mu ,{F}_{z\mathrm{f}}\right)$$
$$\underline{{F_{{y{\text{fnew}}}} }} = \psi _{y} \left( {\underline{{\alpha _{{{\text{fnew}}}} }} ,\mu ,F_{{z{\text{f}}}} } \right)$$
(15)

With limiting \({F}_{y\mathrm{f}}\) by Eq. (14), the vehicle stability and steering capacity can be guaranteed for extreme drive cases. Its effectiveness and benefits will be demonstrated in the following section of validations.

Remark 3: By the proposed bounds in Eq. (14), the constraint number is reduced from 3 to 1 to reduce the control complexity. Moreover, Eq. (14) is related to control input (i.e., the lateral force of front tires), rather than state constraints, which contributes to two advantages as follows. First, it can reduce computing burdens for some controllers, such as MPC. Second, the proposed bounds are applicable to stabilize vehicles for general state feedback controllers (such as proportional integral and SMC) with ease by adding a saturation process of control inputs. One should note that it is difficult to merge the state constraints into general state feedback controllers with superior performance. For example, the control barrier function is delegated for state constraints handling in Ref. [22], but entails small smoothness in controls.

4.2.2 External Yaw Moment Torques Constraint

The external yaw moment is limited considering the physical constraints of IWMs:

$$\underline{{\Delta M_{z} }} \le \Delta M_{z} \le \overline{{\Delta M_{z} }}$$
(16)

where \(\overline{\Delta {M }_{z}}=-\underline{\Delta {M}_{z}}=\frac{2{d}_{\mathrm{s}}{T}_{\mathrm{max}}}{{r}_{\mathrm{w}}}\). \({T}_{\mathrm{max}}\) is the IWMs’ torque limit, and \({d}_{\mathrm{s}}\) is the track width.

Remark 4: Benefited by \(\Delta {M}_{z}\), the system has more control DOFs to adjust vehicle motion in PF, which also influences the \({F}_{y\mathrm{f}}\) bounds in Eq. (14). For example, under an extreme drive case, \({F}_{y\mathrm{f}}\) and \(\Delta {M}_{z}\) contribute to change vehicle motion for expected PF, while moving away from the equivalent point of vehicle stability. The range of bounds in Eq. (14) will shrink according to the feedback states. Therefore, although the vehicle stability is considered in the control of \({F}_{y\mathrm{f}}\), \({F}_{y\mathrm{f}}\) and \(\Delta {M}_{z}\) can synergistically complete the PF and vehicle stabilization.

4.2.3 Closed-loop Stability Constraint

To make the closed-loop stability of PF control, the Lyapunov-based constraint is added:

$$\frac{{\partial V}}{{\partial \user2{x}}}f\left( {\user2{x}\left( 0 \right),\user2{u}\left( 0 \right),d\left( 0 \right)} \right) - \frac{{\partial V}}{{\partial \user2{x}}}f\left( {\user2{x}\left( 0 \right),\user2{u}_{{{\mathbf{aux}}}} \left( 0 \right),d\left( 0 \right)} \right) \le 0$$
(17)

where \({{\varvec{u}}}_{\mathbf{a}\mathbf{u}\mathbf{x}}\) is the auxiliary control law, and \(V\) is the corresponding Lyapunov function. The introduction of Eq. (17) allows the NMPC controller to inherit the stability properties of \({{\varvec{u}}}_{\mathbf{a}\mathbf{u}\mathbf{x}}\left(0\right)\), so as to analytically characterize a guaranteed region of attraction (ROA).

The process to gain \(V\) and \({{\varvec{u}}}_{\mathbf{a}\mathbf{u}\mathbf{x}}\) are shown: Define one Lyapunov function as \({V}_{1}=\frac{1}{2}{{y}_{\mathrm{e}}}^{2}+\frac{1}{2}{{\psi }_{\mathrm{e}}}^{2}\), and make \({\dot{y}}_{\mathrm{e}}=-{k}_{1}{y}_{\mathrm{e}}\), \({\dot{\psi }}_{\mathrm{e}}=-{k}_{2}{\psi }_{\mathrm{e}}\), where \({k}_{1}>0\) and \({k}_{2}>0\) are two specific gain constants. By Eq. (1), if the virtual controls are

$${v}_{y\mathrm{r}}={v}_{y}=-{k}_{1}{y}_{\mathrm{e}}-{v}_{x}{\psi }_{\mathrm{e}}$$
(18)
$${\gamma }_{\mathrm{r}}=\gamma =-{k}_{2}{\psi }_{\mathrm{e}}+{\dot{\psi }}_{\mathrm{r}}$$
(19)

it yields:

$${\dot{V}}_{1}=-{k}_{1}{{y}_{\mathrm{e}}}^{2}-{k}_{2}{{\psi }_{\mathrm{e}}}^{2} \le 0$$
(20)

However, the real values for \({v}_{y}\) and \(\gamma\) are not the same with the virtual controls \({v}_{y\mathrm{r}}\) and \({\gamma }_{\mathrm{r}}\), respectively. Thus, the second Lyapunov function is defined:

$${V}_{2}=\frac{1}{2}{\left({v}_{y}-{v}_{y\mathrm{r}}\right)}^{2}+\frac{1}{2}{\left(\gamma -{\gamma }_{\mathrm{r}}\right)}^{2}$$
(21)

Further set up

$${\dot{v}}_{y}-{\dot{v}}_{y\mathrm{r}}=-{k}_{3}\left({v}_{y}-{v}_{y\mathrm{r}}\right)$$
(22)
$$\dot{\gamma }-{\dot{\gamma }}_{\mathrm{r}}=-{k}_{4}\left(\gamma -{\gamma }_{\mathrm{r}}\right)$$
(23)

where \({k}_{3}>0\) and \({k}_{4}>0\) are two specific gain constants. Arranging Lyapunov function as \(V={V}_{1}+{V}_{2}\), there is

$$\dot{V}=-{k}_{1}{{y}_{\mathrm{e}}}^{2}-{k}_{2}{{\psi }_{\mathrm{e}}}^{2}-{k}_{3}{\left({v}_{y}-{v}_{y\mathrm{r}}\right)}^{2}-{k}_{4}{\left(\gamma -{\gamma }_{\mathrm{r}}\right)}^{2} \le 0$$
(24)

Setting \({{\varvec{u}}}_{\mathbf{a}\mathbf{u}\mathbf{x}}={\left[{F}_{y\mathrm{f}-\mathrm{aux}},\Delta {M}_{z-\mathrm{aux}}\right]}^{\mathrm{T}}\) and by Eqs. (5), (18), (19), (22), and (23), it has

$${F}_{y\mathrm{f}-\mathrm{aux}}=-m{k}_{1}{k}_{3}{y}_{\mathrm{e}}-m\left({k}_{1}+{k}_{3}\right){\dot{y}}_{\mathrm{e}}+m{v}_{x}{\dot{\psi }}_{\mathrm{r}}-{F}_{y\mathrm{r}}$$
(25)
$$\Delta {M}_{z-\mathrm{aux}}=-{I}_{z}{k}_{4}\gamma -{I}_{z}{k}_{4}{k}_{2}{\psi }_{\mathrm{e}}-{I}_{z}{k}_{2}{\dot{\psi }}_{\mathrm{e}}+{I}_{z}{k}_{4}{\dot{\psi }}_{\mathrm{r}}+{I}_{z}{\ddot{\psi }}_{\mathrm{r}}-{l}_{\mathrm{a}}{F}_{y\mathrm{f}-\mathrm{aux}}+{l}_{\mathrm{b}}{F}_{y\mathrm{r}}$$
(26)

The recursive feasibility and closed-loop stability for the established NMPC problem are analyzed:

Assumption 1: The desired path is smooth, and the corresponding target heading angle together with its derivatives is smooth and bounded, holding that \(0\le{}\left\| {\dot{\psi }_{{\text{r}}} } \right\|{}\le\overline{{p_{{{\text{r}}1}} }} < \infty\) and \(0 \le \left\| {\ddot{\psi }_{r} } \right\| \le \overline{{p_{{{\text{r}}2}} }} < \infty\).

Assumption 2: The command \({F}_{y\mathrm{f}}\) is close to the real value, and their difference is small and can be ignored [8].

Lemma 1: Given that the vehicle is controlled by auxiliary control law \({{\varvec{u}}}_{\mathbf{a}\mathbf{u}\mathbf{x}}\), lateral velocity \({v}_{y}\), yaw rate \(\gamma\), lateral position error rate \({\dot{y}}_{\mathrm{e}}\), and heading angle error rate \({\dot{\psi }}_{\mathrm{e}}\), are bounded with:

$${\Vert {v}_{y}\Vert }_{\infty } \le \left(1+{k}_{1}+{v}_{x}\right){\Vert {\varvec{\eta}}\left(0\right)\Vert }_{2}$$
(27)
$${\Vert \gamma \Vert }_{\infty }=\overline{{\chi }_{\gamma }} \le \left(1+{k}_{2}\right){\Vert {\varvec{\eta}}\left(0\right)\Vert }_{2}\le+\overline{{p }_{\mathrm{r}1}}$$
(28)
$${\Vert {\dot{y}}_{\mathrm{e}}\Vert }_{\infty }=\overline{{\chi }_{\mathrm{y}1}} \le \left(1+{k}_{1}+2{v}_{x}\right){\Vert {\varvec{\eta}}\left(0\right)\Vert }_{2}$$
(29)
$${\Vert {\dot{\psi }}_{\mathrm{e}}\Vert }_{\infty }=\overline{{\chi }_{\uppsi 1}} \le \left(1+{k}_{2}\right){\Vert {\varvec{\eta}}\left(0\right)\Vert }_{2}+2\overline{{p }_{\mathrm{r}1}}$$
(30)

where \({\varvec{\eta}}\left(t\right)={\left[{y}_{\mathrm{e}},{\psi }_{\mathrm{e}},{v}_{y}-{v}_{y\mathrm{r}},\gamma -{\gamma }_{\mathrm{r}}\right]}^\text{T}\).

Proof: See Appendix 1.

Theorem 1: Suppose Assumption 1 and Assumption 2 can hold. If the following conditions can be satisfied

$$\overline{{\chi _{{\text{F}}} }} + \left\| {\frac{{\overline{{F_{{y{\text{fnew}}}} }} + \underline{{F_{{y{\text{fnew}}}} }} }}{2}} \right\| \le \left\| {\frac{{\overline{{F_{{y{\text{fnew}}}} }} - \underline{{F_{{y{\text{fnew}}}} }} }}{2}} \right\|$$
(31)
$${I}_{z}{k}_{4}\overline{{\chi }_{\gamma }}+{I}_{z}{k}_{4}{k}_{2}{\Vert {\varvec{\eta}}\left(0\right)\Vert }_{2}+{I}_{z}{k}_{2}\overline{{\chi }_{\uppsi 1}}+{I}_{z}{k}_{4}\overline{{p }_{\mathrm{r}1}}+{I}_{z}\overline{{p }_{\mathrm{r}2}}+2{l}_{\mathrm{a}}\overline{{\chi }_{\mathrm{F}}} \le \overline{\Delta {M }_{z}}$$
(32)

with \(\overline{{\chi }_{\mathrm{F}}}=\frac{{l}_{\mathrm{a}}}{{l}_{\mathrm{a}}+{l}_{\mathrm{b}}}\left[m{k}_{3}{k}_{1}{\Vert {\varvec{\eta}}\left(0\right)\Vert }_{2}+\left(m{k}_{3}+m{k}_{1}\right)\overline{{\chi }_{\mathrm{y}1}}+m{v}_{x}\overline{{p }_{\mathrm{r}1}}\right]\), the NMPC problem admits recursive feasibility.

Proof: See Appendix 2.

Theorem 2: With Assumption 1, Assumption 2, and recursive feasibility of controller, the closed-loop system of NMPC (i.e., under Eqs. (25) and (26)) is asymptotically stable regarding PF equilibrium \(\left[{y}_{\mathrm{e}},{\psi }_{\mathrm{e}}\right]=\left[0,0\right]\).

Proof: See Appendix 3.

4.3 Constraint Handling Method and Problem Reformulation

The original C/GMRES algorithm cannot directly handle the inequality constraints, thus the relaxation function is applied [36]:

$$\xi \left(z\right)=\zeta \left(\frac{1}{1+{e}^{\vartheta \left(z-{z}_{\mathrm{min}}\right)}}+\frac{1}{1+{e}^{\vartheta \left({z}_{\mathrm{max}}-z\right)}}\right)$$
(33)

and the NMPC problem can be changed to an unconstrained one

$$J={\int }_{0}^{{N}_{\mathrm{p}}-1}Ldt={\int }_{0}^{{N}_{\mathrm{p}}-1}\left({{\varvec{y}}}^{\mathrm{T}}{\varvec{Q}}{\varvec{y}}+{{\varvec{u}}}^{\mathrm{T}}{\varvec{R}}{\varvec{u}}+\sum_{j=1}^{3}{\xi }_{j}\left(\cdot \right)\right)\text{d}t$$
(34)

where \({\xi }_{j}\) is the jth constraints, \(j=1,2,3\), corresponding to Eqs. (14), (16), and (17). \(z\) denotes the limited variable. \({z}_{\mathrm{max}}\) and \({z}_{\mathrm{min}}\) are the maximum and minimum for \(z\), respectively. \(\zeta\) is a penalty coefficient, and \(\vartheta\) is a positive variable that determines the varying rate of function value in Eq. (33). In Eq. (33), the shape of function value is influenced by \(\zeta\) and \(\vartheta\). That is for different \(z\), \({z}_{\mathrm{max}}\) and \({z}_{\mathrm{min}}\), the orders of magnitudes for \(\xi \left(z\right)\) may differ greatly, which will worsen the optimization effects. One method for handling this issue is to specially design two adjustment factors \(\zeta\) and \(\vartheta\) for each constraint, making similar orders of magnitudes among each \(\xi \left(z\right)\), but bringing the huge parameter calibration burdens. To this end, Eq. (33) is modified by normalization:

$$\xi \left(z\right)=\zeta \left(\frac{1}{1+{e}^{\vartheta \left(\widehat{z}-{\widehat{z}}_{\mathrm{min}}\right)}}+\frac{1}{1+{e}^{\vartheta \left({\widehat{z}}_{\mathrm{max}}-\widehat{z}\right)}}\right)$$
(35)

where \(\widehat{z}=\frac{2z-\left({z}_{\mathrm{max}}+{z}_{\mathrm{min}}\right)}{{z}_{\mathrm{max}}-{z}_{\mathrm{min}}}\), \({\widehat{z}}_{\mathrm{max}}=1\),\({\widehat{z}}_{\mathrm{min}}=-1\). Figure 5 shows an example of Eq. (35) for the allowable range of \(z\in\)[-4,10] and \(\zeta\)=10. When \(-1<\widehat{z}<1\), \(\xi \left(z\right)\) closes to zero. Instead, if \(\widehat{z}\) approaches to the bounds, \(\xi \left(z\right)\) smoothly enlarges and reaches \(\zeta\). Therefore, in the NMPC controller, when the optimized variable closes to bounds, the objective cost will increase, and the algorithm must find the best solution to minimize the objective cost, thus satisfying the constraints. To discuss the reasonable \(\vartheta\) range, Fig. 6 illustrates the \(\xi \left(z\right)\) profiles for \(\zeta\)=10 and different \(\vartheta\). Generally, it is expected to avoid interferences for optimization until the variables are close to bounds. Therefore, \(\vartheta \ge 10\) is considered a good choice.

Fig. 5
figure 5

Illustration of relaxation function after normalization

Full size image
Fig. 6
figure 6

Profiles of relaxation function cost in Eq. (35) by different \({\vartheta }\)

Full size image

4.4 C/GMRES Algorithm Application

According to Eqs. (5) and (34), the Hamiltonian function is written as \(H=L+{{\varvec{\lambda}}}^{\mathrm{T}}\dot{{\varvec{x}}}\), where \({\varvec{\lambda}}\) denotes the co-state vector. Based on the minimum principle [37], the necessary conditions to gain the optimal control sequences are expressed:

$$\left\{\begin{array}{c}{{\varvec{x}}}^{\boldsymbol{*}}\left(k+1\right)={{\varvec{x}}}^{\boldsymbol{*}}\left(k\right)+f\left({\varvec{x}}\left(k\right),{\varvec{u}}\left(k\right),d\left(k\right)\right)\Delta t\\ {{\varvec{x}}}^{\boldsymbol{*}}\left(0\right)={{\varvec{x}}}_{0}\\ {H}_{{\varvec{u}}}\left({{\varvec{x}}}^{\boldsymbol{*}}\left(k\right),{{\varvec{\lambda}}}^{\boldsymbol{*}}\left(k\right),{{\varvec{u}}}^{\boldsymbol{*}}\left(k\right)\right)=0\\ {{\varvec{\lambda}}}^{\boldsymbol{*}}\left(k\right)={{\varvec{\lambda}}}^{\boldsymbol{*}}\left(k+1\right)+{{H}_{{\varvec{x}}}}^\text{T}\left({{\varvec{x}}}^{\boldsymbol{*}}\left(k+1\right),{{\varvec{\lambda}}}^{\boldsymbol{*}}\left(k+1\right),{{\varvec{u}}}^{\boldsymbol{*}}\left(k+1\right)\right)\Delta t\\ {{\varvec{\lambda}}}^{\boldsymbol{*}}\left({N}_{\mathrm{p}}-1\right)=0\end{array}\right.$$
(36)

where \({H}_{{\varvec{x}}}\) and \({H}_{{\varvec{u}}}\) represent the partial derivative of \(H\) regarding \({\varvec{x}}\) and \({\varvec{u}}\), respectively. Here the optimized variables are defined as \({\varvec{U}}=\left[{\varvec{u}}\left(0\right),...,{\varvec{u}}\left(k\right),...,{\varvec{u}}\left({N}_{\mathrm{p}}-1\right)\right]\). By the Hamiltonian function and Eq. (36), the optimization problem can be rewritten as

$${\varvec{F}}\left({\varvec{U}},{\varvec{x}}\left(0\right)\right)=\left[\begin{array}{c}{H}_{{\varvec{u}}}\left({{\varvec{x}}}^{\boldsymbol{*}}\left(0\right),{{\varvec{\lambda}}}^{\boldsymbol{*}}\left(0\right),{{\varvec{u}}}^{\boldsymbol{*}}\left(0\right)\right)\\ \vdots \\ {H}_{{\varvec{u}}}\left({{\varvec{x}}}^{\boldsymbol{*}}\left({N}_{\mathrm{p}}-1\right),{{\varvec{\lambda}}}^{\boldsymbol{*}}\left({N}_{\mathrm{p}}-1\right),{{\varvec{u}}}^{\boldsymbol{*}}\left({N}_{\mathrm{p}}-1\right)\right)\end{array}\right]=0$$
(37)

The above root-finding problems can be solved by the iterative Newton method, but they suffer from the expensive computation in evaluating Jacobians, Hessian, and inverses [38]. To avoid these, the C/GMRES algorithm is proposed. Equation (37) can be approximated as a dynamic system \(\dot{{\varvec{F}}}\left({\varvec{U}},{\varvec{x}},t\right)={{\varvec{A}}}_{{\varvec{s}}}{\varvec{F}}\left({\varvec{U}},{\varvec{x}},t\right)\), where \({{\varvec{A}}}_{{\varvec{s}}}\) is a stable matrix to stabilize \({\varvec{F}}\) at the origin. Then, the forward difference approximation is used, i.e., \({{\varvec{F}}}_{{\varvec{U}}}\dot{{\varvec{U}}}=\left({{\varvec{A}}}_{{\varvec{s}}}{\varvec{F}}-{{\varvec{F}}}_{{\varvec{x}}}\dot{{\varvec{x}}}-{{\varvec{F}}}_{{\varvec{t}}}\right)\), where \({{\varvec{F}}}_{{\varvec{U}}}\), \({{\varvec{F}}}_{{\varvec{x}}}\), and \({{\varvec{F}}}_{t}\) represent the partial derivative of \({\varvec{F}}\) regarding \({\varvec{U}}\), \({\varvec{x}}\), and time \(t\), respectively. Given a small positive value \(\sigma\), there is.

$$D_{\sigma } {\varvec{F}}\left( {{\varvec{U}},{\varvec{x}} + \dot{\user2{x}}\sigma ,t + \sigma :\dot{\user2{U}},0,0} \right) = {\varvec{A}}_{{\mathbf{s}}} {\varvec{F}}\left( {{\varvec{U}},{\varvec{x}},t} \right) - D_{\sigma } {\varvec{F}}\left( {{\varvec{U}},{\varvec{x}},t:0,\dot{\user2{x}},1} \right).$$

Finally, the residuals can be defined as

$$\widetilde{{\varvec{r}}} = {{\varvec{A}}}_{\mathbf{s}}{\varvec{F}}\left({\varvec{U}},{\varvec{x}},t\right)-{D}_{\sigma }{\varvec{F}}\left({\varvec{U}},{\varvec{x}},t:0,\dot{{\varvec{x}}},1\right)-{D}_{\sigma }{\varvec{F}}\left({\varvec{U}},{\varvec{x}}+\dot{{\varvec{x}}}\sigma ,t+\sigma :\dot{{\varvec{U}}},0,0\right)$$
(38)

Minimizing the residuals between both sides of Eq. (37) is equivalent to minimizing the approximated one in Eq. (38). To do so, the forward approximation GMRES (FDGMRES) algorithm is applied for fast solving, i.e.,

$$\dot{\user2{U}}^{\user2{*}} = FDGMRES\left( {{\varvec{U}}_{0} ,\dot{\user2{U}}_{0} ,{\varvec{x}},\dot{\user2{x}},{\varvec{F}},e_{{{\text{tol}}}} ,k_{{{\text{max}}}} ,\sigma } \right),$$

where \({{\varvec{U}}}_{0}\) and \({\dot{{\varvec{U}}}}_{0}\) are the initial guesses with respect to \({\varvec{U}}\) and \(\dot{{\varvec{U}}}\), respectively. \({e}_{\begin{array}{c}\text{tol}\end{array}}\) is the allowable maximum error toleration, and \({k}_{\mathrm{max}}\) is the maximum iterative number. Considering the limited space, the descriptions of FDGMRES are not illustrated here. Interested readers can find more details in Refs. [29, 38,39,40]. For the first sample time in NMPC, the initial guesses \({{\varvec{U}}}_{0}\) and \({\dot{{\varvec{U}}}}_{0}\) are given, and the optimal control sequence increment \({\dot{{\varvec{U}}}}^{\boldsymbol{*}}\) is gained by the FDGMRES algorithm. For the given sample period \(\Delta t\), the optimal control sequence is calculated by \({{\varvec{U}}}^{\boldsymbol{*}}={{\varvec{U}}}_{0}+{\dot{{\varvec{U}}}}^{\boldsymbol{*}}\Delta t\). Herein, the “warm start-up” mechanism is applied for the expected convergence of optimization [41].

5 Inversive Tire Model Application and Torque Allocation

With the \({F}_{y\mathrm{f}}\) optimized by NMPC controller, the control command \(\delta\) can be determined according to Eq. (4):

$$\delta =\varPhi \left({F}_{y\mathrm{f}},\mu ,{F}_{z\mathrm{f}}\right)+\left({v}_{y}+{l}_{\mathrm{a}}\gamma \right)/{v}_{x}$$
(39)

where \(\varPhi \left(\cdot \right)\) is the affine function of \({F}_{y\mathrm{f}}\), \(\mu\), and \({F}_{z\mathrm{f}}\), and there is \({\alpha }_{\mathrm{f}}=\Phi \left({F}_{y\mathrm{f}},\mu ,{F}_{z\mathrm{f}}\right)\). In \(\phi \left(\cdot \right)\), the inversive calculations are applicable because: the unique \({\alpha }_{\mathrm{f}}\) exists by giving the certain \({F}_{y\mathrm{f}}\), \(\mu\), and \({F}_{z\mathrm{f}}\), as long as the front tires locate in the unsaturated region. By traversing all the possible \({\alpha }_{\mathrm{f}}\) candidates, the 3-D relationship \(\varPhi \left(\cdot \right)\) can be stored as the look-up tables for online applications. Here the selected ranges are \({F}_{y\mathrm{f}}\) of \(\left[-\mu {F}_{z\mathrm{f}}:5:\mu {F}_{z\mathrm{f}}\right]\), \(\mu\) of \(\left[0.2:0.05:1\right]\), and \({F}_{z\mathrm{f}}\) of \(\left[0:200:8000\right]\). When reaching the saturate \({F}_{y\mathrm{f}}\), \({\alpha }_{\mathrm{f}}\) in look-up tables are set as the maximum allowable one, i.e., \(\mu {F}_{z\mathrm{f}}\), to make the interpolations feasible and avoid the tire saturation of front tires. Figure 7 yields the illustration of \(\varPhi \left(\cdot \right)\) for cases of \({F}_{z\mathrm{f}}=8000\) N and \({F}_{z\mathrm{f}}=2400\) N. Given the constant \(\mu\) and \({F}_{z\mathrm{f}}\), \({\alpha }_{\mathrm{f}}\) monotonously increases with enlarging \({F}_{y\mathrm{f}}\). For smaller \({F}_{z\mathrm{f}}\) and/or \(\mu\), \({\alpha }_{\mathrm{f}}\) increases more sharply with the enlarging \({F}_{y\mathrm{f}}\).

Fig. 7
figure 7

A 3-D look-up table for affine function of \({\alpha }_\text{f}\)

Full size image

For torque allocation, the cost function of torque allocation is set up as

$${J}_{\mathrm{TA}}={{{\varvec{u}}}_{\mathbf{T}\mathbf{A}}}^{\mathrm{T}}{{\varvec{P}}}_{1}{{\varvec{u}}}_{\mathbf{T}\mathbf{A}}+{\left({\varvec{B}}{{\varvec{u}}}_{{\varvec{T}}{\varvec{A}}}-{\varvec{\nu}}\right)}^{\mathrm{T}}{{\varvec{P}}}_{2}\left({\varvec{B}}{{\varvec{u}}}_{\mathbf{T}\mathbf{A}}-{\varvec{\nu}}\right)$$
(40)

where \({{\varvec{u}}}_{\mathbf{T}\mathbf{A}}={\left[{T}_{\mathrm{fl}},{T}_{\mathrm{fr}},{T}_{\mathrm{rl}},{T}_{\mathrm{rr}}\right]}^\text{T}\) is the torque vector. \({{\varvec{P}}}_{1}=\mathrm{diag}\left(\left[\frac{1}{{{r}_{\mathrm{w}}}^{2}{\mu }^{2}{{F}_{z\mathrm{fl}}}^{2}},\frac{1}{{{r}_{\mathrm{w}}}^{2}{\mu }^{2}{{F}_{z\mathrm{fr}}}^{2}},\frac{1}{{{r}_{\mathrm{w}}}^{2}{\mu }^{2}{{F}_{z\mathrm{rl}}}^{2}},\frac{1}{{{r}_{\mathrm{w}}}^{2}{\mu }^{2}{{F}_{z\mathrm{rr}}}^{2}}\right]\right)\) is the weight matrix for tire workloads minimization. \({{\varvec{P}}}_{2}=\mathrm{diag}\left({p}_{{T}_{\mathrm{tot}}},{p}_{\Delta {M}_{z}}\right)\) is the weight vector for satisfying the virtual torques, where

$$\left\{\begin{aligned}\varvec{B} & =\left[\begin{array}{cccc}1& 1& 1& 1\\ -\frac{{d}_{\mathrm{s}}}{2{r}_{\mathrm{w}}}& \frac{{d}_{\mathrm{s}}}{2{r}_{\mathrm{w}}}& -\frac{{d}_{\mathrm{s}}}{2{r}_{\mathrm{w}}}& \frac{{d}_{\mathrm{s}}}{2{r}_{\mathrm{w}}}\end{array}\right]\\ \varvec\nu & ={\left[{T}_{\mathrm{tot}},\Delta {M}_{z}\right]}^\text{T}\end{aligned}\right.$$
(41)

where \({T}_{\mathrm{tot}}\) is the total traction torque. The constraints are arranged as,

$$\underline{{{\varvec{u}}}_{\mathbf{T}\mathbf{A}}} \le {{\varvec{u}}}_{\mathbf{T}\mathbf{A}} \le \overline{{{\varvec{u}} }_{\mathbf{T}\mathbf{A}}}$$
(42)
$$\overline{{{\varvec{u}} }_{\mathbf{T}\mathbf{A}}}=-\underline{{{\varvec{u}}}_{\mathbf{T}\mathbf{A}}}=\left[\begin{array}{c}\text{min}\left({T}_{\mathrm{max}},{r}_{\mathrm{w}}\sqrt{{\mu }^{2}{{F}_{z\mathrm{fl}}}^{2}-{{F}_{y\mathrm{fl}}}^{2}}\right)\\ \text{min}\left({T}_{\mathrm{max}},{r}_{\mathrm{w}}\sqrt{{\mu }^{2}{{F}_{z\mathrm{fr}}}^{2}-{{F}_{y\mathrm{fr}}}^{2}}\right)\\ \text{min}\left({T}_{\mathrm{max}},{r}_{\mathrm{w}}\sqrt{{\mu }^{2}{{F}_{z\mathrm{rl}}}^{2}-{{F}_{y\mathrm{rl}}}^{2}}\right)\\ \text{min}\left({T}_{\mathrm{max}},{r}_{\mathrm{w}}\sqrt{{\mu }^{2}{{F}_{z\mathrm{rr}}}^{2}-{{F}_{y\mathrm{rr}}}^{2}}\right)\end{array}\right]$$
(43)

which is imposed to meet the limits of motor torque and tire friction circle, simultaneously [42]. In this paper, a KKT conditions-based optimization method is applied for fast torque allocation, which is simple, globally optimal, and insensitive to initial solutions. Due to the limited space and study emphasis, please find more details in the previous research [43].

6 Validations and Analysis

The validations are carried out in CarSim and MATLAB/Simulink by a desktop computer with 16 GB of RAM and a Core i5 processor of 2.9 GHz. The vehicle parameters are \(m=1412\) kg, \({l}_{\mathrm{a}}=1.015\) m, \({l}_{\mathrm{b}}=1.895\) m, \({d}_{\mathrm{s}}=1.675\) m, \({r}_{\mathrm{w}}=0.308\) m, and \({I}_{z}=1536.7\) kg·m2. The controller parameters are \({q}_{1}\)=7 × 104, \({q}_{2}\)=6 × 102, \({r}_{1}\)=7 × 102, \({r}_{2}\)=2.4 × 102, \(\vartheta\)=25, \({\zeta }_{1}\)=0.8296, \({\zeta }_{2}\)=12.8, \({\zeta }_{3}\)=20, \(\Delta t\)=0.02 s, \({N}_{\mathrm{p}}\)=10, \({e}_{\begin{array}{c}\text{tol}\end{array}}\)=10–3, and \({k}_{1}\)=\({k}_{2}\)=\({k}_{3}\)=\({k}_{4}\)=10–3. Moreover, two methods are adopted for comparisons:

  1. (1)

    Linear quadratic regulator (LQR) method: LQR, derived from the optimal control theory, is a state feedback control method. Since nominal LQR cannot handle the inequality constraints, the saturation operations of control constraints Eqs. (9) and (16) are imposed. The state update function of Eq. (5) is applied, and the objective function is set as \({{\varvec{y}}}^{\mathbf{T}}{\varvec{Q}}{\varvec{y}}+{{\varvec{u}}}^{\mathbf{T}}{\varvec{R}}{\varvec{u}}\). Moreover, given that the nominal LQR can only apply to linear models, the cornering stiffness of rear tires is linearized. To adapt the influences of vertical tire forces and tire-road friction factor, the lateral force of rear tires is calculated by \({F}_{y\mathrm{r}}=2{C}_{y\mathrm{r}}\left(\mu ,\frac{{F}_{z\mathrm{rl}}+{F}_{z\mathrm{rr}}}{2}\right)\times {\alpha }_{\mathrm{r}}\), where \({C}_{y\mathrm{r}}\left(\cdot \right)\) is the mapping relationship about cornering stiffness of rear tires when \({\alpha }_{\mathrm{r}}=0\), as shown in Fig. 8. At each sampling moment, the LQR control gains are calculated online by solving Riccati equation according to the feedback states and the calculated \({F}_{y\mathrm{r}}\). Then, the controls of \({F}_{y\mathrm{f}}\) and \(\Delta {M}_{z}\) can be determined.

  2. (2)

    NMPC by SQP Algorithm (named as “SQP-NMPC”): The cost function is the same as the proposed strategy, i.e., Eq. (6), and the sequential quadratic programming (SQP) algorithm is used for rolling optimization. Unlike the proposed one, this method adopts the parallelogram envelope and limits of \({F}_{y\mathrm{f}}\) and \(\Delta {M}_{z}\) as constraints, namely Eqs. (7) to (9) and (16). Since the SQP algorithm can handle the inequality constraints, the relaxation function is not imposed.

Fig. 8
figure 8

Cornering stiffness of rear tires in LQR controller

Full size image

For fairness, in LQR and SQP-NMPC controllers, all the parameters are set the same as that of the proposed strategy, and the KKT conditions-based optimization method is employed for torque allocation.

6.1 Path Following Effects

The double lane change (DLC) and sinusoid cycles are applied, as shown in Fig. 9, and two extreme drive conditions are given: (1) target \({v}_{x}\)=100 km/h and \(\mu\)=0.8, and (2) target \({v}_{x}\)=80 km/h and \(\mu\)=0.4.

Fig. 9
figure 9

Test cycles in validations

Full size image

Figures 10 and 11 illustrate the PF results under the DLC cycle of target \({v}_{x}\)=100 km/h and \(\mu\)=0.8, and under a sinusoid cycle of target \({v}_{x}\)=80 km/h and \(\mu\)=0.4, respectively. The PF errors by the LQR method are greater than the other two methods, because LQR is essentially a linear controller that cannot optimize the system’s nonlinear dynamics in a rolling time horizon. From Figs. 10a and 11a, the proposed strategy can achieve a smaller magnitude of lateral error, compared with SQP-NMPC. Moreover, from the zoomed-in subfigures in Figs. 10 and 11, the proposed strategy yields a much faster and smoother convergence than the SQP-NMPC.

Fig. 10
figure 10

PF errors under DLC cycle of target \({{\varvec{v}}}_{{\varvec{x}}}\)=100 km/h and \(\mu\)=0.8

Full size image
Fig. 11
figure 11

PF errors under sinusoids cycle of target \({{\varvec{v}}}_{{\varvec{x}}}\)=80 km/h and \(\mu\)=0.4

Full size image

It is noteworthy that theoretically, although the approximations are carried out in the proposed C/GMRES algorithm, the control effects by the two MPC methods should be similar [29], which is inconsistent with the results in Figs. 10 and 11. Figure 12 illustrates the Lyapunov stability constraint profile of the proposed strategy, and all the values are below zero. That means the Lyapunov stability constraint is satisfied, and the ROA for the designed control law \({{\varvec{u}}}_{\mathbf{a}\mathbf{u}\mathbf{x}}\) is inherited in the proposed strategy. Given this, superior tracking performance is yielded by the proposed strategy. For example, combining Fig. 10a with Fig. 12a, for the position of global X 50, 80, 110, 140, and 170 m, the stability constraints in the proposed strategy contribute to restricting the Lyapunov function for improved PF convergence, leading to the differences between two MPCs’ control effects. Moreover, the relaxation function is verified to be effective in constraint handling in Fig. 12.

Fig. 12
figure 12

Lyapunov stability constraint by the proposed strategy

Full size image

More intuitively, Fig. 13 showcases the quantized results of PF errors for three methods. The mean square errors (MSE) regarding lateral errors and heading errors by the proposed strategy are much smaller than that of LQR, making up reductions of 68.22% and 90.31%, respectively. Roughly, compared with the SQP-NMPC method, the proposed strategy conducts similar MSEs in lateral errors and heading errors. In particular, under DLC cycles, the MSE of lateral errors by the proposed method is significantly smaller than SQP-NMPC’s, which reaches more than 30% performance improvements. This is because, with the higher cornering requirements of the DLC cycle than the sinusoids cycle, the restrictions of Lyapunov stability constraint in the proposed strategy are more intense, bringing more desirable tracking convergence to reduce PF errors.

Fig. 13
figure 13

MSE results of PF errors

Full size image

6.2 Vehicle Stability Effects

To verify the effectiveness of the proposed stable bounds, a test cycle, that is more extreme than above, is arranged here, i.e., the DLC cycle of target \({v}_{x}\)=120 km/h and \(\mu\)=0.8.

Figure 14 illustrates the PF results. The proposed strategy can effectively track the target path with smooth transient performance, while the SQP-NMPC approach exhibits greater errors in lateral position and heading angle.

Fig. 14
figure 14

PF errors

Full size image

Figures 15 and 16 demonstrate \({F}_{y\mathrm{f}}\) and vehicle state results by the proposed and SQP-NMPC strategies, respectively. For the proposed strategy in Fig. 15, \({F}_{y\mathrm{f}}\) is effectively restricted within the bounds, so \(\gamma\), \({\alpha }_{\mathrm{f}}\), \({\alpha }_{\mathrm{r}}\), and \({a}_{y}\) stay within the allowable range, indicating the vehicle stability. Moreover, since the lateral velocity differential \({\dot{v}}_{y}\) is introduced into \(\gamma\) bounds in the proposed strategy, the greater allowable range of \(\gamma\) is provided compared with the traditional one (i.e., \(\pm \mu g/{v}_{x}\)=\(\pm 0.2354\)) during steering, as the results of around 2, 2.7, 4, 4.5, and 5.5 s in Fig. 15 (b). Therefore, the vehicle steering capacity is improved, leading to the expected PF performance in Fig. 14. Additionally, from Fig. 15a, it is effective to apply the proposed relaxation function for constraint handling.

Fig. 15
figure 15

Vehicle state results by proposed strategy

Full size image
Fig. 16
figure 16

Vehicle state results by SQP-NMPC strategy

Full size image

With the constraints Eqs. (7) to (9), the vehicle steady drives by SQP-NMPC strategy, but \({F}_{y\mathrm{f}}\), \(\gamma\), and \({\alpha }_{\mathrm{f}}\) reach the boundaries several times. The vehicle steering capacity is limited, resulting in greater PF errors in Fig. 14. For example, at a moment of around 3 s, greater \(\gamma\) is expected to realize the more satisfactory PF effects. However, to guarantee vehicle stability, \({F}_{y\mathrm{f}}\) and \(\gamma\) are limited within their boundaries. Meanwhile, there exists no more control degree of freedom to reduce PF errors since \(\Delta {M}_{z}\) can only adjust vehicle yaw rate from Eq. (5). Hence, the PF errors cannot be eliminated well, as shown in Fig. 14. This explanation is also applicable for cases of other moments, e.g., at around 3, 5, and 5.7 s, as yielded in Fig. 16a, b. Finally, the PF errors by the SQP-NMPC method are accumulated and rise greater than that of the proposed strategy.

Figure 17 depicts the external yaw moment results. In Fig. 17a, the smaller magnitude of \(\Delta {M}_{z}\) is implemented by the proposed method. The SQP-NMPC controller repeatedly adjusts the external yaw moment with greater magnitude for expected PF. To illustrate, at around 5.7 s, \({F}_{y\mathrm{f}}\) reaches the bound, and \(\Delta {M}_{z}\) increase to stay \(\gamma\) within the allowable range, as shown in Fig. 16a, b. Even so, due to its adopted static yaw rate constraints limiting steering capacity, the PF errors are hard to be eliminated, as shown in Fig. 14a.

Fig. 17
figure 17

External yaw moment \(\Delta {M}_{\varvec{z}}\)

Full size image

Figure 18 yields the phase plane portrait under a parallelogram envelope. The phase trajectories by the proposed strategy are outside the parallelogram envelope; however, the vehicle is stable according to the results in Fig. 15. This is because the parallelogram envelope is developed on the basis of \({v}_{y}=0\) and only considers the static yaw rate bounds \(\mu g/{v}_{x}\). The maximum allowable \(\gamma\) for vehicle stability is derived from \(\left|{v}_{x}\gamma +{\dot{v}}_{y}\right|=\left|{a}_{y}\right| \le \mu g\), that is possibly greater than \(\mu g/{v}_{x}\), as discussed in Sect. 4.2.1.

Fig. 18
figure 18

Phase plane portrait with parallelogram envelope

Full size image

To sum up, it can be concluded that the proposed strategy and stable bounds are beneficial for satisfactory performance in PF and vehicle stability under extreme drive conditions.

6.3 Calculation Time

Figure 19 shows the results of calculation time and iterations by the proposed and SQP-NMPC strategies. Under three drive cycles, the calculation time by the proposed strategy is limited to below 0.01 s and much smaller than the sample time of 0.02 s, testifying the real-time applicability.

Fig. 19
figure 19

Calculation time and iterations for proposed and SQP-NMPC strategies

Full size image

In contrast, the maximum calculation time by the SQP algorithm is distinctly higher than that by the C/GMRES algorithm. Under the DLC cycle of \({v}_{x}\)=120 km/h and \(\mu\)=0.8, the SQP-NMPC strategy repeatedly adjusts the controls to satisfy the static yaw rate limits (see Fig. 16b), leading to the increased iterations and calculation time to meet the error toleration value of 10–3. This is why its calculation time per sample reaches up to around 0.3 s in Fig. 19c.

7 Conclusions

A real-time NMPC-based strategy is proposed for path following (PF) and vehicle stability under extreme steering conditions. By \({v}_{y}\)-\(\gamma\) phase plane analysis, the novel lateral force bounds of front tires are developed and adopted in the NMPC controller, which can define the stable zone of vehicles and will not limit the steering capacity under extreme conditions. Additionally, the Lyapunov-based constraint is developed to guarantee the closed-loop system stability, and its recursive feasibility is proved. The NMPC problem is established with the objective of the minimum PF errors, and the constraints are arranged by the proposed stable bounds of \({F}_{y\mathrm{f}}\), \(\Delta {M}_{z}\) bounds, and the Lyapunov stability constraint. For fast optimization, the C/GMRES algorithm is proposed, and the relaxation function is adopted to handle the constraints. After NMPC optimization, the target lateral force of front tires and external yaw moment is acquired. The target lateral force of front tires is transformed to be the steering angle command by the inverse tire model. Moreover, according to the total traction torque and external yaw moment, the KKT conditions-based allocation method is employed to gain the IWMs’ torque commands. The proposed strategy is validated and compared with LQR and SQP-NMPC methods, which implement superior performance and real-time applicability in PF and vehicle stability. Moreover, the developed stable bounds are verified to be effective in guaranteeing stability and improving steering capacity under extreme drive conditions. The conclusions are summed up:

  1. (1)

    By the proposed strategy, the PF performance is greatly superior to that of the LQR controller. Owing to the developed Lyapunov stability constraint, the proposed strategy demonstrates much faster and smoother convergence than the SQP-NMPC in PF.

  2. (2)

    Compared with the parallelogram envelop [8], the proposed stable bounds of lateral forces can realize vehicle stability while improving the steering capacity. Owing to the consideration of lateral velocity differential, the proposed stable bounds can effectively relieve the conflicts between the PF and vehicle stability for extreme drive conditions, benefiting from superior PF effects.

  3. (3)

    The computing time of below 0.01 s per sample is conducted by the proposed C/GMRES algorithm, much smaller than the set sample time of 0.02 s. Instead, by the SQP algorithm, the optimization per sample is completed by up to around 0.3 s, which is hard to be applied in real-time.

The future works are the experimental validations of real-world vehicles and the improvements of the strategy’s transient performance as well as robustness.