1 Introduction

Electromobility is becoming increasingly important in terms of reducing CO\(_2\) emissions. Therefore, the mobility sector is undergoing the most profound transformation in recent decades. Political and legal requirements in the main sales markets demand a significant reduction in CO\(_2\) fleet emissions. Competitive pressure and diversification of the growing market are increasing enormously. For example, the global electric car sales rose by around \(140\,\%\) compared to the same period in 2020 [1] and existing policies around the world suggest a growth in the future. The Stated Policies Scenario predicts that the electric vehicle (EV) stock across all modes (except two / three-wheelers) reaches 145 million in 2030, accounting for \(7\,\%\) of the road vehicle fleet [1].

The efficiency of the powertrain has an immense leverage effect in terms of range increase and competitiveness. Efficiency-optimized powertrains enable an increase in vehicle range or a reduction in costs by limiting the required capacity of the traction battery and the other system components since electric axle drives are used not only in battery electric vehicles (BEVs) but also in P4 hybrid vehicles and fuel cell electric vehicles (FCEVs) and can thus be developed with an open perspective [2, 3]. The transmission in electric axle drives plays a key role here because, in contrast to internal combustion engine powertrains, a significantly higher proportion of the total losses occur in the transmission. The bidirectional speed-torque conversion during recuperation also doubles the efficiency improvements.

Most of the concepts available on the market are currently single-speed transmissions (SST) [4, 5]. The transmission ratio of electric axle drives with a single reduction gear represents a compromise between the conflicting goals of maximum traction torque through a high transmission ratio and maximum vehicle speed through the application of a low transmission ratio [2]. However, multi-speed concepts enable a significant increase in the development parameters of efficiency, performance, and gradeability [6, 7]. More advantages of electric drive systems with two-speed transmissions (TST) are: the higher maximum vehicle speed and increased traction torque of the vehicle, which is particularly beneficial for performance, sport utility vehicle (SUV), and commercial vehicle applications [8, 9], the increased overall powertrain efficiency compared to single-speed drivetrains, cost advantages for electric machines (EM), and pulse inverters by reducing the number of pole pairs of the EM and limiting the phase currents of the pulse inverter [2, 3]. However, the additional shifting elements, especially the oil-cooled multi-plate clutches, can offset the efficiency advantages. What is needed here is a detailed and fast simulation of the individual transmission losses and efficiencies of multi-speed transmissions, which takes into account limitations about the use of common parts and installation space restrictions and does not represent a purely theoretical consideration.

The characteristics of single-speed or two-speed gearboxes have already been investigated in several publications [10,11,12,13]. In most cases, a single-speed transmission was simulated and compared with a two-speed transmission. The EM was not varied. In Ref. [13, 14] a BEV with a permanent-magnet synchronous motor (PMSM) was investigated. The two-speed transmission is a dual-clutch transmission (DCT). No statement was made about the consideration of the transmission losses. The BEV with two-speed transmission showed a consumption advantage of \(6\,\%\) in the New European Driving Cycle (NEDC). Laitinen et al. [11] also examined a BEV with a PMSM. A constant efficiency was assumed for the analysis of transmission losses. As a result, a consumption advantage of 3.1%~5.8% between the two-speed transmission and the single-speed transmission is described in this paper. In Ref. [12], a BEV with PMSM is studied in the US drive cycles like the Federal Test Procedure (FTP75) and the Highway Fuel Economy Driving Schedule (HWFET). Again, a constant efficiency was assumed for the transmission. Here, the BEV with two-speed transmission had a consumption advantage of 3%–6% . Lacerte et al. [10] investigated a BEV with PMSM and two-speed transmission with dog-clutch / Eddy Current Torque Bypass Clutch. Here, the overall transmission losses were not investigated. The focus was only on the consideration of the shifting element losses. In the investigated driving cycles like the US06, SC03, and FTP75, the energy consumption can be improved by \(7.2 \,\%\) with the two-speed transmission. As in the publications described, it can be seen that transmission losses have not been considered in detail here. In some cases, no information was given or a constant efficiency was assumed. In this context, the transmission in electric vehicles has a major influence on the overall consumption of the vehicle. It is therefore important to examine the transmission losses in detail to show the differences between the single-speed transmission and the two-speed transmission.

This study aims to fill this gap in research by presenting a simulation model for detailed modeling of transmission losses and integrating the loss maps into whole vehicle models. This study evaluates different transmission concepts with transmission lossmaps created by a lossmap-based simulation model. Two different two-speed transmissions are examined and compared to a single-speed transmission as a reference. To evaluate the different transmission concepts, the transmission losses are compared in the WLTC. The driving cycle is calculated via a reverse simulation representing the optimal operation of the vehicle. And the transmission concepts are calculated via a forward simulation, which more accurately represents the real operation of the vehicle. Therefore, the transmission concepts are not only examined regarding the total power loss in the driving cycles but also regarding their loss component distribution. Based on the transmission losses occurring in the driving cycles, the concepts and simulation models are compared and evaluated.

In Sect. 2, the transmission loss calculation is described and the loss map generation is demonstrated in more detail. In Sect. 3, the two overall vehicle models are presented and the differences are discussed. In Sect. 4, the transmission concepts investigated are presented and the transmission ratio values are determined. In Sect. 5, the vehicle parameters and performance requirements are described. Finally, in Sect. 6 and 7 the results are discussed and the evaluation is presented.

2 Lossmap-Based Simulation Model

In this section, the transmission losses are simulated via the lossmap-based simulation model for the different transmission concepts, and then automatically integrated into the two different overall vehicle simulations.

2.1 Transmission Losses

The main transmission losses in a vehicle include gear losses (\(P_{\mathrm {VZ}}\)), bearing losses (\(P_{\mathrm {VL}}\)) and seal losses (\(P_{\mathrm {VD}}\)), as well as other losses (\(P_{\mathrm {VX}}\)). Other losses include, for example, losses of shifting elements [15, 16]. The losses described can also be divided into load-dependent and load-independent losses [15, 16]:

  • gearing losses \(P_{\mathrm {VZ}}\)

    • Frictional losses, load-dependent, \(P_{\mathrm {VZP}}\)

    • Hydraulic losses, load-independent, \(P_{\mathrm {VZ0}}\)

  • bearing losses \(P_{\mathrm {VL}}\)

    • friction losses, load-dependent, \(P_{\mathrm {VLP}}\)

    • lubrication losses, load-independent, \(P_{\mathrm {VL0}}\)

  • sealing losses \(P_{\mathrm {VD}}\)

    • Frictional losses due to radial shaft seals at the shaft endings and due to piston rings for sealing of pressure oil at shifting elements, load-independent, \(P_{\mathrm {VD}}\)

  • losses of other components and aggregates \(P_{\mathrm {VX}}\)

    • lubrication losses, load-independent, \(P_{\mathrm {VX0}}\)

The gear losses and bearing losses are composed of a load-dependent part (\(P_{\mathrm {VZP}}\) and \(P_{\mathrm {VLP}}\)) and a speed-dependent part (\(P_{\mathrm {VZ0}}\) and \(P_{\mathrm {VL0}}\)). The load-dependent losses are caused by static or fluid friction, and the load-independent losses belong to the hydraulic losses that occur in seals or switching elements. The other losses are counted among the load-independent losses [15, 16].

The lossmap-based simulation model is established based on calculation approaches for the individual transmission components. The underlying calculation approaches have been partially modified and validated in research activities at the Institute of Automotive Engineering (IAE) via component and overall transmission measurements on test rigs. For more detailed information on these research activities, please check the following publications [17,18,19,20,21,22].

2.2 Generating the Transmission Lossmap

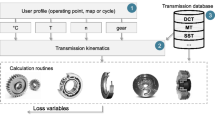
The lossmap-based simulation model from Ref. [18] is used to simulate the transmission losses from Sect. 2.1 for transmission concepts in the early development stage. At this stage, detailed information about the transmission concepts is not available yet. From the gear synthesis, the mathematical description of the concepts is given. In addition, the gear ratios, as well as mechanical connections and shift elements, are known. With this information, the map-based simulation model creates the lossmaps of the transmission concepts. Using the speeds and torques at the wheel, the speeds and torques of all components can be determined via the modular simulation model. These are stored in the operating point matrix, which is shown in Fig. 1 on the top left-hand side.

Fig. 1
figure 1

Generating the transmission lossmap

Full size image

In the second step, the simplified gear kinematics are then set up via the mathematical description of the transmission concepts and all variables for the loss analysis are determined. For the various loss components such as bearings, gear sets, and seals, maps of different sizes are stored, which are usually used in vehicle transmissions.

Cylindrical roller bearings, deep groove ball bearings, tapered roller bearings as well as radial and axial needle roller bearings are considered. The deep groove ball bearings on the driveshaft are sealed deep groove ball bearings. The mean diameters of the bearings are between 40 and \(70\, \mathrm {mm}\) and the outside diameters range from 50 to \(90\, \mathrm {mm}\). Rotary shaft seals are used as sealing elements. These are stored for inside diameters from 30 to \(60\, \mathrm {mm}\). Dry and wet multi-plate clutches with diameters from 100 to \(200\, \mathrm {mm}\) are integrated to consider losses due to switching elements. The gear losses are modeled using a uniform wheelset. Bearings and seals are automatically selected for the different shafts. In this way, it can be taken into account that the output shaft has larger bearings than the input shaft, for example, due to greater loads. For the different loss components, characteristic diagrams are simulated and stored as a function of influencing variables, so that losses can be interpolated accordingly.

The losses are then interpolated from maps using information about the operating point and information about installed transmission elements such as bearings and seals. The interpolated component losses are then stored in the overall lossmap. Since in an electric vehicle the operating points of the electric machine in the reverse simulation depend only on wheel speed and torque, this results in a two-dimensional operating point matrix and a two-dimensional lossmap. The lossmap-based simulation model is verified via the detailed simulation model [18]. Here, it is shown that the map-based simulation model provides a good approximation to simulate transmission concepts in the early development stage.

2.3 Integration into the Operating Strategy

The total lossmap now contains total losses and individual component losses for each operating point and gear. In order to optimize the modular simulation model, the total lossmap can now be integrated into the transmission model from Fig. 3 in the next step. In Fig. 2, the drivetrain of an electric vehicle is shown schematically.

Fig. 2
figure 2

Integration of the lossmap into the operating strategy of the vehicle simulation models

Full size image

By incorporating the transmission losses, the operating strategy can now determine the respective operating points more precisely. Thus, the accuracy of the efficiency analysis can be optimized within the modular simulation model. As a result, the transmission losses can then be evaluated over the particular cycle, for example, the WLTC, which is shown in Fig. 2. The different transmission concepts can therefore be examined and compared in much greater detail.

3 Vehicle Simulation Models

In this section, the employed simulation programs are presented. The overall vehicle models are the modular simulation model (MSM), which is a backward simulation, and a 3D simulation model, which is structured as a forward simulation.

3.1 Modular Simulation Model (MSM)

To evaluate conventional, hybrid, or electric powertrains in terms of their optimal efficiency and performance, the modular simulation model [23] is used at the Institute of Automotive Engineering (IAE). The model is designed as a backward simulation and can be used to evaluate the powertrain synthesis or transmission synthesis [24] also available at the IAE. In Fig. 3, the modular simulation model is shown schematically.

Fig. 3
figure 3

Modular simulation model [23]

Full size image

In the vehicle module on the right side, the vehicle parameters, as well as the driving cycles, are defined. Using information from the vehicle module, driving resistances can be calculated for the defined vehicle and driving cycle, which then provides speed and torque at the wheel. Since this is a backward simulation, wheel speed and torque at the wheel are input parameters to the transmission model. The transmission concepts are described mathematically. This includes information about the mechanical connection of the individual elements and information about shifting elements and operating modes. The lossmaps previously calculated using the lossmap-based simulation model in Sect. 2.2 are integrated into the transmission model, which allows transmission efficiency to be represented accurately. Hybrid transmission concepts with up to nine electric machines can be integrated into the transmission model. All transmission speeds and torques can be calculated via mathematical connections. The input speed and torque of the transmission are then used as input variables in the launch element model due to the backward simulation. Various shifting elements are integrated into the launch element model. In this way, clutches, torque converters, and direct connections can be modeled. The speeds and torques of the starting element model are also output variables of the propulsion model. Conventional and hybrid drive concepts, as well as purely electric drive concepts, can be simulated. The efficiency of the drive unit is represented by characteristic diagrams that are integrated into the simulation. These can be measured or simulated maps. For different electric machines, the lossmaps can be scaled according to the power.

3.2 Equivalent Consumption Minimization Strategy (ECMS)

To compare the concepts on a theoretical level, optimal operating points are calculated. The determination of optimal operating points in the corresponding driving cycle is used via the equivalent consumption minimization strategy (ECMS) as a modular solution for comparing individual concepts. Here, the ECMS is similar to the operating strategy described in Refs. [25, 26], and [27]. In the ECMS, petrochemical energy \(E_{\mathrm {Tank}}\) is compared to electrochemical energy \(E_{\mathrm {Battery}}\) to minimize equivalent fuel consumption \(E_{\mathrm {Equivalent}}\). To compare petrochemical energy to electrochemical energy, the petrochemical energy is multiplied by an equivalence factor \(k_{\mathrm {E1}}\). This ensures balanced energy consumption. The state of charge (SOC) is thereby maintained at neutral operation for the defined vehicle. To ensure that a reliable SOC is achieved, the cycle is iterated several times, and the SOC is included in the weighting each time with the equivalence factor \(k_{\mathrm {E2}}\). The equivalent energy is thereby calculated using the following equation [23]:

$$\begin{aligned} E_{\mathrm {Equivalent}} = E_{\mathrm {Tank}}+(k_{\mathrm {E1}}+k_{\mathrm {E2}} \cdot \varDelta \, \mathrm{SOC}) \cdot E_{\mathrm {Battery}} \end{aligned}$$
(1)

Several criteria have been added to the ECMS to ensure good drivability. For example, a certain duration is defined for which a gear must be held. In addition, a certain shift strategy is integrated. This applies equally to all two-speed transmissions; thus, a more realistic gear selection is simulated.

3.3 3D Simulation Model (3D SM)

The 3D simulation model is a forward simulation model and is based on the model presented in Ref. [28]. At first, the structure of this particular model is described and then the adaptions made in this paper are presented afterward.

In general, the 3D simulation model in Ref. [28] is based on an already established 3D simulation model by Küçükay used to calculate fuel consumption and component behavior close to reality [29]. It consists of three parts interacting with each other: Driver, Driving environment and Driven vehicle along with all drivetrain components. This model has been further developed for various applications at the IAE. In Ref. [28], it was further developed to simulate a variety of hybrid electric vehicles realized by a modular simulation structure. This allows to not only simulate conventional vehicles but also hybrid vehicles with various drivetrain topologies and different voltage levels.

Based on the driving environment which can be represented by legal cycles or realistic cycles based on customer data, the driving resistances are simulated which need to be overcome to operate the vehicle. For legal cycles, the driver is realized by two controllers, one each for the accelerator and brake pedal. For real driving customer data, the driver behavior is implemented by statistics generated by customer data, e.g., statistics for accelerator and brake pedal end positions and gradients. These statistics highly depend on the driving style of the driver which can be sporty, average, or mild. The driver interacts in different ways with the vehicle based on these three driving styles. The last part is the driven vehicle. A resulting traction force necessary to overcome the driving resistances calculated by the driving environment is transformed into speeds and torques of the drivetrain components at current vehicle speed. The drivetrain components are modeled by their physical behavior in combination with maps that model specific behavior. The electric machine with its corresponding power electronics can generate power at various positions of the drivetrain regarding the desired drivetrain topology. For hybrid electric vehicles, an operating strategy is implemented to decide on power distribution between the electric machine and combustion engine. The power split is based on rules considering best energy efficiency and drivability.

This paper aims at an electric vehicle. Thus, the above described 3D simulation model is adapted. This is realized by deactivating the combustion engine so that the operating strategy powers the vehicle by the electric machine only. Due to the modular structure of the 3D simulation model, all other dependencies, such as inertias at various component positions as well as component behavior, are adapted to the deactivation of the combustion engine automatically. The resulting structure of the 3D simulation model is shown in Fig. 4.

Fig. 4
figure 4

3D simulation model

Full size image

Figure 4 shows the driver, driving environment, and driven vehicle. The last one consists of several modules: the electric machine as the energy converter with power electronics (PE) and battery, gearbox, wheels, and resulting vehicle states. The 3D simulation model by Küçükay et al. [29] has been verified for several applications. In Ref. [30], a simulated P2 high voltage hybrid electric vehicle showed high accordance to test bench data. In Ref. [31], a specific electric vehicle was verified by vehicle measurement data. The 3D simulation model in Ref. [28] was applied in a simulation of a conventional vehicle equipped with a manual gearbox and an electrified clutch in the WLTC. It showed a nearly identical simulated fuel consumption compared to measurements of this particular conventional vehicle on the test bench. Due to these verifications, the 3D simulation model in this paper is assumed as robust and reliable regarding simulated energy consumption and components behavior.

3.4 Differences Between the Simulation Models

The two simulation models used here are fundamentally different in structure. The modular simulation model is built as a backward simulation and the 3D simulation model as a forward simulation. The backward simulation is based on the cycle profile (speed and time). In contrast, a driver model is implemented in the forward simulation. Through the driver model, legal cycles, but also realistic driving behavior of a customer can be simulated. Customer cycles generated based on the 3D method of the IAE can be integrated into the modular simulation model [29, 32].

The aggregate modeling in the 3D simulation model and their loss approaches are more detailed than in the modular simulation model. For example, the resulting speeds and torques are simulated in the 3D simulation model in individual submodels, in which the driver’s load requirement, deceleration elements, and inertia influences are taken into account. In combination with integrated maps for the aggregates, this makes the simulation more realistic. In the modular simulation model, the speed and torque of the electric machine are determined without inertial influence via the backward calculation.

The characteristic diagrams from the lossmap simulation are integrated into both simulation programs to consider transmission losses. As already described, the transmission losses are calculated using detailed loss approaches. The gear kinematics is described mathematically so that all loss components are taken into account. As a result, the transmission losses are very well represented in both simulations.

In the modular simulation model, no temperature behavior is taken into account, but a constant temperature is calculated for the operating temperature state. In comparison, thermal models are integrated into the 3D simulation model, which means that the derating of the electric machine can be considered, for example. Furthermore, the braking behavior or the braking system is mapped differently. In the 3D simulation model, brake distribution and recuperation are modeled in more detail by taking into account realistic component behavior in combination with lossmaps.

Another difference is in the determination of operating points. In the modular simulation model, a consumption-optimal approach (ECMS) is integrated, as described in Sect. 3.1. In comparison, a realistic rule-based operating strategy is implemented in the 3D simulation model. Thus, different conclusions can be drawn from the simulation results.

The legal cycles or customer cycles are simulated in the simulation models with a different calculation frequency. In the modular simulation model, calculations are performed at a frequency of \(1\,\mathrm {Hz}\) and in the 3D simulation model at a frequency of \(1000\,\mathrm {Hz}\). This allows dynamic processes in the overall vehicle simulation to be simulated in much greater detail and more realistically.

However, the simulation of the 3D simulation model is more complex, including the parameterization and the simulation time. The modular simulation model is significantly faster in the parameterization and the simulation time since different simulations can also be parallelized and thus the entire computing capacity can be used best. In summary, both models have their advantages and disadvantages and can be used depending on their merits.

4 Transmission Concepts

For this paper, three different transmission concepts are evaluated. Two different two-speed transmissions are compared with a single-speed transmission of the IAE. All concepts use an identical electric machine. The EM has a peak power of \(148 \, \mathrm {kW}\) and a maximum torque of \(300 \, \mathrm {Nm}\). The transmission concepts are designed in such a way that they have a similar package space and the two-speed transmission could be integrated into the same vehicle instead of the single-speed transmission without major package constraints. The first concept is the single-speed transmission. As shown in Fig. 5, the concept is a two-stage transmission. The input shaft is supported by two deep groove ball bearings. The intermediate shaft is supported via a fixed/free bearing by a deep groove ball bearing and a cylindrical roller bearing. The axle is supported by tapered roller bearings. To seal the gear unit, the input shaft is sealed with a rotary shaft seal. The output shaft is sealed by two rotary shaft seals. The single-speed transmission is used in this configuration in the majority of current electric vehicles.

Fig. 5
figure 5

Single-speed transmission (C1 SST)

Full size image

The second transmission concept is also a two-stage transmission, which is shown in Fig. 6. This is a two-speed transmission. A wet double clutch is mounted on the driveshaft as the shifting element. Via the double clutch, the two idler gears on the driveshaft can be coupled according to the selected gear. On the driveshaft are the fixed gear wheels and the gear wheel for the output. The axle equals the axle of the input transmission. The bearings of the shafts are identical to those of the single-speed transmission. In this concept, however, in addition to the radial shaft seals, Torlon seals are also required due to the coupling, so two Torlon seals are installed. The double clutch is controlled and lubricated by an electric pump.

Fig. 6
figure 6

Two-speed transmission with one driveshaft and one dual-clutch (C2 TST)

Full size image

Figure 7 shows the second two-speed transmission concept. In contrast to the first two-speed transmission concept, this one has an additional driveshaft. Therefore, the concept has four shafts. The fixed gears of the transmission are positioned on the driveshaft.

Fig. 7
figure 7

Two-speed transmission with two driveshafts and two clutches (C3 TST)

Full size image

The third concept has a simple wet multi-plate clutch on each driveshaft, which couples the corresponding gear wheel according to the selected gear. In addition to the radial shaft seals on the input shaft and the two radial shaft seals on the output shaft, the concept has a Torlon seal on each driveshaft due to the wet multi-plate clutch. The input shaft is supported by deep groove ball bearings. The two driveshafts are supported by a fixed bearing arrangement with a deep groove ball bearing and a cylindrical roller bearing. As with the other concepts, the output shaft is supported via two tapered roller bearings.

4.1 Optimizing of the Gear Ratio Values

To select the optimum gear ratios for the transmission concepts, a parameter space is created with the MSM and the energy consumption is calculated for all combinations. The results are plotted against acceleration time in Fig. 8.

Fig. 8
figure 8

Gear ratio selection: SST (yellow) and TST (blue) and the selected variant (red)

Full size image

The gear ratio is varied from 10 to 12 for the single-speed transmission and from 11 to 14 for the first gear and from 6 to 10 for the second gear of the two-speed concepts. The performance requirements from Sect. 5 are examined and, if necessary, invalid variants are excluded. For the input transmission, the optimal variant with minimum acceleration time and energy consumption has a total gear ratio of \(i_{g1} = 11.12\). For the two-speed transmission, the result is shown in Fig. 8. A compromise between low acceleration time and low energy consumption is selected as the optimal variant. The gear ratio for the first gear is \(i_{g1} = 11.6\) and for the second gear \(i_{g2} = 6.8\), which applies to both two-speed concepts.

5 Vehicle Parameter and Performance Requirements

A representative electric vehicle is defined for the simulative investigation of the different transmission concepts. This is a battery electric C-segment vehicle (BEV) with rear-wheel drive (RWD). The defined vehicle parameters are listed in Table 1. The vehicle has a mass of \(1750 \, \mathrm {kg}\). The weight effect caused by the additional gear is neglected in this study.

Table 1 Vehicle parameter C-segment BEV (RWD)
Full size table

In addition, the same performance requirements are set for all three transmission concepts so that the individual transmission concepts can be compared with each other. It defines the power requirements for discharging operation and charging operation. In Fig. 9, the traction force for the single-speed transmission and both two-speed transmission concepts are shown over the vehicle velocity.

Fig. 9
figure 9

Traction force rear axle for each gear of the single-speed transmission (orange) and the two-speed transmissions (blue)

Full size image

The vehicle is capable of reaching the traction limit till \(40 \, \mathrm {km/h}\). This criterion is especially important for climbing ability and acceleration. Due to the different gear ratios, the vehicle is capable of reaching different top speeds with the different transmission concepts. In terms of performance, the requirement for this paper is to achieve better performance than existing BEVs on the market. For this, various catalog values of typical C-Segment BEV can be taken as a basis. For example, the Volkswagen ID.3 Pro Performance with an EM power of \(150\,\mathrm {kW}\) and a mass of \(1812 \, \mathrm {kg}\) accelerates from 0 to \(100\,\mathrm {km/h}\) in \(7.1 \, \mathrm {s}\) [33]. Another example is the Airways U5 Premium with the same EM power of \(150\,\mathrm {kW}\) and a mass of \(1770 \, \mathrm {kg}\). The acceleration time is \(7.8 \, \mathrm {s}\) [34]. Thus, the minimum requirement for acceleration from 0 to \(100\,\mathrm {km/h}\) is at least \(7.1 \, \mathrm {s}\). In addition, to comply with highway cycles and example concepts, the maximum vehicle speed is defined to be at least \(160 \, \mathrm {km/h}\).

These requirements apply equally to all transmission concepts and reflect realistic performance requirements for current electric vehicles.

6 Evaluation of Transmission Losses in BEV

For all transmission concepts to be investigated, lossmaps are integrated into the simulation programs and the WLTC is simulated. The results are evaluated and explained below. Figure 10 shows the power loss of the modular simulation model in the WLTC. In the first subplot of Fig. 10, the velocity profile of the WLTC is shown. Furthermore, it is shown in green and yellow which gear is currently selected. As already mentioned, power loss over time is shown in the second subplot. By including lossmaps from Sect. 2.2, the total losses can be divided into the individual loss components. Separation is made between bearing losses, load-dependent gear losses, load-independent gear losses, sealing losses, losses due to shifting elements, and air gap losses. Figure 10 shows the C2 TST with a double-clutch on the input shaft. It is noticeable that losses increase with speed, especially at high speeds in the cycle and thus high speeds in the transmission, load-independent losses, such as the load-independent gear losses, the sealing losses, and also air gap losses, have a large effect since the friction losses increase at high speeds. In phases of acceleration, in contrast, the load-dependent losses are predominant. Between 1200 and \(1400\,\mathrm {s}\), it can be seen how the load-dependent losses are greatly reduced in the thrust phase. Since lower torques occur in the phases of recuperation and therefore the load-dependent losses such as bearing and gearing losses are lower.

Fig. 10
figure 10

Power losses C2 TST MSM

Full size image

Figure 10 can be created for all concepts and both simulation programs. However, for clarity, the total power loss of the C2 TST for the two simulation models is only shown for one concept in the following figure. This allows the differences between the backward simulation of the MSM and the forward simulation of the 3D simulation model to be shown.

Fig. 11
figure 11

Power losses MSM vs 3D SM for the C2 TST

Full size image

In Fig. 11, it can be seen that the power losses of the two models are very close to each other over the complete range in the cycle. During the first section of the WLTC at low speeds, it can be seen that the 3D simulation model has slightly larger power losses during accelerations. In the later part of the WLTC, precisely at the up-shift between first and second gear, the 3D simulation model exhibits significantly greater power losses. This is because the forward simulation simulates much more dynamically and can thus represent processes in the powertrain more realistically.

This phenomenon can be seen more clearly in a diagram in which rotational speeds of the EM for the two simulation models are shown in one figure. Figure 12 shows the EM speed on the first subplot and torque on the second subplot.

Fig. 12
figure 12

Speed (a) and torque (b) of the EM in the WLTC for the C2 TST and both simulation models

Full size image

The speed curve of the two simulation models is very similar over the entire cycle. This is because the gear ratios are identical and there is almost no influence from reverse or forward simulation. With the torque curve of the EM, it can be seen that the torques differ greatly at some points. The higher torques in the forward simulation lead to increased losses, as already shown in Fig. 11.

To enable the results for the different transmission concepts to be presented clearly, the loss energy in the WLTC is shown in Fig. 13. The component losses are shown as a bar chart for the different concepts and simulation models. The colors of component losses are chosen as identical.

Fig. 13
figure 13

Comparison of energy losses in the WLTC

Full size image

The SST has the lowest losses. Both TSTs have greater losses in each case, with the two-speed transmission with the double-clutch on the input shaft having the greatest losses. The two-speed concept with two intermediate shafts and one clutch each has only slightly larger losses than the C1 SST. The bearing losses are lowest for the C2 TST. The transmission concept has almost the same bearing arrangement as the C1 SST, but due to the larger number of gears on the input shaft and intermediate shaft, the axial forces from the gearing are partially compensated, which reduces bearing load and consequently also the load-dependent share of bearing losses. Another reason is due to lower speeds in the cycle since in the two-speed transmission the speeds in the second gear are much lower than in the single-speed transmission. The C3 TST has the largest bearing losses. This is because this transmission has one more shaft bearing due to the second intermediate shaft. The lower speeds in the cycle due to the second gear cannot compensate for the additional bearings either.

A similar explanation can be given for the load-dependent gear losses. In comparison, significantly greater differences occur with the load-independent gearing losses. The lower speeds of the two-speed concepts do not lead to lower losses in this case. The SST has the lowest load-independent losses. In the two-speed transmission, the larger number of gears has a greater influence on the load-independent gearing losses. With the C2 TST, this point is even more significant, since this concept has one intermediate shaft. Due to the additional gear, it is additionally immersed in the oil and thus strongly increases the splash and slippage losses, resulting in large load-independent gear losses.

In terms of sealing losses, the single-speed transmission has the lowest losses. The two-speed transmissions can approximately reduce the losses due to the lower speed in the second gear on the input shaft. However, this advantage is neutralized by the additional Torlon seals due to the clutches. Since the C2 TST concept has the clutch on the input shaft, resulting in higher differential speeds, this concept has the highest sealing losses.

The points just mentioned also apply to the shifting element losses, which means that the C2 TST concept also has the highest losses here. The C3 TST has two clutches, each of which is arranged on an intermediate shaft. This results in lower differential speeds in the clutch, which means that the drag losses of the clutch are lower than the C2 TST. The C1 SST has no shifting elements, so no losses occur.

The distribution of air gap losses is different. Here, the two-speed concepts have almost half as large losses as the C1 SST. Since air gap losses of the EM are directly dependent on EM speed, the transmission ratio of the second gear and thus speed reduction has a major influence on losses. This means that the air gap losses decrease with a smaller gear ratio in the second gear.

Table 2 lists the transmission efficiency of the transmission concepts over the full duration of the WLTC for the two simulation models. For the modular simulation model, the transmission efficiencies range from \(94\,\%\) to almost \(96\,\%\). The C1 SST has the highest transmission efficiency, due to the lowest transmission losses. It is followed by the C3 TST and then the C2 TST. The C3 TST has lower transmission losses compared to the C2 TST, resulting in better efficiency. The losses between the C1 SST and the C3 SST are relatively similar. Because of the different power passing through the transmissions, which results in different speeds and torques depending on the ratio of the second gear, the better efficiency results for the C1 SST.

Table 2 Transmission efficiency in the WLTC with the MSM and the 3D SM
Full size table

For the 3D SM, the transmission efficiencies show identical distribution results compared to the MSM in Table 2. The C1 TST has the best transmission efficiency with \(92.08\,\%\). The C2 TST, with the highest losses, also has the worst transmission efficiency of \(89.56\,\%\). The C3 TST is slightly below the C1 SST with an efficiency of \(91.63\,\%\). As mentioned above, the 3D simulation model has a much more dynamic simulation of the complete vehicle, which results in considerably higher torques in the transmission resulting from the driver which directly impacts the torque by the accelerator and braking pedal. Therefore, the resulting power also differs. In this case, this results in the efficiency of the C1 SST being slightly better than the C3 TST.

The question now is whether, when considering the vehicle as a whole, the advantage of the second gear is compensated by the greater losses in the transmission, or whether it can still lead to an improvement when considered as a whole. Therefore, Fig. 14 shows the energetically weighted operating points of the EM for the SST and both vehicle simulation models in one WLTC. The operating points are shown in the efficiency map of the EM. It can be seen that the operating points are similar across the speeds of the EM. However, the different torques of the EM result in a different weighting in detail. In the case of the MSM, there are operating points during recuperation that lie in efficiency-optimal areas of the EM efficiency map. As a result, the average efficiency is higher with the MSM.

Fig. 14
figure 14

Energetically weighted parts of the EM operating points of the C1 SST drivetrain in the MSM (a) and 3D SM (b) for one WLTC simulation

Full size image

Figure 15 shows the energetically weighted operating points of the EM for the two-speed transmission in the WLTC with the different simulation models.

Fig. 15
figure 15

Energetically weighted parts of the EM operating points of the C2 TST drivetrain in the MSM (a) and 3D SM (b) for one WLTC simulation

Full size image

Compared to Fig. 14, it can be seen clearly that the additional gear of the transmission concept and the smaller transmission ratio shift the speeds from the high speed range to the lower speed range. As a result, more operating points now occur in a medium speed range.

As a result, the operating points also shift into ranges with higher efficiency, which means that the average efficiency of the EM in the WLTC for the two-speed transmission is higher than for the single-speed transmission. It can thereby achieve an efficiency improvement of about 3%~4% as listed in Table 3. As already seen in Fig.12, the torques between the two simulation models differ significantly in some cases. This results from higher EM power and losses resulting from a more dynamic simulation. Because of the high simulation frequency of \(1000\,\mathrm {Hz}\), the individual loss components can be simulated in detail, resulting in more realistic behavior. This also leads to differences in the weighted operating points, which results in the different efficiencies of the EM in the two simulation models.

Table 3 EM efficiency in the WLTC with the MSM and the 3D SM
Full size table

7 Conclusions

This paper presents a simulation program to determine transmission losses for transmission concepts in the early development stage. The transmission lossmaps are created for different transmission concepts for electric vehicles and integrated into two complete vehicle simulations to evaluate the transmission concepts in the WLTC. One of the vehicle simulations is the modular simulation model, which is a reverse simulation. The other simulation model is the 3D simulation model, which is a forward simulation. Three different transmission concepts are studied. One single-speed transmission as a reference and two different two-speed transmissions. One concept has one intermediate shaft and the other concept has two. The two two-speed concepts have wet multi-plate clutches as shifting elements. The first two-speed transmission with one intermediate shaft has a double-clutch on the input shaft and the other transmission concept has one clutch per intermediate shaft. The transmission concepts are evaluated in terms of transmission losses as well as transmission and EM efficiencies. The influence of the overall vehicle simulation is also investigated and analyzed.

The transmission lossmaps from the lossmap-based simulation model can be integrated into both the modular simulation model and the 3D simulation model, which is an innovation compared to current research. In this way, transmission losses can be simulated on a component basis for the different concepts and compared in detail. This makes it possible to investigate optimizations to the transmission concept, such as a different bearing arrangement for the shaft in the early stage of development.

The 3D simulation model as a forward simulation is capable of dynamically simulating the individual power and representing it more realistically. This is also reflected in the results. Different operating points result in different transmission and EM efficiencies, whereby the efficiencies of the 3D simulation model are lower compared to the MSM. The EM efficiency of the two TST has a \(3\,\%\) better efficiency compared to the SST, which confirms various other studies on this field. The transmission efficiencies are on a similar level with the SST, at least for the C3 TST. The transmission concept with the double-clutch on the input shaft has significantly higher losses due to the double-clutch, which means that the transmission efficiency is lower. It can be concluded that a two-speed transmission can certainly be beneficial for electric vehicles and has efficiency advantages if the transmission losses are not too high. The simulation models can be used to identify and investigate the individual sources of transmission losses to find possible optimization potential for a suitable two-speed transmission. Therefore, whole vehicle simulation models are a useful tool for investigating transmission concepts in the early development stage and reducing development effort.