1 Introduction

Safety, mobility and environmental impacts (e.g., the fuel efficiency and exhaust gas emissions) are current concerns of the transportation system highlighted by the Department of Transportation United States [1]. An emerging solution is the use of connected-vehicle technology, which has been reported to be capable of reducing vehicle crashes by 79%, idling time by 4.2 billion hours and gas consumption by 2.8 billion gallons and thus reducing annual costs by $87.2 billion [2, 3]. In the state-of-the-art connected-vehicle environment, vehicle state information can be shared among vehicles via vehicle-to-vehicle (V2V) communication, while signal phase and timing (SPAT) information is also accessible to the vehicles via vehicle-to-infrastructure (V2I) communication [4].

In recent years, connected-vehicle technology has been developed to improve the mobility and fuel economy of vehicles [1, 5]. Recent studies have reported that vehicle connectivity can improve the fuel economy of vehicles through the formation of a platoon, where vehicles have similar behaviors and the number of sharp acceleration and braking events is reduced [6, 7]. It is known that the fuel economy of vehicles depends on the powertrain characteristics, vehicle aerodynamics and driver behaviors [8]. Advanced control methods, such as model-based control, are now being developed, allowing for fully predictive and forward-looking powertrain control that increases the possibility of fuel savings [9, 10]. However, model-based control cannot be implemented in real applications without preview information of the future driving cycle [10]. As a result, powertrain operation is rendered non-optimal regarding maximization of the fuel economy [11]. This problem can potentially be addressed with the emerging connected-vehicle technology using additional and exogenous information for real-time control of the vehicles as well as powertrains [12, 13]. It is envisioned that in the near future, V2V and V2I communications will facilitate extensive automated collaborative operation for reduced fuel consumption and speed harmonization for the mitigation of congestion [14].

A number of recent studies used the concept of vehicle connectivity to generate the optimal velocity profiles that balance the fuel efficiency and mobility while guaranteeing vehicle safety. Kamal et al. [14] formulated a model predictive control (MPC) problem to improve the fuel economy of connected vehicles considering current traffic conditions. Mandava et al. [15] used SPAT information to develop an arterial velocity planning algorithm that minimizes the number of accelerations and decelerations. De Nunzio et al. [16] considered a driver-in-the-loop scenario and proposed a graph discretizing approach to generate the most fuel-efficient velocity profile. However, the aforementioned studies consider only the one-vehicle scenario and neglected vehicle interactions. To address this issue, other works investigated multiple-vehicle scenarios. Kundu et al. [17] presented an eco-speed control approach for the generation of the optimal velocity of a platoon of vehicles. HomChaudhuri et al. [1, 6, 18] formulated decentralized MPC for a group of connected vehicles under urban road conditions using SPAT information. Lin et al. [19] proposed a hierarchical controller for the generation of the optimal velocity profile and energy management control of a group of connected vehicles. Du et al. [20] closed the loop of the hierarchical controller by feeding back the efficiencies of the lower-level controller within certain update time windows.

The most popular approach for the prediction of the optimal velocity profiles of connected vehicles is MPC incorporating SPAT, where the general idea is to reduce sharp accelerations and stoppages at red lights while guaranteeing collision avoidance [15, 19]. To the best of the authors’ knowledge, because deriving an explicit expression of exact engine fuel consumption is not easy, most of the existing literature uses approximate fuel consumption models in the MPC cost function and those models are basically polynomial functions of the velocity and acceleration. Some studies [2, 5, 15, 18] have modeled the fuel consumption rate for the conventional vehicle as the summation of fuel consumption rates in two scenarios: (1) the vehicle is cruising and (2) the vehicle is accelerating. Other studies [1, 4, 19, 20] have proposed a longitudinal vehicle-dynamics-based fuel consumption model for a hybrid electric vehicle. However, the aforementioned approximate fuel consumption models neglect the behaviors and characteristics of the engine and transmission. They may therefore be incapable of reflecting the real fuel consumption rate of the vehicle [18]. Therefore, optimization with an approximate fuel consumption model may not result in the best fuel economy. Furthermore, although some approximate fuel consumption models have been validated by experiments, fitting such approximate fuel consumption models is time consuming and may require much data from simulations or real experiments [14, 21].

Motivated by the aforementioned problems, we propose an engine-map-based predictive fuel-efficient control strategy for a group of connected vehicles. We extend our previous work [1, 3, 4] by substituting the longitudinal vehicle-dynamics-based approximate fuel economy model with the real-time engine-map-based fuel consumption model in the MPC cost function. The MPC problem is thus developed on the basis of knowledge of the engine and transmission behaviors and characteristics. To save time tuning the weight factors, we normalize each term in the cost function by dividing the terms with their reference values. Additionally, to guarantee the avoidance of vehicle collisions, we give extra cost to the vehicle safety term when the inter-vehicle distance drops to a predefined critical value. In addition, in the case of vehicles running a red light, we give another extra cost to the velocity tracking term when the traffic light is red. Finally, we validate the proposed method for different scenarios through simulation.

The remainder of the paper is organized as follows. Section 2 presents a mathematical description of the modeling of vehicle components and the procedures for generating an engine-map-based fuel consumption model. Section 3 formulates the proposed engine-map-based MPC problem. Section 4 performs simulation studies, and Sect. 5 presents conclusions and considers future work.

2 Modeling of the Vehicle

We present an engine-map-based fuel-efficient control strategy for a group of connected vehicles. To achieve the engine-map-based fuel consumption, we employ a backward continuously variable transmission (CVT)-based conventional vehicle model in the MPC cost function. This section presents the modeling of the main vehicle components and discusses the procedures for generating the engine-map-based fuel consumption model.

2.1 Driver Model

The driver model established in this study is a typical proportional–integral–derivative (PID)-based model that generates the torque request and power request of the vehicle. The driver model can be expressed as:

$$ T_{\text{req}} = K_{\text{p}} \left( {v - v_{0} } \right) + K_{\text{i}} \int {\left( {v - v_{0} } \right){\text{d}}t} + K_{\text{d}} \cdot \frac{{{\text{d}}\left( {v - v_{0} } \right)}}{{{\text{d}}t}} $$
(1a)
$$ P_{\text{req}} = f_{1} (T_{\text{req}} ,v) $$
(1b)

where Treq and Preq are, respectively, the torque request and power request of the vehicle; v is the driving cycle velocity (predicted velocity), and v0 is the real output velocity of the vehicle; and Kp, Ki and Kd, respectively, denote the proportion, integration and differentiation coefficients of the PID controller.

2.2 Engine Model

For the backward vehicle simulation model used in this paper, the engine model consists of the fuel consumption model and efficiency model and is expressed as:

$$ \dot{m}_{\text{f}} = f_{2} (T_{\text{e}} ,n_{\text{e}} ) $$
(2a)
$$ \eta_{\text{e}} = f_{3} (T_{\text{e}} ,n_{\text{e}} ) $$
(2b)

where \( \dot{m}_{\text{f}} \) is the fuel consumption rate of the engine; Te and ne are, respectively, the torque request and speed request of the engine; and ηe is the efficiency of the engine.

The engine fuel consumption model and efficiency model are, respectively, illustrated in Fig. 1a, b.

Fig. 1
figure 1

Engine fuel consumption and efficiency model. a Fuel consumption model, b efficiency model

Full size image

2.3 CVT Model

The CVT model employed in this paper is a data-based model expressed as:

$$ i_{\text{CVT}} = f_{4} \left( {P_{\text{req}} ,v} \right) $$
(3a)
$$ \eta_{\text{CVT}} = f_{5} \left( {T_{\text{CVT}} ,i_{\text{CVT}} } \right) $$
(3b)
$$ n_{{{\text{CVT}}\_{\text{out}}}} = n_{{{\text{CVT}}\_{\text{in}}}} /i_{\text{CVT}} $$
(3c)

where iCVT is the CVT transmission ratio; TCVT is the torque request of CVT; ηCVT is the CVT efficiency; and nCVT_in and nCVT_out are, respectively, the CVT input and output speeds.

The CVT transmission ratio iCVT with regard to the power request of the vehicle Preq and predicted velocity v is illustrated in Fig. 2a, while the CVT efficiency ηCVT corresponding to torque request Treq and CVT transmission ratio iCVT is illustrated in Fig. 2b. It is noted that the mechanical efficiencies of the power components are defined as the output power divided by the input power.

Fig. 2
figure 2

CVT model. a Transmission ratio model, b efficiency model

Full size image

2.4 Vehicle Model

The longitudinal dynamics equation of the vehicle is

$$ F_{\text{t}} = \frac{{C_{\text{D}} \rho_{\text{a}} A_{\text{f}} v_{0}^{2} }}{2} + mgf\cos \theta + mg\sin \theta + \delta m\frac{{{\text{d}}v_{0} }}{{{\text{d}}t}} $$
(4)

where Ft is the traction force; CD is the drag coefficient; ρa is air density; Af is the frontal area of the vehicle; m is the gross weight of the vehicle; f is the rolling resistance coefficient; θ is the road slope; and δ is the correction coefficient of a rotating mass.Because the vehicle model employed is a backward model, the procedures for obtaining the engine fuel consumption rate are as follows.

  1. 1.

    With the predicted velocity v and the real output velocity v0 of the vehicle at the current optimization time k, the torque request Treq and power request Preq of the vehicle are calculated through a PID controller in the driver model.

  2. 2.

    With the predicted velocity v and power request Preq of the vehicle, the CVT transmission ratio iCVT and engine speed request ne are obtained.

  3. 3.

    With the torque request Treq of the vehicle and CVT transmission ratio iCVT, the CVT efficiency ηCVT is obtained. Moreover, the engine torque request Te is obtained after several algebraic operations.

  4. 4.

    With the engine torque request Te and speed request ne, the fuel consumption rate \( \dot{m}_{\text{f}} \) and efficiency ηe of the engine are obtained.

After algebraic operations for each vehicle block, the real output velocity v0 of the vehicle is calculated and fed back to the driver model for calculation of the power request Preq and torque request Treq of the vehicle.

3 MPC Formulation

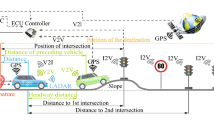
This section formulates a decentralized engine-map-based MPC framework that maximizes the fuel economy and mobility for a group of connected vehicles while guaranteeing safe inter-vehicle distances. In the connected-vehicle environment, each vehicle is assumed to have access to position and velocity information of the preceding vehicle via V2V communication and SPAT information of the traffic light via V2I communication. On the basis of local information, the MPC generates the optimal velocity profile for each individual vehicle. Figure 3 is a schematic of the problem.

Fig. 3
figure 3

Schematic of the problem

Full size image

The longitudinal dynamics of vehicle i are given by [1, 4,5,6]

$$ \dot{x}_{i} \left( t \right) = F_{i} \left( {x_{i} \left( t \right),u_{i} \left( t \right)} \right) $$
(5a)
$$ \begin{aligned} & F_{i} \left( {x_{i} \left( t \right),u_{i} \left( t \right)} \right) \\ & = \left[ {\begin{array}{*{20}c} {v_{i} \left( t \right)} \\ { - \frac{1}{{2m_{i} }}C_{\text{D}} \rho_{\text{a}} A_{{{\text{f}}i}} v_{i} \left( t \right)^{2} - \mu g - g\sin \theta + u_{i} \left( t \right)} \\ \end{array} } \right] \\ \end{aligned} $$
(5b)
$$ x_{i} \left( t \right) = [s_{i} \left( t \right),v_{i} \left( t \right)]^{\text{T}} $$
(5c)
$$ v_{{i{\rm {min}} }} \le v_{i} \left( t \right) \le v_{{i{\rm {max}} }} $$
(5d)
$$ u_{{i{\rm {min}} }} \le u_{i} \left( t \right) \le u_{{i{\rm {max}} }} $$
(5e)

where x is the state variable and s is the position of the vehicle; u is the longitudinal acceleration (control variable) with lower bound umin and higher bound umax; vmin and vmax are, respectively, the higher and lower bounds of the vehicle velocity; and i is the vehicle index.

In the MPC problem, SPAT information is used to calculate the target velocity range that reduces the number of red-light stoppages of the vehicles. Moreover, to maximize the mobility of vehicles, the target velocity is chosen as the higher bound of the target velocity range. The target velocity range is given by [5]

$$ \begin{aligned} & v_{{i{\text{hb}}}} \left( t \right) = \\ & \left\{ {\begin{array}{*{20}l} {\frac{{d_{{i{\text{a}}}} \left( t \right)}}{{K_{\text{w}} t_{\text{c}} - t_{\text{g}} - t}}} \hfill & {{\text{if light}} = {\text{red}}} \hfill \\ {v_{{i{\rm {max}} }} } \hfill & {{\text{if light}} = {\text{green and}} \frac{{d_{{i{\text{a}}}} \left( t \right)}}{{K_{\text{w}} t_{\text{c}} - t}} \le v_{{i{\rm {max}} }} } \hfill \\ {\frac{{d_{{i{\text{a}}}} \left( t \right)}}{{K_{\text{w}} t_{\text{c}} + t_{\text{r}} - t}}} \hfill & {{\text{if light}} = {\text{green and otherwise}}} \hfill \\ \end{array} } \right. \\ \end{aligned} $$
(6a)
$$ \begin{aligned} & v_{{i{\text{lb}}}} \left( t \right) = \\ & \left\{ {\begin{array}{*{20}l} {\frac{{d_{{i{\text{a}}}} \left( t \right)}}{{K_{\text{w}} t_{\text{c}} - t}}} \hfill & {{\text{if light}} = {\text{red}}} \hfill \\ {\frac{{d_{{i{\text{a}}}} \left( t \right)}}{{K_{\text{w}} t_{\text{c}} - t}}} \hfill & {{\text{if light}} = {\text{green and}} \frac{{d_{{i{\text{a}}}} \left( t \right)}}{{K_{\text{w}} t_{\text{c}} - t}} \le v_{{i{\rm {max}} }} } \hfill \\ {\frac{{d_{{i{\text{a}}}} \left( t \right)}}{{(K_{\text{w}} + 1)t_{\text{c}} - t}}} \hfill & {{\text{if light}} = {\text{green and otherwise}}} \hfill \\ \end{array} } \right. \\ \end{aligned} $$
(6b)
$$ v_{{i{\text{target}}}} \left( t \right) = v_{{i{\text{hb}}}} \left( t \right) $$
(6c)

where vitarget is the target velocity of vehicle i bounded by vimin ≤ vitarget ≤ vimax; vihb and vilb are, respectively, the higher and lower bounds of the target velocity range; dia is the distance between vehicle i and the upcoming traffic light a; and Kw denotes the cycle number of traffic signal lights obtained from the floor value of the division of t by tc, with tc being the period of the cycle of traffic signal lights that equals the summation of the green-light duration tg and red-light duration tr.

With the target velocity, position information of the current vehicle and the preceding vehicle, and engine-map-based fuel consumption model, we formulate a decentralized MPC problem over a finite time horizon. In this paper, we employ the MPC framework that penalizes the fuel economy, safety, mobility and acceleration proposed in our previous work [1, 4,5,6] subject to modifications: (1) the approximate fuel consumption model is substituted with the engine-map-based fuel consumption model, (2) we normalize each term in the cost function by dividing it with its reference value and give constant weights to the fuel consumption term and control variable term, (3) to guarantee the avoidance of collisions, we give an extra cost to the safety term when the distance between adjacent vehicles drops to a predefined value, and (4) to avoid the violation of traffic rules, we give another extra cost to the velocity tracking term to ensure no vehicle passes through a red light. The new MPC problem is given by:

$$\begin{aligned} & \mathop {\arg \hbox{min} }\limits_{{u_{i} (t)}} \left\{ \sum\limits_{t = k}^{k + T - 1} \left[ \omega_{1} \left( {\frac{{\dot{m}_{{i{\text{f}}}} (t)}}{{\dot{m}_{{{\text{f}}\_{\text{ref}}}} }}} \right)^{2} + \left[ {\omega_{2} \left( {\frac{{S_{ij} \left( t \right)}}{{S_{\text{ref}} }}} \right)^{2} + a} \right] \right.\right.\\ & \left.\left. \quad + \left[ {\omega_{3} \left( {\frac{{v_{i} \left( t \right) - v_{{i{\text{target}}}} \left( t \right)}}{{\delta v_{\text{ref}} }}} \right)^{2} + b} \right] + \omega_{4} \left( {\frac{{u_{i} \left( t \right)}}{{u_{\text{ref}} }}} \right)^{2} \right] \right\} \end{aligned} $$
(7a)
$$ S_{ij} \left( t \right) = S_{0} + t_{\text{h}} \left[ {v_{i} \left( t \right) - v_{j} \left( t \right)} \right] + \left[ {s_{i} \left( t \right) - s_{j} \left( t \right)} \right] $$
(7b)

where ωii (ii = 1, 2, 3, 4) is the weight factor; T is the MPC horizon with step ∆t; \( \dot{m}_{{{\text{f}}\_{\text{ref}}}} \) is the reference value of the engine fuel consumption rate; Sij is the deviation of the distance between vehicles i and j from the desirable value with reference value Sref; a and b are extra costs for the safety term and velocity tracking term and are sufficiently large constants; δvref is the reference value of the deviation of the vehicle velocity from the target velocity; uref is the reference value of the control variable; th is the headway time; S0 is the desirable distance between vehicles; and sj and vj are, respectively, the position and velocity of vehicle j that precedes vehicle i. In this paper, the fuel consumption rate of vehicle i is calculated with Eq. (2a) and the backward simulation model is written in the MPC cost function using MATLAB code. The MPC uses the fuel consumption rate calculated with the backward simulation model to optimize the velocity profile of the vehicle. It is noted that the MPC cost function should also satisfy the constraints of the longitudinal vehicle dynamics presented in Eq. (5).

After introducing the engine-map-based fuel consumption model, the computational burden may be higher than that when using the approximate model. In this paper, we use the fast MPC (FMPC) approach proposed in our previous work [3, 18] to solve the MPC problem. The FMPC method is an approximation-based method in which the dynamics of the vehicle are rewritten in a linearized form by introducing a state-independent parameter. The computation is accelerated by exploiting the structure of the control problem, block elimination and Cholesky factorization [18]. As theoretical research, we focus on the fuel saving potential using a more accurate fuel consumption model and it is acceptable that the computational burden is increased and the fuel saving potential compromised. After solving the MPC problem, the optimal control variable is obtained, and the optimal velocity (i.e., predicted velocity) can be calculated from the longitudinal dynamics of the vehicle.

4 Simulation Studies

This section presents the simulation results of the proposed method and baseline method. The main idea proposed in this paper is the implementation of the engine-map-based fuel consumption model in the MPC cost function with extra costs for safety and traffic rule violations as well as normalization of the cost function. Because this paper is extended from our previous work [1, 4], we choose the method proposed in [1, 4] as the baseline method.

This paper considers the scenario of four identical conventional vehicles traveling along a single-lane road with traffic lights every 500 m. The basic parameters of the considered vehicles are tabulated in Table 1. To emulate a congested urban road, the signal timing is sampled with a uniform distribution where the average red-light duration is 40 s and the average green-light duration is 15 s. The higher and lower bounds of the velocity are, respectively, 20 and 0 m/s, and the higher and lower bounds of the control variable are, respectively, 1.5 and − 1.5 m/s2. The initial positions (with intervals ranging 15–20 m) and velocities (ranging 10–15 m/s) of the vehicles are generated randomly with uniform distributions. The headway time is 1.5 s and the desirable distance between adjacent vehicles is 5 m. The critical distance is chosen as 0.1 m in the case of collisions. The reference values in the normalized cost function are \( \dot{m}_{{{\text{f}}\_{\text{ref}}}} = 2\;{\text{g/s}} \), Sij_ref = 15 m, δvref = 10 m/s and uref = 1.5 m/s2. The finite MPC horizon is 8 s with a step of 0.5 s, and the total simulation time is 400 s.

Table 1 Basic parameters of the considered vehicle
Full size table

This paper considers three scenarios, namely (1) a normalized cost function with constant weights, (2) a non-normalized cost function with time-varying weights, and (3) different penetration rates, to demonstrate the effectiveness of the proposed control method. For the first scenario, to save time tuning the constant weight factors, we choose the weights of the fuel consumption term and acceleration term to be reasonable fixed constants.

In the first scenario, the cost functions of the proposed method and baseline method are normalized with the weight factors ω1 = 0.2, ω2 = 0.2, ω3 = 0.4 and ω4 = 0.2. The simulation results for this scenario are shown in Fig. 4. Figure 4a shows the trajectories of the vehicles. Red bars in the figure denote the red-light windows, while blank spaces between red bars are the green-light windows. Figure 4a shows that within the simulation time of 400 s, all four vehicles pass through eight consecutive traffic lights without intersecting with the red-light windows, which means none of the vehicles stop at red lights after the engine-map-based fuel consumption model is implemented in the MPC framework. Furthermore, all four vehicles operate cooperatively and none of their trajectories intersect with another, meaning the vehicles do not collide with one another. Figure 4b clearly shows that the distances between vehicles are always greater than zero, again meaning that the vehicles do not collide with one another. Moreover, after a quick regulation from the initial values, the distances between adjacent vehicles converge to the desired value of 5 m with desirable fluctuations. Figure 4c shows that the velocity profiles of the vehicles have similar behaviors and no profile drops to zero, further confirming that the vehicles never stop in the simulation period. Figure 4d compares the velocity profiles generated with our proposed method and the baseline method. Because the velocity profiles of the vehicles are similar, for simplicity, we only present the comparison of the velocity profiles of vehicle 4. It is observed that by implementation of the engine-map-based fuel consumption model, (1) the velocity profiles of the proposed method and baseline method have similar behaviors and similar general shapes and (2) the velocity profile of the proposed method has lower accelerations and decelerations (which play a major role in the fuel economy) than the velocity profile of the baseline method.

Fig. 4
figure 4

Simulation results for the normalized cost with constant weights ω1 = 0.2, ω2 = 0.2, ω3 = 0.4 and ω4 = 0.2. a Trajectories of the vehicles, b Relative distances of the vehicles, c Velocity profiles of the vehicles, d Velocity profile for vehicle 4

Full size image

To demonstrate the advantage of using the engine-map-based fuel consumption model, we present the fuel economy results obtained using the proposed method and baseline method in Table 2. The table shows that the fuel economy obtained using the proposed method is 5.47%, 5.22%, 5.36% and 5.95% better than that obtained using the baseline method for vehicles 1–4, respectively. The average improvement in the fuel economy of the vehicle group is 5.50%.

Table 2 Comparison of fuel economy
Full size table

To explain the better fuel economy for the proposed method than for the baseline method, the operating points of the engine are shown in Fig. 5. The figure shows that the engine operating points are clustered in a higher efficiency area for the proposed method than for the baseline method. It is noted that the average CVT efficiency is 0.8032 for the proposed method and 0.7941 for the baseline method. Meanwhile, the average power request for the vehicle to run with the velocity profile generated using the proposed method is 8.01 kW while that in the case of the baseline method is 8.19 kW. It is thus concluded that (1) a lower average power request, (2) a higher average engine operating efficiency and (3) a higher average CVT efficiency contribute to the improvement of the fuel economy of the proposed method.

Fig. 5
figure 5

Engine operating points for the proposed and baseline methods

Full size image

Furthermore, we study the scenario that the MPC cost functions of the proposed method and baseline method are not normalized and time-varying weight factors are used. The new weight factors for this scenario are ω1 = 10 + 100 × exp(0.05v_range), ω2 = 200 × exp(− 0.1(sj–si)/(vi–vj + 0.001)–th), ω3 = 10 + 500 × exp (− 0.07v_range) and ω4 = 2000 + 1000 × exp(0.05v_range), where v_range = vihb–vilb. Simulation results for this scenario are shown in Fig. 6. From Fig. 6a–c, it is concluded that with the proposed method and the time-varying weight factors, a cooperative platoon forms where the vehicles do not collide or stop at red lights. Moreover, Fig. 6d shows that, although the velocity profile of the proposed method has behaviors similar to those of the profile of the baseline method, it is smoother with lower accelerations and decelerations.

Fig. 6
figure 6

Simulation results for a non-normalized cost and time-varying weights. a Trajectories of the vehicles, b Relative distances of the vehicles, c Velocity profiles of the vehicles, d velocity profile for vehicle 4

Full size image

The fuel economy results for this scenario are given in Table 3. Table 4 shows that the fuel economy of the proposed method is better than that of the baseline method for each individual vehicle, with the average improvement being 3.64%.

Table 3 Comparison of fuel economy
Full size table
Table 4 Comparison of the average fuel economies for different penetration rates
Full size table

In practical applications, there is the possibility of there being mixed traffic with unconnected vehicles. To validate the control performance of the proposed method for different connectivity penetration rates (i.e., the percentages of vehicles that are connected), we further studied heterogeneous scenarios extended from the first scenario. In these heterogeneous scenarios, the connected vehicles have access to state information (i.e., velocity and position) of the preceding connected vehicle via V2V communication and SPAT information via V2I communication so that MPC can be employed for the prediction of the optimal velocities. For unconnected vehicles and connected vehicles with a preceding unconnected vehicle, the state information is no longer available. In this case, connected cruise control [1, 22] is applied for the calculation of the velocity profiles. In this paper, five penetration rates (i.e., 0%, 25%, 50%, 75% and 100%) are considered for our case study. No vehicle is connected for a penetration rate of 0%, vehicle 2 is unconnected for a penetration rate of 25%, vehicles 2 and 4 are unconnected for a penetration rate of 50%, vehicles 2–4 are unconnected for a penetration rate of 75% and all vehicles are unconnected for a penetration rate of 100%. The average fuel economies of the four vehicles are given in Table 4. The table shows that, compared with the result for the baseline method, the average fuel economy of the proposed method shows an improvement of 0.95%, 2.69%, 4.22%, and 5.50% for penetration rates of 25%, 50%, 75%, and 100%, respectively.

5 Conclusions and Future Work

We developed a new decentralized predictive fuel economy control strategy for a group of connected vehicles to balance the fuel economy and mobility while guaranteeing the safety of the vehicles. Simulation results show that:

  1. 1.

    By substituting the approximate fuel consumption model with the engine-map-based fuel consumption model, the basic advantages of MPC based on the concept of vehicle connectivity can be guaranteed.

  2. 2.

    The fuel economy for each individual vehicle and the average fuel economy of the vehicle group are better for the proposed method than for the baseline method under different scenarios. The average improvement for the scenario with normalized cost and constant weights is 5.5%, the average improvement for the scenario with none-normalized cost and time-varying weights is 3.64%, and the improvements for penetration rates of 25%, 50%, 75% and 100% are 0.95%, 2.69%, 4.22% and 5.5%, respectively.

The methodology proposed in this paper may be useful in considering more accurate engine fuel consumption models in the MPC framework for the realization of better fuel economy.

The limitation of this research is that real-world communication uncertainties (e.g., disturbances, delays and drops of packets) are not considered. Future work will use vehicle connectivity for the decision of engine cylinder deactivation with the aforementioned limitations addressed.