Continuous outcome decision tasks have come to play an important role in the study of how attention, memory, and decision processes combine to translate perception into action. Unlike traditional two-alternative or n-alternative decision tasks, decisions in these tasks are made on continuous spatial scales. The most widely studied of them involve decisions about stimulus attributes like color, orientation or direction of motion, in which the response alternatives form a closed circular domain — or, in the more precise language of differential geometry, in which the set of responses form a circular manifold, \(S^1\) (Boothby, 1986). Historically, the continuous-outcome task has its antecedents in the method of adjustment of classical psychophysics (Woodworth & Schlosberg, 1954), in which people adjusted the intensity of a variable stimulus to match a standard. The task was reintroduced to contemporary cognitive psychology by Blake et al. (1997) and Prinzmetal et al. (1998) to study the perception of motion and the effect of attention on perceptual variability, respectively. It was subsequently adapted by Wilken & Ma (2004) to study how the precision of visual working memory (VWM) changes with memory load. It has since become the method of choice for many VWM researchers (Adam et al., 2017; Bays et al., 2009; Oberauer & Lin, 2017; van den Berg et al., 2014; Zhang & Luck, 2008) because it yields entire distributions of retrieval errors rather than just error rates. It has also been used in related settings to study perception of, or memory for, color (e.g., Bae & Luck 2019; Hardman et al. 2017; Persaud & Hemmer 2016), the perception of motion direction (Bae et al., 2015; Smith et al., 2022), and associative recall from episodic memory (Harlow & Donaldson, 2013; Zhou et al., 2021).

Along with the increasing use of continuous outcome tasks in experiments has come an interest in developing formal models of the decision processes they engage. The tasks yield joint distributions of errors and RTs that provide a rich and empirically constrained picture of the time course of decision making. The development of models that can characterize the decision process at the level of these distributions has consequently become a question of considerable theoretical interest. To date, there have been three models of continuous-outcome decisions: the circular diffusion model (CDM) of Smith and colleagues (Smith, 2016; Smith et al., 2020) and its spherical generalization (Smith et al., 2022); the spatially continuous diffusion model (SCDM) of Ratcliff (1978); and the multiply anchored accumulation model (MAAT) of Kvam et al. (2022). These models generalize, respectively, the single-process Wiener diffusion model of Ratcliff (1978), the racing, parallel diffusion models of Ratcliff & Smith (2004) and Usher & McClelland (2001), and others, and the linear ballistic accumulator of Brown & Heathcote (2008). Our focus in this article is on the first of these models, the CDM. Compared to competitor models, the CDM has three attractive features that recommend it. First, its properties closely parallel those of the diffusion model of two-choice decisions (Ratcliff & McKoon, 2008), which, to date, has been the most successful and widely-applied model of two-choice decision making in basic and applied settings (Ratcliff et al., 2016). Second, there exist explicit expressions for the CDM’s predicted joint distributions of decision times and decision outcomes. These expressions offer insights into the theoretical basis of representational and response precision and facilitate fitting the model to data. Third, the model characterizes the behavior of a maximum-likelihood decision maker, so it embodies a well-defined sense of statistical optimality.

Our specific focus in this article is a methodological one. We present a new method that substantially improves the numerical stability of the predictions of the model, which greatly simplifies the task of fitting it to data. As described in detail below, the predicted joint distributions of the model are obtained by applying the Girsanov change-of-measure theorem to the first-passage time distribution of the Bessel process. The latter process describes the Euclidean distance of a two-dimensional (2D) zero-drift Wiener process from its starting point. The first-passage time distribution of the Bessel process is expressed as an infinite series whose terms involve Bessel functions and zeros of Bessel functions (i.e., points at which the functions cross the x-axis). Because of the finite precision of floating point computations, there is residual numerical noise in the resulting expression for the first-passage time distribution, which is most apparent at small values of time. Although the magnitude of the noise is very small (around \(10^{-15}\) or \(10^{-14}\)), it is magnified by the change-of-measure computation, in which the first-passage time distribution is multiplied by an exponential function of the product of two of the model parameters: the decision criterion and the drift rate. These parameters characterize, respectively, the amount of evidence used to make a decision and the quality of the information in the stimulus. In some parts of the parameter space, specifically, when decision criterion or drift rate or both are large, the exponential term can be of the order of \(10^{14}\). As a result, the noise in the product of the two terms can be large enough to significantly distort the representation of the joint distribution. This typically appears, intermittently, as an artifactual spike of probability mass at short values of decision time, most often when fitting data in which response accuracy is very high or RTs are very long.

A similar, although not identical, problem has previously been discussed in the literature in relation to the infinite-series representation of the first-passage time probability density function for the two-choice diffusion model (Ratcliff, 1978). The standard representation of the density function for the model is an infinite sum of exponential and trigonometric terms (Feller, 1968; Smith, 1990). Because the trigonometric terms are oscillatory, truncating the series after a finite number of terms can create numerical stability problems at small values of time. To deal with this problem, Van Zandt and colleagues (Van Zandt, 2000; Van Zandt et al., 2000) suggested using an alternative series representation to compute the density function for short times (Feller, 1968; Ratcliff, 1978) and the standard series for long times. Whereas the standard “long time” series converges rapidly for long values of time but slowly for short values of time the alternative “short time” series has the converse properties. Navarro & Fuss (2009) analytically characterized the truncation error for both series as a function of time and proposed a criterion for switching between them to maximize computational efficiency.

Unlike the convergence problem analyzed by Navarro & Fuss (2009), the numerical stability problem in the CDM is not caused by truncating an infinite series, but instead is associated with finite precision floating point representations of Bessel functions. Consequently, it is not ameliorated by increasing the number of terms in the series representation of the density of the Bessel process. In our published work (Smith, 2016; Smith et al., 2020; Smith & Corbett, 2019; Zhou et al., 2021) we have typically used a series of 50 terms, which more than suffices to yield an accurate representation of the density function in most parts of the parameter space. However, in the parts of the space in which the numerical artifact appears, increasing the number of terms to 500 or 5000 does not diminish its magnitude. This difference notwithstanding, our approach is conceptually similar to the one advocated by Van Zandt and colleagues and Navarro and Fuss, in that it uses one representation of the first-passage time distribution of the Bessel process at short times and another at long times. Instead of an alternative, short-time series, we use an asymptotic approximation that gives a very accurate representation of the leading edge of the first-passage time density function for the Bessel process, which is the region of the function in which the artifact appears. The approximation becomes inaccurate at long times but its long-time properties are immaterial as we use it only at those times for which the computations are affected by noise, which are the ones associated with the leading edge of the distribution. We show by example that the new method provides a simple and practical way of stabilizing the predictions of the model in those parts of the parameter space that are of interest in fitting data. The method applies to higher-dimensional generalizations of the model, specifically, to the spherical diffusion model (Smith et al., 2023) and the hyperspherical diffusion model (Smith & Corbett, 2019). It also applies to versions of the model with normally-distributed across-trial variability in drift rates, with either independent or correlated components (Smith, 2019).

Fig. 1
figure 1

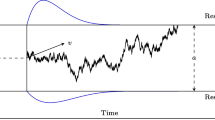
The circular diffusion model. Evidence is accumulated on the interior of a disk of radius a by a 2D Wiener process, \(\varvec{X_t}\), with components \((X_t^1, X_t^2)'\). The point at which the process hits the bounding circle, \(\varvec{X_\theta }\), is the decision outcome and the time, T, taken to hit it is the decision time. The drift rate is vector-valued, \(\varvec{\mu }\), with components \((\mu _1, \mu _2)'\), with norm \(\Vert \varvec{\mu }\Vert \) and phase, or polar, angle \(\theta _\mu \). The polar angle represents the encoded stimulus identity and the norm represents the quality of the encoded representation

Full size image

The Circular Diffusion Model

Figure 1 shows the main properties of the CDM. Evidence is accumulated by a two-dimensional (2D) Wiener diffusion process, \(\varvec{X_t} = (X_t^1, X_t^2)'\), on the interior of a disk of radius a. In this notation, bold-face symbols denote vector or matrix valued quantities, the prime denotes matrix transposition, and the superscripts index the coordinates. Random variables are denoted by upper-case Roman symbols; constants and deterministic functions are denoted by Greek or lower-case Roman symbols. The growth of evidence over time is characterized by a vector-valued stochastic differential equation,

$$\begin{aligned} \varvec{dX_t} = \varvec{\mu } \,dt + \varvec{\sigma }\, \varvec{dW_t}, \end{aligned}$$
(1)

where \(\varvec{dW_t} = (dW_t^1, dW_t^2)'\), is the differential of a 2D Wiener, or Brownian motion, process. The components of \(\varvec{dW_t}\) describe the horizontal and vertical parts of the random change in the process \(\varvec{X_t}\) during a small interval of length dt. The information in the stimulus is represented by a vector-valued drift rate, \(\varvec{\mu } = (\mu _1, \mu _2)'\), shown in the figure as an arrow at \(45^\circ \) (\(\pi /4\) rad). The rate at which the process diffuses towards the boundaries is represented by a dispersion matrix \(\varvec{\sigma } = \sigma \varvec{I}\), where \(\varvec{I}\) is a \(2 \times 2\) identity matrix. The dispersion matrix describes a Wiener process composed of two independent components, each with infinitesimal standard deviation \(\sigma \) (diffusion coefficient \(\sigma ^2\)). In polar coordinates, the drift rate has a length or norm, \(\varvec{\Vert \mu \Vert } = \sqrt{\mu _1^2 + \mu _2^2}\), and a phase, or polar, angle, \(\theta _\mu = \arctan ({\mu _2/\mu _1})\). The polar angle determines the average direction in which evidence diffuses and the norm determines the average rate at which it does so. Psychologically, the polar angle represents the encoded stimulus identity and the norm represents the encoded stimulus quality.

In the psychological model, the process starts at the center of the disk at the beginning of a trial, \(\varvec{X_0} = (0, 0)'\). On presentation of a stimulus, it diffuses until it hits a point on the bounding circle. The radius of the bounding circle, a, represents the decision criterion for the task and is assumed to be under the decision-maker’s strategic control. The irregular trajectory in the Figure 1 represents the sample path of the process (i.e., the accumulating evidence) on a single experimental trial. The hitting point on the boundary is denoted by \(\varvec{X_T}\), where the use of capitalized symbols for both the process and the time subscript indicates that the hitting point and hitting time are both random variables. This is represented in an alternative, more explicit, notation in the figure as a pair, \((\varvec{X_\theta }, T)\), which denotes the hitting time and the hitting point as independent variables, where \(\theta \) is the polar angle of the hitting point. The polar and Cartesian representations of the hitting point are related by the expressions \(X^1_T = a\cos \theta \) and \(X^2_T = a\sin \theta \).

To characterize the joint distribution of decision outcomes and decision times explicitly, we denote by \(d\tilde{P}_t(\theta )\) the joint probability density that a 2D Wiener diffusion process with drift rate \(\varvec{\mu }\) hits the bounding circle a at the point \(\varvec{X_T} = \left( a\cos \theta , a\sin \theta \right) '\) at a random time T. This density is the product of two components, denoted \(\varvec{Z_t}(\varvec{X_T})\) and \(dP_t(a)\),

$$\begin{aligned} d\tilde{P}_t(\theta ) = \varvec{Z_t}(\varvec{X_T}) dP_t(a). \end{aligned}$$
(2)

The component \(dP_t(a)\) is the probability density that a 2D, zero-drift process, started at the center of the circle at time zero, hits a point on its circumference at time t, and takes the form

$$\begin{aligned} dP_t(a) = \frac{\sigma ^2}{2\pi a^2} \sum _{k=1}^\infty \frac{j_{0,k}}{J_1(j_{0,k})} \exp \left( -\frac{j_{0,k}^2\sigma ^2}{2a^2} t\right) . \end{aligned}$$
(3)

Equation 3 is obtained from the first-passage time probability density function for the 1D Euclidean distance, or Bessel, process, which characterizes the Euclidean distance of a zero-drift Wiener process from its starting point (Borodin & Salminen, 1996, p. 297; Hamana & Matsumoto, 2013, Equation 2.7). If a zero-drift Wiener process starts at the origin then its first-passage time distribution through a circular boundary will be circularly symmetrical and identical, up to a scaling factor of \(2\pi \), to that of the 1D Bessel process. The factor of \(2\pi \) in the denominator of Eq. 3 transforms the first-passage time function for the 1D Bessel process into that of a 2D process whose probability mass around the circumference of the response circle integrates to unity when it is combined with \(\varvec{Z_t}(\varvec{X_T})\) in Eq. 2

In Eq. 3, \(J_1(x)\) is a first-order Bessel function of the first kind (Abramowitz & Stegun , 1965, p. 360) and the \(j_{0,k}\) terms are the zeros of a Bessel function of the first kind of order zero, \(J_0(x)\), that is, they are the points at which the function crosses the x-axis (see Smith (2016) for graphs of these functions). The terms \(J_1(j_{0,k})\) in the denominator represent values of \(J_1(x)\) evaluated at the zeros of \(J_0(x)\). Note that \(dP_t(a)\) is a function of time only and is independent of the hitting point on the criterion circle. Parametrically, it depends only on the diffusion coefficient, \(\sigma ^2\), and the radius of the criterion circle, a. The distribution of hitting points on the criterion circle is characterized by the second term, \(\varvec{Z_t}(\varvec{X_T})\), given by the Girsanov change-of-measure theorem (Karatzas & Shreve, 1991), which takes the form

$$\begin{aligned} \varvec{Z_t}(\varvec{X_T}) = \exp \left[ \frac{1}{\sigma ^2}{\left( \varvec{\mu } \cdot \varvec{X_T}\right) - \frac{1}{2\sigma ^2}} \varvec{\Vert \mu \Vert }^2t\right] , \end{aligned}$$
(4)

where \(\left( \varvec{\mu }\cdot \varvec{X_T}\right) = a\mu _1\cos \theta + a\mu _2\sin \theta \) is the dot product of the drift rate vector and the vector of coordinates of hitting points on the boundary. The function \(\varvec{Z_t}(\varvec{X_T})\) factorizes into a product of two exponential terms: one that depends on time and is independent of the hitting point and another that depends on the hitting point and is independent of time.

When there is across-trial variability in drift rate, Eq. 4 is replaced by another expression, whose form depends on whether the components of the distribution of drift rate are independent or correlated. When the components are independent, with means \(\nu _1\) and \(\nu _2\) and standard deviations \(\eta _1\) and \(\eta _2\), the change-of-measure function takes the form

$$\begin{aligned} \varvec{\bar{Z}_t}(\varvec{X_T}) \!=\! \prod _{i=1}^2 \frac{1}{\sqrt{(\eta _i/\sigma )^2 t + 1}}\exp \left\{ \!-\!\frac{\nu _i^2}{2\eta _i^2} \!+\! \frac{[X_T^i(\eta _i/\sigma )^2 \!+\! \nu _i]^2}{2\eta _i^2[(\eta _i/\sigma )^2t \!+\! 1]} \right\} , \end{aligned}$$
(5)

(Smith & Corbett, 2019; Smith et al. 2023). As in Eq. 4, \(\varvec{X_T}\) denotes the locus of hitting points on the criterion circle. In components, as functions of the polar angle of the hitting point, \(X_T^1 = a\cos \theta \) and \(X_T^2 = a\sin \theta \). The overbar notation suggests averaging or marginalization and is intended to imply that the distribution of hitting points and hitting times is obtained by marginalizing Eq. 4 across a distribution of drift rates. When the components of drift rate are correlated rather than independent Eq. 5 is replaced by a more complex expression given by Smith (2019). Drift-rate variability allows the model to predict a continuous-outcome version of the slow-error property of the two-choice diffusion model (Ratcliff & McKoon, 2008), in which the slowest responses are also the least accurate responses. As in two-choice decisions Luce (1986, p. 233), slow errors are found in continuous-outcome tasks in which the discriminability of the stimulus is low and the decision is difficult (Smith et al., 2023)

The Problem and its Solution

Equations 3 and 4 (or 3 and 5) suffice to compute predicted joint distributions of decision times and decision outcomes as functions of drift rate, drift-rate variability, and decision criterion, which are the quantities of interest in experiments. However, as indicated in the introduction, there are conditions under which these expressions can become numerically unstable. The first-passage time function for the Bessel process in Eq. 3 is a sum of terms that depend on the Bessel function, \(J_1(x)\), evaluated at \(j_{0,k}\), the roots of the Bessel function \(J_0(x)\), all of which are computed with finite floating point precision. The joint distribution is obtained by multiplying the series in Eq. 3 by the exponential function \(\varvec{Z_t}(\varvec{X_T})\), which factorizes into a product of two terms, \(\exp \left[ \left( \varvec{\mu } \cdot \varvec{X_T}\right) /\sigma ^2\right] \) and \(\exp \left[ -\varvec{\Vert \mu \Vert }^2t/(2\sigma ^2)\right] \). The second of these terms is not problematic because it is bounded by unity, but the first term is an exponential function of \(\varvec{\mu } \cdot \varvec{X_T} = a\mu _1\cos \theta + a\mu _2\sin \theta \), the dot product of the drift rate and the hitting point on the boundary. For some values of drift rate and criterion, this term may become very large. (In applications of the model to data, we treat the diffusion coefficient, \(\sigma ^2\), as a fundamental scaling constant of the model and set it to unity. In what follows, we assume the process has been scaled in this way and will accordingly omit \(\sigma ^2\) from the discussion.)

Fig. 2
figure 2

Marginal predictions of response error and RT for circular diffusion model for a VWM task for single-item displays (\(n = 1\)). The panels in the top three rows show predictions from the model using the series representation of the first-passage time density function for the Bessel process. The RT distribution in the top row shows the artifact caused by amplification of floating point noise in the series representation. The bottom row shows predictions using the asymptotic approximation of Eq. 6 to compute the function’s leading edge. The artifact in Fig. 2a appears with a drift rate of \(\varvec{\mu } = 6.0\) and a decision criterion \(a = 4.0\). It is eliminated in Fig. 2b and c when the drift rate is reduced to \(\varvec{\mu } = 5.0\) or the criterion is reduced to \(a = 3.5\). In the corrected solution in Fig. 2d there is no artifact even when the drift rate of \(\varvec{\mu } = 6.0\) and the criterion is increased to \(a = 6.0\). The nondecision time parameters were \(T_{er} = 0.3\) s and \(s_t = 0.1\) s

Full size image

Figure 2 shows a worst-case example of what can go wrong in some parts of the parameter space. The figure shows a portion of a fit to data from a color VWM task, which is one of the most highly-studied tasks in the literature (Wilken & Ma, 2004; Zhang & Luck, 2008). The stimuli consisted of arrays of variable numbers of highly discriminable color patches that were presented for a few hundred milliseconds while they were encoded into VWM. After encoding, at the end of a short retention interval, one of the display locations was probed and the participant was required to indicate the color of the item at that location by matching it to a point on a surrounding color wheel. We used an eye-movement decision task, similar to the one used by Smith et al. (2020), in which participants made saccadic eye movements from a home circle to a matching point on the color wheel. RT was measured as the first time at which the eyes deviated by more than 90% of the distance from the center of the screen to the response circle (around \(3.5^\circ \)) and the decision outcome was the point of the last fixation before the participant pressed a button to terminate the trial. Displays of 1, 2, 3, and 4 items were presented in random order in each experimental block. The distributions shown in Fig. 2, which were based on around 400 experimental trials, are from one participant for displays of size \(n = 1\). We focus on this condition because it was the one in which the participant was most accurate and the estimated drift rate was largest. Consequently, the numerical artifact was most severe.

The predictions in Fig. 2a were obtained with drift rate norm \(\varvec{\Vert \mu \Vert } = 6.0\) and decision criterion \(a = 4.0\). As is usual in diffusion process modeling, we assumed that RT was the sum of a decision time, given by Eq. 4, and an independent, uniformly-distributed nondecision time with mean \(T_{er}\) and range \(s_t\). The full data set shows evidence of slow errors and is best-fit by a model with drift-rate variability (i.e., by a combination of Eqs. 3 and 5). However, the problem shown in Fig. 2 does not depend on whether drift rate variability is included in the model, although it is accentuated when drift rate variability is large. The predictions in the figure are not intended to be a best-fitting model; they simply show its behavior in a part of the parameter space that is of interest when fitting these data.

As can be seen from Fig. 2a, there is a large artifactual spike of probability mass located near the leading edge of the function. For comparison purposes, Fig. 2b and c shows what happens when either the criterion is held constant and the drift rate is reduced (Fig. 2b) or the drift rate is held constant and the criterion is reduced (Fig. 2c). In either instance the visible artifact is eliminated. These comparisons highlight how sensitive the artifact is to the values of the drift rate and the criterion. This accords with our observation that it is a function of the dot product in the term \(\exp \left[ {\left( \varvec{\mu } \cdot \varvec{X_T}\right) }/\sigma ^2\right] \), the state-dependent part of the function \(\varvec{Z_t}(\varvec{X_T})\), which depends jointly on the drift rate norm and the criterion. In fact, the better performance of the model in Fig. 2b and c is misleading as these predictions included an ad hoc correction we used in previous applications in which the density function for the Bessel process in Eq. 3 is set to zero to all values of time less than some specified index, \(t \le t_\textrm{bad}\). For the predictions in Fig. 2a to c, \(t \le t_\textrm{bad}\) was set to around 450 ms. Although this approach usually provides a way to stabilize the model, it has two significant drawbacks. First, the choice of \(t_\textrm{bad}\) is context-dependent and may need to be different for different participants and different conditions. Second, for large enough values of drift rate and criterion, the artifact begins to merge with the body of the distribution, making it hard to choose a value of \(t_\textrm{bad}\) that controls it without truncating the probability mass. The method we describe here, the results of which are depicted in the “corrected” predictions shown in Fig. 2d, overcomes both of these limitations.

Fig. 3
figure 3

Leading edge of the first-passage time density of the Bessel process computed using the infinite series with (a) \(k = 50\) or (b) \(k = 500\) terms (irregular lines) and the asymptotic approximation \(dQ_t(a)\) (smooth line)

Full size image

Figure 3 provides a precise characterization of the problem and why it arises. The figure shows a highly magnified representation (note the y-axis scaling) of the leading edge of the first-passage time density function for the Bessel process on the range \(0-0.34\) s, computed using Eq. 3. Figure 3a shows the function computed with \(k = 50\) terms in the series and Fig. 3b shows the same function computed with \(k = 500\) terms. In both instances, the functions show high-frequency oscillations, or “floating-point noise,” attributable to the finite-precision (64 bit) floating point computations. Increasing the number of terms in the series does not reduce the noise in the function; instead, it concentrates it in the neighborhood of \(t = 0\) but does not reduce it between 0.30 and 0.34 s, where the leading edge of function begins to diverge significantly from zero, For \(k = 50\), the maximum amplitude of the noise is around \(1.5 \times 10^{-15}\); for \(k = 500\) it is around \(2.2 \times 10^{-14}\). For a stimulus with a drift norm of \(\varvec{\Vert \mu \Vert } = 6.0\), a decision criterion of \(a = 4.0\), a diffusion coefficient of \(\sigma ^2 = 1.0\), and a response made at \(\theta = \pi /4\) rad (\(45^\circ \)), the exponentiated inner product \(\exp \left[ \left( \varvec{\mu } \cdot \varvec{X_T}\right) /\sigma ^2\right] \) in Eq. 4 is equal to \(\exp [24 \cos (\pi /4) + 24 \sin (\pi /4)] = 5.5 \times 10^{14}\), which is a similar order of magnitude to the noise. Consequently, although the magnitude of the noise in \(dP_t(a)\) is very small, when it is multiplied by \(\varvec{Z_t}(\varvec{X_T})\) to obtain \(d\tilde{P}_t(\theta )\) it becomes similar in magnitude to the function itself, leading to the artifact seen in Fig. 2a. Figure 3b makes clear why increasing the number of terms in the series does not ameliorate the problem.

Our solution to the problem shown in Fig. 3a is to use an alternative representation of the first-passage time density function of the Bessel process, which is not subject to noise in the same way as is the series representation, to evaluate the function in the neighborhood of its leading edge. The representation we use is an asymptotic approximation, originally derived by Małecki et al. (2016) and used to study the first-passage time density of the Bessel process by Serafin (2017). In the mathematics literature, the class of Bessel processes is defined by a parameter, usually denoted \(\nu \), which characterizes the dimensionality of the associated Wiener process (Hamana & Matsumoto, 2013). Specifically, if \(2\nu + 2\) is a positive integer then the Bessel process of order \(\nu \) has the same probability law as the radial motion of a \((2\nu + 2)\)-dimensional Wiener process; that is, it describes the Euclidean distance of the process from its starting point. The 2D Wiener process in the CDM is characterized by a Bessel process of order \(\nu = 0\), while 3D and 4D processes in the spherical and hyperspherical diffusion models (Smith & Corbett, 2019; Smith et al., 2022) are characterized by Bessel processes of order \(\nu = 1/2\) and \(\nu = 1\), respectively. Serafin’s results apply to Bessel processes of all orders, so the method we describe here, although we have focused specifically on the CDM, is equally applicable to these higher-dimensional models. Note that this use of \(\nu \) to denote the order of the Bessel process is unrelated to its use in Eq. 5 to denote the mean of the distribution of drift rates.

For our purposes, the key result is the one stated in Serafin’s (2017) Theorem 3.3. His theorem gives a short-time approximation, \(q_1^{(\nu )}(t, x)\), to the first-passage time density function for a Bessel process of order \(\nu \) (Serafin uses \(\mu \) to denote the order), starting at x, \(x \in (0, 1)\), through the level 1.0. The set of possible starting points is stipulated to be open and to exclude zero for technical reasons, because Bessel processes of different orders behave differently at zero. The zero starting point case is the theoretically interesting one in the CDM because the Bessel process is used in the model to describe the first-passage time density function for a 2D Wiener process starting at the origin through a circular boundary a. This is not a limitation in practice because x may be taken as close to zero as desired. Serafin’s result is

$$\begin{aligned} q_1^{\nu }(t, x) \approx \frac{(1 - x)(1 + t)^{\nu + 2}}{(x + t)^{\nu + 1/2} t^{3/2}} \exp \left[ -\frac{(1 - x)^2}{2t} - \frac{1}{2}j^2_{\nu ,1}t\right] . \end{aligned}$$
(6)

As in Eq. 3, \(j_{\nu ,1}\) is the first root (zero-crossing) of the Bessel function of the first kind of order \(\nu \), \(J_\nu (x)\). Unlike Eq. 3, the function in Eq. 6 has a simple algebraic form. Importantly, it does not require summing an infinite series and so is not subject to the same floating-point precision problems as is that function. Serafin stated his results for a process with a diffusion coefficient \(\sigma ^2 = 1\) through a level (i.e., a boundary) of \(a = 1\), but noted that the results for the general case may be obtained by scaling. The relevant scaling is

$$\begin{aligned} dQ_t(a) = \lim _{x \rightarrow 0} \left( \frac{\sigma }{a}\right) ^2 q_1^{\nu }(\sigma ^2 t/a^2, \, \sigma ^2 x/a^2), \end{aligned}$$
(7)

where we use differential notation for the density function, analogous to the notation in Eq. 3.

Fig. 4
figure 4

Infinite-series representations of the first-passage time density functions for Bessel processes of orders \(\nu = 0\), 1/2, and 1, corresponding to the radial motion of 2D, 3D, and 4D Wiener processes, respectively (solid lines) and asymptotic approximations (dotted lines) given by Eq. 7. The functions in the figure are for a boundary of \(a = 1.2\), a diffusion coefficient \(\sigma ^2 = 1.0\), and a starting point \(x = 0.001\)

Full size image

Figure 4 provides a comparison of the series representation of the first-passage time density of the Bessel process for 2D, 3D, and 4D processes (i.e., the processes in the CDM and the spherical and hyperspherical models) to the representations obtained from Eq. 7 with \(\nu = 0\), 1/2, and 1. The series representation for the general case is obtained by differentiating Equation 2.7 of Hamana and Matsumoto (2013). The explicit forms of these functions can be found in Smith & Corbett (2019) and Smith et al. (2022),

$$\begin{aligned} dP_t(a) = \frac{\sigma ^2}{a^2(2\pi )^{\nu +1}} \sum _{k=1}^\infty \frac{j_{\nu ,k}^{\nu +1}}{J_{\nu +1}(j_{\nu ,k})} \exp \left( -\frac{j_{\nu ,k}^2\sigma ^2}{2a^2} t\right) . \end{aligned}$$
(8)

The denominator of Eq. 8 includes a scaling term that transforms the first-passage time density of the 1D Euclidean-distance Bessel process into a symmetrical \((2\nu + 1)\) density that integrates to unity. The representation of the change-of-measure term, \(\varvec{Z_t(X_T)}\), in Eq. 4 is a general one, in which the inner product, \(\varvec{(\mu \cdot X_T)}\), and the drift-rate norm, \(\varvec{\Vert \mu \Vert }\), vary as a function of the dimensionality of the process. Instead of a single polar angle, \(\theta \), the 3D process requires two polar angles, \(\theta \) and \(\phi \), and the 4D process requires three, \(\theta \), \(\phi \), and \(\psi \). These angles map the locus of hitting points, \(\varvec{X_T}\), on the surface of the criterion sphere for the 3D model and the hypersphere for the 4D model. For the 3D model the locus of hitting points is described in spherical coordinates,

$$\begin{aligned} X_T^3= & {} a \cos \phi \nonumber \\ X_T^2= & {} a \sin \phi \sin \theta \nonumber \\ X_T^1= & {} a \sin \phi \cos \theta . \end{aligned}$$
(9)

For the 4D model it is described in hyperspherical coordinates,

$$\begin{aligned} X_T^4= & {} a \cos \psi \nonumber \\ X_T^3= & {} a \sin \psi \cos \phi \nonumber \\ X_T^2= & {} a \sin \psi \sin \phi \cos \theta \nonumber \\ X_T^1= & {} a \sin \psi \sin \phi \sin \theta , \end{aligned}$$
(10)

where \(-\pi \le \theta < \pi \), \(0 \le \phi \le \pi \) and \(0 \le \psi \le \pi \). The use of spherical and hyperspherical coordinates in the 3D and 4D models is discussed in Smith et al. (2022) and Smith & Corbett (2019), respectively. When there is independent, across-trial variability in drift rate the function \(\varvec{Z_t(X_T)}\) of Eq. 4 is replaced with its marginalized counterpart, \(\varvec{\bar{Z}_t(X_T)}\), of Eq. 5, with the number of terms equal to the dimensionality of the process.

Figure 4 shows that the asymptotic approximation provides a good characterization of the leading edge of the function but misses the peaks and tails badly. This is consistent with the intended purpose of Serafin’s derivation, which was to provide an accurate and easily-computable representation of the function’s leading edge. Figure 3 shows just how accurate this approximation is in the 2D case with a decision boundary \(a = 5.0.\) Once the values of the series solution get above the noise floor, the two curves lie on top of one another and the two solutions are indistinguishable. At larger values of t the functions diverge, as shown in Fig. 4, but at small values they are in very close agreement. The agreement suggests a simple algorithm to control the numerical instability, namely, use the asymptotic approximation for small values of t, in the neighborhood of the noise floor, and switch to the series solution for larger values. The only place where some judgment is required is in relation to where to make the switch. Figure 4 shows that the two representations begin to diverge well before the function’s peak, so the best algorithm will be one that uses no more of the time axis than is necessary to avoid the noise in the change-of-measure calculation. Figure 3 suggests that the noise floor is of the order of \(10^{-14}\) or less and that its effects become apparent when the exponentiated inner product in \(\varvec{Z_t(X_T)}\) is of the order \(10^{14}\). Our algorithm simply finds the smallest time, \(t^*\), at which the asymptotic approximation exceeds \(y_\textrm{floor} = 10^{-12}\) and uses the asymptotic approximation for all t less than this value. Explicitly,

$$\begin{aligned} t^* = \min \{t: \; dQ_t(a) \ge y_\textrm{floor}\} \end{aligned}$$

and

$$\begin{aligned} dP_t(a)_\textrm{corr} = \left\{ \begin{array}{l} dQ_t(a); \hspace{0.5cm} t < t^* \\ dP_t(a); \hspace{0.5cm} t \ge t^*. \end{array}\right. \end{aligned}$$
(11)

There is a degree of arbitrariness in the use of \(10^{-12}\) as a criterion, but it is an order of magnitude above the noise floor in the computed series but still leads to a value of \(t^*\) that is much less than the point at which the two functions begin to diverge. Figure 2d shows the effects of using the corrected function \(dP_t(a)_\textrm{corr}\) to compute predictions for \(\varvec{\Vert \nu \Vert } = 6.0\) and \(a = 6.0\), which jointly lead to a greater value of \(\exp [\varvec{(X_T \cdot \mu )}]\) than the one that resulted in the artifact in Fig. 2a. As is evident from the figure, the correction provides an effective way to control the artifact, even at large values of drift rate and criterion.

Fig. 5
figure 5

Fit of the circular diffusion model to the marginal distributions of accuracy and RT for one participant in the VWM experiment. The panels are for set sizes of 1, 2, 3, and 4 items. The predicted values were generated using the corrected version of the first-passage time density function for the Bessel process, \(dP_t(a)_\textrm{corr}\), of Eq. 11 in Eq. 2, with drift-rate variability given by Eq. 5. The main parameters were \(\Vert \nu _1\Vert = 4.95\), \(\Vert \nu _2\Vert = 3.99\), \(\Vert \nu _3\Vert = 3.62\), \(\Vert \nu _4\Vert = 3.49\), and \(a = 4.18\). The nondecision time parameter, \(T_{er}\), was 0.161 s for single-item displays and 0.191 s for larger displays with \(s_t = 0.06\) s for all conditions. Estimated nondecision times for diffusion model fits to VWM data are typically shorter when there is only a single item in the display because the identity of the item to be reported is known at the time of presentation (Sewell et al., 2016)

Full size image

As a further proof of concept, Fig. 5 shows a fit of the CDM to the full data set that was excerpted in Fig. 2. In addition to drift rate, criterion, and nondecision time, the complete model includes drift rate variability parameters (the \(\eta \) parameters of Eq. 5) and drift-rate bias parameters. The drift rate variability parameters allow the model to predict slow errors and the bias parameters allow it to predict differences in speed and accuracy for stimuli in different parts of the color space. The effects of these parameters appear only indirectly in the marginal distributions of decision outcomes and RT in Fig. 5, but become evident in plots of the joint distributions of outcomes and RT and plots of speed and accuracy conditioned on the location of the stimuli in color space. We omit the details of these aspects of the fit and will present them elsewhere. The reader is referred to Smith et al. (2022) for accounts of the role of drift rate variability and bias parameters in fitting color and motion data, respectively. For our purposes, the primary interest of the data in Fig. 5 is that accuracy was uniformly high for all set sizes and RTs were relatively short, especially in the \(n = 1\) condition, leading to large estimates of drift rates. The figure shows our method provides an effective way to fit data in this part of the parameter space.

We investigated the sensitivity of the computed log-likelihoods to the choice of the noise threshold parameter, \(y_\textrm{floor}\), in Eq. 11. With \(y_\textrm{floor} = 10^{-12}\), the negative log-likelihood of the fitted model shown in Fig. 5 was \(-LL = 794.6\). This value was unchanged to four significant figures with \(y_\textrm{floor}\) varying over several orders of magnitude from \(10^{-13}\) to \(10^{-6}\). Overall, then, the method appears to be robust to variations in the choice of the noise floor parameter.

Discussion and Conclusions

Many empirical studies of continuous-outcome tasks consider distributions of decision-outcomes only and seek to model them using ideas based on, or related to, signal detection theory (Schurgin et al., 2020; Tomić & Bays, 2022) and do not consider RT. Among models that jointly predict outcomes and RTs, the CDM has two features that make it stand out. First, it is a stochastic evidence accumulation model that provides a theoretical solution to what Smith (2023) called “von Neumann’s problem” — namely, the synthesis of reliable organisms from unreliable components. The components in question are neural elements subject to moment-to-moment stochastic perturbation or neural noise. Second, explicit mathematical expressions exist for the CDM’s joint distributions of RT and accuracy (Smith, 2016). These expressions lead to two theoretical benefits not shared by other models. The first is that the model predicts, analytically, that the decision outcomes will follow a von Mises distribution. This property is important because most empirical studies of continuous-outcome tasks characterize accuracy using von Mises distributions or mixtures of von Mises distributions. Instead of simply being an empirical summary of the data, the CDM provides a theoretical account of why von Mises distributions of outcomes should arise psychologically, through accumulation of noisy evidence to a response criterion. The second is that the model provides a theoretical decomposition of the von Mises precision parameter, \(\kappa \), into interpretable cognitive components. Precision is inversely related to the spread or dispersion of a distribution and in empirical studies of continuous-outcome tasks it is often treated as a free parameter when fitting models to data. In contrast, the predicted von Mises precision in the CDM depends on the components of the decision model. Specifically, it is

$$\begin{aligned} \kappa = \frac{a\varvec{\Vert \mu \Vert }}{\sigma ^2}, \end{aligned}$$
(12)

as shown in Equation 29 of Smith (2016). That is, precision is equal to the radius of the criterion circle multiplied by the drift-rate norm, divided by the diffusion coefficient. Expressed otherwise, it equals the amount of evidence used to make a response multiplied by the quality of the evidence in the stimulus, divided by the noisiness of the evidence accumulation process. This expression parallels a similar expression derived by Link (1975) for an unbiased random-walk or diffusion model for two-choice decisions. The two-choice expression is, in turn, closely related to the expression for sensitivity in the Luce Choice Model version of signal detection theory (Luce, 1963; McNicol, 1972/2005).

These evident theoretical benefits of the CDM notwithstanding, its practical utility is limited if it cannot be fitted to data in a straightforward way. The problem we have addressed often arises in scientific computing, because the special functions of mathematics and physics can only be represented with finite precision in floating-point arithmetic. The Girsanov change-of-measure calculation, which is at the heart of the predictions for the model, involves multiplying very small numbers by very large numbers, which magnifies noise in the former. The resulting numerical instability in some parts of the parameter space appreciably complicates the task of fitting the model to data, because individual fits need to be inspected visually for artifact. The artifact can often be controlled by forcing the first-passage time density function for the Bessel process to be zero for all times less than some specified index but this approach has significant limitations, as we discussed earlier. It becomes onerous when the number of participants is large because the index may differ for different participants and different conditions and it makes the model unsuitable for use in hierarchical Bayesian settings because artifacts like the one in Fig. 2a would be hard to detect in posterior distributions marginalized across participants.

The solution we have provided here, of using an alternative asymptotic representation of the first-passage time density function of the Bessel process, offers a fast, simple, and easy-to-implement solution to the problem. As the example of Fig. 5 shows, use of a correction for the leading edge of the first-passage time density function for the Bessel process yields stable, artifact-free representations of the distributions of error and RT when drift rate is high or the decision criterion is large. The corrected solution could be used by a researcher wishing to use hierarchical Bayesian methods to fit the model to data from a sample of participants simultaneously, using a model in which the decision criteria and the drift rates are random samples from population-level distributions. These kinds of methods are useful when there are data from many participants, each of whom have contributed relative few experimental trials (Ratcliff & Childers, 2015).

To assist researchers wishing to investigate the CDM further, the accompanying online materials, at https://osf.io/wn7rp/, contain example code written in C/Matlab, R, and Python. The C-code is in the form of a mex file called from Matlab. Because C is a statically-compiled language, the code is very fast. Each of the code examples give \(d\tilde{P}_t(\theta )_\textrm{corr}\), the joint density function of decision outcomes and RT for a process with across-trial variability in drift rates, embodying the correction factor described here. We have not provided fitting routines, because these need to be tailored to specific experimental designs and to reflect the assumptions a researcher wishes to make about how model parameters vary across conditions. Instead, the routines provide a basis for researchers wishing to adapt the model to their own problems. Example Matlab code for fitting the model by maximum likelihood, without the correction factor, to a continuous-outcome task can be found at https://osf.io/8ptxd. The code in that example is for a continuous-outcome random dot motion task, analyzed by Smith et al. (2022) using the circular and spherical diffusion models.