Bayes Factors for Mixed Models: a Discussion

Abstract

van Doorn et al. (2021) outlined various questions that arise when conducting Bayesian model comparison for mixed effects models. Seven response articles offered their own perspective on the preferred setup for mixed model comparison, on the most appropriate specification of prior distributions, and on the desirability of default recommendations. This article presents a round-table discussion that aims to clarify outstanding issues, explore common ground, and outline practical considerations for any researcher wishing to conduct a Bayesian mixed effects model comparison.

Marginality, Interactions, and Defaults

Opening Statement

One of the central topics in this special issue has been the principle of marginality. Discussion on this principle dates back to Yates (1935), and has been repeatedly referred to in the (mixed) linear modeling literature. The main argument in favor of this principle is that models that include an interaction are rarely theoretically meaningful when they do not also include the constituent main effects. Specifically, it is hard to conceive of plausible cases where an effect is perfectly balanced, such that the average effect is 0, while different from 0 for certain covariates. The principle of marginality implies that the most commonly used model comparison for factorial designs (i.e., the Balanced null comparison, or its frequentist analogue type 3 sum of squares) ought to be replaced as the default option by the more theoretically meaningful Strict null comparison (or its frequentist analogue type 2 sum of squares). As noted by Rouder et al. (2022), this does not release researchers from the obligation of carefully considering their modeling choices, but the Strict null comparison may serve as a better starting point. In the context of mixed effects models, we are already excluding certain models a priori because they are not considered meaningful (e.g., a model without random intercepts or fixed effect, but with random slopes¹), so why not remove one more model from the mix? The critical issues seem to be (a) whether or not particular models should be excluded beforehand; (b) if so, what models these should be. Has anybody changed their mind on the issues since reading the other contributions (specifically the Rouder et al. paper)?

Andrew Heathcote and Dora Matzke

Our objection to adhering to marginality is illustrated in Fig. 1, which construes the same data set in two different ways. Despite both construals having two null effects, and being based on the same data, adhering to marginality produces a contradictory outcome, licensing interpretation of the non-null effect in Fig. 1b but not Fig. 1a. One might object to “fine-balance” required for the null effects, but a further analogous example described in the figure caption shows such null effects are plausible in an experiment using commonplace controls, and again contradictory outcomes are produced by adhering to marginality. We believe these examples illustrate why adhering to the principle of marginality can lead to an unfortunate dependence of the statistical models one is licensed to test on the intentions and opinions of the analyst.

Fig. 1

The figure depicts results for a design in which raters (Republicans or Democrats) indicate their approval for actions performed by two groups (Hunters and Hippies). a One researcher analyzes these data in terms of this literal design and finds no main effects but a strong interaction. b Another plots it in terms of their theoretical prediction that approval is higher for groups whose beliefs are more congruent with those of the raters (Republicans = Hunters, Democrats = Hippies), and finds a strong main effect of this factor without the other main or the interaction effect. The same outcome could occur when the rated groups are novel (“Snurgels”/“Wurgels”) with characteristics and scenarios developed to elicit equal average ratings, and participants are randomly allocated to provide ratings from the point of view of someone with “Snurgelish” or “Wurgelish” characteristics. In this case, both rater and group factors can be reasonably assumed to have null effects in expectation. Note that these examples are not meant to imply that theory-based construals can or will always correspond to non-null main effects rather than interactions, the obverse seems to us equally plausible

In summary, our original commentary found a rigorous mathematical basis for the principle of marginality only with continuous covariates, not in ANOVA designs. We think examples like the foregoing reject the assertion of Nelder (1977) that marginality-violating ANOVA models are “of no practical interest” (p. 50) because in general they clearly do not always correspond to what he claimed are “unrealistic hypotheses” (p. 51). We do not deny that there can be situations in which particular models should be excluded because they do not make psychological sense, but we believe that marginality does not provide general guidance on this issue with fixed effects, and it is unclear to us why that should be different for random effects.

Jeff Rouder

The principle of marginality does not rule out the crossover interactions in Fig. 1a nor does it prevent the data recoding in Fig. 1b. What it says is that perfect crossovers are not likely; instead, crossover interaction likely entails corresponding main effects. In the current example with Democrats and Republicans and hippies and hunters, there are two main effects. The first is about the favorability of hippies and hunters averaged across Democrats and Republicans. Is there a perfect balance here so that the average favorability is the same? How about hunters vs. Black-Lives-Matter protesters; would that upset this perfect balance? Or hippies vs. pro-life protesters? The second main effect is about Democrats or Republicans. Do we really believe there is no overall effect of party affiliation on rating people in general? Maybe Democrats by their nature are big-city snobs who rate everyone lower; maybe it is just the opposite. And would it not depend on how we defined a Democrat/Republican or whether we included certain regions (say lifelong Democrat vs. recent Democrat; including Guam and Puerto Rico vs. not)? I suspect that perfect balance of main effects does not exist conditional on an interaction.

The principle of marginality is not about the presence of crossover interactions. It is about the corresponding main effects. Assuming there are no main effects (of Democrat-vs-Republican or of hippy-vs-hunter) when testing for an interaction is dangerous as it implies perfect balance. And this perfect balance relies on magical levels, that is, just the right definition of Democrat or Republican and of hippie and hunter. In science, there is no magic, so include main effects in models with interactions. It’s not a matter of math or statistics or rigor; it is just common sense. It would be helpful if someone could provide a scenario where exact balance might conceivably hold.

David Kellen

Summarizing Rouder, the marginality principle establishes that interactions are in all likelihood accompanied by main effects. An interaction-only model is deemed implausible because of the perfect balance that it implies.

The example provided by Heathcote and Matzke shows how main effects and interactions can “switch places” as a function of how variables are coded (e.g., absolute vs. relative terms). To make the point clear to everyone, Tables 1 and 2 show the zero-sum contrast coding associated with the two scenarios in Fig. 1—notice the swap between the rightmost two columns (in bold and italics).

Table 1 Zero-sum contrast coding associated with the scenario in Fig. 1a

Table 2 Zero-sum contrast coding associated with the scenario in Fig. 1b

What Heathcote and Matzke’s example shows is that the suspicions being raised by the marginality principle do not apply to the contrast codes themselves—which is all that the ANOVA model “knows”—but to the analyst’s thinking; i.e., how they are coding their variables. After all, it’s the exact same model in both cases.

Now, I’m all for developing ways to sharpen or discipline researchers’ thinking. But I don’t see how that is to be achieved by issuing a ban on an arguably abstract model comparison and/or summoning all kinds of thorny ontological considerations (are point nulls or perfect cancellations realistic?) based on how we name a vector. The effort appears to be misplaced. I am more in favor of the kind of recommendations found in the social-psychological literature, which focus on appeals to theory and richer experimental designs (see Brauer and Judd, 2000).

Henrik Singmann

The argument that model comparison should adhere to the principle of marginality is in my view a statistical “no true scotsman” fallacy, essentially an argument about statistical purity. The question Rouder poses is as follows: Can there be a cross-over interaction that perfectly cancels out the main effect? Whereas one can probably come up with examples where this might be the case, Rouder is right that it is unlikely. Given this unlikeliness—which seems to be nothing more than a violation of an imagined statistical purity—he demands we ban the corresponding models from our statistical toolbox.

The problem with this argument is that it places statistical purity before statistical practice. In statistical practice, models that violate marginality serve a clear purpose; to test whether a lower-order effect is zero while allowing the higher-order effect to be accounted for. Even though a perfect cross-over interaction that cancels out a main effect is unlikely for factorial ANOVA, we still want to know whether for our concrete data we have evidence for the main effect. Likewise, even though a zero fixed effect but non-zero random slope might be unlikely in a mixed model, we still want to know whether for our concrete data we have evidence for the fixed-effect.

Banning certain models for reasons of statistical purity unduly restricts statistical practice. The alternatives, such as Rouder’s Strict null comparison, simply do not permit the type of inference that are of primary interest in an applied setting. Let’s not throw out the substantive baby with the statistical bathwater.

Richard Morey

I take it for granted that all discussants agree on the idea of modeling as an iterative, judgment-laden process, and likewise that no person (including the authors of the Rouder et al commentary) believe in a “ban” on particular model specifications. “Interaction” is an idea that has at least two senses: there is the mathematical idea, as expressed in contrast coefficients or the “parallel lines” heuristic; then, there is the scientific idea, which is less precise. Perhaps, the clearest way we can see the dissociation between the mathematical and scientific use of “interaction” is that we can find spurious interactions from, say, ceiling/floor effects. These are, mathematically definitely interactions: there is no way for effects to be additive when there is an upper/lower bound. There is nothing “spurious” about these interactions, in a purely mathematical sense. There is definitely a lack of additivity. Rather, an interaction depending on a ceiling or floor effect is spurious because it depends on the representation of the problem, which leads to a more complicated expression of a data pattern than necessary. Sometimes if we change the representation of the problem, we can get a much simpler way of expressing what’s going on.

Heathcote and Matzke’s example shows another example: if we change the representation of the factors, the interaction “disappears.” This means that the “literal” representation of the factors was lacking something. If an interaction can be represented as a main effect, then that says something important about the problem: In the example, for instance, it means that congruence in identity appears fundamental.

Any modeling exercise must begin with a choice of problem representation, and that representation can be revised. If we can code important insights in the representation, instead of in a multiplicity of models, we should.

If we do this, then an interaction can be removed by a mere recoding. What then? It means we need to revise what we think an “interaction” is. I’ll leave aside issues of transformations of the measure for now (though the need to consider them is a corollary of my view²), but one might demand that an interaction not be removable by mere recoding: that is, we need all the available degrees of freedom to account for the data pattern. This is the best representation of the idea that “the effect depends on the factor levels, so something complicated is going on.”

If we can accept that the idea of an interaction requires all available degrees of freedom, then this implies that we include all main effects with an interaction, because this model best represents the “it’s complicated” idea. The pure crossover implies “let’s rethink this.” Rouder et al’s point might have better been qualified by “once we’re happy with the representation of the problem.”

David Kellen

In my view, the second question posed by Van Doorn et al., “what are the relevant model comparisons for an interaction effect in a two-factorial design?” presupposes the existence of a general answer that can be figured out “in the abstract,” without any consideration for the substantive matters that different researchers are dealing with. The appeals to authority, which Heathcote and Matzke (this issue) criticize in their response, reinforce this view that we are dealing with an issue that can be settled from the bench. What Singmann et al. (this issue) tried to convey is that this is not the right question to ask: Anything other than encouraging people to be free to tailor model comparisons to the specific questions that they are trying to address (along with proper justification) is an excessively prescriptive move. It creates a barrier, something that researchers will have to overcome in case they don’t think that a certain set of pre-specified comparisons suits their specific problem.

Now, I most certainly sympathize with Richard’s proposal (if I understand it correctly) of a “metalinguistic maxim” according to which the construction of variables should prioritize the characterization of phenomena by means of main effects. After all, the “talk of variables in Psychology” is a centennial big ol’ mess whose cleaning is going to need as much attention and intellectual muscle as it can muster (see Danziger 1997, chap. 9; see also Menger (1954) and Rozeboom (1956)). However, I fear that this specific proposal, if strictly enforced as I predict it to be (just look at all the strict views on preregistration that are out there these days), will inhibit researchers from exploring a number of legitimate alternative hypotheses. As discussed by Brauer and Judd (2000), different variable codings (absolute vs. relative) invite substantively different interpretations of the same data, many of which can be disentangled using tailored experimental designs. Disallowing certain codings appears to sweep these legitimate interpretations off the table. I also note that the aforementioned maxim seems to (at least in part) draw from the notion that interactions are of a lower status given that they are often removable, as famously demonstrated by Geoff Loftus in 1978. I feel compelled to point out that removability is not intrinsic to interactions—main effects can also be removable (see Garcia-Marques et al.2014).

Michael Kalish

The rule-of-thumb some of us articulated was “don’t do statistics you don’t understand”—this is vague (we are all left to decide if we understand) and specific (relative to an individual’s understanding). The paper proposes a different rule-of-thumb, based on the experiences of experts and their views about likely data patterns. The argument seems to be whether these experiences are sufficiently general to warrant a rule, or only a corollary to the general principle (something like “Don’t do statistics you don’t understand, and you probably don’t understand ANOVA if you are looking for interactions without main effects”). I think this corollary is flawed, because it conflates the statistical concerns about (in this case) removable effects with substantive concerns about effects—which is, as far as I can tell, entirely Kellen’s point. A weaker version (“be extra careful when testing for interactions without main effects”) is practically tautological (“always be extra careful” is a good stats tip).

The concern about vanishing interactions strikes me as related to the notion of coordination, which the response misses. A latent variable is essentially unobservable; we attempt, through the process of coordination, to develop measures of these variables and to understand their meanings (what the variable is) simultaneously—I take it that this is the ordinary practice of science. Psychology is cursed with latent variables whose technical meanings are cluttered with the residue of our ordinary vocabulary (e.g., “attention”) so coordination has a harder time getting going since it requires a technical vocabulary free from pre-theoretic semantics. The problem of coordination is not one of reduction; reduction assumes a realist stance about latent variables that is warranted only by a conceptually confused metaphysics on which persons don’t really make decisions etc. but only their brains do. This is irrelevant to the problem of coordination, which deals with the relationship between a measurement and its meaning. The critical point about coordination is that there is no reason to assume it is linear; some lucky results in the past (see, e.g, temperature) notwithstanding, linearity might strike some as optimistic in the realm of psychological measurement (e.g., warmth). The use of, e.g., drift rate as a measure for the rate at which a person accumulates evidence is an example of where coordination has not been established. If the linearity assumption is questionable, then the best rule-of-thumb might be “Don’t use linear models.” On the other hand, as Abelson (2012) puts it, “You can do anything you choose, and ponder the potential meaning of the results for your research.”

Clintin Davis-Stober

Much of this discussion can be boiled down to highlighting the importance of letting substantive concerns drive modeling decisions, subject to the interpretive limitations of the modeling framework. As it should be. In an effort to sharpen these points, I’d like to draw a distinction between “theory-rich” and “theory-poor” environments. I think this is where general recommendations become tricky, as these two environments implicitly set different goals and the same statistical framework can be applied to both.

In theory-rich environments, the modeling framework serves as an operationalization of the theory being tested, with model comparisons driven by substantive questions (as motivated in Rouder et al., 2022). Functional relationships can be specified among the variables, with appropriate choices of coordination functions reflecting reasonable scientific thought, as argued by Singmann et al. (2021) and Michael’s comment. Priors can be selected to help instantiate the theory itself (Lee and Vanpaemel, 2018; McCausland et al., 2020) and are easily set for unstandardized values. What a bright, lovely world to live in.

In theory-poor environments, the collection of effects become things “in and of themselves.” This is a dark, cold world, but I’m willing to believe that there exist scientifically informative effects of this kind. The motivation for the modeling has changed substantially for this case. The effect is now a thing to be detected and estimated (in and of itself). The problem has shifted from adjudicating competing scientific theories to one that is almost forecasting: Can we reliably detect and estimate this effect, which is a function of random variables? All of the previous comments on interpreting main effects and interactions still apply, in fact, they are more important - is the effect a “real” thing or simply a coding artifact?

Given that most psychology investigations lie somewhere between these two extremes, I think recommendations need to harmonize with the theory environment. For example, in theory-poor environments, I might be more interested in choosing priors that solve forecasting problems (e.g., recruiting teams of experts to construct priors), which would impact how I think about defaults. Perhaps eschewing direct model comparisons altogether would be better in this situation (Heck & Bockting, 2021) given that there is not much theory to motivate them.

Daniel Heck

Davis-Stober’s comment highlights an important distinction: Only in theory-rich environments, researchers may have strong prior beliefs about plausible distributions of parameters. Moreover, and more importantly for the current debate, researchers may also have strong expectations about which statistical models should be considered and which are implausible a priori. The consequence of the latter type of prior beliefs becomes especially clear from the perspective of model selection or model averaging, where it is unavoidable to specify prior probabilities for all models. In some contexts, researchers may have sufficient theoretical arguments to exclude some models a priori (e.g., those violating the principle of marginality). In other contexts, this may not be possible given only weak theoretical background knowledge. However, even in the latter scenario, it is still infeasible to consider “all possible models,” given the combinatorial explosion in factorial designs and the fact that the “number of possible models” is infinite. Hence, one always has to focus on a certain subset of models, thereby committing to some (auxiliary) assumptions.

What do such considerations imply for deriving pragmatic heuristics for applied researchers? From a methodological perspective, any recommendation should ensure a certain robustness across various modeling contexts. Such robustness can be achieved by regularly considering not only two competing models, but a set of models. Hence, one could simply recommend to at least consider whether it makes sense to include more than two models in the comparison. This does not imply that one always has to run model comparisons; sometimes, comparing two models might be sufficient. However, by highlighting the ambiguity in selecting some statistical models for the analysis a priori, the inherent uncertainty in model specification is made transparent. If more than two models are actually fitted, the uncertainty will also be reflected by the results of the statistical analysis. As a corollary, such a recommendation would imply that one has to consider whether specific model versions are meaningful at all in a certain context (e.g., by drawing on the present debate).

Regarding the principle of marginality, it appears to be important to distinguish between interactions of two factors that represent theoretical constructs (i.e., fixed-effects interactions) and interactions of a theoretical factor with person characteristics (i.e., random slopes). It is not clear whether the arguments supporting the necessity to include main effects in the presence of interactions generalize from the former to the latter scenario. Variance in person-specific effects of the independent variable can emerge for various reasons that are not theoretically meaningful. For instance, unsystematic nuisance variables may induce individual random-effects (e.g., lack of attention, response bias, fatigue, and testing effects). Such psychological side effects can be statistically relevant depending on details of the experimental design (i.e., whether the order of trials and stimuli is randomized, how many trials are included for each factorial combination, and whether there are breaks). Importantly, nuisance variables may not only affect the average response level of the dependent variable (resulting in non-zero random-intercept variance) but also result in differences between the factor levels at the individual level (resulting in non-zero random-slope variance). Whereas nuisance effects may cancel out at the group level given a sufficient number of participants, they do not necessarily cancel out at the individual level, especially when the number of responses is small. Hence, it may be difficult to assign a prior probability of zero to mixed models that assume the absence of an effect at the group level while allowing for random slopes (i.e., an interaction of the theoretical factor and the person).

Greg Cox

The discussion around the principle of marginality is intended to help researchers decide what their “default” model should be: “[t]he principle of marginality implies that the most commonly used model comparison for factorial designs (i.e., the Balanced null comparison, or its frequentist analogue type 3 sum of squares) ought to be replaced as the default option [emphasis mine] by the more theoretically meaningful Strict null comparison.” I wanted to take a moment to synthesize some recent comments, think about what a “default” is, why they are used, and what sorts of principles might better guide the search for useful “defaults.”

All technology comes with “default” settings. A new TV comes with its brightness, contrast, saturation, etc., set to particular values. An office chair comes with the seat at a particular height. Computer programs have parameters with values that are initially set by their programmers. Statistics is part of the technology of science, and so it is natural that there should be “default” statistical approaches as well. Indeed, statistics has even been called the “science of defaults.” Why are defaults necessary at all? As the examples illustrate, a default serves two functions: The first function is to enable technology to operate at all without the user needing to set every parameter. You can turn on your TV and see something without first adjusting its image quality. You can sit in your chair without first needing to raise or lower it. You can run an optimization routine without first needing to set each of its parameters. As Morey says in regard to statistics, modeling is an “iterative, judgment-laden process”. A default statistical model is one that at least works “right out of the box.” The iterative nature of modeling makes having a starting point valuable because often it is not even clear what judgments need to be made at all, let alone what the “right answer” is. Heathcote and Matzke’s example is a good one in that a researcher who first plots their data in the form shown in Fig. 1a may then realize that the recoding in Fig. 1b is more revealing of a theoretically interesting relationship. Often by seeing our initial attempts fail are we guided toward a more appropriate and insightful model. To know how to set the height of the chair, we first have to sit in it.

The second function of a default is more germane to the present discussion, and is nicely summarized in Heck’s comment: “any recommendation [for a default approach] should ensure a certain robustness across various modeling contexts.” To paraphrase, a default is meant to do a good-enough job in the majority of use cases, something that a user could employ without making any substantive choices, but which nonetheless performs the desired function to within some tolerance. The image settings on a TV are meant to be “good enough” for most people. The height of a chair is set based on an “average” body size. A programmer believes that certain parameter values will work most of the time for their optimization routine. In statistics, the “default” model is one that “we” (in the royal sense) believe applies to the majority of research scenarios. As such, many of the arguments about what is “plausible” or “implausible” are really arguments about what people believe are more frequent use cases for different statistical models.

Heck enumerates a number of important concerns that can help inform which models should be considered plausible or implausible in any particular scenario. But it is telling that these are theoretically meaningful considerations, regarding latent psychological variables like “lack of attention, response bias, fatigue, testing effects.” As Heck says, these theoretical issues are statistically important because they help define the set of models that represent reasonable theories of how the data should be partitioned so as to be most informative with respect to the causal mechanisms that produced the data. To then relate this to Davis-Stober’s remarks regarding “theory-richness,” any attempt to provide general recommendations or “defaults” is only feasible when it is possible to enumerate the theoretical constructs that might profitably explain the data. This is also the crux of Heathcote and Matzke’s example—theory about political attitudes suggests a model structure (framed around the [latent] construct of “congruency”) that aligns with not just a description, but an explanation of the resulting data. Attempts to use vague statistical principles like “marginality” to motivate a default model are quickly overwhelmed by the need to use theory to guide modeling choices.

To nonetheless advocate for a specific default is problematic because just as theory can constrain a statistical model, a statistical model implies a theory. This is the tail wagging the dog. To be sure, a researcher can pick a default to start with and then depart from it. If so, then the default is serving the first function I outlined above, to just “get things started.” Personally, I see no problem with this in itself. But if the default is used to serve its second function, to be “good enough,” then I think this is a problem. It is a problem because it means either that (a) the research scenario is not well-specified enough to enumerate the theoretical concerns that would guide the development of a more appropriate model, or (b) the researcher is not critically examining the implicit theoretical assumptions of the default model as applied to their scenario. The Heathcote and Matzke example shows a potential case of (b).

So what should guide our choice of default recommendations, if anything? Defaults can be useful in the first sense (to get things going), but problematic in the second (to be “good enough”). So I suggest, half-facetiously but half-seriously, that our default recommendations lead to the worst possible model that nonetheless maps onto the structure of the data. I admit I don’t have a good general definition of “worst,” but one example of something that would qualify is given by Davis-Stober et al. (2022). Their “worst possible model” assumes that effects have random directions, essentially severing the coordination function that connects constructs in the model and observable quantities. The point is to ensure that anyone who adopts a default model will not stick with it or, if they do, only because they have critically considered the theoretical concerns they are trying to address and concluded that the default really does represent a plausible theory for their data.

E.-J. Wagenmakers

I agree with much of what was said before. But to place our initial contribution in context, consider a continuum of informed analysis. On the one end, we have Nirvana: the analyst fully understands the statistical methodology, has deep theory to guide predictions, and uses expert background knowledge. On the other end, we have the methodology that is currently dominant, that is, the frequentist null-hypothesis significance test in which a finding is deemed present whenever p < .05 (e.g., Singmann et al., 2020, for the afex package in R). With this continuum in mind, I would like to emphasize that Nirvana is almost fully out of reach. Psychologists are not trained to be statisticians, deep theory is absent in 99.9% of situations in which psychological scientists desire a test, and expert prior knowledge is virtually never used. This will not change in the foreseeable future. Our goal should therefore be modest—we aim for improvement, not perfection. And when practical researchers wish to apply a Bayesian mixed model hypothesis test to their data (a move in the direction of Nirvana, in my opinion), the question immediately arises what specific models ought to be applied. In this regard even those who argue against any default method issue strong opinions. For instance, Singmann et al. (2021) write: “Therefore, it seems generally appropriate to designate the model with maximal random-effects as the alternative model.” This appears to rule out a number of other models, ones that are taken seriously by other contributors (e.g., Rouder et al., 2022; Heck and Bockting, 2021). I believe that there do exist general statistical arguments over what models are appropriate in what scenarios. Outlining these arguments will be helpful to the practitioner (who after all is not a statistician, lacks any guiding theory whatsoever, and is unwilling to specify background knowledge). Note that in our original article we did not advocate for any specific default—rather we wanted to initiate a discussion among experts as to what model comparisons were useful.

David Kellen

If I understand E.-J. Wagenmakers correctly, your argument is that our position is perhaps naively idealistic because it does not take into consideration the reality of the “practical researcher,” who “ is not a statistician, lacks any guiding theory whatsoever, and is unwilling to specify background knowledge.” Basically, the idea is that these people are unwilling/unable to change, and they are going to be out there doing things no matter what. But if we manage to build this convenient statistical infrastructure around them, chock-full of good advice and nutritional value, we can at least try to keep them out of trouble and hope for a better future.

I apologize for the colorful analogy, but in all seriousness this reminds of how in the late 1990s, politicians in my home country (Portugal) realized that instead of penalizing drug addicts, it was better to treat them as chronic patients and provide them with clean rooms alongside a steady supply of syringes and methadone. This way, we could try to keep them out of trouble and hope for a better future. And apparently it worked then, so I guess you have a point here. I sincerely hope that you’re right.

Still, a couple of reactions:

• 1. I remain skeptical about the ability to automate or streamline scientific inference by determining “in the abstract” what models are useful and which ones are not. If anything, because any such a determination requires the researcher to establish goals; i.e., useful for what? It’s like trying to determine the fitness of an agent without specifying an environment and a loss function. As an example, let’s take the recommendation for maximal random effects: it simply states that researchers should keep in mind that their data are the outcome of “encounters” between randomly sampled units, such as people and items. And that ignoring this aspect can have negative consequences (e.g., inflated estimates and type-I errors), when assuming certain goals. But in other cases, ignoring it is perfectly acceptable (e.g., a given ordinal prediction to be tested is unaffected by aggregation). As a matter of fact, even the partitioning of variance into main effects and interactions is very often a questionable move—planned contrasts or order constraints are superior options. Moreover, I don’t think that we can get a lot of mileage out of deracinated scenarios simply because the exact same data structure can be interpreted in many different ways. The 2 × 2 example that Andrew, Dora, and I discussed shows that what might seem appalling in some cases is perfectly reasonable in others. And as Heck and Cox pointed out, even when discussing general desiderata such as “robustness,” subject-matter considerations end up being unavoidable. It turns out that at the end of the day, researchers are going to have to live up to what is expected from any professional class, namely knowing something about what they’re doing and making use of it.

• 2. Maybe what separates certain communities within psychology (perhaps the “practical researchers”?) is not so much a matter of intellectual ability, training opportunities, or resources but values. More concretely, the prioritization of showmanship and grand oratory over careful thinking and a concern for getting things right. I don’t think that creating the aforementioned statistical infrastructure will lead to any meaningful positive change with respect to that target audience. Quite sadly, I expect it to have the opposite effect: Namely, the additional patina of sophistication (“did I mention that our analyses uses Bayes factors?”) and credentialing (“oh, and as you can see by the badges, everything is certified!”) is only gonna make things harder to change. As the historiography of the discipline tells us, one of its original sins is the (enduring) misconception that its foundational challenges can be solved by methodological and/or technological means (see Danziger 1990).

Frederik Aust

I want to steer the discussion about the principle of marginality towards the cases we outlined in our initial discussion paper, namely, away from fixed effect interactions towards random slopes. My thinking about the relevant model comparisons has substantially evolved through our exchange. I think both have their place and I want to offer some thoughts on two perspectives that I think can guide the decision.

Rouder et al. argue for adherence to the principle of marginality with respect to random slopes based on substantive considerations. They consider the ambiguous result of the strict null comparison “more a feature than a limitation”. The maximal Model 6 assumes that the magnitudes of effects on each individual follow a normal distribution with some mean (the fixed effect) and variance (the random slope variance). In essence, Rouder et al. argue that there is little value in examining the mean of this distribution in isolation—researchers should examine the full distribution of effects. The reasoning is that the mean (expected value) of the distribution is of relevance only to the degree that it is a fair summary of the population—that is, when the mean is large relative to the variance. To illustrate, consider a positive mean effect of 0.5 with a population standard deviation of 1. In this case, 30% of individuals have negative effects. If we were to make a prediction about the direction of the effect in a new individual based on the positive population mean, we would be wrong with a probability of 30%. So the benefit of the ambiguity in the strict null comparison is that it encourages the analyst to consider the full distribution of individual effects and to interpret the fixed effect estimate in relation to the variance of effects. Evidence in favor of Model 6 cannot be the end result, it simply indicates that there is something worth investigating further—at least one individual shows an effect.

And here we get to the heart of the argument: If one is interested in inference at the level of individuals, I think it is fair to say that it is of limited interest to test the fixed effect in the presence of random slopes (the balanced null). To claim an effect for (the majority of) individuals, it is most relevant whether the fixed effect is large relative to the random slope variance, not whether it differs from zero. Unfortunately, this question is not directly addressed by the strict null comparison—more sophisticated modeling is required (e.g., Haaf & Rouder 2017, 2019).

Yet, I think a test of the fixed effect (the balanced null comparison) is relevant when one is interested in inference at the population level. Consider the following example: To address a lack of organ donors, it is prudent to study the effectiveness of switching from an opt-in to an opt-out approach: Will there be more organ donors if everyone defaults to donating? Switching to opt-out may plausibly cause reactance in some individuals making them less willing to donate organs. Yet, the success of a change to public policy is largely determined by whether the new policy yields an overall increase in the number of donors. Opposite effects on a minority subset of individuals are of subordinate interest.

In medicine, an analogous distinction is made between two targets of inference: conditional and marginal treatment effects (e.g., Remiro-Azócar et al., 2021), each of which has their place. Conditional treatment effects are relevant in clinical practice when a decision is made for a given patient (conditional on their covariate manifestations³), whereas marginal treatment effects are relevant to public policy, which affects the population as a whole.

Based on these considerations it seems that Singman et al. believe that most researchers are interested in marginal effects (“they are just interested in the average effect,” p. 5), whereas Rouder et al. think that conditional effects are of primary concern (“We worry here if the mean is useful when a sizable proportion of individuals has a true effect in the opposite direction,” p. 9).

With all this said, my current thinking is that there are two perspectives on the decision between strict vs. balanced null comparisons. First, we take the null models seriously as a theoretical statement (e.g., no individual differences without non-zero average effect). The substantive appropriateness of each null must then be carefully considered in each application anew. Personally, I find this perspective very satisfying but it can make the decision difficult and contentious. Second, we consider the null model as an approximate representation or a useful skeptic’s position. In this case, the decision should depend on the target on inference—individuals or population. If the target is individuals, the strict null comparison seems most relevant but, when an effect is claimed, should always be followed by an examination of the population distribution. If the target is the population, the balanced null seems relevant. Denying the relevance of the balanced null comparison in this context would imply denying the relevance of any between-subject research design.

Effect Size Standardization

Frederik Aust and Julia Haaf

Although it is common to report standardized effect sizes in psychological research (and recommended by the APA guidelines, American Psychological Association (2010, 2020); but see Wilkinson 1999), the merits of standardized effect sizes continue to be subject of debate (Baguley, 2009; Cheung, 2009; Kline, 2013; Pek & Flora, 2018). Proponents of standardized effect sizes argue that they facilitate across-study comparisons, interpretation of the magnitude of an effect when the measure is arbitrarily scaled, and meta-analyses. In contrast, opponents argue that standardized effect sizes do more harm than good—standardized effect sizes obfuscate the true magnitude of the effect, depend on the research design, and discourage researchers from developing meaningful dependent variables. As pointedly put by Tukey (1969):

Why then are correlation coefficients so attractive? Only bad reasons seem to come to mind. Worst of all, probably, is the absence of any need to think about units for either variable. […] [W]e think we know what r = −.7 means. Do we? How often? Sweeping things under the rug is the enemy of good data analysis. […] Being so disinterested in our variables that we do not care about their units can hardly be desirable.

The issue of standardization is relevant to the current discussion for two reasons. First, we brought up the issue in van Doorn et al. (2021) because standardization of effect sizes in mixed models is generally difficult as it is unclear which variance should be used for standardization. Vasishth et al. (2022) argue that “effect sizes should generally not be standardized”. Relatedly, Rouder et al. (2022) caution that the average population effect is only interesting if it is a good summary of the population distribution, that is, if it is large relative to the population standard deviation, which implies that an effect size standardized by the random slope variance would be most meaningful. The critical issues here appear to be (1) whether to standardize effect sizes or not and, if so, (2) how to construct an effect size that is meaningfully standardized, i.e., what variance should we standardize by? Has anybody changed their mind on these issues since reading the other contributions?

The second reason to discuss standardization is a bit more subtle. The influential approach to Bayesian mixed models and ANOVA developed by Rouder et al. (2012) uses a parameterization that standardizes model parameters by the residual error variance. Consequently, all priors distributions are specified in standardized effect size units. Singmann et al. (2021) critique the standardized model parameterization as difficult to interpret and reason about. In addition, they note that the specification of prior distributions is difficult in many contexts. On the other hand, these default Bayes factors developed by Rouder et al. (2012) have many desirable statistical properties such as scale invariance and consistency. Given the critique by Singman et al., however, we may discuss (3) whether the benefits of the standardized parameterization outweigh the drawbacks, and/or (4) whether it needs adjustments.

Henrik Singmann

Standardized effect sizes are an instance of what I like to call pretend science; by moving from the concrete and easy to understand unit of the dependent variable to the standardized unit, we pretend to become more scientific or objective, when in reality we just add another layer of abstraction that hides the actual research from proper scrutiny. The reasons for why this additional layer of abstraction obscures rather than objectifies research are well known and aptly summarized by Aust and Haaf above.

In addition to the substantive arguments for why standardized effect sizes should be avoided, I feel there is another more nefarious issue looming. Standardized effect sizes give a piece of research the veneer of being generalizable beyond the methodology that is employed, inviting the type of broad theoretical conclusions that are so common in the field, but hardly justifiable given the evidence provided. To be more blunt, standardized effect sizes are one cause of the theoretical storytelling that stunts actual cumulative progress in psychology.

The question this perspective leaves open is whether there is a place for standardized effect sizes in Bayesian statistics, where they are necessary to enable the calculation of default Bayes factors. This issue can be discussed on two levels, once in general and once in the particular case of mixed models.

For the specific case of mixed models, we (Singmann et al., 2021) have argued that there are several problems with the current solution of using the residual variance term as the standardization constant (e.g., the corresponding standardized effect sizes are in many cases even more difficult to interpret than “regular” standard effect sizes). However, we also mentioned the related problem that within a mixed model framework, no other variance term can be used for standardization because of a fundamental problem. The defining feature of a mixed model, partial pooling across the levels of a grouping factor, leads to shrinkage—a downward bias—on all variance terms, with the exception of the residual variance (e.g., Gelman and Pardoe 2006). Using such biased terms as standardization constants would lead to inflated standardized effect size estimates. Clearly, an undesirable feature for any widely used default Bayes factor.

Nevertheless, Aust and Haaf still ask, “what variance should we standardize by?”. Maybe they believe the argument above is purely theoretical, without any relevance in practice. In other words, maybe they believe that in practice shrinkage is not too large and variance estimates are usually well estimated. Unfortunately, nothing would be further from reality. Random variance terms that are estimated as approximately zero and the resulting convergence problems that appear in a frequentist framework are so common that they are discussed in virtually all important (i.e., well cited) applied mixed model introductions of the last years (e.g., Barr 2013; Matuschek et al., 2017; Brauer & Curtin 2018, see also Bates et al., 2015). So even if we really wanted to use a different variance term for standardization, anything but the residual variance will lead to inflated effect sizes in practice. So for mixed models, there is simply no good solution.

This leaves the general question of using standardized effect sizes for default Bayes factors. Are there situations where the benefits of using default Bayes factors outweigh the problems associated with standardized effect sizes? I do not believe so. If we are in a situation in which the standardized effect size is meaningful—that is, we have such a good understanding of the design and dependent variable that the we have a good intuition regarding the magnitude of the variance, the standardization constant—we are in a situation where we could calculate an equivalent unstandardized Bayes factor. If we do not have a good enough understanding of design and dependent variable, calculating the default Bayes factor based on the obfuscating standardized effect size just produces more pretend science. We just add another layer of abstraction, in this case the default Bayes factor, that hides the actual results.

Shravan Vasishth

Standardizing effect sizes seems to me to move us further away from the details of the research question we are studying. For example, when we record reading times in an eyetracking study, we usually work with several different dependent measures, on the millisecond scale. We use first-pass reading time, the proportion of leftward eye movements (regression probability), re-reading time, regression path duration, and total reading time (among others). All of these dependent measures are generated from different latent processes that can be modeled at a pretty low level (see, e.g., Engbert et al., 2005; Rabe et al., 2021). Psycholinguists already (mistakenly) try to interpret these different measures as if they are telling us the same thing about the underlying cognitive processes of interest (e.g., syntactic or semantic processing). What will happen with measures like first-pass reading time is that the effects will be tiny on the ms scale because first-pass reading times are relatively short. By contrast, total reading time differences between conditions can be huge in comparison; this is just because total reading time includes possibly many revisits and refixations on a word after passing it to the right. Standardizing these estimates adds a layer of abstraction that takes us even further away from the underlying latent process, which is what we really want to model. It would be comparing apples and oranges to think about the effect sizes of early vs. late measures by standardizing them, but that is what will happen if we start standardizing. Regarding Bayes factors, we have written about using informative priors on the variance components and effect sizes in the paper by Schad et al. (2022). In all the Bayes factors-based work we do, we use this approach and it works really well, in the sense that the conclusions are realistic. Currently, I don’t understand why I would need to switch to standardizing effect sizes to do my Bayes factors calculations. Modeling the dependent variable that is of interest, and defining the latent processes that we think produced the observed values seems to me to be the most reasonable way forward. Maybe there are some scientific fields out there in which standardization makes sense, but not in the work I have encountered in cognitive psychology and psycholinguistics.

David Kellen

It’s worth highlighting that the problem identified by Henrik—decontextualized effect sizes—is an almost logical implication of a much bigger issue in psychology, namely the questionable ways in which we tend to write (and think) about our objects of inquiry. Texts are often completely devoid of people engaging in concrete actions/behaviors. Instead, they are almost entirely populated by “fictional objects” created through nominalization; e.g., “people categorizing X in context C” is replaced with “categorization” (Billig, 2011). Now, there is nothing wrong with nominalization per se, in fact it plays a very important role in theoretical development (see Gilbert et al., 1984; Halliday 2004). But if we are not careful enough, it can lead to all sorts of problems and confusions; e.g., the reification of “parameters” or “effects” as “things out there in the world” (e.g., Maraun and Gabriel, 2013; Maraun et al., 2009). The reason why talking/thinking about standardized effect sizes feels so comfortable to many, and why the criticisms made by Henrik, myself, and others can be so hard to swallow, is that we as a field have accumulated a number of intellectual bad habits.

Don van Ravenzwaaij

This may seem like a cop-out to some, but in my opinion there’s no need to be prescriptive about whether or not to go with standardized effect sizes, as long as it’s clear from the reporting what variance was used in standardization. Zooming out a bit: A lot of what has come up in all discussions here has reminded me of the slew of many-analyst papers we have seen (e.g., Silberzahn et al., in press; Hoogeveen et al., 2022; Dongen et al., 2019). Some may feel there’s a “best” approach in these kinds of papers, but to me it seems that as long as the analytical strategy is clearly reported and well-argued, there can be many feasible strategies (even if the outcomes are very different).

Sometimes these strategies can be ridiculously simple, such as for instance in the many-RT-model paper by Dutilh et al. (2019), where the analytical strategy of Evans and Brown was to “… inspect[ed] the joint cumulative density function (CDF; method explained below) plots, as well as plots of the median reaction time (RT) and accuracy for each condition and response option, averaged over participants. This approach sounds subjective, but we think it is an important and often-overlooked element of most researchers’ inference.” At the time, this strategy was unusual in a field of formal cognitive modelers, but I do not believe it was “wrong” or “inferior” because of that. The strategy was well argued, and in terms of performance it did just fine (see supplementary material of Dutilh et al., available at https://osf.io/egrnn).

What does this have to do with the reporting of standardized effect sizes? In my opinion, every reported statistical analysis is a balancing act between being (1) (as) appropriate (as possible); and (2) (as) interpretable (as possible). The latter includes familiarity through common usage and digestibility for different levels of statistical literacy. So yes, I think standardized effect sizes have their place, but their utility stands or falls with the clarity of reporting (how was standardization achieved?). The more statistically literate reader can parse what’s going on and the less statistically literate reader can at least attempt to compare to other papers that have reported similar metrics.

João Veríssimo

The comments above (by Singmann, Vasishth, and Kellen) all make compelling points against the use of standardized effects, but I found the arguments about the particular difficulties with standardization in mixed-effects models to be less convincing. Singmann (comment above) and Singmann et al. (2021) view partial pooling as a “fundamental problem” for standardization. They argue that shrinkage produces biased estimates of random-effect variance components (downward) and can “contaminate” the estimates of residual variance (upward), so that neither should be used as a basis for standardization.

I doubt that the scenario they describe is a common one. The purpose of partial pooling is precisely to separate the between—and within—cluster variances, so that less biased estimates of the different variance components can be obtained. As I see it, the shrunken random effects have actually been “decontaminated” from residual variance (and vice-versa).

A simple simulation can illustrate this point (code at https://osf.io/x9h2g). I sampled data for 50 participants in two conditions, with a true random slope SD of 0.5. True residual SD was either 1 or 5 and there were either 50 observations per participant/condition or only 5. Table 3 shows the mean estimates across 10 Bayesian mixed-effects models and 1000 frequentist models. The results showed that (a) the residual SD was very well-recovered throughout, even when data were sparse and in the presence of substantial shrinkage of the observed effects; (b) random slope SDs were also well-recovered, at least when the residual variance was small (but still 4 times larger than the between-participant variance); and (c) when the residual variance was much larger than the between-participant variance (100 times larger) and data were sparse, estimates of the random-effect SD were indeed biased… but upward, not downward! (one could say that, in these cases, shrinkage has failed to apply enough.)

Table 3 Mean estimates across 10 (Bayesian mixed-effects models) and 1000 data sets (frequentist mixed-effects models)

Residual variances thus seem to be resilient to even high shrinkage and, in that respect, could serve as an appropriate quantity for standardization; often, random slope variances will also be appropriately estimated. Moreover, if there are indeed cases in which the variance components show “contamination” between them (as claimed by Singmann et al.), the problem might be ameliorated by using the total variance as a basis for standardization rather than any individual variance (at least for some common research designs; see Brysbaert and Stevens, 2018; Westfall et al., 2014).

To be clear, I am not arguing for the broad use of standardized effect sizes. My point is that the issues raised by Singmann et al. with regards to partial pooling may be less problematic than they claim they are.

Henrik Singmann

João’s thoughtful analysis is a perfect example of how nuanced these issues are and how easy it is for technical concepts to be blurred by ordinary discourse (mea culpa).⁴

The random slope variance estimate in a mixed model is of course not biased compared to the true value, when the data generating process is the very same mixed model being fit (the inability to recover itself would be a pretty disastrous outcome for mixed models). When talking about a “downward bias” of the random slope estimates, we⁵ used the term “bias” in a more liberal sense and not in the proper technical sense of the “bias of an estimator”.

What we meant was that the random slope estimate shows a downward bias compared to the SD of the observed effects. With “SD of the observed effects,” we mean the sample SD of the individual-participant effects in a within-subject design. Usually, standardized effect sizes are directly calculated using observed quantities, such as the SD of the observed effect. But in the case of mixed models, we are dealing with a model-based SD estimate that is different from the observed estimate in two ways: it is smaller and subjected to shrinkage (i.e., “downward biased”). Consequently, effect-sizes calculated with the latter will be greater.⁶

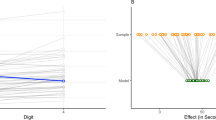
This understanding of “downward bias” can already be seen in João’s table (compare “Observed SD” with “Random SD”), but becomes clearer in Fig. 2 below, which shows distributions of different SD estimates based on João’s simulation code.⁷ Each row shows results from 1000 simulations for one sample size (10, 25, or 50 participants). The left column shows the distribution of the SDs of the observed effects, the central column shows the distribution of the random slope SD estimates from the data generating maximal model (with random intercept, random slopes, and correlation between both random terms), and the right column shows the distribution of the random slope SD estimates from the mixed model without correlation between random intercept and random slope (I added this model to his simulation). The true (data generating) random slope SD value of 0.5 is shown as the vertical black line.

Fig. 2

Distribution of three SD estimates for the within-subjects condition effect when simulating from a mixed model with (true) random slope SD of 0.5 (shown as vertical line) across 1000 simulations per sample size (one row per sample size). The left column shows the distribution of the SDs of observed individual effects, the central column shows the random slope SD estimates from the maximal model (i.e., the true data-generating model), and the right panel shows the random slope SD estimates from the no-correlation (NC) model. The other parameters of the simulation are: random intercept SD of 0.5, correlation between random slope and random intercept of 0.5, residual SD of 1, and 5 observations per participant and condition. Each panel also shows the mean (M), median (Md), standard deviation (SD), and skewness (skew) of each distribution

Figure 2 shows several interesting and relevant patterns. Firstly, as shown in the second column, the random slope estimator is indeed not biased when the fitting model is identical to the data generating model. However, as soon as there is even a small amount of model misspecification—fitting the mixed model without correlation (third column) to the data generated with correlation—we see a bias in the random slope estimator.⁸ In this case, this is an upward bias compared to the true value, but it seems conceivable that in other cases of model misspecification this might also be a downward bias (although this is immaterial to the current issue).

If we compare the distribution of the SD of the observed individual effects with the random slope estimates, we see a shift in the mean between both distributions. Whereas the mean random slope is at the true value of 0.5, the mean SD of the observed effect is around 0.8. In other words, the two SDs are on a different scale. Standardized effect sizes calculated with one or the other SD would not be directly comparable. This difference in scale is likely a consequence of the difference in variance partition between the mixed model and the SD of the observed effect. Hence, I can imagine that it is possible (for someone with the skills in mathematical statistics) to derive a formula bringing these two SD estimates on the same scale.

But even if the two SD variants are brought onto the same scale, the main problem with the random slope estimates is not their mean, but the shape of their distributions, which show a “downward bias.” Across the board we see that the random slope distributions are negatively skewed, whereas a negative skew is absent in the distribution of the observed SDs. In some cases, especially with small N, the random slope estimates are even approaching zero which would lead to impossibly large standardized effect sizes. This negative skew is a consequence of the defining feature of a mixed model, hierarchical shrinkage (or partial pooling), which ensures that extreme individual level effects are shrunk towards the group mean. Whereas such shrinkage is generally a desirable statistical property (e.g., Efron and Morris, 1977), it makes the random slope SD estimates simply unsuitable as standardization constants. As soon as the N is somewhat on the smaller side, one would risk having dramatically inflated standardized effect sizes when the random slope estimates approach zero.

Lastly, we also argued against using the residual standard deviation as the standardization constant. The main thrust of our argument was that in many situations the meaning of the residual standard deviation is unclear, which leads to standardized effect sizes that are not clearly interpretable. However, we also argued that the residual standard deviation can be contaminated by shrinkage. To be clear, there is no shrinkage being directly applied on the residual standard deviation (the distribution of which shows neither negative nor positive skew). The specific problem here is that the variance decomposition is a zero-sum operation. Because the total variance has to be distributed across all variance components, it follows that if one variance takes a smaller share, the other components need to take a larger share. This means that, if shrinkage is applied to the random slope estimate, then the residual variance is contaminated as a consequence. One way to understand this zero-sum relationship is by looking at the correlation between the proportions of random slope variance and residual variance of the total variance, which is shown in Fig. 3. We see an obvious negative relationship (r between − .22 and − .37) showing a contamination of the residual variance when shrinkage affects the random slope estimate.

Fig. 3

Relationship between the ratio of random slope variance and total variance and the ratio of residual variance and total variance across the simulation results. Individual data points are shown semi-transparently so that overlapping points appear darker. The blue line shows the linear regression line for each panel

Taken together, this extended look at João’s simulation results hopefully clears up two points. Firstly, I explain in more detail what we meant with “biased,” a bias compared to the SD of the observed effect. Furthermore, the simulation results show that the random slope estimator of the mixed model is not biased (in the technical sense) if fitted model matches the data generating model. But as soon as the fitting model is misspecified (a condition that likely holds in all real mixed model applications), we can expect a bias in the technical sense with unknown consequences for subsequent effect size estimates.

Secondly, I explained why any SD estimate in a mixed model is unsuitable for standardization of effect sizes. Although the residual variance term is largely unaffected by shrinkage itself, it is often unclear what it means and can be contaminated if other variance terms are estimated poorly (which is one reason for using mixed models in the first place). Furthermore, compared to the observed SDs the random slope estimates are affected by shrinkage which leads to a downward bias, making them completely unsuitable as standardization constants.

As argued in Singmann et al. (2021), the consequence of these issues is that it seems better to abandon standardized effect sizes in mixed models altogether. Which also means abandoning default Bayes factors for mixed models.

João Veríssimo

I appreciate Henrik’s clarification, which truly illustrates how taking a position on the larger issues often requires a discussion of the finer points. I found the demonstration of random-slope bias in models without a correlation parameter particularly striking. I will only point out that the consequences of model misspecification are not specific to variance components or standardized effects, and that all sorts of misspecification (e.g., inclusion/exclusion of covariates) can result in bias of the unstandardized effects as well.

Daniel Schad, Shravan Vasishth, and Bruno Nicenboim

The original target article by van Doorn et al. (2021) illustrates (some aspects of) the use of aggregated data for Bayes factor analyses in Bayesian mixed effects models. The van Doorn et al article seems to suggest in several places that, when carrying out Bayes factor analyses with hierarchical models, aggregating data has the advantage that one can remove the variance associated with the grouping factor that is aggregated over (e.g., in a by-subjects aggregation, each subject’s repeated measures from multiple items in each condition can be reduced to one data point per condition). For example, the authors write: “a benefit of aggregation is that it greatly reduces the impact of random slopes in the inference for a fixed effect and therefore eliminates the inflation of Type 1 and Type 2 error rates that ignoring random slopes typically entails”; and in their discussion section, they write “The data can be aggregated, which minimizes the impact of the random effects in the inference for a fixed effect.” As we also pointed out in our response article (Vasishth et al., 2022), aggregation should in general never be done. One reason is that hiding a source of variance is not an advantage but a disadvantage, because one is losing information about one source of variability. Another reason is the one we outline below and discuss in detail in another article (Schad et al., 2022).

A second issue with aggregation is that potential biases that may arise during data aggregation. To perform data aggregation in a repeated measures design, the mean of the dependent variable is computed for each condition for each subject. A Bayesian mixed effects model is then fit to these aggregated data. We argue that in this case (for the balanced null comparison), if the sphericity assumption is violated, data aggregation can lead to biased estimates for the resulting Bayes factors, and should therefore in general be avoided. We outline the details of this argument in a recent arXiv paper (Schad et al., 2022), and we summarize the key points here.

It is well-known from frequentist repeated measures ANOVA that aggregating data to the by-subject level confounds random slope variances with residual noise. Indeed, repeated measures ANOVA, as well as mixed effects models fit to aggregated data, assume sphericity. In mixed effects model terms, they assume that the variances of all random slopes are equal. For frequentist tools, it has been shown that a violation of the sphericity assumption leads to anti-conservative test statistics (inflated alpha error; Box, 1954). It is therefore common practice to test for violations of sphericity (Mauchly, 1940) and—if violation is detected—to perform corrections of the degrees of freedom (Greenhouse and Geisser, 1959; Huynh & Feldt, 1976) to obtain adequate test statistics. An alternative (and arguably better) solution to this problem is to fit (frequentist) mixed effects models to unaggregated data, and to explicitly estimate the variance of each random slope term, which is then taken into account when computing test statistics. We think that this issue is of practical relevance: a quick citation analysis suggests that violations of the sphericity assumption seem to occur often in data sets in cognitive science and psychology (Greenhouse & Geisser, 1959, have been cited 5520 times in Google Scholar, and 3220 of these citations contain the word “cognitive”).

What we argue here (see Schad et al., 2022, for details) is that these problems and biases are also present when using aggregated data to perform Bayes factor tests (based on the balanced null comparison) using Bayesian mixed effects models. We recently showed that the accuracy versus bias of Bayes factor estimates can be determined using simulation-based calibration (Schad et al., 2022). In simulation-based calibration for Bayes factors, models and parameters are sampled from their priors, are then used to simulate data, and Bayes factors are estimated from the simulated data. If the average posterior model probability is equal to the prior model probability, then this indicates that the Bayes factor is unbiased. If the average posterior model probability deviates from the prior model probability (i.e., if it is larger/smaller than the prior probability), then this indicates a (liberal/conservative) bias in the Bayes factor estimate.

We (Schad et al., 2022) performed simulation-based calibration for Bayesian mixed models, while assuming the sphericity assumption is violated. We implemented a repeated measures design with one factor with 3 factor levels, which were modeled using treatment contrasts. One contrast was assumed to have a small random slope variance (SD = 10), and the other was assumed to have a large random slope variance (SD = 90). We performed null-hypothesis Bayes factor tests on the simulated data to test each contrast estimate to a null model where the contrast was excluded. For details concerning the simulations, see Schad et al. (2022). The results (see Fig. 4, left panel) show that for aggregated analyses, for the contrast with a large random slope variance (SD = 90), Bayes factor estimates have a liberal bias (i.e., Bayes factor estimates are too large), and for the contrast where the random slope variance is small (SD = 10), Bayes factor estimates have a conservative bias (i.e., the Bayes factor estimates are too small). These biases can be avoided by running Bayesian mixed effects models on the non-aggregated data, and by estimating a maximal random effects structure (see Fig. 4, right panel): in this situation, the average posterior model probabilities didn’t differ from the prior model probability, suggesting absence of bias.

Fig. 4

Results from simulation-based calibration for model inference when sphericity is violated. The average posterior model probability together with 95% confidence intervals is shown for effects with a small (10) versus a large (90) standard deviation of the random slopes, reflecting small or large variation of the effect across subjects. The horizontal solid line is the prior probability for the H1, and deviations from this line indicate estimation bias in Bayes factor estimation. Results are shown for null hypothesis Bayes factor analyses based on aggregated data (left panel) versus on non-aggregated data (right panel). They show that aggregating data for null hypothesis tests can lead to biased Bayes factors, which deviate from the true Bayes factor. Bayes factors are more accurate for non-aggregated analyses, where the posteriors do not deviate from the prior probability

Based on these simulation results, we suggest that using aggregated data for the analysis of Bayesian mixed effects models can be risky: when the sphericity assumption is violated, this may lead to biased Bayes factor estimates. Instead, we suggest that the default approach to Bayes factors should be to estimate Bayesian mixed effects models on non-aggregated data and to estimate the maximal (Barr, 2013) or parsimonious (Matuschek et al., 2017) random effects structure. If one wants to perform analyses on aggregated data, then evidence should be provided that the sphericity assumption is not violated for the given data set.

Richard Shiffrin

There are hints in these various commentaries of what I believe is the fundamental underlying issue: Should we be using statistical inference to govern scientific decision making, or should we be careful to use statistics sparingly so as not to distort what scientists in their best judgment would infer from the data? I believe the primary goal of scientists, statisticians and methodologists should be drawing the best possible inference concerning the processes producing the observed data, based in good part on the history of relevant empirical findings and theories. In the kinds of studies being discussed, data are aggregated over numerous variables such as participants, stimuli, trials, and much more. How best to draw scientific conclusions from such data is not a purely statistical matter. Making a case for this assertion would require a long article or a book, not a brief commentary. I will simply state my belief that scientific inference and statistical inference are not the same, and we should be careful not to confuse the two.

Concluding Thoughts

When we started this special issue, the plan was simple: compose three hypothetical examples, pose several questions that arise, and have teams of experts debate about the answer. When they reach a final consensus, a neat set of guiding principles could be produced, aiding any researcher interested in Bayesian mixed model comparison. Reality has proven that last part to be very much wishful thinking and has underscored statistical inference as an inherently subjective process. However, we prefer to celebrate this subjectivity, since the disagreement has urged further dissemination of information and has demonstrated the limitations of certain default options. While few questions from the target article have received a definitive answer, the discussion unveiled crucial elements of statistical inference, and mixed model comparison specifically.⁹ Simply put, the current format has illuminated the components that require consideration when the researcher is told to “carefully think about their stuff.”