Introduction

In our original article we elaborated on how FBST ev violates several desiderata for scientific evidence (Ly & Wagenmakers, in press). Specifically, a proper measure of evidence should at least (i) be able to quantify support for both the null and the alternative hypothesis; (ii) increase in favor of the null as data accumulate that are (exactly) consistent with the null; (iii) allow practitioners to consult it at any moment in time without this practice predetermining the conclusions; and (iv) be exactly balanced when the data are evidentially irrelevant, that is, equally likely under both models.

In response, Kelter agrees with our assessment that FBST ev violates these desiderata, but counters that the FBST ev does not need to adhere to these natural rules:

“The identified problems hold only under a specific class of prior distributions which are required only when adopting a Bayes factor test. However, the FBST explicitly avoids this premise, which resolves the problems in practical data analysis.”

Kelter argues that the Bayes factor involves the assignment of non-zero mass to a point-null hypothesis, in many practical applications supposedly a dubious act that the FBST ev avoids. If the point-null hypothesis is never true, as FBST assumes, then it may not be relevant what ought to happen whenever the point-null hypothesis is true. We are grateful for Kelter’s comment on our paper: the central issue has been debated for decades, and Kelter’s main argument—the point-null hypothesis is never true, and this is a blow against Bayes factors—has been made many times before (see the references in the Kelter article). We appreciate the opportunity to explain why we believe our conclusion stands, and the discussion on the validity on a point-null hypothesis is (and has always been) a red herring. Below we first examine Kelter’s main claim, and then discuss several issues that we believe require clarification and sometimes rectification.

The Point-Null Hypotheses Is Not the Problem

Kelter agrees that FBST ev performs poorly whenever the null hypothesis holds true, but disputes the relevance of this fact. Indeed, Kelter surmises that point-null hypotheses are almost never realistic and can therefore be ignored.

There exist multiple counterarguments to this philosophical position. First, the very fact that the null hypothesis is being tested is an indication of it being possibly true. And if the null holds true, then the statistical method should be able to accumulate evidence in its favor. If a person can never be acquitted, then why the charade of taking them to court? We reiterate our position that even in FBST ev the null value is of special interest—one tests the hypothesis \({{\mathscr{H}}}_{0} : \delta =0\), and not, say, \({{\mathscr{H}}}_{0}^{\prime }: \delta = 0.00177567\). In many statistical applications, the hypothesis \({{\mathscr{H}}}_{0}: \delta = 0\) corresponds to the exclusion of a parameter, such as the effect of a covariate.

Second, the rejection of point-null hypotheses is an implicit rejection of all models. As detailed below, any model can be extended to a larger model, for instance, by adding a covariate or an across-trial parameter. Hence, every model can eventually be identified with a point-null hypothesis. Discarding all point-null hypotheses out of hand implies that researchers would always be forced to use the most complex model, and add a variable for every new data point. This would make impossible any ability for generalization and in fact prohibit any kind of scientific progress (e.g., Poincaré, 1913, pp. 119–120). Thus, tests against a point-null constitute an epistemic firewall against needless complexity. They protect against the whimsical adoption of vague models that overfit the data and generalize poorly (e.g., Myung et al., 2000; Roberts & Pashler, 2000). Point-null tests allow researchers to develop generalizable models in a controllable fashion (e.g., Haaf et al., 2019; Ioannidis, 2019).

Third, and crucially, the problems for FBST ev that we identified do not vanish when the point-null is abandoned. Suppose we accept, for the sake of argument, the common complaint that point-null hypotheses are never true exactly. Also suppose we also accept, again for the sake of the argument, that this realization would invalidate the usual Bayes factor of a point-null hypothesis \({\mathscr{H}}_{0}\) versus \({\mathscr{H}}_{1}\). This knowledge should not cause any researcher to abandon the entire Bayes factor testing framework and embrace the FBST ev estimation framework instead; when a roofer examines their work and finds a broken tile, they generally do not propose to remove the entire roof and declare the problem solved. Rather, in order to incorporate the advance knowledge that the point-null hypothesis is implausible we may replaced it by a peri-null hypothesis.Footnote 1 For instance, the point-null hypothesis \({\mathscr{H}}_{0}: \delta =0\) may be replaced with the peri-null hypothesis \({\mathscr{H}}_{\widetilde {0}}: \delta \sim N(0,\epsilon )\), where 𝜖 accommodates the notion that \({\mathscr{H}}_{0}\) is used only as a mathematically convenient approximation. Importantly, such a change from point-null to peri-null leaves most of our critiques against FBST ev conceptually intact.

Specifically, a Bayes factor test with a peri-null still allows evidence to be collected in favor of the peri-null, and this evidence would increase as data accumulate that are more consistent with the peri-null than with the alternative. The evidence would not increase indefinitely, but be subject to an upper bound—such inconsistency is the price that is paid for adopting a peri-null rather than a point-null (Ly & Wagenmakers, 2022). Similarly, the Jeffreys-Lindley paradox also holds in the case of a peri-null hypothesis, albeit in a less extreme form—as sample size increases and the p-value remains fixed, the evidence will eventually support the peri-null hypothesis over the alternative hypothesis, but the extent of this support is bounded (see Eq. 3 and Fig. 2 in Wagenmakers & Ly, in press). This is a key observation, as it is a common misperception in the statistical literature that the Jeffreys-Lindley paradox is caused by the presence of a point-null hypothesis. It also remains the case that the Bayes factor with a peri-null hypothesis will indicate perfect indifference when confronted with data that are equally likely under the peri-null hypothesis and the alternative hypothesis.

Hence, we believe Kelter’s main thesis is incorrect—our critique against FBST ev as a measure of evidence does not require the assignment of prior mass to a point. We wish to stress that our critique does not concern FBST ev wholesale; in fact, FBST ev may be used as a method to quantify surprise (e.g., Good, 1981, 1983). But when the quantification of evidence is in order, it is important not just to consider the surprise under a single model, but also the surprise under a competing model; specifically, the data provide evidence for model A over model B if and only if model A predicted those data better than model B.

We now turn to a more detailed analysis of Kelter’s arguments, which demands that we also clarify some of our own assumptions.

The Nature of Testing

Kelter’s arguments are motivated from an alternative-model only perspective. In contrast, we believe that a test, in its simplest form, involves at least two models: The null model \({\mathscr{M}}_{0}\) corresponding to the null hypothesis \({\mathscr{H}}_{0}\), and the alternative model \({\mathscr{M}}_{1}\) corresponding to the alternative hypothesis \({\mathscr{H}}_{1}\). By hypotheses we mean assertions regarding (unobservable) parameters of interest, and by a (psychological) model we mean a (proposed) mathematical description of the underlying processes with which these parameters generate the (behavioral) data (e.g., Ly et al., 2017). Provided with data, a test can then be used to distinguish the competing models.

For instance, for speeded decision-making tasks both Ratcliff’s drift diffusion model (DDM, e.g., Boehm et al., 2018; Ratcliff, 1978), or Brown and Heathcote’s linear ballistic accumulator model (LBA, e.g., Brown & Heathcote, 2008) can be used to describe the distribution of response times. Similarly, to describe the relationship between physical dimensions, such as light intensity, and their psychological counterpart, such as brightness, Steven’s model or Fechner’s model can be used (Myung et al., 2000). Analogously, to describe normally distributed data Y, a Gaussian distribution with a mean fixed at zero, or, alternatively, a Gaussian distribution where the mean is free to vary can be used, that is,

$$\begin{array}{@{}rcl@{}} \mathcal{M}_{0} : Y \sim \mathcal{N} (0, \sigma^{2}), \text{ and } \mathcal{M}_{1} : Y \sim \mathcal{N} (\mu, \sigma^{2}) \end{array}$$
(1)

respectively. In the last example the models are easily seen to be nested. For the model comparison Eq. (1) the test addresses the question of whether or not the mean should be estimated, or—equivalently—whether the observed sample mean \(\bar {x}\) should either be regarded as random noise (i.e., when \({\mathscr{M}}_{0}\) holds true) or as a reliable indication of μ (i.e., when \({\mathscr{M}}_{1}\) holds true). In contrast, an estimation problem addresses the “how much” question, by providing a best guess of the magnitude of the population mean given that it is not zero, i.e., when \({\mathscr{M}}_{1}\) holds true.

Regardless of whether or not the models are nested, the Bayesian assessment of the uncertainty between models is the same. This procedure requires prior model probabilities \(0 < P({\mathscr{M}}_{0}), P({\mathscr{M}}_{1}) < 1\) with \(P({\mathscr{M}}_{0}) + P({\mathscr{M}}_{1}) = 1\) if only these two models are believed to be viable for the data. After observing outcomes y, these prior model probabilities are then updated using Bayes’ rule to yield posterior model probabilities, as follows:

$$\begin{array}{@{}rcl@{}} P(\mathcal{M}_{1} | y) = \frac{ \text{BF}_{10}(y) P(\mathcal{M}_{1})} { \text{BF}_{10}(y) P(\mathcal{M}_{1}) + P(\mathcal{M}_{0})} \text{ and } P(\mathcal{M}_{0} | y) = 1 - P(\mathcal{M}_{1} | y), \end{array}$$
(2)

where BF10(y) is the Bayes factor indicating the evidence in the outcomes y for \({\mathscr{M}}_{1}\) over \({\mathscr{M}}_{0}\).Footnote 2 The prior model probabilities \(P({\mathscr{M}}_{0}), P({\mathscr{M}}_{1})\) represent the researcher’s subjective beliefs, or uncertainty, regarding the models and associated hypotheses. For instance, before data observation, a researcher might believe that the LBA and DDM provide equally viable descriptions of response time distributions, and accordingly set \(P({\mathscr{M}}_{0}) = P({\mathscr{M}}_{1}) = 1/2\). Note that these prior model probabilities are not derived from the prior densities that describe the uncertainty within each model. In particular, \(P({\mathscr{M}}_{0})\) is not derived from the prior density regarding the free parameters within \({\mathscr{M}}_{1}\). The parameters of the LBA and DDM are interpreted within their own contexts (e.g., Osth et al., 2017).

Kelter’s Representations of the Bayes Factor

We believe that Kelter’s representation of the Bayes factor conflates the null hypothesis, the statement regarding the parameter of a, say, Gaussian model such as \({\mathscr{H}}_{0} : \delta = \mu / \sigma = 0\), and the null value 0. Specifically, Kelter argues that \(P({\mathscr{M}}_{0})\) has to be zero, once a continuous prior density \(\pi (\delta | {\mathscr{M}}_{1})\) is selected, because such a prior density gives zero prior probability to {0}, where {0} is the set which only contains the null value. However, we dispute the idea that the prior density \(\pi (\delta | {\mathscr{M}}_{1})\) defined on the parameters within the alternative model should dictate the prior model probability of the null model \(P({\mathscr{M}}_{0})\).

In his analysis, Kelter takes the alternative model as a point of departure, and from this perspective it should not come as a surprise that the null model is argued to be false. This alternative-only perspective is also apparent when Kelter discusses the Bayes factor as a ratio of marginal likelihoods. For concreteness, we consider again the model comparison Eq. (1), that is, the Bayesian t-test. The alternative model allows both the effect size \(\delta \in (- \infty , \infty )\), and standard deviation \(\sigma \in (0, \infty )\) to vary freely, whereas the null model has only one free parameter \(\sigma \in (0, \infty )\). The specification of the Bayes factor now requires a pair of priors resulting in

$$\begin{array}{@{}rcl@{}} \text{BF}_{10}(y) = \frac{ {\int}_{- \infty}^{\infty} {\int}_{0}^{\infty} f(y | \delta, \sigma, \mathcal{M}_{1}) \pi(\delta, \sigma | \mathcal{M}_{1}) \mathrm{d} \sigma \mathrm{d} \delta}{{\int}_{0}^{\infty} f(y | \delta=0, \sigma, \mathcal{M}_{0}) \pi(\sigma | \mathcal{M}_{0}) \mathrm{d} \sigma} . \end{array}$$
(3)

Kelter’s presumption that only the alternative model matters translates to the claim that the marginal likelihood (i.e., the denominator in Eq. (3)) has to be zero.Footnote 3

This claim neglects the fact that the priors densities \(\pi (\delta , \sigma | {\mathscr{M}}_{1})\) and \(\pi (\sigma | {\mathscr{M}}_{0})\) are conditional on their respective models that provide contexts to the parameters. In fact, direct computations with \(\pi (\sigma | {\mathscr{M}}_{0}) \propto \sigma ^{-1}\) show that the marginal likelihood is not zero (for details, see, e.g., Ly et al., 2016a, b).

The marginal likelihood in fact is a predictive score, one that does not depend on either of the candidate models being “true” (e.g., O’Hagan and Forster, 2004, pp. 166-167; Kass & Raftery, 1995, p. 777). This can be appreciated by writing the marginal likelihood as a sum of one-step-ahead prediction errors (e.g., Wagenmakers et al., 2006), by interpreting the Bayes factor as a specific case of cross-validation (e.g., Gneiting & Raftery, 2007), or by noting the close relation with model comparison methods that obey the Minimum Description Length principle (e.g., Grünwald et al., 2005; Grünwald, 2007; Ly et al., 2017).

Suppose that researchers wish to compare Fechner’s law of psychophysics (which can account only for negatively accelerating curves) against Steven’s law of psychophysics (which can account for negatively and positively accelerating curves). The researchers view both accounts as sequential forecasting systems (e.g., Dawid, 1984) and use the Bayes factor to quantify the models’ relative predictive performance. They then consult the statistical literature and read, to their surprise, that Fechner’s law is nested under Stevens’ law (Kvålseth, 1992). Does the realization that the models are nested invalidate the conclusion that Fechner’s model has outpredicted Steven’s model? Should we resign ourselves to the position that it is impossible to collect positive evidence for Fechner’s law over Stevens’ law? We don’t think so. In fact we believe that if the data had consistently showed negatively accelerating curves, Stevens’ law would not even have been proposed.

Fig. 1
figure 1

The two-dimensional Lebesgue measure is the natural measure that gives rectangles with width w and height h an area of w × h in, say, square meters m2

Full size image

Null Sets

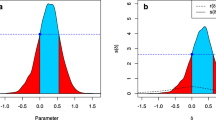
Kelter’s assertion that in practical applications the denominator in Eq. (3) is zero is argued based on the notion of null sets. A null set is a relative concept defined with respect to a certain (probability) measure and the space it works on. For instance, the natural measure on two-dimensional (Euclidean) space \(\mathbb {R}^{2}\) is the so-called two-dimensional Lebesgue measure λ2, which gives the rectangle [− 6,− 2] × [0.5,2.5], see Fig. 1, an area of 4 × 2 = 8 in, say, square meters m2. A lower dimensional object such as the bottom edge of the aforementioned rectangle (i.e., the line segment [− 6,− 2] ×{0.5}) has λ2-measure zero. This just means that this line segment has no area. It does not mean that the line itself has no intrinsic worth, nor that it is uninteresting. When we take into account the intrinsic dimension of the line we get the natural measure in one-dimensional Euclidean space \(\mathbb {R}\).Footnote 4 This natural measure is known as the one-dimensional Lebesgue measure λ and assigns to the line segment a length of 4 in, say, meters m, as one might expect.

Kelter’s claim that the marginal likelihood of \({\mathscr{M}}_{0}\) is zero follows from him letting the two-dimensional prior density \(\pi (\delta , \sigma | {\mathscr{M}}_{1})\) abuse its null sets onto the one-dimensional prior density \(\pi (\sigma | {\mathscr{M}}_{0})\). Note again that the null sets of \(\pi (\delta , \sigma | {\mathscr{M}}_{1})\) defined for \({\mathscr{M}}_{1}\) are made to intrude on \(\pi (\sigma | {\mathscr{M}}_{0})\), which is defined on the different context given by \({\mathscr{M}}_{0}\). Similarly, the within-model uncertainty of the LBA model should not dictate the priors on the parameters of the DDM model. The parameters in each of these models affect the data differently, even if they are given similar interpretations (e.g., Osth et al., 2017).

As mentioned above, Kelter’s argument of having the prior density \(\pi (\sigma | {\mathscr{M}}_{0})\) be violated by the higher-dimensional prior density \(\pi (\delta , \sigma | {\mathscr{M}}_{1})\) leads to an infinite regress. Concretely, suppose that in addition to the models in Eq. (1), we also entertain the model

$$\begin{array}{@{}rcl@{}} \mathcal{M}_{2}: Y | x_{1} \sim \mathcal{N}(\mu + \beta_{1} x_{1}, \sigma^{2}), \end{array}$$
(4)

or equivalently

$$\begin{array}{@{}rcl@{}} \mathcal{M}_{2}: Y = \mu + \beta_{1} x_{1} + \epsilon, \text{ where } \epsilon \sim \mathcal{N}(0, \sigma^{2}) , \end{array}$$
(5)

where β1 is the effect of x1 on Y, where x1, for instance, could represent age, or a factor on which the data could be stratified, such as gender.

By taking β1 = 0 in \({\mathscr{M}}_{2}\), we retrieve \({\mathscr{M}}_{1}\), and note that \({\mathscr{M}}_{2}\) is three-dimensional with free parameters μ,β1,σ. Kelter’s argument leads to \(\pi (\mu , \beta _{1}, \sigma | {\mathscr{M}}_{2})\) forcing its null sets onto \(\pi (\mu , \sigma | {\mathscr{M}}_{1})\) making the marginal likelihood of \({\mathscr{M}}_{1}\) zero. Because the marginal likelihood of \({\mathscr{M}}_{1}\) is the normalizing constant of the posterior on μ,σ, Kelter would then have to conclude that the posterior density \(\pi (\mu , \sigma | y, {\mathscr{M}}_{1})\) does not exist. This implies that also no FBST ev can be computed. Observe that the whole argument is reasoned from the perspective of \({\mathscr{M}}_{2}\) in which both \({\mathscr{M}}_{1}\) and \({\mathscr{M}}_{0}\) are false to begin with. Every model can be further extended by including a possibly not relevant covariate, resulting in a higher-dimensional model. This argument can be repeated indefinitely, resulting in posteriors that are always ill-defined from a certain perspective. The way out is to give intrinsic value to each model, and have each their own prior densities in their own rights.

The FBST ev Behaves as a p-Value

In Ly and Wagenmakers (in press) we elaborated on a theorem derived by, amongst others, the advocates of FBST ev (Diniz et al., 2012). The clarification we added was the mode of convergence which is “in distribution” resulting in

$$\begin{array}{@{}rcl@{}} ev \overset{d}{\rightarrow} 1 - F_{\dim({{\varTheta}}_{1})} [ F_{\dim({{\varTheta}}_{1}) - \dim({{\varTheta}}_{0})}^{-1}(1- p)] , \end{array}$$
(6)

see the discussion surrounding Equation 3 in Ly and Wagenmakers (in press) for further details. Equation (6) implies that the sampling distribution of FBST ev can be accurately approximated by the distribution of a (transformed) p-value. It shows that for general priors, FBST ev behaves as a p-value. This qualitative statement provides sufficient insights to why FBST ev does not act as a proper measure of evidence. Furthermore, Kelter’s claim that Eq. (6) cannot hold for discrete models is unfortunately incorrect. Converge in distribution does not depend on the underlying probability spaces (e.g., van der Vaart, 1998, p. 5). This mode of convergence formalizes exactly what it means for the intuitive clear idea of a discrete uniform distribution on the interval (0,1) with n bins each occurring with chance 1/n to converge to the continuous uniform distribution on the interval (0,1). Another example is given by a Galton board, which demonstrates how a binomial distribution can be well approximated by a normal distribution Galton (p. 63, 1889). It is in this sense that the distribution of FBST ev can be well approximated by the distribution of a p-value based on the likelihood ratio statistic. In Ly and Wagenmakers (in press) we elaborated on how this relationship between FBST ev and the p-value causes FBST ev to not act as a proper measure of scientific evidence.

Concluding Comments

Kelter’s main counterargument to our critique on FBST ev as a measure of evidence is that in scientific practice, the point-null hypothesis is never true exactly. Hence, the epistemic defects of FBST ev are judged to be practically irrelevant. Presumably it does not matter that FBST ev cannot quantify evidence in favor of the point-null, because the point-null is never true anyway. According to Kelter, the problem lies instead with methodologies such as the Bayes factor, that do assign credence to a point-null hypothesis. Kelter’s line of argumentation is relatively well-known in the field of statistics. For statisticians, it would be good news if the Kelter line of argumentation were correct, because hypotheses could then be evaluated using a methodology that is straightforward—much more straightforward than Bayes factors, which depend critically on the specification of prior distributions (e.g., Bayarri et al., 2012; Grünwald et al., 2020; Jeffreys, 1961; Ly et al., 2016b, 2016a, 2020).

In this rejoinder we have stressed the following points that are underappreciated in the statistical literature:

  1. 1.

    Bayes factors compare predictive performance between any two models, nested or non-nested. Researchers who abhor the point-null hypothesis may still prefer the Bayes factor as a method for model comparison.

  2. 2.

    Researchers allergic to the point-null may replace it with a peri-null. Crucially, this does not affect the key aspects of our critique on FBST ev (Ly & Wagenmakers, 2022). In particular, it does not change the fact that FBST ev suffers from the Jeffreys-Lindley paradox (Wagenmakers & Ly, in press).

  3. 3.

    The Bayes factor quantifies relative predictive performance and does not depend on any of the two models under consideration or the prior densities being “true”.Footnote 5

  4. 4.

    The prior distribution for the test-relevant parameter in the alternative model does not dictate the prior model probability for the null hypothesis, nor the prior density within the null model. Doing so leads to an infinite regress.

Therefore we maintain that the epistemic defects of FBST ev are more than just a theoretical possibility. In practice, a skeptic who is confronted with compelling FBST ev support against the null has every right to remain doubtful; after all, the skeptic’s model—whether instantiated as a point-null or a peri-null hypothesis—may predict the data as well or better than the alternative model. This does not mean that the FBST ev is useless or inherently flawed; in fact, it may serve well as a measure of surprise (Good, 1981), attending the researcher to the fact that a single hypothesized model may be in need of reappraisal or adjustment. Thus, FBST ev may be particularly useful in an early stage of model-development, where clearly articulated alternative models are still lacking. However, in a later stage researchers will want to use the developed models to quantify evidence (e.g., for a treatment effect in medical clinical trials). In this stage, a between-model perspective appears to be essential. In sum, we remain convinced that even though FBST ev may be useful as a within-model measure of surprise, it is not a genuine measure of evidence.