Introduction

The view of the brain as a passive input–output device is losing prominence with the emerging understanding of the importance of spontaneous brain-wide dynamics in perceiving and acting upon the environment. Key in regulating these ongoing brain-wide dynamics are global fluctuations of neural gain: the degree to which neural signaling is amplified or suppressed (Aston-Jones & Cohen, 2005; Eldar et al., 2013, 2016; Mather et al., 2016; Servan-Schreiber et al., 1990; Shine et al., 2021). An increase in global gain is thought to enhance both excitatory and inhibitory neural signals, thereby increasing the contrast between weak and strong connections.

Global fluctuations in neural gain are made possible through brain-wide neuromodulation arising from brainstem arousal systems, including the locus coeruleus (LC), whose noradrenergic projections innervate a large part of the central nervous system (Aston-Jones & Cohen, 2005; Berridge & Waterhouse, 2003; Joshi et al., 2016). The ability to flexibly modulate brain-wide neural dynamics through changes in the activity of the LC and other neuromodulatory systems provides the brain with a powerful tool for appropriately adapting behavior in a rapidly changing and unpredictable environment, both from moment to moment and over slower timescales. What exactly prompts changes in this activity, and how subsequent fluctuations in neural gain impact interactions with the environment are important, yet largely unanswered questions.

Although it is impossible to directly measure neural gain in human participants, an increasing body of research suggests that changes in neuromodulatory activity (and consequently neural gain), most prominently of the LC, can be non-invasively tracked by measuring pupil diameter (Breton-Provencher & Sur, 2019; Joshi et al., 2016; Murphy, O’Connell, et al., 2014; Murphy, Vandekerckhove, et al., 2014; Reimer et al., 2016). In particular, the first derivative (rate of change) of pupil size may be best suited to capture neural gain effects following noradrenergic neuromodulation (Joshi et al., 2016; Murphy et al., 2021; Reimer et al., 2016; van den van den Brink, Murphy, et al., 2016). Using pupil size measures as a proxy for neural gain, researchers have found evidence of the expression of neural gain effects in cortical network activity and the rate of hippocampal sharp-wave ripples (Eldar et al., 2013; McGinley et al., 2015; van den van den Brink, Pfeffer, et al., 2016; Vinck et al., 2015; Warren et al., 2016). Furthermore, several studies have found behavioral correlates of neural gain effects in for example the domains of learning (Eldar et al., 2013), perceptual processing (Eldar et al., 2016), and decision-making under time pressure (Murphy et al., 2016).

While rapid progress is being made in linking inferred changes in neural gain to measurable behavioral outcomes, the domain of cognitive control remains rather unexplored in this regard. Cognitive control encapsulates the set of cognitive processes that allow us to flexibly respond to the environment in a goal-directed manner, instead of being subject to the constraints of automaticity. The limitations of cognitive control are exemplified in the classic Stroop task; even when participants manage to limit the number of errors, there is a robust slow down of the reaction time (RT) in trials where the stimulus dimensions are conflicting (e.g., the word BLUE shown in green text) compared to neutral trials (e.g., the string XXXX shown in red text). Moreover, participants often respond quicker when the stimulus dimensions match (e.g., the string BLUE shown in blue text) than on neutral trials. The mechanisms underlying these Stroop interference and facilitation effects have been subject to intensive study for several decades since these effects could elucidate important characteristics of the capacity for cognitive control. An influential theory attempting to explain these phenomena states that cognitive control can be simulated as the sustained (proactive) pattern of activation across a set of task-demand representations that creates a top-down bias leading to the production of a response other than the one prepotently associated with a given stimulus (Botvinick et al., 2001; Cohen & McClelland., 1990; Cohen & Huston, 1994; Miller & Cohen, 2001). More recently, this theory has been extended by introducing the concept of task conflict (i.e., the simultaneous activation of conflicting task-demand representations) and by distinguishing proactive and reactive modes of cognitive control (Braver, 2012; Kalanthroff et al., 2018). Hereby, the proactive mode is characterized by sustained activation of task-demand representations while the reactive mode is characterized by a more transient response-to-trial-evoked conflict (Cohen & Servan-Schreiber, 1992; Servan-Schreiber et al., 1990).

This theory is capable of explaining an impressive array of behavioral results from the Stroop task. However, even though early computational modeling work based on this theory of cognitive control did touch upon the subject of gain modulation (Cohen & Servan-Schreiber, 1992; Servan-Schreiber et al., 1990), it is still unclear whether the theory can be extended to incorporate effects of changes in neural gain (and dynamical brain states in general). More generally, as both the modulation of behavior by gain and the more directed modulation of behavior by cognitive control influence many aspects of our interactions with the environment, it is imperative to elucidate how these specific systems interact with each other. The class of computational models described above—in which both gain modulation and cognitive control are formally defined in the algorithms that translate stimulus input into behavior—provide a testbed for addressing these questions.

Here, we set out to investigate this interaction by computationally and empirically exploring the effect of neural gain modulation in the context of cognitive control. To this end, we implemented fluctuations in neural gain in the proactive control/task conflict (PC-TC) model, the most recent instantiation of the theory introduced above, which accounts for a wide range of phenomena associated with Stroop-task performance (Kalanthroff et al., 2018). We also assessed empirically—by assessing performance of human participants on a standard Stroop task with simultaneous measurements of pre-trial baseline pupil size—whether the framework can be extended to capture the effects of pupil-linked changes in neural gain.

Below, we show that the PC-TC model is robust in explaining Stroop data even when accounting for changes in inferred neural gain states. The PC-TC model correctly predicts the overall decrease of reaction time with increased global gain (larger pupil rate of change), accompanied by a relative increase in Stroop interference and decrease in Stroop facilitation. By comparison, an earlier model grounded in the same theory (Cohen & Huston, 1994) predicts the overall decrease in reaction time, but cannot account for the gain-related increase in interference.

We conclude by analyzing the mechanisms through which the PC-TC model recapitulates the empirical findings, highlighting the representation and use of task conflict as key for the theory to successfully incorporate the effects of changing neural gain.

Methods

Participants

Twenty-eight individuals (11 males, aged 18–35) participated in the study. They spoke fluent Dutch and received monetary compensation for their participation. The study was approved by the Psychology Research Ethics Committee of Leiden University (CEP code: 2,806,978,983), and participants signed informed consent prior to their inclusion in the study.

Task

Participants performed a Stroop color-naming task (Fig. 1a) with three word stimuli (Dutch equivalents of blue, green, and red) and three neutral non-word stimuli (“XXXXX,” “SSSSS,” “ZZZZZ”) which were presented in blue, green or red Helvetica font color (size 36) in the middle of a black screen, using Psychtoolbox for MATLAB. Equal numbers of incongruent, neutral, and congruent trials were presented in random order. The words were presented until the participant responded, with a maximum duration of 2 s. During the response-to-stimulus interval (RSI), the letter string was replaced by a white fixation point for 3.3 s, allowing the evoked pupil response to return to baseline level before measurement of baseline pupil diameter on the subsequent trial (Supplementary Fig. 1).

Fig. 1
figure 1

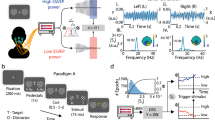
Results of the empirical study and the PC-TC model simulations. a Top: example of an incongruent trial followed by a neutral trial. In the first trial the correct answer is “blue,” in the second trial the correct answer is “green.” Bottom: mean RT (left) and accuracy (right). Orange line indicates the simulated RTs from the Kalanthroff model. Error bars indicate SEM. b Architecture of the PC-TC model. c Empirical data: RT as a function of pupil derivative. d Empirical data: interference (incongruent RT–neutral RT) and facilitation (neutral RT–congruent RT) as a function of pupil derivative. For c and d, single-trial data were first z-scored within participants, then all data were pooled across participants and sorted by pupil derivative into equal-sized bins. e Simulation data: RT as a function of gain. f Simulation data: interference (incongruent RT–neutral RT) and facilitation (neutral RT–congruent RT) as a function of gain. ISI, interstimulus interval; RT, reaction time; C, congruent; N, neutral; I, incongruent; PC, proactive control; z, z-score; log, log transformed; Δ, difference. Note that the legend in e and f also applies to respectively c and d

Full size image

Participants first received automated task instructions to respond to the font color using the left, down, and right arrow keys for red, green, and blue, with their right index, middle, and ring fingers, respectively. They were also asked to respond as quickly as possible, but without making any errors. The participants then completed a practice block of 36 trials with feedback provided through a brief change in the color of the fixation point: green or red for correct and incorrect responses, blue indicating “too late” if no response was given after 2 s. This feedback was only present in the practice block. After the practice block, participants were presented with 6 blocks of 126 trials, each block lasting approximately 8.5 min, with 2-min breaks in between. This amounts to 756 trials in total, evenly divided over the three conditions (incongruent, neutral, and congruent). Participants were shown their mean block accuracy at the end of each block.

Pupillometry

Pupil diameter was recorded under low levels of ambient light (< 7.2 cd/m2) at a sampling rate of 250 Hz, with an EyeLink 1000 eye-tracker which was calibrated before each block of trials. The participant’s head was supported by a chinrest at a viewing distance of 65 cm. Pupil diameter was recorded in arbitrary pixels and subsequently converted to mm using data recorded from an artificial pupil of precisely known diameter. The data were low-pass filtered (fourth-order Butterworth) at a cutoff frequency of 6 Hz and segmented into epochs from − 0.5 to 0 s relative to the onset of each stimulus. Trials with a blink (as defined by the manufacturer’s software) or gaze shift exceeding 3 degrees of visual angle from fixation were excluded from all analyses. The remaining epochs that violated amplitude (any sample < 1 mm) or gradient (any difference in consecutive samples > 0.02 mm) criteria, both measured in the pre-filtered data, were also rejected from the analysis. This resulted in an average of 6.0% (standard deviation = 8.0%) rejected trials.

Similar to previous reports (Gilzenrat et al., 2010; Murphy, O’Connell, et al., 2014; Murphy, Vandekerckhove, et al., 2014), single-trial measures of pre-trial baseline pupil diameter were estimated in the cleaned datasets by computing the average pupil size during the 0.5-s pre-stimulus window. Measures of pupil derivative were estimated for the same trials by computing the signed change in pupil diameter over the two consecutive samples directly preceding stimulus onset (thus capturing the “instantaneous” rate of change of pupil diameter, in keeping with how this measure has been defined in other work; Murphy et al., 2021; Reimer et al., 2016).

Other work has examined stimulus-evoked pupil dilations associated with Stroop conflict (Hershman & Henik, 2019) and other manifestations of processing conflict and reactive control (van der Wel & van Steenbergen, 2018). Unlike in this work, our stimuli were not matched for luminance, and luminance-related differences in evoked pupil responses to individual stimuli would significantly confound the single-trial analyses of relationships between pupil size and behavior that are our focus. Thus, we restrict our analyses to pupil size at or before stimulus onset, which is not subject to such luminance effects.

Statistical Analysis

We conducted the statistical analyses in R-Studio using the lme4 package for building and fitting linear models (Bates et al., 2015). The full reproducible code is available in the supplementary materials. We ran two linear models, one using baseline pupil size and the other using the pupil derivative as regressors, but otherwise equal. The pupil regressors were first z-scored within blocks to minimize slow between-block fluctuations potentially due to non-cognitive factors (e.g., differences in position relative to the eye-tracker) and then concatenated across blocks. The dependent variable RT was log transformed, concatenated across blocks, and then z-scored. Trials on which the z-scored RT exceeded 3.5 were excluded. All other regressors were mean-centered. We fitted the following linear regression model:

$$R\mathrm{T }\sim 1+\mathrm{congruent}+\mathrm{incongruent}+\mathrm{pupil}+(\mathrm{congruent}\times \mathrm{pupil})+(\mathrm{incongruent}\times \mathrm{pupil})+\mathrm{crep}+\mathrm{wrep}+\mathrm{repalt}+\mathrm{cae}+\mathrm{ntrial}$$

where congruent and incongruent are binary regressors that were set to 1 in congruent and incongruent conditions, respectively. Pupil represents single-trial baseline pupil size or pupil derivative. Several other binary regressors were included to capture additional sources of variance in Stroop-task performance following the recommendations of Notebaert and Verguts (2007): crep, which was set to 1 when the trial was a color repetition; wrep, which was set to 1 when the trial was a word repetition; repalt, which was set to 1 in case of a complete repetition or alternation (both color and word same or different than on the previous trial); and cae, the conflict adaptation variable, which was set to 1 if the congruency status was the same as on the previous trial. We also included the continuous regressor ntrial (trial number with block), to account for within-block time-on-task effects on RT. As Notebaert and Verguts did not find any effect of previous trial congruency on RT, we did not include that regressor in the model (see (Notebaert & Verguts, 2007; table 1).

The model was fit to each participant’s data separately, after which we conducted a one-sample t-test comparing the group distribution of coefficients to zero and inspected the statistical results for our regressors of interest. Similar conclusions were reached using nested model comparisons.

The Stroop GRAIN Model

We performed all computational modeling using the PsyNeuLink package (PsyNeuLink, http://www.psyneuln.deptcpanel.princeton.edu). The Stroop GRAIN (graded, random, activation-based, interactive, and nonlinear) model (Fig. 3a) includes color and lexical input layers with units that represent the stimulus color and word (Cohen & Huston, 1994). These connect to a single response layer with units representing potential responses. In Fig. 3a, the thicker lines (stronger connection weights) from the lexical layer to the response layer reflect the assumption that stimulus–response associations in the word-reading pathway are generally stronger than those in the color-naming pathway. To exert control, units in a task-demand layer provide a top-down bias to the color or lexical layer, depending on whether the task is to name the color or read the word. This top-down bias in turn helps overcome the response competition caused by activation of the task-irrelevant pathway. The units within each layer inhibit each other. An important characteristic of the model is that the lexical and color input layers have bidirectional excitatory connections with the response layer and the task-demand layer. Consequently, not only do the task-demand units inject a sustained bias to processing in the color- and word-processing pathways (thus exerting proactive cognitive control), but the input units also activate the corresponding task-demand units in a bottom-up fashion. Because we used non-lingual neutral stimuli (unpronounceable letter strings), the neutral unit was not connected with the task-demand unit representing the word task.

All model parameters and functions were adopted from the original paper (Cohen & Huston, 1994) with a few exceptions (Supplementary Table 1). We fitted the model (with gain fixed at 1; see below) to our group-averaged empirical behavioral data (mean correct RTs for congruent, neutral, and incongruent conditions) by adjusting the value of the within-layer inhibition parameter, and the slope and intercept of a linear function that converted model processing cycles to milliseconds. Furthermore, to simulate the effects of global gain modulation, we added a neuromodulatory gain unit to the fitted model that multiplicatively scaled the slope of the network’s activation function relating a unit’s input x to its corresponding output F(x). The activation function of the response layer and task layer is as follows:

$$F\left(x\right)=\left(\frac{1}{1+ {e}^{-(x)}}\right)\times \mathrm{gain}$$

while the activation function of the stimulus layers is as follows:

$$F\left(x\right)=\left(\frac{1}{1+ {e}^{-(x-4)}}\right)\times \mathrm{gain}$$

The neuromodulatory unit affected the gain of all units in the network equally, simulating the diffuse and global effects of brainstem arousal systems such as the noradrenergic system. See the next section for a note on the specific formulation of gain modulation we focus on here and other alternatives we considered.

The PC-TC Model

The proactive control/task conflict (PC-TC) model (Kalanthroff et al., 2018) is similar to the Stroop GRAIN model except for three assumptions. First, the simultaneous activation of the units in the task-demand layer leads to task conflict, which is defined as the product of the activation values of the two task-demand units multiplied by a task inhibition parameter. This task conflict inhibits the two units in the response layer until the conflict is resolved, which slows down RTs. This assumption reflects the idea that uncertainty about what task needs to be performed puts a temporary brake on action selection, and constitutes a form of reactive cognitive control. Second, in the PC-TC model, the connection between the lexical/color layers and the response layers is unidirectional (from word/color to response) instead of bidirectional as in the GRAIN model. Third, a central idea of the PC-TC model is that the degree of task conflict is partly determined by the amount of proactive control that can be recruited in advance of the Stroop stimulus. Higher proactive control leads to quicker resolution of task conflict, and thereby a faster increase in activation in the response layer. While in the Stroop GRAIN model, the sustained top-down input is fixed, the PC-TC model explicitly allows for varying levels of sustained top-down input to the task-relevant task-demand unit. Lowering proactive control renders the task-demand representations vulnerable to task-irrelevant bottom-up input from the lexical input layer. This increases task conflict, resulting in increased reactive control through suppression of activity in the response layer. This slows down responses but protects the model from making errors.

We fitted the model to our empirical data by doing a grid search to find the combination of proactive control, task inhibition, and linear cycles-to-RT function (intercept, slope) parameters that best matched the mean correct RTs in the different conditions (Supplementary Table 2). Furthermore, we added a gain parameter to the network’s activation function in the same manner as with the GRAIN model. The adapted activation function for the PC-TC model is as follows:

$$F\left(x\right)=\left(\frac{1}{1+ {e}^{-4(x-1)}}\right)\times \mathrm{gain}-c$$

Hereby, c is defined as \(\frac{1}{1+ {e}^{4}}\) ≈ 0.0180. As in the GRAIN model, gain acts as a multiplicative factor for all units in the network. We note that there are several possible ways to implement gain modulation through the activation functions of both the PC-TC and GRAIN models. One implementation involves the application of a multiplicative term to the exponent in the denominator of the activation function. We observed that in the presence of an additive constant term in the exponent (there in both the PC-TC function and the function for the GRAIN stimulus layer), this implementation has the unexpected consequence of suppressing weak excitatory inputs when gain is high. Such an effect is inconsistent with the enhancement of weak inputs that is generally considered to be a cardinal feature of increased gain, so we do not consider this implementation further. Instead, we focus primarily on an implementation, whereby the gain term is applied multiplicatively to the entire activation function (sometimes referred to as “multiplicative gain”; Munn et al., 2021). We additionally considered a third form whereby a multiplicative term is applied only to the input x in the exponent. This implementation similarly yielded the overall RT speeding, a clear decrease in Stroop facilitation, and a weaker increase in Stroop interference with increasing gain that we report below, albeit under a more restricted range of gain values outside of which the model generated unrealistically slow or fast RTs (data not shown).

Simulation Method

For both models, we simulated congruent, neutral, and incongruent conditions for different levels of gain to investigate the impact of changing gain on Stroop-task performance. Before the start of each simulated trial, all units were initialized to zero. Each trial started with a settling period of 500 cycles, which simulated the time before stimulus presentation. During this settling period input was provided to the appropriate task-demand unit, and the system was allowed to settle into a “ready state” for that task. In the PC-TC model, the continuous input to the appropriate task-demand unit originated from the proactive control unit. In the GRAIN model, the value of the appropriate task-demand unit was simply set to 1. After the settling period, the inputs representing the Stroop stimulus for that trial were set to 1 for the remaining duration of the trial. The activation of the color and lexical units set in motion a cascade of unit-updating cycles that continued until one of the response units reached the pre-specified threshold. The simulated RT was defined as the number of update cycles from stimulus presentation until the threshold crossing, passed through a linear function (with free slope and intercept parameters, see above) to convert cycles to milliseconds. The intercept of the linear function was assumed to capture the duration of sensory encoding and motor execution—the non-decision component of the RT.

Results

Empirical and Simulated Behavior

Empirical RTs showed significant Stroop facilitation (neutral-congruent = 20 ms, t(27) = 4.68, p < 0.001) and interference effects (incongruent-neutral = 51 ms, t(27) = 7.80, p < 0.001; Fig. 1a). Accuracy showed a pattern consistent with these effects on RT but was near ceiling.

To constrain the PC-TC model, we fitted the model to the empirical RTs on correct trials (see “Methods” for the fitting procedure and Supplementary Table 2 for model parameter values). After model fitting and applying the linear function to convert RT in cycles to RT in milliseconds, the simulations produced identical Stroop facilitation (20 ms) and near-identical interference (52 ms; Fig. 1a).

Gain-Behavior and Pupil-Behavior Relationships

Using the constrained PC-TC model, we systematically varied the level of global gain to examine the effect of gain on RT. Increasing gain was associated with a strong overall speeding of RTs (Fig. 1e). Furthermore, increasing gain was associated with a monotonic increase in Stroop interference in combination with a monotonic decrease in Stroop facilitation (Fig. 1f). These predictions were robust to a range of values of Gaussian noise input in the task-demand layer and the response layer (0.1 ≤ σ ≤ 1).

Next, we compared these model predictions to empirically observed pupil-behavior relationships, as established using a multiple linear regression model (see “Methods” for regression equation and Supplementary Tables 3 and 4 for the full results). A cardinal effect of gain modulation common across candidate models of the Stroop task (PC-TC, GRAIN, as well as a well-known predecessor; Cohen et al., 1990, data not shown) is the general speeding of RTs with increased gain described for the PC-TC model above. We leveraged this effect to arbitrate between two candidate pupillometric proxies for gain state that have been described in the literature: pre-stimulus “baseline” pupil diameter (Eldar et al., 2013; Gilzenrat et al., 2010; Jepma et al., 2009; Murphy et al., 2021; Warren et al., 2016) and its first derivative (i.e. rate of change; Murphy et al., 2021; Reimer et al., 2016; van den van den Brink, Murphy, et al., 2016; van den Brink, Pfeffer, et al., 2016). We found a robust main effect of pupil derivative (mean β ± s.e.m. = -0.031 ± 0.008, t(27) = -3.78, p < 0.001) but not baseline pupil diameter (mean β ± s.e.m. = 0.024 ± 0.014, t(27) = 1.84, p = 0.07) on RT, and this derivative effect was in the predicted direction (increased derivative, putatively reflecting states of higher gain, being associated with faster RTs; Fig. 1c). We, therefore, focused on pupil derivative as our candidate proxy for changes in gain state.

We found that increased pupil derivative was associated with increased Stroop interference as captured by the incongruent term in our multiple linear regression model (mean β ± s.e.m. = 0.038 ± 0.016, t(27) = 2.31, p < 0.05). Moreover, increased pupil derivative was associated with decreased Stroop facilitation as captured by the congruent term in our multiple linear regression model (mean β ± s.e.m. = 0.041 ± 0.018, t(27) = 2.41, p < 0.05) (Fig. 1d). Thus, these results support key predictions of the PC-TC model about the effect of global gain changes on Stroop-task performance: all three predicted effects (general speeding, increased interference, decreased facilitation) were observed in the relationship between RT and pupil derivative. As was the case for the RT main effect, neither the interference (mean β ± s.e.m. =  − 0.024 ± 0.017, t(27) = -0.22, p = 0.83) nor facilitation (mean β ± s.e.m. = -0.004 ± 0.018, t(27) =  − 1.40, p = 0.17) effects were observed for baseline pupil diameter.

We note that some disparities remain between the model predictions (Fig. 1e,f) and observed pupil derivative-behavior relationships (Fig. 1c,d). In particular, the overall strength of the RT main effect, captured by the steepness of the negative-going lines in Fig. 1c and e, appears stronger in the model than in the data; and, there is an apparent asymmetry in the magnitude of the effect of gain on Stroop facilitation and interference that is present in the model (stronger effect of gain on facilitation; Fig. 1f) but absent in the data (Fig. 1c). In general, we adopted a conservative fitting approach, fitting a noise-free version of the model only to the mean RTs across the three trial types of the Stroop task and leaving zero degrees of freedom to optimize the fit to the observed pupil-behavior relationships; and we note that fine-tuning of the model parameterization has the capacity to resolve the abovementioned discrepancies. Specifically, further simulations showed that injecting noise into the stimulus, task demand, and/or response layers of the model serves to decrease the overall strength of all gain-RT relationships, while leaving the relative pattern of facilitation and interference effects intact (data not shown); increasing the level of proactive control serves to selectively increase the slope of the relationship between gain and Stroop interference without substantially affecting the gain-facilitation effect (Supplementary Fig. 2).

Unit Activation Trajectories

To understand how the specific pattern of gain effects described above is produced by the PC-TC model, we examined the unit activation trajectories during simulated trials with low (0.9) and high (1.1) gain (Fig. 2). High gain produces a general speeding of RTs because all signals are amplified, leading the network to generally reach decisions triggered by a fixed response threshold more quickly. One consequence of this general amplification, however, is an increase in the activations of the two task-demand units. This increases task conflict, which acts to slow down responses through the reactive control mechanism of task-conflict-to-response inhibition. Importantly, this latter chain of events occurs only on congruent and incongruent trials, on which the task-irrelevant word-reading task unit is activated by bottom-up input from the lexical input layer. Because our neutral stimuli are non-lingual letter strings, they evoke minimal task conflict (Monsell et al., 2001), and hence there is no task-conflict-to-response inhibition for these stimuli, regardless of the level of gain. Because higher gain produces greater RT-slowing conflict for congruent and incongruent RTs, but not neutral RTs, it increases Stroop interference (incongruent RT minus neutral RT) and decreases Stroop facilitation (neutral RT minus congruent RT).

Fig. 2
figure 2

Task demand and response unit activation trajectories from the PC-TC model across a single noiseless trial in low gain (left) and high gain (right) conditions. The gray numbers depict the number of cycles before the response threshold (horizontal dashed gray line) is reached

Full size image

GRAIN Model

If the effects of gain on Stroop interference and facilitation are indeed mediated by gain effects on task-conflict-to-response inhibition, then a model without task conflict should not produce these effects. To test this prediction, we repeated our simulations using the GRAIN model of the Stroop task (Cohen & Huston, 1994), which formed the basis for the PC-TC model but does not include task-conflict-to-response inhibition (Fig. 3a; see Supplementary Table 1 for model parameter values). As noted above, we found that this model also produced a general speeding of RTs with increased gain (consistent with our empirical result for pupil derivative, but not baseline pupil diameter; Fig. 3b). However, contrary to the PC-TC model, the GRAIN model did not produce the gain-related increase in Stroop interference observed in the empirical data, but rather a decrease in interference (Fig. 3c). Similar results were obtained when we ran the PC-TC model simulations after removing the task-conflict-to-response inhibition link. These results confirm the notion that the effects of gain on cognitive control reflect an interaction between gain, task conflict, and the resulting reactive cognitive control, at least in the context of the Stroop task.

Fig. 3
figure 3

Results of the GRAIN model simulations. a Model architecture. Note the absence of the proactive control sustained bias and the task-conflict-to-response inhibition depicted for the PC-TC model in Fig. 1a. b RT as a function of gain. c Interference (incongruent RT–neutral RT) and facilitation (neutral RT–congruent RT) as a function of gain. RT, reaction time; log, log transformed; Δ, difference

Full size image

Discussion

We aimed to examine the effects of neural gain on cognitive control, using a classic Stroop task, pupillometry, and computational modeling. To simulate the effects of global gain modulation, we added a neuromodulatory gain unit to the PC-TC model (Kalanthroff et al., 2018) and examined the effects of a range of gain values on the model’s Stroop task-performance. Increasing gain led to an overall speeding of RTs, increased Stroop interference, and decreased Stroop facilitation. Pupil analyses revealed that our empirical proxy of neural gain, the pre-trial pupil derivative (i.e., rate of change), showed the same diagnostic relationship with task performance: a larger pupil derivative was associated with an overall speeding of RTs accompanied by opposing effects on Stroop interference and facilitation.

An analysis of the internal dynamics of the PC-TC model suggested that high gain produces a general speeding of RTs because all signals are amplified and, coupled with a fixed response threshold, the network thus settles on a decision more quickly. Furthermore, this general signal amplification increases the degree of task conflict present in congruent and incongruent trials, which works against the general speeding effect to slow down responses (and protect accuracy) on these trials through a (within-trial) increase in reactive control. This increase in reactive control produces a counter-intuitive rise in interference (incongruent minus neutral RT) and a drop in facilitation (neutral minus congruent RT), thus accounting for our simulated and empirical Stroop findings. In contrast, very similar models without a task conflict-control loop (Cohen & Huston, 1994) could not account for these findings. Thus, the concept of task conflict is vital in understanding the effects of neural gain on cognitive control processes in the Stroop task.

A psychological process that may correspond to the pre-stimulus fluctuations in pupil-linked neural gain that we capitalized on here is temporal expectation, the ability to actively predict the timing of upcoming sensory input. Growing temporal expectation is accompanied by a gradual increase in pupil size (Jennings et al., 1998; Shalev & Nobre, 2022) and neural gain (Auksztulewicz et al., 2019). Interestingly, phasic alerting, a purely exogenous surge of temporal attention, increases flanker and Simon interference (but not Stroop interference), while speeding up overall RTs (Macleod et al., 2010; Nieuwenhuis & de Kleijn, 2013; Schneider, 2019)—a pattern resembling the behavioral consequences of increased gain. This suggests that neural gain may be the mechanism that instantiates the surge in temporal attention. Future work should examine the relationships between phasic alerting vis-à-vis pupil size and neural gain.

How might our findings relate to the large body of existing work on experimental manipulations affecting performance on the Stroop task? To our knowledge, there are no commonly accepted manipulations of neural gain that can be applied to human participants. However, we consider the effects on Stroop-task performance of two types of manipulation that may qualify. First, evidence from rodents and human participants shows that locomotion is accompanied by a dilating pupil (Cao et al., 2020; McGinley et al., 2015) and an increase in the gain of visual responses (Polack et al., 2013; Reimer et al., 2014). We found one study in which the Stroop task was administered during low-intensity walking (Alderman et al., 2014). Stroop interference was increased compared to a seated control condition, consistent with our findings. However, it should be noted that, although pupil size is increased during locomotion, pupil-linked arousal and locomotion actually make distinct contributions to cortical activity patterns and stimulus encoding (Vinck et al., 2015) and so their effects on neural processing appear to be at least partially dissociable. Second, we reviewed the literature about the effects on Stroop-task performance of moderate- and high-intensity auditory noise, another condition that is associated with increased pupil size (Asgeirsson & Nieuwenhuis, 2017). The effects of noise on Stroop interference are mixed (e.g., Hartley & Adams, 1974; Houston, 1969), possibly because the effects of auditory noise on human task performance depend on various factors, including noise intensity, exposure duration, and type of noise (Smith, 1989)—factors that often differ between studies. Altogether, we must be cautious in directly relating this work on locomotion and noise to our key findings on pupil-linked gain and Stroop-task performance.

If amplified task conflict through an increase in global gain can explain our empirical results, could our results also be explained by amplified task conflict through a reduction in proactive control? PC-TC model simulations confirm that a reduction in proactive control increases Stroop interference and reduces Stroop facilitation (Kalanthroff et al., 2018, p. 10; Supplementary Fig. 2), in line with our findings. However, a reduction in proactive control slows down RTs and therefore does not mimic the overall speeding of RTs that we observed with enhanced gain and increased pupil derivative. Elsewhere, Chiew and Braver (2013) found that increased pre-trial baseline pupil size was associated with increased rather than decreased proactive control. This positive association with proactive control would predict opposite relationships between pupil size and Stroop interference/facilitation to what we observed presently for pupil derivative and, importantly, this study restricted analysis to baseline pupil size and did not examine the pupil derivative. In summary, our pattern of findings cannot be explained by changes in proactive control. Instead, our explanation is consistent with a growing literature relating pupil size and its derivative to global gain (Eldar et al., 2013; Murphy et al., 2016; Warren et al., 2016).

The degree of Stroop interference in an individual is commonly used as a measure of cognitive control in a range of clinical patient populations. This assumption is in line with a wealth of neuropsychological and neuroimaging evidence for a key role of the prefrontal cortex in Stroop-task performance (reviewed in Cohen et al., 1990). Furthermore, PC-TC model simulations by Kalanthroff and colleagues (2018) suggest that abnormal behavioral patterns of Stroop performance in various psychiatric patient populations may be caused by impaired proactive control, reduced sensitivity to task conflict, or other aspects of cognitive control. Nonetheless, other work highlights the important contributions of other types of cognitive processes to individual differences in Stroop interference (e.g., stimulus processing speed and lateral inhibition; Naber et al., 2016), and challenges the view that the Stroop task primarily assesses cognitive control. The present results, like the seminal work by Cohen and Servan-Schreiber (1992), suggest that abnormal gain (in the prefrontal cortex and/or other parts of the brain) may be an important additional factor for explaining aberrant cognitive control in clinical populations, many of which can be characterized by disturbed neuromodulatory gain control (Hauser et al., 2016; Parr et al., 2018).

Lastly, the present work offers a clear example of the utility of computational modeling for understanding what can be nuanced and counter-intuitive behavioral effects arising from relatively simple neurocognitive manipulations—in this case, the suite of effects of global gain modulation on Stroop-task performance. In leveraging the PC-TC model to provide a highly parsimonious account of the complex relationships between fluctuations in pupil size and Stroop RT—which could not be achieved with earlier models—our results also provide novel empirical support for the unique feature of the PC-TC model that differentiates it from those earlier iterations: the computation of task conflict and its use in the deployment of reactive cognitive control. Our incorporation of gain modulation into the PC-TC model also furnishes novel predictions; in particular, relating to how the relationship between gain modulation and Stroop behavior may depend on the level of proactive control (Supplementary Fig. 2). Future work could look to test these predictions by deploying task designs thought to manipulate proactive control (Entel et al., 2015).