Generalization at Retrieval Using Associative Networks with Transient Weight Changes

Abstract

Without having seen a bigram like “her buffalo”, you can easily tell that it is congruent because “buffalo” can be aligned with more common nouns like “cat” or “dog” that have been seen in contexts like “her cat” or “her dog”—the novel bigram structurally aligns with representations in memory. We present a new class of associative nets we call Dynamic-Eigen-Nets, and provide simulations that show how they generalize to patterns that are structurally aligned with the training domain. Linear-Associative-Nets respond with the same pattern regardless of input, motivating the introduction of saturation to facilitate other response states. However, models using saturation cannot readily generalize to novel, but structurally aligned patterns. Dynamic-Eigen-Nets address this problem by dynamically biasing the eigenspectrum towards external input using temporary weight changes. We demonstrate how a two-slot Dynamic-Eigen-Net trained on a text corpus provides an account of bigram judgment-of-grammaticality and lexical decision tasks, showing it can better capture syntactic regularities from the corpus compared to the Brain-State-in-a-Box and the Linear-Associative-Net. We end with a simulation showing how a Dynamic-Eigen-Net is sensitive to syntactic violations introduced in bigrams, even after the associations that encode those bigrams are deleted from memory. Over all simulations, the Dynamic-Eigen-Net reliably outperforms the Brain-State-in-a-Box and the Linear-Associative-Net. We propose Dynamic-Eigen-Nets as associative nets that generalize at retrieval, instead of encoding, through recurrent feedback.

Introduction

The ability to learn the structure underlying serially ordered events, be it parsing a sentence, following a melody, or tying one’s shoes, is a hallmark of intelligent behaviour. A learning theoretic account must specify how statistical regularities derived from a small subset of congruent serially ordered representations can encode sufficient constraints for the system to recognize the entire set of possible congruent sequences. Restricting ourselves to the linguistic domain,¹ how can we tell what serial ordering of words is congruent and what serial ordering is incongruent without having seen all congruent permutations of words? When recognition is not an option, structural generalization is required to determine which words can follow which other words. How is it that learners can generalize the structure of an infinite combinatorial domain based on a finite number of exemplar sequences?

One approach is to abstract away the contextual details of the contents of experience during encoding to form a generic representation. Assuming that memories are stored as connectivity weights in a network of simple processing units, a generalization-at-encoding view (e.g. Hinton, 1990) implies that at the time of storage (and perhaps also during sleep, Stickgold, & Walker, 2013) gradual changes to the connectivity of the network fine-tune the system for transforming its input into some desired output. The transformation compresses (summarizes) the input into a lower-dimensional representation that retains information relevant to the mapping. Some difference between the generated pattern and a desired pattern is used to obtain an error. The error is used to adjust the connectivity weights in the direction that reduces the error, and the whole cycle is repeated until the error is minimized. If the input was every word in a sentence, except for one target word that was treated as the desired output, over many iterations with many sentences, words of similar syntactic and semantic classes would cluster together in the compressed space (e.g. Westbury & Hollis, 2019). If the bigram “you know” was never seen, but “I know” and “they know” were seen, the system can align the representations and infer that “you know” is congruent since “you” is very similar to “they” and “I” and “know” and both “I” and “know” can precede “know”. Linguists have long discussed the importance of capturing relations between words that can be used interchangeably—i.e. paradigmatic relations (de Saussure, 1974)—and recently various computationally tractable models have been proposed to learn such relations (e.g. Sloutsky et al., 2017).

One way higher-order relations, such as paradigmatic relations, can be induced is by projecting the raw input patterns into a latent space. The mapping of input into a latent space brings out higher-order co-occurrence structures that are not explicit in the original space (Landauer & Dumais, 1997; Grefenstette, 1994). In word2vec (Mikolov et al., 2013), words surrounding a target word are compressed into a low-dimensional representation that is used to predict the target word itself. The network is optimized to make the mapping with small subsequences (contexts) sampled from a large text-corpus. Words that co-occur in the same contexts (e.g. “squirrel” and “chipmunk”) map to similar representations in the lower-dimensional space.

Error-based neural architectures are widely employed in cognitive models to formalize various theories of human information processing (see Rogers & McClelland, 2014, for a review), but they have some limitations. Compressing the input into a lower-dimensional representation renders encoded patterns more vulnerable to cross-talk. When a sufficient number of new patterns are encoded, interference can completely wipe out previously encoded representations (Mannering & Jones, 2020; McCloskey & Cohen, 1989; Ratcliff, 1990). Interference can be reduced by making the changes to the weights very small for a given learning trial (i.e. each forward pass of an input through the network followed by a backward propagation of error). When the weight changes are small, the network requires about an order of magnitude more learning trials (e.g. around 600) to match human learners (e.g. around 10 trials) on the same task (McCloskey & Cohen, 1989), and interference is still far greater in the network than what is observed with human learners (Barnes & Underwood, 1959).²

An alternative generalization-at-retrieval view (Hintzman, 1986; McClelland, 1981; see Jones, 2019, for a recent overview) is that instead of assuming a mapping of the input into some latent space, a noisy copy is directly encoded into the connectivity structure. The presentation of a cue activates some of the processing-units, which then initiate a cascade of signals that reverberate through the network until the mutual constraints imposed by the connectivity structure dynamically resolve to complete retrieval (Hintzman, 1986). The encoded patterns are not abstractions. Spreading activation drives abstraction as retrieval stabilizes to a pattern formed through the integration of all previously encoded patterns in resonance with the retrieval cue.

While generalization at retrieval is not mutually exclusive with generalization during encoding, it has been argued that deferring generalization until retrieval better meets the flexibility demands of the environment (Hintzman, 1988). One reason is that the system has access to the relevant cues when attempting to generalize, hence escaping the need to prospectively assume a generic form that can meet later requirements. During retrieval, constraints (i.e. memories) that are relevant to the immediate circumstances can be selected and integrated online. The absence of dimensionality reduction allows the system to freely add new constraints with little immediate concern for how they will impact performance on other representations.

MINERVA 2 (Hintzman, 1988, 1986) is a commonly used memory model that assumes generalization during retrieval instead of encoding. Each new instance of experience is stored by appending a noisy copy to the end of a rectangular matrix, say E; the width of the matrix grows with experience. At retrieval, a cue is compared with every instance in memory, in parallel, and a retrieved pattern is constructed by summing all instances into a single vector, each weighted by its similarity to the retrieval cue. Jamieson and Mewhort (2009, 2010, 2011; Chubala & Jamieson, 2013) demonstrated that a MINERVA 2 variant is capable of distinguishing congruent and incongruent strings in artificial grammar tasks, where learners are presented with a set of strings generated from a probabilistic Finite State Automaton, and are later queried to discriminate between strings that are generated from the same rules and strings that violate the rules in some way. Dennis (2005; also see Kwantes, 2005) provided a large-scale instance-based model, trained on natural language text, that captured various phenomena in semantic composition by inferring paradigmatic relations between words based on their shared contexts. Johns & Jones (2015) have provided simulations that capture various phenomena in the sentence reading literature by equipping an instance-based model with semantic vectors constructed using the BEAGLE algorithm (Jones & Mewhort, 2007; for more recent results, see Johns et al., 2020).

An alternative class of models, called associative nets,³ employs a generalization-at-retrieval approach without adding memory patterns to a limitless memory store. By doing away with a compressed representation (i.e. a hidden layer), associative nets are also distinct from error-driven neural networks with hidden layers. Associative nets provide a mechanistic account of memory retrieval through the collective action of a mass of associations. They have been used to model phenomena as varied as categorical perception (Anderson et al., 1977), serial recall (Farrell & Lewandowsky, 2002), reading comprehension (Kintsch, 1998), and letter perception (McClelland & Rumelhart, 1981).

Following Hebb (1949), Hebbian associative nets assume that synapses between pairs of “neurons” strengthen when the neurons activate within a short time interval. If a single neuron encodes a single feature in a stimulus (e.g. colour or size), then the strengthened synapses encode co-occurrence patterns between features that compose the stimulus. Stimulus patterns are represented as vectors, where the value in each element stands for the rate of firing of a particular neuron.⁴ A geometric interpretation of the state vector is a point in a high-dimensional space, making state vectors the dynamic analogues to semantic vectors (e.g. word2vec). Whereas new memories are appended to a wide matrix in MINERVA 2, an associative net encodes new memories by superimposing each memory pattern’s outer product, with itself, into a weight matrix of fixed dimensionality. In essence, the Hebb rule binds coactive features into an assembly of neurons that can mutually excite one-another later during retrieval. If we treat the rectangular memory used in MINERVA 2 as the collection of experiences to which the system is exposed, memory in an associative net is proportional to the product of the experience matrix with its transpose, W ∝ EE^T (c.f., the co-occurrence matrix).

Associative nets have suffered from one of two problems. On the one hand, systems like the Interactive Activation and Competition model (Rumelhart & McClelland, 1987) and Construction Integration networks (Kintsch, 1998) require handcrafted connection weights, and have been difficult to scale beyond toy problems. On the other hand, associative networks like the Hopfield net (Hopfield, 1982) and the Brain-State-in-a-Box (Anderson et al., 1977) have been restricted to memory retrieval tasks; they do not generalize beyond the reconstruction of encoded patterns. In this paper, we propose a mechanism that extends the generalization capabilities of associative networks to allow them to more effectively compete with instance-based models. By generalization we mean structural generalization: deciding if permutations of symbols come from a combinatorial domain, based on experience with just a small subset of instances. We use the terms “structural generalization” and “combinatorial generalization” interchangeably throughout the manuscript, and will often opt to simply use “generalization”. We demonstrate how generalization during retrieval may accomplish a simplified grammar induction task: judging the serial order congruity of word pairs.

The network dynamics in an associative net are defined by a first-order difference equation—a recurrence relation. Recurrence drives retrieval by specifying how the weight matrix, W, and the momentary state vector, x^T_t, interact to yield the next momentary state vector, x^T_t+1. Geometrically, the recurrence relation defines a law of motion in a high-dimensional feature-space. During retrieval, an input probe, x^T₀ initializes the state for the first time-point. The state at the next time-point is a function, f, of the vector–matrix multiplication of the current state and the weight matrix, x^T_t+1 = f(x^T_tW). In the Linear-Associative-Net, the function f is simply unit-normalization. The process is carried out iteratively until further cycles have no additional effect on the state vector (i.e. when x^T_t+1 ≈ x^T_t). Recurrence spreads activation until the co-occurrence statistics from previously learned patterns and activation from the probe reach an equilibrium (steady) state—the retrieved pattern.

The weight matrix can be decomposed into a set of orthogonal dimensions that capture the degree of change corresponding to different aspects of experience. Multiplying a vector with a matrix and unit-normalizing, as done with the Linear-Associative-Net, pushes the state vector closer to the direction of variance that captures the maximum amount of variance in the encoded experience, a direction corresponding to the dominant eigenvector of W. Unless every dimension of variance capturing the encoded memories accounts for the same magnitude of variance—i.e. if W has a flat eigenspectrum—or a probe is completely orthogonal to the dominant eigenvector, a Linear-Associative-Net always settles to the dominant eigenvector. It is only capable of generating a single response. In order to increase the size of the response set, Anderson et al., (1977; Anderson, 1995) introduced saturation in the Brain-State-in-a-Box by bounding each neuron’s activation by a constant. Saturation constraints possible states of activation within a box and forces convergence to one of the corners. The bounding box halts the system before the state gets dominated by the lead eigenvector, therefore allowing a larger number of steady states, or responses.

The Brain-State-in-a-Box assumes the encoded patterns are corners of a hypercube (i.e. mutually orthogonal bi-polar vectors with an equal number of 1’s and -1’s). When the encoded patterns are orthogonal, they become the eigenvectors of the weight matrix. Therefore, each encoded memory forms its own eigenvector in the Brain-State-in-a-Box. Although saturation enables a larger possible set of responses, the Brain-State-in-a-Box is limited because it restricts steady states to single eigenvectors corresponding to previously encoded patterns. A desirable property for a system that is capable of combinatorial generalization is the ability to combine constraints from multiple eigenvectors, but this is not easily achieved in the Brain-State-in-a-Box.

Previous attempts have been made to remedy the generalizability of associative nets, but they have been limited when dealing with correlated structure among memory patterns. Strategies used to overcome those limitations introduce further complicating assumptions. Amari (1977) explored the effect of encoding correlated patterns in associative nets, where non-linearity was introduced by using a binary-threshold activation function. The output of each element of the state-vector was set to one, if, and only if, it passed some fixed threshold, and was zero otherwise. Using several variations of the Hebb rule, Amari showed that fine-tuning the threshold parameter can mitigate against noise introduced by the cross-talk between correlated patterns, however, the cross-talk quickly became unwieldy when additional noise was introduced at encoding. The noise intolerance suggests the system will not scale to deal with an input stream resembling raw experience.

Here, we assume that input to the system enhances the conductance between connections that link the input elements to each other, in addition to affecting the initial state. For instance, if you are shown words such as “the cat sat on the mat”, the connections linking each of the words in the sentence to each of the other words are assumed to be facilitated for the duration of the time the sentence is maintained in working memory. The facilitation forces the emergence of a neural assembly that induces a positive feedback loop between the input elements—a reverberatory loop. It changes the dominant eigenvector to a point that is close to the original input, one that is a mixture of the eigenvectors of the original weight matrix and the input probe. The new equilibrium balances the influence of the input and the structure encoded along the eigenvectors. In the model we present, we assume that each time the system is probed, a neural assembly is temporarily superimposed over the static weights that were learned during previous encoding. The input-driven connectivity changes are not permanent, but remain present while the system is approaching equilibrium and are reset after.

We explore the system in relation to the eigenvectors of the weight matrix and show how transient assemblies re-weight various eigenvectors (directions of variance) encoded in memory, dampening the impact of some and magnifying the impact of others. We show that transient assemblies provide a linear alternative to saturation for overcoming the dominant eigenvector problem. A transient assembly reweights the contribution of each eigenvector based on its similarity to the input pattern. Therefore, we call the system a Dynamic-Eigen-Net. The additional gain-control on the eigenstructure prevents saturation to a single eigenvector and enables mixed-eigenstates, or retrieved states that are spread across multiple eigenvectors.

In this paper, we present several simulations to demonstrate how spreading activation with the Dynamic-Eigen-Net outperforms both the Linear-Associative-Net and the Brain-State-in-a-Box. We first provide some toy simulations to demonstrate the essential characteristics of Dynamic-Eigen-Nets, in relation to the two baseline models. We then scale up the system to encode bigram information from a naturalistic text corpus. Using the exact same memory representation, but only changing the algorithm for spreading activation, our simulations show that the Dynamic-Eigen-Net is more sensitive to syntactic structure than the two baseline models. The Dynamic-Eigen-Net best accounts for priming effects in lexical decision tasks that manipulate the syntactic congruity between primes and targets. Noting the paucity of experiments that use bigrams to manipulate syntactic variables, we augment previous empirical data with data from a 2AFC bigram acceptability task. As we show later, our model’s performance provides the best match to human data out of the three models. We end by demonstrating the superiority of the Dynamic-Eigen-Net for generalization, by deleting associations between word-pairs (e.g. association between “her” to “buffalo”) and checking if the network can distinguish between the congruent form (“her buffalo”) and its incongruent counterpart (“she buffalo”).

Properties of Associative Nets

We now illustrate some key properties of three spreading activation algorithms. The first variant is a simple Linear-Associative-Net, the second is the Brain-State-in-a-Box, and the third is a Dynamic-Eigen-Net.

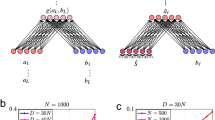
The encoded patterns and retrieval cues are identical across simulations of the spreading activation variants; we only change the algorithm driving the system towards equilibrium following a probe – the recurrence relation. The Linear-Associative-Net and the Dynamic-Eigen-Net do not make any particular assumptions about representation, but the Brain-State-in-a-Box requires that memories correspond to Walsh vectors, or mutually orthogonal bi-polar vectors that are corners of a hyper-cube. Hence we use Walsh vectors as our representational primitive. For the toy demonstrations, we define four Walsh vectors, each with dimensionality set to four and assign a single word in English to each vector. We use [1, 1, 1, 1]^T for “the”, [-1, 1, -1, 1]^T for "cat", [1, -1, -1, 1]^T for "a", and [1, 1, -1, -1]^T for “dog”. The capital letter “T” superscript stands for the transposition operation (i.e. swapping rows for columns or vice-versa). We assume that input to the system is an eight-dimensional vector, and construct bigram vectors by concatenating pairs of individual word vectors. Hence, bigrams are encoded with the word in the first serial position active in the first slot and the word in the second serial position active in the second slot. Since the concatenation of two Walsh vectors is also a Walsh vector, our bigram representations are also corners of a hyper-cube.

The bigrams for “the cat” and “a dog” can be constructed by concatenating the respective word-vectors, in sequence. When the two bigram vectors are encoded with unequal strength, the Linear-Associative-Net always responds with the stronger pattern, even when the other pattern is only fractionally weaker. We unit-normalize each bigram vector, m_i, and sum their weighted outer-products, each pattern with itself, into a single matrix to initialize the connection weights. We set the strength of the stronger pattern to 1.2 and the strength of the weaker pattern to 1.1. For all following simulations in the toy demonstrations, we assume a weight matrix,

$$\mathrm{W}={1.2\mathrm{m}}_{the-cat}{{\mathrm{m}}^{T}}_{the-cat}+{1.1\mathrm{m}}_{a-dog}{{\mathrm{m}}^{T}}_{a-dog}$$

where m_the-cat and m_a-dog are the bigram vectors corresponding to “the cat” and “a dog”, respectively.

A probe is initialized by taking an 8-dimensional vector and populating one, or both, of the slots with individual word vectors. Zero-mean Gaussian noise is added to each probe and the result is unit-normalized prior to cueing the system. The addition of noise allows us to explore each system’s robustness and also captures random variation in people’s responses. Gaussian noise is superimposed onto the pattern via, ϵ, an 8-dimensional vector of samples from a zero-mean Gaussian distribution with its standard deviation, σ = 0.3. We set the probe as,

$$\begin{array}{cc}{\mathrm{x}}_{0}= \frac{\mathrm{x}+ \epsilon }{\Vert \mathrm{x}+ \epsilon \Vert } \mathrm{where},& \epsilon =\mathcal{N}(0,\sigma )\end{array}$$

The vector, x, has dimensionality 8. The double vertical bars denote vector length.

The system’s state at each time-point can be characterized in terms of the level of activation for the primitive word vectors, yielding four activation values in the first slot and four activation values in the second slot. To compute the activation values for each slot, we segment the state vector from the middle and take the first half as the first slot and the second half as the second slot. We set the activation value for a word in position one (or two) as the absolute value (c.f., Farrell & Lewandowsky, 2002) of the vector cosine of its primitive vector and the first slot (or second).

Linear Associative Net

In a Linear-Associative-Net, we define the recurrence relation in terms of the unit-normalized vector–matrix multiplication of the current state vector and the weight matrix. It is given by,

$${\mathrm{x}}_{t+1}^{T}= \frac{{\mathrm{x}}_{t}^{T}\mathrm{W}}{\Vert {\mathrm{x}}_{t}^{T}\mathrm{W}\Vert }$$

A small fraction, c, sets the stopping criterion by terminating retrieval when change from one time-point, to the next, falls below the threshold, i.e. || x^T_t+1—x^T_t ||< c. We set the convergence criterion to 1e-07 for all the following toy simulations.

The eigenstructure of the weight matrix can be captured by decomposing it into a superposition of the outer-products of its eigenvectors, each weighted by its respective eigenvalue, λ_i, W = Σ(λ_iê_iê_i^T), where ê_i stands for the i’th eigenvector of W. Dropping the normalization, we then have,

$${\mathrm{x}}_{t+1}^{T}= {\mathrm{x}}_{t}^{T}\mathrm{W}= {\mathrm{x}}_{t-1}^{T}\mathrm{WW}= {\mathrm{x}}_{0}^{T}{\mathrm{W}}^{t}=\;\sum\limits_{i=1}^{N}\left(\left({\lambda }_{i}^{t}{\mathrm{x}}_{0}^{T}{\widehat{e}}_{i}\right){\widehat{e}}_{i}^{T}\right)$$

We include parentheses around the term, λ^t_ix^T₀ê_i, to emphasize that it is a scalar. Because of the exponent over the eigenvalues, and because the eigenvalues are monotonically decreasing in magnitude, from the first to the last, in the limit, as we multiply the vector with the matrix and unit-normalize, x^T_t+1 converges to the dominant eigenvector, ê_max, except when the initial probe is orthogonal to the dominant eigenvector, x^T₀ê_max = 0, or if all the eigenvalues are the same, λ_i = λ_j, for all i ≠ j.⁵ Orthogonality between the initial cue and the top eigenvector is unlikely if we assume any level of noise, meaning x^T₀ê_max will rarely equal zero, and forcing the eigenvalues to be uniform prevents the system from tracking the relative probability of different stimuli. When the two criteria are not met, spreading activation with the Linear-Associative-Net always settles to the dominant eigenvector.

Table 1 shows the probability of each response (along the columns) as a function of each probe (along the rows). In the Linear-Associative-Net, the system always converges to the dominant pattern (“the cat”) regardless of the input. The probability values in Table 1 are based on 1000 runs as each run is different because of the noise term, ϵ, added to the probe. The same procedure was applied for the results generated from the other spreading activation algorithms (Tables 2, 3, 4,  5).

Table 1 Probabilities of response across probes show how a Linear-Associative-Net is restricted to a single response

Table 2 Probabilities of response across probes show how persistent Linear-Associative-Net is susceptible to structurally misaligned steady-states

Sometimes the persistent variant of the Linear-Associative-Net is used, where the initial input is included in the update function,

$${\mathrm{x}}_{t+1}^{T}= \frac{{\mathrm{x}}_{t}^{T}\mathrm{W}+{\mathrm{x}}_{0}^{T}}{\Vert {\mathrm{x}}_{t}^{T}\mathrm{W}+ {\mathrm{x}}_{0}^{T}\Vert }$$

As we show in the “Dynamic-Eigen-Net” section, where we analyze the Dynamic-Eigen-Net, simply including the initial pattern does not fully exploit the interaction between the eigenstructure and the input pattern.

Table 2 has the same form as Table 1, but shows steady-state activations for the persistent Linear-Associative-Net. The persistent Linear-Associative-Net settles to misaligned patterns more often than we desire. For instance, when probed with “dog the”, the system settles to “dog the” 50.9% of the time and “the the” 28% of the time. Likewise, when probed with “cat a”, it settles to “the a” 42.3% of the time. Table 2 demonstrates how including the initial probe into the update function has some difficulties constraining the system’s state-space to structurally aligned patterns.

Brain-State-in-a-Box

The Brain-State-in-a-Box remedies the dominant eigenvector problem by introducing saturation, forcing a maximum and minimum over the range of activations. The modified recurrence relation is given by,

$${\mathrm{x}}_{t+1}^{T}=S\left({\mathrm{x}}_{t}^{T}\mathrm{W}\right)$$

where.

$$S\left({\mathrm{x}}_{i}\right)= \left\{\begin{array}{c}1 \\ {\mathrm{x}}_{i}\\ -1\end{array}\begin{array}{c}{\mathrm{x}}_{i} \ge 1\\ -1 < {\mathrm{x}}_{i} <1\\ {\mathrm{x}}_{i} \le - 1\end{array}\right.$$

with 1 being the saturation constant. Normalizing is no longer used with saturation and instead of using a small fraction for the stopping criterion, convergence in the Brain-State-in-a-Box is defined as the state where the absolute value of all vector elements is equal to the saturation constant (i.e. when the state reaches one of the corners of the hypercube).

Table 3 shows the probability of responses (columns) as a function of different probes (rows). Whereas the Linear-Associative-Net always settled to the dominant pattern, “the cat”, the Brain-State-in-a-Box settles to “the cat” when probed with “the cat” and “the _”, and settles to “a dog” when probed with “a dog” or “a _”. Because of the noise and the larger region of attraction for “the cat”, probing the system with the weaker pattern settles to “the cat” about half the time. The partial probes demonstrate the pattern-completion capabilities of the system. The preference to reach steady state near the stronger pattern, even when probed with a partial pattern that better matches the weaker bigram, shows the system’s bias towards the stronger pattern. The underscore denotes an empty slot, where the elements are populated by Gaussian noise.

Table 3 Probabilities of response across probes show how a Brain-State-in-a-Box is restricted to previously stored patterns

The second two probes, “the dog” and “a cat”, are novel combinations of the primitive word vectors. Both “the” and “a” have been encoded in the first slot and both “dog” and “cat” have been encoded in the second slot. Therefore, they structurally align with the encoded patterns. Despite their alignment with the eigenstructure of the system, the responses generated by the Brain-State-in-a-Box are restricted to previously stored patterns, with a preference for the stronger pattern, shown in the fifth and sixth rows. The final two probes, “dog the” and “cat a”, are the same novel combinations, except that the two words have been swapped so that they are no longer aligned with the encoded structure. The system always responds with “the cat” regardless of the probe. Critically, the system mainly settles to previously encoded patterns, with a very low probability of settling to novel patterns that were not encoded.

In some implementations of the Brain-State-in-a-Box (e.g. Anderson, 1995), the initial state is also included in the recurrence relation. We can include the initial state, as in:

$${\mathrm{x}}_{t+1}^{T}=S\left({\mathrm{x}}_{t}^{T}\mathrm{W}+ {\mathrm{x}}_{0}^{T}\right)$$

We call this the persistent Brain-State-in-a-Box variant. As shown in Table 4, including the initial state in the update function does not facilitate generalization in the Brain-State-in-a-Box. Persistence changes performance in the Brain-State-in-a-Box by reducing its bias towards more strongly encoded patterns. The steady states are still limited to the two encoded patterns, showing that the persistent variant is no better at generalizing than the simple Brain-State-in-a-Box algorithm.

Table 4 Probabilities of response across probes show how a Brain-State-in-a-Box is restricted to previously stored patterns even with the persistent input

Dynamic-Eigen-Net

Transient assemblies enable the system to generalize to novel patterns based on combinations of multiple eigenvectors. A transient assembly is a temporary increase in the weights corresponding to the active entries in the input. The temporary change follows the presentation of the input and persists for the duration of the subsequent set of iterations. After convergence, the weights are reset. Transient assemblies can be modeled by superimposing the outer-product of the probe, with itself, into the weight matrix. The state-vector is unit-normalized after each iteration, as in the Linear-Associative-Net. Because the corresponding system is linear, its dynamics can be characterized by analyzing the eigenstructure of the weight matrix.

The recurrence relation for a Dynamic-Eigen-Net is given by,

$${\mathrm{x}}_{t+1}^{T}= \frac{{\mathrm{x}}_{t}^{T}\left(\mathrm{W}+ {\mathrm{x}}_{0}{\mathrm{x}}_{0}^{T}\right)}{\Vert {\mathrm{x}}_{t}^{T}\left(\mathrm{W}+{\mathrm{x}}_{0}{\mathrm{x}}_{0}^{T}\right)\Vert }$$

In both a Linear-Associative-Net and the Brain-State-in-a-Box, convergence filters out any component orthogonal to the encoded eigenvectors. In a Dynamic-Eigen-Net the input pattern persists and is integrated into other components that do align with the eigenstructure.

If we let x^T_∞ be the state in the limit, and λ_∞ be the primary eigenvalue of W + x₀x^T₀, the following equation describes the steady-state:

$${\mathrm{x}}_{\infty }^{T} \left(\mathrm{W}+ {\mathrm{x}}_{0}{\mathrm{x}}_{0}^{T}\right)= \sum\limits_{i=1}^{N}\left(\left({\uplambda }_{i}{\mathrm{x}}_{\infty }^{T}{\widehat{e}}_{i}\right){\widehat{e}}_{i}^{T}\right)+ \left({\mathrm{x}}_{\infty }^{T}{\mathrm{x}}_{0}\right) {\mathrm{x}}_{0}^{T}= {\uplambda }_{\infty }{\mathrm{x}}_{\infty }^{T}$$

The term, λ_∞x^T_∞, follows from the fundamental eigenvalue identity because x^T_∞ is the primary eigenvector of W + x₀x^T₀. For the term, Σ_i((λ_ix^T_∞ ê_i)ê_i^T), the eigenvectors and eigenvalues correspond to the original weight matrix before the outer-product of the initial pattern was added.

The parentheses around λ_ix^T_∞ ê_i and x^T₀x₀ are added to emphasize that they are scalar terms. The activation pattern converges toward the direction of each of the eigenvectors, weighted by each eigenvector’s dot-product with the current state and the eigenvalue, plus the initial pattern, weighted by its dot-product with the current state. Since the states are assumed to have unit-normal length, the dot-products correspond to vector cosines. Adding the outer-product into the weight matrix not only dynamically weights each eigenvector, but also forces the persistence of the initial pattern.

Post-multiplying both sides with x^T_∞, yields an equation for the dominant eigenvalue of the converged state, λ_∞:

$${\uplambda }_{\infty }= \sum\limits_{i=1}^{N}\left({\left({\uplambda }_{i}{\mathrm{x}}_{\infty }^{T}{\widehat{e}}_{i}\right)}^{2}\right)+ {\left({\mathrm{x}}_{\infty }^{T}{\mathrm{x}}_{0}\right)}^{2}$$

In the limit, the lead eigenvalue is the squared sum of the similarity of the state and each eigenvector, weighted by the corresponding eigenvalue, plus the square of the similarity of the state and the initial probe. The lead eigenvalue is similar to Smolensky’s (1987) measure of harmony and the global strength used in MINERVA 2 (Hintzman, 1986, 1988), and we will use it as a measure of familiarity.

The persistent Linear-Associative-Net is equivalent to the Dynamic-Eigen-Net, but only for the first iteration:

$${\mathrm{x}}_{1}^{T}= {\mathrm{x}}_{0}^{T} \left(\mathrm{W}+ {\mathrm{x}}_{0}{\mathrm{x}}_{0}^{T}\right)= {\mathrm{x}}_{0}^{T}\mathrm{W}+ {\mathrm{x}}_{0}^{T}$$

Ignoring normalization, in the second iteration, for the Dynamic-Eigen-Net, we have,

$${\mathrm{x}}_{2}^{T}= \left({\mathrm{x}}_{0}^{T}\mathrm{W}+ {\mathrm{x}}_{0}^{T}\right)\left(\mathrm{W}+ {\mathrm{x}}_{0}{\mathrm{x}}_{0}^{T}\right)= \sum\limits_{i=1}^{N}\left(\left({\lambda }_{i}^{2}+ {\lambda }_{i}\right){\mathrm{x}}_{0}^{T}{\widehat{e}}_{i}{\widehat{e}}_{i}^{T}\right)+ \left(\sum\limits_{i=1}^{N}\left({\lambda }_{i}{\left({\mathrm{x}}_{0}^{T}{\widehat{e}}_{i}\right)}^{2}\right)+1\right){\mathrm{x}}_{0}^{T}$$

In the persistent Linear-Associative-Net, we have,

$${\mathrm{x}}_{2}^{T}= \left({\mathrm{x}}_{0}^{T}\mathrm{W}+ {\mathrm{x}}_{0}^{T}\right) \mathrm{W}+ {\mathrm{x}}_{0}^{T}= \sum\limits_{i=1}^{N}\left(\left({\lambda }_{i}^{2}+ {\lambda }_{i}\right){\mathrm{x}}_{0}^{T}{\widehat{e}}_{i}{\widehat{e}}_{i}^{T}\right)+ {\mathrm{x}}_{0}^{T}$$

For the second iteration, the Dynamic-Eigen-Net includes an additional weight for the initial state, i.e. Σ_i(λ_i(x₀^Tê_i)²), which enables the similarity between the initial state and the eigenspectrum of the weight matrix to modulate the relative weight given to the initial state. In general, each additional iteration in the Dynamic-Eigen-Net introduces a new high-order mixture of weights that correspond to interactions between the initial state and the eigenstructure. The high-order mixture terms help balance the contribution of the eigenstructure and the structure of the input during recurrence.

Table 5 shows the probability of responses as a function of the probe for a Dynamic-Eigen-Net. The first two probes (“the cat” and “a dog”) yield a similar pattern of response as the Brain-State-in-a-Box. One notable difference is that the Dynamic-Eigen-Net is not limited to previously stored patterns (e.g. sometimes it responds with “the dog” when probed with “a dog”). One similarity with the Brain-State-in-a-Box, is that the Dynamic-Eigen-Net is sensitive to the relative strength of the encoded items. The system settles to “a dog”, the weaker pattern, with a less than one probability whereas when probed with the stronger pattern, it always settles to “the cat”. In contrast to the Brain-State-in-a-Box, the Dynamic-Eigen-Net settles to the weaker pattern with much greater probability. Sensitivity to differences in the encoded strengths gives the system a way to track prior probabilities of stimuli in the environment because in a continuously learning system, higher probability signals will have an increased basin of attraction.

Table 5 Probabilities of response across probes show how a Dynamic-Eigen-Net accommodates novel patterns

The pattern completion dynamics are evident in the next two probes, “the _” and “a _”. The system always completes the stronger pattern in accordance with the encoded bigram (i.e. “the _” to “the cat”), but it sometimes completes the partial probe corresponding to the weaker pattern (“a _”) with the noun that was in the stronger pattern (“a cat”) and sometimes overrides the partial probe with the stronger pattern entirely (i.e. “a _” settles to “the cat”). Whereas the Brain-State-in-a-Box almost always favoured the strong pattern, the Dynamic-Eigen-Net has a weaker bias towards the strong pattern. Critically, it sometimes even settles to a pattern that is closest to the novel pattern, “a cat”.

The probes “the dog” and “a cat” in Table 5 show the response probabilities for the structurally aligned novel bigrams. Although the system sometimes converges to the originally encoded patterns, it settles to novel inputs with high probability, hence generalizing to structurally consistent patterns. Finally, the last two probes, “dog the” and “cat a”, show the probabilities of responding when the words in the novel bigrams swap serial-positions, resulting in novel combinations that misalign with the encoded structure. The system never settles to the misaligned patterns (the columns corresponding to “dog the” and “cat a” have zero probability). In the case of misaligned novel patterns, the system defaults to the strongest memory: “the cat”. Hence, although the system assimilates novel patterns that structurally align with the encoded patterns, it rejects misaligned patterns through interaction terms between the initial state and the eigenstructure.

Figure 1 shows the activation of the four words, in each slot, across recurrence iterations (horizontal axis), between the persistent Linear-Associative-Net (pLAN), the Brain-State-in-a-Box (BSB), the persistent Brain-State-in-a-Box (pBSB), and the Dynamic-Eigen-Net (DEN), when probed with the novel pattern, “a cat”. For each model, the left-hand panel shows activations (vertical axis) in the first slot and the right-hand panel shows the activations in the second slot. The examples correspond to the most probable steady-state activations for each model. In the persistent Linear-Associative-Net, the original cue was included in the recurrence function with a weight of 1, but in the persistent Brain-State-in-a-Box the weight was set to 0.1 because larger weights did not converge.

Fig. 1

The pattern of activation across recurrence iterations in the first (left column) and second (right column) slots across four spreading activation algorithms (rows), when cued with the aligned novel pattern, “a cat”

Across all models, cueing with “a cat” activates “a” (green dotted line) and “the” (blue line) in the first slot. The reason “the” is activated is because of its association with “cat” in the second slot. In the second slot, the words “cat” and “dog” are activated in all four models, but “dog” is quickly suppressed across iterations. The reason “dog” is activated is because of its association with “a” in the first slot. Whereas activation for “the” fully surpasses activation for “a” in the two Brain-State-in-a-Box variants, “the” remains highly active in the persistent Linear-Associative-Net and the Dynamic-Eigen-Net, but does not exceed the activation for “a”. Likewise, whereas in the persistent Linear-Associative-Net and the Dynamic-Eigen-Net, the word “dog” maintains a non-zero activation in the steady-state, activation for “dog” is pushed to zero by the time the Brain-State-in-a-Box variants settle. Despite the pattern’s novelty, both the persistent Linear-Associative-Net and the Dynamic-Eigen-Net settle to a point closest to the novel pattern, whereas the Brain-State-in-a-Box algorithm always settles to the closest studied pattern, “the cat”. Since the steady-states in the Brain-State-in-a-Box variants are corners of a hypercube, retrieval induces an all-or-none competition between the two studied patterns. In contrast, both the persistent Linear-Associative-Net and the Dynamic-Eigen-Net enable steady-states that combine information across the encoded eigenvectors.

Figure 2 mirrors Fig. 1 by illustrating the dynamics of activations when each model is cued with the novel pattern, but with the words swapped (“cat a”) to no longer align with structure encoded from the two studied patterns. Across all models, recurrence suppresses “cat” in the first slot, in favour of “the”. Likewise, recurrence suppresses “a” in the second slot, in favour of “cat”. All variants settle to the pattern, “the cat”, which was studied, but the Brain-State-in-a-Box variants show greater suppression of the misaligning words. The persistent Linear-Associative-Net and the Dynamic-Eigen-Net reach steady-states with a similar profile of activations, with “the” becoming most active in the first slot, followed by “cat”. One difference between the two models is that the activation for “cat” is very close to the activation for “the” for the persistent Linear-Associative-Net, whereas in the Dynamic-Eigen-Net, the activation for “cat” is pushed further down relative to “the”. A similar pattern is present in the second slot, where activation for “cat” is dominant in both models, but the misaligned words are more suppressed in the Dynamic-Eigen-Net.

Fig. 2

The pattern of activation across recurrence iterations in the first (left column) and second (right column) slots across four spreading activation algorithms (rows), when cued with the misaligned novel pattern, “cat a”

Greater suppression of misaligned activations in the Dynamic-Eigen-Net relative to the persistent Linear-Associative-Net suggests that the former is more sensitive to the serial-order structure of the input domain. The first and last rows of Fig. 1 show how cueing with the novel pattern, “a cat”, elicits activation of “the”, in the first slot, and “dog”, in the second slot, for both the persistent Linear-Associative-Net and the Dynamic-Eigen-Net. The corresponding rows in Fig. 2 show how for both models, “cat” remains active in the first slot and “a” and “the” remain active in the second slot. The Dynamic-Eigen-Net shows greater discrimination between activations that are part of the cue, but dissonant with structure in memory, and those that are part of the cue and resonate with the encoded structure.

Focusing on the persistent Linear-Associative-Net, the first row of Fig. 1 shows how the activation for “the” in the first slot and “dog” in the second slot remain strong until steady-state, a desirable property for capturing the paradigmatic relation between “a” and “the”, and between “cat” and “dog”. However, when probed with the misaligned pattern, the first row of Fig. 2 shows how the activations for the misaligning words remain relatively high (i.e. “cat” in the first slot and “a” and “the” in the second slot). The difference in activation between the misalining and aligning words is much greater for the Dynamic-Eigen-Net, as evident when comparing the fourth rows of Figs. 1 and 2. For the aligning pattern (Fig. 1), the activation for “the” in the first slot is far greater than the activation for “cat” in the misaligned pattern (Fig. 2).

From Theory to Data

Having shown that the Dynamic-Eigen-Net is better at generalizing than the alternative models, in a toy demonstration, we scale up the models using a text corpus meant to approximate the variable and unstructured input experienced by human observers. To preserve the simplicity of representation, we continue with a two-slot model as before. The subsequent simulations are not meant as complete cognitive models, but are presented to showcase the Dynamic-Eigen-Net’s superior generalization capability relative to other spreading activation algorithms, at scale. A more complete model will require further architectural assumptions that are beyond the scope of the present manuscript.

We consider two tasks that can be adapted to deal with bigrams as stimuli: the lexical decision task and the judgment-of-grammaticality task. The lexical decision task requires participants to decide whether strings of letters with which they are presented are words or nonwords. The judgment-of-grammaticality task requires subjects to decide whether a sequence of words forms a well-formed utterance or not. More generally, in the following simulations we explore the extent to which the Dynamic-Eigen-Net algorithm yields more discriminant familiarity signals when comparing congruent and incongruent bigrams relative to the persistent-Linear-Associative-Net and the persistent Brain-State-in-a-Box. If a serial-order association exists in memory between the pair of words in a congruent bigram and not for the corresponding incongruent bigram, then a difference in familiarity simply demonstrates recognition. To show that the system can generalize, we must demonstrate that it is able to exploit the structure in the weight matrix to yield higher familiarity for congruent strings over incongruent strings, without any knowledge of the specific congruent strings queried. In our final simulation, we delete the associations, both forward and backward,⁶ between the words in the syntactically congruent bigram before comparing its familiarity to the corresponding incongruent bigram.

Scaling Up

In the toy demonstrations, we initialized the weight matrix by simply adding in the outer-products of the to-be-encoded patterns. In order to scale up the system to deal with more realistic data streams, we made several modifications to how the weight matrix is initialized. We count adjacent word co-occurrence by sliding a two-word window across the text corpus to encode all the lag-one sequential dependencies, similar to the toy examples. We use the TASA corpus in all, but one, of the simulations; we use a French wikipedia corpus for one of the simulations. The French corpus was based on a subset of a POS-tagged Wikipedia corpus called WikipediaFR2008 (http://redac.univ-tlse2.fr/corpus/wikipedia/wikipediaFR-2008-06-18.tag.7z). Both corpora were tokenized prior to encoding, such that tokens corresponded to words or common morphological units. For instance, the abbreviated term “don’t” was tokenized into “do” and “n’t”. Punctuation symbols, other than the apostrophe, were treated as separate tokens. Our corpus also included a hash (“#”) to mark the beginning of each sentence. For ease of conversation, we will refer to the tokens as words, however, it would be most precise to refer to them more generally as symbols.

The raw co-occurrence matrix is not well-suited for a memory system when the input domain follows a Zipfian distribution. That is, when the most frequent word in the corpus is about twice as frequent as the second-most frequent word in the corpus, and so forth for the third-most frequent word relative to the second-most and so on. For two words, A and B, if they occur independently, then their joint-probability will be the product of their marginal probabilities. Under the independence assumption, the ratio of their joint-probability and the product of their marginal probabilities will be one. Taking the log transform of the ratio as a measure of association ensures that independent events have zero associative strength. If two words have a higher-than-chance probability of occurring together, the ratio will be larger than one, and the logarithm of the ratio will be positive. In contrast, if the two words have a less-than-chance probability of co-occurring, the ratio will be less than one, in which case the logarithm of the ratio will be negative. We adopt the same measure of association, known in the wider literature as the pointwise mutual information (PMI; Church & Hanks, 1990).

In a model where two slots are concatenated, the co-occurrence matrix can be partitioned into four submatrices. The top-left submatrix maps each word in the first slot to itself as does the lower-right submatrix for each word in the second slot. The top-right submatrix encodes the number of times a word in the second slot follows another word in the first slot, i.e. it yields the forward serial dependency counts. The bottom-left submatrix encodes the backward serial dependencies and is the transpose of the top-right submatrix. Let C_ij^pq be the co-occurrence count between the i’th and j’th word, corresponding to the (p, q)’th submatrix. The submatrix indices for the top-left, top-right, bottom-left, and bottom-right are (0, 0), (0, 1), (1, 0), and (1, 1), respectively. The i and j indices range between one and V, where V is the number of unique terms in the studied corpus. The full weight matrix, W, for a two-slot model has dimensionality 2 V x 2 V. We add a small smoothing constant, ɑ, to all co-occurrence counts before applying PMI to prevent taking the log of zero. The (i, j)’th cell in the (p, q)’th submatrix of the weights is given by,

$${\mathrm{W}}_{ij}^{pq}= {\mathrm{log}}_{2}\left(\frac{Pij}{PiPj}\right)$$

where,

$$Pij= \frac{{C}_{ij}^{pq}+ \alpha }{T+ \alpha {V}^{2}}$$

$$Pi= \frac{{\sum }_{j=1}^{V}\left({C}_{ij}^{pq}\right)+ \alpha V}{T+ \alpha {V}^{2} }$$

$$Pj= \frac{{\sum }_{j=1}^{V}\left({C}_{ij}^{pq}\right)+ \alpha V}{T+ \alpha {V}^{2} }$$

$$T= \sum_{j=1}^{V}\sum_{i=1}^{V}{C}_{ij}^{pq}$$

The smoothing parameter, ɑ, was set to 0.1 for the following simulations.

The PMI does not sufficiently normalize against the Zipfian distribution of the input. Figure 3 shows the top twenty eigenvalues corresponding to the weight matrix, W. The first eigenvalue is very large relative to the subsequent eigenvalues. We scale the transient assemblies by, β = λ_max + 0.001⋅ λ_max to ensure that the initial cue has a greater driving force than the dominant eigenvector. As a result, because the dominant eigenvector of the unmodified weight matrix, ê_max, has a much larger eigenvalue, λ_max, than the other eigenvectors in the unmodified weight matrix, steady-states will be dominated by the initial cue and the dominant eigenvector of the unmodified matrix, x_∞ ≈ ê_max + x₀. Reducing the strength of the dominant eigenvector of the unmodified matrix, ê_max, by subtracting part of its outer-product from the weight matrix prevents the dominant eigenvector from saturating all the variance. The dominant eigenvector is inhibited by by subtracting some proportion, η, of its outer-product, with itself, ê_maxê^T_max, further weighted by its corresponding eigenvalue, λ_max, from the original weight matrix,

Fig. 3

Shows how the eigenvalue of the primary eigenvector towers over the other eigenvalues corresponding to the weight matrix after normalizing using the pointwise mutual information (PMI). The top twenty eigenvalues are shown

$$\widehat{\mathrm{W}}=\mathrm{W}-{\lambda }_{max}\eta {\widehat{\mathrm{e}}}_{max}{\widehat{\mathrm{e}}}_{max}^{T}$$

The parameter, η, was set to 0.55 for all the following simulations. The convergence criterion was set to 1e-07 for the Dynamic-Eigen-Net and the persistent Linear-Associative-Net.

The Dynamic-Eigen-Net is a general spreading activation algorithm that works with either localist or distributed representations, however, the Brain-State-in-a-Box requires each symbol (e.g. word) to be a Walsh vector. Projecting the localist space into a distributed one by changing from the standard basis to one that is spanned by corners of a hypercube, meets the Walsh-vector requirement. Corners of a 2 ^k hypercube can be represented by columns of a Walsh matrix (Golubov et al., 1991), H(k). A k of 14 was used for the following simulations.

Since each column of H(k) has 2 ^k elements with either a positive or negative one, the normalizing constant √2 ^k makes each vector unit-length. The (p, q)’th submatrix, U^pq, in the distributed representation is given by,

${\mathrm{U}}^{pq}= \frac{1}{{2}^{k}}\mathrm{H}\left(k\right){\widehat{\mathrm{W}}}^{pq}\mathrm{H}{(k)}^{T}$where the matrix H(k) is defined recursively as,

$$\mathrm{H}\left(k\right)=\left\{\begin{array}{ll}+1& \mathrm{if} k=0\\ \left[\genfrac{}{}{0pt}{}{\mathrm{H}\left(k-1\right)}{\mathrm{H}\left(k-1\right)} \genfrac{}{}{0pt}{}{\mathrm{H}\left(k-1\right)}{-\mathrm{H}\left(k-1\right)}\right]& \mathrm{otherwise}\end{array}\right.$$

In the scaled-up simulations, we compare the Dynamic-Eigen-Net with the persistent Brain-State-in-a-Box, and the persistent Linear-Associative-Net. We use the persistent variants and set the persistence weight for the latter two models to be the same as the transient weight constant in the Dynamic-Eigen-Net (i.e. β), to facilitate comparison. The Brain-State-in-a-Box, requires another parameter, the constant of saturation, which was set to 10. Smaller constants of saturation result in a reduction in the volume of the state-space in the Brain-State-in-a-Box, reducing the time it takes for the initial state to reach one of the corners of the hypercube. With a saturation constant of 1, the system reached the corners after a single recurrence iteration, whereas a saturation constant of 10 led to longer settling time, leaving more room for the global structure encoded in the weight matrix to determine the final state. The code for both the toy examples and the scaled-up simulations can be found through the OSF (https://osf.io/g4axy/).

Table 6 shows the steady-state activations of the top six most active symbols for the Dynamic-Eigen-Net (DEN), persistent Brain-State-in-a-Box (pBSB), and the persistent Linear-Associative-Net (pLAN) when the cue is placed in either the first or second slot, respectively (c.f., Table 1 in Sahlgren et al., 2008 and Table 4 in Jones & Mewhort, 2007).⁷ The Dynamic-Eigen-Net and persistent Linear-Associative-Net evoke the same responses for the top six most active symbols, but as we will show, the Dynamic-Eigen-Net outperforms the persistent Linear-Associative-Net when discriminating between congruent and incongruent bigrams, particularly when the association corresponding to the congruent bigram is erased and the system is forced to generalize. For the persistent Brain-State-in-a-Box, the information encoded in the partial cue quickly vanishes as the network approaches a corner of the hypercube. Ultimately, it terminates near the same region regardless of the cue. Attempts to prevent the persistent Brain-State-in-a-Box, or its simpler non-persistent variant, from always terminating to a single pattern using partial cues were unsuccessful, but we include the results for the sake of completeness. Overall, the Dynamic-Eigen-Net and persistent Linear-Associative-Net show promise for scalability, but the persistent Brain-State-in-a-Box does not appear to scale well to deal with corpus-derived statistics.

Table 6 The generated responses to a set of cues shows that the persistent Linear-Associative-Net and the Dynamic-Eigen-Net favour the same top six activations, whereas the persistent Brain-State-in-a-Box always drifts to the same dominant pattern

In the following simulations, we compute a familiarity signal as the vector length of the state, prior to normalization, for the final recurrence iteration (i.e. ||x_∞||). We subtract the familiarity for each incongruent bigram from the familiarity for its corresponding, congruent, bigram as an index of their relative familiarity strength. The ideal spreading activation algorithm should reliably yield positive familiarity differences for pairs of congruent-incongruent bigrams.

Goodman et al. (1981)

Using a lexical decision task, Goodman et al. (1981) found that participants were approximately 35 msc slower to make a lexical decision for words that were preceded with a syntactically incongruent word. We simulate their task by randomly constructing different sets of congruent-incongruent bigram pairs using their method.

The left-most panel in Fig. 4 summarises the pattern of response times presented in Table 3 of Goodman et al. (1981), and their item Analysis of Variance (ANOVA), where they showed faster responses for noun primes, relative to verbs, and faster responses to syntactically congruent bigrams (blue) relative to incongruent bigrams (red). Faster response times should correspond to larger familiarities. Therefore, the model-derived familiarities should be larger for congruent bigrams relative to incongruent bigrams, and they should be larger for nouns relative to verbs.

Fig. 4

Mean Reaction Times and Model Familiarites for Goodman et al. (1981). Whereas familiarities derived from the Brain-State-in-a-Box model show little sensitivity to syntactic congruity, both the persistent Linear-Associative-Net and the Dynamic-Eigen-Net attribute higher familiarity to congruent bigrams (blue) over incongruent bigrams (red). *** indicates p < .001. Error-bars show the estimated 95% confidence intervals

We obtained familiarity values for 120 of each four types of bigrams consisting of the factorial combination of Congruity and part-of-speech (PoS), yielding 480 different bigrams. Half of the bigrams were congruent (240) and the other half were incongruent, each with 120 using a verb as the second word and 120 using a noun as the second word. Because the familiarity values are not on the same scale across models, we analyzed each model separately using a congruity (congruent vs incongruent) by part-of-speech (noun vs verb) between-group ANOVA. The other three panels in Fig. 4 show the marginal means of familiarity and the corresponding 95% confidence intervals for congruent and incongruent bigrams, separately for nouns and verbs, across the three models.

Congruity and part-of-speech did not account for much of the variance in familiarities derived using the persistent Brain-State-in-a-Box algorithm (r² ≈ 0.007) and neither congruity, part-of-speech, or their interaction reached statistical significance (all ps > 0.15). Congruity and part-of-speech accounted for more variance in the familiarity values derived from the persistent Linear-Associative-Net (r² ≈ 0.106) with significantly greater familiarity for congruent bigrams indicated by a main effect of congruity, F(1, 476) = 47.60, MSE = 1709.92, p < 0.001, accounting for the majority of the explained variance (η²_p ≈ 0.09). The main effect of part-of-speech was marginally significant, F(1, 476) = 2.86, MSE = 102.72, p ≈ 0.092, η²_p ≈ 0.01, but was complicated by an interaction. There was a difference-of-slopes Congruity x PoS interaction driven by a greater difference between congruent and incongruent bigrams for nouns relative to verbs, F(1, 476) = 6.56, MSE = 235.56, p ≈ 0.011, η²_p ≈ 0.01. The two factors explained yet more variance in familiarities derived from the Dynamic-Eigen-Net (r² ≈ 0.25), mainly driven by a main effect of congruity, F(1, 476) = 141.12, MSE = 1791.27, p < 0.001 (η²_p ≈ 0.23). The main effect of part-of-speech was not statistically significant (p > 0.6), but a difference-of-slopes Congruity x PoS interaction, driven by a greater congruity cost for nouns relative to verbs, accounted for the rest of the explained variance, F(1, 476) = 20.83, MSE = 264.35, p < 0.001 (η²_p ≈ 0.04). The statistically significant main effects are indicated by horizontal bars in Fig. 4.

The greater familiarity for congruent bigrams relative to incongruent bigrams in the persistent Linear-Associative-Net and the Dynamic-Eigen-Net is consistent with faster lexical verification of the second word in the congruent bigrams, relative to the incongruent bigrams, used by Goodman et al. (1981). The slower response-times for bigrams with a verb prime relative to a noun prime was not explained by the models, except for a marginal trend in the persistent Linear-Associative-Net. To the extent to which syntactic congruity and part-of-speech capture important structural characteristics of the text corpus, the variance accounted for in the familiarities derived from the three models suggest the Dynamic-Eigen-Net (around 25%) to be most sensitive, and the persistent Linear-Associative-Net (around 10%) to be somewhat less sensitive to the structure. The Brain-State-in-a-Box, as implemented here and with our choice of weight matrix, did not show sensitivity to the regularities captured by syntactic congruity or part-of-speech.

Colé et al. (1994)

In a similar task, Colé and Segui (1994) presented subjects with pairs of letter-strings and asked them to respond “yes”, only if both were valid words in French—a double-lexical decision. They used French, because French nouns have inherent gender: some words are considered masculine and others feminine. For example, the word “chat” (“cat”) is a noun that is both singular and masculine. When preceded by the singular and masculine possessive pronoun, “mon” (“my”), or the singular and masculine adjective “joli” (“pretty”), the bigrams “mon chat” and “joli chat” are syntactically congruent because of the noun’s agreement in both gender and number. When “chat” is preceded by the plural pronoun, “mes”, or the feminine pronoun, “ma”, the resulting bigram disagrees in either number or gender, respectively. When “chat” is preceded by the singular and masculine adjective, “joli”, the corresponding bigram is syntactically congruent, but when it is preceded by the plural, “jolis”, or the feminine, “jolie”, then the bigram mismatches in either number or gender, respectively. The bigrams containing different possessive pronouns were part of the closed-class condition whereas the bigrams containing adjectives were part of the open-class condition.

The left-most panel in Fig. 5 shows mean RT as a function of congruity and vocabulary type from the first experiment in Colé and Segui (1994). Mixed-effects ANOVAs revealed a main effect of congruity (congruent vs incongruent) and a main effect of vocabulary (closed vs open). The lexical verification accuracy mirrored the RTs for congruity (i.e. higher accuracy for congruent over incongruent), as indicated by a significant main effect, but the closed-open distinction did not reliably impact accuracy. Hence, as with Goodman et al. (1981) subjects were slower to verify syntactically incongruent bigrams relative to congruent bigrams. In addition, they were faster in responding to bigrams whose initial word was closed-class relative to bigrams whose first word was open-class. Open-class words (e.g. adjectives, nouns, verbs etc.) correspond to content words and closed-class words (e.g. determiners, pronouns, prepositions) correspond to function words. The former group allows for the addition of new members (e.g. new nouns or adjectives), but the latter group does not.

Fig. 5

Mean Reaction Times and Model Familiarities for Colé et al. (1994). Familiarity is significantly higher for closed-class words relative to open-class words for all three models, and the congruent bigrams are more familiar for the persistent Linear-Associative-Net and the Dynamic-Eigen-Net. *** indicates p < .001. Error bars show 95% confidence intervals

Because syntactic violations resulted in faster response-time for closed-class bigrams compared to open-class bigrams, Colé and Segui speculated that the two classes may be stored separately, an idea previously entertained by Garrett (1978). If model-derived familiarities for closed-class bigrams are larger in magnitude compared to familiarities for open-class bigrams, we have an existence proof that distinct performance signatures can be obtained between the two classes without assuming qualitative differences in encoding or representation.

We used a French Wikipedia corpus to simulate Colé et al. (1994), and replicated their method for constructing sets of paired congruent and incongruent bigrams. For each congruent bigram we constructed two incongruent bigrams, with the second word in each bigram mismatching the first word in either gender or number. First we collected 415 target words and used each to construct a congruent closed-class bigram and a congruent open-class bigram. Then, for each kind of congruent bigram (closed and open), we constructed two incongruent bigrams, one mismatching in gender and another mismatching in number.

Colé et al. (1994) collapsed over the two kinds of mismatch because they did not yield statistically reliable effects. We likewise collapse over the two kinds of mismatch by averaging the familiarities of gender-mismatching bigrams and number-mismatching bigrams. We conducted a separate congruity (congruent vs. incongruent) by vocabulary (closed vs. open) mixed-effects ANOVA for familiarities derived from each of the three spreading activation algorithms, with items (i.e. different sets of bigrams, each with the same target word) as the random effect. The other panels in Fig. 5 show the marginal mean familiarities for congruent and incongruent bigrams, broken down based on whether the bigram contains a closed-class or both open-class words, separately for each model. The error bars show the 95% confidence intervals, and statistically significant main effects are indicated by the horizontal bars.

The two fixed effects, congruity and vocabulary, accounted for some variance in familiarity scores derived using the persistent Brain-State-in-a-Box (r²_m ≈ 0.041; see Nakagawa & Schielzeth, 2013 for details on deriving accounted variance in mixed effect models). The addition of the item factor as a random effect doubled the accounted variance (r²_c ≈ 0.093). There was no main effect of congruity (p > 0.35), but familiarities for the closed-class bigrams were significantly larger than familiarities for the open-class bigrams, F(1, 1242) = 68.585, MSE = 4.4263e + 12, p < 0.001. The interaction between congruity and vocabulary was significant, F(1, 1242) = 5.952, MSE = 3.8414e + 11, p = 0.015, driven by a tendency toward greater familiarity in congruent bigrams relative to incongruent bigrams for closed-class bigrams but not for open-class bigrams.

Congruity and vocabulary accounted for much more variance in familiarities derived using the persistent Linear-Associative-Net (r²_m ≈ 0.53) and the addition of the item factor as a random effect further increased the accounted variance (r²_m ≈ 0.7). In contrast to the persistent Brain-State-in-a-Box, familiarities from the persistent Linear-Associative-Net were reliably greater for congruent relative to incongruent bigrams as indicated by a main effect of congruity, F(1, 1242) = 766.818, MSE = 21,223.212, p < 0.001. The main effect of vocabulary was also significant, indicating greater familiarity for closed-class relative to open-class bigrams, F(1, 1242) = 2162.490, MSE = 59,851.226, p < 0.001. The congruity by vocabulary interaction was nonsignificant (p > 0.35).

Familiarity from the Dynamic-Eigen-Net was somewhat more sensitive to congruity and vocabulary (i.e. closed vs open) relative to the persistent Linear-Associative-Net (r²_m ≈ 0.59) and the combined variance for by both fixed and random effects accounted for about the same amount of variance as the persistent Linear-Associative-Net (r²_m ≈ 0.711). As with the persistent Linear-Associative-Net, variance in familiarities from the Dynamic-Eigen-Net drove a main effect of congruity, F(1, 1242) = 2409.757, MSE = 18,485.039, p < 0.001, and a main effect of vocabulary, F(1, 1242) = 949.907, MSE = 7286.659, p < 0.001. Familiarity was greater for congruent over incongruent bigrams, and also greater for closed-class relative to open-class bigrams. In contrast to the persistent Linear-Associative-Net, there was a marginal interaction between congruity and vocabulary, F(1, 1242) = 3.252, MSE = 24.946, p = 0.072. The results show that the persistent Brain-State-in-a-Box model is not sensitive to the congruity and vocabulary type of bigrams, whereas both the persistent Linear-Associative-Net and the Dynamic-Eigen-Net show high sensitivity to the two variables, yielding a pattern of familiarities that is consistent with data reported by Colé et al. (1994).

Experiment

Münte et al. (1993) constructed bigrams composed of a pronoun followed either by a noun or a verb, such as “my cat” and “you think”. They introduced violations by swapping possessive pronouns with personal pronouns, or vice versa, as in “me cat” and “your think”. They then presented each bigram to participants, and asked them to decide whether it was “grammatical” or not. They found a response-time advantage when subjects responded to syntactically valid bigrams, relative to invalid bigrams. Münte et al. (1993) used English stimuli, but did not provide a list of their materials. We extended the manipulations employed by Münte et al. (1993) with seven additional syntactically congruent and incongruent pairs. Instead of using a yes–no judgment task as in Münte et al. (1993), we used a 2AFC design, where congruent–incongruent bigram pairs were presented simultaneously and participants had to decide which was easier to read.

We recruited 20 native English speakers, with normal or corrected to normal vision, from Amazon’s Mechanical Turk. The participants were told about the task and provided consent prior to taking part. The study was approved by the Melbourne Psychological Sciences Board of Ethics.

Materials

We used the Stanford Part-of-speech (POS) tagger (Toutanova et al., 2003) to tag words in the TASA corpus with their syntactic class; we did this in context and not with the words in isolation. We then grouped bigrams based on their syntactic composition. Starting from the most frequent bigram compositions (e.g. a determiner followed by a noun), we searched for bigram types that could be easily altered to render them ill-formed (e.g. by swapping the noun for the determiner to have a noun followed by a determiner). Working down the most frequent bigram types, we found nine different bigram compositions with a straightforward way to introduce violations. For each of nine different syntactic compositions, we used the 80 most frequent bigrams as our congruent set. More specifically, we used the top 80 bigrams of each composition group, after discarding bigrams whose isolated POS tags predicted by another tagger (Honnibal et al., 2016) conflicted with the Stanford tagger’s prediction. We also attempted to discard bigrams that contained a word whose POS varied depending on context (e.g. “bear”). We then constructed an incongruent bigram for each bigram in the congruent set. A listing of the bigrams is provided in the Table A1 of Appendix, along with mean response-time and accuracy measures collected in the present study.

The first column in Table 7 shows the valid (left) and invalid (right) bigram compositions used, each with an example in the corresponding row, in the second column. For example, in a bigram consisting of a possessive pronoun and a noun (POSS-NOUN), we can construct an incongruent bigram by turning the possessive pronoun into a personal pronoun (i.e. PRON-NOUN). If the POSS-NOUN bigram is “her cat”, the incongruent PRON-NOUN bigram would be “she cat”. For a determiner-noun bigram (DET-NOUN), such as “the cat”, we can construct a corresponding incongruent bigram, “cat the”, by swapping the two words (NOUN-DET). The POSS-NOUN versus PRON-NOUN and PRON-VERB(pres) versus POSS-VERB(pres) comparisons correspond to Münte et al. (1993), but the rest are novel violations that we have added.

Table 7 Bigram composition violations along with an example for the nine sets of bigrams used in the acceptability task

Procedure

The study was conducted through the participant’s web-browser, using jsPsych (de Leeuw, 2015). Participants judged all pairs of bigrams from each of the nine violation types. Before making the judgments, we instructed participants to “put the index finger of your left hand on the 'A' key and the index finger of your right hand on the 'L' key”. We informed the participants that they would see pairs of bigrams presented on different sides of the screen, and that their job was to determine “which pair you find easier to read”. We asked that they “respond as fast as possible, while making sure you are also accurate”.

For each pair, the “correct” and “incorrect” bigrams were simultaneously displayed on opposite sides of the center of the screen. The bigrams remained on screen until the participant made a key press. The next bigram pair was immediately displayed following a response. Whenever the participants responded faster than 200 mscs or slower than 7500 mscs, we notified them that they were responding “too quick” or “too slow”, respectively. The position of the “correct” bigram was randomized.

We first had participants complete eighteen practice trials, using bigram pairs that were not used in the main study phase. After practice, we reminded them about their finger placement on the keyboard. Upon a final key press, we presented them 720 bigram pairs (9 × 80). All 720 bigrams were shuffled at random, separately for each participant.

Results and Simulations

We did not exclude any data from the analysis. To assess the performance of the models, we tallied the proportion of times each congruent bigram had a larger familiarity value than its corresponding congruent bigram, across the three models.

The first column in Table 8 shows the nine different bigram comparison types, followed by the proportion of times each of the three models favoured the congruent over the incongruent bigrams. The final column shows the accuracy obtained from the 20 participants in the study. Out of the three models, performance is near chance for the persistent Brain-State-in-a-Box, and much higher for the persistent Linear-Associative-Net. The Dynamic-Eigen-Net is somewhat more accurate than the persistent Linear-Associative-Net. Human performance slightly lags behind the persistent Linear-Associative-Net.

Table 8 The probability of choosing the congruent bigram over the paired incongruent bigram is near chance for the persistent Brain-State-in-a-Box, but much higher for the persistent Linear-Associative-Net and the Dynamic-Eigen-Net

Greater differences in familiarity between the congruent versus incongruent bigrams should correspond to faster and more accurate responses from participants in the study. We computed a difference measure for each bigram comparison by subtracting familiarity for each of the incongruent bigrams from the corresponding congruent bigram’s familiarity. Figure 6 shows mean RT (left-side vertical axis) and proportion correct (right-side vertical axis) as a function of mean familiarity difference (horizontal axis), derived from each of the three models (different panels). The error-bars correspond to 95% confidence intervals for either mean RT (red) or proportion correct (blue).

Fig. 6

Mean Response Time and Probability Correct as a function of Discriminability across Models. Mean response time (left vertical axis; red) and probability of correctly choosing the congruent bigram (right vertical axis; blue) are both better predicted by mean familiarity difference (discriminability) derived from the Dynamic-Eigen-Net (bottom panel) compared to the persistent Linear-Associative-Net and the Brain-State-in-a-Box. NOUN: singular or mass noun, PREP: preposition, VERB: verb, ADV(comp): comparative adverb, VERB(sing/3rd): third-person, singular, and present tense verb, NOUN(s): plural noun, VERB(pres): non-third-person, present tense-verb, VERB(ing): gerund or present-tense verb, DET: determiner, ADJ: adjective, PRON: personal-pronoun, POSS: possessive pronoun

We fit a separate linear regression for each model, regressing mean RT on mean familiarity difference. Table 9 summarises the results. Whereas mean familiarity difference did not reliably predict mean RT for the persistent Brain-State-in-a-Box or the persistent Linear-Associative-Net, the mean familiarity difference was a statistically significant predictor for Dynamic-Eigen-Net, accounting for about 68.1% of the variance in mean response times across comparisons.

Table 9 Three separate linear models regressing mean RT on discriminability derived from each of three models shows the Dynamic-Eigen-Net (DEN) captures the most variance

We applied the same analysis with probability correct. As before, we fit a separate linear regression for each model. Table 10 summarizes the results. Regressing probability correct on mean familiarity difference mirrored results shown in Table 9. Mean familiarity differences derived from Brain-State-in-a-Box and the persistent Linear-Associative-Net were not statistically significant predictors of probability correct, however, mean familiarity differences from the Dynamic-Eigen-Net reliably predicted accuracy, accounting for about 54.6% of variance.

Table 10 Three separate linear models regressing probability correct on discriminability derived from each of three models shows the Dynamic-Eigen-Net (DEN) captures the most variance

Overall participants were slowest to judge the NOUN–VERB(sing/3rd) to NOUN–VERB(pres), NOUN-PREP to PREP-NOUN,VERB-ADV(comp) to ADV(comp)-VERB, and NOUN(s)-VERB(pres) to NOUN–VERB(pres) pairs. They were also the least discriminable for the Dynamic-Eigen-Net. In contrast, participants were fastest when making judgements about the ADJ-NOUN to NOUN-ADJ, PREP-VERB(ing) to PREP-VERB(pres), PRON-VERB(pres) to POSS-VERB(pres), PRONS-NOUN to PRON-NOUN, and DET-NOUN to NOUN-DET pairs. Consistent with the data, they were also the most discriminable for the Dynamic-Eigen-Net. Out of the four bigram comparisons that were most difficult, low accuracy and discriminability for the VERB-ADV(comp) to ADV(comp)-VERB may be linked to the generally low frequency of bigrams of the form VERB-ADV(comp) such as “becoming more”. The other three bigram comparisons with low accuracy and discriminability were more likely to be ambiguous in their well-formedness.

The bigram comparisons so far were based on paired bigrams, where the congruent and incongruent bigrams are roughly matched by frequency since the congruent counterparts to the incongruent bigrams often have one or more words in common. It should be straight-forward for people to judge which of two bigrams, congruent versus incongruent, is easier to read without needing the two to closely match in their type of composition (e.g. “your know” vs “his dog”). To better understand how the models perform, we counted the number of times the familiarity for each congruent bigram exceeded the familiarity for each incongruent bigram, without stratifying the comparisons. For each of the 81 comparisons (i.e. each of the nine congruent bigram sets compared with each of the nine incongruent bigram sets), we obtained 80² = 6400 familiarity differences comparing each of the 80 congruent bigrams with each of the 80 incongruent bigrams.

Figure 7 (left panel) shows the proportion with which the correct bigram was chosen for each comparison. For each model, the congruent bigram types are listed along the rows and the incongruent bigram types are listed along the columns. The cells with less than 50% of comparisons (out of 6400) favouring congruent over incongruent bigrams are indicated with red font (light green background), whereas comparisons favouring the congruent over incongruent bigrams are indicated with white font (dark green background).

Fig. 7

The Probability that Familiarity is Greater for the Congruent Bigrams relative to the Incongruent Bigrams. Lower probabilities of choosing congruent over incongruent bigrams for the persistent Brain-State-in-a-Box show that it is not sensitive to syntactic congruity, whereas both the persistent Linear-Associative-Net and the Dynamic-Eigen-Net show an affinity for congruent bigrams. For the two latter models, the affinity for congruent bigrams is somewhat diminished when memory for the congruent bigram is lesioned, but is relatively robust

For the Brain-State-in-a-Box, the probability that any congruent bigram is attributed greater familiarity compared to any incongruent bigram is at chance (47.34% for all 81 comparisons). For the persistent Linear-Associative-Net, the familiarities are generally greater for the congruent bigrams relative to the incongruent bigrams (76.55% of the time). Finally, the familiarities are yet more likely to be higher for congruent over incongruent bigrams for the Dynamic-Eigen-Net (83.24%).

The Dynamic-Eigen-Net performs best out of the three models. With the exception of four cells, the rest of the bigram comparisons all favoured the congruent bigram over the incongruent bigram at least 50% of the time or more. Incongruent bigrams that include a preposition followed by a noun (PREP-NOUN; e.g. “of group”) are generally more familiar compared to the other congruent bigrams, a pattern also evident in the persistent Linear-Associative-Net. Out of the congruent bigram types, verbs followed by a comparative adverb (VERB-ADV(comp); e.g. “learn more”) are less familiar relative to the NOUN-DET and PREP-NOUN incongruent bigrams. Overall, the persistent Linear-Associative-Net shows good discriminability, but it trails behind the Dynamic-Eigen-Net.

The frequency of the bigram in the corpus and the frequencies of the constituents composing the bigram have an impact on the familiarity values. For instance, for the Dynamic-Eigen-Net, the DET-NOUN bigrams are more familiar than all other incongruent bigrams. Our explorations of the eigenvectors of the weight matrix suggest that items falling into the DET class load strongly on the top eigenvectors. In general, the loadings on the top eigenvectors favour closed-class words, likely because of their high frequency, which explains how we obtained greater familiarity for closed-class bigrams relative to open-class bigrams when modeling Colé et al. (1994). Closed-class words are not qualitatively distinct from the rest of the words, however, they form fixed dimensions of variation within the representational space. Since frequency is a potent organizational variable in the eigenspectrum of the system, a key question is whether frequency information alone can predict the response times in the bigram acceptability task.

Table 11 shows the mean frequency of congruent (column labeled with G_bg) and incongruent (UG_bg) bigrams in the TASA corpus, along with the frequency of the bigram constituents (G or UG subscripted with the position of the word: 1 or 2). To examine how much frequency information may be driving people’s performance, we regressed mean RT on the six frequency measures in a single model. A summary of the results is presented in Table 12. Results show that mean frequency of the congruent bigrams is the only statistically significant predictor: participants were faster to choose the congruent bigrams over the incongruent bigrams, when the frequency for the congruent bigram was higher in the corpus.

Table 11 Mean corpus frequency of the congruent and incongruent bigrams and their constituents greatly vary across bigram comparisons

Table 12 Multiple regression of mean RT on six different frequency measures shows how higher mean grammatical bigram frequency leads to faster responses

G_bg denotes the congruent bigram and UG_bg denotes the incongruent bigram, while G₁ corresponds to the first constituent of the congruent bigram and G₂ corresponds to the second constituent. The same notation is used for the incongruent set. A significant b-weight indicates the beta-weight and semi-partial correlation are also significant. b represents unstandardized regression weights. beta indicates the standardized regression weights. LL and UL indicate the lower and upper limits of a confidence interval, respectively. * indicates p < 0.05. ** indicates p < 0.01.

Given that the mean bigram frequency for the congruent bigrams predicts mean RT, it is possible that we can predict people’s response times by simply using the frequency. In order to combine the central tendencies of the familiarity differences with the overall spread, we took the means of the familiarity differences, separately across comparisons, and divided them by the standard deviation to yield a measure of discriminability, similar to d’ or Cohen’s d. We regressed the mean RT on both discriminability and mean congruent bigram frequency, in a single model. Table 13 shows the result of the regression analysis. Discriminability derived from the Dynamic-Eigen-Net remains a statistically significant predictor of mean RT, even when including mean congruent bigram frequency. Table 14 shows the same analysis, but using probability correct as the to-be-predicted variable. Table 14 mirrors results from Table 13, showing discriminability to remain a statistically reliable predictor of probability correct, even when combined with the frequency measure. Therefore, we conclude that the Dynamic-Eigen-Net is sensitive to structure beyond what is captured purely by frequency information.

Table 13 Regressing discriminability from DEN and mean congruent bigram frequency on mean response time favours discriminability

Table 14 Regressing discriminability from DEN and mean congruent bigram frequency on probability correct favours discriminability

Generalization

The simulations we have presented have been limited to recognition. That is, all of the associations connecting the words in the congruent bigrams were encoded into memory. The system cannot rely on a simple match to memory to show generalization; it needs to rely purely on the structural properties encoded in the system. Suppose you are shown a pair of bigrams, “you know” and “your know”. If an association between “you”, in the first slot, and “know”, in the second slot, exists in memory and an association between “your”, in the first slot, and “know”, in the second slot, does not exist or is much weaker, you can correctly pick out the congruent bigram by relying on recognition. Lesioning the association between “you” and “know” prevents reliance on a simple recognition process, pushing the system to generalize. In the next simulation, we modeled the bigram discriminability task as before, but deleted the association between the two words making up each congruent bigram, prior to probing the system with either the congruent bigram or its incongruent counterpart. Before moving on to each new pair of congruent and incongruent bigrams, the association was reset to its pre-lesioned state. The association between the two words making up the corresponding incongruent bigram was left intact.

Table 15 shows the different violation types in the first column, an example for each violation in the second column, followed by the discriminabilities obtained when the association for the congruent bigram is left intact (“intact”), and when the association for the congruent bigram is deleted (“lesioned”), separately for the persistent Linear-Associative-Net and the Dynamic-Eigen-Net. We exclude the persistent Brain-State-in-a-Box because performance was at chance regardless of lesioning. Figure 10 in the appendix shows the distribution of the corresponding familiarity differences across the nine bigram violations, for the lesioned case, separately for the Dynamic-Eigen-Net and the persistent Linear-Associative-Net.

Table 15 The model shows good discriminability between valid and invalid bigrams across various syntactic violations

As evident in Table 15, both the persistent Linear-Associative-Net and the Dynamic-Eigen-Net obtain positive discriminability for all but one bigram comparison despite no memory of the congruent bigrams. Overall, the discriminabilities are lower when the association is removed relative to when it is intact, showing the contribution of recognition to discriminability. Because discriminability in the lesioned case cannot rely on recognition, both models are exploiting the global structure from the corpus based on the encoded associations. Both the persistent Linear-Associative-Net and the Dynamic-Eigen-Net are able to exploit the structure encoded in the eigenvectors to generalize without relying on recognition.

The persistent Linear-Associative-Net and the Dynamic-Eigen-Net yield a similar pattern of generalizability. Out of the nine comparisons, the persistent Linear-Associative-Net and the Dynamic-Eigen-Net only fail to generalize for the NOUN–VERB(sing/3rd) to NOUN–VERB(pres) violations. Whereas the mean familiarity differences are significantly greater than zero in all other comparisons, they are significantly less than zero for the NOUN–VERB(sing/3rd) to NOUN–VERB(pres) violations.

For a more granular comparison of the generalization capability of the different spreading activation algorithms, we compared the number of times the familiarity for each congruent bigram exceeded that of each of the incongruent bigrams across 81 comparisons, as we did earlier with the intact system. The probability that any congruent bigram was attributed greater familiarity compared to any incongruent bigram was near chance for the persistent Brain-State-in-a-Box model (around 46.98% for all 81 comparisons), whereas it was around 63.12% for the persistent Linear-Associative-Net, and 78.28% for the Dynamic-Eigen-Net. The right column of Fig. 7 shows the proportion of times the congruent bigram had a larger familiarity than the incongruent bigram, separately for each of the 81 comparisons, in the lesioned condition.

The lightly shaded heatmaps for the persistent Brain-State-in-a-Box, the first row, illustrate its inability to capture the structure required for distinguishing congruent and incongruent bigrams. Many more cells are darkly shaded for the persistent Linear-Associative-Net, indicating a notable improvement over the persistent Brain-State-in-a-Box. Despite the improvement over the persistent Brain-State-in-a-Box, the persistent Linear-Associative-Net discriminates between a more limited range of comparisons compared to the Dynamic-Eigen-Net. The better performance using the Dynamic-Eigen-Net relative to the persistent Linear-Associative-Net is clear in the lesioned cases, showing that it is better at generalization.

Our use of the term incongruent is out of convenience and only true in the sense that the members in the set very rarely occur in natural language. In some cases, they only appear odd in a bigram. Some examples of the VERB-ADV(comp)-vs-NOUN-DET comparisons include the bigram pairs, “tell more” vs “child the”, “go more” vs “money the”, and “mature more” vs “government the”. For the VERB-ADV(comp)-vs-PREP-NOUN comparisons, some examples include, “promote more” vs “for money”, “suffer more” vs “of price”, and “retain more” vs “of understanding”. Some example bigram pairs for the NOUN–VERB(sing/3rd)-vs-PREP-NOUN included “birds sing” vs “from home”, “symptoms include” vs “for food”, and “atoms combine” vs “of quality”. Some examples for the NOUN–VERB(sing/3rd)-vs-PREP-NOUN bigrams include, “food gives” vs “of life”, “brain sends” vs “in life”, and “theory suggests” vs “of section”. The examples make it clear that, although rare, some of the incongruent bigrams may be plausible in larger sentential contexts. For example, the examples corresponding to the NOUN-DET bigrams may be plausible in larger utterances such as in “give the child the toy”, “when given the money the man laughed”, and “they told the government the truth”. Some of the clearly incongruent bigrams include, “of advantage”, “of bit”, “of plenty”, and “of lot”. Except for some of the ambiguous comparisons, the Dynamic-Eigen-Net shows good generalizability.

How then is the system generalizing? On the one hand, the incongruent bigrams are more likely to have an inhibitory association, connecting the composite words. On the other hand, words that are activated during recurrence are more likely to be mutually inhibitory for incongruent bigrams relative to congruent bigrams. In the first iteration the symbol⁸ in the first slot activates symbols in the second slot, and the symbol in the second slot activates symbols in the first slot. On each following iteration, the symbols that had become activated in a previous iteration either inhibit or activate other symbols in the adjacent slot. For instance, given the probe “you know”, the symbol “you”, in the first slot, may activate symbols such as “‘re” and “think” in the second slot while the symbol “know”, in the second slot, may activate symbols such as “‘n't”, “i”, and “we”, in the first slot. When the two symbols form an incongruent pair, as in “your know”, the symbols activated by the input symbols (i.e. “your” and “know”) are more likely to inhibit one-another. For instance, the symbol “your” in the first slot may activate “body” and “own” in the second slot. Because “body” and “own” are inconsistent with symbols activated in the first slot by the symbol “know”, they are more likely to be mutually inhibitory than facilitatory.

Figure 8 illustrates the steady state of the lesioned Dynamic-Eigen-Net, when probed with either “you know”, shown in panel A, or “your know”, shown in panel B. Within each panel, the top five most active symbols in the first slot (left) and the second slot (right) are shown as separate nodes, and the connections linking them are shown as lines, whose width corresponds to the strength of association. Symbols with higher activations are shown in darker shades of blue and symbols that are inhibited (less-than-0 activation) are shown in darker shades of red. Excitatory connections are shown in blue while inhibitory connections are shown in red. The association connecting “you” to “know” was removed. In addition to the negative association between symbols in the incongruent bigram, activations are more inhibited for the incongruent pair compared to the congruent pair based on the cross-connections of the other activated symbols. Despite the absence of the association between the words in the congruent pair, the greater familiarity for congruent bigrams emerges through the mutual constraints encoded in the system.

Fig. 8

shows how the scaled-up Dynamic-Eigen-Net distinguishes between congruent (panel A: “you know”) and incongruent (panel B: “your know”) bigrams, even when the association forming the congruent form has been lesioned. Within each panel, the top ten most active terms in each bank (first slot on the left and the second lot on the right) are indicated by separate nodes, coloured based on their relative activation. Darker shades of blue correspond to more active nodes whereas darker shades of red correspond to the less active, or inhibited, nodes. The activations correspond to the steady-state of the system after each probe. When the probe is syntactically congruent, excitatory connections (blue) outnumber inhibitory connections (red) between the top most active terms, whereas the pattern is reversed in the case of syntactically incongruent probes

Discussion

We started by asking how a system may use a limited set of exemplars to infer the structure of an infinite set that is defined by constraints on how symbolic representations within each exemplar combine. We explored generalization in a combinatorial domain—the set of all well-formed bigrams, and contrasted our generalization-at-retrieval approach with systems that attempt to generalize the structure during encoding, through error-driven learning, and proposed a modified variant of associative nets. We proposed the use of a Linear-Associative-Net equipped with dynamic connections that change the association strength between elements in the network based on the input that is processed. We provided an eigenspectrum analysis of the resulting system and described how changing weights based on input adds dynamics to the eigenspectrum of the system and expands its space of equilibria in a way that respects mutual constraints encoded in memory from prior experience.

After a series of toy demonstrations showing how the resulting system has greater generative potential than previous versions of associative nets, we turned to some empirical work using bigrams in order to explore the model’s scalability and capacity to match human performance. We supplemented previous work with a bigram acceptability task, showed that discriminability derived from a variant of the Dynamic-Eigen-Net can predict the speed with which human participants make bigram acceptability judgements, and that such discriminability is superior to simple frequency measures. We showed that the Dynamic-Eigen-Net is more sensitive to syntactic structure compared to a persistent Linear-Associative-Net, a Linear-Associative-Net with the original input added to the state-vector during each recurrence iteration, and the persistent Brain-State-in-a-Box. Finally, to show that the system can generalize at scale, we modeled the bigram acceptability task but deleted the associations corresponding to congruent bigrams before probing the system. Our results showed that despite some discriminability loss, the system is able to exploit global associative structure to correctly distinguish congruent bigrams from incongruent bigrams, in the absence of knowledge about the specific bigram. Although the persistent Linear-Associative-Net was also capable of generalization, performance was superior for the Dynamic-Eigen-Net.

In order to scale up the Dynamic-Eigen-Net, we introduced some requirements for the eigenspectrum encoded in the weight matrix. The first requirement was that the magnitude of the transient assemblies must exceed the largest eigenvalue of the weight matrix. The second requirement was to partially dampen the contribution of the dominant eigenvector of the weight matrix. Our way of meeting the two requirements is only provisional and may easily be accomplished in other ways. The contribution of the current manuscript is the Dynamic-Eigen-Net spreading activation algorithm.

We used PMI to normalize the raw co-occurrence counts. Again, we do not propose that using PMI is necessary, as other normalization measures may be used, however, it is possible that inhibitory connections are required. Recently, Johns et al. (2019) showed how negative information greatly improves semantic benchmarks for various representations of meaning. Our use of PMI for normalizing the weight matrix is likely benefiting from the resulting negative information. When the co-occurrence between a pair of words falls below the base-rate co-occurrence expected if the two were independent (i.e. the product of each of their probabilities), the resulting PMI yields a negative association between the two words. Our work complements work by Johns et al. (2019) by further showing how the influence of negative information can best emerge through iterative feedback to drive generalization in a dynamical system. Despite using the same weight matrix, the Dynamic-Eigen-Net algorithm outperformed both the persistent Linear-Associative-Net and the Brain-State-in-a-Box.

We reiterate that the current model is not meant as a complete description. The main goal of our simulations is to show that generalization is possible when the connectivity of the network is altered by the input. Our way of representing serial-order can be considered a concatenation model, where mutually disjoint subsequences of a single vector code the temporal order of the input stream. As pointed out by one of the reviewers, concatenation models of serial-order do not predict interference if two bigrams are encoded, with the same word (e.g. “apple”) appearing in the first slot in one bigram (“apple tree”) and in the second slot in another bigram (“juicy apple”). In one of the earliest demonstrations of same-item interference, Primoff (1938) had subjects study pairs of items in a list and later cued them with an item either in the first position or the second. The cues indicated whether the to-be-recalled paired associate was on the left or right side of the cue word. Primoff (1938) found superior cued recall for items that only appeared once in a list relative to items that appeared twice – once as the first member of a pair and another time as the second member of a different pair. Recently, Rehani and Caplan (2011) replicated the findings and suggested that they require modifications to models that encode serial-position through concatenation, as we have done here.

We may be able to accommodate the result based on the interaction between serial-order and syntagmatic associations. Syntagmatic associations correspond to order-independent links between words that occur in the same context. The simulations presented here only incorporated the former kind of association, however, we believe that a more complete model will require the addition of the latter. Figure 9 shows one way the two kinds of associations may interact. In addition to encoding serial-order associations in the first two slots as we have done here, a third slot may be added to include syntagmatic associations. For instance, when a subject studies the pair A-B, the unit for A would be turned on (e.g. set to one) in the first slot, the unit for B would be turned on in the second slot, and both units A and B would be turned on in the third slot. The outer-product of the vector with itself would encode forward associations in the top-middle submatrix and backward associations in the middle-left submatrix. The lower-right submatrix would encode syntagmatic associations (i.e. many to many links) and the two submatrices above and the two submatrices to the left would encode item associations (i.e. one to many links). If we assume another pair, B-C that was encoded, probing the system with B (i.e. turning on the unit for B in the first and third slots) would activate both associates A-B and B-C via spreading activation through the item and syntagmatic associations, leading to interference (c.f. Kato & Caplan, 2017). Murdock (1974) provides an in-depth examination of order and item information, and Dennis (2005) shows how syntagmatic and paradigmatic relations can be combined (the SP model) to capture several problems in semantic composition.

Fig. 9

One-way serial-order information can interact with item and syntagmatic information. The elongated rectangle above the square partitioned table corresponds to the pair A-B. The item, A, is active in the first slot and the item, B, is active in the second slot. Both A and B are active in the third slot. The outer-product of such input with itself yields a block-matrix that can be partitioned into forward (FW), backward (BW), item (ITEM), and syntagmatic (SYN) associations

An open question remains as to how serial-order and syntagmatic associations may interface. The experiments conducted by Goodman et al. (1981) and Münte et al. (1993) manipulated both syntactic and semantic congruity in their tasks, however, we have only explored syntactic congruity in the current work in order to demonstrate structural, or combinatorial, generalization. One way semantic congruity is explored is in lexical decision tasks where the second word in two adjacent word-present trials is synonymous (e.g. “feline cat”) with the first word or when it is associatively related (“cat fluffy”). Some of the work exploring the interaction between syntactic and semantic congruity (e.g. Goodman et al., 1981; Münte et al., 1993; Seidenberg et al., 1984) has led to the suggestion that syntactic and semantic primes tap into different processing loci, with the overall theme being that semantic effects are stronger, automatic, and occur earlier in processing while syntactic effects are weaker, controlled, and occur later in processing. A major challenge has been to orthogonally manipulate both semantic and syntactic variables, as they are typically highly confounded, i.e. syntactically anomalous utterances are also often semantically anomalous. Our current view is that associations of different kinds underlie semantic and syntactic effects, and that the interactions between the two occur within a highly interactive system. The addition of syntagmatic associations to serial-order associations would be a natural path forward for capturing some of the semantic-syntactic interactions documented in the literature.

The recurrent architecture of associative nets was originally motivated by the observation that cortical pyramidal cells are subsumed in a vast network of feedback connections (e.g. Douglas et al., 1995). Similarly, Hebbian encoding has long been considered the computational analogue to Long-Term Potentiation (Collingridge & Bliss, 1995). In the same way, transient assemblies in the Dynamic-Eigen-Net may be grounded in synaptic plasticity that spans time-scales ranging from hundreds of milliseconds to a few minutes, referred to generally as Short-Term-Plasticity⁹ (Masse et al., 2020). Our simulations with the Dynamic-Eigen-Net suggest that Short-Term-Plasticity may have a stabilizing effect on the formation of steady states.

As evident from our results, we were unsuccessful when scaling up the persistent Brain-State-in-a-Box to deal with naturalistic input. We explored various alternatives in our attempts, but they all proved highly susceptible to interference from high frequency symbols. The Brain-State-in-a-Box’s requirement for steady states to be corners of a hypercube implies that the absolute value of all elements of the state-vector need to reach a constant. Based on observations of the evolution of activations across banks during recurrence, we speculate that initially the state-space yields sensible patterns (i.e. the symbols that populate the banks have obvious interpretations in their serial-order alignment). However, the finer-grain activation patterns correspond to states where a large proportion of elements in the vector have not reached the saturation constant. When all elements are saturated, not only is the resulting pattern orthogonal to other patterns, by definition, but much of the granularity in the representation is lost. Therefore one possibility is that the bounding box constraint that defines the Brain-State-in-a-Box collapses over the dynamic range along which structurally relevant information is encoded. The Dynamic-Eigen-Net and the persistent Linear-Associative-Net do not suffer the same problem because they allow a larger space of steady-states. Instead of the corners of a hypercube, in the latter two models, the span of possible steady states fall on the surface of the hyper unit-sphere.

Improved performance through the introduction of transient assemblies, or weights, resonates with earlier cognitive models (e.g. Gardner-Medwin, 1989; Burgess & Hitch, 1999; Plaut & Shallice, 1993; Feldman, 1982). The various implementations make different architectural and processing assumptions, but generally show that including transient assemblies has several advantages over networks with static connectivity. For instance, in a Hebbian net, Gardner-Medwin (1989) assumes transient assemblies are multiplicatively combined with long-term weights whereas Burgess and Hitch (1999) assume the additive combination of the two. Gardner-Medwin (1989) provides information-theoretic analyses showing capacity advantages using their implementation of transient weight changes and Burgess and Hitch (1999) rely on transient assemblies to capture a set of memory benchmarks. Plaut and Shallice (1993) additively combine transient assemblies to long-term weights, trained using error-driven learning, to model perseveration in their model of deep dyslexia and Feldman (1982) suggests transient assemblies as one possible mechanism for feature-binding through attention.

Transient weights have also been explored in the broader machine-learning literature, however, the implementations rely on neural networks with hidden layers that are trained through error-driven learning. For instance, Ba et al. (2016) suggest encoding a set of recent hidden states into a fast-decaying set of short-term weights as a way to model greater facilitation for states corresponding to the system’s recent hidden state history. They propose the mechanism for recurrent neural nets which use error-driven learning for training the long-term connectivities. Reliance on error-driven learning limits the system’s ability to meet human-level cognitive benchmarks such as one-shot learning, due to the slow formation of novel associations. The associations form directly in an associative net without the need to funnel stimuli through a hidden, lower dimensional, layer. The lower dimensionality facilitates generalization, however, it also increases interference between encoded representations. Instead of relying on projection through a hidden layer to induce generalization, spreading activation through an associative net using the Dynamic-Eigen-Net algorithm induces generalization by driving the activation of an initial cue into resonance with the entire knowledge-base.

In conclusion, our demonstrations show that including transient assemblies in Linear-Associative-Nets increases their generative complexity. Given that generalization requires exploiting structural regularities with little surface-level information, and the Dynamic-Eigen-Net’s ability to assimilate novel patterns based on structure, we propose our model as one candidate for the spreading of activation in an associative net capable of structural generalization at retrieval.

Appendix A

Fig.

Fig. 10

Distributions of familiarity differences (congruent minus the incongruent) across the nine bigram comparison types, after deleting the associations for the congruent bigrams, show that the Dynamic-Eigen-Net can generalize well for most of the comparisons. The red vertical line marks the zero-point. The distributions that fall on the right of the zero-point indicate good generalizability. NOUN: singular or mass noun, PREP: preposition, VERB: verb, ADV(comp): adverb (comparative), VERB(sing/3rd): verb, (third-person singular present tense), NOUN(s): plural noun, VERB(pres): non-third-person verb (singular present tense), VERB(ing): gerund verb (present participle), DET: determiner, ADJ: adjective, PRON: personal-pronoun, POSS: possessive pronoun

10