Introduction

Over the past decades, the “FBST ev” has been proposed as a Full Bayesian Significance Test (de Bragança Pereira and Stern 1999; de Bragança Pereira et al. 2008) that offers distinct advantages over both frequentist p-values and Bayes factors (e.g., Madruga et al. 2003). The FBST ev has been applied in economics, genetics, signal processing, time series analysis, biology, astronomy, medicine, and other fields (see de Bragança Pereira and Stern J. M. in press and references therein). Recently, the FBST ev has also been introduced to the field of psychology (e.g., Kelter 2020b; Kelter in press). However, we believe that the method has specific limitations that warrant discussion. Below we first introduce the FBST ev and describe its similarities to conventional p-values. Next we outline four features that we perceive to be particularly problematic.

A Brief Definition of the FBST e v

The FBST ev (sometimes called “e-value” Footnote 1) is a posterior tail probability, where the tail area is defined by a so-called posterior surprise function, which is defined below. For concreteness we focus on a point null hypothesis that fixes a parameter of interest to a specific value: \( {\mathscr{H}}_{0}: \theta = \theta _{0} \). The alternative hypothesis relaxes the restriction on 𝜃, and it is assumed that a prior distribution \( \pi (\theta | {\mathscr{H}}_{1}) \) is assigned to 𝜃, which in light of the observed data can then be updated to a posterior \( \pi (\theta | y, {\mathscr{H}}_{1}) \) using Bayes’ rule.

The posterior surprise function is the ratio of the posterior over a reference function. One of the most common reference functions, and the one we use throughout this manuscript, is the prior distribution, and leads to \( \pi (\theta | {\mathscr{H}}_{1}, y) / \pi (\theta | {\mathscr{H}}_{1}) \) — a common Bayesian measure of evidence or support (e.g., Evans, 2015). The support associated with the null hypothesis is defined as the largest support for parameter values restricted by the null, that is, \( \sup _{\theta \in {\varTheta }_{0}} \pi (\theta | {\mathscr{H}}_{1}, y) / \pi (\theta | {\mathscr{H}}_{1}) \), where Θ0 is the parameter space Θ1 restricted according to \( {\mathscr{H}}_{0} \). For a point null hypothesis this simply yields \( \pi (\theta _{0} | {\mathscr{H}}_{1}, y) / \pi (\theta _{0} | {\mathscr{H}}_{1}) \). The tail area T used to define the FBST ev consists of all parameter values 𝜃 that have posterior support less than the support associated with the null hypothesis, that is,

$$ T = \left\{ \theta \in {\varTheta}_{1} \left| \frac{\pi(\theta ~|~ y, \mathcal{H}_{1})}{\pi(\theta ~|~ \mathcal{H}_{1})} \leq \frac{\pi(\theta_{0} ~|~ y, \mathcal{H}_{1})}{\pi(\theta_{0} ~|~ \mathcal{H}_{1})} \right \} \right., $$
(1)

where Θ1 is the unrestricted parameter space. The FBST ev for \( {\mathscr{H}}_{0}: \theta = \theta _{0} \) is defined as the posterior mass in area T, that is,

$$ ev = {\int}_{T} \pi(\theta ~|~ y, \mathcal{H}_{1}) \text{d} \theta . $$
(2)

When ev is low, or \( \bar {ev}= 1 - ev \) is high, the data are said to cast doubt on \( {\mathscr{H}}_{0} \).

As a concrete example, consider a binomial test of \( {\mathscr{H}}_{0}: \theta = \frac {1}{2} \) versus \( {\mathscr{H}}_{1}: \theta \in {\varTheta }_{1} = (0, 1) \) and a beta(1, 1) prior (i.e., a uniform prior from 0 to 1). The posterior surprise function then equals the posterior distribution. Consequently, the set T that defines the posterior tail area are those 𝜃 s that lead to a posterior value \( \pi (\theta | y, {\mathscr{H}}_{1}) \leq \pi (\frac {1}{2} | y, {\mathscr{H}}_{1}) \). Equivalently, \( \bar {ev} = 1 - ev \) defines the posterior probability of \( \bar {T} = {\varTheta }_{1} \setminus T \), the complement of the tail area T.

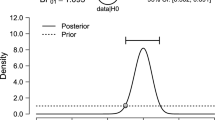
For observed data consisting of s = 15 successes and f = 5 failures the posterior is a beta(16, 6) distribution. The support for the null is \( \pi (\frac {1}{2} | y, {\mathscr{H}}_{1}) = 0.31 \) and the area of parameter values that have more support is \( \bar {T} = [\frac {1}{2}, 0.92] \); thus, the tail area is \( T= (0, \frac {1}{2}) \cup (0.92, 1) \). The area under the curve shown in Fig. 1 equals \( \bar {ev} = 1 - ev = .98 \), and hence ev = .02, which combined with the standard threshold of .05 leads to a rejection of the null hypothesis (de Bragança Pereira et al. 2008, Definition 2.3).

Fig. 1
figure 1

Example of the FBST ev for a binomial test of \( {\mathscr{H}}_{0}: \theta = \frac {1}{2} \) versus \( {\mathscr{H}}_{1}: \theta \in {\varTheta }_{1} = (0, 1) \) with a beta(1,1) prior for s = 15 successes out of n = 20 observations. Shown is the beta(16,6) posterior distribution. Area \( \bar {T} = [\frac {1}{2}, 0.92] \) contains all values of 𝜃 with at least as much support from the data as \( \theta = \frac {1}{2} \). The posterior mass on \( \bar {T} \) equals 0.98, and hence ev = 1 − 0.98 = 0.02. Figure based on the JASP module Learn Bayes

Full size image

The advantage of the FBST ev is that the procedure promises to work with non-subjective priors such as Jeffreys’s transformation-invariant priors (e.g., Jeffreys 1946; Ly et al., 2017), or reference priors (e.g., Berger et al. 2009; Bernardo 1979) as long as the posterior is proper. In contrast, Bayes factors prohibit the use of improper priors on the test-relevant parameter, and the construction of default Jeffreys’s Bayes factors requires the statistician to select a class of priors that fulfil certain desiderata (e.g., Bayarri et al. 2012; Jeffreys 1961; Li and Clyde 2018; Ly et al. 2016a; Ly et al. 2016b). Hence, the FBST procedure is more or less automatic whenever non-subjective priors are available (de Bragança Pereira and Stern J. M. in press), as it does not require additional difficulties of prior selection. Moreover, Diniz et al. (2012) mention that it is an advantage that the FBST procedure avoids the introduction of a prior probability on the null hypothesis. Below we show that the automatic use of the FBST can lead to problematic inferences. The root of the problem, we believe, is due to the fact that the behavior of FBST ev is similar to that of p-values.

The FBST e v as an Approximate p-value

Fig. 1 highlights the conceptual similarity between the FBST ev and the frequentist p-value from null hypothesis significance testing. One key difference is that the p-value violates the Likelihood Principle (e.g., Berger and Wolpert 1988; Wagenmakers, 2007), but the FBST ev does not, because it relies on the posterior distribution. Footnote 2

Another key difference is that for p-values the tail event consists of the set of more extreme outcomes than what is observed across the sample space, whereas for the FBST ev the tail area consists of parameter values that receive less support than the null value. This difference between the spaces is noticeable in the binomial example, as the tail event of the p-value is comprised of discrete outcomes, e.g., the sets {0,1,2,3,4,5} and {15,16,17,18,19,20}, whereas the tail area for FBST ev consists of two continuous intervals, e.g., \( (0, \frac {1}{2}) \) and (0.92,1).

There are specific cases where the FBST ev and the p-value (for a fixed-n sampling plan and without possible corrections for multiplicity) are exactly equal. In particular, this occurs when data are normally distributed with population mean μ and variance σ2 = 1 and the null hypothesis is \( {\mathscr{H}}_{0}: \mu = 0 \), whereas the alternative allows μ to vary freely, that is, \( {\mathscr{H}}_{1} : \mu \in \mathbb {R} \). Using the (improper) uniform prior (i.e., the “uninformative” Jeffreys’s transformation-invariant prior) then results in the FBST ev and the p-value being exactly equal (e.g., Diniz et al. 2012). More generally, consider Bayesian parameter estimation for the location parameter μ of a statistical model from the exponential family. Assume the prior on μ is uniform on the real line. Then the proportion of the posterior distribution with mass lower than zero equals the one-sided frequentist p-value (e.g., Lindley 1965; Pratt et al. 1995). This means that for a symmetric posterior distribution, the FBST ev equals the two-sided frequentist p-value. For non-uniform priors the relation between FBST ev and p-value is only approximate; however, as sample size grows the data quickly dominate the posterior distribution (e.g., Wrinch and Jeffreys 1921), such that the approximation will be increasingly close.

The large-sample connection between the FBST ev and the p-value holds even more generally, whenever the (asymptotic) p-value is derived from the (generalized) likelihood ratio statistic. This connection is made rigorous via Wilks’ theorem (Wilks 1938), which states that the likelihood ratio statistic asymptotically has a χ2-distribution, and the Bernstein von-Mises theorem (e.g., LeCam 1986; Ghosal and van der Vaart 2017; van der Vaart 1998), which states that, under general conditions, the posterior is asymptotically normal. Both theorems were used by Diniz et al. (2012) to derive the following (asymptotic) functional relationship

$$ ev \overset{d}{\rightarrow} 1 - F_{\dim({\varTheta}_{1})} [ F_{\dim({\varTheta}_{1}) - \dim({\varTheta}_{0})}^{-1}(1- p)] , $$
(3)

as \( n \rightarrow \infty \), where p in the right-hand side is the asymptotic p-value of the generalized likelihood ratio statistic, Fk and \( F_{k}^{-1} \) are the cumulative distribution function and the quantile function of a χ2-distribution with k degrees of freedom, respectively. For instance, for the binomial example \( \dim ({\varTheta }_{1}) = 1 \), since there is only one parameter that is free to vary in \( {\mathscr{H}}_{1} \) and \( \dim ({\varTheta }_{0}) = 0 \), since it is a singleton. As such, whenever \( \dim ({\varTheta }_{1}) = \dim ({\varTheta }_{1}) - \dim ({\varTheta }_{0}) \), Eq. (3) states that the difference between FBST ev and the asymptotic p-value becomes negligible as the sample sizes increase.

In the remainder of the paper we highlight how the FBST procedure can result in problematic inferences. Our conclusions are to some extent predicated on the notion that evidence is the degree to which the data change our conviction about competing accounts of the world (Evans 2015; Morey et al. 2016).

Problem 1: The FBST e v Cannot Quantify Evidence in Favor of the Null Hypothesis

Our first demonstration concerns the case of pure induction: a universal generalization is stipulated and an unbroken string of n confirmatory instances is observed. The evidence in favor of the universal generalization ought to increase with n; we consider this axiomatic. The mathematician George Polya termed this regularity the “fundamental inductive pattern”:

“This inductive pattern says nothing surprising. On the contrary, it expresses a belief which no reasonable person seems to doubt: The verification of a consequence renders a conjecture more credible. With a little attention, we can observe countless reasonings in everyday life, in the law courts, in science, etc., which appear to confirm to our pattern.” (Polya 1954, pp. 4–5)

The FBST ev violates the fundamental inductive pattern. Concretely, a universal generalization posits that all instances have property x, that is, \( {\mathscr{H}}_{0}: \theta = 1 \) for a binomial likelihood kernel. Regardless of their number n, the confirmatory instances are best predicted by 𝜃 = 1, and consequently this value receives more support than any other value of 𝜃. This means that \( \bar {ev}=0 \) and ev = 1 regardless of the number of confirmatory instances and regardless of the prior distribution under \( {\mathscr{H}}_{1} \). Note that the p-value suffers from the exact same problem (e.g., Jeffreys1980; Ly et al. 2020; Wrinch and Jeffreys 1919).

Our second demonstration concerns a binomial test of \( {\mathscr{H}}_{0}: \theta = \frac {1}{2} \) versus \( {\mathscr{H}}_{1}: \theta \in {\varTheta }_{1} = (0, 1) \) and a beta(α,α) prior that is symmetric around \( \frac {1}{2} \). Suppose that the data consist of just as many successes s as failures f (i.e., \( s=f=\frac {n}{2} \)). In this scenario, the evidence for \( {\mathscr{H}}_{0} \) ought to increase with n. However, for any n the data are best predicted by \( \theta = \frac {1}{2} \). As in the first demonstration, this means that ev = 1 regardless of n.

These demonstrations show that the FBST ev cannot quantify evidence in favor of a null hypothesis. Data maximally consistent with the null hypothesis ought to offer stronger support when sample size is high rather than low; however, this regularity is not reflected in FBST ev. This inability means that the FBST ev also cannot discriminate between evidence for absence and absence of evidence (e.g., Keysers et al. 2020).

Problem 2: The FBST ev is Susceptible to Sampling to a Foregone Conclusion

Not only is the FBST ev incapable of quantifying evidence for the null, it will lead to a sure rejection of the null if a sufficiently patient researcher monitors the FBST ev and stops whenever it dips below a fixed threshold such as ev < .05. When \( {\mathscr{H}}_{0} \) is true, this is certain to happen (i.e., the decision to reject \( {\mathscr{H}}_{0} \) based on an indefinite accumulation of observations is a foregone conclusion). This makes an observed rejection of the null based on a sequential application of the FBST procedure ambiguous and uninterpretable.

The reason why monitoring the FBST ev is problematic stems from its intimate (asymptotic) relationship with the p-value. As noted earlier, the asymptotic behavior of the p-value also describes the asymptotic behavior of the FBST ev; and for p-values, it can be proven that there is no convergence to a single value — instead, p-values meander randomly in the (0,1)-interval (Feller 1940; 1968). Hence, the FBST ev will eventually cross the threshold of, say, ev < .05. A concrete demonstration is given in Wagenmakers et al. (2018, intuition 5).

A Bayesian interpretation of this phenomena is that the FBST ev is approximately a test for the direction of an effect (Casella and Berger 1987; Marsman and Wagenmakers 2017). Recall that in many applications, the FBST ev consists of the sum of two posterior areas: the right tail and the left tail (cf. Fig. 1). Focusing on the left tail (i.e., the posterior mass on values of parameter values 𝜃 lower than 𝜃0), we note that it equals the probability that 𝜃 is lower than 𝜃0 as opposed to higher than 𝜃0. Specifically, assume a prior distribution for 𝜃 under \( {\mathscr{H}}_{1} \) that is centered on 𝜃0, and assume that the posterior is symmetric such that the area in the left tail equals that in the right tail. The posterior probability that 𝜃 is lower than 𝜃0 then equals ev/2.

Consider now the scenario where data are generated under \( {\mathscr{H}}_{0} \), and accumulate indefinitely (cf. Kelter2020a). In our interpretation, the FBST ev is an approximate test for direction; because the true value is exactly in between the positive and negative values, the FBST ev will therefore meander randomly — the probability (or odds) has nothing to converge to.

To conclude, the FBST ev can be interpreted as an approximate test for direction. This means that whenever data are generated under \( {\mathscr{H}}_{0} \), the truth is exactly in the middle and the FBST ev will drift randomly and be susceptible to sampling to a foregone conclusion (Rouder 2014; Wagenmakers et al. 2018). Because the asymptotic behavior of the FBST ev equals that of the frequentist p-value, the proofs on sampling to a foregone conclusion in Feller (1968) also pertain to the FBST procedure.

Problem 3: The FBST e v Violates the Principle of Predictive Irrelevance

The principle of predictive irrelevance implies that if two models yield exactly the same predictions for to-be-observed data, then actually observing the data should not change our preference for one model over the other. As an example, consider the binomial test of \( {\mathscr{H}}_{0}: \theta = \frac {1}{2} \) versus \( {\mathscr{H}}_{1}: \theta \in {\varTheta }_{1} = (0, 1) \) with a beta(α,α) prior, which is symmetric around \( \frac {1}{2} \). Under \( {\mathscr{H}}_{0} \), the probability that the next observation is a success equals \( \frac {1}{2} \). This is also the case under \( {\mathscr{H}}_{1} \), as the prior predictive of \( {\mathscr{H}}_{1} \) is then a symmetric beta-binomial distribution with mean \( \alpha / (2 \alpha ) = \frac {1}{2} \) which equals the probability of the next observation being a success.

To see that the FBST ev violates the principle of predictive irrelevance, note that if α = 1 and the first observation is a success then under \( {\mathscr{H}}_{1} \) we have \( \theta \sim \text {beta}(2,1) \); ev is then the posterior mass on \( \theta < \frac {1}{2} \), which equals ev = .25. If, instead, the first observation is a failure, then under \( {\mathscr{H}}_{1} \) we have \( \theta \sim \text {beta}(1,2) \) and ev is also equal to .25. Hence, upon observing the new datum, the posterior changes and consequently the FBST ev changes — even though the datum is predictively irrelevant.

More generally, any symmetric posterior distribution \( \theta \sim \text {beta}(\alpha +n/2,\alpha +n/2) \) under \( {\mathscr{H}}_{1} \) has ev = 1 (see Problem 1 above). The occurrence of a new datum will decrease that FBST ev to indicate some evidence against \( {\mathscr{H}}_{0} \), even though the datum is predictively irrelevant and even though the decrease occurs regardless of the nature of the datum (i.e., success or failure). This analysis can be extended to data sequences of arbitrary length (Wagenmakers et al. 2020).

In contrast, Jeffreys’s Bayes factor does behave in accordance with the principle of predictive irrelevance, because it is defined as the ratio of the prior predictives evaluated at the observed data, that is, the ratio of marginal likelihoods. Whenever \( {\mathscr{H}}_{0} \) and \( {\mathscr{H}}_{1} \) make identical predictions for the next datum, Jeffreys’s Bayes factor is unaltered when that datum is observed, indicating perfect predictive equivalence: “The first member sampled is bound to be of one type or the other, whether the chance is \( \frac {1}{2} \) or not, and therefore we should expect it to give no information about the existence of bias.” (Jeffreys 1961, p. 257). More generally, when the beta prior distribution is symmetric and s = f observations have been made, the prior distribution for the analysis of the next observation is a beta(α + s,α + f) distribution. Because this distribution is symmetric around \(\theta =\frac {1}{2}\), the predictions for the upcoming observation are again identical under \( {\mathscr{H}}_{0} \) and \( {\mathscr{H}}_{1} \), and therefore the Bayes factor remains unchanged irrespective of its outcome. “Thus if at a certain stage the sample is half and half, the next member, which is bound to be of one type or the other, gives no new information.” (Jeffreys 1961, p. 257). Another case consist of an asymmetric \( \theta \sim \text {beta}(\alpha ,\upbeta ) \) distribution which is updated with unequal s and f such that α + s =β +f; the next observation will not change the Bayes factor for \( {\mathscr{H}}_{0} \) versus \( {\mathscr{H}}_{1} \).

In other words, whenever the distribution for 𝜃 under \( {\mathscr{H}}_{1} \) is symmetric around \( \frac {1}{2} \) (either before or during data collection), the next observation is predictively irrelevant, and will leave the Bayes factor unaffected (see Wagenmakers et al. 2020 and references therein). Jeffreys notes “In that case the posterior [model] probabilities are equal to the prior [model] probabilities; in other words the new data do nothing to help us decide between the hypotheses. This is the case of irrelevance.” (Jeffreys1973, p. 31; italics in original) and “...if the data were equally likely to occur on any of the hypotheses, they tell us nothing new with respect to their credibility, and we shall retain our previous opinion, whatever it was.” (Jeffreys 1961, p. 29) In contrast, the FBST ev suggest that the observation of predictively irrelevant data ought to change our previous opinion.

Problem 4: The FBST e v Suffers from the Jeffreys-Lindley Paradox

The Jeffreys-Lindley paradox (e.g.,Jeffreys 1935; Jeffreys 1937; Jeffreys1939; Lindley 1957; see also Bernardo1980; Cousins2017; Good 1980a; Good 1980b) refers to the fact that, as sample size increases indefinitely and the threshold for the p-value remains constant at any non-zero value (e.g., p < .005), we inevitably arrive at a conflict between p-values and Bayes factors, in the sense that the p-value would suggest that \( {\mathscr{H}}_{0} \) be rejected, whereas the Bayes factor would indicate that \( {\mathscr{H}}_{0} \) decisively outpredicts \( {\mathscr{H}}_{1} \). This conflict will arise regardless of the prior distribution on the test-relevant parameter under \( {\mathscr{H}}_{1} \) (under regularity conditions) and regardless of the p-value under consideration. As explained earlier, the FBST ev is an approximate p-value, and hence the conflict arises for the FBST ev as it does for the p-value.

For reasons that are unclear to us, the Jeffreys-Lindley paradox is sometimes been used to argue against the Bayes factor and motivate the search for a model comparison metric that does not ‘suffer’ from the paradox. For instance, de Bragança Pereira et al. (2008, p. 80) state: “However, whenever the posterior is absolutely continuous and the null hypothesis sharp, the use of Bayes Factors for significance testing is controversial” and then refer to Lindley (1957). In another article, de Bragança Pereira and Stern (1999, p. 109) state that the Jeffreys-Lindley paradox is due to the fact that the Bayes factor privileges the null hypothesis by giving it separate prior mass.

However, Lindley (1957) argued explicitly that the paradox revealed a shortcoming of the p-value, not of the Bayes factor:

Now in our example we have taken situations in which the significance level is fixed because, as explained above, we wish to see whether its interpretation as a measure of lack of conviction about the null hypothesis does mean the same in different circumstances. The Bayesian probability is all right, by the arguments above; and since we now see that it varies strikingly with n for fixed significance level, in an extreme case producing a result in direct conflict with the significance level, the degree of conviction is not even approximately the same in two situations with equal significance levels. 5% in today’s small sample does not mean the same as 5% in tomorrow’s large one. Lindley 1957, p. 189)

Similarly, throughout his work on Bayes factor hypothesis testing in the 1930s Harold Jeffreys argued that a rational measure of evidence against the null hypothesis cannot be based on a constant multiple of the standard error, as is the case for the p-value. For instance,

“A constant significance limit, in relation to the standard error, would however be equivalent to saying that the prior probability of a zero value varies with the number of observations, which is absurd; or, alternatively, that the chance of a real difference exceeding the standard error is the same no matter how small the standard error is made by increasing the number of observations.” (Jeffreys 1937, p. 259)

With respect to the question of prior model probabilities, note that the Bayes factor quantifies relative predictive performance of two rival models, and is thus independent of the prior beliefs about the hypotheses (e.g., Wrinch and Jeffreys1921):

$$ \underbrace{ \frac{P(\mathcal{H}_{1} ~|~ y)}{P(\mathcal{H}_{0} ~|~ y)}}_{\substack{\text{Posterior beliefs}\\ \text{about the models}} } = \underbrace{ \frac{P(\mathcal{H}_{1})}{P(\mathcal{H}_{0})}}_{\substack{\text{Prior beliefs}\\ \text{about the models}} } \times \underbrace{ \frac{p(y ~|~ \mathcal{H}_{1})}{p(y ~|~ \mathcal{H}_{0})}}_{\substack{\text{Bayes factor} } }. $$
(4)

One might argue that in order for the conditioning in the marginal likelihood \( p(y | {\mathscr{H}}_{i}) \) to be well-defined, each model \( {\mathscr{H}}_{i} \) must at least have some prior probability 𝜖 > 0. Footnote 3 But when the aim is to test \( {\mathscr{H}}_{0} \) it appears entirely reasonable for \( {\mathscr{H}}_{0} \) to have separate prior mass. Instead, it seems remarkable to assign \( {\mathscr{H}}_{0}: \delta =0 \) a prior probability of zero, deeming the hypothesis impossible from the outset, and then proceeding to test it anyway. Why then test δ = 0, and not, say, δ = 0.02144347729918..., δ = 0.010101010101..., or δ = e/30? The reason is that \( {\mathscr{H}}_{0}: \delta =0 \) is a value of special interest: it represents a simple model in which an effect is entirely absent, and for that ‘sampling noise-only’ model to be abandoned the data must offer evidence against it. The Laplacean practice of not assigning the point-null value any separate prior mass, i.e., estimating only, “expresses a violent prejudice against any general law, a totally unacceptable description of the scientific attitude.” (Jeffreys 1974, p. 1)

Admittedly there exist many problems in which the point-null hypothesis is not believable, not even as an approximation. For instance, there is usually no reason to assume that interrater agreement equals zero exactly, or that two politicians are exactly equally popular. Jeffreys labelled such scenarios problems of estimation. But with problems of testing, a specific value of the parameter stands out; the desire to assess that value (out of an infinity of other values that could be assessed) already suggests that its prior probability is not exactly zero.

At its core, however, the Jeffreys-Lindley paradox is sufficiently general that it does not even require a Bayesian mindset. Good (1980a) (in modern notation) explains it in terms of simple versus simple likelihood ratio tests, as follows:

Dr. Deborah Mayo raised the following question. How could one convince a very naive student, Simplissimus, that a given tail-area probability (P-value), say 1/100, is weaker evidence against the null hypothesis when the sample is larger? Although this fact is familiar in Bayesian statistics the question is how to argue it without (explicit) reference to Bayesian methods.

One can achieve this aim, without even referring to power functions, in the following manner.

Take a very concrete example, say the tossing of a coin, and count the number [s] of heads (“successes”) in [n] trials. Ask Simplissimus to specify any simple non-null hypothesis for the probability [𝜃] of a head. Suppose he gives you a value [𝜃 = 0.5 + 𝜖]. First compute a value of [n] so that a 𝜖 value of [s] approximately equal to [n(0.5 + 𝜖/7)] would imply a tail-area probability close to 1/100. Then point out that the fraction 0.5 + 𝜖/7 of successes is much closer to 0.5 than it is to 0.5 + 𝜖 and therefore must support the null hypothesis as against the specific rival hypothesis proposed by Simplissimus. Thus, for any specified simple non-null hypothesis, [n] can always be made so large that a specified tail-area probability supports the null hypothesis more than the rival one. This should convince Simplissimus, if he had been listening, that the larger is [n] the smaller the set S of simple non-null hypotheses that can receive support (as compared with [𝜃 = 0.5]) in virtue of a specified P-value. If the tail-area probability, for example 1/100, is held constant, the set S converges upon the point [𝜃 = 0.5] when [n] is made larger and larger.” (Good 1980a, pp. 307–308; italics in original)

For instance, assume Simplissimus specifies their simple non-null hypothesis as 𝜃 = 0.57 with 𝜖 = 0.07. Then our target value for the number of successes s equals n(0.5 + 0.07/7) = n × 0.51. So for a sample proportion of 0.51 we now seek n such that the two-sided tail area probability equals .01. We find that n = 16700—consisting of 8517 heads, for a sample proportion of s = 8517/16700 = 0.51, as stipulated—yields a tail area just below .01. But the sample proportion of 0.51 is much closer to the null hypothesis (i.e., 𝜃 = 0.50) than to the non-null hypothesis specified by Simplissimus (i.e., 𝜃 = 0.57).

Returning to an explicit Bayesian perspective, suppose the estimate of the test-relevant parameter is within one standard error from zero. This will provide some evidence in favor of \( {\mathscr{H}}_{0} \). Now assume that sample size increases indefinitely, but the estimate remains within one standard error from zero. As implied by Good’s scenario concerning Simplissimus, the range of parameter values under \( {\mathscr{H}}_{1} \) that are consistent with the observed data continually shrinks: with large sample size and an estimate within a standard error of the null value, parameter values far away from zero predict so poorly that they can be effectively excluded from consideration. For any sample size there will be a set of parameter values that are still in contention with the null value, but this set will shrink to zero. Of course, for any specific sample size it is possible to select with the maximum likelihood estimator and claim that the data support it over the null value; for instance, after seeing the data Simplissimus might argue that their non-null choice of 0.57 was overly optimistic, and that a choice of 0.51 would have been more apt. Of course, Good’s game could be played anew, and Simplissimus would be forced to select ever smaller values of 𝜃. In other words, Simplissimus is cherry-picking. In the Bayes factor formalism, such cherry-picking is counteracted by averaging predictive performance across the prior distribution; when sample size increases but the estimate remains within a constant multiple of the standard error from the null value, a growing proportion of the prior distribution under \( {\mathscr{H}}_{1} \) will start to predict poorly, driving down the average performance (cf. Jeffreys1937, pp. 250–251).

Thus, the prior distribution can be viewed as an automatic method to prevent cherry-picking, that is, to prevent the selection of those parameter values that the data happen to support. In the Bayes factor methodology, any prior distribution fulfils this purpose, and will therefore produce the Jeffreys-Lindley paradox. Instead, the FBST ev is based on an assessment of the posterior distribution, and therefore lacks the Bayesian correction for cherry-picking. As a result, the evidence against the null hypothesis is overstated; moreover, the FBST ev is inconsistent, meaning that the support for \( {\mathscr{H}}_{0} \) will not increase without bound if the data accumulate indefinitely and \( {\mathscr{H}}_{0} \) is the true data-generating model. The FBST ev avoids the Jeffreys-Lindley conflict between a Bayesian measure of evidence and the p-value, but this is not something that needs avoiding — quite the opposite, it is something to embrace.

In sum, to paraphrase Lindley, we claim that the degree of conviction is not even approximately the same in two situations with equal FBST ev s. An FBST ev of .05 in today’s small sample does not mean the same as an FBST ev of .05 in tomorrow’s large one.

Concluding Comments

The FBST ev provides a Bayesian hypothesis testing analogue of the frequentist p-value. The FBST ev is easy to use and it arguably offers several distinct Bayesian advantages (e.g., the result does not depend on the sampling plan). However, we believe that the FBST ev falls short on several counts. As detailed above, the FBST ev cannot quantify evidence in favor of \( {\mathscr{H}}_{0} \), it is susceptible to sampling to a foregone conclusion, it violates the principle of predictive irrelevance, and it suffers from the Jeffreys-Lindley paradox in the sense that its assessment of evidence is asymptotically equal to a constant multiple of the standard error. Footnote 4 These limitations are fundamental.

In conclusion, we agree with the statement from de Bragança Pereira et al. (2008) that the FBST ev is a “genuine Bayesian measure of evidence” in the sense that the FBST ev is a genuinely Bayesian procedure; the FBST ev is not, however, a genuine measure of evidence.