Introduction

Psychology has long aimed to discover fundamental laws of behavior that place the field on the same footing as “hard” sciences like physics and chemistry (Schultz and Schultz 2015). Perhaps the most visible and overarching set of such laws, developed in the early twentieth century to explain perceptual and attentional phenomena, are the Gestalt principles (Wertheimer 1923). These principles have had a tremendous impact on modern psychology (Kimchi 1992; Wagemans et al. 2012a; Wagemans et al. 2012b; Schultz and Schultz 2015). Although Gestalt psychology has faced some criticism over a lack of rigor (Wagemans et al. 2012a; Westheimer 1999; Schultz and Schultz 2015), investigators have successfully operationalized its concepts (Ren and Malik 2003), and it has influenced work in medicine (Bender 1938), computer vision (Desolneux et al. 2007), therapy (Zinker 1977), and design (Behrens 1998).

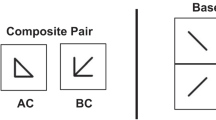
The Gestalt principles describe how visual elements are grouped and interpreted. For example, the Gestalt principle of closure asserts that human visual perception tends to “close the gap” by grouping elements that can jointly be interpreted as a complete figure or object. The principle thus provides a basis for predicting how viewers will parse, interpret, and attend to display fragments such as those in Fig. 1a, b. The linking of fragments such as those in Fig. 1a hampers access to the constituent fragments but facilitates rapid recognition of the completed shape (Rensink and Enns 1998).

Fig. 1
figure 1

a A circle formed from fragments via closure; b the same fragments but rearranged to prevent closure; c fragments from two circles which can be segmented using closure

Full size image

The Gestalt principles can support object perception by grouping together strongly interrelated features—features likely to belong to the same object, allowing features of that object to be processed apart from the features of other objects (e.g., Fig. 1c). Consistent with this role of grouping, the Gestalt principles have long been considered to have ecological validity in the natural world (Brunswik and Kamiya 1953). That is, natural image statistics have been shown to justify many of the Gestalt principles, including good continuation, proximity, and similarity (Elder and Goldberg 2002; Geisler et al. 2001; Krüger 1998; Sigman et al. 2001).

Gestaltism was in part a reaction to Structuralism (Titchener 1909; Wundt 1874), the perspective that association and grouping is a consequence of experience (Kimchi 1992). The Gestaltist tradition considered the principles to be innate and immutable. Although the role of learning was acknowledged, the atomic Gestalt principles were considered primary (Todorovic 2008). Even the aforementioned research examining natural image statistics has presumed that the principles either evolved to support ordinary perception or fortuitiously happen to have utility for perception.

However, ample evidence supports the notion that perceptual grouping can be modulated by experience. For example, figure-ground segregation is affected by object familiarity: a silhouette is more likely to be assigned as the figure if it suggests a common object (Peterson and Gibson 1994; Peterson 2019). And perceptual grouping can be altered with only a small amount of experience in a novel stimulus environment (Zemel et al. 2002). In these experiments, participants were asked to report whether two features in a display matched. Consistent with previous work (Duncan 1984), participants are faster to respond when the two features—notches on the ends of rectangles—belong to the same object (Fig. 2a) relative to when they belong to different objects (Fig. 2b). Although participants treat Fig. 2a, b as one rectangle occluding another, the two small squares in Fig. 2c are treated as distinct objects. However, following brief training on stimuli such as the zig-zag shape in Fig. 2d, the two small squares are treated as parts of the same object, relative to a control condition in which the training consisted of fragments as in Fig. 2e.

Fig. 2
figure 2

Examples of stimuli used in Zemel et al. (2002). a Same-object notches. b Different-object notches. c Same or different object? d “Single object” training. e “Double object” training

Full size image

If perceptual grouping can be modulated by experience, perhaps the Gestalt principles are not innate and immutable but rather are developmentally acquired as a consequence of interacting with the natural world. Ordinary perceptual experience might suffice to allow a learner to discover the Gestalt principles, given that the statistical structure of the environment is consistent with the Gestalt principles (Elder and Goldberg 2002; Geisler et al. 2001; Krüger 1998; Sigman et al. 2001). In the present work, we use deep learning methods to investigate necessary and sufficient conditions on this hypothesis.

We focus on closure (Fig. 1a, c). Closure is a particularly compelling illustration of the Gestalt perspective because fragments are assembled into a meaningful configuration and perceived as a unified whole (Wertheimer 1923). Closure has been studied experimentally via measures that include electrophysiology (Brodeur et al. 2006; Marini and Marzi 2016; Pitts et al. 2012), shape discrimination latency or accuracy (Elder and Zucker 1993; Kimchi 1994; Pomerantz et al. 1977; Ringach and Shapley 1996), and attentional capture (Kimchi et al. 2016; Kramer and Jacobson 1991).

Closure is a form of amodal completion, which corresponds to the naturalistic case of an occluded shape where the occluder is not visible. As a result of occlusion, some features are visible and others are missing. In contrast, modal completion refers to an occluder shape, camouflaged against the background, whose borders are delineated by illusory contours. Figure 3a illustrates both modal perception (the white occluding triangle in the foreground) and amodal perception (the black outline triangle, occluded by the white triangle).

Fig. 3
figure 3

a The Kanisza triangle, an illustration of modal (white triangle in the foreground defined by illusory contours) and amodal (occluded black outline triangle) perception; b fat and thin squares used as stimuli by Baker et al. (2018); c aligned fragments—the minimal visual cues required to induce closure; d a complete triangle; and edisordered fragments, which should be insufficient to induce closure

Full size image

Traditional cognitive models have been designed to explain modal completion (e.g., Grossberg 2014) or to provide a unified explanation for both modal and amodal completion (e.g., Kalar et al. 2010). We are not aware of cognitive models aimed specifically at amodal completion, though the topic has been of interest in the computer vision community (e.g., Oliver et al. 2016). These past models adopt the assumption of innateness in that they are built on specialized mechanisms designed to perform some type of filling in. We examine whether a deep neural net trained on natural images exhibits amodal closure effects naturally and as a consequence of its exposure to its environment.

The most closely related work to ours is an investigation of Baker, Kellman, Erlikhman, and Lu (2018) into whether neural nets “perceive” illusory contours (see also Ehrensperger et al. 2019). They studied modal perception in displays consisting of fragments that could be completed as either fat or thin rectangles (Fig. 3b, left and right images, respectively). Using AlexNet (Krizhevsky et al. 2012), a convolutional net pretrained for image classification, they removed the output layer which represents every object class and replaced it with a single unit that discriminates fat from thin rectangles. The weights from the penultimate layer to the output unit were trained on complete (non-illusory) fat and thin rectangles presented in varying sizes, aspect ratios, and positions in the image. This additional training extracts information available from the original model for fat versus thin classification. Following training, the network could readily discriminate fat and thin rectangles, whether real or illusory. Baker et al. then borrowed a method from the human behavioral literature, classification images (Gold et al. 2000), to infer features in the image that drive responses. Essentially, the method adds pixelwise luminance noise to images and then uses an averaging technique to identify the pixels that reliably modulate the probability of a given response. In humans, this method infers the illusory contours of the rectangles suggested by the stimuli in Fig. 3b. In contrast, Baker et al. found no evidence that pixels along illusory contours influence network classification decisions. They conclude that “deep convolutional networks do not perceive illusory contours” (the title of their article).

This work does not directly bear on ours because it focuses on modal perception; we focus on amodal. It also contrasts with our work in the modeling approach taken. Baker et al. adopt a traditional approach in which a model is trained to perform a cognitive task and is evaluated by comparing its behavior to humans’. Although this paradigm allows networks to be treated as a black box, one advantage of network experiments over human experiments is that representations can be observed directly. With humans, the classification image paradigm is a necessary and clever means of reverse-engineering representations; with models, we can inspect network internal representations directly.

Assessing Closure via Internal Representations

In our work, we examine the internal representations of a neural network trained on natural scenes and then tested on simple line drawings (Fig. 3c–e), similar to stimuli used in classic human studies (e.g., Elder and Zucker 1993; Kimchi et al. 2016; Kimchi 1992). We investigate whether aligned fragments (Fig. 3c) yield a representation closer to that of a complete triangle (Fig. 3d) than do disordered fragments (Fig. 3e). We perform critical control experiments to ensure that the similarity we observe is not due to abstract properties of the representations, not simple pixel overlap. Our approach is similar to fMRI analyses that use the subtraction method to determine the (dis)similarity of an experimental condition to a baseline condition.

Focusing on similarity of internal representations allows us to evaluate the Gestalt perception of shape without complicating assumptions of behavioral read out. We can definitively conclude that a neural network does not exhibit closure if we find that aligned fragments are no more similar to complete triangles than are disordered fragments. Similarity of representation is fundamental to generalization in any neural network. Consequently, without similarity of representation, no possible read-out mechanism could yield behavioral responses indicative of closure (or of functional filling in or grouping).

However, representational similarity consistent with closure does not ensure that the model will replicate quantitative behavioral patterns of human subjects in a particular experimental paradigm. To construct traditional cognitive models that simulate an individual performing a perceptual task, we require additional assumptions about response formation and initiation. It is our experience that these additional assumptions provide modelers with enough flexibility that it’s not terribly challenging to fit data, especially when only two conditions are being compared (closure vs. non-closure displays).

We return to the issue of data fitting later in the article. For now, we focus on obtaining evidence of a differential neural response to collections of fragments depending on whether or not their elements are consistent with a simple Gestalt figure. It is far from obvious that such a differential response will be obtained given that we are testing networks on synthetic images very unlike what they are trained on.

Methods

Our stimuli are images of complete, aligned, and disordered shapes, varying in a number of irrelevant dimensions to ensure robustness of effects we observe (Fig. 4a, b). The stimuli are fed into a pretrained deep convolutional neural net (hereafter, ConvNet) that maps the image to an m-dimensional internal representation, which we refer to as the embedding (Fig. 4c). We estimate the expected relative similarity of aligned and disordered fragments to the complete image using a closure measure, \(\bar {\mathcal {C}} \in [-1,+1]\), where a larger value indicates that the representation of the complete triangle is more like the representation of the aligned fragments than the representation of the disordered fragments (Fig. 4d).

Fig. 4
figure 4

Outline of the stimuli and methodology to test closure in pretrained neural networks. a The tested shapes varied in global orientation and the disordered images also varied in local orientation of their elements. b Examples of stimulus variation for the three experimental conditions (depicted in the rows), and for five properties (depicted in the columns). c Images are fed into a deep ConvNet trained to classify images, where there is one output neuron per class. In most of our simulations, the penultimate layer, with m units is used as a deep embedding of the input image. d Computing a closure measure, \(\bar {\mathcal {C}}\), where a larger value indicates that the representation of the complete triangle is more similar to the representation of the aligned fragments than to the representation of the disordered fragments. Note that \(\bar {\mathcal {C}}\) is an expectation over many image triples, not depicted in the equation

Full size image

Models

In our large simulation experiments, we leverage a state-of-the-art, pretrained image classification network, Inception, trained on the 1000-class ImageNet data set (Szegedy et al. 2016). Most images in this data set consist of one or multiple instances of a given object in the foreground with a naturalistic background (e.g., fruit on a plate on a tablecloth); some involve more complex scenes (e.g., a family at a dinner table eating ice cream for dessert); and some are at a larger spatial scale (e.g., sporting events, street scenes, underwater coral reefs). Input to this model is a 150 × 150 pixel color (RGB) image, and output a 1001-dimensional activation vector whose elements indicate the probability that the image contains the corresponding object class. (The ImageNet task involves 1000 classes; the additional class is a “none of the above” category.) Inception has been trained on 1.2 million images from the ImageNet data set (Deng et al. 2009) to assign each image to one of a thousand object classes. Standard data augmentation methods were used including: horizontal flips, feature-wise normalization, aspect ratio adjustment, shifts, and color distortion. In most simulations, we read out representations from the penultimate layer of the net, known as Mixed_7c, which consists of a 2048-dimensional flat vector. The penultimate layer of a deep net is commonly assumed to embody a semantic representation of the domain (visual objects). For example, in transfer learning and few-shot learning models, this layer is used for encoding novel object classes (e.g., Scott et al. 2018; Yosinski et al. 2014). One of our experiments reads out from earlier layers of the network.

We also explore a simple convolutional architecture consisting of three pairs of alternating convolutional and max pooling layers followed by a fully connected layer and a single output unit trained to discriminate between three classes, randomly chosen from ImageNet. A fully connected variant of the architecture replaces the convolutional and pooling blocks with fully connected layers. For these simple models, the embedding is the penultimate layer of the network.

For the sanity-check experiments (CD and BD models), we used the simple convolutional architecture with a single output trained to perform a binary discrimination (disordered versus complete and aligned for CD; black backgrounds versus white backgrounds for BD). The CD and BD models are trained on 75% of the 768 distinct complete-aligned-disordered triples; the remainder form a validation set, which reaches 100% accuracy and is used for evaluating the model. Five replications of the CD and BD models are trained with different random initial seeds to ensure reliability of results.

Further details on all models are provided in the Supple- mental Information.

Stimuli

We compare three critical conditions (Fig. 3c–e): complete triangles, triangle fragments with aligned corners, and fragments with disordered corners. Each stimulus is rendered in a 150 × 150 pixel image and the Euclidean distance between vertices is 116 pixels. Rather than testing models with more elaborate images (e.g., Fig. 3a, b), we chose to use the simplest images possible that could evoke closure effects, for two reasons. First, with more complex and naturalistic images, we found that it was difficult to control for various potential confounds (e.g., the amount of input activation, which affects the level of output activation). Second, the simplistic shapes we studied are quite unlike ImageNet images which are used for training the model. Any observed closure effects cannot be attributed to the possibility that the stimuli were part of a model’s training set.

We manipulated various properties of the stimuli, as depicted in Fig. 4. For all conditions, the stimuli varied in the global orientation of the triangle or fragments, which we refer to as 𝜃global, the background (light on dark versus dark on light), and the position of the object center in the image. For the disordered condition, we varied the orientation of the corners with respect the orientation of corners in the aligned fragment condition, which we refer to as 𝜃local. And finally, for the disordered and aligned conditions, we varied the length of the edges extending from the fragment corners, which we refer to as edge length.

Edge length is centrally related to the phenomenon of interest. Edge length, or equivalently, the gap between corners, influences the perception of closure, with smaller gaps leading to stronger closure (Elder and Zucker 1993; Jakel et al. 2016). The remaining properties—background color, local and global orientation, and image position—are manipulated to demonstrate invariance to these properties. If sensitivity to any of these properties is observed, one would be suspicious of the generality of results. Further, these properties must be varied in order to avoid a critical confound: the complete image (Fig. 3d) shares more pixel overlap with the aligned fragments (Fig. 3c) than with the disordered fragments (Fig. 3d). We therefore must ensure that any similarity of response between complete and aligned images is not due to pixel overlap. We accomplished this aim by always comparing the response to complete and fragment images that have different 𝜃global and different image positions. However, when comparing representations, we always match the images in background color because neural nets tend to show larger magnitude responses to brighter images.

The background color has two levels, black and white. The position is varied such that the stimuli could be centered on the middle of the image or offset by − 8 pixels from the center in both x and y directions, resulting in two distinct object locations. The global orientation is chosen from eight equally spaced values from 0∘ to 105∘. (Symmetries make additional angles unnecessary. A 120∘ triangle is identical to a 0∘ triangle.) The local orientation of the disordered corners is rotated from the aligned orientation by 72∘, 144∘, 216∘, or 288∘. The edge length is characterized by the length of an edge emanating from the vertex; we explored six lengths: 3, 8, 13, 18, 24, and 29 pixels, which corresponds to removal of between 95% and 50% of the side of a complete triangle to form an aligned image. These manipulations result in 2 × 2 × 8 = 32 complete triangles, 2 × 2 × 8 × 6 = 192 aligned fragments, and 2 × 2 × 8 × 6 × 4 = 768 disordered fragments, totalling 992 distinct stimulus images.

Quantitative Measure of Closure

We compare model internal representations via a quantitative measure of closure:

$$ \mathcal{C}_{i} = s(f(\boldsymbol{a}_{i}), f(\boldsymbol{c}_{i})) - s(f(\boldsymbol{d}_{i}), f(\boldsymbol{c}_{i})) , $$

where i is an index over matched image triples consisting of a complete triangle (ci), aligned fragments (ai), and disordered fragments (di); \(f(.) \in \mathbb {R}^{m}\) is the neural net mapping from an input image in \(\mathbb {R}^{150\times 150}\) to an m-dimensional embedding, and s(.,.) is a similarity function (Fig. 4). Consistent with activation dynamics in networks, we use a standard similarity measure, the cosine of the angle between the two vectors,Footnote 1

$$ s(\boldsymbol{x}, \boldsymbol{y}) = \frac{f(\boldsymbol{x}) f(\boldsymbol{y})^{\mathrm{T}} }{|f(\boldsymbol{x})|~ |f(\boldsymbol{y})|} . $$

The triples are selected such that ai and di are matched in 𝜃global position, both differ from ci in 𝜃global, and all three images have the same background color (black or white). These constraints ensure that there is no more pixel overlap (i.e., Euclidean distance in image space) between complete and aligned images than between complete and disordered images.

We test 768 triples by systematically pairing each of the 768 distinct disordered images with randomly selected aligned and complete images, subject to the constraints in the previous paragraph. Each of the 192 aligned images in the data set is repeated four times, and each of the 32 complete images is repeated 24 times.

We compute the mean closure across triples, \(\bar {\mathcal {C}} \in [-1,+\) 1]. This measure is + 1 when the complete image yields a representation identical to that of the aligned image and orthogonal to that of the disordered image. These conditions are an unambiguous indication of closure because the closure measure cannot distinguish the complete triangle from the aligned fragments. Mean closure \(\bar {\mathcal {C}}\) is 0 if the complete image is no more similar to the aligned than disordered images, contrary to what one would expect by the operation of Gestalt grouping processes that operate based on the alignment of fragments to construct a coherent percept similar to that of the complete triangle. Mean closure \(\bar {\mathcal {C}}\) may in principle be negative, but we do not observe these values in practice.

Although our measure of representational similarity is common in the deep learning literature, the neuroimaging literature has suggested other notions of similarity, e.g., canonical correlation analysis (Härdle and Simar 2007) and representational similarity analysis (Kriegeskorte et al. 2008). These measures are particularly useful for comparing signals of different dimensionality (e.g., brain-activity measurement and behavioral measurement).

Results

Sanity Check

We conduct a proof-of-concept experiment to show that we can distinguish models that produce closure from those that do not. To ensure that the models have these properties, we train simple ConvNets from scratch solely on our set of complete, aligned, and disordered images. The networks are trained to perform one of two binary classification tasks: closure discrimination (CD), which produces output 1 for complete and aligned images and output 0 for disordered images, and background discrimination (BD), which produces output 1 for black backgrounds and 0 for white backgrounds. The CD net will necessarily treat complete and aligned as more similar than complete and disordered, and should therefore produce a positive \(\bar {\mathcal {C}}\) score. In contrast, the BD net needs to extract color not shape information from images, and if it ignores shape altogether, it will yield a \(\bar {\mathcal {C}}\) score of 0. Our aim in this contrast is to present the pattern of results obtained in these two conditions as signatures of closure (for CD) and lack of closure (for BD).

Figure 5 presents the closure measure (\(\bar {\mathcal {C}}\)) for the CD and BD models, as a function of the edge length (Fig. 4b). The measure is computed using the activations in the penultimate layer of the net. The CD model, trained to treat aligned and closure as identical, produces linearly increasing closure as the edge length increases. The BD model, trained to focus on background color, produces a flat function of closure with edge length. Thus, when a model necessarily treats aligned and complete as identical, it produces a monotonic ramp with edge length. When a model has no constraint on how it treats the different types of images, it fails to produce closure at any edge length. We therefore use these curves as signatures of closure and failure to exhibit closure, respectively.

Fig. 5
figure 5

Sanity check experiment. CD networks, trained to discriminate complete and aligned from disordered images, show increasing closure with edge length. BD networks, trained to discriminate background color, show no closure. The simulation is replicated multiple times with different random initial seeds, and statistics of each value are depicted via a standard box-and-whisker diagram which shows the median value, first and third quartiles, as well as individual outlier points

Full size image

Given that the CD model was trained to treat aligned images as equivalent to complete triangles, regardless of edge length, it is surprising that internal representations of the model remain sensitive to edge length, as evidenced by increasing closure with edge length. Because the task requires determining how edges align in Gestalt shapes, it seems to be impossible for the CD model not to preserve information about edge length, albeit task irrelevant. This feature of the model is consistent with findings that human performance also varies as a continuous, monotonic function of the edge length, whether the behavioral measure of closure is discrimination threshold (Ringach and Shapeley 1996), search latency (Elder and Zucker 1993), or memory bias (Holmes 1968). Similarly, neurons in area 18 of the visual cortex of alert monkeys responding to illusory contours show an increased strength of response as the edge length increases (von der Heydt et al. 1984). These empirical results give further justification to treating the profile of the CD model in Fig. 5 as a signature of closure.

The Role of Natural Image Statistics

We now turn to the main focus of our modeling effort: to evaluate the hypothesis that natural image statistics, in conjunction with a convolutional net architecture, are necessary and sufficient to obtain closure in a neural net. We perform a series of simulations that provide converging evidence for this hypothesis. Each experiment compares a base model to a model that varies in a single aspect, either its architecture or training data. Our base model is a state-of-the-art pretrained image classification network, Inception (Szegedy et al. 2016).

Natural Images Versus White Noise

Figure 6a compares the base model to an identical architecture trained on white noise images. The base model and white-noise net share not only the same architecture but also training procedure and initial weight distribution; they differ only in that the white-noise net does not benefit from natural image statistics. Nonetheless, the network has the capacity to learn a training set of 1.2 million examples (same number as normal ImageNet training set) from 1001 randomly defined classes. Each pixel in these images is sampled from a uniform [− 1,+ 1] distribution, the range of values that the model has for natural images after preprocessing. The base model shows a closure effect: a monotonic increase in \(\bar {\mathcal {C}}\) with edge length, whereas the white-noise net obtains \(\bar {\mathcal {C}}=0\) regardless of edge length. Performing a two-way analysis of variance with stimulus triple as the between-condition random factor, we find a main effect of model (F(1,1188) = 2507,p < 0.0001), a main effect of edge length (F(5,1188) = 254,p < 0.0001), and an interaction (F(5,1188) = 254,p < 0.0001).

Fig. 6
figure 6

Exploration of how closure is influenced by various aspects of the neural net. We test Inception with 1000 classes (panels a–d) and a smaller ConvNet architecture with 3, 6, or 9 classes (panels e–h). Each graph compares a standard ConvNet architecture trained on natural images to an alternative: a comparing standard Inception to white-noise trained model, b comparing standard Inception to model trained on shuffled pixels, c comparing standard Inception to untrained model, d comparing standard Inception to model trained on shuffled labels, e comparing small ConvNet to white-noise trained model, f comparing small ConvNet to model trained on shuffled pixels, g comparing small ConvNet to untrained model, h comparing small ConvNet to model trained on shuffled labels

Full size image

Original Images Versus Shuffled Pixels

Training on white noise might be considered a weak comparison point because the low-order statistics (e.g., pairs of adjacent pixels) are quite different from those natural images. Consequently, we tested an input variant that looks quite similar to white noise to the human eye but matches pixelwise statistics of natural images: images whose pixels have been systematically shuffled between image locations. While these shuffled images contain the same information as natural images, the rearrangement of pixels not only prevents the human eye from detecting structure but also blocks the network from learning structure and regularities due to the local connectivity of the receptive fields. Nonetheless, large overparameterized neural networks like Inception have the capacity to learn the shuffled-pixel training set, although they will not generalize to new examples (Zhang et al. 2016).

Figure 6b shows that Inception trained on shuffled pixels does not obtain a closure effect. Performing a two-way analysis of variance, we find a main effect of model (F(1,888) = 1249.6,p < .0001), a main effect of edge length (F(5,888) = 253.3,p < .0001), and an interaction (F(5,888) = 126.7,p < .0001).

Trained Versus Untrained Networks

Our white-noise and shuffled-pixel experiments indicate that training on corrupted inputs prevents closure. Now we ask whether an untrained network naturally exhibits closure, which is then suppressed by training in the case of corrupted images.

Figure 6c compares our base model to the same model prior to training, with random initial weights. The untrained model exhibits a weaker closure effect as indicated by an interaction between condition and edge length (F(5, 1188) = 166.9,p < .0001). Averaging over edge lengths, the magnitude of the random-weight closure effect is nonzero (t(599) = 19.7,p < 0.0001), indicating that some amount of closure is attributable simply to the initial architecture and weights. This finding is not entirely surprising as researchers have noted the strong inductive bias that spatially local connectivity and convolutional operators impose on a model, making them effective as feature extractors with little or no data (Ulyanov et al. 2018; Zhang et al. 2020). In the Supplemental Information, we show that the amount of training required for the network to reach its peak \(\bar {\mathcal {C}}\) is fairly minimal, about 20 passes through the training set, about 1/6th of the training required for the network to reach its asymptotic classification performance.

Systematic Versus Shuffled Labels

We have argued that the statistics of natural image data are necessary to obtain robust closure, but we have thus far not explored what aspect of these statistics are crucial. Natural image data consist of {image, label} pairs, where there is both intrinsic structure in the images themselves—the type of structure typically discovered by unsupervised learning algorithms—and associative structure in the systematic mapping between images and labels. Associative structure is crucial in order for a network to generalize to new cases.

In Fig. 6d, we compare our base model with a version trained on shuffled labels, which removes the associative structure. Our model has the capacity to memorize the randomly shuffled labels, but of course it does not generalize. The shuffled-label model exhibits a weaker closure effect as indicated by an interaction between condition and edge length (F(5,1188) = 143.0,p < .0001). Averaging over edge lengths, the magnitude of the shuffled-label closure effect is nonzero (t(599) = 18.5,p < 0.0001), indicating that some amount of closure is attributable simply to intrinsic image structure. We conjecture that the network must extract this structure in order to compress information from the original 150 × 150 × 3 pixel input into the more compact 2048-dimensional embedding, which will both allow it to memorize idiosyncratic class labels and—as a side effect—discover regularities that support closure. By this argument, supervised training on true labels further boosts the network’s ability to extract structure meaningfully related to class identity. This structure allows the network to generalize to new images as well as to further support closure.

We chose to eliminate associative structure by shuffling labels, but an alternative approach might be to train an unsupervised architecture that uses only the input images, e.g., an autoencoder. We opted not to explore this alternative because label shuffling was a more direct and well-controlled manipulation; it allows us to reuse the base model architecture as is.

Replication on Simpler Architecture

To examine the robustness of the results we’ve presented thus far, we conducted a series of simulations with a smaller, simpler architecture. This architecture has three output classes, chosen randomly from the ImageNet data set, and three layers, each consisting of a convolutional mapping followed by max pooling. We train 8–10 networks with the same architecture and different weight initializations.

Figure 6e–h show closure results for the simple architecture that correspond to the results from the larger architecture in Fig. 6a–d. This simple architecture produces the same pattern of closure effects as the larger Inception model, suggesting that closure is robust to architecture. Closure also appears to be robust to stimulus image diversity: Inception is trained on images from 1000 distinct classes; the simple net is trained on images from only 3 classes. However, we have observed lower bounds on the required diversity: When we train either model on one example per class, closure is not obtained.

The Role of Convolutional Operators and Local Connectivity

The success of deep networks in vision is partially due to the adoption of some basic architectural features of the mammalian visual system, specifically, the assumptions of local connectivity and equivariance (Fukushima et al. 1983). Local connectivity in a topographic map indicates that a detector in one region of the visual field receives input only from its local neighborhood in the visual field. Equivariance indicates that when presented with the same local input, detectors in different parts of the topographic map respond similarly. These properties are attained in deep nets via convolutional architectures with weight constraints.

To evaluate the role of these architectural constraints, we compare a ConvNet with the generic alternative, a fully connected architecture (FCNet) with dense (non-local) connectivity and no built in equivariance. Because FCNets do not perform as well on complex vision tasks, we were unable to train an FCNet on the full ImageNet data set to achieve performance comparable to our baseline ConvNet. Without matching the two architectures on performance, any comparison confounds architecture and performance. Consequently, we trained small instances of both architectures on just three randomly selected classes from ImageNet, allowing us to match the ConvNet and FCNet on performance. We replicated this simulation 7 times for robustness.

Figure 7 compares the closure effect for ConvNets and FCNets. The penultimate layer of representation is used to assess closure for both architectures. While the ConvNet evidences closure, the FCNet does not. Taking this finding together with the fact that the untrained ConvNet exhibits some degree of closure (Fig. 6c and g), we infer that some aspect of the ConvNet structure facilitates the induction of closure.

Fig. 7
figure 7

Exploring closure on convolutional versus fully connected architectures. Only the convolutional net achieves a closure effect, as indicated by the nonzero slope of the edge length vs. closure function

Full size image

Levels of Representation and Closure

Thus far, we have investigated closure at the penultimate layer of a network, on the assumption that this representation would be the most abstract and therefore most likely to encode object shape. However, the deep Inception architecture we tested has 16 major layers, some of which involve multiple convolutional transformation and pooling operations. A priori, observing closure in early layers seems unlikely because the receptive fields of neurons in these layers have spatially constrained receptive fields, and closure requires the registration of Gestalt properties of the shapes. (Our test of closure will not false trigger based on local visual edge similarity because we compare images with distinct 𝜃global.)

In Fig. 8a, we show the closure effect for representations in the last eleven layers of Inception. “Mixed_7c” is the layer whose representation we have previously reported on. The graph legend is ordered top to bottom from shallowest to deepest layer. While all of the eleven layers show closure, closure is weaker for the shallower layers, labeled “Mixed_5”, than the deeper layers, labeled “Mixed_6” and “Mixed_7”. We do not have a definitive explanation for why the effect is slightly weaker in the deeper “Mixed_7” layers than in the shallower “Mixed_6” layers, though we suspect it is a consequence of training the model for classification. Classification does not require any information other than class labels to be transmitted through the network. Consequently, the net is not encouraged to preserve a shape representation through all layers, and the net possibly discards irrelevant shape information in order to optimize inter-class discrimination.

Fig. 8
figure 8

a The closure effect for the final eleven layers of the Inception architecture. Previously, we assessed closure only at layer “Mixed_7c”, but the lower layers also show varying degrees of closure. b The closure effect for each layer of the small ConvNet. Previous results have read out from the “fc_finale” layer. In both graphs, variability over images in the strength of closure is shown with uncertainty shading

Full size image

In Fig. 8b, we depict the closure curves for layers of the simple net, from the shallowest hidden layer, “conv2d_1”, to the penultimate layer, “fc_finale”. For this architecture, only the penultimate layer shows closure. In the penultimate layer, each neuron can respond to information anywhere in the visual field.

Consistent across Inception and the simple net, representations at the shallow layers are not sufficiently abstract to encode Gestalt closure. This follows from the local feedforward connectivity of the architectures and gradual collapsing (pooling) of information across increasingly wider receptive fields at deeper stages of both architectures.

Although filling in phenomena are observed in early stages of visual cortex (von der Heydt et al. 1984), it is possible that these effects are not causally related to Gestalt perception or are due to feedback projections, which our models lack. But our results are otherwise consistent with the view that lower stages of neural nets capture spatially local, low-order statistics whereas higher stages capture spatially global, high-order statistics (Bau et al. 2017; Mozer 1991).

Discussion

Our work follows a long tradition in computational modeling of using neural network models to explain qualitative aspects of human perception (e.g., Rumelhart et al. 1988; Mozer 1991). The strength of computational methods over behavioral or neuroscientific methods as an investigative tool is that models can be precisely manipulated to determine the specific model properties and inputs that are necessary and sufficient to explain a phenomenon. Further, we can do more than merely observe a model’s input-output behavior; we can probe its internal representations and directly determine what it is computing.

We began with the conjecture that Gestalt laws need not be considered as primitive assumptions underlying perception, but rather, that the laws themselves may arise from a more fundamental principle: adaptation to statistics of the environment. We sought support for this conjecture through the detailed study of a key Gestalt phenomenon, closure. Using a state-of-the-art deep neural network model that was pretrained to classify images, we showed that in the model:

  • Closure depends on natural image statistics. Closure is obtained for large neural networks trained to classify objects, and even for a smaller net trained to discriminate only a few object classes, but it is not obtained when a net is trained on white noise images or shuffled-pixel images. While shuffled-pixels have the same statistics as natural images, networks with local receptive fields are unable to extract spatially local structure due to the fact that the pixel neighborhood has been randomly dispersed in a shuffled image.

  • Closure depends on learning to categorize the world in a meaningful way. Networks trained to associate images with their correct categorical label produce much larger closure effects than networks trained to associate images with random labels. In the former case, the labels offer a clue about what features should be learned to systematically discriminate categories (Lupyan 2012). In the latter case, the labels misdirect the net to discover features that, by chance, happen to be present in a random collection of images that were assigned the same label.

  • Closure depends on the architecture of convolutional networks. The extraction of image regularities is facilitated by two properties of ConvNets: spatially local receptive fields and equivariance. Fully connected networks, which lack these forms of inductive bias, do not obtain closure. The inductive biases are sufficiently strong that even an untrained ConvNet obtains a weak degree of closure, indicative of a synergy between innate structures and experience.

Our simulation experiments suggest that these three dependencies are necessary and sufficient conditions for a computational system to produce closure. The system need not be prewired to perform closure, nor does it need to learn closure per se. Rather, closure emerges as a synergy between architectural structures and learning to represent real-world objects and categories.

One limitation of our work is that our model does not “produce closure” per se. That is, we have not fleshed out a full-fledged cognitive model that can replicate human behavioral responses in a particular experimental paradigm. Nonetheless, the model—in producing readily discriminable representations for aligned versus disordered fragments—is consistent with neural signatures of closure identified in electrophysiological studies (Brodeur et al. 2006; Marini and Marzi 2016; Pitts et al. 2012). Further, it is not much of a stretch to imagine read-out mechanisms that would explain behavioral data. For example, Elder and Zucker (1993) studied closure in a visual-search task, finding that latency to detect a target formed from aligned fragments is faster than one formed from non-aligned fragments, and the more of the edges that are present, the faster detection is. To account for such data, one might make two assumptions. First, add an output unit to the model that detects a complete triangle (much as Baker et al. 2018, added output units for fat and thin squares). Second, allow this output to drive a drift-diffusion process (Ratcliff and McKoon 2008) that guides attention or initiates a response. More activation of the complete triangle unit will lead to shorter latencies. Due to the similarity structure in the model, aligned fragments will yield shorter latencies than disordered fragments, and as the edge length of the aligned fragments is increased, latencies will drop, consistent with the behavioral data.

Although our argument has been focused specifically on closure, the same argument should apply to other Gestalt laws that have underpinnings in natural scene statistics (Brunswik and Kamiya 1953; 2001; Elder and Goldberg 2002; Geisler et al. 2001; Krüger 1998; Sigman et al. 2001). In support of this proposition are simulations conducted by Amanatiadis et al. (2018) contemporaneously with ours. Their work is a nice complement to ours in that they aim for a breadth of coverage, whereas we aimed for depth. They examined pretrained ConvNets to evaluate their sensitivity to a range of Gestalt laws—not only closure but also proximity, continuation, similarity, figure-ground, and symmetry. They find that the ConvNets exhibit behavior consistent with a sensitivity to all these Gestalt laws. They use classification accuracy of a perturbed image as a measure of Gestalt law sensitivity rather than examining internal representations. This measure has limitations (e.g., they cannot test novel shapes as we have), and their experiments lack some important control experiments that we have done (e.g., comparing to disordered fragments, and failing to rule out pixel overlap as an explanation). Nonetheless, both their work and ours suggest that the Gestalt laws can emerge via adaptation to the statistical structure of the environment. Given structure in the environment and the existence of powerful learning architectures and mechanisms, one need not consider the Gestalt laws as primitives.

In the late 1980s, the Connectionist movement focused on the role of learning in perception and cognition, demonstrating that abilities that one might previously have thought to have been built into a cognitive system could emerge as a consequence of simple learning rules. Most connectionist architectures were fairly generic—typically fully connected neural networks with one hidden layer. While such architectures showed promise, it was far from clear that these architectures could scale up to human-level cognitive abilities. Modern deep learning architectures have clearly scaled in a manner most did not imagine in the 1980s. Large language models show subtle linguistic skills and can express surprisingly broad knowledge about the world (Raffel et al. 2019); large vision models arguably match or surpass human abilities to label images (Xie et al. 2019). Our work suggests that in the modern era, the combination of a sophisticated neural architecture (e.g., a ConvNet) and scaling the size of models may be sufficient to broaden the range of cognitive phenomena that are emergent from more basic principles of learning and adaptation. Our work bridges the gap between analyses indicating that perceptual mechanisms are consistent with natural scene statistics (Burge et al. 2010; Brunswik and Kamiya 1953) and claims that statistical learning is essential to understanding human information processing (Frost et al. 2019). The synthesis leads to a view of the human perceptual system that is even more elegant than the Gestaltists imagined: a single principle—adaptation to the statistical structure of the environment—might suffice as fundamental.