Abstract
There is a growing body of evidence that the human brain may be organized according to principles of predictive processing. An important conjecture in neuroscience is that a brain organized in this way can effectively and efficiently approximate Bayesian inferences. Given that many forms of cognition seem to be well characterized as a form of Bayesian inference, this conjecture has great import for cognitive science. It suggests that predictive processing may provide a neurally plausible account of how forms of cognition that are modeled as Bayesian inference may be physically implemented in the brain. Yet, as we show in this paper, the jury is still out on whether or not the conjecture is really true. Specifically, we demonstrate that each key subcomputation invoked in predictive processing potentially hides a computationally intractable problem. We discuss the implications of these sobering results for the predictive processing account and propose a way to move forward.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The predictive processing account is becoming increasingly popular as an account of perceptual, behavioral, and neural phenomena in cognitive neuroscience. According to this account, the brain seeks to predict its sensory inputs using a hierarchy of probabilistic generative models (Clark 2013, 2016; Hohwy 2013). The account integrates ideas from different traditions, including (1) classical views on perception as an inferential process combining sensory input and prior knowledge (von Helmholtz 1867; Barlow 1961); (2) the view of the brain as encoding and processing uncertain information using Bayesian mechanisms (Dayan et al. 1995; Knill and Pouget 2004); (3) the view of the brain as a series of hierarchical generative (inverse) models (Friston 2008); and (4) the free energy principle in theoretical biology (Friston 2010). In addition, the account draws inspiration from computer science (e.g., the predictive coding approach in signal processing Vaseghi 2000) and philosophy (e.g., the work by Kant 1999/1787 on cognition and perception). While originally rooted in visual perception research (Lee and Mumford 2003; Rao and Ballard 1999; Hohwy et al. 2008), it has been successfully extended to combine action and perception in so-called active inference theories (Brown et al. 2011; Adams et al. 2013), in computational psychiatry (Edwards et al. 2012; Horga et al. 2014; Sterzer et al. 2018; Van de Cruys et al. 2014), to explain action understanding (Kilner et al. 2007a, b; Den Ouden et al. 2012), as well as explaining phenomena as dreaming (Hobson and Friston 2012), hallucinations (Brown and Friston 2012), conscious presence (Seth et al. 2011; Seth 2015), self-awareness (Seth and Tsakiris 2018), synesthesia (Rothen et al. 2018), and psychedelics (Pink-Hashkes et al. 2017).
Some of the popularity of the predictive processing account seems to hinge on its presumed ability to give a neurally plausible and computationally feasible explanation of how Bayesian inferences can be efficiently implemented in brains. It is well known that Bayesian inference is in general an intractable problem (Cooper 1990; Shimony 1994) that remains intractable even when approximated (Dagum and Luby 1993; Abdelbar and Hedetniemi 1998) and so Knill and Pouget note that:
… unconstrained Bayesian inference is not a viable solution for computation in the brain. (Knill and Pouget 2004, p. 758)
Both Clark (2016, p. 298) and Thornton (2016, p. 6) have argued that the predictive processing account demands approximate Bayesian inferences to be computationally tractable. However, the abovementioned intractability results imply that approximate inference may be necessary, but are definitely not sufficient, to ensure tractability of Bayesian computations (Kwisthout 2018; Donselaar 2018). That is, more is needed than an appeal to approximation as cure for the ailment of Bayesian intractability (Kwisthout et al. 2011).
It is claimed, however, that predictive processing allows for tractability. As Andy Clark (2013) has put it:
It is thus a major virtue of the hierarchical predictive coding account that it effectively implements a computationally tractable version of the so-called Bayesian Brain Hypothesis. (Clark 2013, p. 191)
[The] predictive processing story, if correct, would rather directly underwrite the claim that the nervous system approximates, using tractable computational strategies, a genuine version of Bayesian inference. (Clark 2013, p. 189)
If Clark is right, then the hypothesis that brains are organized according to the principles of predictive processing is not only of great importance for neuroscience—as a hypothesis about the modus operandi of the human brain—but also for contemporary cognitive science. After all, it would directly suggest a candidate explanation of how the probabilistic computations postulated by the many Bayesian models in cognitive science (Chater et al. 2006; Griffiths et al. 2008, 2010) may be realistically implemented in the human brain. The promise that the predictive processing framework would yield a tractable way to perform (approximate) Bayesian inference seems all the more important in light of the fact that Bayesian models of cognition have been plagued by complaints about their apparent computational intractability (e.g., Gigerenzer 2008; Kwisthout et al. 2011). Having a candidate neural story on offer about how Bayesian inference may yet be tractable for human brains would, of course, further strengthen the already strong case for the Bayesian approach in cognitive science (see, e.g., Chater et al. 2006; Tenenbaum2011).
In this paper, we set out to analyze to what extent the framework already makes true on this promise, or otherwise could in the future. The approach that we take is as follows. We formally model each required subcomputation postulated by the predictive processing framework for the forward (bottom–up) and backward (top–down) chains of processing. Our models characterize these computations at Marr’s (1982) computational level, i.e., in terms of the basic input–output transformations that they are assumed to perform. This means that our analyses will be independent of the nature of the algorithmic- or implementational-level processes that the brain may use to perform these transformations (van Rooij 2008; van Rooij et al. 2019). We distinguish three key transformations: prediction, error computation, and explaining away. We will show that, unless the causal models underlying these subcomputations are somehow constrained, both making predictions and explaining away prediction errors are in and of itself intractable to compute (e.g., NP-hard), whether exactly or approximately.Footnote 1
The remainder of this paper is organized as follows.Footnote 2 First, we explain the basic ideas of the predictive processing framework in more detail. After providing the necessary preliminaries, definitions, and notational conventions in “Preliminaries and Notation”, we present our formal models of its postulated subprocesses in “Computational Modeling”. We then give an overview of the computational (in)tractability results for these formal models (“Results”), and discuss the implications of our findings for the presumed tractability of a predictive processing account of the Bayesian brain (“Discussion”).
The Predictive Processing Framework
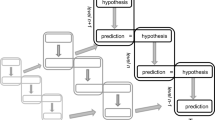
In the predictive processing framework, it is assumed that the brain continuously tries to predict its sensory inputs on the basis of a hierarchy of hypotheses about the world (Friston 2008; Clark 2016). The predictions are formed by the so-called backward chain (top–down processing), in which higher order hypotheses (stemming from generative models) are transformed to lower order hypotheses and eventually predictions about sensory inputs. This form of top–down processing augments the “forward chain” (bottom–up processing) in which sensory inputs are transformed to increasingly more abstract hypotheses. Figure 1 presents a schematic illustration.
A schematic depiction of the way in which the backward chain (left) and the forward chain (right) in the hierarchical predictive coding framework interact. The gray arrows denote the causal direction of the generative models, relating hypotheses about causes to predictions about effects. The black arrows are labeled by the key computational transformations that we analyze in this paper: Prediction, Error-Computation, and Explaining Away. See the text for more details
By comparing predicted observations at each level n in this hierarchy with the actual observations at the same level n in this hierarchy, the system can determine the extent to which its predicted observations in the backward chain match the observations arising from the forward chain, and update its hypotheses about the world accordingly. An example of the explanatory uses of the predictive processing framework is its explanation of binocular rivalry in vision (Hohwy et al. 2008; Weilnhammer et al. 2017). When an image of a house is presented to the left eye, and an image of a face to the right eye, the subjective experience of the images alternates between a face and a house, rather than some combination of the separate stimuli. As we are not familiar with blended house-faces, such a combination would have a low prior probability, hence either a house or a face is predicted to be observed. The actual observation, however, triggers a prediction error: a mismatch between what was predicted (e.g., a face), and what was observed (both a house and a face). This mismatch then leads to an updated hypothesis; taking prior probabilities as well as the prediction error into account, the hypothesis will then shift toward a house, rather than a combination of a face and a house.
In predictive processing, three separate processes are assumed to operate on the generative models: viz., prediction (computing the observations that are predicted at level n, given the causal model at level n and the predictions at level n + 1 in the backward chain); error computation (computing the divergence between the predicted observations at level n in the backward chain and the actual observations at level n in the forward chain); and explaining away prediction errors. The latter process can be further distinguished into hypothesis updating (updating hypotheses at level n of the forward chain based on the prediction error between predicted and actual observations at level n); model revision (revising the parameters or structure of the generative model); active inference (actively intervening in the world, bringing its actual state closer to the predicted state); or adding observations (gathering information on the state of contextual cues or other hidden variables in the generative model).
Although several task- or domain-specific computational models have been developed that apply the ideas underlying the predictive processing framework to the analysis of particular perceptual and neural processes (e.g., Grush 2004; Jehee and Ballard 2009; Rao and Ballard 1999), such specific models cannot directly be used to address our research question: “Is Bayesian inference tractable when implemented in a predictive processing architecture?” To address this question, we need instead generic computational models, i.e., models that are general enough to be applicable, in principle, to any cognitive domain. In particular, these models should allow for the representation of structured information (Griffiths et al. 2010). We propose such generic models in “Computational Modeling.” We now first provide for the necessary preliminaries.
Preliminaries and Notation
In this section, we introduce mathematical concepts and notation that we use throughout. To start, a causal Bayesian network \(\mathcal {B} = (\mathbf {G}_{\mathcal {B}}, \text {Pr}_{\mathcal {B}})\) is a graphical structure that models a set of stochastic variables, the conditional independences among these variables, and a joint probability distribution over these variables (Pearl 1988). \(\mathcal {B}\) includes a directed acyclic graph \(\mathbf {G}_{\mathcal {B}}=(\mathbf {V}, \mathbf {A})\), modeling the variables and conditional independences in the network, and a set of conditional probability tables (CPTs) \(\text {Pr}_{\mathcal {B}}\) capturing the stochastic dependences between the variables. The network models a joint probability distribution \(\text {Pr}({\mathbf {V}}) = {\prod }_{i=1}^{n} \text {Pr}({V_{i}}|{\pi (V_{i})})\) over its variables, where π(Vi) denotes the parents of Vi in \(\mathbf {G}_{\mathcal {B}}\) (Kiiveri et al. 1984). The arcs have a causal interpretation; the semantics of which is given by the do-calculus (Pearl 2000). By convention, we use uppercase letters to denote individual nodes in the network, uppercase bold letters to denote sets of nodes, lowercase letters to denote value assignments to nodes, and lowercase bold letters to denote joint value assignments to sets of nodes. We use the notation Ω(Vi) to denote the set of values that Vi can take. Likewise, Ω(V) denotes the set of joint value assignments to the set of variables V. For brevity and readability, we often omit the set of variables over which a probability distribution is defined if it is clear from the context.
Predictive processing is often construed as using a hierarchy of Bayesian generative models, where posterior probabilities on one level of the hierarchy provide priors for its subordinate level (e.g., Kilner et al. 2007b; Lee and Mumford 2003; Rao and Ballard 1999). Consistent with our earlier work (Kwisthout et al. 2017), we propose a general computational model where each level of the hierarchy can be seen (for the sake of computational analysis) as a separate causal Bayesian network \(\mathcal {B}_{L}\), where the variables are partitioned into a set of hypothesis variables Hyp, a set of prediction variables Pred, and a set of intermediate variables Int, describing contextual dependences and (possibly complicated) structural dependences between hypotheses and predictions. We assume that all variables in Hyp are source variables, all variables in Pred are sink variables, and that the Pred variables in \(\mathcal {B}_{L}\) are identified with the Hyp variables in \(\mathcal {B}_{L+1}\) for all levels of the hierarchy save the lowest one. We distinguish between the prior probability of a set of variables (such as Hyp) in the network, which we assume is stable over time, and the current inferred distribution over that set. For example, given that we identify the Pred variables in \(\mathcal {B}_{L}\) with the Hyp variables in \(\mathcal {B}_{L+1}\), any inferred probability distribution for Pred in \(\mathcal {B}_{L}\) is “copied” to Hyp variables in \(\mathcal {B}_{L+1}\), independent of the prior distribution over Hyp. Technically, we establish this by means of so-called virtual evidence (Bilmes 2004).
As predictive processing is claimed to be a unifying mechanism describing all cortical processes (Clark 2013), we do not impose additional a priori constraints on the structure of the network or the nature of the probability distributions that describe the stochastic relationships (Griffiths et al. 2010). Motivated by the assumption that global prediction errors are minimized by local minimization (Kilner et al. 2007b), we will focus on the computations in a single level of the network. Figure 2 gives an illustrative example of the hierarchy and the constituting causal Bayesian networks.
The Kullback–Leibler (KL) divergence (or relative entropy) is a measure of how much two probability distributions diverge from each other, or how well one distribution approximates another one (Kullback and Leibler 1951). In particular in predictive processing, it is used to represent the size of the prediction error at a particular level of the hierarchy. The KL divergence between Pr(Obs) and Pr(Pred), expressed in bits, is defined as
As all logarithms have base 2 in this paper, we will omit the base in the remainder for brevity. Conform the definition of the KL divergence, we will interpret the term 0log 0 as 0 when appearing in this formula, as \(\lim _{x \to 0} x \log x = 0\); similarly, any term 0log 0/0 will be interpreted as 0. The KL divergence is undefined if for any p, PrPred(p) = 0 while PrObs(p)≠ 0. In the remainder of this paper, to improve readability, we abbreviate DKL(Pr(Obs)∥Pr(Pred)) to simply DKL when the divergence is computed between Pr(Obs) and Pr(Pred); we sometimes include brackets DKL[ψ] to refer to the divergence under some particular value assignment, parameter setting, or observation ψ.
Note that the size of the prediction error is not to be confused with the prediction error itself. We define the prediction error between observation and prediction as the difference between the two probability distributions Pr(Obs) and Pr(Pred) defined over the set of variables Pred. More formally, when two distributions Pr, Pr′ are defined over a set of variables P, we define the prediction error \(\delta _{(\text {Pr},\text {Pr}^{\prime })}\) as δ(p ∈Ω(P)) = Pr(p) −Pr′(p). Figure 3 gives an example of two probability distributions Pr(Pred) and Pr(Obs) and the prediction error δ(Obs,Pred) between Pr(Pred) and Pr(Obs). Note that DKL = 0 iff. ∀p∈Ω(Pred)δ(p) = 0, that is, the size of the prediction error is 0 if and only if the two distributions are identical.
The Hamming distance dH(p, p′) is a measure of how two joint value assignments p and p′ to a set of variables P diverge from each other; it simply adds up the number of values in the joint value assignment where the two joint value assignments disagree (Hamming 1950). It can be seen as the size of the prediction error when predictions and observations are defined as joint value assignments, rather than distributions. For ease of exposition, in the remainder, we abbreviate dH(pObs, pPred) to dH when the distance between predicted and observed joint value assignments to Pred is computed.
Again, also in this formalization, the size of the prediction error is not to be confused with the prediction error itself. We define the prediction error d(p, p′) as a difference function such that for all paired elements (p, p′) of the joint value assignments p and p′ to the prediction variables Pred, d(p, p′) = nil if p = p′ and d(p, p′) = p if p≠p′; here, nil is a special blank symbol. Note that the prediction error dH = 0 if and only if the prediction error is vacuous.
Computational Modeling
The hierarchy of coupled subcomputations that we sketched above and in Fig. 1 can be seen as a scheme for candidate algorithmic level explanations of how perceptual and cognitive inferences—often well-captured by Bayesian models situated at the computational level of Marr (1982) and presumably living higher up in such hierarchies—could be computed by human brains. For such an algorithm to be tractable, all of its subcomputations need to be tractable. Here, we present models of the three subcomputations prediction, error computation, and explaining away also situated at Marr’s computational level. That is, the models merely characterize the nature of the transformation the subcomputations achieve while not committing to any further hypotheses of how these subcomputations are again further subdivided in sub-subcomputations.
Before presenting our models, we note that it is difficult to settle on a single candidate computational-level model per subcomputation, because several different—sometimes mutually inconsistent—interpretations of the predictive processing framework can be found in the literature (e.g., Friston 2002, 2005; Hohwy et al. 2008; Kilner et al. 2007b; Lee and Mumford 2003; Knill and Pouget 2004). The most prominent aspects in which interpretations diverge are in the conceptualization of predictions and of hypothesis revision. Some authors interpret the inference steps as updating one’s probability distribution over candidate hypotheses (Lee and Mumford 2003, p. 1437), and others interpret them as fixating one’s belief to the most probable ones (Kilner et al. 2007b, p. 161). These two notions correspond to two different computational problems in Bayesian networks, viz., the problem of computing a posterior probability distribution and the problem of computing the mode of a posterior probability distribution (i.e., the joint value assignment with the highest posterior probability). Following conventions in the machine learning literature, we apply the suffix SUM to the distribution updating variants, and MAX to the belief fixation model variants.
When explaining away prediction errors by hypothesis updating (that is, adapting our current best explanation of the causes of the observations we make, contrasted to, e.g., active inference), there are again two possible conceptualizations in both the SUM and MAX variants. In the belief updating conceptualization, the current hypothesis distribution (SUM) or current belief (MAX) is updated by computing the posterior hypothesis distribution given the observed distribution (SUM) or the hypothesis that has the highest posterior probability given the evidence (MAX); in either situation, both the likelihood and the prior probability of the hypotheses are taken into account (Friston 2002, p. 13). In contrast, in the belief revision conceptualization, the current hypothesis distribution (SUM) or current belief (MAX) is revised such that the prediction error is minimized, that is, replacing the current hypothesis distribution (SUM) or current belief (MAX) by one that has a higher likelihood given the observations (Kilner et al. 2007b, p. 161). Note that the crucial distinction between both conceptualizations is that, in the belief update conceptualization, the priors of the hypotheses are taken into consideration while they are ignored in the belief revision conceptualization. The rationale behind this is that in belief updating the aim is to globally reduce prediction error over several levels of the hierarchy, while in belief revision the aim is to minimize local prediction error within one level of the hierarchy.
In addition to hypothesis updating, there are several other mechanisms for explaining away prediction error: specifically active inference (intervention (i.e., acting) in the world in order to minimize prediction error) (Brown et al. 2011), sampling the environment (i.e., adding observations) to lower uncertainty (Friston et al. 2012), and revising the generative model to accommodate future predictions (Friston et al. 2012). We will formalize all these computational models, in both SUM and MAX variants, in the definitions below and summarize them in Table 1. A conceptual overview of hypothesis updating, model revision, intervention, and adding observations is given in Fig. 4.
Explaining away prediction error by means of updating hypotheses, revision of the generative model, adding observations, or intervening on variables. Figure adapted from Kwisthout et al. (2017)
SUM Variants
The SUM variant of prediction is defined as the computation of the marginal probability distribution \(\text {Pr}({\text {Pred}}) = {\sum }_{\mathbf {h}}\text {Pr}({\text {Pred}}|{\text {Hyp} = \mathbf {h}})\times \text {Pr}({\text {Hyp} = \mathbf {h}})\) over the prediction nodes Pred, given virtual evidence Pr(Hyp). Note that this computation is non-trivial as it involves integrating the current distribution over the hypothesis nodes Hyp with the likelihood of the predictions given the hypotheses, where the latter may represent complex dependences mediated by intermediate variables.
Prediction (SUM)
Instance: A causal Bayesian network \(\mathcal {B}_{L}\) with designated variable subsets Pred and Hyp, probability distribution Pr(Hyp) over Hyp.
Output:\(\text {Pr}({\text {Pred}}) = {\sum }_{\mathbf {h}}\text {Pr}({\text {Pred}}|{\text {Hyp} = \mathbf {h}})\times \text {Pr}({\text {Hyp} = \mathbf {h}})\), i.e., the updated marginal probability distribution over the prediction nodes Pred.
The computation of the prediction error is defined in the SUM-variant as the computation of the difference between the observed distribution Pr(Obs) and predicted distribution Pr(Pred) over the set of prediction variables Pred. The computation of the size of the prediction error is defined as the computation of the KL divergence between these distributions.
Error-Computation (SUM)
Instance: A set of variables Pred and two probability distributions Pr(Obs) and Pr(Pred) over Pred.
Output: The prediction error δ(Obs, Pred).
Error-Size-Computation (SUM)
Instance: As in Error-Computation (SUM).
Output: The size of the prediction error DKL.
Explaining away prediction errors can be accomplished by updating hypotheses, by revision of the generative model, by adding observations to previously unobserved intermediate variables, or by intervening on the state of intermediate variables. For Hypothesis-Updating we discriminate between Belief-Updating (formalized in the SUM variant as recomputing the hypothesis distribution via Jeffrey’s rule of conditioning Jeffrey 1965) and Belief- Revision (revising the current probability distribution over the hypothesis variables such that prediction error is minimized). Note that the input of these problem instances is the prediction and the prediction error (not the observation; also, not the size of the prediction error but the actual prediction error); still, this does not underdefine the problem as the observation can be inferred from prediction and prediction error as the prediction error is defined as the difference between prediction and observation.
Belief-Updating (SUM)
Instance: A causal Bayesian network \(\mathcal {B}_{L}\) with designated variable subsets Hyp and Pred, a probability distribution Pr(Pred) over Pred, and a prediction error δ(Obs,Pred).
Output: The posterior probability distribution \({\sum }_{\mathbf {p}}\text {Pr}({\text {Hyp}}|{\text {Pred} = \mathbf {p}})\times \text {Pr}_{\text {Obs}}(\text {Pred} = \mathbf {p})\).
Belief-Revision (SUM)
Instance: As in Belief-Updating.
Output: A (revised) prior probability distribution \(\text {Pr}_{(\text {Hyp})^{\prime }}\) over Hyp such that \(D_{\text {KL}}{[\text {Hyp}^{\prime }]}\) is minimal.
In the Model-Revision problem definition, we restrict the “degrees of freedom” in revision to a particular set of parameter probabilities that are subject to revision. We elaborate more on the question of what constitutes model revision in “Model Revision Revisited”.
Model-Revision (SUM)
Instance: As in Belief-Updating; furthermore, a set \(\mathbf {P}\subset \text {Pr}_{\mathcal {B}_{L}}\) of parameter probabilities.
Output: A combination of values 𝜃 to P such that DKL[𝜃] is minimal.
Gathering additional observations for unobserved (intermediate) variables and intervening on the values of these variables can be seen as computational-level models of sampling the world (Friston et al. 2012), respectively, active inference (Brown et al. 2011). We assume here that we cannot directly intervene on the values of the hypotheses, only indirectly via intermediate variables (hence, A is a subset of Int, not of Hyp). For example, we can reduce proprioceptive prediction errors by sending motor commands that will cause our arm to move; the intervention here is on the motor commands, not on the actual position of our arm.
Add-Observations (SUM)
Instance: As in Belief-Updating; furthermore, a designated and yet unobserved subset O ⊆Int.
Output: An observation o for the variables in O such that DKL[o] is minimal.
Intervention (SUM)
Instance: As in Belief-Updating; furthermore, a designated subset A ⊆Int.
Output: An intervention a to the variables in A such that DKL[a] is minimal.
MAX Variants
The MAX variant of prediction is defined as the computation of the most probable joint value assignment to the prediction nodes, that is, the joint value assignment that has maximum posterior probability given the joint value assignment to the hypothesis nodes. Again, this computation is non-trivial as it requires maximization over candidate joint value assignments without direct access to the probability of these assignments.
Prediction (MAX)
Instance: A causal Bayesian network \(\mathcal {B}_{L}\) with designated variable subsets Pred and Hyp, a joint value assignment h to Hyp.
Output: argmaxpPr(Pred = p|Hyp = h), i.e., the most probable joint value assignment p to Pred, given Hyp = h.
The computation of the prediction error is defined in the MAX-variant as the computation of the difference between the observed and predicted joint value assignment to the prediction variables Pred. The computation of the size of the prediction error is defined as the computation of the Hamming distance between these joint value assignments.
Error-Computation (MAX)
Instance: A set of variables Pred and two joint value assignments p and p′ to Pred.
Output: The prediction error d(p′, p).
Error-Size-Computation (MAX)
Instance: As in Error-Computation (MAX).
Output: The size of the prediction error dH.
As in the SUM variants, we make a distinction in Hypothesis-Updating between Belief-Updating, where we compute the most probable hypothesis given the observation (taking the prior probabilities of the hypotheses into consideration), and Belief-Revision, where we compute the most likely hypothesis that would minimize prediction error.
Belief-Updating (MAX)
Instance: A causal Bayesian network \(\mathcal {B}_{L}\) with designated variable subsets Hyp and Pred, a joint value assignment p to Pred, and the prediction error d(p′, p) such that p′ = p + d(p′, p).
Output:\(\text {argmax}_{\mathbf {h}^{\prime }}\text {Pr}({\text {Hyp}=\mathbf {h}^{\prime }}|{\text {Pred}=\mathbf {p}^{\prime }})\), i.e., the most probable joint value assignment h′ to Hyp, given Pred = p′
Belief-Revision (MAX)
Instance: As in Belief-Updating.
Output: A (revised) joint value assignment h′ to Hyp such that dH[h′] is minimal.
The remaining computational problems are similar to their SUM variants:
Model-Revision (MAX)
Instance: As in Belief-Updating; furthermore, a set \(\mathbf {P}\subset \text {Pr}_{\mathcal {B}_{L}}\) of parameter probabilities.
Output: A combination of values p to P such that dH[p] is minimal.
Add-Observations (MAX)
Instance: As in Belief-Updating; furthermore, a designated and yet unobserved subset O ⊆Int.
Output: An observation o for the variables in O such that dH[o] is minimal.
Intervention (MAX)
Instance: As in Belief-Updating; furthermore, a designated subset A ⊆Int.
Output: An intervention a to the variables in A such that dH[a] is minimal.
Results
Intractability Results
For our (in)tractability analyses, we build on concepts and techniques from computational complexity theory (see, e.g., Garey and Johnson 1979; Arora and Barak 2009). In line with the literature (Gigerenzer 2008; Bossaerts and Murawski 2017; Frixione 2001; Parberry 1994; Thagard and Verbeurgt 1998; Tsotsos 1990; van Rooij et al. 2019), we will adopt NP-hardness as a formalization of the notion of “intractability.” A computation that is NP-hard cannotFootnote 3 be computed in so-called polynomial time, i.e., a time taking on the order of nc steps, where n is a measure of the input size (e.g., n may the number of the nodes in the Bayesian network), and c is a (small) constant. In other words, all algorithms performing an NP-hard computation require super-polynomial (e.g., exponential) time, at least for some of the inputs. Most Bayesian computations are NP-hard, both to compute exactly and to approximate (Kwisthout and van Rooij 2013a; Kwisthout 2015); we show that (by and in itself) “low prediction error” is not sufficient to render the computations in predictive processing tractable. More specifically, we have derived the following intractability results. For full proofs and technical details, we refer to the Supplementary Materials.
Result 1PredictionisNP-hard, both in the SUM and MAX variants, even if all variables are binary, there is only a singleton hypothesis variable, and there is only a singleton prediction variable.
Result 2Error-ComputationandError-Size-Computationcan be computed in polynomial time, both in the SUM and MAX variants.
Result 3Belief-UpdatingandBelief-RevisionareNP-hard, both in the SUM and MAX variants, even if all variables are binary, there is only a singleton hypothesis variable, there is only a singleton prediction variable, and (forBelief-Revision) the size of the prediction error is arbitrarily small.
Result 4Model-RevisionisNP-hard, both in the SUM and MAX variants, even if all variables are binary, there is only a singleton hypothesis variable, there is only a singleton prediction variable, and there is just a single parameter that can be revised.
Result 5Add-ObservationsandInterventionareNP-hard, both in the SUM and MAX variants, even if all variables are binary, there is only a singleton hypothesis variable, there is only a singleton prediction variable, and there is just a single variable that can be observed, respectively, intervened on.
Some important observations and implications can be drawn from our results: Without constraints on the network, Prediction, Hypothesis-Updating, Model- Revision, Intervention, and Add-Observations are all intractable (NP-hard) for either the SUM or the MAX interpretation, and for either the “prediction error minimization” and “best explanation” interpretation of Hypothesis-Updating. These findings make clear that a predictive processing implementation of Bayesian inference does not yet make the latter tractable; i.e., the subcomputations can themselves also be intractable. This intractability holds even under stringent additional assumptions, such as that each level in the hierarchy contains a causal model with at most one binary hypothesis variable and at most one binary observation variable. Finally, the size of the initial prediction error does not contribute to the hardness of Belief-Revision, as the intractability result holds even if the prediction error is arbitrarily close to zero. It is likely that this result can also be extended to Model-Revision, Add-Observations, and Intervention, but we did not yet succeed to prove this.
Tractability Results
The previous section reports intractability (NP-hardness) results for unconstrained causal models in hierarchical predictive coding. It is known, however, that a computation that is NP-hard on unconstrained inputs can sometimes be computed in a time that is non-polynomial only in some (possibly small) parameter of the input and polynomial in the size of the input. More formally, given an NP-hard computation Q, with input parameters k1, k2,…, km, there may exist a procedure for computing Q that runs in time f(k1, k2,…, km)na, where f is a function and a is a constant independent of the input size n. A fixed-parameter (fp-) tractable procedure can perform an otherwise intractable computation quite efficiently, even for large inputs, provided only that the parameters k1, k2,…, km are small (e.g., for k = 3 and n = 35 an fp-tractable running time on the order of 2kn = 280 compares favorable with an exponential running time 2n > 1010). Here, we investigate whether or not such fp-tractable procedures also exist for the sub-computations in the hierarchical predictive coding framework. In our analyses (full formal details appear in the Supplementary Materials; see footnote 2), we consider the following parameters:
-
The maximum number of values each variable in the Bayesian network can take (c);
-
The treewidth of the network (t), a graph-theoretical property that can loosely be described as a measure on the “localness” of connections in the network (Bodlaender 1993);
-
The size of the prediction space (|Pred|) or hypothesis space (|Hyp|);
-
The number of probability parameters that may be revised (|P|);
-
The size of the observation space (|O|) or action repertoire (|A|); and
-
The probability of the most probable prediction or most probable hypothesis (1 − p).
Our main findings are that both the subcomputations Prediction and Hypothesis-Updating can be performed tractably when the topological structure of the Bayesian network is constrained (small t), and each variable can take a small number of distinct values (small c), and the search space of possible predictions and hypotheses is small (small |Pred| and small |Hyp|). Specifically, both SUM and MAX variants are computable in fp-tractable time O(c|Pred|⋅ ct ⋅ n) for Prediction, and O(c|Hyp|⋅ ct ⋅ n) for Hypothesis-Updating. In addition, the MAX variants are also tractable when the prediction or hypothesis space may be large, but instead the most probable prediction (hypothesis) has a high probability (i.e., 1 − p is small). Specifically, Prediction and Hypothesis-Updating are then computable in fp-tractable time \(O\left (c^{\frac {\log (p)}{log(1-p)}}\cdot c^{t} \cdot n\right )\). For Model-Revision, Intervention, and Add-Observations similar tractability results hold, but in addition to these parameters also the the number of revisable problem parameters, action repertoire, or observation space needs to be constrained.
Theoretical Predictions for Neuroscience
By combining the intractability and (fixed-parameter) tractability results from the previous two sections, we can derive a few theoretical predictions. First off, the intractability results in “Intractability Results” establish that a brain can tractably implement predictive processing’s (Bayesian) subcomputations only if each level of the hierarchy encodes a Bayesian network that is properly constrained.Footnote 4 Second, the tractability results in “Tractability Results” present constraints that are sufficient for tractability. Specifically, each tractability result identifies a set of parameters {k1, k2,…, km} for which a given subcomputation (Prediction, Hypothesis-Updating etc.) is efficiently computable for relatively large Bayesian networks provided only that the values of k1, k2,…, km are relatively small. This means that the predictive processing account can be empirically shown to meet the conditions for tractability if it can be shown that the brain’s implementation respects these constraints.Footnote 5 As explained in van Rooij (2008) and van Rooij et al. (2019), fixed-parameter tractability results are necessarily qualitative in nature, because exact numerical predictions are not possible at this level of abstraction. But as a rule of thumb, one can consider parameters in the range of, say, 2 to 10 relatively small, and in the range of, say, 100 to 10,000 relatively large.Footnote 6
Empirically testing if the brain’s predictive processing hierarchy respects these (qualitative) constraints is beyond the scope of this paper. Moreover, it is beyond state-of-the art knowledge about the relationship between the high-level (computational-level) parameters that we analyzed in this paper and putative parameters measurable with empirical neuroscience methods. In order to make the relationship transparent, more theoretical neuroscience research may need to be done to explore this relationship more directly and in a way designed to map out the relevant bridging hypotheses (i.e., about how the parameters at the computational-level map to parameters of the neural implementation). For instance, at present, it is known that the types of Bayesian computations that we analyzed at the computational level can, in principle, be (approximately) computed by spiking artificial neural networks (Buesing et al. 2011; Habenschuss et al. 2013; Maass 2014). Also, it is known that the number of spiking neurons needed to approximate Bayesian computations is directly related to computational-level parameters, such as t and c considered in “Tractability Results” (i.e., the number of neurons is proportional to ct, Pecevski et al.2011). However, since such implementations at present still make biologically implausible assumptions about how the implementation is achieved,Footnote 7 it is too early to know how the size of the higher level parameters will correspond to the size (or other) of the putative parameters of biological neural networks in the brain. We hope that our computational-level analyses provide an incentive to prioritize theoretical and empirical neuroscience investigations into how computational-level parameters relate to parameters of the biological implementation. Because one thing is certain: our complexity-theoretic proofs show that without proper parametric constraints at the biological level it is impossible for a predictive brain to engage in Bayesian subcomputations tractably.
A Note on Approximation
As we argued elsewhere (Kwisthout et al. 2011; Kwisthout and van Rooij 2013a; Kwisthout 2015), an approximation assumption itself cannot buy tractability. In particular, the sampling approximation algorithms that are typically assumed to be representative of the brain’s approximate computations (Maass 2014; Habenschuss et al. 2013) are provably intractable in general.Footnote 8 Heuristical approaches, such as Laplace or mean field approximations, have no guarantees on the quality of the approximation; while in structured mean field approximations, settling the trade-off between factorization and coupling of variables might in itself be an intractable problem.Footnote 9 However, recent advances in the study of the computational complexity of such approximate algorithms (Kwisthout 2018; Donselaar 2018) suggest that, while still intractable in general, these algorithms may be rendered tractable for certain sub-classes of inputs. Whether these tractable sub-classes include the sorts of approximation problems the brain is faced with is still an open problem.
Model Revision Revisited
In the context of this paper, we make a distinction between learning and revising generative models. We interpret learning as the process of gradually shaping generative models, including the hyperparameters that describe their precision, by Bayesian updating. An illustrative example could be the development of a generative model that describes the outcome of a coin toss, i.e., the probability distribution over the outcomes and the precision of that model, based on several experiences with coin tosses. In contrast, we interpret model revision as the process of accommodating a dynamic, changing world in the light of unexpected prediction errors; that is, the adaptation of generative models with the aim of lowering prediction error. In this paper, we operationalize model revision as parameter tuning, as a sort of “baseline” of the most straightforward and established way of revising generative models. However, in reality, this is an oversimplification: One can also revise models by adding new variables or adding values of variables such as to accomodate for contextual influences. For example, one’s generative model that describes the expected action “hand-shake” as predicted by the assumed intention “friendly greeting” can be updated by including a contextual variable “age” (young/old) and adding the action “fist-bump” to the repertoire. In addition, we might need to generate new hypotheses and integrate them to our generative models; a process known as abduction proper (c.f. Blokpoel et al.2018). These aspects of model revision are yet to be studied in the context of the predictive processing account.
Discussion
The hypothesis that a predictive processing implementation of a Bayesian brain may harbor some intractable subcomputations, especially when the account is assumed to scale to all of cognition (Kwisthout et al. 2017; Otworowska et al. 2014), has been put forth before (Blokpoel et al. 2012). In this paper, we support and have extended this hypothesis by assessing the computational resource demands of each key subcomputation required for a predictive Bayesian brain. To this end, we formulated explicit computational-level characterizations of the subcomputations, while accommodating for different possible interpretations in the literature.
Complexity analyses of the subcomputations reveal that most are intractable (in the sense of NP-hard; see Result 1 and Results 3, 4, 5), unless the causal models that are coded by the hierarchy are somehow constrained.
These complexity-theoretic results are important for researchers in the field to know about, given that part of the popularity of the predictive processing account seems due to its claims of computational tractability: For instance, the account postulates that, by processing only the prediction error rather than the whole input signal, tractable inferences can be made provided that the prediction error is small. However, our results show that these claims are not substantiated for generative models based on the structured representations (such as causal Bayesian networks) that are required for higher cognitive capacities (Kwisthout et al. 2017; Otworowska et al. 2014; Tenenbaum 2011).
We realize that our mathematical proofs and results may seem counterintuitive given that it is often tacitly assumed or explicitly claimed that the computations postulated by predictive processing can be tractable approximated by algorithms implemented by the brain (e.g., Bruineberg et al. 2018; Clark 2013; Swanson 2016). The apparent mismatch between such claims and our findings can be understood as follows (see also “A Note on Approximation”): the claims of tractable approximation in the literature are in one way or another based on simplifying representational assumptions. These can be, for instance, the assumption of Gaussian probability distributions as in Laplace approximation (Friston et al. 2007) or the assumption of independence of variables (despite their potential dependence in reality) as in variational methods (Bruineberg et al. 2018). These assumptions specifically prohibit richly structured representations that have been argued to be essential as models of cognition and are therefore pursued by Bayesian modelers in cognitive science (Chater et al. 2006; Griffiths et al. 2008, 2010; Tenenbaum 2011); see also Kwisthout et al. (2017).
Holding onto overly simplified representational assumptions may buy one tractability, but it would not support the predictive processing framework to scale to higher cognition. This route would severely limit the framework’s relevance for cognitive neuroscience, a route we suspect few predictive processing theorists would prefer. Moreover, the complexity-theoretic results presented in this paper establish that the popular “approximation” methods cannot genuinely approximate predictive processing computations over structured representations, as their outputs will be arbitrarily off from the outputs corresponding to the predictive processing subcomputations defined over Bayesian networks for most inputs.
To forestall misunderstanding, we would like to clarify that we do not wish to suggest that the brain cannot tractably implement the Bayesian inferences required for human cognition, nor do we suggest that the brain cannot do so using a predictive processing architecture. In fact, we think that the hypothesis that the brain implements tractable Bayesian inferences, possibly using predictive processing, is not implausible. What our results show, however, is that if the brain indeed tractably implements Bayesian inference, then that is not because the inferences are implemented using predictive processing per se. Furthermore, our results suggest that the key to tractable inference in the brain may rather lie in the properties of the causal models that it represents at the different levels of such hierarchy. Our complexity results thus confirm earlier theoretical work that shows that while theoretical models at the neuronal level (e.g., spiking neural networks) can be shown to be able to approximate posteriors in arbitrary Bayesian networks, the number of nodes grows exponentially with the order of stochastic relations (and thus also with the treewidth of the network) in the probability distribution (Pecevski et al. 2011).
With our fixed-parameter tractability analyses (see “Tractability Results”), we illustrate how one may go about identifying the properties that make Bayesian inference tractable (see also Blokpoel et al. 2012, 2013; Kwisthout 2011; Kwisthout et al. 2011). Some of these properties are topological in nature (i.e., the structure of the causal models), whereas others pertain to the number of competing hypotheses that the brain considers per level of the hierarchy. In light of our findings, we propose that an important topic of empirical and theoretical investigations in cognitive neuroscience should be to investigate whether or not the brain’s causal models, and their biological implementations (“Theoretical Predictions for Neuroscience”), have the properties that are necessary for tractable predictive processing. It seems that this is the only way in which the tractability claims about predictive processing can be more than castles in the air.
Notes
Relative to common and widely endorsed assumptions in theoretical computer science; in particular, the assumptions that P≠NP (Goldreich 2008) and that BPP≠NP (Clementi et al. 1998). Here, BPP (short for bounded-error probabilistic polynomial-time) is the class of problems that enjoy efficient randomized algorithms.
More technical preliminaries from complexity theory and full details of the formal intractability proofs can be found in the Supplementary Materials.
Again, assuming P≠NP.
This is a necessary condition for tractability, even when approximate computation is assumed (see “A Note on Approximation”).
To illustrate, assume that c = 2, |Pred| = 8 and t = 5. Then, say, O(c|Pred|⋅ ct ⋅ n) would be upperbounded by a polynomial O(n2) for n ≥ 8,200.
Including, for example, hand-crafted deterministic dependences between variables in order to represent higher order stochastic interactions.
Under the common complexity-theoretical assumption that BPP≠NP (Clementi et al. 1998)
Nils Donselaar, personal communications.
References
Abdelbar, A.M., & Hedetniemi, S.M. (1998). Approximating MAPs for belief networks is NP-hard and other theorems. Artificial Intelligence, 102, 21–38.
Adams, R., Shipp, S., Friston, K. (2013). Predictions not commands: active inference in the motor system. Brain Structure and Function, 218(3), 611–643.
Arora, S., & Barak, B. (2009). Complexity theory: a modern approach. Cambridge: Cambridge University Press.
Barlow, H.B. (1961). Possible principles underlying the transformation of sensory messages. In W.A. Rosenblith (Ed.) Sensory Communication, (Vol. 3 pp. 217–234). Cambridge,MA: MIT Press.
Bilmes, J. (2004). On virtual evidence and soft evidence in Bayesian networks. Tech. Rep UWEETR-2004-0016, University of Washington, Department of Electrical Engineering.
Blokpoel, M., Kwisthout, J., van Rooij, I. (2012). When can predictive brains be truly Bayesian? Frontiers in Theoretical and Philosophical Psychology, 3, 406.
Blokpoel, M., Kwisthout, J., van der Weide, T., Wareham, T., van Rooij, I. (2013). A computational-level explanation of the speed of goal inference. Journal of Mathematical Psychology, 57(3-4), 117–133.
Blokpoel, M., Wareham, H., Haselager, W., Toni, I., van Rooij, I. (2018). Deep analogical inference as the origin of hypotheses. Journal of Problem Solving, 11(1), 3.
Bodlaender, H.L. (1993). A tourist guide through treewidth. Acta Cybernetica, 11, 1–21.
Bossaerts, P., & Murawski, C. (2017). Computational complexity and human decision-making. Trends in Cognitive Sciences, 21(12), 917–929.
Brown, H., & Friston, K. (2012). Free-energy and illusions: the cornsweet effect. Frontiers in Psychology, 3, 43.
Brown, H., Friston, K., Bestmann, S. (2011). Active inference, attention, and motor preparation. Frontiers in Psychology, 2(218), 1–9.
Bruineberg, J., Kiverstein, J., Rietveld, E. (2018). The anticipating brain is not a scientist: the free-energy principle from an ecological-enactive perspective. Synthese, 195(6), 2417–2444.
Buesing, L., Bill, J., Nessler, B., Maass, W. (2011). Neural dynamics as sampling: A model for stochastic computation in recurrent networks of spiking neurons. PLoS Computational Biology, 7(11), e1002, 211.
Castillo, E., Gutiérrez, J., Hadi, A. (1997). Sensitivity analysis in discrete Bayesian networks. IEEE Transactions on Systems Man, and Cybernetics, 27, 412–423.
Chater, N., Tenenbaum, J., Yuille, A. (2006). Probabilistic models of cognition: conceptual foundations. Trends in Cognitive Sciences, 107, 287–201.
Clark, A. (2013). Whatever next? Predictive brains, situated agents, and the future of cognitive science. Behavioral and Brain Sciences, 36(3), 181–204.
Clark, A. (2016). Surfing uncertainty: prediction action, and the embodied mind. Oxford: Oxford University Press.
Clementi, A., Rolim, J., Trevisan, L. (1998). Recent advances towards proving P=BPP. In E. Allender, A. Clementi, J. Rolim, L. Trevisan (Eds.) EATCS (p. 64).
Cooper, G.F. (1990). The computational complexity of probabilistic inference using Bayesian belief networks. Artificial Intelligence, 42(2), 393–405.
Dagum, P., & Luby, M. (1993). Approximating probabilistic inference in Bayesian belief networks is NP-hard. Artificial Intelligence, 60(1), 141–153.
Darwiche, A. (2009). Modeling and reasoning with Bayesian networks. Cambridge: CU Press.
Dayan, P., Hinton, G.E., Neal, R.M. (1995). The helmholtz machine. Neural Computation, 7, 889–904.
Den Ouden, H., Kok, P., De Lange, F. (2012). How prediction errors shape perception, attention, and motivation. Frontiers in Psychology, 3, e548.
Donselaar, N. (2018). Parameterized hardness of active inference. In Proceedings of the international conference on probabilistic graphical models, PMLR, (Vol. 72 pp. 109–120).
Edwards, M., Adams, R., Brown, H., Pare’/es, I., Friston, K. (2012). A bayesian account of ‘hysteria’. Brain, 135(11), 3495–512.
Friston, K. (2002). Functional integration and inference in the brain. Progress in Neurobiology, 590, 1–31.
Friston, K. (2005). A theory of cortical responses. Philosophical Transactions of the Royal Society B, 350, 815–836.
Friston, K. (2008). Hierarchical models in the brain. PLoS Computational Biology, 4(11), e1000,211.
Friston, K. (2010). The free-energy principle: a unified brain theory? Nature Reviews Neuroscience, 11(2), 127–138.
Friston, K., Mattout, J., Trujillo-Barreto, N., Ashburner, J., Penny, W. (2007). Variational free energy and the Laplace approximation. Neuroimage, 34, 220–234.
Friston, K., Adams, R., Perrinet, L., Breakspear, M. (2012). Perceptions as hypotheses: Saccades as experiments. Frontiers in Psychology, 3, e151.
Frixione, M. (2001). Tractable competence. Minds and Machines, 11, 379–397.
Garey, M., & Johnson, D. (1979). Computers and intractability. A guide to the theory of NP-completeness. W.H Freeman and Co., San Francisco, CA.
Gigerenzer, G. (2008). Why heuristics work. Perspectives in Psychological Science, 3(1), 20–29.
Gill, J.T. (1977). Computational complexity of probabilistic Turing Machines. SIAM Journal of Computing 6(4), 675–695.
Goldreich, O. (2008). Computational complexity: a conceptual perspective. Cambridge: Cambridge University Press.
Griffiths, T., Kemp, C., Tenenbaum, J. (2008). Bayesian models of cognition. In R. Sun (Ed.) The Cambridge handbook of computational cognitive modeling (pp. 59–100): Cambridge University Press.
Griffiths, T., Chater, N., Kemp, C., Perfors, A., Tenenbaum, J. (2010). Probabilistic models of cognition: Exploring representations and inductive biases. Trends in cognitive sciences, 14(8), 357–364.
Griffiths, T., Lieder, F., Goodman, N. (2015). Rational use of cognitive resources: levels of analysis between the computational and the algorithmic. Topics in Cognitive Science, 7, 217–229.
Grush, R. (2004). The emulation theory of representation: Motor control, imagery, and perception. Behavioral and Brain Sciences, 27, 377–442.
Habenschuss, S., Jonke, Z., Maass, W. (2013). Stochastic computations in cortical microcircuit models. PLoS Computational Biology, 9(11), e1003, 037.
Hamming, R. (1950). Error detecting and error correcting codes. Bell System Technical Journal, 29(2), 147–160.
Hobson, J., & Friston, K. (2012). Waking and dreaming consciousness: Neurobiological and functional considerations. Progress in Neurobiology, 98(1), 82–98.
Hohwy, J. (2013). The predictive mind. Oxford: Oxford University Press.
Hohwy, J., Roepstorff, A., Friston, K. (2008). Predictive coding explains binocular rivalry: an epistemological review. Cognition, 108(3), 687–701.
Horga, G., Schatz, K., Abi-Dargham, A., Peterson, B. (2014). Deficits in predictive coding underlie hallucinations in schizophrenia. The Journal of neuroscience, 34(24), 8072–8082.
Jeffrey, R. (1965). The logic of decision. New York: McGraw-Hill.
Jehee, J., & Ballard, D. (2009). Predictive feedback can account for biphasic responses in the lateral geniculate nucleus. PLoS Computational Biology, 5, 1–10.
Kant, I. (1999/1787). Critique of pure reason. The Cambridge edition of the Works of Immanuel Kant. Cambridge: Cambridge University Press.
Kiiveri, H., Speed, T.P., Carlin, J.B. (1984). Recursive causal models. Journal of the Australian Mathematical Society Series A Pure mathematics, 36(1), 30–52.
Kilner, J.M., Friston, K.J., Frith, C.D. (2007a). The mirror-neuron system: a Bayesian perspective. Neuroreport, 18, 619–623.
Kilner, J.M., Friston, K.J., Frith, C.D. (2007b). Predictive coding: an account of the mirror neuron system. Cognitive Process, 8, 159–166.
Knill, D., & Pouget, A. (2004). The Bayesian brain: the role of uncertainty in neural coding and computation. Trends in Neuroscience, 27(12), 712–719.
Kostopoulos, D. (1991). An algorithm for the computation of binary logarithms. IEEE Transactions on computers, 40(11), 1267–1270.
Kullback, S., & Leibler, R.A. (1951). On information and sufficiency. The Annals of Mathematical Statistics, 22, 79–86.
Kwisthout, J. (2009). The computational complexity of probabilistic networks. PhD thesis Faculty of Science, Utrecht University, The Netherlands.
Kwisthout, J. (2011). Most probable explanations in Bayesian networks: complexity and tractability. International Journal of Approximate Reasoning, 52(9), 1452–1469.
Kwisthout, J. (2014). Minimizing relative entropy in hierarchical predictive coding. In L. van der Gaag, & A. Feelders (Eds.) Proceedings of PGM’14, LNCS, (Vol. 8754 pp. 254–270).
Kwisthout, J. (2015). Tree-width and the computational complexity of map approximations in Bayesian networks. Journal of Artificial Intelligence Research, 53, 699–720.
Kwisthout, J. (2018). Approximate inference in Bayesian networks: parameterized complexity results. International Journal of Approximate Reasoning, 93, 119–131.
Kwisthout, J., & van der Gaag, L. (2008). The computational complexity of sensitivity analysis and parameter tuning. In D. Chickering, & J. Halpern (Eds.) Proceedings of the 24th conference on uncertainty in artificial intelligence (pp. 349–356): AUAI Press.
Kwisthout, J., & van Rooij, I. (2013a). Bridging the gap between theory and practice of approximate Bayesian inference. Cognitive Systems Research, 24, 2–8.
Kwisthout, J., & van Rooij, I. (2013b). Predictive coding: intractability hurdles that are yet to overcome [abstract]. In M. Knauff, M. Pauen, N. Sebanz, I. Wachsmuth (Eds.) Proceedings of the 35th annual conference of the cognitive science society Austin, TX: Cognitive Science Society.
Kwisthout, J., Wareham, T., van Rooij, I. (2011). Bayesian intractability is not an ailment approximation can cure. Cognitive Science, 35(5), 779–784.
Kwisthout, J., Bekkering, H., van Rooij, I. (2017). To be precise, the details don’t matter: On predictive processing, precision, and level of detail of predictions. Brain and Cognition, 112(112), 84–91.
Lee, T.S., & Mumford, D. (2003). Hierarchical Bayesian inference in the visual cortex. Journal of the Optical Society of America America, 20(7), 1434–1448.
Lieder, F., & Griffiths, T.L. (2019). Resource-rational analysis: understanding human cognition as the optimal use of limited computational resources. Behavioral and Brain Sciences. https://doi.org/10.1017/S0140525X1900061X.
Littman, M.L., Goldsmith, J., Mundhenk, M. (1998). The computational complexity of probabilistic planning. Journal of Artificial Intelligence Research, 9, 1–36.
Maass, W. (2014). Noise as a resource for computation and learning in networks of spiking neurons. Proceedings of the IEEE, 102(5), 860–880.
Majithia, J.C., & Levan, D. (1973). A note on base-2 logarithm computations. Proceedings of the IEEE, 61 (10), 1519–1520.
Marr, D. (1982). Vision: A computational investigation into the human representation and processing of visual information. New York: Freeman.
Otworowska, M., Kwisthout, J., van Rooij, I. (2014). Counter-factual mathematics of counterfactual predictive models. Frontiers in Consciousness Research, 5, 801.
Papadimitriou, CH. (1994). Computational complexity. Reading: Addison-Wesley.
Parberry, I. (1994). Circuit complexity and neural networks. Cambridge: MIT Press.
Park, J.D., & Darwiche, A. (2004). Complexity results and approximation settings for MAP explanations. Journal of Artificial Intelligence Research, 21, 101–133.
Pearl, J. (1988). Probabilistic reasoning in intelligent systems: networks of plausible inference. Palo Alto: Morgan Kaufmann.
Pearl, J. (2000). Causality: models, reasoning and inference. Cambridge: MIT Press.
Pecevski, D., Bueling, L., Maass, W. (2011). Probabilistic inference in general graphical models through sampling in stochastic networks of spiking neurons. PLoS Computational Biology, 7(12), 1–25.
Pink-Hashkes, S., van Rooij, I., Kwisthout, J. (2017). Perception is in the details: a predictive coding account of the psychedelic phenomenon. In Proceedings of the 39th annual meeting of the cognitive science society (pp. 2907–2912).
Rao, R., & Ballard, D. (1999). Predictive coding in the visual cortex: a functional interpretation of some extra-classical receptive-field effects. Nature neuroscience, 2, 79–87.
Rothen, N., Seth, A., Ward, J. (2018). Synesthesia improves sensory memory, when perceptual awareness is high. Vision Research, 153, 1–6.
Seth, A. (2015). Presence, objecthood, and the phenomenology of predictive perception. Cognitive neuroscience, 6(2-3), 111–117.
Seth, A., & Tsakiris, M. (2018). Being a beast machine: the somatic basis of selfhood. Trends in Cognitive Sciences, 22(11), 969– 981.
Seth, A., Suzuki, K., Critchley, H. (2011). An interoceptive predictive coding model of conscious presence. Frontiers in Psychology, 2, e395.
Shimony, S.E. (1994). Finding MAPs for belief networks is NP-hard. Artificial Intelligence, 68(2), 399–410.
Sterzer, P., Adams, R., Fletcher, P., Frith, C., Lawrie, S., Muckli, L., Petrovic, P., Uhlhaas, P., Voss, M., Corlett, P. (2018). The predictive coding account of psychosis. Biological Psychiatry, 84(9), 634–643.
Stockmeyer, L. (1977). The polynomial-time hierarchy. Theoretical Computer Science, 3, 1–22.
Swanson, L. (2016). The predictive processing paradigm has roots in Kant. Frontiers in Systems Neuroscience, 10, 79.
Tenenbaum, J.B. (2011). How to grow a mind: statistics, structure, and abstraction. Science, 331, 1279–1285.
Thagard, P., & Verbeurgt, K. (1998). Coherence as constraint satisfaction. Cognitive Science, 22, 1–24.
Thornton, C. (2016). Predictive processing is Turing complete: a new view of computation in the brain.
Torán, J. (1991). Complexity classes defined by counting quantifiers. Journal of the ACM, 38(3), 752–773.
Tsotsos, J. (1990). Analyzing vision at the complexity level. Behavioral and Brain Sciences, 13, 423–469.
Van de Cruys, S., Evers, K., Van der Hallen, R., Van Eylen, L., Boets, B., de Wit, L., Wagemans, J. (2014). Precise minds in uncertain worlds: Predictive coding in autism. Psychological Review, 121(4), 649–675.
van Rooij, I. (2008). The Tractable Cognition Thesis. Cognitive Science, 32, 939–984.
van Rooij, I., Blokpoel, M., Kwisthout, J., Wareham, T. (2019). Cognition and intractability: a guide to classical and parameterized complexity analysis. Cambridge: Cambridge University Press.
Vaseghi, S. (2000). Advanced digital signal processing and noise reduction, 2nd. New Jersey: Wiley.
von Helmholtz, H. (1867). Handbuch der Physiologischen Optik. Leipzig: Leopold Voss.
Wagner, K.W. (1986). The complexity of combinatorial problems with succinct input representation. Acta Informatica, 23, 325–356.
Weilnhammer, V., Stuke, H., Hesselmann, G., Sterzer, P., Schmack, K. (2017). A predictive coding account of bistable perception-a model-based fMRI study. PLoS Computational Biology, 13(5), e1005, 536.
Acknowledgements
We are grateful to Mark Blokpoel, Lieke Heil, Maria Otworowska, and Nils Donselaar for helpful discussions and comments on earlier versions of this manuscript, and to the anonymous reviewers for very constructive feedback. This paper builds on preliminary results presented at CogSci 2013 (Kwisthout and van Rooij 2013b) and in a conference paper (Kwisthout 2014). This research was funded by a NWO-TOP grant (407-11-040) awarded to IvR; NWO had no involvement in study design, collection, analysis and interpretation of data, in the writing of the report, or in the decision to submit the article for publication.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Kwisthout, J., van Rooij, I. Computational Resource Demands of a Predictive Bayesian Brain. Comput Brain Behav 3, 174–188 (2020). https://doi.org/10.1007/s42113-019-00032-3
Published:
Issue Date:
DOI: https://doi.org/10.1007/s42113-019-00032-3