Abstract
A steel high-rise building (HRB) with plan irregularity is a major challenge in engineering design, especially under seismic loads. Soil–structure interaction (SSI) is one of the most important factors in designing steel high-rise structures. Herein, a T-shape in plan steel HRB subjected to four different earthquakes will mitigate the vibration and control the displacements and base straining actions resulting from earthquakes by using tuned mass dampers (TMDs) systems, and the most controlling arrangement of TMDs, in the fixed base HRB model and in the SSI HRB model, will be examined. Three-dimensional models of the steel high-rise building (HRB) with a T-shape in the plan subjected to four different earthquakes fixed or with the SSI effect were analyzed to investigate the seismic mitigation effect of six different plan arrangements of TMDs applied on the top plan of the fixed HRB model, while for the SSI HRB model, these TMDs distributions were applied on the top plan and additionally on two intermediate plans along the HRB height. The TMDs for the T-shape in plan steel HRB are more effective in the SSI model than in the fixed base model. In the SSI effect model, the distributions of the TMDs not only on the top plan of the model but also through the model (on two additional plan levels along the height) further reduced the HRB seismic response and this three-level TMDs distribution was required for the plan arrangement of 2 or 4 TMDs.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Steel structures are the most appropriate types in high-rise buildings because of the speed of construction and their light weight. Irregularity of a building may be used because of the usage of such a building or because of the shortage of construction lands. The performance of steel structures (damping coefficient equals 2%) under seismic loads is complex in design and especially in high-rise buildings. The irregular in-plan high-rise buildings, especially those subjected to earthquakes performed as vulnerable structures even though they were designed for special loads. Many studies have dealt with such problems of irregular in-plan steel high-rise buildings.
Abd-el-rahim and Farghaly (2010) studied seismically different irregular in plan building models and concluded that the T-shape in plan models has the worst behavior when subjected to an earthquake in increasing base shear and top displacements, and they also suggested that structural separation of the T, L, or U shape in plan, is a good solution to decrease the straining actions resulting from an earthquake.
Farghaly and Ahmed (2012) studied the TMD optimum distribution in a square in plan tall building and concluded that the distribution of TMDs on the floor plan and through the building elevation, controls the vibration effectively and reduces floor displacements and straining actions.
Gutierrez Soto (2012) studied the seismic performance of irregular buildings and used bidirectional TMD as a control method and concluded that bidirectional tuned mass damper (BTMD) performs consistently better than pendulum tuned mass damper (PTMD) for the reduction of the maximum displacement, acceleration, and base shear. BTMD is advantageous over PTMD because it can be tuned for two modes of vibrations and therefore can be used as an alternative to using two TMDs.
Chunyu et al. (2012) studied experimentally a 1/20 scaled model of an existing irregular high-rise building using a shaking table for small, moderate and large earthquake levels, and concluded that the structural irregularities, including plan reduction, little top tower, and un-continuous columns, caused damages under large earthquakes and suggested specific strengthening measures.
Varadharajan (2014) reviewed the seismic response of irregular RC buildings, pointed out that the seismic design codes have quantified the irregularities in terms of magnitude only ignoring the effect of irregularity location, proposed a single parameter to quantify mass, stiffness and strength irregularity in terms of both magnitude and location based on the dynamic characteristics of the building and concluded that his proposed index can be effectively used for the assessment of seismic damage.
Pnevmatikos and Hatzigeorgiou (2014) studied the seismic response of active or semi-active control for irregular buildings based on eigenvalues modification, by proposing a reduction of the seismic response of irregular structures by control devices equipped with the pole placement control algorithm, and concluded that this control strategy can achieve a sufficient reduction of the response of irregular buildings and can be applied to one story or to multi-story irregular buildings.
Bigdeli et al. (2014) studied the vibration control of 3D irregular buildings by using a developed neuro-controller strategy and their results showed that the proposed control algorithm is effective in structural control.
Stathi et al. (2015) proposed a reliable index (ratio of torsion) capable of assessing the torsional effect in plan irregular buildings and found that the proposed index provides a reliable prediction of the magnitude of the torsional effect for all test examples considered.
Hirde and Aher (2016) studied the performances of T shape and L shape irregular buildings located in a severe earthquake zone and identified the most vulnerable building among them to be the T shape and retrofitted it with X steel bracings.
Khan and Rao (2016) compared the dynamic results of an irregular L-shape 10-story building in various zones, and demonstrated that the total story drift responses ratio increases as the floor plane irregularity increases up to the third floor, the middle stories are more affected than lower and upper stories in drift story, the displacements gradually increases from ground story to top story, and concluded that plan irregularity has a significant effect on the seismic response of buildings.
Naveen and Chaya (2016) studied regular and irregular in-plan 3D buildings subjected to an earthquake and concluded that the responses of irregular buildings are bigger than the responses of regular buildings.
Ghos et al. (2016) studied the seismic performance of horizontally irregular multi-story RC buildings, namely L-shaped, H-shaped, and U-shaped.
Hallale and Bai (2016) studied the structural behavior of irregular in-plan buildings subjected to earthquakes compared with regular buildings and found that the plan irregularity increased the top displacement, top acceleration, time period and member forces, and showed that the infill frame action developed additional lateral stiffness and reduced all these except the base shear.
Farghaly (2017a) studied the TMD control of a L-shape in plan RC high-rise building considering soil–structure interaction (SSI) and concluded that the length-to-width ratio affects the response and that when the soil gets stronger the best TMDs distribution is on the top at the model corners, while when the soil gets softer the best TMDs distribution is through the elevation of the model.
Farghaly (2017b) studied the seismic analysis of adjacent buildings subjected to double pounding (i.e., pounding at the superstructure and at the foundation level) considering soil–structure interaction.
He et al. (2017) proposed a new type of tuned mass damper with tuned mass blocks, orthogonal poles, and torsional pendulums (TMDPP) to simultaneously control the translational responses and the torsional angle of asymmetry structures. The damping capacity of the TMDPP was verified by the time history analysis of an eccentric structure, multidimensional earthquake excitations were considered, and the results showed that the performance of TMDPP is superior to the traditional TMD.
Bekdaş and Nigdeli (2017) proposed a metaheuristic-based optimization approach for the optimum design of tuned mass dampers (TMDs) implemented to seismic structures considering soil–structure interaction (SSI), where two metaheuristic algorithms (namely the harmony search algorithm and the bat algorithm) were employed, and the bat algorithm was found to be advantageous in minimizing the optimization objective and finding a precise optimum value.
Mirzai et al. (2017) proposed optimum parameters of tuned mass dampers (TMDs) using a gravity search algorithm (GSA) and particle swarm optimization (PSO) to reduce the responses of tall and typical buildings.
Rahman et al. (2017) proposed a new type of mass damper system for controlling wideband earthquake vibrations, called multiple wall dampers (MWD); this proposed passive energy dissipation system does not require additional mass for the damping system because the boundary wall mass of the building was used as a damper mass, and the obtained structural responses under different earthquake forces demonstrated that the MWD is one of the most capable tools for reducing the responses of new and existing multi-storied buildings.
Philip and Elavenil (2017) analyzed irregular in-plan high-rise buildings subjected to earthquake and showed that story displacements increase linearly with the height of the building while the values of story shear force decrease linearly with height, and also higher displacements, story drifts and story shears were observed for the irregular building compared to the regular building.
Joshy and Santhi (2018) studied RC high-rise buildings with plan irregularity subjected to earthquake and concluded that the story displacement increases as the plan irregularity of the building increases, the maximum displacement will be at places where story stiffness is less, the L shape model has displaced more compared to C, T, Z and regular buildings and finally, the lower story column size needs to be increased to prevent collapse due to plastic hinge formation in case of a building with plan irregularity.
Nazarimofrad and Zahrai (2018) developed a mathematical model for the seismic control of an irregular plan multi-story building using two active tuned mass dampers (ATMDs) at the center of mass on the top floor with fuzzy logic control algorithm considering SSI effect.
Amini et al. (2018) showed that the simple adaptive control method (SACM) is successful in reducing the response of asymmetric buildings with rotationally non-linear behavior under seismic loads and furthermore, the results of the SACM were very close to those of the LQR algorithm.
Kontoni and Farghaly (2018) studied the seismic response of adjacent unequal buildings subjected to double pounding considering soil–structure interaction (SSI).
Naderpour et al. (2019) investigated the effectiveness of a hybrid control strategy, combining base isolation and non-traditional tuned mass dampers (TMDs) (i.e., TMDs with dashpots directly connected to the ground) in suppressing the seismic vibrations of high-rise buildings.
Kontoni and Farghaly (2019a) investigated the mitigation of the seismic response of a cable-stayed bridge with soil–structure interaction (SSI) effect subjected to four different earthquakes by using tuned mass dampers and spring dampers with different placements in four different mitigation schemes.
Kontoni and Farghaly (2019b) studied the effect of base isolation and tuned mass dampers (TMDs) on the seismic response of reinforced concrete (RC) high-rise buildings considering soil–structure interaction; a comprehensive study of the combination of TMDs with three different base-isolator types for three different soil types and under five different earthquakes was conducted to show the most suitable hybrid passive vibration control system.
Kaveh et al. (2020a) investigated the optimum design of a tuned mass damper inerter (TMDI) to control a 10-story base-excited shear building by selecting the H2 and H∞ norms of three different objective functions to tune two different single and double inerter TMDI configurations using a metaheuristic technique, and concluded that the TMDI is most effective when the optimization goal is to reduce the floor accelerations.
Kaveh et al. (2020b) studied the optimum design of a tuned mass damper inerter (TMDI) to control a 10-story base shear building under seismic loading by minimizing the H∞ norm of the roof displacement transfer function as the objective function for robust building control, and they recommended to optimize and design the TMDI using the MDOF model and not the SDOF model.
Kaveh et al. (2020c) compared the H2 and H∞ algorithms for the optimum design of tuned mass dampers (TMDs) under near-fault and far-fault earthquake motions and concluded that the H∞ objective function is superior to the H2 objective function under NF and FF earthquake excitations.
Kontoni and Farghaly (2020) investigated the TMD effectiveness for a steel high-rise building of 15 stories under the dynamic load of wind or four different earthquakes taking into consideration the effect of soil–structure interaction (SSI) and the TMDs were found to be a successful passive resistance method.
Farghaly and Kontoni (2022) studied the mitigation of seismic pounding (due to five different earthquakes) between two adjacent RC twin high-rise buildings, founded on raft foundation supported on piles inside a liquefaction-prone soil, considering SSI. Contact pounding elements between the two buildings (distributed at all floor levels and at the raft foundation level) were used. The three mitigation methods investigated were the base isolation, the tuned mass damper (TMD) method, and the pounding tuned mass damper (PTMD) method (using PTMDs connected between the two buildings) and it was found that the PTMD method was more efficient than the other two methods in mitigating the earthquake-induced pounding risk.
Farghaly and Kontoni (2023) investigated the mitigation of the seismic pounding between two L-shape in plan high-rise buildings (HRBs) subjected to earthquake in three different direction cases, including the SSI effect, and found that the most effective technique to mitigate the seismic pounding and help in seismically protecting these adjacent HRBs is the use of a combination of pounding tuned mass dampers (PTMDs) all over the height (at the connection points) together with tuned mass dampers (TMDs) on the top of both buildings.
Kontoni and Farghaly (2023) investigated the enhancement of the earthquake resistance of RC and steel high-rise buildings by bracings, shear walls and TMDs considering SSI.
The irregular in-plan buildings may be a solution to the architectural design due to the lack of area or due to the function of such buildings. The challenge which the structural designer faces in the irregularity of a building is that the forces and the displacements are increased due to the irregularity of the building so a special design for such structures especially those subjected to earthquakes is required. A steel high-rise building (HRB) subjected to earthquake vibrations represents a big challenge to the safety design. In this paper, a T-shape in plan steel HRB subjected to four different earthquakes will mitigate vibration and control the displacements and base straining actions resulting from earthquakes by tuned mass dampers (TMDs) systems and the most controlling TMDs system in the fixed base and in the SSI effect HRB models will be investigated.
Model description
A three-dimensional steel high-rise building (HRB) of a T-shape in the plan without and with the effect of SSI was seismically analyzed to investigate the best TMD control system, using the SAP2000 version 17 (2015) software. The specifications of the steel structures with a damping coefficient of 2% represent a critical challenge in the resistance of earthquakes in addition to the effect of plan irregularity and the effect of SSI. All beams and columns are designed according to the Egyptian code of steel structures (ECP-205, 2008). The structural plan of the repeated floors consists of BFIBs No. 40 beams connected to the columns which are BFIBs No. 60, and each floor is similar in beam cross-sections covered with a plate of thickness of 50 mm. The height of each floor is 3 m, and the total number of floors is 30. The dimensions of each bay of the plan of the model are 5 × 5 m. Figure 1 shows the SAP2000 model of the T-shape in plan steel tall building with a height of 90 m. The own weight of the steel is calculated by the program SAP2000 on the base of the true weights of these elements, and the live load on the deck was assumed to be 2 kN/m2. The material nonlinear time history analysis was used in analyzing all HRB model cases.
Seismic loads
The steel HRB model is subjected to four different earthquakes equal in the x and y directions. These earthquakes, with accelerograms as shown in Fig. 2, are the 1961 Hollister earthquake near central California with a magnitude of 5.2, the 1940 El Centro earthquake in California with a magnitude of 6.9, the 1989 Loma Prieta earthquake in Northern California with a magnitude of 6.9, and the 1995 Kobe earthquake in the southern part of Hyōgo Prefecture, Japan with a magnitude of 6.9.
Tuned mass dampers
Figure 3 shows the placement of tuned mass dampers (TMDs) at the top of the HRB model and the examined six different arrangements. Figure 3a shows the TMDs arrangement at the corners of the horizontal part, Fig. 3b shows TMDs arrangement at the vertical part, Fig. 3c shows TMDs arrangement at the horizontal part, Fig. 3d shows TMDs arrangement at the center of gravity of the model, Fig. 3e shows 18 TMDs at all intersection points of the model, and Fig. 3f shows TMDs arrangement at all corners of the model. The type of TMD used herein is the bidirectional TMD (with components in x and y directions) as shown in Fig. 3g.
The parameters of TMDs as per Zahrai and Ghannadi-Asl (2008), are shown below:
where, αopt is the optimum frequency ratio, ζ is the damping ratio, ζopt is the optimum damping, kd is the spring stiffness, cd is the damping, md is the damper mass, μ is the mass ratio μ = md/ms (ratio of damper mass md to building mass ms). Using the values of αopt and ζopt, optimum values of damping cd and stiffness kd of the TMD can be calculated. Each different distribution of TMDs is considered separately in order to find the TMD parameters.
Results and discussion
Fixed base HRB model
Figures 4, 5, 6 and 7 show the maximum lateral displacements and Figs. 8, 9 and 10 display the maximum base forces and moments of the HRB model under four different earthquakes and for six different arrangements of the TMDs at the top of the model with fixed base for this first stage, to investigate the most effective arrangement of TMDs in reducing the displacements and straining actions of the HRB model.
Figure 4 shows the displacements in the x and y directions of the model under the Hollister earthquake. Figure 4a shows the x-displacements of the HRB model, the “8TMDs V”, 18TMDs, 12TMDs, 4TMDs, and 8TMDs group systems reduce the lateral x displacements by nearly 4 times than the fixed case without TMDs. In Fig. 4b, the 12TMDs, 8TMDs, 18TMDs, and 4TMDs group systems reduce the lateral displacements in y direction by nearly 1.8 times than the fixed case without TMDs (all cases are close in values).
Figure 5 shows the displacements in the x and y directions of the model under the El Centro earthquake. Figure 5a shows the x-displacements of the model, where the “8TMDs V” group system reduces the lateral x displacements by nearly 2.3 times than the fixed case without TMDs. In Fig. 5b the 12TMDs group system reduces the lateral displacements in the y direction by nearly 2.5 times than the fixed case without TMDs (all cases are close in values).
Figure 6 shows the displacements in the x and y directions of the model under the Loma-Prieta earthquake. Figure 6a shows the x-displacements of the model, where the “8TMDs V” system reduces the lateral x displacements by nearly 1.5 times than the fixed case without TMDs. In Fig. 6b, the 12TMDs group system reduces the lateral displacements in the y direction by nearly 1.8 times than the fixed case without TMDs (all cases are close in values).
Figure 7 shows the displacements in the x and y directions of the model under the Kobe earthquake. Figure 7a shows the x-displacements of the model, where the 18TMDs, 12TMDs, 4TMDs, 8TMDs, and “8TMDs V” group systems reduce the lateral x displacements by nearly 1.4 times than the fixed case without TMDs. In Fig. 7b, the “8TMDs V” group system reduces the lateral displacements in y direction by nearly 2.5 times than the fixed case without TMDs.
Figure 8 shows the base shear for the fixed model subjected to four different earthquakes with TMDs group systems. Figure 8a shows the base shear in the x direction, where the 12TMDs group system reduces the base shear in the x direction by nearly 2.4, 3.2, 1.8, and 1.1 times than the fixed case without TMDs (“f”) in the Hollister, El Centro, Loma Prieta and Kobe earthquake cases respectively. Figure 8b represents the base shear in the y direction, where all values in the four earthquake cases are close, and the TMDs reduce the base shear in the y direction nearly by 2.5 times than the fixed case without TMDs (“f”).
Figure 9a shows the base moments in the x direction, where all TMDs group systems reduce the base moments in the x direction by nearly 5.5, 2, 1.7, and 2.7 times than the fixed case without TMDs (“f”) in the Hollister, El Centro, Loma Prieta and Kobe earthquake cases, respectively. Figure 9b represents the base moments in the y direction, where all TMD group systems behave similarly in reducing the base moments; the 12TMDs group system reduces the base moments in the y direction nearly by 2.4, 3, 1.7, and 1.1 times than the fixed case without TMDs (“f”) in the Hollister, El Centro, Loma Prieta and Kobe earthquake cases, respectively.
Figure 10 shows the base axial force, where all the TMD group systems behave similarly and reduce the base axial forces by nearly 1.1, 1.2, 1.1, and 1.1 times than the fixed case without TMDs (“f”) in the Hollister, El Centro, Loma Prieta and Kobe earthquake cases, respectively.
SSI HRB model
The second stage of investigation is taking into consideration the effect of SSI for the T-shape in plan steel HRB model. The raft foundation has a thickness of 2.5 m and 2 m projection at each side of the model limits, and the reinforcements with a top mesh of 8ϕ25 mm/m and a bottom mesh of 8ϕ25 mm/m. The soil type was medium soil (E = 30 MPa, ν = 0.4, G = 14.35 MPa, γ = 16 kN/m3), and the soil model was taken as 3D soil element model (as shown in Fig. 11) in which the soil elements are represented as springs and dampers (as, e.g., in Farghaly & Ahmed, 2013) The equations used to find the parameters of the 3D soil elements (stiffness Kx, Ky, Kz and damping Cx, Cy, Cz) can be found e.g. in Newmark and Rosenblueth (1971), Dowrick (2009), etc.
Figures 12, 13, 14 and 15 show the maximum lateral displacements in x and y directions and Figs. 16, 17 and 18 show the maximum base forces and moments for the steel T-shape in plan HRB subjected to four different earthquakes (Hollister, El Centro, Loma Prieta and Kobe), including SSI effect and with six different arrangements of the TMDs group system only at the top plan of the HRB model or at the top plan of the HRB model and also at every 30 m of height through the HRB model (i.e., three groups).
Figure 12 represents the displacements in x and y directions for the HRB model with the SSI effect subjected to the Hollister earthquake for one TMDs group at the top of the model only, or three TMDs groups through the model. Figure 12a represents the x-displacements of the model, the biggest displacements appear in the SSI only case (without any TMDs); the 2TMDs × 3 (i.e., 2TMDs at CG of the model at the top and through the model at every 30 m of height), 8TMDs × 3, “8TMDs V” × 3, 4TMDs × 3 and 12TMDs group systems give the best values in reducing the horizontal displacements of the model and the foremost reduction of the TMDs group systems is nearly 5 times than the SSI only case (with no TMDs). Figure 12b shows the y-displacements of the model; all displacements are in the same direction, while the “8TMDs V”, 4TMDs × 3, and 2TMDs × 3 group systems give the smallest displacements, and the foremost reduction of the TMDs group systems is nearly 1.6 times than the SSI only case (with no TMDs), but all these results are close; the y-displacements are bigger in the SSI case (with no TMDs), the 2TMDs and 4TMDs top group systems.
Figure 13 represents the displacements in the x and y directions for the HRB model with SSI effect subjected to the El Centro earthquake. Figure 13a represents the x-displacements of the model, the biggest displacements appear in the SSI only case (without TMDs); with respect to using only one TMDs group system at the top of the model and when using three TMDs group systems through the model, the 2TMD × 3 (2TMDs at CG of the model at the top and through the model at every 30 m of height), 8TMDs × 3, “8TMDs V” × 3, 4TMDs × 3 and 12TMDs group systems give the best values of reduced horizontal displacements of the model, and the foremost reduction of the TMDs group systems is nearly 8 times than SSI case (with no TMDs). Figure 13b shows the y-displacements of the model; all displacements are in the same direction, the 8TMDs, 4TMDs × 3, and 2TMDs × 3 group systems give the smallest displacements, the y-displacements are bigger in the SSI case (with no TMDs), 2TMDs and 4TMDs top group systems; the foremost reduction of the TMDs group systems is nearly 2 times than SSI case (with no TMDs), but all these results are close.
Figure 14 represents the displacements in the x and y directions for the HRB model with the SSI effect subjected to the Loma Prieta earthquake. Figure 14a represents the x-displacements of the model, the bigger displacements appear in the SSI case (without TMDs); with respect to using only one TMDs group system at the top of the model and when using three TMDs groups systems through the model, the 2TMD × 3 (2TMDs at CG of the model at the top and through the model at every 30 m of height), 8TMDs × 3, 4TMDs × 3, 8TMDs and 12TMDs group systems give the best values of reduced horizontal displacements of the model, and the foremost reduction of the TMDs group system is nearly 4 times than the SSI case (with no TMDs). Figure 14b shows the y-displacements of the model, all displacements are in the same direction, the 8TMDs, 4TMDs × 3 and 2TMDs × 3 give the smallest displacements, and the foremost reduction of the TMDs group systems is nearly 2.4 times than the SSI case (with no TMDs), but all these results are close; the y-displacements are bigger in the SSI only case (with no TMDs), the 2TMDs and 4TMDs top group systems.
Figure 15 represents the lateral displacements in the x and y directions for the HRB model with the SSI effect subjected to the Kobe earthquake. Figure 15a represents the x-displacements of the model subjected to the Kobe earthquake, where the biggest displacements appear in the SSI only case (without any TMDs); with respect to using only one TMDs group system at the top of the model and when using three TMDs group systems through the model, the 2TMD × 3 (2TMDs at CG of the model at the top and through the model at every 30 m of height), 8TMDs × 3, “8TMDs V” × 3, 4TMDs × 3 and 12TMDs group systems give the best values of reduced horizontal displacements of the model, and the foremost reduction of the TMDs group systems is nearly 4 times than the SSI case (with no TMDs). Figure 15b shows the y-displacements of the model, where all displacements are in the same direction, the “8TMDs V” × 3, 4TMDs × 3, 2TMDs × 3 and 12TMDs × 3 group systems give the smaller displacement values, and the foremost reduction of the TMDs group systems is nearly 2.40 times than the SSI case (with no TMDs); the y-displacements are bigger in the SSI (with no TMDs), the 2TMDs and 4TMDs top group systems.
Figure 16a represents the base shear in the x direction of the HRB model with SSI effect; all TMDs group systems give similar behavior in reducing the base shear in x direction except the 2TMDs case, the most effective TMDs group systems reduce the base shear by nearly 15 times than the SSI case (with no TMDs). Figure 16b shows the y direction base shear of the HRB model with SSI effect; all TMDs group systems show the same behavior in reducing the base shear except the 4TMDs and 2TMDs group cases, the most effective TMDs group systems reduce the base shear by nearly 12.5 times than the SSI case (with no TMDs).
Figure 17a represents the base moment in the x direction of the model of the HRB model with SSI effect; all TMDs group systems give similar behavior in reducing the base moment in x direction except the 4TMDs and 2TMDs cases, the most effective TMDs group systems reduce the base shear by nearly 15 times than the SSI case (no TMDs). Figure 17b shows the y direction base moment of the HRB model with SSI effect; all TMDs group systems show the same behavior in reducing base moment except the 2TMDs group case, the most effective TMDs group systems reduce the y direction base moment by nearly 12.5 times than the SSI case (no TMDs).
Figure 18 represents the base axial force of the HRB model subjected to four different earthquakes with SSI effect; all TMDs group systems give similar behavior for the base axial force, the 2TMDs × 3 (2TMDs at CG of the model at the top and through the model at every 30 m of height) shows an increase in the axial force, but most values are close. The TMDs group systems do not significantly affect the axial force values with respect to the SSI effect. All these values are also related to the weight of the TMDs group systems used.
Conclusions
Three-dimensional models of a steel high-rise building (HRB) with a T-shape in the plan subjected to four different earthquakes fixed or with the SSI effect were analyzed to show the seismic mitigation effect of six different arrangements of TMDs on the top plan of the HRB model while for the SSI HRB model, these TMDs distributions were additionally applied on two intermediate plans along the HRB height (specifically at every 30 m of height through the HRB model, i.e., three groups in total).
The lateral displacements in the x and y directions and the base straining actions were compared for each of these TMDs systems to point out the most effective distributions of TMDs in reducing the effect of the earthquakes. From the presented results, the following conclusions can be drawn:
-
The TMDs for the T-shape in plan steel HRB are effective in controlling the seismic response in the fixed and in the SSI model.
-
In the fixed model, the distributions of the TMDs on the top plan of the model are effective on the seismic response control of the steel HRB model and reduced the lateral displacements and base straining actions.
-
The TMDs for the T-shape in plan steel HRB are more effective in the SSI model than in the fixed base model.
-
In the SSI effect model, the distributions of the TMDs not only on the top plan of the model but also through the model (on two additional plan levels along the height) further reduced the HRB seismic response, and this three-level TMDs distribution was required for the plan arrangement of 2 or 4 TMDs.
Data availability
The data used to support the findings of this study are included within the article.
References
Abd-el-rahim, H. H. A., & Farghaly, A. A. (2010). Influence of structural irregularity in plan floor shape on seismic response of buildings. Journal of Engineering Sciences, Assiut University, 38(4), 911–928. https://jesaun.journals.ekb.eg/article_125548_4319632d55e7d3c77ad069d63e0e9ca9.pdf
Amini, F., Rezazadeh, H., & Afshar, M. A. (2018). Adaptive control of rotationally non-linear asymmetric structures under seismic loads. Structural Engineering and Mechanics, 65(6), 721–730. https://doi.org/10.12989/SEM.2018.65.6.721
Bekdaş, G., & Nigdeli, S. M. (2017). Metaheuristic based optimization of tuned mass dampers under earthquake excitation by considering soil–structure interaction. Soil Dynamics and Earthquake Engineering, 92, 443–461. https://doi.org/10.1016/j.soildyn.2016.10.019
Bigdeli, Y., Kim, D., & Chang, S. (2014). Vibration control of 3D irregular buildings by using developed neuro-controller strategy. Structural Engineering and Mechanics, 49(6), 687–703. https://doi.org/10.12989/SEM.2014.49.6.687
Chunyu, T., Junjin, L., Hong, Z., & Jinzhe, C. (2012). Experimental study on seismic behavior of an irregular high-rise building. In Proceedings of the Fifteenth World Conference on Earthquake Engineering, Lisbon (15 WCEE), Lisboa Portugal, 2012, 10 pages. http://www.iitk.ac.in/nicee/wcee/article/WCEE2012_3618.pdf
Dowrick, D. J. (2009). Earthquake resistant design and risk reduction (2nd ed.). Wiley.
ECP-205. (2008). Egyptian code of practice for steel construction, load and resistance factor design (LRFD), ECP-205. Housing and Building National Research Center, Ministry of Housing, Utilities and Urban Planning.
Farghaly, A. A. (2017a). Self-control of high rise building L-shape in plan considering soil structure interaction. Coupled Systems Mechanics, 6(3), 229–249. https://doi.org/10.12989/csm.2017.6.3.229
Farghaly, A. A. (2017b). Seismic analysis of adjacent buildings subjected to double pounding considering soil–structure interaction. International Journal of Advanced Structural Engineering, 9, 51–62. https://doi.org/10.1007/s40091-017-0148-y
Farghaly, A. A., & Ahmed, H. H. (2013). Contribution of soil–structure interaction to seismic response of buildings. KSCE Journal of Civil Engineering, 17(5), 959–971. https://doi.org/10.1007/s12205-013-0261-9
Farghaly, A. A., & Ahmed, M. S. (2012). Optimum design of TMD system for tall buildings. ISRN Civil Engineering, 2012, 716469. https://doi.org/10.5402/2012/716469
Farghaly, A. A., & Kontoni, D.-P. N. (2022). Mitigation of seismic pounding between RC twin high-rise buildings with piled raft foundation considering SSI. Earthquakes and Structures, 22(6), 625–635. https://doi.org/10.12989/EAS.2022.22.6.625
Farghaly, A. A., & Kontoni, D.-P. N. (2023). Mitigation of seismic pounding between two L-shape in plan high-rise buildings considering SSI effect. Coupled Systems Mechanics, 12(3), 277–295. https://doi.org/10.12989/csm.2023.12.3.277
Ghos, S., Khandker, R. Z., & Rokonuzzaman, Md. (2016). Effect of horizontal irregularity on the behavior of multi-storey R/C buildings due to horizontal loads. In Proceedings of the 3rd International Conference on Civil Engineering for Sustainable Development (ICCESD 2016), 12–14 February 2016, KUET, Khulna, Bangladesh (ISBN: 978-984-34-0265-3), ICCESD, pp. 910–915. http://www.iccesd.com/proc_2016/Papers/ICCESD-2016-588.pdf
Gutierrez Soto, M. (2012). Investigation of passive control of irregular building structures using bidirectional tuned mass damper. MSc Thesis, Civil Engineering, Ohio State University, 126 pages. http://rave.ohiolink.edu/etdc/view?acc_num=osu1354596462, http://orcid.org/0000-0003-2408-0351
Hallale, S., & Bai, H. S. (2016). Seismic behavior of buildings with plan irregularity with and without structural infill action. International Journal of Recent Advances in Engineering & Technology (IJRAET), 4(4), 97–101. http://www.irdindia.in/journal_ijraet/pdf/vol4_iss4/22.pdf
He, H., Wang, W., & Xu, H. (2017). Multidimensional seismic control by tuned mass damper with poles and torsional pendulums. Shock and Vibration, 2017, 5834760. https://doi.org/10.1155/2017/5834760
Hirde, S. K., & Aher, R. A. (2016). Seismic evaluation of irregular structures. International Journal of Current Engineering and Technology, 6(5), 1665–1672. https://inpressco.com/wp-content/uploads/2016/09/Paper331665-1672.pdf
Joshy, D., & Santhi, M. H. (2018). Seismic performance evaluation of high rise building with plan irregularity. International Journal of Civil Engineering and Technology (IJCIET), 9(4), 570–577. Available online at http://www.iaeme.com/ijciet/issues.asp?JType=IJCIET&VType=9&IType=4, http://www.iaeme.com/MasterAdmin/UploadFolder/IJCIET_09_04_063/IJCIET_09_04_063.pdf
Kaveh, A., Fahimi Farzam, M., & Hojat Jalali, H. (2020a). Statistical seismic performance assessment of tuned mass damper inerter. Structural Control and Health Monitoring, 27(10), e2602. https://doi.org/10.1002/stc.2602
Kaveh, A., Fahimi Farzam, M., Hojat Jalali, H., & Maroofazar, R. (2020b). Robust optimum design of a tuned mass damper inerter. Acta Mechanica, 231(9), 3871–3896. https://doi.org/10.1007/s00707-020-02720-9
Kaveh, A., Fahimi Farzam, M., & Maroofazar, R. (2020c). Comparing H2 and H∞ algorithms for optimum design of tuned mass dampers under near-fault and far-fault earthquake motions. Periodica Polytechnica Civil Engineering, 64(3), 828–844. https://doi.org/10.3311/PPci.16389
Khan, I. U., & Rao, S. S. E. S. (2016). Seismic analysis of irregular L-shape building in various zones. International Journal of Innovative Research in Science, Engineering and Technology, 6(8), 16529–16536. https://doi.org/10.15680/IJIRSET.2017.0608247
Kontoni, D.-P. N., & Farghaly, A. A. (2018). Seismic response of adjacent unequal buildings subjected to double pounding considering soil–structure interaction. Computation, 6(1), 10. https://doi.org/10.3390/computation6010010
Kontoni, D.-P. N., & Farghaly, A. A. (2019a). Mitigation of the seismic response of a cable-stayed bridge with soil–structure-interaction effect using tuned mass dampers. Structural Engineering and Mechanics, 69(6), 699–712. https://doi.org/10.12989/sem.2019.69.6.699
Kontoni, D.-P. N., & Farghaly, A. A. (2019b). The effect of base isolation and tuned mass dampers on the seismic response of RC high-rise buildings considering soil–structure interaction. Earthquakes and Structures, 17(4), 425–434. https://doi.org/10.12989/eas.2019.17.4.425
Kontoni, D.-P. N., & Farghaly, A. A. (2020). TMD effectiveness for steel high-rise building subjected to wind or earthquake including soil–structure interaction. Wind and Structures, 30(4), 423–432. https://doi.org/10.12989/was.2020.30.4.423
Kontoni, D.-P. N., & Farghaly, A. A. (2023). Enhancing the earthquake resistance of RC and steel high-rise buildings by bracings, shear walls and TMDs considering SSI. Asian Journal of Civil Engineering. https://doi.org/10.1007/s42107-023-00666-6
Mirzai, N. M., Zahrai, S. M., & Bozorgi, F. (2017). Proposing optimum parameters of TMDs using GSA and PSO algorithms for drift reduction and uniformity. Structural Engineering and Mechanics, 63(2), 147–160. https://doi.org/10.12989/SEM.2017.63.2.147
Naderpour, H., Naji, N., Burkacki, D., & Jankowski, R. (2019). Seismic response of high-rise buildings equipped with base isolation and non-traditional tuned mass dampers. Applied Sciences, 9(6), 1201. https://doi.org/10.3390/app9061201
Naveen, G. M., & Chaya. S. (2016). Study on regular and irregular building structures during an earthquake. International Journal of Latest Engineering Research and Applications (IJLERA), 1(8), 42–48. http://www.ijlera.com/papers/v1-i8/5.201611171.pdf
Nazarimofrad, E., & Zahrai, S. M. (2018). Fuzzy control of asymmetric plan buildings with active tuned mass damper considering soil–structure interaction. Soil Dynamics and Earthquake Engineering, 115, 838–852. https://doi.org/10.1016/j.soildyn.2017.09.020
Newmark, N. M., & Rosenblueth, E. (1971). Fundamentals of earthquake engineering (p. 640). Prentice-Hall.
Philip, A., & Elavenil, S. (2017). Seismic analysis of high rise buildings with plan irregularity. International Journal of Civil Engineering and Technology (IJCIET), 8(4), 1365–1375. http://www.iaeme.com/MasterAdmin/Journal_uploads/IJCIET/VOLUME_8_ISSUE_4/IJCIET_08_04_154.pdf
Pnevmatikos, N. G., & Hatzigeorgiou, G. D. (2014). Seismic response of active or semi active control for irregular buildings based on eigenvalues modification. Earthquakes and Structures, 6(6), 647–664. https://doi.org/10.12989/eas.2014.6.6.647
Rahman, M. S., Chang, S., & Kim, D. (2017). Multiple wall dampers for multi-mode vibration control of building structures under earthquake excitation. Structural Engineering and Mechanics, 63(4), 537–549. https://doi.org/10.12989/SEM.2017.63.4.537
SAP2000® Version 17. (2015). Integrated software for structural analysis and design. Computers and Structures, Inc. https://www.csiamerica.com/products/sap2000
Stathi, C. G., Bakas, N. P., Lagaros, N. D., & Papadrakakis, M. (2015). Ratio of torsion (ROT): an index for assessing the global induced torsion in plan irregular buildings. Earthquakes and Structures, 9(1), 145–171. https://doi.org/10.12989/eas.2015.9.1.145
Varadharajan, S. (2014). Study of irregular RC buildings under seismic effect. PhD Thesis, Department of Civil Engineering, National Institute of Technology, Kurukshetra, India. http://nitkkr.ac.in/nit_kuk/docs/SVRAJAN_phd_2015.pdf
Zahrai, S. M., & Ghannadi-Asl, A. (2008). Seismic performance of TMDs in improving the response of MRF buildings. Scientia Iranica, 15(1), 21–33. http://scientiairanica.sharif.edu/article_2979_6d8a8cfd751f7c24eb11113da3682197.pdf
Funding
Open access funding provided by HEAL-Link Greece. This research received no external funding.
Author information
Authors and Affiliations
Contributions
Both authors (D-PNK and AAF) significantly contributed to all stages of this research work and approved the manuscript to be published.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that there is no conflict of interest regarding the publication of this paper.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kontoni, DP.N., Farghaly, A.A. Seismic control of T-shape in plan steel high-rise buildings with SSI effect using tuned mass dampers. Asian J Civ Eng 25, 1725–1739 (2024). https://doi.org/10.1007/s42107-023-00873-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s42107-023-00873-1


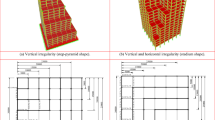



 ) arrangements at the top plan of the model
) arrangements at the top plan of the model













