Introduction

One of the steel structural systems which has gained significant attention across the world is steel special truss moment frames (STMFs). The system was first assessed by Itani and Goel in (1990), and it was considered as one of the allowed structural systems by AISC 341-05 in 2005 (AISC, 2005). Since truss girder is used instead of plate-girder, it is considered as one of the suitable lateral load bearing systems for structures which need to have long spans where the use of plate-girder is not cost-effective or suitable (Goel & Itani, 1994). Moreover, using steel moment resisting frames with heavy plate girders, seems not to be an appropriate design when taking other considerations into account, such as economy, structural and architectural limitations, the need for passing electrical and mechanical facilities, among others. Indeed, STMFs appear to be the best choice in such situations. Furthermore, one of the other features of these structural systems is devising a special segment at the middle of the truss girder to increase ductility and dissipate the energy that the structure receives from an earthquake. Two types of special segments have been presented by AISC 341-05 (AISC, 2005); one is the Vierendeel panel consisting of two parallel chord members and the other is the Vierendeel panel accompanied with X-type bracing members that increase its degree of indeterminacy. These two types of STMFs are shown schematically in Fig. 1.

Fig. 1
figure 1

STMF with a Vierendeel panel, b Vierendeel panel accompanied with X-type bracing members

Full size image

Goel and Itani (1994) compared the seismic behavior of steel STMFs with steel Special Moment Resisting Frames (SMRF). They showed that STMFs are more economical than SMRF and in addition they offer inherently more resistance. Furthermore, they conducted a study to investigate the seismic performance of Ordinary Truss Moment Frames (OTMFs) (Goel & Itani, 1994). It was concluded that, because of buckling of diagonal members of truss girder, more than 70% of the stiffness of the frame is lost within the initial loading cycles resulting in avoidance of energy dissipation and probably early instability. Basha (1994) investigated the seismic behavior of STMFs with X-type and Vierendeel special segments using experimental specimens. They showed that the Vierendeel type of special segment results in a more stable hysteresis curve compared with the X-type one. Moreover, it was concluded that the Vierendeel type of special segment led to a 7% reduction in the steel material required. Basha and Goel (1995) presented a methodology for the design of special truss moment frames which was considered the basis of seismic design of such structural systems in AISC 341-10 provisions (AISC, 2010). Based on the methodology, the design of STMFs should be such that when the special segment members enter the plastic range, the first ends of the columns at the base are permitted to yield, and the other members remain elastic. Besides, some limitations were introduced for the geometrical dimensions of the special segment, the depth of the truss girder, and the truss-girder length. After that, as an update to the above method, Chao and Goel (2008) proposed a plastic-based design methodology (Mokhtar-zadeh and Kaveh 1999) considering the seismic energy concept in which the input energy demand was equaled with the plastic energy dissipated by the special segments.

Peckan et al. (2009) proposed a new special segment encompassing a buckling restrained brace (BRB) located at the mid-span length of truss girder diagonally. They also presented a design methodology for the STMFs equipped with diagonal BRBs. The superiority of the new configuration compared to Vierendeel type was proved using inelastic static and dynamic analyses. Wongpakdee et al. (2012) presented a methodology for STMFs equipped with buckling restrained knee braces. In their proposed structural system, the truss girder was designed to remain elastic, and the braces were designed to be capable of dissipating the seismic energy demand. Longo et al. (2012) used energy dissipation devices located at the ends of the truss girders at the bottom chord level. They proposed a seismic design approach for STMFs to guarantee a yield mechanism of global type (Kaveh and Jahanshahi 2008). Using several finite element analyses, Ölmez and Topkaya (2011) proposed an equation to design the special segment chord members and showed that the equation recommended by AISC 341-05 (AISC, 2005) may perform poorly in certain cases. Kim and Park (2014) investigated the progressive collapse capacity of STMFs in different scenarios of column removal. Variables such as span length, number of stories and length of the special segment were considered in the study. It was shown that all structures collapse as the consequence of a sudden removal of a column. Heidari and Gharehbaghi (2015) proposed a new configuration associated with a damage and energy-based seismic design methodology for STMFs equipped with energy dissipation devices. The efficiency of the methodology was proven in comparison with the current STMFs with special segment of Vierendeel type using both inelastic static and dynamic analyses. Simasathien et al. (2017) examined the effect of using double-hollow steel sections (HSS) instead the other cross sections such as single-angle, single-HSS, double-angle and double-channel. Using a full-scale STMF sub-assemblage with a truss girder made of double-HSS subjected to both monotonic and cyclic loading, it was shown that double-HSS truss members could be alternatively used as the cross sections of the truss-girder members. They also proposed plastic hinge models for double-HSS sections required for computer analysis and design of non-yielding members. Kim and Park (2014) compared the seismic performance of STMFs with SMRFs using fragility analyses. It was shown that STMFs have larger stiffness and strength, but smaller ductility compared with SMRFs. Moreover, to retrofit the STMFs, they used viscus dampers diagonally located at the special segment and concluded that the method could significantly improve the performance of STMFs in the complete damage state. Gade and Sahoo (2016) assessed the seismic collapse of STMFs designed by force-based seismic design as per AISC 341-10 provisions (AISC, 2010) and performance-based plastic design (Chao et al., 2008). It was shown that the adjusted collapse margin ratio of those frames designed based on plastic method is higher and it cannot be achieved in an acceptable range for the other frames designed based on the force method. Dastigerdi et al. (2018) designed STMFs equipped with viscus dampers using optimization techniques. The viscous dampers were located at the ends of the truss girders at the bottom chord level. Using the inelastic dynamic analysis method, the efficiency of the approach was investigated in two case studies, with and without the use of the viscus damper. More recently, Jiansinlapadamrong et al. (2019) investigated the behavior of a very long-span STMF made of high-depth truss girder with members having double-channel sections. They investigated the performance of this type of frame in both design basis and maximum considered earthquake levels. They also recommended a modification to the axial load limit of chord members in current seismic provisions.

Generally, although STMFs exhibit many advantages over SMRFs, a limited number of studies have dealt with the seismic behavior of STMFs structural systems in comparison with SMRFs. As mentioned above, Simasathein et al. (2017) recommended double-HSS cross sections to be used for the truss-girder members. Most of the studies so far on STMFs have used double-channel and double-angle sections. In addition, the values recommended by ASCE7-16 (American Society of Civil Engineers, 2016) for seismic parameters such as seismic behavior factor (R), over-strength factor (Ω) and displacement modification factor Cd, for STMFs rely on these studies. Therefore, the investigation of these seismic parameters for STMFs is of great importance.

In this paper, certain basic parameters such as μ, R, Ω and Cd, for the STMFs made of truss girders with double-HSS cross-section are evaluated in two limit states, the one of life safety (LS) and the one of collapse prevention (CP). The inelastic static analysis method is used to determine these parameters. The effect of various variables on the main parameters is investigated, including the number of stories and the special segment length. SAP2000 software (Computers & Structures Inc., 2001) is used for both the analysis and the design steps of the methodology. It should be noted that, most of the STMFs whose seismic performance has been investigated in the literature had the truss girder constructed with double-angle or channel cross-section.

In the next sections, the main aspects and design of STMFs are first presented. Then, the modeling approach is investigated and verified with an experimental frame. After that, the seismic parameters are described. Next, the employed methodology used to reach the aims of this study is described. Finally, numerical examples are presented, and the relevant results are discussed.

Design of steel STMFs

Design provisions

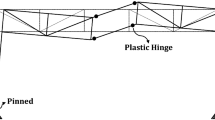
The idea behind the design of steel STMFs is that all the members outside the special segment including columns (except for bottom end of base columns), chords, diagonals and vertical members of the truss girder remain essentially elastic under the forces generated by the fully yielded and strain-hardened special segment members. Also, it is expected that the special segment members will enter the plastic range to dissipate seismic energy demand during a strong earthquake. In effect, the STMFs are designed to limit inelastic deformations to occur only in the special segment members under the design basis earthquake. A schematic view of a STMF composed of a Vierendeel panel and its laterally deformed shape with expected plastic hinges at Vierendeel special segment and bottom end of base columns are shown in Fig. 2. Some parameters of a STMF composed of a Vierendeel panel are characterized on Fig. 2(a). The dimensional limitations on the parameters recommended by AISC 341-10 (AISC, 2010) are listed in Table 1. It is worth mentioning that in the case where the special segment is composed of one Vierendeel panel, Ls is equal to Lp.

Fig. 2
figure 2

A schematic view of: a STMF composed of a Vierendeel panel with the specified dimensions, b Laterally deformed STMF with the expected plastic hinges

Full size image
Table 1 The dimensional limitations applied for STMF (AISC, 2010)
Full size table

Design process

The design process of STMFs is started by initially designing all the members including columns, special and non-special segment members under standard load combinations. The design loads include factored non-seismic and seismic loads based on the Load and Resistant Factor Design (LRFD) method conformed to AISC 360-16 (AISC, 2016). To determine the internal design forces, all the STMF members are modeled as beam-column elements and the elastic analysis method is adopted. In the next step, non-special segment members need to be redesigned if they enter the plastic range at a target displacement. In this step, a design checking based on the plastic analysis approach shall be performed. For this purpose, a nonlinear static analysis is performed considering a given target displacement at roof level where special chord members are fully yielded and strain-hardened. In this step, all members are modeled by nonlinear beam-column elements. Then, since all the non-special segment members shall behave elastically, if this condition is not satisfied, the member of interest shall be redesigned and the nonlinear static analysis is repeated to make sure that all the non-special segment members remain always elastic. It is worth mentioning that bottom ends of base columns (at the first story) may enter the plastic range. Therefore, to avoid designing unrealistically large columns, an upper limit of 0.005 radians is suggested for the plastic rotation at the base column (Jiansinlapadamrong et al., 2019). As an alternative method, column tree method with considering plastic analysis approach is also suggested by AISC341-10 (AISC, 2010). In this method, a deformed shape of the structure is assumed with a roof displacement by which special chord members fully yield and strain-hardened and bottom ends of base columns enter the plastic range. The ultimate shear force assumed for the method is suggested by AISC 341-10 (AISC, 2010) as follows:

$$V_{ne} = 3.6R_{y} \frac{{M_{nc} }}{{L_{s} }} + 0.036EI\frac{L}{{L_{s}^{3} }},$$
(1)

in which, EI is the bending rigidity of a chord member of the special segment; Mnc is the nominal flexural strength of a chord member of the special segment; and Ry is the ratio of the expected yield stress to the specified minimum yield stress. The method has been described by Chao and Goel (2008) in detail. Herein, the first method is adopted using the analysis software.

It has to be noted that, to avoid the local buckling under combined flexure and axial compression of columns, the selected column sections should satisfy the width-to-thickness ratio of flanges and webs required for compact sections.

Model verification

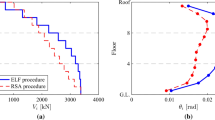
To verify the structural analysis model, an experimental specimen presented by Simasathein et al. (2017) was chosen. The model is a single-bay single-story STMF composed of a Vierendeel special segment. A schematic view of the experimental specimen and the numerical model in SAP2000 are shown in Fig. 3. Its span size is 9695 mm (approximately 9.70 m) with a story height of 3220 mm. The supports of the model are pinned at the base. All the members of the truss girder are made of double-HSS steel built-up sections and the columns are made of W-section. The double-HSS built-up sections of HSS203.2 × 101.6 × 12.7 was used for all top and bottom chord members of the truss girder, as well as the two vertical members at both sides of special segment. 2HSS127 × 127 × 9.5 was used for the vertical and diagonal members outside of the special segment. The vertical members at the ends of special segment were the same sections. Additional detailed information about this structure can be found in (Simasathien et al., 2017)

Fig. 3
figure 3

a The subject experimental STMF by Simasathien et al., (2017) as the reference model, and b the corresponding numerical model in SAP2000 at collapse state

Full size image

.

To verify the model used in this study, the pushover curve of the analysis model is compared with those for experimental specimen (Simasathien et al., 2017). For this purpose, a target displacement of 140 mm was considered and it was gradually applied on the frame using displacement control. All the chords were modeled as beam-column elements. Plastic hinges were defined at the two ends of all members using the lumped plasticity model approach. Steel material of ASTM A500/A500M Gr. B with yield stress 315 MPa and ultimate stress equal to 400 MPa was used. The moment-rotation relationship (hinge model) proposed by Simasathein et al. (2017) for double-HSS built-up sections was used for the plastic hinges of the chord members. The top beam, as shown in Fig. 3, was modeled using a simple beam element. Nonlinear moment-rotation hinge properties in accordance with P-M yield interaction surfaces were considered at the ends of columns and other elements. As shown in Fig. 4 the pushover curve of the numerical model used in this study is in an excellent agreement with that for the experimental specimen by (Simasathien et al., 2017), confirming the accuracy of the numerical model used in this work.

Fig. 4
figure 4

Pushover curve of the reference model (Simasathien et al., 2017) and the one obtained numerically in this study

Full size image

Seismic design parameters

It has well been recognized that structures designed based on current design codes are supposed to experience controlled nonlinear responses during design basis earthquakes. To capture the real nonlinear structural response under earthquake loading, one would need to use nonlinear analysis techniques which require great computational effort and are usually time consuming and difficult. For this reason, seismic codes allow the use of the equivalent linear static and/or linear dynamic analysis methods as simple and computationally more efficient alternatives, to estimate the design forces and deformations. To capture the effect of nonlinear behavior of a structure, the design forces and displacements are modified using some parameters, such as the ductility factor, response modification factor, over-strength factor and displacement amplification factors, which are studied herein.

Response modification factor

To design structures using a simple elastic analysis method, where they are supposed or expected to experience nonlinear deformations during an earthquake, the design base shear is divided with a factor known as R. This factor is computed as the product of certain parameters, as follows (Uang, 1991):

$$R = R_{s} R_{\mu } R_{r} R_{\zeta } ,$$
(2)

in which Rs, Rμ, Rr and \(R_{\zeta }\) are the reduction factors due to over-strength, ductility, degree of indeterminacy and damping, respectively. Rr and \(R_{\zeta }\) are assumed to be equal to 1.0 herein. Rμ can be computed as follows:

$$R_{\mu } = \frac{{V_{E} }}{{V_{y} }},$$
(3)

in which VE and Vy are the elastic and yielding base shear forces, respectively, which can be computed using a linear and nonlinear analysis. Different equations have been so far reported for computing Rμ. In this work, the Newmark-Hall equation (Newmark & Hall, 1982) is used for computing Rμ, as follows:

$$R_{\mu } = \left\{ {\begin{array}{*{20}c} {\sqrt {2\mu - 1} \,\,\,\,\,\,\,\,\,T \le 0.5s} \\ {\mu \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,T > 0.5s} \\ \end{array} } \right.,$$
(4)

in which T is the natural period of vibration of the structure, and is the ductility factor, which can be computed as follows:

$$\mu = \frac{{\Delta_{\max } }}{{\Delta_{y} }},$$
(5)

where Δmax is the maximum experienced displacement at the roof level corresponding to the performance level of interest, and Δy is the yield displacement obtained from the idealized pushover curve. The over-strength factor Rs is examined in the next subsection.

Over-strength factor

The over-strength factor quantifies the difference between the real, available strength of a structural system after it has been built, in comparison to its required (or assumed at design phase) strength. It is an indicator of the ability of a structure to redistribute forces and the over-strength demands in other structural elements (Falborski et al., 2020). Mwafy and Elnashai (2002) defined the factor as the ratio of the yielding base shear to the elastic strength of the structural system. Previous research on the performance of buildings during severe earthquakes indicated that the structural over-strength plays a very important role in protecting buildings from collapse (Falborski et al., 2020; Torres-Rodas et al., 2021; Zareian & Kanvinde, 2013). The factor has three sources, namely design over-strength, material over-strength, and structural system over-strength. It can be computed as follows:

$$R_{s} = R_{s0} R_{s1} R_{s2} ,$$
(6)

Ellingwood et al. (1980) showed that, for structural steel, the value of Rs1 may be taken as 1.05. Rs2 may be used to consider the increase in yield stress as a result of the strain rate effect during an earthquake excitation. A value of 1.1, i.e., a 10% increase because of the strain rate effect, could be used (Ellingwood et al., 1980). Rs0 is computed as follows:

$$R_{s0} = \frac{{V_{u} }}{{V_{d} }},$$
(7)

where Vu is the base shear corresponding to the undertaken limit state, and Vd is the design base shear which is computed as below:

$$V_{d} = C_{s,design} \,W,$$
(8)

in which Cs,design is the design base shear coefficient and W is the seismic weight. Another definition for the over-strength factor (Ω) is recommended by ASCE41-13 which is the ratio of the maximum strength of the fully yielded system to the design base shear:

$$\Omega = \frac{{V_{\max } }}{{V_{d} }},$$
(9)

in which Vmax is the maximum strength of the structure based on pushover analysis. Note that, based on Eqs. (7) and (9), when Vmax is equal to Vu, Rs0 and Ω are equal.

Displacement amplification factor

In seismic design of structures, when elastic analysis is employed, the obtained displacement values are smaller than the actual ones and they need to be amplified. For this purpose, the displacement amplification factor is used which can be computed as follows:

$$C_{d} = \frac{{\Delta_{u} }}{{\Delta_{s} }},$$
(10)

where Δu and Δs are the maximum roof displacement at the subject performance level and the roof displacement at the first actual yielding of the structure, respectively. Figure 5 shows all the base shear and roof displacement characteristic parameters defined in the above subsections. The figure also shows the actual and the idealized base shear-roof displacement curves. In this figure, ΔE is the displacement corresponding to the VE and Vs is the displacement corresponding to ΔE.

Fig. 5
figure 5

Actual and idealized pushover curve and characteristic parameters

Full size image

Scope and objectives

The main contribution of this paper is to determine the seismic parameters of R, Ω and Cd of STMFs with Vierendeel special segment and truss girder made of steel double-HSS sections. These can be considered as the most important parameters in earthquake-resistant design of structures according to contemporary design codes. The independent variables used in this work include the number of stories of the structure and the length of the special segment members. In particular, it is examined how these variables affect the previously mentioned seismic parameters. The nonlinear static analysis method considering the first mode-based load pattern is used to determine the seismic parameters. In addition, two approaches, one based on Uang (1991) and another based on ASCE41-13 recommendations (ASCE/SEI 2012) are employed for the idealization of the pushover curve needed for computing the seismic parameters. Two performance levels, namely LS and CP are considered in computing the seismic parameters. In addition to the mentioned parameters, the pushover curves of the frames considered are evaluated, and the formation of plastic hinges at large roof displacements is investigated in terms of the number of the stories and the length of the special segments. Moreover, the cumulative dissipated energy is investigated, calculated as the area confined by the pushover curve. The next section describes and discusses the worked numerical examples and the corresponding analysis results.

Numerical examples

Assumptions

In this section, the worked numerical examples are described in detail. The plan view shown in Fig. 6, with three bays in both X- and Y-directions, was considered as standard for all the frames examined. To simplify the analysis procedures, a two-dimensional STMF carrying half of the gravity and lateral loads was studied. Half of the seismic masses were attributed to each STMF. Loads and seismic masses at each joint were determined based on the respective tributary area. Twelve 3-bay STMFs with 3, 5, 7 and 9 stories and with three lengths of special segment members including 1.0, 1.5 and 2.0 m were considered as the numerical models of the study. Elevation views of the worked frame models are shown in Fig. 7. An abbreviation name is considered for each case. For example, the naming 3B9S indicates a STMF with 3 bays and 9 stories. The span length was set to L = 10 m for all the examined frames, which is less than the allowable upper limit based on Table 1 (i.e. 20 m). The length of the special segment was considered as 1.0, 1.5 and 2.0 m. Hence, the obtained ratios of Ls to L are 0.10, 0.15 and 0.20, which are within the allowable range shown in Table 1. The height of the first story was taken equal to 4.0 m, while the heights of the other stories were considered as 3.0 m. The depth of truss girder (d) is the same for all stories and was considered equal to 1.4 m, therefore, the ratio of d to L, which is 0.14, is within the allowable range specified in Table 1. The overall height (H) of the 3-story STMF is computed as 1 × 4.0 + 2 × 3.0 + 3 × 1.4 = 14.2 m. H is equal to 23.0, 31.8 and 40.6 m for 5-, 7- and 9-story STMFs, respectively, which are permitted as per ASCE7-16 recommendations (American Society of Civil Engineers, 2016).

Fig. 6
figure 6

The plan view of the building and the STMF selected

Full size image
Fig. 7
figure 7

Elevation views of the STMFs considered as numerical models

Full size image

Two types of steel material have been used for the columns and the truss-girder elements. All the properties of the materials are described in Table 2. The same values for the dead and the live loads are considered for all the stories. The standard load combinations are used as per ASCE7-16 requirements (American Society of Civil Engineers, 2016). The six load combinations used in the design are expressed as follows:

$$\begin{gathered} 1:\,\,1.4DL \hfill \\ 2:\,\,1.2DL + 1.6LL \hfill \\ 3,4:\,\,1.2(DL + 0.2S_{DS} ) + 0.5LL \pm \rho E \hfill \\ 5,6:\,\,0.9(DL - 0.2S_{DS} ) \pm \rho E \hfill \\ \end{gathered}$$
(11)

in which DL, LL and E are the dead load, live load and earthquake load, respectively. The values of DL and LL were considered as 5.0 and 3.0 kPa, respectively; and SDS is the short period design spectral acceleration. ρ was assumed to be equal to 1.0. The structure was assumed to be constructed in a site located at 32.71573° N and 117.16171° W corresponding to San Diego, California, USA as a high seismicity zone. Based on the location, the design map detailed report was downloaded from the United States Geological Survey (USGS) (USGS, 2018). The seismic design properties based on the specific site are summarized in Table 3.

Table 2 Properties of materials used for the structural members
Full size table
Table 3 Assumed parameters for the worked examples
Full size table

Some seismic design parameters based on the all the structures properties including the period (T), base shear coefficient of design (Cs,design) and power k in distribution of base shear over the height of structures (floors) are listed in Table 4. It has to be noted that the frames with different lengths of special segment have the same Cs,design since they have equal structural height.

Table 4 Seismic design parameters for each STMF examined
Full size table

The hinge model used for the special segment members is extracted from the work of Simasathein et al. (2017) and defined as shown schematically in Fig. 8, which shows a generalized moment-rotation relationship for plastic hinge of the steel double-HSS built-up sections. In this figure, Mp,exp is the expected plastic moment capacity, Mu is the ultimate moment capacity, Mr is the rest moment capacity and Z is the plastic modulus of the section.

In computing the seismic parameters, the maximum inter-story drift ratios equal to 0.025 and 0.05 were considered to find the target roof displacements corresponding to LS and CP performance levels. (Federal Emergency Management Agency (FEMA) 2000).

Herein, the truss-girder members are named and shown in Fig. 9. For instance, the cross sections of designed 3-story 3-bay STMF with Ls equal to 1.5 m are listed in Table 5.

Fig. 8
figure 8

The hinge model considered for HSS sections of truss-girder members

Full size image
Fig. 9
figure 9

Labels of different truss-girder members

Full size image
Table 5 Sections of the designed 3-bay 3-story STMF with Ls = 1.5 m
Full size table

Results and discussion

First, the pushover curves of all the STMFs are generated and investigated. Then, their monotonic energy dissipation capacity is examined. Next, the formation of plastic hinges is investigated at a roof displacement corresponding to the roof drift ratio of 0.03 (Chao & Goel, 2008). In addition, the results of the parameters µ, R, Ω and Cd obtained for all the STMFs at both LS and CP levels are presented and the effect of the two variables on them, i.e. the number of stories and Ls is investigated. To capture the effect of the number of stories on the four mentioned parameters, all the results are presented as average values across Ls. Likewise, the effects of Ls on the seismic parameters are investigated as average values across the number of stories. Finally, the average values of the seismic parameters are compared with those proposed by ASCE7-16 (American Society of Civil Engineers, 2016). Likewise, the effects of Ls on the seismic parameters are investigated in average across the number of stories.

Comparison of pushover curves

In this section, the pushover curves of all STMFs are compared with each other. To present a clearer investigation, the roof displacement and the normalized base shear (base shear to seismic weight) are considered as the horizontal and vertical axis of the pushover curve. To clarify the effect of variations of Ls, as shown in Fig. 10, four sets of curves corresponding to the 3-, 5-, 7- and 9-story STMFs are presented. The final point of the curves corresponds to CP performance level where the inter-story drift ratio is equal to 0.03.

Fig. 10
figure 10

Pushover curves of STMFs with different Ls: a 3-story, b 5-story c 7-story, d 9-story

Full size image

The pushover curves of the 3-story STMF are depicted in Fig. 10(a). As shown in Fig. 10(a), for the 3-story STMF, the initial stiffness of the STMFs with Ls = 1.0 m (black line) and Ls = 2.0 m (red dotted line) are almost equal, while the difference lies in the post-yield stiffness and the ultimate strength values where the ones of Ls = 2.0 m are much higher. Moreover, both the initial stiffness and the ultimate strength of the 3-story STMF with Ls = 1.5 m is significantly higher than those of the other two cases. Moreover, although the ultimate roof displacement is almost equal for the cases Ls = 1.5 m and Ls = 2.0 m, the former has higher ultimate strength. Based on the results, it can be concluded that the STMF with Ls = 1.5 m exhibits better performance. As can be seen in Fig. 10(b), for the 5-story case, as Ls increases, the initial stiffness, post-yield stiffness and ultimate strength also increase. In addition, the ultimate roof displacement for the case Ls = 1.0 m is much lower than that of the other cases.

Based on Fig. 10(c), for the 7-story case, the pushover curves of STMF with Ls = 1.5 and Ls = 2.0 m almost coincide, and these frames exhibit clearly more ductile behavior than the one of the case Ls = 1.0 m. Moreover, by increasing the Ls value, the ultimate roof displacement also increases. As their yield displacements are almost the same, the displacement ductility ratio is increased as Ls increases. As shown in Fig. 10(d), for the 9-story STMFs, the initial stiffness, post-yield stiffness and ultimate strength all increase as the Ls value increases.

In general, the STMF with Ls = 1.0 m is more brittle than the ones with other Ls values (1.5 m and 2.0 m). In addition, for low-rise STMFs, i.e. the 3- and 5-story ones, the Ls = 1.5 m case exhibits the desired behavior compared with the other frames with the same number of stories. By increasing the number of stories, the behavior of STMF with Ls = 2.0 m becomes better than the ones of the others. Furthermore, by increasing the number of stories, the initial stiffness of the frames with the same story tends to be equal, for different Ls values.

Next, the area confined by the pushover curve and the displacement axis is computed for all the frame models. This area is an indicator of the monotonic energy dissipation capacity of the structure. The corresponding parameter, as an energy curve, is shown for all the frames in Fig. 11 versus the number of displacement steps of the pushover procedure. As shown in this figure, the monotonic energy dissipation capacity is increased as Ls increases from 1.0 m to 2.0 m and this is true for all models except the 3-story STMF in which the capacity is greater for Ls = 1.5 m. To make a clearer comparison of the energy capacity of the frames, the variations of the ultimate energy capacity of the STMF models are measured with respect to the frames with Ls = 1.0 m and the results are presented in Table 6. As shown in this table, by increasing the Ls value from 1.0 m to 1.5 m, in average, the ultimate energy capacity increases by 64%, while the corresponding increase when Ls increases from 1.0 m to 2.0 m is 83%.

Fig. 11
figure 11

Energy curves of STMFs with different Ls values: a 3-story, b 5-story c 7-story, d 9-story

Full size image
Table 6 Variation (increase) of the maximum energy, in relation to the corresponding Ls = 1.0 m case
Full size table

Plastic hinges formation

Herein, the formation of plastic hinges at a roof displacement corresponding to the roof drift ratio of 0.03 is investigated. For illustration purposes, the 5-story STMFs with Ls = 1.5 is investigated herein and the other frames are shown in Appendix A for the interested reader. As shown in Fig. 12, all the members of the special segment have fully yielded while the other members have remained elastic, which satisfies the fundamental concept behind the seismic design with STMFs. Also, the distribution of the plastic hinges is uniform over the height of the structure which shows a desired and satisfactory design for the frame. It should be noted that plastic hinges were defined (and were able to form) for all members.

Fig. 12
figure 12

Formation of plastic hinges for the 3-story STMF with Ls = 1.5 m and roof drift ratio of 0.03

Full size image

Evaluation of the seismic parameters μ, R, Ω and C d

Effect of the number of stories

The average values of µ, R, Ω and Cd for the LS and CP performance levels corresponding to the number of stories are presented in Tables 7 and 8, respectively. Note that, for µ and R parameters, the results are obtained based on both Uang (1991) and ASCE41-13 (ASCE/SEI 2012) methods.

Table 7 Variations of average µ, R, Ω and Cd for STMFs vs. number of stories for LS performance level
Full size table
Table 8 Variations of average μ, R, Ω and Cd for STMFs vs. number of stories for CP performance level
Full size table

Based on Table 7, it is shown that, as the number of stories increases, µ decreases from 2.39 to 1.93 (19.2% decrease) for the Uang method and from 2.09 to 1.93 (7.6% decrease) for the ASCE41-13 method. In addition, the differences between the results of the two methods drastically decreases as the number of stories increases and the results are practically the same in the case of the tallest, 9-story STMF. The values of µ and R corresponding to CP level are shown in Table 8. As shown, as the number of stories increases, µ decreases from 3.38 to 1.96 (42% decrease) and from 2.85 to 1.95 (31.6% decrease) for the Uang and the ASCE41-13 methods, respectively. The decrease of µ with increasing the number of stories is more pronounced in the CP performance level in comparison to the LS level.

As shown in Table 7, by increasing the number of stories from 3 to 9, the values of R decrease from 10.9 to 6.95 for the Uang method, and decrease from 10.21 to 6.96 for the ASCE41-13 method. 36 and 32% decrease in the values of R are observed for the Uang and ASCE41-13 methods, respectively. In addition, as shown for the CP performance level in Table 8, the values of R decrease from 17.96 to 8.03, i.e. 55% decrease for the Uang method and accordingly from 16 to 8.01, i.e. 50% decrease for the ASCE41-13 method, confirming the point that R decreases as the number of stories increase. These effects are due to the decrease in the ductility ratio (µ) as the number of stories increases. It can be also stated that, the Uang method almost results in higher values for R compared with those of the ASCE41-13 method. The reductions of µ and R versus increasing the number of stories are more pronounced for the CP level, compared with those of the LS performance level.

As shown in Tables 7 and 8, as the number of stories increases, the value of Ω decreases from 4.9 to 3.52 for LS and from 5.32 to 3.54 for CP performance level. By increasing the number of stories from 3 to 9, the value of Ω is almost 28.16 and 33.46% decreased, respectively, for the LS and the CP performance levels. Moreover, except for the 3-story frame, the difference between LS and CP levels is almost negligible.

For the Cd parameter, which highly depends on µ, as shown in Tables 7 and 8, by increasing the number of stories from 3 to 9, it decreases from 4.24 to 3.08 for LS and from 8.17 to 5.91 for CP performance level. These results show almost 28% reduction in both LS and CP performance levels. Moreover, the values of Cd for CP are almost twice the ones for the LS level.

The results of both Tables 7 and 8 show that the metrics are sensitive to the increasing of the height of the frames. The main reason is that by increasing the number of stories, the ratio of yielding base shear to weight, ductility and the ability of the frame to redistribute forces and deformations are decreased and plasticity cannot be uniformly distributed over the height.

Effect of the special segment length (L s)

Herein, the effect of Ls on the seismic parameters µ, R, Ω and Cd is assessed. Table 9 shows the average values of µ, R, Ω and Cd for different Ls of 1.0, 1.5 and 2.0 m corresponding to LS level for both the Uang and the ASCE41-13 methods. In addition, the mentioned parameters corresponding to the CP level are shown in Table 10.

Table 9 Variations of average μ, R, Ω and Cd for STMFs with different Ls for LS performance level
Full size table
Table 10 Variations of average μ, R, Ω and Cd for STMFs with different number of stories for CP performance level
Full size table

Based on Table 9, it is indicated that, as the Ls value increases, µ increases from 1.64 to 2.36 (43.9% increase) and from 1.6 to 2.23 (39.38% increase) for the Uang and the ASCE41-13 methods, respectively. In addition, the values of µ corresponding to CP level are shown in Table 10. As shown, as the Ls value increases, µ increases from the small value of 1.5 to 3.16 (110.67% increase) and from 1.47 to 2.85 (93.88% increase) for the Uang and the ASCE41-13 methods, respectively. Thus, it can be concluded that, µ significantly increases as the Ls value increases from 1.0 to 2.0 m.

As can be seen from Table 9, for the ASCE41-13 method, R is equal to 9.87 for Ls = 1.5 m which is higher than the corresponding R for the other Ls values, which are 6.7 and 9.17 for the 1.0 and 2.0 m cases, respectively. Likewise, for the Uang method, R is equal to 10.17 for Ls = 1.5 m which is higher than 6.81 and 9.43 corresponding to the Ls values of 1.0 and 2.0 m, respectively.

In addition, Table 10 shows the results of R corresponding to CP for both the Uang and the ASCE41-13 methods. The value of R increases from 6.81 to 15.2 for the Uang method. For the ASCE41-13 method, R is equal to 14.32 for Ls = 1.5 m which is higher than the ones for the other Ls values of 1.0 and 2.0 m which are 6.7 and 14.09, respectively. In the other words, for the ASCE41-13 method, 123.2 and 110.3% increases are observed in R values when Ls increases from 1.0 to 1.5, and 1.0 to 2.0 m, respectively. These variations are significantly greater than those for the LS level. Finally, for CP level similar to LS level, the value of R increases as Ls increases.

Tables 9 and 10 also show the values of Ω for both the LS and CP performance levels. As observed, the value of Ω increases from 3.8 to 4.39 for LS level (i.e. 15.53% increase) and from 3.8 to 4.76 for CP level (i.e. 25.26% increase), as Ls increases from 1.0 to 2.0 m.

Moreover, Cd values are listed in Tables 9 and 10 for the LS and CP levels, respectively. As shown, by increasing Ls from 1.0 to 2.0 m, the value of Cd decreases from 3.61 to 3.42 for the LS level which corresponds to 5.26% increase. As well, the value of Cd for CP level increases from 6.04 to 7.38 (i.e. 22.19% increase) as Ls increases from 1.0 to 1.5 m, and it is almost the same for Ls values of 1.5 and 2.0 m.

In general, all the values of R, Ω and Cd show higher variations when Ls changes from 1.0 to 1.5 m compared with the corresponding variations when it changes from 1.5 to 2.0 m. It can be concluded that by increasing the length of the horizontal chord members of special segment at the top and bottom level of the truss girder, the condition to experiencing more degree of plasticity of special segment members is provided and ductility is increased. In addition, the potential for redistribution of forces and deformation is provided to a greater extent.

Comparison of R s with Ω, and C d with µ

Herein, the Rs values are compared with Ω using a ratio of X defined as follows:

$$X = \frac{\Omega }{{R_{s} }},$$
(12)

In addition, the ratio of Cd to µ is assessed using the following ratio of Y as:

$$Y = \frac{{C_{d} }}{\mu },$$
(13)

The results for the X and Y ratios corresponding to LS and CP levels are depicted in Fig. 13. Note that, Rs and µ considered herein are based on the Uang method. For each ratio, the minimum, maximum and average values are shown on the figure. As shown in Fig. 11(a), for LS level, X varies from 0.89 to 1.22 with the average value of almost 1.0 indicating that they are the same on average. Likewise, for CP level, X ratio is in the range of 0.79 to 1.24 with the average value 0.9 indicating 10% differences between Rs and Ω. As can be seen from Fig. 13(b), the Y ratio varies from 1.35 to 2.4 with the average value of 2.4 for LS level, and it is in the range of 1.86 to 4.37 with an average value of 3.08 for CP level. It can be said that, on average, Cd is about 2.4 and 3.0 times the value of µ for LS and CP levels, respectively.

In addition, the Pearson correlation coefficient r was computed for Rs and Ω corresponding to all models. The obtained value of r was 0.80 and 0.88, respectively, for LS and CP levels, indicating good agreement. Moreover, r was also computed for Cd and µ with obtained values 0.29 and 0.8. The values of Cd and µ show a good agreement for the CP level while a very poor correlation for LS level, which is reasonable.

Fig. 13
figure 13

Results of X and Y ratios for all studied models

Full size image
Comparison with ASCE7-16

Herein, the values of R, Ω and Cd are compared with those of proposed by ASCE7-16 (American Society of Civil Engineers, 2016). R = 7.0, Ω = 3.0 and Cd = 5.5 are considered for the design of STMFs based on ASCE7-16. The results of R show that, by increasing the number of stories, the differences between the obtained values in this work (for both performance levels) and ASCE7-16 are decreasing. This is also true for Ω. Regarding Cd, it is the same for the CP level.

To make a valid general comparison, the average values of R, Ω and Cd for all 12 STMFs, for both LS and CP performance levels are compared with those proposed by ASCE7-16. The average results of R, Ω and Cd and those proposed by ASCE7-16 are listed in Table 11 and their differences are presented. As shown in this table, the average values of R, Ω and Cd, respectively, show almost 23% and 39% higher values and 36% lower value for LS level in comparison with those proposed by ASCE7-16. Again, if the CP level is considered as the basis of comparison, the average values of R, Ω and Cd, respectively, give almost 67%, 45% and 28% higher values compared with those of ASCE7-16.

Table 11 Comparing the average values of R, Ω and Cd with those proposed by ASCE7-16
Full size table

Conclusions

In this research work, the seismic parameters R, Ω and Cd of twelve STMFs composed of Vierendeel special segments were determined and assessed. The problem variables used in the parametric analysis were the number of stories, including 3, 5, 7 and 9 stories, and the length of the special segment considering the cases 1.0, 1.5 and 2.0 m. These variables combined together, resulted in 12 different STMFs designed based on AISC41-13 and ASCE7-16 provisions. The nonlinear static analysis method was used to derive the pushover curves. The main findings of the study, when HSS sections properties was chosen, are the following:

  • For both LS and CP performance levels, by increasing the number of stories, R, Ω and Cd decrease.

  • In general, for both LS and CP performance levels, as the length of special segment increases, µ increases, and R, Ω and Cd also therefore increase.

  • In general, the cumulative energy dissipation capacity (monotonic type) of the models with Ls = 2.0 m is greater the one of other models while the differences tend to be very small for low-rise frames.

  • In general, for low-rise STMFs, such as the ones with 3- and 5-stories, the frames with Ls = 1.5 m exhibit a better and more desirable behavior.

  • By increasing the number of stories, the behavior of STMF with Ls = 2 m becomes more desirable than the others.

  • Although the average values of R, Ω and Cd have significant differences with respect to the ASCE7 recommended values, by increasing the number of stories, the differences become practically negligible.