A New Surface Node Method to Accurately Model the Mechanical Behavior of the Boundary in 3D State-Based Peridynamics

Abstract

Peridynamics is a non-local continuum theory capable of modeling crack initiation and propagation in solid bodies. However, the layer near the boundary of the body exhibits a stiffness fluctuation due to the so-called surface effect and the inaccurate way of imposing the boundary conditions. Moreover, in numerical models discretized using the meshfree method with uniform grid spacing, there are no nodes on the external surface of the body where the boundary conditions should be applied. Inspired by the method of the fictitious nodes with the Taylor-based extrapolation, we propose an innovative method that introduces a new type of nodes lying on the external surface of the body, i.e., the surface nodes. These nodes represent the interactions between the nodes within the body and the fictitious nodes surrounding the body, and they are used to mitigate the surface effect and properly impose the boundary conditions via the concept of force flux. Moreover, a procedure to compute the analytical solution of peridynamic problems is developed: a manufactured displacement field is prescribed and the volume and surface forces, to obtain that displacement field, are computed. The benefits of the surface node method are shown by means of several 2D and 3D quasi-static examples by comparing the numerical results with other methods with or without boundary corrections.

1 Introduction

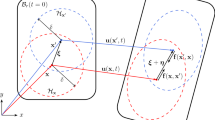
Peridynamics is a non-local continuum theory of solid mechanics devised to intrinsically model discontinuities in the displacement field, such as crack initiation and propagation [1, 2]. This is possible because peridynamic equations do not contain any spatial derivatives, but only integrals. Peridynamic points interact with each other if their distance is smaller than or equal to a prescribed value $\delta$, called the horizon size. Therefore, the interactions of a point are contained in a sphere, named neighborhood, centered in that point with a radius $\delta$.

The most commonly used method to solve numerically peridynamic integrals is a uniform meshfree discretization with a mid-point quadrature rule [3,4,5,6]. In the literature, there are many examples of the good agreement of peridynamic results compared to mechanical experiments involving fracture [7, 8]. Nonetheless, the non-local nature of Peridynamics leads to three main drawbacks:

• higher computational cost with respect to numerical models based on classical continuum mechanics, such as the Finite Element Method (FEM);

• undesired stiffness fluctuations near the boundary of the body, known as surface effect or skin effect;

• difficulty in imposing properly the boundary conditions.

The coupling between Peridynamics and FEM can be exploited to reduce the computational cost: Peridynamics is used only where cracks are more likely to propagate, whereas FEM-based approaches are used for the rest of the domain [9,10,11,12,13,14,15,16,17,18,19,20]. The surface effect is due to the fact that the neighborhoods near the boundary of the body are incomplete, so that the most external layer of the body has different stiffness properties with respect to the bulk of the body [21,22,23,24,25,26]. Another issue related to the boundary is that external loads and constraints should be distributed over a layer of finite thickness near the boundary [27], but the definition of a standard method for imposing non-local boundary conditions is problematic.

Both the surface effect and the problem of the imposition of the non-local boundary conditions can be reduced by decreasing the horizon size $\delta$ near the boundary with the variable horizon method [24, 28,29,30,31,32,33]. However, this approach inevitably varies the peridynamic solution where the value of $\delta$ is modified. The mechanical properties of the interactions between nodes near the boundary can be tuned to correct the surface effect [23, 27, 34,35,36,37], but the peridynamic solution exhibits some undesired fluctuations near the boundary because of the inaccurate imposition of the boundary conditions [22]. Another approach implies the reformulation of the peridynamic equations via the peridynamic differential operator [38,39,40,41,42].

The method of the fictitious nodes is arguably the most commonly used to mitigate the boundary issues: a layer of nodes is added all around the body to complete the neighborhoods of the nodes close to the boundary, thus the surface effect vanishes [35, 43, 44]. However, the displacements of the fictitious nodes are unknown and may be extrapolated with the displacements of the nodes within the body. Many authors suggested that this extrapolation can be used to enforce boundary conditions [22, 27, 32, 33, 45,46,47,48,49,50,51], but the formulae they used are case-dependent and applicable only to simple geometries. On the other hand, we proposed in [25, 26] that the non-local concept of force flux, i.e., the peridynamic version of stress, should be exploited to coherently impose the boundary conditions. Furthermore, we employed the extrapolation based on the Taylor series expansion, with a general truncation order N, which adopts the nearest-node strategy, to manage more complex body geometry. Nevertheless, the method we proposed is limited to 2-dimensional cases and makes use of the Lagrange multipliers to impose the boundary conditions. The main disadvantages in imposing the boundary conditions via Lagrange multipliers are related to the structure of the matrix to solve [52, 53]:

• the dimensions of the matrix increase because of the higher number of unknowns;

• the matrix is not, in general, positive definite;

• the matrix is not banded;

• there are zeroes on the diagonal of the matrix.

Clearly, these characteristics make the matrix more computationally expensive to invert.

Inspired by [25, 26], this paper aims at developing a novel numerical method to impose the boundary conditions in peridynamic models without the use of Lagrange multipliers. We introduce a new type of nodes, the surface nodes, that represent the external surface of the body. The surface nodes have their own degrees of freedom that can be used during the Taylor-based extrapolation of the displacements. The equations of motion of the surface nodes are based on the concept of force flux, thus they represent the interactions between the fictitious nodes and the nodes within the body. Thanks to this fact, the boundary conditions can be applied directly to the surface nodes, as one would do in a local model, without the use of the Lagrange multipliers. The number of unknowns is still higher than that of a model without corrections at the boundary, but the new unknowns have the physical meaning of the displacements of the external surface of the body. The stiffness matrix is still not, in general, positive definite, but its bandwidth remains the same as that of the peridynamic system without corrections to the boundary issues and there are no zeroes on its diagonal. Hence, the numerical solution to the system of equations can be found more efficiently by a computational standpoint. Furthermore, with respect to the previous method of the fictitious nodes, the surface node method allows for a simpler implementation (the boundary conditions are imposed as one would do in a local model). 3D static numerical examples are presented to show the benefits achieved by the new method. In the Appendix, we also developed a procedure to obtain the peridynamic analytical solutions, which are then employed to compute the errors in the numerical models. The comparison with other methods recently developed to correct the surface effect and impose the peridynamic boundary conditions is provided as well.

The paper is organized as follows: Section 2 reviews briefly the main equations of ordinary state-based Peridynamics and the method of the fictitious layer to correct the boundary issues; Section 3 presents the numerical implementation of the novel method of the surface nodes; Section 4 shows the differences between the models with and without the use of the method of the surface nodes; Section 5 compares the proposed method with three of the most recent methods for boundary corrections; Section 6 draws the conclusions. Furthermore, the Appendix shows a procedure to compute the analytical solutions for peridynamic problems when prescribing an (even complex) displacement field.

2 Review of Peridynamic Theory

A peridynamic interaction between neighboring points $\mathbf {x}$ and $\mathbf {x}'$ is called bond and is identified by the relative position vector in the initial configuration as

$$\begin{aligned} \boldsymbol{\xi } = \mathbf {x}' - \mathbf {x} \, , \end{aligned}$$

(1)

where $\Vert \boldsymbol{\xi } \Vert \le \delta$. Therefore, point $\mathbf {x}$ interacts with all the points in the neighborhood $\mathcal {H}_{\mathbf {x}} = \big \{ \mathbf {x}' \in \mathcal {B}(t_0): \Vert \boldsymbol{\xi }\Vert \le \delta \big \}$, where $\mathcal {B}(t_0)$ is the body in the initial configuration and $\delta$ is the horizon size, as shown in Fig. 1. The relative displacement vector $\boldsymbol{\eta }$ is defined in the deformed configuration $\mathcal {B}(t)$ at time $t>t_0$ as

$$\begin{aligned} \boldsymbol{\eta } = \mathbf {u}(\mathbf {x}',t) - \mathbf {u}(\mathbf {x},t) \, , \end{aligned}$$

(2)

where $\mathbf {u}$ is the displacement field. Note that $\boldsymbol{\xi } + \boldsymbol{\eta }$ is the relative position of points $\mathbf {x}$ and $\mathbf {x}'$ in the deformed configuration.

Fig. 1

Body modelled with Peridynamics in the initial configuration $\mathcal {B}(t_0)$ and deformed configuration $\mathcal {B}(t>t_0)$: the force state $\mathbf {f}$ arises due to the deformation of the body

The peridynamic equation of motion of a point $\mathbf {x}$ is given by [1, 2]:

$$\begin{aligned} \rho (\mathbf {x}) \, \ddot{\mathbf {u}}(\mathbf {x},t) = \int _{\mathcal {H}_{\mathbf {x}}} \mathbf {f}(\mathbf {x},\mathbf {x}',t) \,\mathrm {d}V_{\mathbf {x}'} + \mathbf {b}(\mathbf {x},t) \, , \end{aligned}$$

(3)

where $\rho$ is the material density, $\ddot{\mathbf {u}}$ is the acceleration field, $\mathbf {f}$ is the force state (force per unit volume squared), $\,\mathrm {d}V_{\mathbf {x}'}$ is the differential volume of a point $\mathbf {x}'$ within the neighborhood $\mathcal {H}_{\mathbf {x}}$ and $\mathbf {b}$ is the external force density field. In quasi-static conditions, Eq. (3) becomes the equilibrium equation of point $\mathbf {x}$:

$$\begin{aligned} - \int _{\mathcal {H}_{\mathbf {x}}} \mathbf {f}(\mathbf {x},\mathbf {x}') \,\mathrm {d}V_{\mathbf {x}'} = \mathbf {b} (\mathbf {x}) \, . \end{aligned}$$

(4)

The value of $\mathbf {f}(\mathbf {x},\mathbf {x}')$ is determined in the following.

2.1 Ordinary State-Based Peridynamics

The reference position scalar state $\underline{x}$ represents the bond length in the initial configuration:

$$\begin{aligned} \underline{x} = \Vert \boldsymbol{\xi } \Vert \, . \end{aligned}$$

(5)

On the other hand, the extension scalar state $\underline{e}$ represents the elongation (or contraction) of the bond in the deformed configuration:

$$\begin{aligned} \underline{e} = \Vert \boldsymbol{\xi } + \boldsymbol{\eta } \Vert - \Vert \boldsymbol{\xi } \Vert \, . \end{aligned}$$

(6)

Hereinafter, the Gaussian influence function is adopted:

$$\begin{aligned} \underline{\omega } = \exp \left( -\frac{\Vert \boldsymbol{\xi } \Vert ^2}{\delta ^2} \right) \, \end{aligned}$$

(7)

For later use, the weighted volume m and the dilatation $\theta$ of a point $\mathbf {x}$ are defined respectively as

$$\begin{aligned} m(\mathbf {x}) = \int _{\mathcal {H}_{\mathbf {x}}} \underline{\omega } \, \underline{x}^2 \,\mathrm {d}V_{\mathbf {x}'} \, , \end{aligned}$$

(8)

$$\begin{aligned} \theta (\mathbf {x}) = \frac{c_{\theta }}{m(\mathbf {x})} \int _{\mathcal {H}_{\mathbf {x}}} \underline{\omega } \, \underline{x} \, \underline{e} \,\mathrm {d}V_{\mathbf {x}'} \, , \end{aligned}$$

(9)

where $c_{\theta }$ = 3 [2].

In ordinary state-based Peridynamics, the force state is aligned with the bond direction for any deformation, as depicted in Figure 1. The bond direction is defined as

$$\begin{aligned} \mathbf {m} = \frac{\boldsymbol{\xi }+\boldsymbol{\eta }}{\Vert \boldsymbol{\xi }+\boldsymbol{\eta } \Vert } \, . \end{aligned}$$

(10)

Hence, the force state can be computed as [2]

$$\begin{aligned} \mathbf {f}(\mathbf {x},\mathbf {x}') = \left[ k_{\theta } \left( \frac{\theta (\mathbf {x})}{m(\mathbf {x})} + \frac{\theta (\mathbf {x}')}{m(\mathbf {x}')} \right) \underline{\omega } \, \underline{x} + k_e \left( \frac{1}{m(\mathbf {x})} + \frac{1}{m(\mathbf {x}')} \right) \underline{\omega } \, \underline{e} \right] \mathbf {m} \, , \end{aligned}$$

(11)

with $k_{\theta } = -3(1-4\nu )E/(2(1+\nu )(1-2\nu ))$ and $k_e = 15E/(2(1+\nu ))$, where $\nu$ is the Poisson’s ratio and E is the Young’s modulus. The constants $k_{\theta }$ and $k_e$ are derived by equalizing the peridynamic strain energy density of a point with a complete neighborhood under homogeneous deformation, with the strain energy density in a point subjected to the same deformation in classical continuum mechanics [2].

2.2 Force Flux

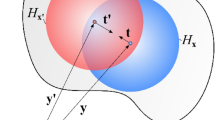
Suppose that the force flux $\boldsymbol{\tau }$, i.e., the peridynamic concept of stress, should be computed at a point $\mathbf {x}$ in the direction of the unit vector $\mathbf {n}$. As shown in Fig. 2, the plane with normal $\mathbf {n}$ passing through point $\mathbf {x}$ is named $\mathcal {P}$. The unit sphere $\Omega$ centered in $\mathbf {x}$ represents all the directions that the bonds passing through $\mathbf {x}$ may have, and $\,\mathrm {d}\Omega _{\mathbf {m}}$ is the differential solid angle on $\Omega$ in direction $\mathbf {m}$ of the considered bond. In order for the bond to pass through the plane $\mathcal {P}$, the points of that bond must lie in the different half-spaces generated by $\mathcal {P}$. Therefore, we define the points of a bond in the direction $\mathbf {m}$ as $\mathbf {x}' = \mathbf {x}-s\mathbf {m}$ and $\mathbf {x}'' = \mathbf {x}+(r-s)\mathbf {m}$, where $0 \le s \le \delta$ and $s \le r \le \delta$ (see Fig. 2).

Fig. 2

The force flux $\boldsymbol{\tau } (\mathbf {x},\mathbf {n})$ computed at point $\mathbf {x}$ in direction $\mathbf {n}$ is the resultant of the forces per unit area of all the bonds passing through plane $\mathcal {P}$ with normal $\mathbf {n}$. The bonds may have any direction $\mathbf {m}$ within the unit sphere $\Omega$ and the two points of the bond are defined by the values s and r as $\mathbf {x}' = \mathbf {x}-s\mathbf {m}$ and $\mathbf {x}'' = \mathbf {x}+(r-s)\mathbf {m}$, where $0 \le s \le \delta$ (dashed line) and $s \le r \le \delta$ (dashdotted line)

The force flux is defined as the resultant of the forces per unit area of all the bonds intersecting $\mathcal {P}$ in $\mathbf {x}$ [54]:

$$\begin{aligned} \boldsymbol{\tau } (\mathbf {x},\mathbf {n}) = \frac{1}{2} \int _{\Omega } \int _{0}^{\delta } \int _{s}^{\delta } \mathbf {f} (\mathbf {x}', \mathbf {x}'') \left( \mathbf {m} \cdot \mathbf {n} \right) \, r^2 \,\mathrm {d}r \,\mathrm {d}s \,\mathrm {d}\Omega _{\mathbf {m}} \, . \end{aligned}$$

(12)

The factor $\left( \mathbf {m} \cdot \mathbf {n} \right)$ in the integrand is required to project the force state along the direction $\mathbf {n}$. Note that the integration limits in Eq. (12) allow to consider every bond passing through point $\mathbf {x}$. However, each bond is repeated twice in the integration domain (for both directions $\mathbf {m}$ and $-\mathbf {m}$), thus the integral is divided by 2.

2.3 Problems at the Boundaries

The non-local formulation of the peridynamic theory exhibits two issues near the boundary: the so-called surface effect and the difficulty of imposing properly the boundary conditions. The former is due to the incomplete neighborhoods of points close to the boundary of the body [22], as shown in Fig. 3. The mechanical properties of peridynamic materials are indeed computed for points with a complete neighborhood, i.e., in the bulk of the body. Note that the lacking part of the neighborhood increases as the points are near the faces, the edges, or the vertices of the body, hence the stiffness fluctuations due to the surface effect are expected to increase accordingly [26].

Fig. 3

Some points in the bulk, as $\mathbf {x}$, have a complete neighborhood, whereas other points near the boundary, as $\mathbf {x}'$ and $\mathbf {x}''$, have an incomplete neighborhood

In local models, boundary conditions are imposed on the points lying on the boundary. This is possible because, for instance, a force applied to a point has a “local” influence only on that point. On the other hand, in non-local models such as Peridynamics, a force applied to a point influences a spherical region surrounding that point (see the concept of force flux in Section 2.2). Therefore, peridynamic boundary conditions should be imposed in a layer of finite thickness near the boundary of the body. Nonetheless, how to “distribute” the boundary conditions over a finite layer of material is still an open issue in Peridynamics.

2.4 Method of the Fictitious Layer

The addition of a layer $\mathcal {F}$ of fictitious points of thickness $\delta$ around the body is a simple way to complete the neighborhoods of the points near the boundary [43], as shown in Fig. 4. The displacements of the fictitious points are evaluated by means of an extrapolation procedure in order to ensure that the fictitious layer keeps deforming as the body.

Fig. 4

When a fictitious layer of thickness $\delta$ is added around the body, all the points of the body have a complete neighborhood

We adopt the Taylor-based extrapolation method with the nearest-node strategy for its simplicity [25, 26]. The displacement vector of a point $\mathbf {x}_f = \{ x_f, y_f, z_f \}^{\top }$ in the fictitious layer $\mathcal {F}$ is determined as the Taylor series expansion truncated at a general order $N \ge 1$ about the closest point $\mathbf {x}_c = \{ x_c, y_c, z_c \}^{\top }$ of the body:

$$\begin{aligned} \mathbf {u} (\mathbf {x}_f) = \mathbf {u} (\mathbf {x}_c) + \sum _{n=1}^{N} \sum _{n_1=0}^{n} \sum _{n_2=0}^{n-n_1} \frac{(x_f-x_c)^{n_1} (y_f-y_c)^{n_2} (z_f-z_c)^{n_3}}{n_1! \, n_2! \, n_3!} \cdot \frac{\partial ^{n_1+n_2+n_3}\mathbf {u}(\mathbf {x}_c)}{\partial x^{n_1} \partial y^{n_2} \partial z^{n_3}} \, , \end{aligned}$$

(13)

where $n_3 = n-n_1-n_2$. Note that the points of the body closest to the fictitious points are the ones at the boundary of the body itself. To mitigate the surface effect, the weighted volume of the fictitious points is computed as if their neighborhoods were complete, thus $m (\mathbf {x}_f) = m (\mathbf {x}_c)$. Moreover, since the dilatation is a measure of strain, that of the fictitious points is evaluated by means of a Taylor series expansion as in Eq. (13) with a truncation order $N-1$. If the displacements are extrapolated with a truncation order $N=1$, then the dilatation of a fictitious point is equal to the dilatation of the closest point of the body: $\theta (\mathbf {x}_f) = \theta (\mathbf {x}_c)$. Otherwise for $N \ge 2$, the dilatation of a fictitious point is determined as

$$\begin{aligned} \theta (\mathbf {x}_f) = \theta (\mathbf {x}_c) + \sum _{n=1}^{N-1} \sum _{n_1=0}^{n} \sum _{n_2=0}^{n-n_1} \frac{(x_f-x_c)^{n_1}}{n_1!} \cdot \frac{(y_f-y_c)^{n_2}}{n_2!} \cdot \frac{(z_f-z_c)^{n_3}}{n_3!} \cdot \frac{\partial ^{n_1+n_2+n_3} \theta (\mathbf {x}_c)}{\partial x^{n_1} \partial y^{n_2} \partial z^{n_3}} \, , \end{aligned}$$

(14)

where $n_3 = n-n_1-n_2$.

The Taylor-based extrapolation method is able to correct the surface effect when the truncation order N matches the order of the displacement field: for instance, if the displacements vary linearly, a Taylor series expansion with $N=1$ exactly extrapolates the displacements in the fictitious layer. For a displacement field of general order, more accurate results are obtained by increasing the truncation order.

In order to impose the boundary conditions in a non-local way, the equation which governs the behavior of the points at the boundary of the body is based on the concept of force flux [25, 26]:

$$\begin{aligned} \boldsymbol{\tau } (\mathbf {x}_c,\mathbf {n}) = \mathbf {p}(\mathbf {x}_c) \, , \end{aligned}$$

(15)

where $\mathbf {n}$ is the outward unit vector normal to the boundary in $\mathbf {x}_c$ and $\mathbf {p}$ is the force per unit area applied to $\mathbf {x}_c$. Because of the definition of force flux (Eq. 12), the external load $\mathbf {p}$ is “spread”, in a non-local way, within the most external layer of the body via the bonds that are passing through $\mathbf {x}_c$.

3 Method of the Surface Nodes

In this section, we show how to implement the method of the fictitious layer in a numerical peridynamic model via the introduction of the surface nodes. The body domain and the fictitious layer are discretized by adopting the meshfree method with a uniform grid spacing h [3, 4], as shown in Fig. 5. The nodes within the body and the fictitious layer are respectively called interior nodes and fictitious nodes. Each node of the grid is representative of a cell with cubic volume $V = h^3$. Since the boundary conditions are imposed on the external surface of the body, we add a new type of nodes, namely the surface nodes (marked by solid squares in Fig. 5), near the most external interior nodes. Each surface node represents a cell face of one of the interior nodes closest to the boundary, i.e., a square area $A = h^2$ of the external surface of the body. Note that, since the surface nodes do not represent a volume cell, they do not have the properties of weighted volume and dilatation. Indeed, a surface node is not connected to any bond but is related to the bonds that intersect its area, as explained in Section 3.4.

Fig. 5

Uniform peridynamic grid of interior nodes (solid circles) and fictitious nodes (empty circles), with the introduction of the surface nodes (solid squares) on the external surface of the body

3.1 Numerical Force States

Consider two nodes i and j that are connected by the bond

$$\begin{aligned} \boldsymbol{\xi }_{ij} = \mathbf {x}_j - \mathbf {x}_i \, . \end{aligned}$$

(16)

Surface nodes are not connected to any bond, therefore nodes i and j can be either interior or fictitious nodes. The relative displacement vector of this bond after the deformation of the body is computed as

$$\begin{aligned} \boldsymbol{\eta }_{ij} = \mathbf {u}_j - \mathbf {u}_i \, , \end{aligned}$$

(17)

where $\mathbf {u}_i$ and $\mathbf {u}_j$ are the displacement vectors of nodes i and j, respectively. If one of these nodes is in the fictitious layer, then its displacements are determined by the Taylor-based extrapolation method described in Section 3.2. The reference position scalar state and the influence function of the bond are evaluated as follows:

$$\begin{aligned} \underline{x}_{ij} = \Vert \boldsymbol{\xi }_{ij} \Vert \, , \end{aligned}$$

(18)

$$\begin{aligned} \underline{\omega }_{ij} = \exp \left( -\frac{\Vert \boldsymbol{\xi }_{ij} \Vert ^2}{\delta ^2} \right) \, . \end{aligned}$$

(19)

Under the assumption of small displacements, the bond direction vector is given as

$$\begin{aligned} \begin{array}{l} \mathbf {m}_{ij} = \frac{\boldsymbol{\xi }_{ij}+\boldsymbol{\eta }_{ij}}{\Vert \boldsymbol{\xi }_{ij}+\boldsymbol{\eta }_{ij} \Vert } \\ {\mathop {\approx }\limits ^{ \Vert \boldsymbol{\eta }_{ij} \Vert \ll \Vert \boldsymbol{\xi }_{ij} \Vert }} \frac{\boldsymbol{\xi }_{ij}}{\Vert \boldsymbol{\xi }_{ij} \Vert } \, . \end{array} \end{aligned}$$

(20)

Similarly, the extension scalar state of the bond is computed as

$$\begin{aligned} \begin{array}{c} \underline{e}_{ij} = \Vert \boldsymbol{\xi }_{ij} + \boldsymbol{\eta }_{ij} \Vert - \Vert \boldsymbol{\xi }_{ij} \Vert \\ {\mathop {\approx }\limits ^{ \Vert \boldsymbol{\eta }_{ij} \Vert \ll \Vert \boldsymbol{\xi }_{ij} \Vert }} \boldsymbol{\eta }_{ij} \cdot \frac{\boldsymbol{\xi }_{ij}}{\Vert \boldsymbol{\xi }_{ij} \Vert } \\ \approx \boldsymbol{\eta }_{ij} \cdot \mathbf {m}_{ij} \, . \end{array} \end{aligned}$$

(21)

In the discretized model, the integrals over the neighborhood $\mathcal {H}_i$ of a node i are evaluated numerically as the summation for each node j with a portion of the cell within $\mathcal {H}_i$, as shown in Fig. 6. Therefore, the weighted volume $m_i$ and the dilatation $\theta _i$ of a node i are determined from Eqs. (8) and (9) as

$$\begin{aligned} m_i = \sum _{j \in \mathcal {H}_i} \underline{\omega }_{ij} \, \underline{x}_{ij}^2 \, \beta _{ij} V_j \, , \end{aligned}$$

(22)

$$\begin{aligned} \theta _i = \frac{3}{m_i} \sum _{j \in \mathcal {H}_i} \underline{\omega }_{ij} \, \underline{x}_{ij} \, \underline{e}_{ij} \, \beta _{ij} V_j \, , \end{aligned}$$

(23)

where $\beta _{ij} V_j$ represents the quadrature weight, with $V_j = V(\mathbf {x}_j)$. Note that, since surface nodes are representative of the external surface of the body, they do not have weighted volumes or dilatations which are volume properties. The quadrature coefficient $\beta _{ij}$ is computed as the volume fraction of the cell lying within the neighborhood [4, 6]. If the cell of node j is completely within the neighborhood, then $\beta _{ij}=1$, otherwise $0<\beta _{ij}<1$, as shown in Fig. 6. The algorithm to compute accurately the quadrature coefficients in 3D peridynamic problems can be found in [6].

Fig. 6

The neighborhood $\mathcal {H}_i$ of a node i is constituted by the nodes (black dots) with a portion of their cell within the neighborhood (blue area). The quadrature coefficient $\beta _{ij}$ is the volume fraction of cell of node j lying inside the neighborhood

Therefore, the force state of the bond is computed from Eq. (11) as

$$\begin{aligned} \mathbf {f}_{ij} = \left[ k_{\theta } \left( \frac{\theta _i}{m_i} + \frac{\theta _j}{m_j} \right) \underline{\omega }_{ij} \, \underline{x}_{ij} + k_e \left( \frac{1}{m_i} + \frac{1}{m_j} \right) \underline{\omega }_{ij} \, \underline{e}_{ij} \right] \mathbf {m}_{ij} \, . \end{aligned}$$

(24)

If either node i or node j is fictitious, then its weighted volume and dilatation are determined by the Taylor-based extrapolation method described in Section 3.2.

3.2 Numerical Taylor-Based Extrapolation Method

The Taylor-based extrapolation method with the nearest-node strategy is employed to determine the values of the displacements, weighted volumes, and dilatations of the fictitious nodes as a function of the corresponding values of the interior nodes. This method has been described in [25, 26]. However, the use of the surface nodes introduces new degrees of freedom in the numerical model, in addition to the degrees of freedom of the interior nodes, and the Taylor-based extrapolation method should be adapted accordingly.

The weighted volumes and dilatations of interior nodes are numerically computed in Eqs. (22) and (23), respectively. The fictitious nodes are used to complete the neighborhoods of the interior nodes close to the boundary of the body, as shown in Fig. 5. Therefore, all the interior nodes have the same value of the weighted volume. This value is assigned also to the weighted volumes of the fictitious nodes, as dictated by the Taylor-based extrapolation method.

Suppose that N is the order of truncation of the Taylor series expansions to extrapolate the displacements of the fictitious nodes. If $N=1$, then the dilatation of a fictitious node is equal to the dilatation of the closest interior node. Otherwise, the dilatations should be extrapolated with Taylor expansions truncated at the order $N-1$. The numerical procedure to determine the dilatation $\theta _f$ of a fictitious node $\mathbf {x}_f$ is carried out as follows:

1.:

find the interior node $\mathbf {x}_b$ which is the closest to node $\mathbf {x}_f$;

2.:

perform a Taylor series expansion of $\theta _f = \theta (\mathbf {x}_f)$ about node $\mathbf {x}_b$:

$$\begin{aligned} \theta _f = \theta _b + \sum _{n=1}^{N-1} \sum _{n_1=0}^{n} \sum _{n_2=0}^{n-n_1} \frac{(x_f-x_b)^{n_1}}{n_1!} \cdot \frac{(y_f-y_b)^{n_2}}{n_2!} \cdot \frac{(z_f-z_b)^{n_3}}{n_3!} \cdot \frac{\partial ^{n_1+n_2+n_3} \theta _b}{\partial x^{n_1} \partial y^{n_2} \partial z^{n_3}} \, , \end{aligned}$$

(25)

where $n_3 = n-n_1-n_2$;

3.:

find the interior nodes $\mathbf {x}_{b_k}$ closest to $\mathbf {x}_b$ so that the set of found nodes includes at least $n_1$ different $x_{b_k}$ coordinates, $n_2$ different $y_{b_k}$ coordinates and $n_3$ different $z_{b_k}$ coordinates for each derivative in Eq. (25), where $n_1$, $n_2$ and $n_3$ are the possible orders of the derivative in the three directions;

4.:

for each of the found nodes k, perform a Taylor series expansion of their dilatations $\theta _{b_k} = \theta (\mathbf {x}_{b_k})$ about node $\mathbf {x}_b$:

$$\begin{aligned} \theta _{b_k} = \theta _b + \sum _{n=1}^{N-1} \sum _{n_1=0}^{n} \sum _{n_2=0}^{n-n_1} \frac{(x_{b_k}-x_b)^{n_1}}{n_1!} \cdot \frac{(y_{b_k}-y_b)^{n_2}}{n_2!} \cdot \frac{(z_{b_k}-z_b)^{n_3}}{n_3!} \cdot \frac{\partial ^{n_1+n_2+n_3} \theta _b}{\partial x^{n_1} \partial y^{n_2} \partial z^{n_3}} \, ; \end{aligned}$$

(26)

5.:

solve the system of equations in Eq. (26) to obtain the derivatives of $\theta _b$ as a function of the dilatations $\theta _b$ and $\theta _{b_k}$:

$$\begin{aligned} \frac{\partial ^{n_1+n_2+n_3} \theta _b}{\partial x^{n_1} \partial y^{n_2} \partial z^{n_3}} = f (\theta _b, \theta _{b_k}) \, ; \end{aligned}$$

(27)

6.:

substitute Eq. (27) in Eq. (25) to obtain the dilatation of the fictitious node as a function of the dilatations of the interior nodes:

$$\begin{aligned} \theta _f = f (\theta _b, \theta _{b_k}) \, . \end{aligned}$$

(28)

On the other hand, the surface nodes can be included in the Taylor-based extrapolation method for the displacements to improve the accuracy of the procedure. Thus, the numerical procedure to determine the displacement vector $\mathbf {u}_f$ of a fictitious node $\mathbf {x}_f$ is carried out as follows:

7.:

find the surface node $\mathbf {x}_s$ which is the closest to node $\mathbf {x}_f$;

8.:

perform a Taylor series expansion of $\mathbf {u}_f = \mathbf {u} (\mathbf {x}_f)$ about node $\mathbf {x}_s$:

$$\begin{aligned} \mathbf {u}_f = \mathbf {u}_s + \sum _{n=1}^{N} \sum _{n_1=0}^{n} \sum _{n_2=0}^{n-n_1} \frac{(x_f-x_s)^{n_1}}{n_1!} \cdot \frac{(y_f-y_s)^{n_2}}{n_2!} \cdot \frac{(z_f-z_s)^{n_3}}{n_3!} \cdot \frac{\partial ^{n_1+n_2+n_3} \mathbf {u}_s}{\partial x^{n_1} \partial y^{n_2} \partial z^{n_3}} \, , \end{aligned}$$

(29)

where $n_3 = n-n_1-n_2$;

9.:

add to the set of interior nodes $\mathbf {x}_{b_k}$ found in Step 3 the surface nodes closest to $\mathbf {x}_s$ so that the new set of found nodes $\mathbf {x}_{s_q}$ includes at least $n_1$ different $x_{s_q}$ coordinates, $n_2$ different $y_{s_q}$ coordinates and $n_3$ different $z_{s_q}$ coordinates for each derivative in Eq. (29);

10.:

for each of the found nodes q, perform a Taylor series expansion of their displacement vectors $\mathbf {u}_{s_q} = \mathbf {u} (\mathbf {x}_{s_q})$ about node $\mathbf {x}_s$:

$$\begin{aligned} \mathbf {u}_{s_q} = \mathbf {u}_s + \sum _{n=1}^{N} \sum _{n_1=0}^{n} \sum _{n_2=0}^{n-n_1} \frac{(x_{s_q}-x_s)^{n_1}}{n_1!} \cdot \frac{(y_{s_q}-y_s)^{n_2}}{n_2!} \cdot \frac{(z_{s_q}-z_s)^{n_3}}{n_3!} \cdot \frac{\partial ^{n_1+n_2+n_3} \mathbf {u}_s}{\partial x^{n_1} \partial y^{n_2} \partial z^{n_3}} ; \end{aligned}$$

(30)

11.:

solve the system of equations in Eq. (30) to obtain the derivatives of $\mathbf {u}_s$ as a function of the displacement vectors $\mathbf {u}_s$ and $\mathbf {u}_{s_q}$:

$$\begin{aligned} \frac{\partial ^{n_1+n_2+n_3} \mathbf {u}_s}{\partial x^{n_1} \partial y^{n_2} \partial z^{n_3}} = f (\mathbf {u}_s, \mathbf {u}_{s_q}) \, ; \end{aligned}$$

(31)

12.:

substitute Eq. (31) in Eq. (29) to obtain the displacement vector of the fictitious node as a function of the displacement vectors of the interior and surface nodes:

$$\begin{aligned} \mathbf {u}_f = f (\mathbf {u}_s, \mathbf {u}_{s_q}) \, . \end{aligned}$$

(32)

Note that the procedure to determine the displacement vectors of the fictitious nodes is same as that to determine their dilatations except for Step 9, in which the number of considered nodes is increased. This is due to the fact that the Taylor series expansion for the displacement vector has a truncation order of N instead of $N-1$.

3.3 Equilibrium Equation for Interior Nodes

An interior node is representative of the volume within its own cells. The behavior of an interior node i is described by the peridynamic equilibrium equation (Eq. 4), which can be written in the discretized form (multiplying both sides of the equation by the cell volume $V_i = V(\mathbf {x}_i)$) as

$$\begin{aligned} - \sum _{j \in \mathcal {H}_i} \mathbf {f}_{ij} \, \beta _{ij} V_j \, V_i = \mathbf {b}_i \, V_i \, , \end{aligned}$$

(33)

where $\mathbf {b}_i$ is the external force density vector applied to node i.

If some of the nodes j within the neighborhood $\mathcal {H}_i$ of node i are fictitious nodes, then the force states $\mathbf {f}_{ij}$ are computed with the dilatations and the displacement vectors obtained with the Taylor-based extrapolation method (see Section 3.2). Since the neighborhood $\mathcal {H}_i$ is complete, the stiffness fluctuations near the boundary of the body due to the surface effect are reduced (and, in some cases, eliminated).

3.4 Equation for Surface Nodes

A surface node represents a portion of the external surface of the body, namely one of the cell faces lying on the external surface (see Fig. 5). The equation of a surface node i (Eq. 15) is based on the concept of force flux:

$$\begin{aligned} \boldsymbol{\tau } (\mathbf {x}_i,\mathbf {n}_i) = \mathbf {p}_i \, , \end{aligned}$$

(34)

where $\mathbf {n}_i$ is the outward unit vector normal to the face of the cell and $\mathbf {p}$ is the force per unit area applied to $\mathbf {x}_i$. Equation 34 equates the externally applied stress ($\mathbf {p}_i$) to the force flux, i.e., the resultant of the forces of the bonds crossing the surface node.

Suppose that $A_i = A(\mathbf {x}_i)$ is the area represented by the surface node. Since a regular grid of peridynamic nodes is used, $A_i = h^2$ where h is the grid spacing. The force flux $\boldsymbol{\tau } (\mathbf {x}_i, \mathbf {n}_i)$ is computed numerically as the sum of the force states (multiplied by the volumes $V_j$ and $V_k$ of the interacting nodes j and k and divided by $A_i$) of all the bonds intersecting the area $A_i$ [26]:

$$\begin{aligned} \boldsymbol{\tau } (\mathbf {x}_i, \mathbf {n}_i) = \frac{1}{A_i} \sum _{\begin{array}{c} \boldsymbol{\xi }_{jk} \, \cap \, A_i \, \ne \emptyset \\ \mathbf {m}_{jk} \cdot \mathbf {n}_i > 0 \end{array}} \alpha _{jk} \, \mathbf {f}_{jk} \, \beta _{jk} V_k \, V_j \, , \end{aligned}$$

(35)

where $\alpha _{jk}$ is a coefficient equal to 1/4 if the bond intersects $A_i$ at a vertex, 1/2 if the bond intersects $A_i$ at a point on the edges or 1 if the bond intersects $A_i$ at any other point. Figure 7a represents the latter case in which the contribution of the bond $\boldsymbol{\xi }_{jk}$ is completely attributed to the force flux of node i ($\alpha _{jk} = 1$). If the bond $\boldsymbol{\xi }_{jk}$ intersects the area $A_i$ at a point on an edge as shown in Fig. 7b, that edge is shared between node i and an adjacent node. Therefore, only half of the force state $\mathbf {f}_{jk}$ contributes to the force flux of node i ($\alpha _{jk} = 1/2$) and the other half to the force flux of the adjacent node. Similarly, if the bond $\boldsymbol{\xi }_{jk}$ intersects the area $A_i$ at a vertex as shown in Fig. 7c, the contribution of that bond is shared equally by the 4 adjacent nodes ($\alpha _{jk} = 1/4$).

Fig. 7

Values of the coefficient $\alpha _{jk}$ used in the computation of the force flux for different types of intersection between the bond $\boldsymbol{\xi }_{jk}$ and the area $A_i$ of the surface node i

Thus, the governing equation for the surface nodes is obtained by substituting Eq. (35) in Eq. (34) and multiplying both sides by $A_i$:

$$\begin{aligned} \sum _{\begin{array}{c} \boldsymbol{\xi }_{jk} \, \cap \, A_i \, \ne \emptyset \\ \mathbf {m}_{jk} \cdot \mathbf {n}_i > 0 \end{array}} \alpha _{jk} \, \mathbf {f}_{jk} \, \beta _{jk} V_k \, V_j = \mathbf {p}_i A_i \, . \end{aligned}$$

(36)

Since the bond $\boldsymbol{\xi }_{jk}$ intersects the area $A_i$ lying on the external surface of the body, at least one of the nodes in the bond is a fictitious node. Therefore Eq. (36) involves many fictitious nodes, the displacement vectors and dilatations of which are determined by means of the Taylor-based extrapolation method illustrated in Section 3.2.

3.5 Peridynamic System of Equations

On the one hand, Eq. (33), which describes the equilibrium of a volume cell, can be applied to every interior node. On the other hand, Eq. (36) can be applied to every surface node. The left-hand side of both Eqs. (33) and (36) can be rewritten as functions of the displacements of the interior and surface nodes, as shown in Sections 3.1 and 3.2. Therefore, the peridynamic system of equation is given in the standard form as

$$\begin{aligned} \mathbf {K} \, \widetilde{\mathbf {u}} = \widetilde{\mathbf {f}} \, , \end{aligned}$$

(37)

where $\mathbf {K}$ is the peridynamic stiffness matrix, $\widetilde{\mathbf {u}}$ is the displacement vector containing the displacements of interior and surface nodes and $\widetilde{\mathbf {f}}$ is the force vector.

Please note that the stiffness matrix $\mathbf {K}$ is different from the one described in [25, 26], in which the introduction of the Lagrange multipliers is required to solve the system of equations. In the new method, the displacements of the surface nodes are considered as degrees of freedom of the system and the stiffness matrix embeds also the equations for those nodes. This allows to solve directly the system of equations shown in Eq. (37), without the use of the Lagrange multipliers. The advantages of this method with respect to the previous Taylor-based extrapolation method are the following:

• the new unknowns introduced in the system have the physical meaning of the displacements of the external surface of the body, so there is a better description of the mechanical behavior of the boundary of the body;

• the boundary conditions can be applied as one would do in a local model, namely by constraining the displacements in the vector $\widetilde{\mathbf {u}}$ of some nodes and by prescribing the forces in the vector $\widetilde{\mathbf {f}}$ acting on the other nodes;

• if elimination techniques are employed to impose numerically the boundary conditions, the dimensions of the stiffness matrix are reduced (this was not possible with the use of the Lagrange multipliers);

• the structure of the stiffness matrix (banded and with no zeroes on the diagonal) allows for a more efficient inversion of the matrix itself;

• the reaction forces at constrained degrees of freedom can be simply obtained by multiplying the corresponding rows of the stiffness matrix $\mathbf {K}$ by the displacement vector $\widetilde{\mathbf {u}}$.

4 Numerical Examples

Consider a body, the properties of which are reported in Table 1. The body is discretized with the meshfree method with a uniform grid spacing h. The ratio between the horizon and the grid spacing is defined as $\overline{m}$-ratio: $\overline{m} = \delta /h$. The $\overline{m}$-ratio is chosen to be equal to 3 as a compromise between the accuracy of the results and the computational cost. The quadrature coefficients for $\overline{m} = 3$ can be found in Table D1 of Appendix D in [6].

Table 1 Properties of the body and its discretization parameters

Two different sets of boundary conditions are imposed on the body in order to verify the accuracy of the results: a simple traction and a manufactured loading. In the former case, the analytical peridynamic solution is a displacement field varying linearly, the same solution which is obtained with classical continuum mechanics [14]. In the latter case, inspired by [5], we suppose that the peridynamic solution is a manufactured displacement field varying more than linearly. By prescribing this displacement field to the body, we are able to compute the force states of the bonds via Eq. (11). Then, the volumetric loading of the interior of the body and the peridynamic stress at the boundary can be obtained by solving respectively Eqs. (4) and (15). Therefore, if these volumetric loading and peridynamic stress at the boundary, i.e., the manufactured loads, are imposed on the body, the analytical peridynamic solution is the displacement field prescribed at the beginning. Note that, since the manufactured displacement field varies more than linearly, the peridynamic solution is different from the analytical solution obtained with classical mechanics. The procedure shown in the Appendix can be repeated with different prescribed displacement fields to obtain other analytical solutions with the peridynamic theory.

The two static examples are solved firstly without the fictitious and surface nodes. In this case, the boundary conditions are applied to the interior nodes closest to the boundary, as one would do in a local model. In particular, since the most external interior nodes are not exactly lying on the boundary (see Fig. 5), the constraints are imposed by assigning to those nodes the analytical value of the displacement field at their position. Subsequently, the same examples are solved by adopting the method of the surface nodes. The numerical results are compared with the analytical peridynamic solution and the magnitude of the error in a node i is computed as

$$\begin{aligned} \Vert \mathbf {\epsilon }_i \Vert = \sqrt{ \left( \frac{u_i-\overline{u}_i}{\overline{u}_{max}} \right) ^2 + \left( \frac{v_i-\overline{v}_i}{\overline{v}_{max}} \right) ^2 + \left( \frac{w_i-\overline{w}_i}{\overline{w}_{max}} \right) ^2 } \, , \end{aligned}$$

(38)

where $u_i$, $v_i$ and $w_i$ are the displacements in the three directions obtained with the numerical model, $\overline{u}_i$, $\overline{v}_i$ and $\overline{w}_i$ are the displacements obtained with the analytical solution computed at $\mathbf {x}_i$ and $\overline{u}_{max}$, $\overline{v}_{max}$ and $\overline{w}_{max}$ are the maximum magnitude of the analytical displacements. The analytical solution will be computed for each example in the following sections.

4.1 Body Under Traction

The boundary conditions of the body subjected to simple traction are shown in Figure 8. The analytical solution in this case is given as

$$\begin{aligned} \mathbf {u} (\mathbf {x}) = \begin{Bmatrix} u (x,y,z) \\ v (x,y,z) \\ w (x,y,z) \end{Bmatrix} = \begin{Bmatrix} \displaystyle \frac{p}{E} \, x \\ \displaystyle \frac{-\nu \, p}{E} \left( y+\frac{\ell _y}{2} \right) \\ \frac{-\nu \, p}{E} \left( z+\frac{\ell _z}{2} \right) \end{Bmatrix} \, , \end{aligned}$$

(39)

where p is the traction load. Thus, the body is elongated along the x-axis and contracted in the other two directions.

Fig. 8

Boundary conditions for the body under the traction $p= {10}\,{MPa}$. The origin of the reference system lies at the center of the constrained face of the body. The constraints are described by the following equations: $u (x=0) =0$, $v (x=0, y=-\frac{\ell _y}{2}) =0$ and $w (x=0, z=-\frac{\ell _z}{2}) =0$

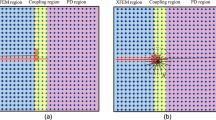
Figure 9a shows the magnitude of the displacement error computed as in Eq. (38) for the peridynamic model without any correction at the boundaries of the body. In this case, there are evident displacement fluctuations near the external surface which are due to the surface effect and the approximated way of imposing the boundary conditions. Note that the errors are much larger especially near the edges and the vertices of the body, as commonly observed in surface effect phenomena [26], reaching a maximum magnitude of more than $30 \%$. On the other hand, when the method of the surface nodes is employed with an order of truncation $N=1$ for the Taylor-based extrapolation, the fluctuations due to the surface effect are eliminated and the peridynamic boundary conditions are imposed properly (see Fig. 9b). Nonetheless, there are still small errors, with a maximum magnitude of $0.06 \%$, due to the discretization of the peridynamic equations.

Fig. 9

Magnitude of the displacement errors when no corrections at the boundaries of the body are adopted (a) and when the method of the surface nodes, with an order of truncation $N=1$ for the Taylor-based extrapolation, is used (b). Note that the colormaps refer to different values in the two plots. The asymmetry of the errors is due to the asymmetric constraints in y and z directions

4.2 Body Under Manufactured Loading

When considering the same mechanical problem, Peridynamics and classical continuum mechanics may provide different solutions [14]. Since Peridynamics has been developed relatively recently, it is difficult to find analytical solutions to benchmark problems. Therefore, inspired by [5], we computed in the Appendix the forces that should be applied to the body to obtain a prescribed displacement field. The boundary conditions of the body subjected to the manufactured loading are shown in Fig. 10. The manufactured volumetric loading is given as

$$\begin{aligned} \mathbf {b} (\mathbf {x}) = \begin{Bmatrix} b_1 (x,y,z) \\ b_2 (x,y,z) \\ b_3 (x,y,z) \end{Bmatrix} = \begin{Bmatrix} - c_w \left( \frac{k_{\theta }}{3} + \frac{2 k_e}{15} \right) \\ - c_u \left( \frac{k_{\theta }}{3} + \frac{2 k_e}{15} \right) - c_v \, \frac{2 k_e}{5} \, x \\ 0 \end{Bmatrix} \, , \end{aligned}$$

(40)

where $c_u = {0.05}\,{\text {m}^{-1}}$, $c_v = {-0.06}\,{\text {m}^{-2}}$ and $c_w = {-0.02}\,{\text {m}^{-1}}$ are randomly chosen constants. The components of the manufactured peridynamic stress tensor $\boldsymbol{\tau } (\mathbf {x})$ can be computed as

$$\begin{aligned} \left\{ \begin{array}{l} \tau _{11} (\mathbf {x}) = c_u \left( \frac{k_{\theta }}{3} + \frac{k_e}{5} \right) y + c_w \left( \frac{k_{\theta }}{3} + \frac{k_e}{15} \right) x \, , \\ \tau _{22} (\mathbf {x}) = c_u \left( \frac{k_{\theta }}{3} + \frac{k_e}{15} \right) y + c_w \left( \frac{k_{\theta }}{3} + \frac{k_e}{15} \right) x \, , \\ \tau _{33} (\mathbf {x}) = c_u \left( \frac{k_{\theta }}{3} + \frac{k_e}{15} \right) y + c_w \left( \frac{k_{\theta }}{3} + \frac{k_e}{5} \right) x \, , \\ \tau _{12} (\mathbf {x}) = c_u \, \frac{k_e}{15} \, x + c_v \left( \frac{k_e}{5} x^2 + \frac{k_e}{35} \frac{\Delta _2}{\Delta _1} \right) \, , \\ \tau _{13} (\mathbf {x}) = c_w \, \frac{k_e}{15} \, z \, , \\ \tau _{23} (\mathbf {x}) = 0 \, , \\ \end{array}\right. \end{aligned}$$

(41)

where $\Delta _1 = \left( \frac{3}{8} \sqrt{\pi } \text {erf} (1) - \frac{5}{4} \exp (-1) \right) \delta ^5$ and $\Delta _2 = \left( \frac{15}{32} \sqrt{\pi } \text {erf} (1) - \frac{29}{16} \exp (-1) \right) \delta ^7$. “erf” and “exp” stand respectively for the Gaussian error function and the exponential function. The surface force, used to impose the surface loading at the free faces of the body, at a point $\mathbf {x}$ on the external surface of the body with an outward normal $\mathbf {n}$ can be computed as $\boldsymbol{\tau } (\mathbf {x},\mathbf {n}) = \boldsymbol{\tau } (\mathbf {x}) \cdot \mathbf {n}$.

If the manufactured loading is applied to the body, then the analytical peridynamic solution is given as

$$\begin{aligned} \mathbf {u} (\mathbf {x}) = \begin{Bmatrix} u (x,y,z) \\ v (x,y,z) \\ w (x,y,z) \end{Bmatrix} = \begin{Bmatrix} c_u \, x \, y \\ c_v \, x^3 \\ c_w \, x \, z \\ \end{Bmatrix} \, . \end{aligned}$$

(42)

The deformation given by this displacement field is shown in Fig. 11.

Fig. 10

Boundary conditions for the body under the manufactured loading. The face at $x=0$ is constrained in all directions, whereas the loads are computed from Eqs. (40) and (41)

Fig. 11

Analytical solution of the displacement field for the body under manufactured loading. The deformation of the body is magnified by 50 times for visualization reasons

Figure 12 shows the magnitude of the displacement error computed as in Eq. (38). The errors obtained without corrections at the boundary (Fig. 9a) are considerably higher than those obtained with the method of the surface nodes (Fig. 9b–d). Indeed, the maximum magnitudes of the displacement errors are respectively over $130 \%$ and below $1 \%$. This is due to the surface effect and, especially, to the approximated way of imposing the boundary conditions. In the model without boundary corrections, the surface loads are indeed applied to the nodes closest to the boundary of the body, which however are distant h/2 from the external surface (where the loads should actually be applied). On the other hand, the surface nodes lie exactly on the external surface of the body and allow to enforce the boundary conditions exactly where they are supposed to be imposed, while also mitigating the surface effect.

Since the analytical solution for the displacement field in Eq. (42) is at most cubic, we expect to capture the proper displacements in the fictitious layer with an order of truncation $N=3$ for the Taylor-based extrapolation. The numerical results indeed show that the magnitude of the errors decreases as the order of truncation is increased from 1 to 3 (compare Fig. 9b–d). However, even if $N=3$ is chosen, there are still small errors, with a maximum magnitude of $0.4 \%$. These residual errors, due to the discretization of the peridynamic equations [6], can be further reduced by increasing the value of the $\overline{m}$-ratio, i.e., decreasing the value of the grid spacing h when the horizon size $\delta$ is kept constant [26].

Fig. 12

Magnitude of the displacement errors when no corrections at the boundaries of the body are adopted (a) and when the method of the surface nodes, with different order of truncation for the Taylor-based extrapolation, is used (b-d). Note that the colormaps refer to different values in the plots. Also, note that the difference between $N=2$ and $N=3$ is very small because the errors due to the truncation of the Taylor series expansions in the displacement extrapolation are negligible compared to the errors due to the discretization of the peridynamic equations

5 Comparison with Other Methods

The surface effect and the imposition of the boundary conditions are two well-known issues in Peridynamics, which were thoroughly analyzed in the literature. Many methods have been indeed devised to mitigate these problems at the boundary (see, for instance, [22]). There are mainly three types of methods for boundary corrections:

• the modification of the stiffness of the bonds near the boundary [23, 27, 34,35,36,37],

• the introduction of the fictitious nodes surrounding the body and the extrapolation of their displacements along with the implementation of the peridynamic boundary conditions [22, 25,26,27, 32, 33, 45,46,47,48,49,50,51],

• the modification of the equations governing the nodes near the boundary thanks to the peridynamic differential operator [38,39,40,41,42].

Even though it employs the fictitious layer as in the second type of methods, the surface node method differs from all the previously proposed methods. The main difference is the introduction of new degrees of freedom at the boundary of the body, governed by new equations based on the concept of force flux. In the following, the most recent versions of the three types of methods are reviewed and compared with the surface node method.

For the comparison, we consider an example of a 2D body under plane strain conditions subjected to simple traction $p={240}\,\text {MPa}$. Note that, under these conditions, the coefficients for the computation of the dilatation and the force state (respectively Eqs. 9 and 11) should be modified to $c_{\theta }=2$, $k_{\theta } = -(1-4\nu )E/((1+\nu )(1-2\nu ))$ and $k_e = 4E/(1+\nu )$. The boundary conditions and the properties of the plate, which are the same as those of a numerical example in [42], are shown respectively in Fig. 13 and Table 2. The quadrature coefficients are computed with the algorithm proposed in Appendix A of [6].

Fig. 13

Boundary conditions for the plate under traction p

Table 2 Properties of the plate and its discretization parameters

The peridynamic analytical solution of this problem, which is the same analytical solution obtained with classical continuum mechanics [14], is given as

$$\begin{aligned} \mathbf {u} (\mathbf {x}) = \begin{Bmatrix} u (x,y) \\ v (x,y) \end{Bmatrix} = \begin{Bmatrix} \displaystyle \frac{-\nu (1+\nu )p}{E} \, x \\ \displaystyle \frac{(1-\nu ^2)p}{E} \, y \end{Bmatrix} \, , \end{aligned}$$

(43)

Therefore, the error in a node i is computed as

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \epsilon _{u_i} = \left\| \frac{u_i-\overline{u}_i}{\overline{u}_{max}} \right\| \, , \\ \displaystyle \epsilon _{v_i} = \left\| \frac{v_i-\overline{v}_i}{\overline{v}_{max}} \right\| \, , \end{array}\right. } \end{aligned}$$

(44)

where $u_i$ and $v_i$ are the displacements in the two directions obtained with the numerical model, $\overline{u}_i$ and $\overline{v}_i$ are the displacements obtained with the analytical solution computed at $\mathbf {x}_i$, and $\overline{u}_{max}$ and $\overline{v}_{max}$ are the maximum magnitude of the analytical displacements.

5.1 Position-Aware Linear Solid (PALS)

The Position-Aware Linear Solid (PALS) constitutive model proposes a kinematic correction that modifies the influence function differently for the dilatation and the deviatoric part of the extension [22, 37]. This method introduces two sets of constraints, called matching deformations, which prescribe homogeneous strain conditions in the whole body. The two sets of matching deformations, representing the deformations either for uniaxial strains or for simple shear, are used to define two linear systems of equations for each node via the Lagrange multipliers. The solution of these two systems, corresponding to the matching deformations for uniaxial strains or simple shear, leads to the determination of the dilatation and deviatoric influence functions, respectively. Since only the influence functions of the nodes near the boundary are automatically modified, the method is called position-aware.

The modification of the bond properties through the dilatation and deviatoric influence functions allows to restore the proper values of stiffness in the whole body, also near the boundaries, under homogeneous deformations. However, the PALS approach does not deal with the problem of the imposition of the peridynamic boundary conditions and exhibits even larger errors when the deformation is non-homogeneous.

5.2 Mirror Node Method (MNM)

The Mirror Node Method (MNM), developed in [50], is based on introducing the fictitious nodes surrounding the peridynamic body. In state-based Peridynamics, the thickness of the fictitious layer for the MNM is equal to $2 \delta$. Each fictitious node is associated with the node within the body closest to the point at the same (symmetric) distance from the boundary, the so-called mirror node. The direction for this search of the mirror node is given by the peridynamic gradient, a vector defined in such a way as to point towards the region of nodes with the more complete neighborhoods, i.e., the bulk of the body. The fictitious nodes are employed to mitigate the surface effect and to impose the boundary condition thanks to the mirror nodes. The displacements of the fictitious nodes are indeed determined depending on the values of the Dirichlet or Neumann boundary conditions at the boundary and on the displacements of the corresponding mirror nodes.

Even if the MNM is similar to the Surface Node Method (SNM) in exploiting the fictitious nodes to deal with both the surface effect and the imposition of the boundary conditions, the two methods differ considerably in the way they do it. Indeed, the Taylor-based extrapolation used in the SNM does not need the computation of the peridynamic gradient but only the search for the nearest node of the body. Moreover, in the SNM, higher-order terms of the Taylor expansion may increase the accuracy in the case of a superlinear displacement field, and the external forces are consistently applied in the peridynamic framework.

5.3 Peridynamic Differential Operator (PDDO)

The Peridynamic Differential Operator (PDDO) was introduced in [38] and then was used to recast the formulation of the bond associated non-ordinary state-based Peridynamics [40]. In this model, the PDDO can be used to correct the surface effect and impose the boundary conditions without the fictitious layer [42]. The domain of the body is partitioned into three subdomains:

• the set of the most external layer of nodes, where the boundary conditions are enforced via the PDDO equations;

• the set of the remaining nodes with a distance from the boundary smaller than $2 \delta$, where the peridynamic equations are modified to correct the surface effect;

• the set of the nodes with a distance from the boundary greater than $2 \delta$, which are governed by the standard peridynamic equations.

To some extent, the PDDO method and the Surface Node Method (SNM) are similar since they use different equations than the standard ones to correct the surface effect and impose the boundary conditions. However, the differences between the two methods to implement the boundary corrections are evident: the PDDO method exploits a layer of nodes within the body, whereas the SNM the fictitious nodes outside the body. This is the reason why, in the SNM, all the nodes in the interior of the body are still governed by the standard peridynamic equations, and crack propagation is naturally included in the peridynamic formulation near the boundary of the body as well.

5.4 Comparison with Surface Node Method (SNM)

The SNM retains the unique quality of having some nodes positioned exactly at the boundary of the body, i.e., the surface nodes, representing the non-local mechanical behavior of the external surface of the body. Thanks to these new nodes, the boundary conditions are not imposed at a distance of h/2 from the boundary as in the other methods, where h is the uniform grid spacing, but can be imposed exactly where they are supposed to. Moreover, the boundary conditions are imposed as one would do in a local model, namely by setting the values of the corresponding degrees of freedom in either the displacement vector or the force vector (in Equation 37). This is a very handy characteristic that is not exhibited in most of the other methods in the literature.

Figures 14 and 15 show the errors, respectively for the displacements in x and y directions, computed with Eq. (44) for the example in Fig. 13. Since the PALS approach is expected to correct the surface effects under homogeneous deformation, the errors in Figs. 14a and 15a are due to the approximated way boundary conditions were imposed. Note that this method reduces the errors of the displacements in the direction of the load (y direction) but still yields significant errors in the perpendicular direction (x direction). The numerical results obtained with the MNM are really close to the analytical solution for the displacements in x direction, except in one of the corners (see Fig. 14a). However, the errors for the displacements in y direction (Fig. 15b) are the highest among the four analyzed methods due to the approximated imposition of the Neumann boundary conditions via the mirror nodes.

Both PALS and MNM are implemented in the same peridynamic framework of the SNM, namely the ordinary state-based Peridynamics, but they provide, on average, larger errors than SNM. The numerical errors obtained with the method involving the PDDO are similar to those obtained with the SNM: both methods do not exhibit fluctuations of the displacements near the boundary and yield, on average, smaller errors than PALS and MNM methods. However, the PDDO method is based on the non-ordinary state-based Peridynamics framework, which is different from the model used for the SNM. Therefore, the comparison between these two methods can be only qualitative. The advantages of using the SNM over the PDDO method are mainly two:

• the complete knowledge of the mechanical behavior of the external surface of peridynamic bodies is achieved solely with the SNM thanks to the surface nodes lying exactly at the boundary,

• the PDDO method is limited to cracks that propagate far from the nodes where boundary conditions are imposed (this limitation is not present in the SNM).

Fig. 14

Errors of the displacements in x direction for the following methods for boundary corrections: a Position-Aware Linear Solid, b Mirror Node Method, c Peridynamic Differential Operator, and d Surface Node Method

Fig. 15

Errors of the displacements in y direction for the following methods for boundary corrections: a Position-Aware Linear Solid, b Mirror Node Method, c Peridynamic Differential Operator, and d Surface Node Method

6 Conclusions

Peridynamics, as typical of non-local theories, exhibits some issues near the boundaries of the body: an undesired stiffness fluctuation due to incomplete neighborhoods close to the external surface of the body, phenomenon known as surface effect, and a difficulty in imposing properly the boundary conditions. In [25, 26], we proposed an innovative method, i.e., the Taylor-based extrapolation method with the nearest-node strategy, to mitigate the surface effect by means of the introduction of the fictitious nodes and to impose properly the peridynamic boundary conditions via the concept of force flux. The main disadvantage of this method is that the system of equations is solved through the use of the Lagrange multipliers, that increases the number of unknowns and leads to an equation structure which is not computationally efficient to solve.

Therefore, we developed the method of the surface nodes which exploits the same concepts of the previous method, but also avoids the use of the Lagrange multipliers. Each surface node represents a portion of the external surface of the body. The displacements of these nodes are new degrees of freedom in the model and their corresponding equations are based on the concept of force flux. In this regard, the surface nodes may be considered as representative of the interactions between the most external layer of the body and the fictitious layer surrounding the body. The boundary conditions can be applied directly to these nodes, exactly as one would do in a local model. Moreover, the Taylor-based extrapolation is adapted by including the contributions of the new degrees of freedom associated to the surface nodes.

For the first time, the concepts of the Taylor-based extrapolation method are applied to 3D peridynamic models: 3D static numerical examples have been carried out to verify the accuracy of the method of the surface nodes. The improvements of the proposed method are evident when compared to a peridynamic model without corrections at the boundary: the undesired stiffness fluctuations near the external surface of the body are sensibly reduced (or even eliminated) and the errors of the numerical solution decrease by 2 orders of magnitude.

Moreover, the advantages of the proposed method are the following:

• it defines in a clear way how the boundary conditions in Peridynamics are imposed and removes the arbitrariness of other methods in distributing the constraints or the external loads over the layer of the body close to the boundary;

• the introduction of the new unknowns, namely the displacements of the surface nodes, allows for a better description of the mechanical behavior of the external surface of the body;

• the implementation of the boundary conditions in peridynamic models is straightforward since it is similar to what one would do in a local model (for instance, by using elimination techniques);

• there is no need to use of the Lagrange multipliers, thus the stiffness matrix can be numerically inverted in a more efficient way.

We compared the proposed method with three of the most recently developed methods for boundary corrections. This comparison highlights that the surface node method yields the most accurate numerical results with respect to the other methods applied in the framework of ordinary state-based Peridynamics. The unique characteristics of the surface nodes, namely the knowledge of the non-local mechanical behavior of the external surface of peridynamic bodies and the imposition of the boundary conditions exactly at the boundary, make the proposed method one of the most attractive to use.

Moreover, we computed the peridynamic analytical solution for a relatively complex displacement field. In the literature, only few analytical solutions are available for peridynamic problems. The Appendix shows a procedure to analytically obtain the volume and surface forces when a displacement field is prescribed. The same procedure can be applied to different displacement fields in order to attain other analytical solutions with the peridynamic theory.

Appendix. Analytical Solution to the Manufactured Problem

A peridynamic problem is said to be manufactured when the forces applied to a body are computed from a given displacement field, which can be arbitrarily chosen (provided that the integrals in the peridynamic equations are explicitly solvable). Therefore, consider an infinite body which is subjected to the following displacement field:

$$\begin{aligned} \mathbf {u} (\mathbf {x}) = \begin{Bmatrix} u (x,y,z) \\ v (x,y,z) \\ w (x,y,z) \end{Bmatrix} = \begin{Bmatrix} c_u \, x \, y \\ c_v \, x^3 \\ c_w \, x \, z \\ \end{Bmatrix} \, , \end{aligned}$$

(45)

where $c_u$, $c_v$ and $c_w$ are arbitrarily chosen constants. The volume forces that should be applied to the infinite body to obtain this displacement field can be computed from Eq. (4) as

$$\begin{aligned} \mathbf {b} (\mathbf {x}) = - \int _{\Omega } \int _{0}^{\delta } \mathbf {f}(\mathbf {x},\mathbf {x}') \, l^2 \,\mathrm {d}\Omega _{\mathbf {m}} \,\mathrm {d}l \, , \end{aligned}$$

(46)

where the differential volume $\,\mathrm {d}V_{\mathbf {x}'}$ has been rewritten as $l^2 \,\mathrm {d}\Omega _{\mathbf {m}} \,\mathrm {d}l$, in which $l= \Vert \mathbf {x}' - \mathbf {x} \Vert$ is the length of the bond and $\,\mathrm {d}\Omega _{\mathbf {m}}$ is the differential solid angle in direction $\mathbf {m}$ of the bond. The direction $\mathbf {m}$ may vary on the unit sphere $\Omega$ centered in $\mathbf {x}$ and the length l of the bond is comprised between 0 and $\delta$, so that all the bonds within the neighborhood $\mathcal {H}_{\mathbf {x}}$ of the point $\mathbf {x}$ are considered within the limits of the integration domain.

However, we would like to consider a body with finite dimensions (imagine to cut out a piece of the infinite body). This means that some forces arise at the external surfaces of the finite body (where the infinite body is cut). Therefore, we need to compute the peridynamic stress tensor as

$$\begin{aligned} \boldsymbol{\tau } (\mathbf {x}) = \frac{1}{2} \int _{\Omega } \int _{0}^{\delta } \int _{s}^{\delta } \mathbf {f} (\mathbf {x}', \mathbf {x}'') \otimes \mathbf {m} \, r^2 \,\mathrm {d}r \,\mathrm {d}s \,\mathrm {d}\Omega _{\mathbf {m}} \, , \end{aligned}$$

(47)

where $r= \Vert \mathbf {x}'' - \mathbf {x}' \Vert$, $s= \Vert \mathbf {x}' - \mathbf {x} \Vert$ and “$\otimes$” stands for the dyadic product. The limits of the integration domain can be visualized in Fig. 2. If the stress tensor is multiplied by the outward unit vector $\mathbf {n}$ normal to the external surface, one can obtain the above-mentioned forces, or force fluxes, arisen at the external surface of the finite body: $\boldsymbol{\tau } (\mathbf {x},\mathbf {n}) = \boldsymbol{\tau } (\mathbf {x}) \cdot \mathbf {n}$.

For later use, we solve hereinafter the integrals that will appear in the computation of the forces. Since both Eqs. (46) and (47) contain an integral over a unit sphere $\Omega$, that integral is equal to 0 whenever the integrand involves an odd exponent for at least one of the components $\mathrm {m}_i$, with $i=1,2,3$, of the vector $\mathbf {m}$ of the bond direction (antisymmetric function integrated over a symmetric domain). The analytical solutions of the integrals which involve the bond direction vector are:

$$\begin{aligned} \int _{\Omega } \,\mathrm {d}\Omega _{\mathbf {m}} = 4 \pi \, , \end{aligned}$$

(48)

$$\begin{aligned} \int _{\Omega } \mathrm {m}_i^{\, 2} \,\mathrm {d}\Omega _{\mathbf {m}} = \frac{4 \pi }{3} \, , \end{aligned}$$

(49)

$$\begin{aligned} \int _{\Omega } \mathrm {m}_i^{\, 4} \,\mathrm {d}\Omega _{\mathbf {m}} = \frac{4 \pi }{5} \, , \end{aligned}$$

(50)

$$\begin{aligned} \int _{\Omega } \mathrm {m}_i^{\, 2} \mathrm {m}_j^{\, 2} \,\mathrm {d}\Omega _{\mathbf {m}} = \frac{4 \pi }{15} \, , \end{aligned}$$

(51)

$$\begin{aligned} \int _{\Omega } \mathrm {m}_i^{\, 4} \mathrm {m}_j^{\, 2} \,\mathrm {d}\Omega _{\mathbf {m}} = \frac{4 \pi }{35} \, , \end{aligned}$$

(52)

where $i,j = 1,2,3$ with $i \ne j$. On the other hand, the integrals involving the bond length l (see Eq. 46) are solved as follows:

$$\begin{aligned} \int _{0}^{\delta } \exp \left( \frac{-l^2}{\delta ^2} \right) l^4 \,\mathrm {d}l = \left( \frac{3}{8} \sqrt{\pi } \text {erf} (1) - \frac{5}{4} \exp (-1) \right) \delta ^5 = \Delta _1 \, . \end{aligned}$$

(53)

where “erf” is the Gaussian error function and “exp” is the exponential function. We name $\Delta _1$ the solution of Eq. (53) to simplify and shorten the next formulae. The solutions for the integrals required to compute the peridynamic stress tensor are:

$$\begin{aligned} \int _{0}^{\delta } \int _{s}^{\delta } \exp \left( -\frac{r^2}{\delta ^2} \right) r^3 \,\mathrm {d}r \,\mathrm {d}s = \Delta _1 \, , \end{aligned}$$

(54)

$$\begin{aligned} \int _{0}^{\delta } \int _{s}^{\delta } \exp \left( -\frac{r^2}{\delta ^2} \right) r^3 (r^2 - 3 s r +3 s^2) \,\mathrm {d}r \,\mathrm {d}s = \left( \frac{15}{32} \sqrt{\pi } \text {erf} (1) - \frac{29}{16} \exp (-1) \right) \delta ^7 = \Delta _2 \, . \end{aligned}$$

(55)

These analytical solutions are valid only for the Gaussian influence function in Eq. (7), but they can be computed also if other influence functions are adopted (the values of $\Delta _1$ and $\Delta _2$ would be different).

The analytical value of the weighted volume of a point $\mathbf {x}$ with complete neighborhood (from Eq. 8) is:

$$\begin{aligned} m (\mathbf {x}) = \int _{\Omega } \int _{0}^{\delta } \exp \left( -\frac{l^2}{\delta ^2} \right) l^4 \,\mathrm {d}l \,\mathrm {d}\Omega _{\mathbf {m}} = 4 \pi \Delta _1 \, . \end{aligned}$$

(56)

We show hereinafter how to compute the volume and surface forces applied to a peridynamic body to obtain the displacement field in Eq. (45).

1.1 A.1 Computation of Volume Forces

Under the assumption of small displacements, the extension scalar state of the bond between points $\mathbf {x}$ and $\mathbf {x}'$ is computed as

$$\begin{aligned} \begin{aligned} \underline{e}&= \left[ \mathbf {u} (\mathbf {x}') - \mathbf {u} (\mathbf {x}) \right] \cdot \mathbf {m} \\&= \left\{ \begin{array}{c} c_u \left( x' y' - x y \right) \\ c_v \left( x'^3 - x^3 \right) \\ c_w \left( x' z' - x z \right) \\ \end{array}\right\} \cdot \left\{ \begin{array}{c} \mathrm {m}_1 \\ \mathrm {m}_2 \\ \mathrm {m}_3 \\ \end{array}\right\} \\&= \left\{ \begin{array}{c} c_u \left( l^2 \mathrm {m}_1 \mathrm {m}_2 + x l \mathrm {m}_2 + y l \mathrm {m}_1 \right) \\ c_v \left( l^3 \mathrm {m}_1^{\, 3} +3x l^2 \mathrm {m}_1^{\, 2} + 3x^2 l \mathrm {m}_1 \right) \\ c_w \left( l^2 \mathrm {m}_1 \mathrm {m}_3 + x l \mathrm {m}_3 + z l \mathrm {m}_1 \right) \\ \end{array}\right\} \cdot \left\{ \begin{array}{c} \mathrm {m}_1 \\ \mathrm {m}_2 \\ \mathrm {m}_3 \\ \end{array}\right\} \\& \begin{aligned}=&\;c_u \left( l^2 \mathrm {m}_1^{\, 2} \mathrm {m}_2 + x l \mathrm {m}_1 \mathrm {m}_2 + y l \mathrm {m}_1^{\, 2} \right) \\&+ c_v \left( l^3 \mathrm {m}_1^{\, 3} \mathrm {m}_2 +3x l^2 \mathrm {m}_1^{\, 2} \mathrm {m}_2 + 3x^2 l \mathrm {m}_1 \mathrm {m}_2 \right) \\&+ c_w \left( l^2 \mathrm {m}_1 \mathrm {m}_3^{\, 2} + x l \mathrm {m}_3^{\, 2} + z l \mathrm {m}_1 \mathrm {m}_3 \right) \, ,\end{aligned} \end{aligned} \end{aligned}$$

(57)

where the equations $x' = x+l \mathrm {m}_1$, $y' = y+l \mathrm {m}_2$ and $z' = z+l \mathrm {m}_3$ have been used.

By substituting Eq. (63) in Eq. (9) (and neglecting the terms of the extension scalar state with an odd exponent for the components of the bond direction vector), the dilatation in a point $\mathbf {x}$ is given as

$$\begin{aligned} \theta (\mathbf {x}) &= \frac{3}{m(\mathbf {x})} \int _{\Omega } \int _{0}^{\delta } \exp \left( -\frac{l^2}{\delta ^2} \right) l^4 \left( c_u y \mathrm {m}_1^{\, 2} + c_w x \mathrm {m}_3^{\, 2} \right) \,\mathrm {d}l \,\mathrm {d}\Omega _{\mathbf {m}} \\& = \frac{3}{4 \pi \Delta _1} \int _{0}^{\delta } \exp \left( -\frac{l^2}{\delta ^2} \right) l^4 \,\mathrm {d}l \left( c_u y \int _{\Omega } \mathrm {m}_1^{\, 2} \,\mathrm {d}\Omega _{\mathbf {m}} + c_w x \int _{\Omega } \mathrm {m}_3^{\, 2} \,\mathrm {d}\Omega _{\mathbf {m}} \right) \\& = \frac{3}{4 \pi \Delta _1} \Delta _1 \left( c_u y \frac{4 \pi }{3} + c_w x \frac{4 \pi }{3} \right) \\& = c_u y + c_w x \, .\end{aligned}$$

(58)

The volume force applied to a point $\mathbf {x}$ is computed by substituting Eq. (11) in Eq. (46) (where $m(\mathbf {x}) = m(\mathbf {x}')$):

$$\begin{aligned} \mathbf {b} (\mathbf {x}) = - \frac{1}{m(\mathbf {x})} \int _{\Omega } \int _{0}^{\delta } \exp \left( -\frac{l^2}{\delta ^2} \right) \left\{ k_{\theta } l \left[ \theta (\mathbf {x}) + \theta (\mathbf {x}') \right] + 2 k_e \underline{e} \right\} \mathbf {m} \, l^2 \,\mathrm {d}\Omega _{\mathbf {m}} \,\mathrm {d}l \, . \end{aligned}$$

(59)

We rewrite the two main terms of the integrand as follows:

$$\begin{aligned} \left[ \theta (\mathbf {x}) + \theta (\mathbf {x}') \right] \mathbf {m} &{} = \left[ c_u \left( y + y' \right) + c_w \left( x + x' \right) \right] \begin{Bmatrix} \mathrm {m}_1 \\ \mathrm {m}_2 \\ \mathrm {m}_3 \\ \end{Bmatrix} \\ &{} = \left[ c_u \left( l \mathrm {m}_2 + 2y \right) + c_w \left( l \mathrm {m}_1 + 2x \right) \right] \begin{Bmatrix} \mathrm {m}_1 \\ \mathrm {m}_2 \\ \mathrm {m}_3 \\ \end{Bmatrix} \\ &{} = \begin{Bmatrix} c_u l \mathrm {m}_1 \mathrm {m}_2 + c_w l \mathrm {m}_1^{\, 2} + \left[ c_u \left( 2y + 2x \right) \right] \mathrm {m}_1 \\ c_u l \mathrm {m}_2^{\, 2} + c_w l \mathrm {m}_1 \mathrm {m}_2 + \left[ c_u \left( 2y + 2x \right) \right] \mathrm {m}_2 \\ c_u l \mathrm {m}_2 \mathrm {m}_3 + c_w l \mathrm {m}_1 \mathrm {m}_3 + \left[ c_u \left( 2y + 2x \right) \right] \mathrm {m}_3 \\ \end{Bmatrix} \, , \end{aligned}$$

(60)

$$\begin{aligned} \begin{aligned} \underline{e} \, \mathbf {m} =&\, c_u l \left\{ \begin{array}{c} l \mathrm {m}_1^{\, 3} \mathrm {m}_2 + x \mathrm {m}_1^{\, 2} \mathrm {m}_2 + y \mathrm {m}_1^{\, 3} \\ l \mathrm {m}_1^{\, 2} \mathrm {m}_2^{\, 2} + x \mathrm {m}_1 \mathrm {m}_2^{\, 2} + y \mathrm {m}_1^{\, 2} \mathrm {m}_2 \\ l \mathrm {m}_1^{\, 2} \mathrm {m}_2 \mathrm {m}_3 + x \mathrm {m}_1 \mathrm {m}_2 \mathrm {m}_3 + y \mathrm {m}_1^{\, 2} \mathrm {m}_3 \\ \end{array}\right\} \\&+ c_v l \left\{ \begin{array}{c} l^2 \mathrm {m}_1^{\, 4} \mathrm {m}_2 + 3 x l \mathrm {m}_1^{\, 3} \mathrm {m}_2 + 3 x^2 \mathrm {m}_1^{\, 2} \mathrm {m}_2 \\ l^2 \mathrm {m}_1^{\, 3} \mathrm {m}_2^{\, 2} + 3 x l \mathrm {m}_1^{\, 2} \mathrm {m}_2^{\, 2} + 3 x^2 \mathrm {m}_1 \mathrm {m}_2^{\, 2} \\ l^2 \mathrm {m}_1^{\, 3} \mathrm {m}_2 \mathrm {m}_3 + 3 x l \mathrm {m}_1^{\, 2} \mathrm {m}_2 \mathrm {m}_3 + 3 x^2 \mathrm {m}_1 \mathrm {m}_2 \mathrm {m}_3 \\ \end{array}\right\} \\&+ c_w l \left\{ \begin{array}{c} l \mathrm {m}_1^{\, 2} \mathrm {m}_3^{\, 2} + x \mathrm {m}_1 \mathrm {m}_3^{\, 2} + z \mathrm {m}_1^{\, 2} \mathrm {m}_3 \\ l \mathrm {m}_1 \mathrm {m}_2 \mathrm {m}_3^{\, 2} + x \mathrm {m}_2 \mathrm {m}_3^{\, 2} + z \mathrm {m}_1\mathrm {m}_2 \mathrm {m}_3 \\ l \mathrm {m}_1 \mathrm {m}_3^{\, 3} + x \mathrm {m}_3^{\, 3} + z \mathrm {m}_1 \mathrm {m}_3^{\, 2} \\ \end{array}\right\} \, . \end{aligned} \end{aligned}$$

(61)

Therefore, keeping only the terms with all even exponents of the components of the bond direction vector, Eq. (59) becomes

$$\begin{aligned} \begin{aligned} \mathbf {b} (\mathbf {x})&= - \frac{1}{m(\mathbf {x})} \int _{\Omega } \int _{0}^{\delta } \exp \left( -\frac{l^2}{\delta ^2} \right) \left( k_{\theta } l^2 \left\{ \begin{array}{c} c_w \mathrm {m}_1^{\, 2} \\ c_u \mathrm {m}_2^{\, 2} \\ 0 \end{array} \right\} + 2 k_e l^2 \left\{ \begin{array}{c} c_w \mathrm {m}_1^{\, 2} \mathrm {m}_3^{\, 2} \\ (c_u + 3 c_v x) \mathrm {m}_1^{\, 2} \mathrm {m}_2^{\, 2} \\ 0 \end{array} \right\} \right) l^2 \,\mathrm {d}\Omega _{\mathbf {m}} \,\mathrm {d}l \\&= - \frac{1}{4 \pi \Delta _1} \int _{0}^{\delta } \exp \left( -\frac{l^2}{\delta ^2} \right) l^4 \,\mathrm {d}l \int _{\Omega } \left( k_{\theta } \left\{ \begin{array}{c} c_w \mathrm {m}_1^{\, 2} \\ c_u \mathrm {m}_2^{\, 2} \\ 0 \end{array} \right\} + 2 k_e \left\{ \begin{array}{c} c_w \mathrm {m}_1^{\, 2} \mathrm {m}_3^{\, 2} \\ (c_u + 3 c_v x) \mathrm {m}_1^{\, 2} \mathrm {m}_2^{\, 2} \\ 0 \end{array} \right\} \right) \,\mathrm {d}\Omega _{\mathbf {m}} \\&= - \frac{1}{4 \pi \Delta _1} \Delta _1 \left( \frac{4 \pi }{3} k_{\theta } \left\{ \begin{array}{c} c_w \\ c_u \\ 0 \end{array} \right\} + \frac{8 \pi }{15} k_e \left\{ \begin{array}{c} c_w \\ c_u + 3 c_v x \\ 0 \end{array}\right\} \right) \\&= \left\{ \begin{array}{c} - c_w \left( \frac{k_{\theta }}{3} + \frac{2 k_e}{15} \right) \\ - c_u \left( \frac{k_{\theta }}{3} + \frac{2 k_e}{15} \right) - c_v \, \frac{2 k_e}{5} \, x \\ 0 \end{array}\right\} \, . \end{aligned} \end{aligned}$$

(62)

This is the volume force that should be applied to the body to obtain the manufactured displacement field and the same formula is reported in Eq. (40).

1.2 A.2 Computation of Surface Forces

Under the assumption of small displacements, the extension scalar state of the bond between points $\mathbf {x}'=\mathbf {x}-s\mathbf {m}$ and $\mathbf {x}''=\mathbf {x}+(r-s)\mathbf {m}$ is computed as

$$\begin{aligned} \begin{aligned} \underline{e}&= \left[ \mathbf {u} (\mathbf {x}'') - \mathbf {u} (\mathbf {x}') \right] \cdot \mathbf {m} \\&= \left\{ \begin{array}{c} c_u \left( x'' y'' - x' y' \right) \\ c_v \left( x''^3 - x'^3 \right) \\ c_w \left( x'' z'' - x' z' \right) \end{array}\right\} \cdot \left\{ \begin{array}{c} \mathrm {m}_1 \\ \mathrm {m}_2 \\ \mathrm {m}_3 \end{array}\right\} \\&= \left\{ \begin{array}{c} c_u \left[ (r^2 - 2 s r) \mathrm {m}_1 \mathrm {m}_2 + x r \mathrm {m}_2 + y r \mathrm {m}_1 \right] \\ c_v \left[ (r^3 - 3 s r^2 + 3 s^2 r) \mathrm {m}_1^{\, 3} + 3 x (r^2 - 2 s r) \mathrm {m}_1^{\, 2} + 3 x^2 r \mathrm {m}_1 \right] \\ c_w \left[ (r^2 - 2 s r) \mathrm {m}_1 \mathrm {m}_3 + x r \mathrm {m}_3 + z r \mathrm {m}_1 \right] \end{array}\right\} \cdot \left\{ \begin{array}{c} \mathrm {m}_1 \\ \mathrm {m}_2 \\ \mathrm {m}_3 \end{array}\right\} \\& \begin{aligned}=&\; c_u \left[ (r^2 - 2sr) \mathrm {m}_1^{\, 2} \mathrm {m}_2 + x r \mathrm {m}_1 \mathrm {m}_2 + y r \mathrm {m}_1^{\, 2} \right] \\& + c_v \left[ (r^3 - 3 s r^2 + 3 s^2 r) \mathrm {m}_1^{\, 3} \mathrm {m}_2 + 3 x (r^2 - 2 s r) \mathrm {m}_1^{\, 2} \mathrm {m}_2 + 3 x^2 r \mathrm {m}_1 \mathrm {m}_2 \right] \\& + c_w \left[ (r^2 - 2sr) \mathrm {m}_1 \mathrm {m}_3^{\, 2} + x r \mathrm {m}_3^{\, 2} + z r \mathrm {m}_1 \mathrm {m}_3 \right] \, , \end{aligned} \end{aligned} \end{aligned}$$

(63)

where the equations $x' = x-s \mathrm {m}_1$, $y' = y-s \mathrm {m}_2$, $z' = z-s \mathrm {m}_3$, $x'' = x+(r-s) \mathrm {m}_1$, $y' = y+(r-s) \mathrm {m}_2$ and $z' = z+(r-s) \mathrm {m}_3$ have been used.

The peridynamic stress tensor of a point $\mathbf {x}$ is computed by substituting Eq. (11) in Eq. (47) (where $m(\mathbf {x}') = m(\mathbf {x}'') = m(\mathbf {x})$):

$$\begin{aligned} \boldsymbol{\tau } (\mathbf {x}) = \frac{1}{2 m(\mathbf {x})} \int _{\Omega } \int _{0}^{\delta } \int _{s}^{\delta } \exp \left( -\frac{r^2}{\delta ^2} \right) \left\{ k_{\theta } r \left[ \theta (\mathbf {x}') + \theta (\mathbf {x}'') \right] + 2 k_e \underline{e} \right\} \mathbf {m} \otimes \mathbf {m} \, r^2 \,\mathrm {d}r \,\mathrm {d}s \,\mathrm {d}\Omega _{\mathbf {m}} \end{aligned}$$

(64)

We rewrite the sum of the dilatations as follows:

$$\begin{aligned} \begin{aligned} \theta (\mathbf {x}') + \theta (\mathbf {x}'')&= c_u \left( y' + y'' \right) + c_w \left( x' + x'' \right) \\&= c_u \left[ (r - 2s) \mathrm {m}_2+2y \right] + c_w \left[ (r - 2s) \mathrm {m}_1+2x \right] \, , \end{aligned} \end{aligned}$$

(65)

Then, by omitting the terms with at least one odd exponent for the components of the bond direction vector, the peridynamic stress tensor is given as

$$\begin{aligned} &\begin{aligned} \boldsymbol{\tau } (\mathbf {x}) = &\;\frac{1}{2 m(\mathbf {x})} \int _{\Omega } \int _{0}^{\delta } \int _{s}^{\delta } \exp \left( -\frac{r^2}{\delta ^2} \right) \left( 2 k_{\theta } r^3 \left( c_u y + c_w x \right) \left[ \begin{array}{ccc} \mathrm {m}_1^{\, 2} &{} 0 &{} 0 \\ 0 &{} \mathrm {m}_2^{\, 2} &{} 0 \\ 0 &{} 0 &{} \mathrm {m}_3^{\, 2} \\ \end{array} \right] \right. \\& + 2 k_e r^3 \left[ \begin{array}{ccc} c_u y \mathrm {m}_1^{\, 4} + c_w x \mathrm {m}_1^{\, 2} \mathrm {m}_3^{\, 2} &{} (c_u x +3 c_v x^2) \mathrm {m}_1^{\, 2} \mathrm {m}_2^{\, 2} &{} c_w z \mathrm {m}_1^{\, 2} \mathrm {m}_3^{\, 2} \\ (c_u x +3 c_v x^2) \mathrm {m}_1^{\, 2} \mathrm {m}_2^{\, 2} &{} c_u y \mathrm {m}_1^{\, 2} \mathrm {m}_2^{\, 2} + c_w x \mathrm {m}_2^{\, 2} \mathrm {m}_3^{\, 2} &{} 0 \\ c_w z \mathrm {m}_1^{\, 2} \mathrm {m}_3^{\, 2} &{} 0 &{} c_u y \mathrm {m}_1^{\, 2} \mathrm {m}_3^{\, 2} + c_w x \mathrm {m}_3^{\, 4} \end{array}\right] \\& \left. + 2 k_e r^3 (r^2 - 3 s r + 3 s^2) \left[ \begin{array}{ccc} 0 &{} c_v \mathrm {m}_1^{\, 4} \mathrm {m}_2^{\, 2} &{} 0 \\ c_v \mathrm {m}_1^{\, 4} \mathrm {m}_2^{\, 2} &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ \end{array}\right] \right) \,\mathrm {d}r \,\mathrm {d}s \,\mathrm {d}\Omega _{\mathbf {m}} \end{aligned}\\&\begin{aligned} \qquad\; = &\;\frac{1}{8 \pi \Delta _1} \left( 2 k_{\theta } \left( c_u y + c_w x \right) \Delta _1 \frac{4 \pi }{3} \left[ \begin{array}{ccc} 1 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \\ \end{array} \right] \right. \\& \left. + 2 k_e \Delta _1 \frac{4 \pi }{15} \left[ \begin{array}{ccc} 3 c_u y + c_w x &{} c_u x +3 c_v x^2 &{} c_w z \\ c_u x +3 c_v x^2 &{} c_u y + c_w x &{} 0 \\ c_w z &{} 0 &{} c_u y + 3 c_w x \\ \end{array}\right] \right. \\& \left. + 2 k_e c_v \Delta _2 \frac{4 \pi }{35} \left[ \begin{array}{ccc} 0 &{} 1 &{} 0 \\ 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ \end{array}\right] \right) \end{aligned} \\& \qquad\; = \left[ \begin{array}{ccc} c_u \left( \frac{k_{\theta }}{3} + \frac{k_e}{5} \right) y + c_w \left( \frac{k_{\theta }}{3} + \frac{k_e}{15} \right) x &{} c_u \frac{k_e}{15} x + c_v \left( \frac{k_e}{5} x^2 + \frac{k_e}{35} \frac{\Delta _2}{\Delta _1} \right) &{} c_w \frac{k_e}{15} z \\ c_u \frac{k_e}{15} x + c_v \left( \frac{k_e}{5} x^2 + \frac{k_e}{35} \frac{\Delta _2}{\Delta _1} \right) &{} c_u \left( \frac{k_{\theta }}{3} + \frac{k_e}{15} \right) y + c_w \left( \frac{k_{\theta }}{3} + \frac{k_e}{15} \right) x &{} 0 \\ c_w \frac{k_e}{15} z &{} 0 &{} c_u \left( \frac{k_{\theta }}{3} + \frac{k_e}{15} \right) y + c_w \left( \frac{k_{\theta }}{3} + \frac{k_e}{5} \right) x \\ \end{array}\right] \, . \end{aligned}$$

(66)

The surface force at a point $\mathbf {x}$ on the external surface of the body with a normal $\mathbf {n}$ can be computed as $\boldsymbol{\tau } (\mathbf {x},\mathbf {n}) = \boldsymbol{\tau } (\mathbf {x}) \cdot \mathbf {n}$. The components of the stress tensor are reported in Eq. 41.