Analysis of Functionally Graded Timoshenko Beams by Using Peridynamics

Abstract

In this study, a new peridynamic formulation is presented for functionally graded Timoshenko beams. The governing equations of the peridynamic formulation are obtained by utilising Euler-Lagrange equation and Taylor’s expansion. The proposed formulation is validated by considering a Timoshenko beam subjected to different boundary conditions including pinned support-roller support, clamped-roller support and clamped-free boundary conditions. Results from peridynamics are compared against finite element analysis results. A very good agreement is obtained for transverse displacements, rotations and axial displacements along the beam.

1 Introduction

Peridynamics was introduced by Silling [1] to overcome the limitations of widely used classical continuum mechanics formulation especially for problems including discontinuities in the displacement field due to existence of cracks. Moreover, it has a length scale parameter, horizon, which gives peridynamics a nonlocal characteristic and defines the range of nonlocal interactions between material points. Peridynamics has been utilised to analyse many different types of material systems including metals [2] and composites [3]. Peridynamics can be utilised for not only structural analysis but also for the solution of other physical fields such as heat transfer [4], porous flow [5], diffusion [6], etc. Peridynamics is not limited to elastic behaviour, but peridynamic plasticity [7], viscoelasticity [8] and viscoplasticity [9] formulations are available. Peridynamic formulations are not limited at macro-scale but can be used for the analysis of polycrystalline materials [10] and nano-structures [11]. An extensive review of peridynamics is given in Javili et al. [12].

The original formulation of peridynamics considers only translational degrees of freedom for material points and is capable of performing 3-dimensional analysis. However, this approach can be computationally expensive for certain geometries such as beam, plate and shell-type structures. To capture the correct deformation behaviour of such structures, additional rotational degrees of freedom may be necessary. Such formulations are currently available in the literature. Amongst these Taylor and Steigmann [13] introduced a peridynamic formulation for thin plates. O’Grady and Foster [14, 15] developed non-ordinary state-based formulations suitable for Euler-Bernoulli beams and Kirchhoff-Love plate theory. Diyaroglu et al. [16] also proposed a state-based formulation suitable for Euler-Bernoulli beams. Yang et al. [17] extended this formulation to Kirchhoff plates. In order to take into account the transverse shear deformations, Diyaroglu et al. [18] introduced Timoshenko beam and Mindlin plate formulations. In addition, Chowdhury et al. [19] developed a state-based formulation for linear elastic shells.

In this study, a new peridynamic formulation is presented suitable for analysis of functionally graded Timoshenko beams. Functionally graded materials have certain advantages with respect to fibre-reinforced composites since they have continuously varying material properties which does not cause stress concentrations that can lead to delamination failure. There are currently numerous studies available in the literature on analysis of functionally graded Timoshenko beams using classical [20, 21] and strain-gradient [22] theories. Peridynamics can be suitable alternative to these approaches. Although there are existing peridynamic formulations available in the literature suitable for the analysis of 2-dimensional and 3-dimensional problems [23, 24], the peridynamic functionally graded Timoshenko beam formulation presented in this study has significant benefits in terms of computational time for the analysis of thin and thick functionally graded beams. Proposed peridynamic formulation is derived using Euler-Lagrange equation and Taylor’s expansion. To validate the current formulation, several benchmark problems are considered, and peridynamic results are compared against finite element analysis results.

2 Timoshenko Beam Formulation for Functionally Graded Materials

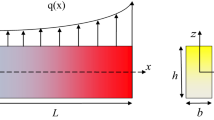
Timoshenko developed first-order shear deformation theory for thick beams which is also known as Timoshenko beam theory. According to the assumptions of the Timoshenko beam theory, the displacement field of any material point can be expressed in terms of the displacement field of a material point along the central axis in xz plane as (see Fig. 1):

$$ u\left(x,z,t\right)=u\left(x,0,t\right)+z\cdotp u{\left(\mathrm{x},0,t\right)}_{,z} $$

(1a)

$$ w\left(x,z,t\right)=w\left(x,0,t\right) $$

(1b)

where u(x, 0, t) and w(x, 0, t) denote the displacement components of the material point along the central axis in x and z directions, respectively, and t is time. Thus, the strain-displacement relationships can be written as:

$$ {\varepsilon}_x=\frac{\partial u}{\partial x}+z\frac{\partial \theta }{\partial x} $$

(2a)

$$ {\gamma}_{xz}=\theta +\frac{\partial w}{\partial x} $$

(2b)

$$ {\varepsilon}_z=0 $$

(2c)

in which $\theta =\frac{\partial u}{\partial z}$ represents the rotation angle and u = u(x, 0, t) and w = w(x, 0, t) represent the displacement components of a particular material point located at (x, 0) along the central (neutral) axis of the beam, respectively.

Fig. 1

Displacement components of the Timoshenko beam formulation

The stress-displacement relationships can also be written as:

$$ {\sigma}_x=E(z)\left(\frac{\partial u}{\partial x}+z\frac{\partial \theta }{\partial x}\right) $$

(3a)

$$ {\tau}_{xz}=G(z)\left(\theta +\frac{\partial w}{\partial x}\right) $$

(3b)

where E(z) and G(z) denote Young’s modulus and shear modulus, respectively, and they are functions of the vertical coordinate, z.

The linear elastic strain energy density of the Timoshenko beam is defined as:

$$ W=\frac{1}{2}\left({\sigma}_x{\varepsilon}_x+\kappa {\tau}_{xz}{\gamma}_{xz}\right) $$

(4)

where κ is introduced as the shear correction factor. Inserting Eqs. (2) and (3) into (4) yields

$$ \mathrm{W}=\frac{1}{2}\left\{E(z)\left[{\left(\frac{\partial u}{\partial x}\right)}^2+{z}^2{\left(\frac{\partial \theta }{\partial x}\right)}^2+2z\frac{\partial u}{\partial x}\frac{\partial \theta }{\partial x}\right]+\kappa G(z){\left(\theta +\frac{\partial w}{\partial x}\right)}^2\right\} $$

(5)

The average strain energy density of a particular material point along the central axis of the beam can be reasonably obtained by integrating the strain energy density function, Eq.(5), over the cross-section and divided by the cross-sectional area, as:

$$ W=\frac{1}{A}{\int}_A WdA $$

(6)

In particular, for a rectangular cross-section, Eq. (6) becomes:

$$ W=\frac{1}{2h}\left[{\int}_{-\frac{h}{2}}^{\frac{h}{2}}E(z) dz\cdotp {\left(\frac{\mathrm{\partial u}}{\partial x}\right)}^2+{\int}_{-\frac{h}{2}}^{\frac{h}{2}}E(z){z}^2 dz{\left(\frac{\partial \theta }{\partial x}\right)}^2+2{\int}_{-\frac{h}{2}}^{\frac{h}{2}}E(z) zdz\frac{\partial u}{\partial x}\frac{\partial \theta }{\partial x}+\kappa {\int}_{-\frac{h}{2}}^{\frac{h}{2}}G(z) dz{\left(\theta +\frac{\partial w}{\partial x}\right)}^2\right] $$

(7)

3 Peridynamic Timoshenko Beam Formulation for Functionally Graded Materials

Peridynamics (PD) is new continuum mechanics formulation introduced by Silling [1]. As opposed to Cauchy’s classical continuum mechanics (CCM) formulation, the material points can interact with each other in a nonlocal manner, and the range of interactions is defined by the region called horizon, H. The governing equations of peridynamics are in the form of integro-differential equations and can be written as:

$$ \rho (x)\ddot{u}\left(x,t\right)={\int}_H\left(t-{t}^{\prime}\right)d{V}^{\prime }+b\left(x,t\right) $$

(8)

where ρ is density, u and $\ddot{u}$ represent displacement and acceleration, respectively, and b is the body load vector. t and t^′ define the peridynamic interaction (bond) forces between two material points located at x and x^′.Analytical solution to Eq. (8) is generally not possible. Numerical techniques are widely used including meshless approach. Therefore, the PD equations of motion for a particular material point k can be expressed in discrete form as:

$$ {\rho}_{(k)}{\ddot{u}}_{(k)}={\sum}_{j=1}^N\left({t}_{(k)(j)}-{t}_{(j)(k)}\right){V}_{(j)}+{b}_{(k)} $$

(9)

where N indicates the total number of family members and V is the volume of a material point. As shown in Fig. 2, the PD force density vector t_(k)(j) represents the force acting on the main material point k by its family member material point j, and, on the contrary, t_(j)(k) represents the force acting on the material point j by its family member material point, k.

Fig. 2

Peridynamic interaction force between two material points k and j and the horizon concept

The PD equations of motion can be derived by utilising Euler-Lagrange equation [25]:

$$ \frac{d}{dt}\frac{\partial L}{\partial {\dot{u}}_{(k)}}-\frac{\partial L}{\partial {u}_{(k)}}=0 $$

(10)

where L = T − U is the Lagrangian which is the difference between the system’s kinetic energy, T, and potential energy, U, that can be expressed as:

$$ T=\frac{1}{2}{\sum}_k\rho {\dot{u}}_{(k)}\cdotp {\dot{u}}_{(k)}{V}_{(k)} $$

(11)

and

$$ U={\sum}_k{W}_{(k)}{V}_{(k)}-{\sum}_k{b}_{(k)}\cdotp {u}_{(k)}{V}_{(k)} $$

(12)

with u and b being the generalised displacement vector and generalised body force density vector, respectively. In this study, they can be defined as:

$$ u={\left(u\kern0.5em \theta \kern0.5em w\right)}^T $$

(13a)

and

$$ b={\left({b}_x\kern0.5em {b}_{\theta}\kern0.5em {b}_z\right)}^T $$

(13b)

Here, the entries of the body force density vector, b_x, b_θ and b_z, correspond to axial force along x-axis, bending moment and transverse force densities, respectively. Considering rectangular cross-section case, inserting Eq. (1) into (11), integrating throughout the thickness and dividing by the thickness give the kinetic energy of the system as:

$$ T=\frac{1}{2}{\sum}_k{\rho}_{(k)}\left({\dot{u}}_{(k)}^2+\frac{h^2}{12}{\dot{\theta}}_{(k)}^2+{\dot{w}}_{(k)}^2\right){V}_{(k)} $$

(14)

The first term of Euler-Lagrange equation can be obtained by substituting Eq. (14) into Eq. (10) as:

$$ \frac{d}{dt}\frac{\partial L}{\partial {\dot{\boldsymbol{u}}}_{(k)}}={\rho}_{(k)}\left\{\begin{array}{c}{\ddot{u}}_{(k)}\\ {}\frac{h^2}{12}{\ddot{\theta}}_{(k)}\\ {}{\ddot{w}}_{(k)}\end{array}\right\}{V}_{(k)} $$

(15)

Unlike the classical elasticity theory, according to PD theory, the strain energy density function has nonlocal form such that the strain energy of a particular material point k depends on both its displacement and displacements of all other material points in its horizon, which can be expressed as:

$$ {W}_{(k)}={W}_{(k)}\left({u}_{(k)},{u}_{\left({1}^k\right)},{u}_{\left({2}^k\right)},{u}_{\left({3}^k\right)},\cdots \right) $$

(16)

where u_(k) is the displacement vector of the material point k and ${u}_{\left({i}^k\right)}$ (i = 1, 2, 3, ⋯) is the displacement vector of the ith material point inside the horizon of the material point k. Therefore, the total potential energy stored in the body can be obtained by summing potential energies of all material points including strain energy and energy due to external loads as:

$$ U=\sum \limits_k{W}_{(k)}\left({u}_{(k)},{u}_{\left({1}^k\right)},{u}_{\left({2}^k\right)},{u}_{\left({3}^k\right)},\cdots \right){V}_{(k)}-\sum \limits_k{b}_{(k)}{u}_{(k)}{V}_{(k)} $$

(17)

Thus, the second term of the Euler-Lagrange equation can be written as:

$$ -\frac{\partial L}{\partial {u}_{(k)}}=\frac{\partial }{\partial {u}_{(k)}}\sum \limits_n{W}_{(n)}\left({u}_{(n)},{u}_{\left({1}^n\right)},{u}_{\left({2}^n\right)},{u}_{\left({3}^n\right)},\cdots \right){V}_{(n)}-\frac{\partial }{\partial {u}_{(k)}}\sum \limits_n{b}_{(n)}{u}_{(n)}{V}_{(n)}=\sum \limits_n\frac{\partial {W}_{(n)}}{\partial {u}_{(k)}}\left({\delta}_{nk}+{\delta}_{n{i}^k}\right){V}_{(n)}-\sum \limits_n{b}_{(n)}{\delta}_{nk}{V}_{(n)}=\left(\frac{\partial {W}_{(k)}}{\partial {u}_{(k)}}{V}_{(k)}+\sum \limits_j\frac{\partial {W}_{(j)}}{\partial {u}_{(k)}}{V}_{(j)}\right)-{b}_{(k)}{V}_{(k)} $$

(18)

Inserting Eqs. (15) and (18) into Euler-Lagrange equation yields:

$$ {\rho}_{(k)}\left\{\begin{array}{c}{\ddot{u}}_{(k)}\\ {}\frac{h^2}{12}{\ddot{\theta}}_{(k)}\\ {}{\ddot{w}}_{(k)}\end{array}\right\}{V}_{(k)}=-\left\{\begin{array}{c}\begin{array}{c}\frac{\partial {W}_{(k)}}{\partial {u}_{(k)}}{V}_{(k)}+\sum \limits_j\frac{\partial {W}_{(j)}}{\partial {u}_{(k)}}{V}_{(j)}\\ {}\frac{\partial {W}_{(k)}}{\partial {\theta}_{(k)}}{V}_{(k)}+\sum \limits_j\frac{\partial {W}_{(j)}}{\partial {\theta}_{(k)}}{V}_{(j)}\end{array}\\ {}\frac{\partial {W}_{(k)}}{\partial {w}_{(k)}}{V}_{(k)}+\sum \limits_j\frac{\partial {W}_{(j)}}{\partial {w}_{(k)}}{V}_{(j)}\end{array}\right\}+\left\{\begin{array}{c}\begin{array}{c}{b}_x^{(k)}\\ {}{b}_{\theta}^{(k)}\end{array}\\ {}{b}_z^{(k)}\end{array}\right\}{V}_{(k)} $$

(19)

The strain energy density function given in Eq. (7) can be written in nonlocal PD form for a particular material point k. To achieve this, it is necessary to transform all differential terms into equivalent PD forms in accordance with the form of PD strain energy density given in Eq. (17). As derived in Appendix 1, the strain energy density function of the material point k and its family member j can be expressed as:

$$ {W}_{(k)}=\frac{1}{2h}\frac{1}{\delta^2A}\left[{\int}_{-\frac{h}{2}}^{\frac{h}{2}}E(z) dz\cdotp {\sum}_i\frac{{\left({u}_{\left({i}^k\right)}-{u}_{\left(\mathrm{k}\right)}\right)}^2}{\left|{\xi}_{\left({i}^k\right)(k)}\right|}{V}_{\left({i}^k\right)}+{\int}_{-\frac{h}{2}}^{\frac{h}{2}}E(z){z}^2 dz{\sum}_i\frac{{\left({\theta}_{\left({i}^k\right)}-{\theta}_{(k)}\right)}^2}{\left|{\xi}_{\left({i}^k\right)(k)}\right|}{V}_{\left({i}^k\right)}+2{\int}_{-\frac{h}{2}}^{\frac{h}{2}}E(z) zdz{\sum}_i\frac{\left({u}_{\left({i}^k\right)}-{u}_{(k)}\right)\left({\theta}_{\left({i}^k\right)}-{\theta}_{(k)}\right)}{\left|{\xi}_{\left({i}^k\right)(k)}\right|}{V}_{\left({i}^k\right)}+\kappa {\int}_{-\frac{h}{2}}^{\frac{h}{2}}G(z) dz{\sum}_i\frac{{\left(\frac{\uptheta_{(k)}+{\theta}_{\left({i}^k\right)}}{2}{\xi}_{\left({i}^k\right)(k)}+{w}_{\left({i}^k\right)}-{w}_{(k)}\right)}^2}{\left|{\xi}_{\left({i}^k\right)(k)}\right|}{V}_{\left({i}^k\right)}\right] $$

(20a)

and

$$ {W}_{(j)}=\frac{1}{2h}\frac{1}{\delta^2A}\left[{\int}_{-\frac{h}{2}}^{\frac{h}{2}}E(z) dz\cdotp {\sum}_i\frac{{\left({u}_{\left({i}^j\right)}-{u}_{(j)}\right)}^2}{\left|{\xi}_{\left({i}^j\right)(j)}\right|}{V}_{\left({i}^j\right)}+{\int}_{-\frac{h}{2}}^{\frac{h}{2}}E(z){z}^2 dz{\sum}_i\frac{{\left({\theta}_{\left({i}^j\right)}-{\theta}_{(j)}\right)}^2}{\left|{\xi}_{\left({i}^j\right)(j)}\right|}{V}_{\left({i}^j\right)}+2{\int}_{-\frac{h}{2}}^{\frac{h}{2}}E(z) zdz{\sum}_i\frac{\left({u}_{\left({i}^j\right)}-{u}_{(j)}\right)\left({\theta}_{\left({i}^j\right)}-{\theta}_{(j)}\right)}{\left|{\xi}_{\left({i}^j\right)(j)}\right|}{V}_{\left({i}^j\right)}+\kappa {\int}_{-\frac{h}{2}}^{\frac{h}{2}}G(z) dz{\sum}_i\frac{{\left(\frac{\uptheta_{(j)}+{\theta}_{\left({i}^j\right)}}{2}{\xi}_{\left({i}^j\right)(j)}+{w}_{\left({i}^j\right)}-{w}_{(j)}\right)}^2}{\left|{\xi}_{\left({i}^j\right)(j)}\right|}{V}_{\left({\mathrm{i}}^j\right)}\right] $$

(20b)

Substituting Eqs. (20a) and (20b) into (18) and renaming the summation indices, the second term of Euler-Lagrange equation becomes:

$$ -\frac{\partial L}{\partial {\boldsymbol{u}}_{(k)}}=\left\{\begin{array}{c}\frac{1}{h}\frac{2}{\delta^2A}\left({\int}_{-\frac{h}{2}}^{\frac{h}{2}}E(z) dz{\sum}_j\frac{u_{(j)}-{u}_{(k)}}{\left|{\xi}_{(j)(k)}\right|}{V}_{(j)}+{\int}_{-\frac{h}{2}}^{\frac{h}{2}}E(z) zdz{\sum}_j\frac{\theta_{(j)}-{\theta}_{(k)}}{\left|{\xi}_{(j)(k)}\right|}{V}_{(j)}\right)+{b}_x^{(k)}\\ {}\frac{1}{h}\frac{2}{\delta^2A}\left(\begin{array}{c}{\int}_{-\frac{h}{2}}^{\frac{h}{2}}E(z){z}^2 dz{\sum}_j\frac{\theta_{(j)}-{\theta}_{(k)}}{\left|{\xi}_{(j)(k)}\right|}{V}_{(j)}+{\int}_{-\frac{h}{2}}^{\frac{h}{2}}E(z) zdz{\sum}_j\frac{\left({u}_{(j)}-{u}_{(k)}\right)}{\left|{\xi}_{(j)(k)}\right|}{V}_{(j)}\\ {}-\frac{1}{2}\kappa {\int}_{-\frac{h}{2}}^{\frac{h}{2}}G(z) dz{\sum}_j\left({w}_{(j)}-{w}_{(k)}+\frac{\theta_{(k)}+{\theta}_{(j)}}{2}{\xi}_{(j)(k)}\right)\mathit{\operatorname{sign}}\left({\xi}_{(j)(k)}\right){V}_{(j)}\end{array}\right)+{b}_{\theta}^{(k)}\\ {}\frac{1}{h}\frac{2}{\delta^2A}\left(\kappa {\int}_{-\frac{h}{2}}^{\frac{h}{2}}G(z) dz{\sum}_j\frac{w_{(j)}-{w}_{(k)}}{\left|{\xi}_{(j)(k)}\right|}+\frac{\theta_{(k)}+{\theta}_{(j)}}{2}\mathit{\operatorname{sign}}\left({\xi}_{(j)(k)}\right){\mathrm{V}}_{(j)}\right)+{b}_z^{(k)}\end{array}\right\} $$

(21)

Therefore, the entire set of equations of motion is given by inserting Eqs. (15) and (21) into Eq. (10) as:

$$ {\uprho}_{(k)}{\ddot{u}}_{(k)}=\frac{1}{h}\frac{2}{\delta^2A}\left({\int}_{-\frac{h}{2}}^{\frac{h}{2}}E(z) dz{\sum}_j\frac{u_{(j)}-{u}_{(k)}}{\left|{\xi}_{(j)(k)}\right|}{V}_{(j)}+{\int}_{-\frac{h}{2}}^{\frac{h}{2}}E(z) zdz{\sum}_j\frac{\theta_{(j)}-{\theta}_{(k)}}{\left|{\xi}_{(j)(k)}\right|}{V}_{(j)}\right)+{b}_x^{(k)} $$

(22a)

$$ {\uprho}_{(k)}\frac{h^2}{12}{\ddot{\theta}}_{(k)}=\frac{1}{h}\frac{2}{\delta^2A}\left({\int}_{-\frac{h}{2}}^{\frac{h}{2}}E(z){z}^2 dz{\sum}_j\frac{\theta_{(j)}-{\theta}_{(k)}}{\left|{\xi}_{(j)(k)}\right|}{V}_{(j)}+{\int}_{-\frac{h}{2}}^{\frac{h}{2}}E(z) zdz{\sum}_j\frac{\left({u}_{(j)}-{u}_{(k)}\right)}{\left|{\xi}_{(j)(k)}\right|}{V}_{(j)}-\frac{1}{2}\kappa {\int}_{-\frac{h}{2}}^{\frac{h}{2}}G(z) dz{\sum}_j\left({w}_{(j)}-{w}_{(k)}+\frac{\theta_{(k)}+{\theta}_{(j)}}{2}{\xi}_{(j)(k)}\right)\mathit{\operatorname{sign}}\left({\xi}_{(j)(k)}\right){V}_{(j)}\right)+{b}_{\theta}^{(k)} $$

(22b)

$$ {\uprho}_{(k)}{\ddot{w}}_{(k)}=\frac{1}{h}\frac{2}{\delta^2A}\left(\kappa {\int}_{-\frac{h}{2}}^{\frac{h}{2}}G(z) dz{\sum}_j\frac{w_{(j)}-{w}_{(k)}}{\left|{\xi}_{(j)(k)}\right|}+\frac{\theta_{(k)}+{\theta}_{(j)}}{2}\mathit{\operatorname{sign}}\left({\xi}_{(j)(k)}\right){V}_{(j)}\right)+{b}_z^{(k)} $$

(22c)

4 Application of Boundary Conditions

Application of boundary conditions is a critical step of peridynamic analysis. Since the PD equations of motion are in the form of integro-differential equations, the approach to apply boundary conditions is different than the approach used in CCM. In this study, to apply displacement boundary conditions, a fictitious region, R_c, is created outside of the actual solution domain, R. The width of the fictitious layer can be chosen as the same size of the horizon. Two common types of boundary conditions including clamped and simply supported boundary conditions are presented below for PD Timoshenko beam formulation for functionally graded materials.

4.1 Clamped Boundary Condition

To implement the clamped boundary condition, a fictitious boundary layer is created outside the actual material domain. The horizon size can be chosen as δ = 3∆x in which the discretisation size is ∆x. Hence, the size of the fictitious region is chosen as δ.

In Timoshenko beam theory, the clamped boundary condition imposes zero transverse displacement, zero axial displacement and zero rotation for the material point adjacent to the clamped end as:

$$ w=0,u=0\ \mathrm{and}\ \theta =0 $$

(23)

In our study, these conditions can be achieved by enforcing mirror image of the transverse displacement field for the material points adjacent to the clamped end and anti-symmetric image of rotational and axial displacements fields, as shown in Fig. 3, such that:

$$ {w}_{(i)}={w}_{\left({i}^{\ast}\right)}\kern0.75em {w}_{(1)}={w}_{\left({1}^{\ast}\right)}=0 $$

(24a)

$$ {u}_{(i)}=-{u}_{\left({i}^{\ast}\right)}\kern0.5em \mathrm{and}\ {\theta}_{(i)}=-{\theta}_{\left({i}^{\ast}\right)}\kern0.75em \mathrm{with}\ \mathrm{i}=1,2,3 $$

(24b)

Fig. 3

Application of clamped boundary conditions in peridynamic theory

Note that enforcing conditions given in Eqs. (24a, b) also implicitly satisfies the conditions related with accelerations of the material point adjacent to the clamped end, i.e. $\ddot{w}=0$, $\ddot{u}=0$ and $\ddot{\theta}=0$.

4.2 Simply Supported Boundary Condition

To implement the simply supported boundary condition, the fictitious layer is introduced outside the real material domain, whose size is again chosen to be equal to δ. In Timoshenko beam theory, the simply supported boundary condition imposes zero transverse displacement and zero curvature for the material point adjacent to the clamped end as:

$$ w=0\ \mathrm{and}\ \frac{\partial \theta }{\partial x}=0 $$

(25)

In our study, the above conditions can be satisfied by enforcing anti-symmetrical transverse displacement field and symmetrical rotational displacement field to the material points in the fictitious region with respect to the actual displacement field, as shown in Fig. 4, which is defined as:

$$ {w}_{(i)}=-{w}_{\left({i}^{\ast}\right)},\kern0.5em {\theta}_{(i)}={\theta}_{\left({i}^{\ast}\right)}\kern1em \mathrm{with}\ i=1,2,3 $$

(26)

Fig. 4

Application of simply supported boundary (pinned support) conditions in peridynamic theory

The discussion about simply supported boundary condition for axial deformation should be separated into two parts, which are pinned support and roller support, respectively. The implementation of axial deformation for pinned support is achieved by enforcing anti-symmetrical displacement field for fictitious material domain with respect to actual material domain, as shown in Fig. 4, which can be defined as:

$$ {u}_{\left({i}^{\ast}\right)}=-{u}_{(i)}\kern0.5em \mathrm{with}\ i=1,2,3 $$

(27)

On the other hand, the implementation for roller support boundary condition requires symmetrical displacement field adjacent to the boundary as (see Fig. 5)

$$ {u}_{\left({i}^{\ast}\right)}={u}_{(i)}\kern0.5em \mathrm{with}\ i=1,2,3 $$

(28)

Fig. 5

Application of simply supported boundary (roller support) conditions in peridynamic theory

5 Numerical Results

To verify the validity of the PD formulation for functionally graded Timoshenko beams, the PD solutions are compared with the corresponding finite element (FE) analysis results. In this study, the functionally graded material properties are chosen as Young’s modulus E(z) and shear modulus G(z), and they are assumed to vary linearly through the thickness as:

$$ E(z)=\left({E}_t-{E}_b\right)\frac{z}{h}+\frac{1}{2}\left({E}_t+{E}_b\right)\kern0.5em (GPa) $$

(29a)

and

$$ G(z)=\frac{E(z)}{2\left(1+0.3\right)} $$

(29b)

where E_t and E_b denote the Young’s modulus of the top and bottom surfaces of the beam and h denotes the total thickness of the beam as shown in Fig. 6. All numerical examples considered in this section are for static analysis, and the numerical solution procedure is given in Appendix 2. For all numerical examples, the horizon size is chosen as δ = 3∆x where ∆x is the distance between material points.

Fig. 6

Material variation along the thickness direction for the functionally graded material

5.1 Timoshenko Beam with Pinned Support-Roller Support Boundary Conditions

A simply supported functionally graded beam with length, width and thickness of L = 1 m, W = 0.01 m and t = 0.1 m is considered as shown in Fig. 7. The beam is constrained by pinned support and roller support at the left and right ends, respectively. Young’s modulus of the top and bottom surfaces is specified as E_t = 200 GPa and E_b = 100 GPa, respectively. The model is discretised into one single row of material points along with the thickness, and the distance between material points is ∆x = 0.002 m. Fictitious regions are introduced outside the actual solution domain as the external boundaries with a width of δ. The beam is subjected to a concentrated transverse load of P_z = 100 N at the central point. The load is converted to a body load of $b=\frac{P_z}{2\Delta V}=2.5e7\ \mathrm{N}/{\mathrm{m}}^3$, and it is applied to two central material volumes of the model (see Fig. 8).

Fig. 7

Timoshenko beam with pinned support-roller support boundary conditions

Fig. 8

Discretisation, applied loading and fictitious region

The FE model of the beam is created by using SHELL181 element in ANSYS with dimensions of 1 m × 0.01 m × 0.1 m. The FE model is meshed with 100 elements along the length. To model the functionally graded beam, the model is divided to 50 layers with varying homogeneous materials properties through the thickness. Young’s modulus varies linearly over the thickness from the first layer E₁ = 101 GPa to the last layer E₅₀ = 199 GPa, as shown in Fig. 9. Poisson’s ratio, ν = 0.3, is applied in ANSYS.

Fig. 9

Material variation in the thickness direction for the finite element model

The PD and FE transverse displacements, w(x), rotations, θ(x), and axial displacements, u(x), are compared in Fig. 10. Both approaches yield similar displacement and rotation variations. These results verify the accurateness of the current PD formulation for a functionally graded beam theory for pinned support-roller support boundary condition.

Fig. 10

Comparison of PD and FE results for (a) transverse displacements, (b) rotations and (c) axial displacements

5.2 Timoshenko Beam with Clamped-Roller Support Boundary Conditions

The Timoshenko beam with clamped-roller supported boundary conditions is under consideration (see Fig. 11). The beam has the same geometrical and elastic properties as previous case. The model is discretised into one single row of material points along with the thickness, and the distance between material points is ∆x = 0.002 m. A fictitious region is introduced outside the ends as the external boundaries with a width of δ. The beam is subjected to a concentrated transverse load of P_z = 100 N at the central point. The load is converted to a body load of $b=\frac{P_z}{2\Delta V}=2.5e7\ N/{m}^3$, and it is subjected to two central material volumes of the model (see Fig. 12).

Fig. 11

Timoshenko beam with clamped-roller support boundary conditions

Fig. 12

Discretisation, applied loading and fictitious region

As depicted in Fig. 13, for transverse displacements, w(x), rotations, θ(x), and axial displacements, u(x), a very good agreement is obtained between PD and FE results.

Fig. 13

Comparison of PD and FE results for (a) transverse displacements, (b) rotations and (c) axial displacements

5.3 Timoshenko Beam with Clamped-Free Boundary Conditions

The performance of a cantilever beam is under investigation (see Fig. 14). The beam has the same geometrical and elastic properties as previous case. The model is discretised into one single row of material points along with the thickness, and the distance between material points is ∆x = 0.002 m. Fictitious regions are introduced outside the ends as the external boundaries with a width of δ. The fictitious region at the free end is included to improve the accuracy of the calculation of the material points adjacent to the free end due to lack of interactions at the free end. The beam is subjected to a bending moment of M = 100 Nm at the free end. The load is converted to a body load of ${b}_{\theta }=\frac{M}{\Delta V}=5e7\ \mathrm{N}/{\mathrm{m}}^2$, and it is applied to the last material point adjacent to the free end (see Fig. 15).

Fig. 14

Timoshenko beam with clamped-free boundary conditions

Fig. 15

Discretisation, applied loading and fictitious region

The transverse displacements, w(x), rotations, θ(x), and axial displacements, u(x), along the beam are obtained from both PD and FE analysis. As shown in Fig. 16, a very good agreement is observed between the two approaches.

Fig. 16

Comparison of PD and FE results for (a) transverse displacements, (b) rotations and (c) axial displacements

6 Conclusions

In this study, a new peridynamic formulation was presented for functionally graded Timoshenko beams. The proposed formulation was validated by considering a Timoshenko beam subjected to different boundary conditions including pinned support-roller support, clamped-roller support and clamped-free boundary conditions. Results from peridynamics were compared against finite element analysis results. A very good agreement was obtained for transverse displacements, rotations and axial displacements along the beam. Therefore, it can be concluded that peridynamics can be a suitable alternative for the analysis of functionally graded Timoshenko beams.

Appendices

Appendix 1

As explained above, the strain energy density function for a functionally graded Timoshenko beam can be expressed as:

$$ W=\frac{1}{2h}\left[{\int}_{-\frac{h}{2}}^{\frac{h}{2}}E(z) dz\cdotp {\left(\frac{\partial u}{\partial x}\right)}^2+{\int}_{-\frac{h}{2}}^{\frac{h}{2}}E(z){z}^2 dz{\left(\frac{\partial \theta }{\partial x}\right)}^2+2{\int}_{-\frac{h}{2}}^{\frac{h}{2}}E(z) zdz\frac{\partial u}{\partial x}\frac{\partial \theta }{\partial x}+\kappa {\int}_{-\frac{h}{2}}^{\frac{h}{2}}G(z) dz{\left(\theta +\frac{\partial w}{\partial x}\right)}^2\right] $$

(30)

In order to obtain the strain energy density function in PD form, it is necessary to transform each term into an equivalent PD expression, and this can be achieved by utilising Taylor’s expansion. If we expand the axial displacement u about a point x and ignore the higher order terms:

$$ u\left(x+\xi \right)-u(x)=\frac{\partial u(x)}{\partial x}\xi $$

(31)

By squaring both sides of Eq. (31) and then dividing each term by |ξ| yields:

$$ \frac{{\left[u\left(x+\xi \right)-u(x)\right]}^2}{\left|\xi \right|}={\left(\frac{\partial u(x)}{\partial x}\right)}^2\left|\xi \right| $$

(32)

Considering x as a fix point and integrating each term of Eq. (32) over the region (−δ, δ) results in:

$$ {\int}_{-\delta}^{\delta}\frac{{\left[u\left(x+\xi \right)-u(x)\right]}^2}{\left|\xi \right|} d\xi ={\left(\frac{\partial u(x)}{\partial x}\right)}^2{\int}_{-\delta}^{\delta}\left|\xi \right| d\xi $$

(33a)

which then gives:

$$ {\left(\frac{\partial u(x)}{\partial x}\right)}^2=\frac{1}{\delta^2}{\int}_{-\delta}^{\delta}\frac{{\left[u\left(x+\xi \right)-u(x)\right]}^2}{\left|\xi \right|} d\xi $$

(33b)

Equation (33b) can be written in discretised form as:

$$ {\left(\frac{\partial {u}_{(k)}}{\partial x}\right)}^2=\frac{1}{\delta^2A}{\sum}_i\frac{{\left({u}_{\left({i}^k\right)}-{u}_{(k)}\right)}^2}{\left|{\xi}_{\left({i}^k\right)(k)}\right|}{V}_{\left({i}^k\right)} $$

(34)

where A represents the cross-sectional area of the beam. Two other terms can be obtained similarly as:

$$ {\left(\frac{\partial {\theta}_{(k)}}{\partial x}\right)}^2=\frac{1}{\delta^2A}\sum \limits_i\frac{{\left({\theta}_{\left({i}^k\right)}-{\theta}_{(k)}\right)}^2}{\left|{\xi}_{\left({i}^k\right)(k)}\right|}{V}_{\left({i}^k\right)} $$

(35)

$$ \frac{\partial {u}_{(k)}}{\partial x}\frac{\partial {\theta}_{(k)}}{\partial x}=\frac{1}{\delta^2A}{\sum}_i\frac{\left({u}_{\left({i}^k\right)}-{u}_{(k)}\right)\left({\theta}_{\left({i}^k\right)}-{\theta}_{(k)}\right)}{\left|{\xi}_{\left({i}^k\right)(k)}\right|}{V}_{\left({i}^k\right)} $$

(36)

If we use Taylor’s expansion for the transverse displacement, w:

$$ w\left(x+\xi \right)-w(x)=\frac{\partial w(x)}{\partial x}\xi $$

(37)

Adding θ(x)ξ to both sides of Eq. (37) yields:

$$ \frac{\uptheta \left(\mathrm{x}\right)+\uptheta \left(x+\xi \right)}{2}\upxi +w\left(x+\xi \right)-w(x)=\left(\frac{\partial w(x)}{\partial x}+\uptheta \left(\mathrm{x}\right)\right)\xi $$

(38)

Squaring both sides of Eq. (38) and then dividing each term by |ξ| gives:

$$ \frac{{\left[\frac{\uptheta \left(\mathrm{x}\right)+\uptheta \left(x+\xi \right)}{2}\upxi +w\left(x+\xi \right)-w(x)\right]}^2}{\left|\xi \right|}={\left(\frac{\partial w(x)}{\partial x}+\uptheta \left(\mathrm{x}\right)\right)}^2\left|\xi \right| $$

(39)

Considering x as a fix point and integrating each term of Eq. (39) over the region (−δ, δ) results in:

$$ {\int}_{-\delta}^{\delta}\frac{{\left[\frac{\uptheta \left(\mathrm{x}\right)+\uptheta \left(x+\xi \right)}{2}\upxi +w\left(x+\xi \right)-w(x)\right]}^2}{\left|\xi \right|} d\xi ={\left(\frac{\partial w(x)}{\partial x}+\uptheta \left(\mathrm{x}\right)\right)}^2{\int}_{-\delta}^{\delta}\left|\xi \right| d\xi $$

(40a)

which then gives:

$$ {\left(\frac{\partial w(x)}{\partial x}+\uptheta \left(\mathrm{x}\right)\right)}^2=\frac{1}{\delta^2}{\int}_{-\delta}^{\delta}\frac{{\left[\frac{\uptheta \left(\mathrm{x}\right)+\uptheta \left(x+\xi \right)}{2}\upxi +w\left(x+\xi \right)-w(x)\right]}^2}{\left|\xi \right|} d\xi $$

(40b)

Equation (40b) can be written in discretised form as:

$$ {\left(\frac{\partial {w}_{(k)}}{\partial x}+{\uptheta}_{(k)}\right)}^2=\frac{1}{\delta^2A}{\sum}_i\frac{{\left(\frac{\uptheta_{(k)}+{\uptheta}_{\left({i}^k\right)}}{2}{\xi}_{\left({i}^k\right)(k)}+{w}_{\left({i}^k\right)}-{w}_{(k)}\right)}^2}{\left|{\xi}_{\left({i}^k\right)(k)}\right|}{V}_{\left({i}^k\right)} $$

(41)

Inserting Eqs. (34), (35), (36) and (39) into (30) results in PD form of strain energy density function for the material point k as:

$$ {W}_{(k)}=\frac{1}{2h}\frac{1}{\delta^2A}\left[{\int}_{-\frac{h}{2}}^{\frac{h}{2}}E(z) dz\cdotp {\sum}_i\frac{{\left({u}_{\left({i}^k\right)}-{u}_{(k)}\right)}^2}{\left|{\xi}_{\left({i}^k\right)(k)}\right|}{V}_{\left({i}^k\right)}+{\int}_{-\frac{h}{2}}^{\frac{h}{2}}E(z){z}^2 dz\sum \limits_i\frac{{\left({\theta}_{\left({i}^k\right)}-{\theta}_{(k)}\right)}^2}{\left|{\xi}_{\left({i}^k\right)(k)}\right|}{V}_{\left({i}^k\right)}+2{\int}_{-\frac{h}{2}}^{\frac{h}{2}}E(z) zdz\sum \limits_{\mathrm{i}}\frac{\left({u}_{\left({i}^k\right)}-{u}_{(k)}\right)\left({\theta}_{\left({i}^k\right)}-{\theta}_{(k)}\right)}{\left|{\xi}_{\left({i}^k\right)(k)}\right|}{V}_{\left({i}^k\right)}+\kappa {\int}_{-\frac{h}{2}}^{\frac{h}{2}}G(z) dz\sum \limits_i\frac{{\left(\frac{\uptheta_{(k)}+{\theta}_{\left({i}^k\right)}}{2}{\xi}_{\left({i}^k\right)(k)}+{w}_{\left({i}^k\right)}-{w}_{(k)}\right)}^2}{\left|{\xi}_{\left({i}^k\right)(k)}\right|}{V}_{\left({i}^k\right)}\right] $$

(42)

Similarly, PD form of strain energy density function for material point j is:

$$ {W}_{(j)}=\frac{1}{2h}\frac{1}{\delta^2A}\left[{\int}_{-\frac{h}{2}}^{\frac{h}{2}}E(z) dz\cdotp \sum \limits_i\frac{{\left({u}_{\left({i}^j\right)}-{u}_{(j)}\right)}^2}{\left|{\xi}_{\left({i}^j\right)(j)}\right|}{V}_{\left({i}^j\right)}+{\int}_{-\frac{h}{2}}^{\frac{h}{2}}E(z){z}^2 dz\sum \limits_i\frac{{\left({\theta}_{\left({i}^j\right)}-{\theta}_{(j)}\right)}^2}{\left|{\xi}_{\left({i}^j\right)(j)}\right|}{V}_{\left({i}^j\right)}+2{\int}_{-\frac{h}{2}}^{\frac{h}{2}}E(z) zdz\sum \limits_i\frac{\left({u}_{\left({i}^j\right)}-{u}_{(j)}\right)\left({\theta}_{\left({i}^j\right)}-{\theta}_{(j)}\right)}{\left|{\xi}_{\left({i}^j\right)(j)}\right|}{V}_{\left({i}^j\right)}+\kappa {\int}_{-\frac{h}{2}}^{\frac{h}{2}}G(z) dz\sum \limits_i\frac{{\left(\frac{\uptheta_{(j)}+{\theta}_{\left({i}^j\right)}}{2}{\xi}_{\left({i}^j\right)(j)}+{w}_{\left({i}^j\right)}-{w}_{(j)}\right)}^2}{\left|{\xi}_{\left({i}^j\right)(j)}\right|}{V}_{\left({i}^j\right)}\right] $$

(43)

Appendix 2

The numerical solution for PD static analysis is obtained by eliminating the inertia forces. Therefore, the PD governing equations given in Eqs. (22a–c) can be reduced as:

$$ \frac{1}{h}\frac{2}{\delta^2A}\left({\int}_{-\frac{h}{2}}^{\frac{h}{2}}E(z) dz\sum \limits_j\frac{u_{(j)}-{u}_{(k)}}{\left|{\xi}_{(j)(k)}\right|}{V}_{(j)}+{\int}_{-\frac{h}{2}}^{\frac{h}{2}}E(z) zdz\sum \limits_j\frac{\theta_{(j)}-{\theta}_{(k)}}{\left|{\xi}_{(j)(k)}\right|}{V}_{(j)}\right)=-{b}_x^{(k)} $$

(44a)

$$ \frac{1}{h}\frac{2}{\delta^2A}\left({\int}_{-\frac{h}{2}}^{\frac{h}{2}}E(z){z}^2 dz\sum \limits_j\frac{\theta_{(j)}-{\theta}_{(k)}}{\left|{\xi}_{(j)(k)}\right|}{V}_{(j)}+{\int}_{-\frac{h}{2}}^{\frac{h}{2}}E(z) zdz\sum \limits_j\frac{\left({u}_{(j)}-{u}_{(k)}\right)}{\left|{\xi}_{(j)(k)}\right|}{V}_{(j)}-\frac{1}{2}\kappa {\int}_{-\frac{h}{2}}^{\frac{h}{2}}G(z) dz\sum \limits_j\left({w}_{(j)}-{w}_{(k)}+\frac{\theta_{(k)}+{\theta}_{(j)}}{2}{\xi}_{(j)(k)}\right)\mathit{\operatorname{sign}}\left({\xi}_{(j)(k)}\right){V}_{(j)}\right)=-{b}_{\theta}^{(k)} $$

(44b)

$$ \frac{1}{h}\frac{2}{\delta^2A}\left(\kappa {\int}_{-\frac{h}{2}}^{\frac{h}{2}}G(z) dz\sum \limits_j\frac{w_{(j)}-{w}_{(k)}}{\left|{\xi}_{(j)(k)}\right|}+\frac{\theta_{(k)}+{\theta}_{(j)}}{2}\mathit{\operatorname{sign}}\left({\xi}_{(j)(k)}\right){V}_{(j)}\right)=-{b}_z^{(k)} $$

(44c)

Eqs. (44a, 44b) can be written in matrix form as:

$$ \left[K\right]\left\{U\right\}=-\left\{B\right\} $$

(45)

where [K], {U} and {B} represent stiffness matrix, displacement and body force vectors, respectively. Thus, displacements can be obtained from Eq. (45) by considering the boundary conditions as explained in Section 4.