Peridynamic Higher-Order Beam Formulation

Abstract

In this study, a novel higher-order peridynamic beam formulation is presented. The formulation is obtained by using Euler-Lagrange equations and Taylor’s expansion. To demonstrate the capability of the presented approach, several different beam configurations are considered including simply supported beam subjected to distributed loading, simply supported beam with concentrated load, clamped-clamped beam subjected to distributed loading, cantilever beam subjected to a point load at its free end and cantilever beam subjected to a moment at its free end. Transverse displacement results along the beam obtained from peridynamics and finite element method are compared with each other and very good agreement is obtained between the two approaches.

1 Introduction

Peridynamic (PD) theory was introduced by Silling [1] to overcome the limitations of widely used classical continuum mechanics (CCM). PD equations do not contain spatial derivatives as opposed to their usage in CCM which allows its equations to be valid even if the displacement field is not continuous due to the existence of cracks. Moreover, it has a length scale parameter called horizon which does not exist in CCM, so that it can capture non-local effects. PD has been applied to many different material systems including metals [2], composite materials [3] and concrete [4]. Moreover, PD is not limited to structural analysis, but can also be used to analyse heat transfer [5], diffusion [6], porous flow [7], fluid flow [8], etc. An extensive review of PD research is given in Javili et al. [9]. Original PD formulation is suitable to analyse 1-Dimensional, 2-Dimensional and 3-Dimensional models by assigning translational degrees of freedom to each material point. However, for certain shapes including beams, plates and shells, such formulations can be computational expensive. Alternatively, simplified beam, plate and shell formulations with additional rotational degrees of freedom per material point can be utilised.

There are several PD formulations available in the literature suitable for beam, plate and shell structures. Amongst these, Diyaroglu et al. [10] proposed a state-based Euler-beam formulation for slender beams. This formulation was further extended by Yang et al. [11] to analyse Kirchhoff plates. O’Grady and Foster [12] developed a non-ordinary state-based model to represent the bending behaviour of Euler-Bernoulli beam. They also introduced a non-ordinary state-based peridynamic model for Kirchhoff-Love plate [13]. In order to take into account transverse shear deformation for thick beams and plates, Diyaroglu et al. [14] presented peridynamic Timoshenko beam and Mindlin plate formulations. Taylor and Steigmann [15] developed a general plate model via bond-based peridynamics and asymptotic analysis. Chowdry et al. [16] proposed a state-based peridynamic formulation for linear elastic shells.

In this study, a novel peridynamic formulation is presented for higher-order beam theory. Higher-order beam theory allows more accurate representation in the thickness direction for thick plates with respect to Timoshenko beam formulation. Moreover, it does not require shear correction factors as in Timoshenko beam models. The formulation is based on Euler-Lagrange equation and Taylor’s expansion. The capability of the proposed formulation is demonstrated by considering several benchmark problems of beams subjected to various boundary and loading conditions. Peridynamic results are compared against finite element method (FEM) results.

2 Peridynamic Formulation

2.1 Classical Strain Energy Density

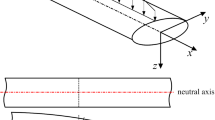
The displacement field of any material point in a beam can be represented in terms of the displacement field of a material point along the central axis in xz plane by using Taylor expansion as (see Fig. 1)

$$ {\left.u\left(x,z\right)=u\Big(x,0\Big)+z\left(\frac{\partial u(x)}{\partial z}\right)\right|}_{z=0}+\frac{1}{2}{z}^2\left(\frac{\partial^2u(x)}{\partial {z}^2}\right){\left|{}_{z=0}+\frac{1}{3!}{z}^3\left(\frac{\partial^3u(x)}{\partial {z}^3}\right)\right|}_{z=0}+\dots $$

(1a)

$$ {\left.w\left(x,z\right)=w\Big(x,0\Big)+z\left(\frac{\partial w(x)}{\partial z}\right)\right|}_{z=0}+\frac{1}{2}{z}^2\left(\frac{\partial^2w(x)}{\partial {z}^2}\right){\left|{}_{z=0}+\frac{1}{3!}{z}^3\left(\frac{\partial^3w(x)}{\partial {z}^3}\right)\right|}_{z=0}+\dots $$

(1b)

where u(x, z) and w(x, z)are the displacement components of the material point in x- and z-directions, respectively. In this study, only flexural deformations are taken into consideration. Thus, eliminating axial deformation effects and higher order terms in Eq. (1), the components of the displacement field can be expressed as:

$$ u\left(x,z\right)= z\theta \left(x,0\right)+{z}^3{\theta}^{\ast}\left(x,0\right) $$

(2a)

$$ w\left(x,z\right)=w\left(x,0\right)+{z}^2{w}^{\ast}\left(x,0\right) $$

(2b)

where θ, θ^∗ and w^∗ are introduced as three new independent variables which are defined respectively as (see Fig. 2)

$$ \theta \left(x,0\right)={\left[\frac{\partial u}{\partial z}\right]}_{z=0} $$

(3a)

$$ {\theta}^{\ast}\left(x,0\right)=\frac{1}{3!}{\left[\frac{\partial^3u}{\partial {z}^3}\right]}_{z=0} $$

(3b)

$$ {w}^{\ast}\left(x,0\right)=\frac{1}{2}{\left[\frac{\partial^2u}{\partial {z}^2}\right]}_{z=0} $$

(3c)

Fig. 1

Cross-section of the beam

Fig. 2

Degrees-of-freedom per node used in higher-order beam theory

In order to simplify the expressions, hereafter w(x, 0), θ(x, 0), w^∗(x, 0)and θ^∗(x, 0)will be written simply as w, θ, w^∗ and θ^∗, respectively. Utilising the expressions given in Eq. (2) for the displacement components, the three well-known strain-displacement relationships of the plane stress elasticity can be written as:

$$ {\varepsilon}_{xx}=z\frac{\partial \theta }{\partial x}+{z}^3\frac{\partial {\theta}^{\ast }}{\partial x} $$

(4a)

$$ {\varepsilon}_{zz}=2{zw}^{\ast } $$

(4b)

$$ {\gamma}_{xz}=\theta +\frac{\partial w}{\partial x}+3{z}^2{\theta}^{\ast }+{z}^2\frac{\partial {w}^{\ast }}{\partial x} $$

(4c)

Note that the strain-displacement relationships given in Eq. (4a–c) are much more realistic with respect to Timoshenko beam theory where the axial normal strain, ε_xx, and transverse shear strain, γ_xz,vary linearly in the thickness direction and the transverse normal strain, ε_zz, is equivalent to zero. This also eliminates the need for the introduction of shear correction factor which is widely used in Timoshenko beam analysis.

Assuming the material is isotropic and plane-stress condition is applicable, the stress-strain relationships can be expressed as:

$$ \left\{\begin{array}{c}{\sigma}_{xx}\\ {}{\sigma}_{zz}\\ {}{\tau}_{xz}\end{array}\right\}=\frac{E}{1-{\nu}^2}\left[\begin{array}{ccc}1& \nu & 0\\ {}\nu & 1& 0\\ {}0& 0& \frac{1-\nu }{2}\end{array}\right]\left\{\begin{array}{c}{\varepsilon}_{xx}\\ {}{\varepsilon}_{zz}\\ {}{\gamma}_{xz}\end{array}\right\} $$

(5)

where E and ν represent elastic modulus and Poisson’s ratio, respectively. Substituting Eq. (4a–c) into Eq. (5) yields:

$$ {\sigma}_{xx}=\frac{Ez}{1-{\nu}^2}\left(\frac{\partial \theta }{\partial x}+2\nu {w}^{\ast}\right)+\frac{E}{1-{\nu}^2}{z}^3\frac{\partial {\theta}^{\ast }}{\partial x} $$

(6a)

$$ {\sigma}_{zz}=\frac{Ez}{1-{\nu}^2}\left(\nu \frac{\partial \theta }{\partial x}+2{w}^{\ast}\right)+\frac{E}{1-{\nu}^2}{z}^3\left(\nu \frac{\partial {\theta}^{\ast }}{\partial x}\right) $$

(6b)

$$ {\tau}_{xz}=G\left(\theta +\frac{\partial w}{\partial x}\right)+G{z}^2\left(3{\theta}^{\ast }+\frac{\partial {w}^{\ast }}{\partial x}\right) $$

(6c)

The strain energy density can then be defined as:

$$ W=\frac{1}{2}\left({\sigma}_{xx}{\varepsilon}_{xx}+{\sigma}_{zz}{\varepsilon}_{zz}+{\tau}_{xz}{\gamma}_{xz}\right) $$

(7)

Substituting Eqs. (4) and (6) into Eq. (7) results in:

$$ W=\frac{1}{2}\left\{\begin{array}{c}\frac{E}{1-{\nu}^2}\left[{z}^2\left({\left(\frac{\partial \theta }{\partial x}+2{w}^{\ast}\right)}^2-4\left(1-\nu \right){w}^{\ast}\frac{\partial \theta }{\partial x}\right)+2{z}^4\frac{\partial {\theta}^{\ast }}{\partial x}\left(\frac{\partial \theta }{\partial x}+2\nu {w}^{\ast}\right)+{z}^6\frac{\partial {\theta}^{\ast }}{\partial x}\frac{\partial {\theta}^{\ast }}{\partial x}\right]+\\ {}G\left[{\left(\theta +\frac{\partial w}{\partial x}\right)}^2+{z}^4{\left(3{\theta}^{\ast }+\frac{\partial {w}^{\ast }}{\partial x}\right)}^2+2{z}^2\left(\theta +\frac{\partial w}{\partial x}\right)\left(3{\theta}^{\ast }+\frac{\partial {w}^{\ast }}{\partial x}\right)\right]\end{array}\right\} $$

(8)

The average strain energy density of a material point along the central axis of the beam can be obtained by integrating the strain energy density function given in Eq.(8) through the transverse direction and divided by the thickness, h, as:

$$ W=\frac{1}{2h}\left\{\begin{array}{c}\frac{E}{1-{\nu}^2}\left[\frac{h^3}{12}\left(\frac{\partial \theta }{\partial x}\frac{\partial \theta }{\partial x}+4{\left({w}^{\ast}\right)}^2+4\nu {w}^{\ast}\frac{\partial \theta }{\partial x}\right)+\frac{h^5}{40}\frac{\partial {\theta}^{\ast }}{\partial x}\left(\frac{\partial \theta }{\partial x}+2\nu {w}^{\ast}\right)+\frac{h^7}{448}\frac{\partial {\theta}^{\ast }}{\partial x}\frac{\partial {\theta}^{\ast }}{\partial x}\right]+\\ {}G\left[h{\left(\theta +\frac{\partial w}{\partial x}\right)}^2+\frac{h^5}{80}{\left(3{\theta}^{\ast }+\frac{\partial {w}^{\ast }}{\partial x}\right)}^2+\frac{h^3}{6}\left(\theta +\frac{\partial w}{\partial x}\right)\left(3{\theta}^{\ast }+\frac{\partial {w}^{\ast }}{\partial x}\right)\right]\end{array}\right\} $$

(9)

2.2 Peridynamics

Peridynamics (PD) is a non-local theory and it is different than the classical local continuum mechanics since state of each material point is not only influenced by the material points located in its immediate vicinity but also influenced by material points which are located within a region of finite radius named as “horizon”, H. The equation of motion of a material point located at x can be expressed as:

$$ \rho (x)\ddot{u}\left(x,t\right)=\underset{H}{\int}\mathbf{f}\left(u\left({x}^{\prime },t\right)-u\left(x,t\right),{x}^{\prime }-x\right)\;d{V}^{\prime }+b\left(x,t\right) $$

(10)

where ρ(x) represents the density of the material, t represents time, u(x, t), $\ddot{\mathbf{u}}\left(\mathbf{x},t\right)$ and b(x, t) are the displacement, acceleration and body load of the material point located at x. In Eq. (10), f(u^′ − u, x^′ − x) defines the peridynamic interaction (bond) force between the material point located at x and another material point inside its horizon located at x^′ (see Fig. 3).

Fig. 3

Peridynamic interaction force and horizon concept [17]

Obtaining a closed-form solution for Eq. (10) is usually not possible. Numerical techniques including meshless approach is widely used by discretising the solution domain into small volumes and assigning a point to represent the associated volume. Therefore, the PD equations of motion for a particular material point k can be written in discrete form as:

$$ {\rho}_{(k)}{\ddot{\mathbf{u}}}_{(k)}=\sum \limits_{j=1}^N{\mathbf{f}}_{(k)(j)}{V}_{(j)}+{\mathbf{b}}_{(k)} $$

(11)

where the summation takes over the family members of the material point k, N indicates the total number of family members, and V is the volume of the material point. The PD equation of motion can be obtained by using Euler-Lagrange equation as:

$$ \frac{d}{dt}\frac{\partial L}{\partial {\dot{\mathbf{u}}}_{(k)}}-\frac{\partial L}{\partial {\mathbf{u}}_{(k)}}=0 $$

(12)

where ${\dot{\mathbf{u}}}_{(k)}$ is the velocity of the material point k and L is the Lagrangian which is the difference between the total kinetic energy of the system, T, and total potential energy of the system, U, i.e. L = T − U.

The total potential energy stored in the body can be obtained by summing potential energies of all material points including strain energy and energy due to external loads as:

$$ U=\sum \limits_k{W}_{(k)}\left({\mathbf{u}}_{(k)},{\mathbf{u}}_{\left({1}^k\right)}-{\mathbf{u}}_{(k)},{\mathbf{u}}_{\left({2}^k\right)}-{\mathbf{u}}_{(k)},{\mathbf{u}}_{\left({3}^k\right)}-{\mathbf{u}}_{(k)},\mathrm{K}\right){V}_{(k)}-\sum \limits_k{\mathbf{b}}_{(k)}{\mathbf{u}}_{(k)}{V}_{(k)} $$

(13)

where i^(k) is the material point inside the horizon of the material point k.

Note that unlike classical continuum mechanics, in peridynamics, the strain energy density function, W_(k), of a certain material point k depends on its displacement and the relative displacement between itself and all other material points in its horizon. The strain energy density of a material point for a higher-order beam theory based on classical continuum mechanics is given in Eq. (9). This expression can be converted into a peridynamic form by transforming the spatial derivative terms to their corresponding peridynamic form as explained in Appendix A. Therefore, by performing the following transformations,

$$ {\left(\frac{\partial {\theta}_{(k)}}{\partial x}\right)}^2+4{\left({w}_{(k)}^{\ast}\right)}^2+4\nu {w}_{(k)}^{\ast}\frac{\partial {\theta}_{(k)}}{\partial x}=\frac{1}{\delta^2A}\sum \limits_{i^k}\frac{{\left({\theta}_{\left({i}^k\right)}-{\theta}_{(k)}\right)}^2+4\nu {w}_{(k)}^{\ast}\left({\theta}_{\left({i}^k\right)}-{\theta}_{(k)}\right){\xi}_{\left({i}^k\right)(k)}+4{\left({w}_{(k)}^{\ast}\right)}^2{\xi}_{\left({i}^k\right)(k)}^2}{\mid {\xi}_{\left({i}^k\right)(k)}\mid }{V}_{\left({i}^k\right)} $$

(14a)

$$ \frac{\partial {\theta}_{(k)}^{\ast }}{\partial x}\left(\frac{\partial {\theta}_{(k)}}{\partial x}+2\nu {w}_{(k)}^{\ast}\right)=\frac{1}{\delta^2A}\sum \limits_{i^k}\frac{\left({\theta}_{\left({i}^k\right)}-{\theta}_{(k)}+2\nu {w}_{(k)}^{\ast }{\xi}_{\left({i}^k\right)(k)}\right)\left({\theta}_{\left({i}^k\right)}^{\ast }-{\theta}_{(k)}^{\ast}\right)}{\mid {\xi}_{\left({i}^k\right)(k)}\mid }{V}_{\left({i}^k\right)} $$

(14b)

$$ {\left(\frac{\partial {\theta}_{(k)}^{\ast }}{\partial x}\right)}^2=\frac{1}{\delta^2A}\sum \limits_{i^k}\frac{{\left({\theta}_{\left({i}^k\right)}^{\ast }-{\theta}_{(k)}^{\ast}\right)}^2}{\mid {\xi}_{\left({i}^k\right)(k)}\mid }{V}_{\left({i}^k\right)} $$

(14c)

$$ {\left({\theta}_{(k)}+\frac{\partial {w}_{(k)}}{\partial x}\right)}^2=\frac{1}{\delta^2A}\sum \limits_{i^k}\frac{{\left({w}_{\left({i}^k\right)}-{w}_{(k)}+{\theta}_{(k)}{\xi}_{\left({i}^k\right)(k)}\right)}^2}{\mid {\xi}_{\left({i}^k\right)(k)}\mid }{V}_{\left({i}^k\right)} $$

(14d)

$$ {\left(3{\theta}_{(k)}^{\ast }+\frac{\partial {w}_{(k)}^{\ast }}{\partial x}\right)}^2=\frac{1}{\delta^2A}\sum \limits_{i^k}\frac{{\left({w}_{\left({i}^k\right)}^{\ast }-{w}_{(k)}^{\ast }+3{\theta}_{(k)}^{\ast }{\xi}_{\left({i}^k\right)(k)}\right)}^2}{\mid {\xi}_{\left({i}^k\right)(k)}\mid }{V}_{\left({i}^k\right)} $$

(14e)

$$ \left({\theta}_{(k)}+\frac{\partial {w}_{(k)}}{\partial x}\right)\left(3{\theta}_{(k)}^{\ast }+\frac{\partial {w}_{(k)}^{\ast }}{\partial x}\right)=\frac{1}{\delta^2A}\sum \limits_{i^k}\frac{\left({w}_{\left({i}^k\right)}-{w}_{(k)}+{\theta}_{(k)}{\xi}_{\left({i}^k\right)(k)}\right)\left({w}_{\left({i}^k\right)}^{\ast }-{w}_{(k)}^{\ast }+3{\theta}_{(k)}^{\ast }{\xi}_{\left({i}^k\right)(k)}\right)}{\mid {\xi}_{\left({i}^k\right)(k)}\mid }{V}_{\left({i}^k\right)} $$

(14f)

the strain energy density function given in Eq. (9) can be written in PD form as:

$$ {W}_{(k)}=\frac{1}{2h}\frac{1}{\delta^2A}\left\{\begin{array}{c}\frac{E}{1-{\nu}^2}\left[\begin{array}{c}\frac{h^3}{12}\left(\sum \limits_{i^k}\frac{{\left({\theta}_{\left({i}^k\right)}-{\theta}_{(k)}\right)}^2+4\nu {w}_{(k)}^{\ast}\left({\theta}_{\left({i}^k\right)}-{\theta}_{(k)}\right){\xi}_{\left({i}^k\right)(k)}+4{\left({w}_{(k)}^{\ast}\right)}^2{\xi}_{\left({i}^k\right)(k)}^2}{\mid {\xi}_{\left({i}^k\right)(k)}\mid }{V}_{\left({i}^k\right)}\right)+\\ {}\frac{h^5}{40}\left(\sum \limits_{i^k}\frac{\left({\theta}_{\left({i}^k\right)}-{\theta}_{(k)}+2\nu {w}_{(k)}^{\ast }{\xi}_{\left({i}^k\right)(k)}\right)\left({\theta}_{\left({i}^k\right)}^{\ast }-{\theta}_{(k)}^{\ast}\right)}{\mid {\xi}_{\left({i}^k\right)(k)}\mid }{V}_{\left({i}^k\right)}\right)+\frac{h^7}{448}\left(\sum \limits_{i^k}\frac{{\left({\theta}_{\left({i}^k\right)}^{\ast }-{\theta}_{(k)}^{\ast}\right)}^2}{\mid {\xi}_{\left({i}^k\right)(k)}\mid }{V}_{\left({i}^k\right)}\right)\end{array}\right]+\\ {}G\left[\begin{array}{c}h\left(\sum \limits_{i^k}\frac{{\left({w}_{\left({i}^k\right)}-{w}_{(k)}+{\theta}_{(k)}{\xi}_{\left({i}^k\right)(k)}\right)}^2}{\mid {\xi}_{\left({i}^k\right)(k)}\mid }{V}_{\left({i}^k\right)}\right)+\frac{h^5}{80}\left(\sum \limits_{i^k}\frac{{\left({w}_{\left({i}^k\right)}^{\ast }-{w}_{(k)}^{\ast }+3{\theta}_{(k)}^{\ast }{\xi}_{\left({i}^k\right)(k)}\right)}^2}{\mid {\xi}_{\left({i}^k\right)(k)}\mid }{V}_{\left({i}^k\right)}\right)\\ {}\frac{h^3}{6}\left(\sum \limits_{i^k}\frac{\left({w}_{\left({i}^k\right)}-{w}_{(k)}+{\theta}_{(k)}{\xi}_{\left({i}^k\right)(k)}\right)\left({w}_{\left({i}^k\right)}^{\ast }-{w}_{(k)}^{\ast }+3{\theta}_{(k)}^{\ast }{\xi}_{\left({i}^k\right)(k)}\right)}{\mid {\xi}_{\left({i}^k\right)(k)}\mid }{V}_{\left({i}^k\right)}\right)\end{array}\right]\end{array}\right\} $$

(15)

The generalised displacement vector, u_(k), and the body load vector, b_(k), at point k in the potential energy expression given in Eq. (13) can be written, respectively, as:

$$ {\mathbf{u}}_{(k)}={\left\{{\theta}_{(k)}\kern0.5em {\theta}_{(k)}^{\ast}\kern0.5em {w}_{(k)}\kern0.5em {w}_{(k)}^{\ast}\right\}}^T $$

(16a)

$$ {\mathbf{b}}_{(k)}={\left\{{b}_{\theta (k)}\kern0.5em 0\kern0.5em {b}_{z(k)}\kern0.5em 0\right\}}^T $$

(16b)

The total kinetic energy of the body can be obtained by summing kinetic energies of all material points as:

$$ T=\frac{1}{2}\sum \limits_k{\rho}_{(k)}\left({\dot{u}}_{(k)}^2+{\dot{w}}_{(k)}^2\right){V}_{(k)} $$

(17)

After substituting Eq. (2 a, b) in Eq. (17), Eq. (17) can be rewritten as:

$$ T=\frac{1}{2}\sum \limits_k{\rho}_{(k)}\left[{\left(z{\dot{\theta}}_{(k)}+{z}^3{\dot{\theta}}_{(k)}^{\ast}\right)}^2+{\left({\dot{w}}_{(k)}+{z}^2{\dot{w}}_{(k)}^{\ast}\right)}^2\right]{V}_{(k)} $$

(18)

The average kinetic energy of a material point along the central axis of the beam can be obtained by integrating the kinetic energy expression given in Eq.(18) through the transverse direction and divided by the thickness, h, as:

$$ T=\frac{1}{2}\sum \limits_k\frac{1}{h}{\rho}_{(k)}\left[\frac{h^3}{12}{\dot{\theta}}_{(k)}^2+\frac{h^7}{448}{\left({\dot{\theta}}_{(k)}^{\ast}\right)}^2+\frac{h^5}{40}{\dot{\theta}}_{(k)}{\dot{\theta}}_{(k)}^{\ast }+h{\dot{w}}_{(k)}^2+\frac{h^5}{80}{\left({\dot{w}}_{(k)}^{\ast}\right)}^2+\frac{h^3}{6}{\dot{w}}_{(k)}{\dot{w}}_{(k)}^{\ast}\right]{V}_{(k)} $$

(19)

Thus, the Lagrangian of the body can be written as:

$$ {\displaystyle \begin{array}{c}L=T-U=\frac{1}{2}\sum \limits_k\frac{1}{h}{\rho}_{(k)}\left[\frac{h^3}{12}{\dot{\theta}}_{(k)}^2+\frac{h^7}{448}{\left({\dot{\theta}}_{(k)}^{\ast}\right)}^2+\frac{h^5}{40}{\dot{\theta}}_{(k)}{\dot{\theta}}_{(k)}^{\ast }+h{\dot{w}}_{(k)}^2+\frac{h^5}{80}{\left({\dot{w}}_{(k)}^{\ast}\right)}^2+\frac{h^3}{6}{\dot{w}}_{(k)}{\dot{w}}_{(k)}^{\ast}\right]{V}_{(k)}\\ {}-\sum \limits_k{W}_{(k)}{V}_{(k)}+\sum \limits_k{b}_{\theta (k)}{\theta}_{(k)}{V}_{(k)}+\sum \limits_k{b}_{z(k)}{w}_{(k)}{V}_{(k)}\end{array}} $$

(20)

Finally, Euler-Lagrange equations for higher-order beam theory can be written as:

$$ \frac{d}{dt}\frac{\partial L}{\partial {\dot{\theta}}_{(k)}}-\frac{\partial L}{\partial {\theta}_{(k)}}=0 $$

(21a)

$$ \frac{d}{dt}\frac{\partial L}{\partial {\dot{\theta}}_{(k)}^{\ast }}-\frac{\partial L}{\partial {\theta}_{(k)}^{\ast }}=0 $$

(21b)

$$ \frac{d}{dt}\frac{\partial L}{\partial {\dot{w}}_{(k)}}-\frac{\partial L}{\partial {w}_{(k)}}=0 $$

(21c)

$$ \frac{d}{dt}\frac{\partial L}{\partial {\dot{w}}_{(k)}^{\ast }}-\frac{\partial L}{\partial {w}_{(k)}^{\ast }}=0 $$

(21d)

Substituting Eq. (20) into Eq. (21) gives the PD equations of motion for higher-order beam theory as:

$$ {\displaystyle \begin{array}{c}{\rho}_{(k)}\left(\frac{h^2}{12}{\ddot{\theta}}_{(k)}+\frac{h^4}{80}{\ddot{\theta}}_{(k)}^{\ast}\right)=\\ {}\frac{1}{h}\frac{E}{1-{\nu}^2}\frac{2}{\delta^2A}\left[\frac{h^3}{12}\left(\sum \limits_j\left(\frac{\left({\theta}_{(j)}-{\theta}_{(k)}\right)}{\mid {\xi}_{(j)(k)}\mid }+\nu \left({w}_{(k)}^{\ast }+{w}_{(j)}^{\ast}\right)\operatorname{sign}\left({\xi}_{(j)(k)}\right)\right){V}_{(j)}\right)+\frac{h^5}{80}\sum \limits_j\frac{\left({\theta}_{(j)}^{\ast }-{\theta}_{(k)}^{\ast}\right)}{\mid {\xi}_{(j)(k)}\mid }{V}_{(j)}\right]\\ {}-\frac{G}{h}\frac{1}{\delta^2A}\left\{h\sum \limits_j\left[\left({w}_{(j)}-{w}_{(k)}\right)\operatorname{sign}\left({\xi}_{(j)(k)}\right)+{\theta}_{(k)}|{\xi}_{(j)(k)}|\right]{V}_{(j)}+\frac{h^3}{12}\sum \limits_j\left[\left({w}_{(j)}^{\ast }-{w}_{(k)}^{\ast}\right)\operatorname{sign}\left({\xi}_{(j)(k)}\right)+3{\theta}_{(k)}^{\ast }|{\xi}_{(j)(k)}|\right]{V}_{(j)}\right\}+{b}_{\theta (k)}\end{array}} $$

(22a)

$$ {\displaystyle \begin{array}{c}{\rho}_{(k)}\left(\frac{h^6}{448}{\ddot{\theta}}_{(k)}^{\ast }+\frac{h^4}{80}{\ddot{\theta}}_{(k)}\right)=\\ {}\frac{1}{h}\frac{E}{1-{\nu}^2}\frac{2}{\delta^2A}\left[\frac{h^5}{80}\left(\sum \limits_j\left(\frac{\left({\theta}_{(j)}-{\theta}_{(k)}\right)}{\mid {\xi}_{(j)(k)}\mid }+\nu \left({w}_{(k)}^{\ast }+{w}_{(j)}^{\ast}\right)\operatorname{sign}\left({\xi}_{(j)(k)}\right)\right){V}_{(j)}\right)+\frac{h^7}{448}\sum \limits_j\frac{\left({\theta}_{(j)}^{\ast }-{\theta}_{(k)}^{\ast}\right)}{\mid {\xi}_{(j)(k)}\mid }{V}_{(j)}\right]\\ {}-\frac{G}{h}\frac{3}{\delta^2A}\left\{\frac{h^3}{12}\sum \limits_j\left[\left({w}_{(j)}-{w}_{(k)}\right)\operatorname{sign}\left({\xi}_{(j)(k)}\right)+{\theta}_{(k)}|{\xi}_{(j)(k)}|\right]{V}_{(j)}+\frac{h^5}{80}\sum \limits_j\left[\left({w}_{(j)}^{\ast }-{w}_{(k)}^{\ast}\right)\operatorname{sign}\left({\xi}_{(j)(k)}\right)+3{\theta}_{(k)}^{\ast }|{\xi}_{(j)(k)}|\right]{V}_{(j)}\right\}\end{array}} $$

(22b)

$$ {\displaystyle \begin{array}{c}{\rho}_{(k)}\left({\ddot{w}}_{(k)}+\frac{h^2}{12}{\ddot{w}}_{(k)}^{\ast}\right)=\\ {}\frac{G}{h}\frac{2}{\delta^2A}\left\{h\sum \limits_j\left[\frac{\left({w}_{(j)}-{w}_{(k)}\right)}{\mid {\xi}_{(j)(k)}\mid }+\frac{\left({\theta}_{(k)}+{\theta}_{(j)}\right)}{2}\operatorname{sign}\left({\xi}_{(j)(k)}\right)\right]{V}_{(j)}+\frac{h^3}{12}\sum \limits_j\left[\frac{\left({w}_{(j)}^{\ast }-{w}_{(k)}^{\ast}\right)}{\mid {\xi}_{(j)(k)}\mid }+3\frac{\left({\theta}_{(k)}^{\ast }+{\theta}_{(j)}^{\ast}\right)}{2}\operatorname{sign}\left({\xi}_{(j)(k)}\right)\right]{V}_{(j)}\right\}+{b}_{z(k)}\end{array}} $$

(22c)

$$ {\displaystyle \begin{array}{c}{\rho}_{(k)}\left(\frac{h^2}{12}{\ddot{w}}_{(k)}+\frac{h^4}{80}{\ddot{w}}_{(k)}^{\ast}\right)=\\ {}-\frac{1}{h}\frac{E}{1-{\nu}^2}\frac{2}{\delta^2A}\left[\frac{h^3}{12}\left(\sum \limits_j\left(\nu \left({\theta}_{(j)}-{\theta}_{(k)}\right)\operatorname{sign}\left({\xi}_{(j)(k)}\right)+2{w}_{(k)}^{\ast }|{\xi}_{(j)(k)}|\right){V}_{(j)}\right)+\frac{h^5}{80}\sum \limits_j\nu \left({\theta}_{(j)}^{\ast }-{\theta}_{(k)}^{\ast}\right)\operatorname{sign}\left({\xi}_{(j)(k)}\right){V}_{(j)}\right]\\ {}+\frac{G}{h}\frac{1}{\delta^2A}\left\{\frac{h^3}{6}\sum \limits_j\left[\frac{\left({w}_{(j)}-{w}_{(k)}\right)}{\mid {\xi}_{(j)(k)}\mid }+\frac{\theta_{(k)}+{\theta}_{(j)}}{2}\operatorname{sign}\left({\xi}_{(j)(k)}\right)\right]{V}_{(j)}+\frac{h^5}{40}\sum \limits_j\left[\frac{\left({w}_{(j)}^{\ast }-{w}_{(k)}^{\ast}\right)}{\mid {\xi}_{(j)(k)}\mid }+\frac{3}{2}\left({\theta}_{(k)}^{\ast }+{\theta}_{(j)}^{\ast}\right)\operatorname{sign}\left({\xi}_{(j)(k)}\right)\right]{V}_{(j)}\right\}\end{array}} $$

(22d)

3 Numerical Results

In this section, several different numerical examples are considered to demonstrate the capability of the current PD formulation. A beam with a length of 1 m, a thickness of 0.2 m and a width of 0.005 m is considered. The material properties of the beam are specified as elastic modulus of 200 GPa and Poisson’s ratio of 1/3. PD model is obtained by using discretisation size of Δx = 1/1000 m. The horizon size is chosen as δ = 3.015Δx. The boundary conditions are applied through a fictitious region as explained in Appendix B with a size of 3Δx. All example problems are static problems and the numerical solution is obtained by directly assigning inertia terms in equations of motion given in Eq. (22) to 0 and solving a matrix system of equations. PD results are compared against FEM results generated using ANSYS, a commercial finite element software. Plane182 element type is utilised by creating 100 elements along the beam with 8 elements along the thickness direction.

3.1 Simply Supported Beam with Distributed Load

In the first example, a simply supported beam subjected to a distributed loading of 100 N/m is considered as shown in Fig. 4. Comparison of transverse displacements obtained from PD and FEM analyses are depicted in Fig. 5, and a very good agreement is observed between the two approaches.

Fig. 4

Simply supported beam subjected to distributed loading

Fig. 5

Variation of transverse displacements along the beam

3.2 Simply Supported Beam with Concentrated Load

In the second example, the simply supported beam considered in the previous example is subjected to a concentrated load of P_z = 100 N acting at the centre of the beam as shown in Fig. 6. Based on the comparison given in Fig. 7, PD results agree very well with FEM results.

Fig. 6

Simply supported beam subjected to concentrated load

Fig. 7

Variation of transverse displacements along the beam

3.3 Clamped-Clamped Beam with Distributed Load

In the third example, the simply supported beam subjected to distributed loading considered in the first example case is subjected clamped-clamped boundary conditions as shown in Fig. 8. The distributed load is specified as 100 N/m.

Fig. 8

Clamped-clamped beam subjected to distributed loading

As demonstrated in Fig. 9, a very good agreement is observed between PD and FEM results in terms of transverse displacements.

Fig. 9

Variation of transverse displacements along the beam

3.4 Cantilever Beam Subjected to a Point Load at its Free End

In the fourth example case, a cantilever beam is considered as shown in Fig. 10. The beam is subjected to a point load of P_z = 100 N at its free end. As depicted in Fig. 11, PD results agree very well with FEM results.

Fig. 10

Cantilever beam subjected to a point load at its free end

Fig. 11

Variation of transverse displacements along the beam

3.5 Cantilever Beam Subjected to a Moment at its Free End

In the final example case, the cantilever beam is subjected to a moment of 100 Nm at its free end as shown in Fig. 12. The moment loading is applied through a body load of b_θ = 10⁷ N/m² acting on a single material point at the right edge. As depicted in Fig. 13, there is a very good agreement between PD and FEM results for the transverse displacement along the beam.

Fig. 12

Cantilever beam subjected to a moment at its free end

Fig. 13

Variation of transverse displacements along the beam

4 Conclusion

In this study, a novel higher-order peridynamic beam formulation was presented. The formulation was obtained by using Euler-Lagrange equations and Taylor’s expansion. To demonstrate the capability of the presented approach, several different beam configurations were considered including simply supported beam subjected to distributed loading, simply supported beam with concentrated load, clamped-clamped beam subjected to distributed loading, cantilever beam subjected to a point load at its free end and cantilever beam subjected to a moment at its free end. Transverse displacement results along the beam obtained from peridynamics and finite element method are compared with each other and very good agreement was obtained between the two approaches. Therefore, it can be concluded that the proposed methodology is capable of representing higher-order beam theory in peridynamic framework.

Appendices

Appendix

As explained in Section 2.1, the strain energy density of a material point from classical continuum mechanics can be written as:

$$ W=\frac{1}{2h}\left\{\begin{array}{c}\frac{E}{1-{\nu}^2}\left[\frac{h^3}{12}\left({\left(\frac{\partial \theta }{\partial x}\right)}^2+4{\left({w}^{\ast}\right)}^2+4\nu {w}^{\ast}\frac{\partial \theta }{\partial x}\right)+\frac{h^5}{40}\frac{\partial {\theta}^{\ast }}{\partial x}\left(\frac{\partial \theta }{\partial x}+2\nu {w}^{\ast}\right)+\frac{h^7}{448}{\left(\frac{\partial {\theta}^{\ast }}{\partial x}\right)}^2\right]+\\ {}G\left[h{\left(\theta +\frac{\partial w}{\partial x}\right)}^2+\frac{h^5}{80}{\left(3{\theta}^{\ast }+\frac{\partial {w}^{\ast }}{\partial x}\right)}^2+\frac{h^3}{6}\left(\theta +\frac{\partial w}{\partial x}\right)\left(3{\theta}^{\ast }+\frac{\partial {w}^{\ast }}{\partial x}\right)\right]\end{array}\right\} $$

(A23)

This expression can be expressed in peridynamics by converting spatial derivatives to PD form. To achieve this, first ${\left(\frac{\partial \theta }{\partial x}\right)}^2+4{\left({w}^{\ast}\right)}^2+4\nu {w}^{\ast}\frac{\partial \theta }{\partial x}$ term will be converted. By using Taylor’s expansion and disregarding the higher order terms, following relationship can be obtained:

$$ \theta \left(x+\xi \right)-\theta (x)=\frac{\partial \theta }{\partial x}\xi $$

(A24)

By calculating the square of both sides of Eq. (A2),

$$ {\left[\theta \left(x+\xi \right)-\theta (x)\right]}^2={\left(\frac{\partial \theta }{\partial x}\right)}^2{\xi}^2 $$

(A25)

and adding 4(w^∗(x))²ξ² to both sides, Eq. (A2) will take the following form:

$$ {\left[\theta \left(x+\xi \right)-\theta (x)\right]}^2+4{\left({w}^{\ast }(x)\right)}^2{\xi}^2=\left[{\left(\frac{\partial \theta }{\partial x}\right)}^2+4{\left({w}^{\ast }(x)\right)}^2\right]{\xi}^2 $$

(A26)

Moreover, if both sides of Eq. (A2) is multiplied by 4νw^∗(x)ξ , the following relationship can be obtained:

$$ \left[\theta \left(x+\xi \right)-\theta (x)\right]4\nu {w}^{\ast }(x)\xi =\left(\frac{\partial \theta }{\partial x}\right)4\nu {w}^{\ast }(x){\xi}^2 $$

(A27)

By summing Eqs. (A4) and (A5) yields:

$$ {\left[\theta \left(x+\xi \right)-\theta (x)\right]}^2+4{\left({w}^{\ast }(x)\right)}^2{\xi}^2+\left[\theta \left(x+\xi \right)-\theta (x)\right]4\nu {w}^{\ast }(x)\xi =\left[{\left(\frac{\partial \theta }{\partial x}\right)}^2+4{\left({w}^{\ast }(x)\right)}^2+4\nu \left(\frac{\partial \theta }{\partial x}\right){w}^{\ast }(x)\right]{\xi}^2 $$

(A28)

If both sides of Eq. (A6) is divided by |ξ|:

$$ \frac{{\left[\theta \left(x+\xi \right)-\theta (x)\right]}^2+4{\left({w}^{\ast }(x)\right)}^2{\xi}^2+\left[\theta \left(x+\xi \right)-\theta (x)\right]4\nu {w}^{\ast }(x)\xi }{\mid \xi \mid }=\left[{\left(\frac{\partial \theta }{\partial x}\right)}^2+4{\left({w}^{\ast }(x)\right)}^2+4\nu \left(\frac{\partial \theta }{\partial x}\right){w}^{\ast }(x)\right]\mid \xi \mid $$

(A29)

and integrating both sides of Eq. (A7) over the interval (−δ, δ) by considering x as a fixed point yields

$$ {\left(\frac{\partial \theta }{\partial x}\right)}^2+4{\left({w}^{\ast }(x)\right)}^2+4\nu \left(\frac{\partial \theta }{\partial x}\right){w}^{\ast }(x)=\frac{1}{\delta^2}\underset{-\delta }{\overset{\delta }{\int }}\frac{{\left[\theta \left(x+\xi \right)-\theta (x)\right]}^2+4{\left({w}^{\ast }(x)\right)}^2{\xi}^2+\left[\theta \left(x+\xi \right)-\theta (x)\right]4\nu {w}^{\ast }(x)\xi }{\mid \xi \mid } d\xi $$

(A30)

As the second step, $\frac{\partial {\theta}^{\ast }}{\partial x}\left(\frac{\partial \theta }{\partial x}+2\nu {w}^{\ast}\right)$ term will be converted into PD form. To do this, again Taylor’s expansion is utilised and the following relationships can be obtained:

$$ {\theta}^{\ast}\left(x+\xi \right)-{\theta}^{\ast }(x)=\frac{\partial {\theta}^{\ast }}{\partial x}\xi $$

(A31a)

$$ \theta \left(x+\xi \right)-\theta (x)+2\nu {w}^{\ast }(x)\xi =\left(\frac{\partial \theta }{\partial x}+2\nu {w}^{\ast }(x)\right)\xi $$

(A31b)

After multiplying Eq. (A9a) by Eq. (A9b),

$$ \left[\theta \left(x+\xi \right)-\theta (x)+2\nu {w}^{\ast }(x)\xi \right]\left[{\theta}^{\ast}\left(x+\xi \right)-{\theta}^{\ast }(x)\right]=\frac{\partial {\theta}^{\ast }}{\partial x}\left(\frac{\partial \theta }{\partial x}+2\nu {w}^{\ast }(x)\right){\xi}^2 $$

(A32)

and integrating over the interval (−δ, δ) by considering x as a fix point and multiplying both side of Eq.(A10) with$\frac{1}{\left|\xi \right|}$ yields

$$ \frac{\partial {\theta}^{\ast }}{\partial x}\left(\frac{\partial \theta }{\partial x}+2\nu {w}^{\ast }(x)\right)=\frac{1}{\delta^2}\underset{-\delta }{\overset{\delta }{\int }}\frac{\left[\theta \left(x+\xi \right)-\theta (x)+2\nu {w}^{\ast }(x)\xi \right]\left[{\theta}^{\ast}\left(x+\xi \right)-{\theta}^{\ast }(x)\right]}{\mid \xi \mid } d\xi $$

(A33)

Next, ${\left(\frac{\partial {\theta}^{\ast }}{\partial x}\right)}^2$ will be converted into PD form by using Taylor’s expansion:

$$ {\theta}^{\ast}\left(x+\xi \right)-{\theta}^{\ast }(x)=\frac{\partial {\theta}^{\ast }}{\partial x}\xi $$

(A34)

Calculating the square of Eq. (A12a),

$$ {\left[{\theta}^{\ast}\left(x+\xi \right)-{\theta}^{\ast }(x)\right]}^2={\left(\frac{\partial {\theta}^{\ast }}{\partial x}\right)}^2{\xi}^2 $$

(A35)

and integrating over the interval (−δ, δ) by considering x as a fix point and multiplying both side of Eq.(A13) with$\frac{1}{\left|\xi \right|}$ yields

$$ {\left(\frac{\partial {\theta}^{\ast }}{\partial x}\right)}^2=\frac{1}{\delta^2}\underset{-\delta }{\overset{\delta }{\int }}\frac{{\left[{\theta}^{\ast}\left(x+\xi \right)-{\theta}^{\ast }(x)\right]}^2}{\left|\xi \right|} d\xi $$

(A36)

Finally, by following a similar procedure, ${\left(\theta +\frac{\partial w}{\partial x}\right)}^2$, ${\left(3{\theta}^{\ast }+\frac{\partial {w}^{\ast }}{\partial x}\right)}^2$ and $\left(\theta +\frac{\partial w}{\partial x}\right)\left(3{\theta}^{\ast }+\frac{\partial {w}^{\ast }}{\partial x}\right)$ terms can be converted into PD form as:

$$ {\left(\frac{\partial w}{\partial x}+\theta (x)\right)}^2=\frac{1}{\delta^2}\underset{-\delta }{\overset{\delta }{\int }}\frac{{\left[w\left(x+\xi \right)-w(x)+\theta (x)\xi \right]}^2}{\left|\xi \right|} d\xi $$

(A37a)

$$ {\left(\frac{\partial {w}^{\ast }}{\partial x}+3{\theta}^{\ast }(x)\right)}^2=\frac{1}{\delta^2}\underset{-\delta }{\overset{\delta }{\int }}\frac{{\left[{w}^{\ast}\left(x+\xi \right)-{w}^{\ast }(x)+3{\theta}^{\ast }(x)\xi \right]}^2}{\left|\xi \right|} $$

(A37b)

$$ \left(\frac{\partial w}{\partial x}+\theta (x)\right)\left(\frac{\partial {w}^{\ast }}{\partial x}+3{\theta}^{\ast }(x)\right)=\frac{1}{\delta^2}\underset{-\delta }{\overset{\delta }{\int }}\frac{\left[w\left(x+\xi \right)-w(x)+\theta (x)\xi \right]\left[{w}^{\ast}\left(x+\xi \right)-{w}^{\ast }(x)+3{\theta}^{\ast }(x)\xi \right]}{\mid \xi \mid } d\xi $$

(A37c)

Eqs. (A8), (A11), (A14) and (A15) can also be expressed in the discretized form as:

$$ {\left(\frac{\partial {\theta}_{(k)}}{\partial x}\right)}^2+4{\left({w}_{(k)}^{\ast}\right)}^2+4\nu {w}_{(k)}^{\ast}\frac{\partial {\theta}_{(k)}}{\partial x}=\frac{1}{\delta^2A}\sum \limits_{i^k}\frac{{\left({\theta}_{\left({i}^k\right)}-{\theta}_{(k)}\right)}^2+4\nu {w}_{(k)}^{\ast}\left({\theta}_{\left({i}^k\right)}-{\theta}_{(k)}\right){\xi}_{\left({i}^k\right)(k)}+4{\left({w}_{(k)}^{\ast}\right)}^2{\xi}_{\left({i}^k\right)(k)}^2}{\mid {\xi}_{\left({i}^k\right)(k)}\mid }{V}_{\left({i}^k\right)} $$

(A38a)

$$ \frac{\partial {\theta}_{(k)}^{\ast }}{\partial x}\left(\frac{\partial {\theta}_{(k)}}{\partial x}+2\nu {w}_{(k)}^{\ast}\right)=\frac{1}{\delta^2A}\sum \limits_{i^k}\frac{\left({\theta}_{\left({i}^k\right)}-{\theta}_{(k)}+2\nu {w}_{(k)}^{\ast }{\xi}_{\left({i}^k\right)(k)}\right)\left({\theta}_{\left({i}^k\right)}^{\ast }-{\theta}_{(k)}^{\ast}\right)}{\mid {\xi}_{\left({i}^k\right)(k)}\mid }{V}_{\left({i}^k\right)} $$

(A38b)

$$ \frac{\partial {\theta}_{(k)}^{\ast }}{\partial x}\frac{\partial {\theta}_{(k)}^{\ast }}{\partial x}=\frac{1}{\delta^2A}\sum \limits_{i^k}\frac{{\left({\theta}_{\left({i}^k\right)}^{\ast }-{\theta}_{(k)}^{\ast}\right)}^2}{\mid {\xi}_{\left({i}^k\right)(k)}\mid }{V}_{\left({i}^k\right)} $$

(A38c)

$$ {\left({\theta}_{(k)}+\frac{\partial {w}_{(k)}}{\partial x}\right)}^2=\frac{1}{\delta^2A}\sum \limits_{i^k}\frac{{\left({w}_{\left({i}^k\right)}-{w}_{(k)}+{\theta}_{(k)}{\xi}_{\left({i}^k\right)(k)}\right)}^2}{\mid {\xi}_{\left({i}^k\right)(k)}\mid }{V}_{\left({i}^k\right)} $$

(A38d)

$$ {\left(3{\theta}_{(k)}^{\ast }+\frac{\partial {w}_{(k)}^{\ast }}{\partial x}\right)}^2=\frac{1}{\delta^2A}\sum \limits_{i^k}\frac{{\left({w}_{\left({i}^k\right)}^{\ast }-{w}_{(k)}^{\ast }+3{\theta}_{(k)}^{\ast }{\xi}_{\left({i}^k\right)(k)}\right)}^2}{\mid {\xi}_{\left({i}^k\right)(k)}\mid }{V}_{\left({i}^k\right)} $$

(A38e)

$$ \left({\theta}_{(k)}+\frac{\partial {w}_{(k)}}{\partial x}\right)\left(3{\theta}_{(k)}^{\ast }+\frac{\partial {w}_{(k)}^{\ast }}{\partial x}\right)=\frac{1}{\delta^2A}\sum \limits_{i^k}\frac{\left({w}_{\left({i}^k\right)}-{w}_{(k)}+{\theta}_{(k)}{\xi}_{\left({i}^k\right)(k)}\right)\left({w}_{\left({i}^k\right)}^{\ast }-{w}_{(k)}^{\ast }+3{\theta}_{(k)}^{\ast }{\xi}_{\left({i}^k\right)(k)}\right)}{\mid {\xi}_{\left({i}^k\right)(k)}\mid }{V}_{\left({i}^k\right)} $$

(A38f)

Appendix

In this Appendix, the application of boundary conditions in PD formulation of higher-order beams will be explained. Two common types of boundary conditions, including clamped and simply supported boundary conditions, are considered.

1.1 Clamped boundary condition

To implement the clamped boundary condition, a fictitious boundary layer is created outside the actual material domain. The horizon size can be chosen asδ = 3Δxin which the discretization size is Δx. The clamped boundary condition constrains zero transverse displacement and zero rotation for the material point adjacent to the clamped end. In this study, this can be achieved by enforcing symmetrical displacement fields for w and w^∗ and anti-symmetrical displacement fields for θ and θ^∗, respectively, to the material points in the fictitious region as opposed to the actual displacement field as (see Fig. 14):

$$ {w}_{(i)}={w}_{\left({i}^{\prime}\right)},{w}_{(i)}^{\ast }={w}_{\left({i}^{\prime}\right)}^{\ast },{w}_{(1)}={w}_{\left({1}^{\prime}\right)}={w}_{(1)}^{\ast }={w}_{\left({1}^{\prime}\right)}^{\ast }=0 $$

(B39)

and

$$ {\theta}_{(i)}=-{\theta}_{\left({i}^{\prime}\right)},{\theta}_{(i)}^{\ast }=-{\theta}_{\left({i}^{\prime}\right)}^{\ast}\kern1.32em i=1,2,3 $$

(B40)

Fig. 14

Application of clamped boundary condition in PD theory

1.2 Simply supported boundary condition

To implement the simply supported boundary condition, a fictitious layer is introduced outside the real material domain, whose size is again chosen to be equal to δ. From geometrical point of view, the simply supported boundary condition imposes zero transverse displacement and zero curvature for the material point adjacent to the constrained edge. In this study, this can be achieved by enforcing anti-symmetrical displacement fields for w and w^∗ and symmetrical displacement fields for θ and θ^∗, respectively, to the material points in the fictitious region with respect to the actual displacement field as (see Fig. 15):

$$ {w}_{(i)}=-{w}_{\left({i}^{\prime}\right)},{w}_{(i)}^{\ast }=-{w}_{\left({i}^{\prime}\right)}^{\ast}\kern1em \mathrm{and}\kern1em {\theta}_{(i)}={\theta}_{\left({i}^{\prime}\right)},{\theta}_{(i)}^{\ast }={\theta}_{\left({i}^{\prime}\right)}^{\ast}\kern1.32em i=1,2,3 $$

(B41)

Fig. 15

Application of simply supported boundary condition in PD theory