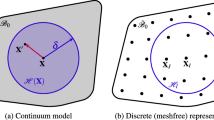
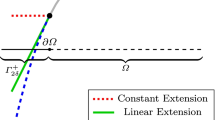
Abstract
The overarching goal of this work is to develop an accurate, robust, and stable methodology for finite deformation modeling using strong-form peridynamics (PD) and the correspondence modeling framework. We adopt recently developed methods that make use of higher-order corrections to improve the computation of integrals in the correspondence formulation. A unified approach is presented that incorporates the reproducing kernel (RK) and generalized moving least square (GMLS) approximations in PD to obtain non-local gradients of higher-order accuracy. We show, however, that the improved quadrature rule does not suffice to handle instability issues that have proven problematic for the correspondence model-based PD. In Part I of this paper, a bond-associative, higher-order core formulation is developed that naturally provides stability without introducing artificial stabilization parameters. Numerical examples are provided to study the convergence of RK-PD, GMLS-PD, and their bond-associated versions to a local counterpart, as the degree of non-locality (i.e., the horizon) approaches zero. Problems from linear elastostatics are utilized to verify the accuracy and stability of our approach. It is shown that the bond-associative approach improves the robustness of RK-PD and GMLS-PD formulations, which is essential for practical applications. The higher-order, bond-associated model can obtain second-order convergence for smooth problems and first-order convergence for problems involving field discontinuities, such as curvilinear free surfaces. In Part II of this paper, we use our unified PD framework to (a) study wave propagation phenomena, which have proven problematic for the state-based correspondence PD framework, and (b) propose a new methodology to enforce natural boundary conditions in correspondence PD formulations, which should be particularly appealing to coupled problems. Our results indicate that bond-associative methods accompanied by higher-order gradient corrections provide the key ingredients to obtain the necessary accuracy, stability, and robustness characteristics needed for engineering-scale simulations.














Similar content being viewed by others
References
Bažant ZP, Luo W, Chau VT, Bessa MA (2016) Wave dispersion and basic concepts of peridynamics compared to classical nonlocal damage models. J Appl Mech 83(11)
Behzadinasab M (2020) Peridynamic modeling of large deformation and ductile fracture. PhD thesis, The University of Texas at Austin
Behzadinasab M, Foster JT (2020a) On the stability of the generalized, finite deformation correspondence model of peridynamics. Int J Solids Struct 182:64–76
Behzadinasab M, Foster JT (2020b) A semi-lagrangian, constitutive correspondence framework for peridynamics. J Mech Phys Solids:103862
Belytschko T, Guo Y, Kam Liu W, Ping Xiao S (2000) A unified stability analysis of meshless particle methods. Int J Numer Methods Eng 48(9):1359–1400
Bobaru F, Zhang G (2015) Why do cracks branch? A peridynamic investigation of dynamic brittle fracture. Int J Fract 196(1-2):59–98
Bobaru F, Foster JT, Geubelle PH, Silling SA (2016) Handbook of peridynamic modeling. CRC Press, Boca Raton
Breitenfeld M, Geubelle P, Weckner O, Silling S (2014) Non-ordinary state-based peridynamic analysis of stationary crack problems. Comput Methods Appl Mech Eng 272:233–250
Breitzman T, Dayal K (2018) Bond-level deformation gradients and energy averaging in peridynamics. J Mech Phys Solids 110:192–204
Chen H (2018) Bond-associated deformation gradients for peridynamic correspondence model. Mech Res Commun 90:34–41
Chen X, Gunzburger M (2011) Continuous and discontinuous finite element methods for a peridynamics model of mechanics. Comput Methods Appl Mech Eng 200(9-12):1237–1250
Geuzaine C, Remacle JF (2007) Gmsh: a three-dimensional finite element mesh generator with built-in pre-and post-processing facilities. In: Proceedings of the Second Workshop on Grid Generation for Numerical Computations, Tetrahedron II
Gould PL, Feng Y (2018) Introduction to linear elasticity, 4th edn. Springer
Ha YD, Bobaru F (2010) Studies of dynamic crack propagation and crack branching with peridynamics. Int J Fract 162(1-2):229–244
Hillman M, Pasetto M, Zhou G (2020) Generalized reproducing kernel peridynamics: unification of local and non-local meshfree methods, non-local derivative operations, and an arbitrary-order state-based peridynamic formulation. Comput Part Mech 7(2):435–469
Kramer SL, Boyce BL, Jones A, et al (2019) The third Sandia Fracture Challenge: predictions of ductile fracture in additively manufactured metal. Int J Fract 218:5–61
Littlewood DJ (2010) Simulation of dynamic fracture using peridynamics, finite element modeling, and contact. In: ASME 2010 International Mechanical Engineering Congress and Exposition, American Society of Mechanical Engineers, pp 209–217
Littlewood DJ (2015) Roadmap for peridynamic software implementation. SAND Report, Sandia National Laboratories, Albuquerque
Liu WK, Li S, Belytschko T, et al (1997) Moving least-square reproducing kernel methods (i) methodology and convergence. Comput Methods Appl Mech Eng 143(1):113–154
Madenci E, Barut A, Futch M (2016) Peridynamic differential operator and its applications. Comput Methods Appl Mech Eng 304:408–451
Madenci E, Dorduncu M, Barut A, Phan N (2018) Weak form of peridynamics for nonlocal essential and natural boundary conditions. Comput Methods Appl Mech Eng 337:598–631
Michell J (1899) On the direct determination of stress in an elastic solid, with application to the theory of plates. Proc Lond Math Soc 1(1):100–124
Moutsanidis G, Koester JJ, Tupek MR, Chen JS, Bazilevs Y (2020) Treatment of near-incompressibility in meshfree and immersed-particle methods. Comput Part Mech 7(2):309–327
Silling SA (2017) Stability of peridynamic correspondence material models and their particle discretizations. Comput Methods Appl Mech Eng 322:42–57
Silling SA, Askari E (2005) A meshfree method based on the peridynamic model of solid mechanics. Comput Struct 83(17):1526–1535
Trask N, You H, Yu Y, Parks ML (2019) An asymptotically compatible meshfree quadrature rule for nonlocal problems with applications to peridynamics. Comput Methods Appl Mech Eng 343:151–165
Tupek MR, Radovitzky R (2014) An extended constitutive correspondence formulation of peridynamics based on nonlinear bond-strain measures. J Mech Phys Solids 65:82–92
Wendland H (2004) Scattered data approximation, vol 17. Cambridge University Press, Cambridge
Zhou K, Du Q (2010) Mathematical and numerical analysis of linear peridynamic models with nonlocal boundary conditions. SIAM J Numer Anal 48(5):1759–1780
Acknowledgements
The authors also thank Nathaniel Trask for helpful discussions on the subject.
Funding
Y. Bazilevs was partially supported through the Sandia contract no. 2111577. J.T. Foster received funding from AFOSR MURI Center for Materials Failure Prediction through Peridynamics: project no. ONRBAA12-020 and Sandia National Laboratories contract no. 1885207.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Behzadinasab, M., Foster, J.T. & Bazilevs, Y. A Unified, Stable, and Accurate Meshfree Framework for Peridynamic Correspondence Modeling—Part II: Wave Propagation and Enforcement of Stress Boundary Conditions. J Peridyn Nonlocal Model 3, 46–66 (2021). https://doi.org/10.1007/s42102-020-00039-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s42102-020-00039-6