Alternative skew Laplace scale mixtures for modeling data exhibiting high-peaked and heavy-tailed traits

Abstract

The search and construction of appropriate and flexible models for describing and modelling empirical data sets incongruent with normality retains a sustained interest. This paper focuses on proposing flexible skew Laplace scale mixture distributions to model these types of data sets. Each member of the collection of distributions is obtained by dividing the scale parameter of a conditional skew Laplace distribution by a purposefully chosen mixing random variable. Highly-peaked, heavy-tailed skew models with relevance and impact in different fields are obtained and investigated, and elegant sampling schemes to simulate from this collection of developed models are proposed. Finite mixtures consisting of the members of the skew Laplace scale mixture models are illustrated, further extending the flexibility of the distributions by being able to account for multimodality. The maximum likelihood estimates of the parameters for all the members of the developed models are described via a developed EM algorithm. Real-data examples highlight select models’ performance and emphasize their viability compared to other commonly considered candidates, and various goodness-of-fit measures are used to endorse the performance of the proposed models as reasonable and viable candidates for the practitioner. Finally, an outline is discussed for future work in the multivariate realm for these models.

1 Introduction

The search for appropriate and flexible models for describing larger data sets, which frequently deviate from normality, remains a major focus in many research fields (Adcock & Azzalini, 2020). The Laplace distribution is among the most well-known parametric models for real valued data, and is preferred to the normal distribution when the empirical distribution is still symmetric but presents heavy-tails and a discernible peak (Kotz et al., 2001; Wilson, 1923). It is often referred to as the double exponential distribution, as it can be thought of as two exponential distributions spliced together back-to-back with an additional location parameter.

The probability density function (PDF) of the Laplace distribution is expressed in terms of the absolute difference from the mean, which is reminiscent of the normal distribution which is expressed in terms of the squared difference from the mean. As a result, the Laplace distribution has heavier tails than the normal distribution (DeCarlo, 1997). The excess kurtosis, defined as kurtosis minus 3 (i.e. the kurtosis of the univariate normal distribution), of the Laplace distribution is fixed at 3 and it is thus leptokurtic. The flexibility of the Laplace distribution is still, however, limited because of this fixed excess kurtosis.

In an attempt to make the tail behaviour of the Laplace more flexible, Punzo and Bagnato (2021) extended this branch of literature by introducing the Laplace scale mixture (LSM) family of distributions to make the Laplace tail behaviour more flexible in order to model the highly-peaked and heavy-tailed return distribution of cryptocurrencies. Due to its symmetric property, the LSM models are not able to model skewness. Punzo and Bagnato (2022a) circumvented this limitation by using the asymmetric Laplace distribution as reference distribution instead, and developed a family of asymmetric Laplace scale mixture (ALSM) distributions capable of modelling, not only highly-peaked and heavy-tailed data, but also, skewness.

Various types of skewed generalisations of the Laplace distribution (1) have sporadically appeared in literature over the past few decades. One of the earliest is introduced by McGill (1962) and a variation thereof is studied by Holla and Bhattacharya (1968). Another generalization is studied by Poiraud-Casanova and Thomas-Agnan (2000), which is a special case of the skewed Laplace distribution of Yu and Jin (2005).

Subbotin (1923) proposed a generalization of the Laplace distribution, which is sometimes referred to as the exponential power function distribution. The Laplace distribution is also a special case of several distributions: the asymmetric power (Komunjer, 2007), double Weibull (Balakrishnan & Kocherlakota, 1985), Sargan (Hadri, 1996), the Laplace normal mixture (Kanji, 1985) and beta Laplace distributions (Kozubowski & Nadarajah, 2008) for example. A variance-mean mixture of multivariate normal distributions in Doğru and Arslan (2023), seeks to define a flexible extension of the Laplace distribution, and an extensive review of the various Laplace distribution generalisations is given in Kozubowski and Nadarajah (2010). The alpha-skew Laplace distribution Harandi and Alamatsaz (2013) is a bimodal distribution, which contains the Laplace distribution as a special case, and is further extended to a discrete alpha skew Laplace (Harandi & Alamatsaz, 2015), the Balakrishnan alpha-skew Laplace (Shah et al., 2019) and the Balakrishnan alpha-beta-skew Laplace distribution (Shah et al., 2023). Other multimodal extensions are proposed in Chakraborty et al. (2014), Doğru and Arslan (2017) and Doğru and Arslan (2021). Fernández and Steel (1998) introduced skewness to a symmetric distribution by converting a symmetric PDF into a skewed one by stipulating inverse scale factors in the positive and negative half lines. This resulted in the asymmetric Laplace distribution studied in Kotz et al. (2001), from which the ALSM distributions were formed upon.

In Sect. 2, we show that other generalizations of the Laplace distribution can be used as reference distributions (Kozubowski & Nadarajah, 2010) and be considered as valid alternatives to the ALSM models introduced in Punzo and Bagnato (2022a); literature contextualizes the choices of the Bernoulli-, shifted exponential-, unimodal gamma-, and power function distributions - which are considered as mixing variables in this paper. Convenient computational tools are reviewed such as moments and sampling schemes. The focus is on using previously unconsidered skew Laplace (SL) models as the reference (conditional) distribution that can leverage skewness. Different mixing random variables on all or part of the real line are considered to develop the skew Laplace scale mixture (SLSM) models in Sect. 3; in this way, the novelty of this paper is thus two-fold. Ultimately, a collection of flexible skew Laplace scale mixture (SLSM) distributions that can model data with peakedness, heavy-tails, skewness and multimodality is proposed. In Sect. 4, finite mixtures consisting of the members of the SLSM models are also explored - further extending the models ability to fit multi-modal data. Methods considered for estimation are described in Sect. 5, followed by applications of the proposed models on the well-known bodily injury claims dataset (Rempala & Derrig, 2005) and the refractive index of glass fragments in Sect. 6. Furthermore, we employ finite mixtures of the members of the SLSM distributions fitting the campaign finance scores, which serve as indicators of the ideological leanings of donors to political candidates in the United States. Finally, Sect. 7 concludes the paper with a view towards future work in the multivariate setting.

2 Essential components

The PDF of the Laplace distribution is expressed as

$$\begin{aligned} f_L(x;\mu ,\beta )=\frac{1}{2\beta }\textrm{e}^{-\frac{|x-\mu |}{\beta }}, \quad -\infty<x<\infty , \end{aligned}$$

(1)

where $\mu \in (-\infty ,\infty )$ and $\beta >0$ are location and scale parameters, respectively. If a random variable X has the Laplace distribution, we denote it by $X\sim Laplace(\mu ,\beta )$. The LSM distribution introduced by Punzo and Bagnato (2021) is presented in Definition 2.1.

Definition 2.1

A random variable X is said to have the LSM distribution with location $\mu \in (-\infty ,\infty )$, scale $\beta \in (0,\infty )$ and tailedness $\varvec{\theta }$, if its PDF is given by

$$\begin{aligned} g_{LSM}(x;\mu ,\beta ,\varvec{\theta })&=\int _{S_h} f_{L}(x;\mu ,\beta /w)h(w;\varvec{\theta })dw, \quad -\infty<x<\infty , \end{aligned}$$

(2)

where $h(w;\varvec{\theta })$ is the mixing PDF of W, with support $S_h \subseteq (0,\infty )$, depending on the vector of parameters $\varvec{\theta }$.

In a similar manner, the SLSM distribution follows in Definition 2.2 which considers a SL distribution as the conditional reference distribution. The proposed SLSM distribution is constituted from two components: the reference (conditional) distribution $f_{SL}(\cdot )$ and the mixing distribution, $h(\cdot )$. This is similar to the ALSM distribution introduced by Punzo and Bagnato (2022a); and the acronym SLSM is used to avoid confusion with the models proposed and discussed in Punzo and Bagnato (2022a).

Definition 2.2

A random variable X is said to have the SLSM distribution with location $\mu \in (-\infty ,\infty )$, scale $\beta \in (0,\infty )$, skewness $\lambda$, and tailedness $\varvec{\theta }$, if its PDF is given by

$$\begin{aligned} g_{SLSM}(x;\mu ,\beta ,\varvec{\theta }, \lambda )&=\int _{S_h} f_{SL}(x;\mu ,\beta /w,\lambda )h(w;\varvec{\theta })dw, \quad -\infty<x<\infty , \end{aligned}$$

(3)

$$\begin{aligned}&\equiv \sum _{w}f_{SL}(x;\mu ,\beta /w, \lambda )h(w;\varvec{\theta }) \end{aligned}$$

(4)

where $h(w;\varvec{\theta })$ is the mixing PDF of W, with support $S_h \subseteq (0,\infty )$, depending on the vector of parameters $\varvec{\theta }$. This is denoted as $X\sim SLSM(\mu ,\beta ,\varvec{\theta })$. (4) follows when W is a discrete random variable.

A SLSM distribution can be thought of as a compound distribution, with the same location $\mu$ and skewness parameter $\lambda$ but with different scale $\beta /w$ due to w (see also Punzo et al. 2018). The component skew Laplace distributions, as conditional reference distribution, are not taken uniformly from the set, but according to a set of “weights" determined by the probabilistic behaviour of W. Note that if W is degenerate in 1 (i.e. $W \equiv 1$ which implies that $P[W=1]=1$) then $f_{SL}(x;\mu ,\beta ,\lambda )$ is obtained, whereas in other cases the tails of $f_{SLSM}$ are heavier compared to $f_{SL}$.

2.1 Formulation of skew Laplace distributions

Azzalini (1985) presented the skew-normal distribution by adding an additional parameter to introduce asymmetry, as described in Definition 2.3. Using this definition, two reference (conditional) candidates will be proposed.

Definition 2.3

Denote a PDF on $\mathbb {R}$ by $f_0(\cdot )$, a continuous cumulative distribution function (CDF) on $\mathbb {R}$ by $G_0(\cdot )$, and a real-valued function on $\mathbb {R}$ by $w(\cdot )$, such that $f_0(-x)=f_0(x)$, $G_0(-x)=1-G_0(x)$ and $w(-x)=-w(x)$ $\forall x\in (-\infty ,\infty )$. Then

$$\begin{aligned} f_X(x)=2f_0(x)G_0{(w(x))} \end{aligned}$$

(5)

is a PDF on $\mathbb {R}$ (Azzalini 1985). Note that $f_0$ is termed the symmetric base PDF, $2G_0{(w(x))}$ is termed the skewing mechanism, and $f_X$ is termed the skewed version of the symmetric base PDF.

2.2 An Azzalini type skew Laplace distribution

Azzalini investigated the case where $w(x)=\lambda x$ for $\lambda \in (-\infty ,\infty )$ and $f_0$ is a standard-normal PDF, which yields the skew-normal distribution. Similarly, as illustrated in Aryal and Nadarajah (2005), a skewed Laplace distribution can be obtained by utilizing (5) and instead using a Laplace distribution as the base distribution; see also Gupta et al. (2002), Jagannathan (2005) and Kozubowski and Nolan (2008). This will be referred to as the skew Laplace type I ($SL_{I}$) distribution, with PDF given by

$$\begin{aligned} f_{SL_{I}}(x;\mu ,\beta ,\lambda )&={\left\{ \begin{array}{ll} \frac{1}{2\beta }\textrm{e}^{\frac{(\lambda +1)(x-\mu )}{\beta }}, \quad &{}x\le \mu , \\ \frac{1}{\beta }\textrm{e}^{-\frac{(x-\mu )}{\beta }}-\frac{1}{2\beta }\textrm{e}^{-\frac{(\lambda +1)(x-\mu )}{\beta }}, \quad &{}x>\mu , \end{array}\right. } \end{aligned}$$

(6)

where $\beta ,\lambda >0$. This is denoted by $X \sim SL_{I}(\mu ,\beta ,\lambda )$.

To obtain valid PDF’s a restriction is placed on $\lambda >0$. The corresponding PDF for $\lambda <0$ can be obtained using the fact that $-X$ has the PDF $2f_L(x;\mu ,\beta )F_L(-\lambda x;\mu ,\beta )$, where $F_{L}(\cdot )$ denotes the CDF of the Laplace distribution. Thus, the $\lambda >0$ restriction does not result in a loss of generality in the distribution (see also Kozubowski and Nolan (2008)). The main feature of the $SL_{I}$ distribution is that the addition of the new parameter $\lambda$ allows for a greater degree of flexibility. If $\lambda =0$, (6) reduces to the PDF of the Laplace distribution (1).

A technique for generating $SL_{I}$ random variables with PDF (6) is the inversion transform sampling method (see Aryal & Nadarajah 2005). Therefore, in this case,

$$\begin{aligned} X\overset{d}{=} {\left\{ \begin{array}{ll} \frac{\beta }{1+\lambda }\textrm{ln}(2U(1+\lambda ))+\mu , \quad &{} 0\le U\le \frac{1}{2(1+\lambda )},\\ \mu -\beta \textrm{ln}\left\{ 1-U+(1-U)\sum _{k=1}^{\infty }\left( {\begin{array}{c}(1+\lambda )k\\ k-1\end{array}}\right) \frac{(1-U)^{\lambda k}}{k2^k(1+\lambda )^k}\right\} , \quad&\frac{1}{2(1+\lambda )}\le U\le 1, \end{array}\right. } \end{aligned}$$

(7)

where $U\sim {Uniform}(0,1)$. Without loss of generality, the kth moment of $X\sim SL_{I}(0,\beta ,\kappa )$ is given by

$$\begin{aligned} \textrm{E}(X^k)={\left\{ \begin{array}{ll} \beta ^k\Gamma (k+1), &{}\text {if }k\text { is even,}\\ \beta ^k\Gamma (k+1) \left\{ 1- \frac{1}{(1+\lambda )^{k+1}}\right\} , &{}\text {if }k\text { is odd.}\\ \end{array}\right. } \end{aligned}$$

(8)

From (8) and the binomial expansion, the kth central moment of X can be calculated as

$$\begin{aligned} \textrm{E}_{SL_{{II}}}\left[ (X-\mu )^k\right] = {\left\{ \begin{array}{ll} \mu ^k + \sum \limits _{j=1}^{k/2} {k\atopwithdelims ()2j} \mu ^{k-2j}\beta ^{2j}\Gamma (2j+1) \\ -\sum \limits _{j=1}^{k/2} {k\atopwithdelims ()2j-1} \mu ^{k-2j+1}\beta ^{2j-1}\Gamma (2j)\left\{ 1-\frac{1}{(1+\lambda )^{2j}}\right\} , &{}\text {if }k\text { is even,}\\ -\mu ^k - \sum \limits _{j=1}^{\frac{k-1}{2}} {k\atopwithdelims ()2j} \mu ^{k-2j}\beta ^{2j}\Gamma (2j+1) \\ +\sum \limits _{j=1}^{\frac{k+1}{2}} {k\atopwithdelims ()2j-1} \mu ^{k-2j+1}\beta ^{2j-1}\Gamma (2j)\left\{ 1-\frac{1}{(1+\lambda )^{2j}}\right\} , &{}\text {if }k\text { is odd.}\\ \end{array}\right. } \end{aligned}$$

(9)

From (8) and (9) it follows that

$$\begin{aligned} \textrm{E}_{SL_{{I}}}(X)&=\mu +\beta \left( 1-\frac{1}{(1+\lambda )^2}\right) ,\nonumber \\ \textrm{Var}_{SL_{{I}}}(X)&=\frac{\beta ^2(2+8\lambda +8\lambda ^2+4\lambda ^3+\lambda ^4)}{(1+\lambda )^4},\nonumber \\ \textrm{Skewness}_{SL_{{I}}}(X)&=\frac{2\lambda (6+15\lambda +20\lambda ^2+15\lambda ^3+6\lambda ^4+\lambda ^5)}{(2+8\lambda +8\lambda ^2+4\lambda ^3+\lambda ^4)^{3/2}},\end{aligned}$$

(10)

$$\begin{aligned} \textrm{Kurtosis}_{SL_{{I}}}(X)&=\frac{3(8+64\lambda +176\lambda ^2+272\lambda ^3+276\lambda ^4+192\lambda ^5+88\lambda ^6+24\lambda ^7+3\lambda ^8)}{(2+8\lambda +8\lambda ^2+4\lambda ^3+\lambda ^4)^2}. \end{aligned}$$

(11)

A comprehensive description of the mathematical properties of the $SL_{I}$ distribution is derived in Aryal and Nadarajah (2005). From (10) and (11) it is evident that the skewness and kurtosis only depend on $\lambda$. Figure 1 illustrates the skewness and kurtosis for varying values of $\lambda$ with skewness between $(-2,2)$ and kurtosis between (5.81, 9), as given in Aryal and Nadarajah (2005).

Fig. 1

Skewness and kurtosis of $SL_{I}$ with PDF (6) as a function of $\lambda$

2.3 A Subbotin type skew Laplace distribution

By applying Azzalini’s skewing method to a generalised normal distribution attributed to Subbotin (1923) as the base distribution, with $w(x)=\sqrt{2}\lambda x$, the PDF of a random variable X with the skew generalised normal (SGN) distribution is given by

$$\begin{aligned} g_{SGN}(x;\mu ,\beta ,\delta ,\lambda )=\frac{\delta }{\beta \Gamma \left( \frac{1}{\delta }\right) }\textrm{e}^{-|\frac{x-\mu }{\beta }|^\delta }\Phi \left( \sqrt{2}\lambda \left( \frac{x-\mu }{\beta }\right) \right) , \quad -\infty<x<\infty , \end{aligned}$$

(12)

where $\Phi (\cdot )$ denotes the CDF of the standard normal distribution, $\mu , \lambda \in (-\infty ,\infty )$ and $\beta ,\delta >0$.

By setting $\delta$ to 1 in (12), we obtain the Skew Laplace type II distribution with the PDF given by

$$\begin{aligned} f_{SL_{{II}}}(x;\mu ,\beta ,\lambda )&=\frac{1}{\beta }\textrm{e}^{-|\frac{x-\mu }{\beta }|}\Phi \left( \sqrt{2}\lambda \left( \frac{x-\mu }{\beta }\right) \right) \nonumber \\&=2f_L(x;\mu ,\beta )\Phi \left( \sqrt{2}\lambda \left( \frac{x-\mu }{\beta }\right) \right) , \quad -\infty<x<\infty , \end{aligned}$$

(13)

where $\mu , \lambda \in (-\infty ,\infty )$ and $\beta >0$, denoted as $X\sim SL_{II}(\mu ,\beta ,\lambda ).$

(13) is often referred to as the skew Laplace normal (SLN) distribution in literature (Gómez et al., 2007), with finite mixtures of the SLN distribution considered in Doğru and Arslan (2017) and Doğru and Arslan (2021). As noted in Bekker et al. (2020), the acceptance-rejection method described in Lange et al. (1999) cannot draw appropriate samples from certain parameter structures from a SGN distribution. Following a similar approach to that of Sadeghkhani and Ghosh (2018), a stochastic representation is given in Algorithm 1 for generating random numbers from a $SL_{II}$ distribution with PDF, $f_{SL_{II}}(x;\mu ,\beta ,\lambda )$, as given in (13).

Algorithm 1

Generating Skew Laplace Type II Random Variables

If $Y\sim SL_{{II}}(0,1,\lambda )$, the rth moment is given as

$$\begin{aligned} \textrm{E}[Y^r]= {\left\{ \begin{array}{ll} \Gamma (r+1), \quad &{}\text {if }r\text { is even},\\ \Gamma (r+1)\left( 2\textrm{E}_{X_1}\left[ \Phi \left( \sqrt{2}\lambda X_1\right) \right] -1\right) , \quad &{}\text {if }r\text { is odd}, \end{array}\right. } \end{aligned}$$

(14)

where $X_1\sim Gamma(r+1,1)$. Therefore, the kth moment of $X=\mu +\beta Y$ is

$$\begin{aligned} \textrm{E}_{SL_{{II}}}[X^k]&=\textrm{E}[(\mu +\beta Y)^k] =\sum _{r=0}^{k}{k\atopwithdelims ()r}\mu ^{k-r}\beta ^r\textrm{E}\left[ Y^r\right] \nonumber \\&=\mu +\beta \left( 2\textrm{E}_{X_2}\left[ \Phi \left( \sqrt{2}\lambda X_2\right) \right] -1\right) , \end{aligned}$$

(15)

where $X_2\sim Gamma(2,1)$. The other centralised moments follow in a similar manner. As illustrated in Fig. 2, the skewness is bounded between $(-2, 2)$, while the kurtosis is bounded by (5.6558,9), with the lower bound being calculated numerically.

Fig. 2

Skewness and kurtosis of $SL_{II}$ with PDF (13) as a function of $\lambda$

3 Skew Laplace scale mixtures

In this section, we introduce some members of the SLSM models (Definition 2.2) by considering different convenient mixing PDFs, denoted by $h(w;\varvec{\theta })$. These members have the ability to nest their respective reference distribution under a suitable choice of $\varvec{\theta }$, which allows the use of the likelihood ratio test to determine whether the SLSM models are significant improvements over the respective SL distributions. Furthermore, the resulting SLSM distributions have closed-form PDFs and we prove that the members are unimodal. The sampling schemes described for the two SL models can also be used to generate SLSM random variables.

3.1 Mode

The SLSM distribution is unimodal, with mode $\mu$. By taking the first derivative with respect to x of $g_{SLSM}(x;\mu ,\beta ,\varvec{\theta },\lambda )$

$$\begin{aligned} g'_{SLSM}(x;\mu ,\beta ,\varvec{\theta }, \lambda )&=\int _{S_h} f'_{SL}(x;\mu ,\beta /w,\lambda )h(w;\varvec{\theta })dw, \quad x>0\\&\equiv \sum _{w}f'_{SL}(x;\mu ,\beta /w_i, \lambda )h(w_i;\varvec{\theta }) \end{aligned}$$

where

$$\begin{aligned} f'_{SL_I}(x;\mu ,\beta /w,\lambda )={\left\{ \begin{array}{ll} \dfrac{w^2\left( {\lambda }+1\right) \textrm{e}^\frac{w\left( {\lambda }+1\right) \left( x-{\mu }\right) }{{\beta }}}{2{\beta }^2}, \quad x\le \mu ,\\ \dfrac{w^2\left( {\lambda }+1\right) \textrm{e}^{-\frac{w\left( {\lambda }+1\right) \left( x-{\mu }\right) }{{\beta }}}}{2{\beta }^2}-\dfrac{w^2\textrm{e}^{-\frac{w\left( x-{\mu }\right) }{{\beta }}}}{{\beta }^2}, \quad x>\mu , \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} f'_{SL_{II}}(x;\mu ,\beta /w,\lambda )={\left\{ \begin{array}{ll} \frac{w^2}{\beta ^2}\left( \textrm{e}^{\frac{(x-\mu )}{\beta /w}}\Phi \left( \sqrt{2}\lambda \frac{x-\mu }{\beta /w}\right) +\sqrt{2}\lambda \textrm{e}^{\frac{(x-\mu )}{\beta /w}}\phi \left( \sqrt{2}\lambda \frac{x-\mu }{\beta /w}\right) \right) , \quad x\le \mu ,\\ \frac{w^2}{\beta ^2}\left( -\textrm{e}^{-\frac{(x-\mu )}{\beta /w}}\Phi \left( \sqrt{2}\lambda \frac{x-\mu }{\beta /w}\right) +\sqrt{2}\lambda \textrm{e}^{-\frac{(x-\mu )}{\beta /w}}\phi \left( \sqrt{2}\lambda \frac{x-\mu }{\beta /w}\right) \right) , \quad x>\mu , \end{array}\right. } \end{aligned}$$

where $\phi (\cdot )$ denotes the PDF of the standard normal distribution, and since $f'_{SL}(x;\mu ,\beta /w,\lambda )>0$ for $x<\mu$, $f'_{SL}(x;\mu ,\beta /w,\lambda )<0$ for $x>\mu$, and $f'_{SL}(x;\mu ,\beta /w,\lambda )=0$ for $x=\mu$ for both $SL_I$ and $SL_{II}$, and recalling $h(w;\varvec{\theta })>0$ for $w>0$, it follows directly the SLSM distribution is unimodal, with mode $\mu$.

Definition 3.1

If Y has a SL distribution with either PDF (6) or (13) and is independent of W, then

$$\begin{aligned} X\overset{d}{=}\frac{Y}{W} \end{aligned}$$

(16)

has a SLSM distribution.

Let $X\sim SLSM(\mu ,\beta ,\lambda ,\varvec{\theta })$. Subsequently, from the representation given in (16), noting that Y and W are stochastically independent, the kth moment is given by

$$\begin{aligned} \textrm{E}_{SLSM}(X^k)=\textrm{E}_{h}[\textrm{E}_{SL}\left( X^k|W=w\right) ]. \end{aligned}$$

(17)

3.2 Skew Bernoulli Laplace distributions

Consider the following mixing Bernoulli distribution

$$\begin{aligned} W= {\left\{ \begin{array}{ll} 1 \quad \text {with probability } \theta _1\\ 1/\theta _2 \quad \text {with probability } 1-\theta _1\\ \end{array}\right. } \end{aligned}$$

(18)

where $\theta _1 \in (0,1)$ and $\theta _2>1$, and corresponding probability mass function (PMF)

$$\begin{aligned} h_{B}(w;\varvec{\theta })=\theta _1^{\frac{w-1/\theta _2}{1-1/\theta _2}}(1-\theta _2)^{\frac{1-w}{1-1/\theta _2}}, \end{aligned}$$

(19)

where $\varvec{\theta }=(\theta _1,\theta _2)$Punzo and Bagnato (2021). It follows that the kth moment of 1/W is

$$\begin{aligned} \textrm{E}\left( \frac{1}{W^k}\right) =\theta _1+(1-\theta _1)\theta _2^k. \end{aligned}$$

(20)

3.2.1 Skew Bernoulli Laplace type I distribution

By applying the SLSM to the $SL_{I}$ distribution with PDF (6) and the Bernoulli mixing PMF $h_B(w;\varvec{\theta })$ in (19), a random variable X has the skew Bernoulli Laplace type I distribution if its PDF is given by

$$\begin{aligned} g_{SBL_{I}}(x;\mu ,\beta ,\theta _1,\theta _2,\lambda )={\left\{ \begin{array}{ll} \frac{\theta _1}{2\beta }\textrm{e}^{\frac{(\lambda +1)(x-\mu )}{\beta }} +\frac{1-\theta _1}{2\beta \theta _2}\textrm{e}^{\frac{(\lambda +1)(x-\mu )}{\beta \theta _2}}, \quad &{}x\le \mu , \\ \theta _1\left( \frac{1}{\beta }\textrm{e}^{-\frac{(x-\mu )}{\beta }}-\frac{1}{2\beta }\textrm{e}^{-\frac{(\lambda +1)(x-\mu )}{\beta }}\right) \\ +(1-\theta _1)\left( \frac{1}{\beta \theta _2}\textrm{e}^{-\frac{(x-\mu )}{\beta \theta _2}}-\frac{1}{2\beta \theta _2}\textrm{e}^{-\frac{(\lambda +1)(x-\mu )}{\beta \theta _2}}\right) , \quad &{}x> \mu ,\\ \end{array}\right. } \end{aligned}$$

(21)

where $x,\mu \in (-\infty ,\infty )$, $\beta >0, \lambda \ge 0$, $\theta _1 \in (0,1)$ and $\theta _2>1$. This is denoted by $X\sim SBL_{I}(\mu ,\beta ,\theta _1,\theta _2,\lambda )$. Figure 3 illustrates (21) for different values of $\theta _1$ and $\theta _2$, with expressions for the moments given in Appendix A.

Fig. 3

$SBL_{I}$ with PDF (21) for $\mu =0,\beta =1,\lambda =1$ and different values of $\theta _1$ and $\theta _2$

The behaviour of the skewness and kurtosis, as a function of $\lambda$, are illustrated in Fig. 4 for varying values of $\theta _1$ and $\theta _2$. From Fig. 4a it is evident that values of $\theta _1$ close to 1 tend to produce the skewness curve obtained for the $SL_{I}$ distribution with PDF (21), as illustrated in Fig. 1a. It can be observed that as $\theta _1$ decreases the skewness increases. Similarly, from Fig. 4c, the kurtosis curve is produced when $\theta _1$ is close to the plot obtained for the $SL_{I}$ distribution. $\theta _1\rightarrow 1$ can thus be considered as bound for the possible range of skewness, i.e. when $\theta _1\rightarrow 1$ the skewness lies between $(-2,2)$, and also acts as a lower bound for the kurtosis. Figure 4b and d demonstrate the skewness and kurtosis behaviour for varying values of $\theta _2$, respectively. When $\theta _2$ is close to one the skewness and kurtosis of the $SL_{II}$ distribution are obtained, and can thus be considered a practical lower bound.

Fig. 4

Skewness and kurtosis of $SBL_{I}$ with PDF (21) as a function of $\lambda$

3.2.2 Skew Bernoulli Laplace type II distribution

Next, the $SL_{II}$ distribution (22) is considered as the conditional reference distribution. A random variable X has the skew Bernoulli type II distribution if its PDF is given by

$$\begin{aligned} \begin{aligned} g_{SBL_{II}}(x;\mu ,\beta ,\theta _1,\theta _2,\lambda )&= 2\theta _1 f_L(x;\mu ,\beta )\Phi \left( \sqrt{2}\lambda \left( \frac{x-\mu }{\beta }\right) \right) \\&\quad + 2(1-\theta _1) f_L(x;\mu ,\theta _2 \beta )\Phi \left( \sqrt{2}\lambda \left( \frac{x-\mu }{\theta _2\beta }\right) \right) , \end{aligned} \end{aligned}$$

(22)

where $x,\mu ,\lambda \in (-\infty ,\infty )$, $\beta >0$, $\theta _1 \in (0,1)$, $\theta _2>1$ and where $f_L(\cdot )$ is given by (1). This is denoted by $X\sim SBL_{II}(\mu ,\beta ,\theta _1,\theta _2,\lambda )$ and illustrated for varying values of $\theta _1$ and $\theta _2$ in Fig. 5.

Fig. 5

$SBL_{II}$ with PDF (22) for $\mu =0,\beta =1,\lambda =1$ and different values of $\theta _1$ and $\theta _2$

In this case, the kth moment is given as

$$\begin{aligned} \textrm{E}_{SBL_{II}}[X^k] =\theta _1\sum _{r=0}^{k}{k\atopwithdelims ()r}\mu ^{k-r}\beta ^r\textrm{E}\left[ Y^r\right] +(1-\theta _1)\sum _{r=0}^{k}{k\atopwithdelims ()r}\mu ^{k-r}(\beta \theta _2)^r\textrm{E}\left[ Y^r\right] , \end{aligned}$$

(23)

where $\textrm{E}[Y^r]$ is given in (14). Using (23), expressions for the mean, variance, skewness and kurtosis can be obtained. Figure 6 illustrates the skewness and kurtosis for varying values of $\theta _1$ and $\theta _2$.

Fig. 6

Skewness and Kurtosis of $SBL_{II}$ with PDF (22) as a function of $\lambda$

Fig. 7

$SSEL_{I}$ with PDF (26) for $\mu =0,\beta =1,\lambda =1$ and different values of $\theta$

The PDFs in (21) and (22) can be viewed as contaminated SL models, i.e. the SL counterpart of the contaminated normal distribution (Tukey, 1960). It should be noted the additional parameters $\theta _1$ and $\theta _2$ have an interpretation of practical interest. $\theta _1$ is the proportion of points from the reference distribution, while the parameter $\theta _2$ denotes the degree of contamination. Since it is common practice to assume that at least half of the observations are considered “good” in robustness studies (Punzo & Bagnato, 2021), we will assume that $\theta _1 \in (0.5,1)$. Because of the assumption that $\theta _2>1$, it can be meant as the increase in variability due to the points which do not come from the reference distribution. Both PDFs reduce to their respective SL distributions given in (6) and (13) when $\theta _1 \rightarrow 1$ and $\theta _2 \rightarrow 1$. In addition, if $\lambda = 0$, (21) and (22) simplifies to the Bernoulli Laplace distribution developed in Punzo and Bagnato (2021). The Laplace distribution with PDF (1) is obtained if $\theta _1 \rightarrow 1$, $\theta _2 \rightarrow 1$ and $\lambda = 0$.

As discussed in Punzo and Bagnato (2021), an advantage of using a contaminated model is that, given ${\mu },{\beta }$, ${\lambda }$, $\theta _1$ and $\theta _2$, it is possible to establish whether a data point x comes from the reference distribution or not via the a posteriori probability

$$\begin{aligned} P(x \text { comes from the reference distribution} )=\frac{\theta _1f_{SL_i}(x;\mu ,\beta ,\lambda )}{g_{SBL_i}(x;\mu ,\beta ,\theta _1,\theta _2,\lambda )} \end{aligned}$$

(24)

for $i=I,II$. If the a posteriori probability in (24) is greater than 0.5 then x can be considered to come from the respective SL distribution in (6) or (13).

3.3 Skew shifted exponential Laplace distributions

As a next candidate for the mixing distribution, consider the shifted exponential distribution with PDF given by

$$\begin{aligned} h_{SE}(w;\theta )=\theta \textrm{e}^{-\theta (w-1)}, \quad w>1, \end{aligned}$$

(25)

where $\theta >0$ Punzo and Bagnato (2021) and the kth moment of 1/W is

$$\begin{aligned} \textrm{E}\left( \frac{1}{W^k}\right) =\theta \textrm{e}^\theta \int _1^\infty \textrm{e}^{-\theta t}/t^kdt=\theta \textrm{e}^\theta E_k(\theta ), \end{aligned}$$

where $E_k(\theta )$ is the exponential integral function.

3.3.1 Skew shifted exponential Laplace type I distribution

If (25) is considered as the mixing PDF in (3), the skew shifted exponential Laplace type I (SSEL$_{I}$) distribution is proposed as

$$\begin{aligned} g_{SSEL_{{I}}}(x;\mu ,\beta ,\theta ,\lambda )={\left\{ \begin{array}{ll} -\dfrac{{\theta }\left[ \left( x-{\mu }\right) \left( {\lambda }+1\right) -{\beta }\left( {\theta }+1\right) \right] \textrm{e}^\frac{\left( {\lambda }+1\right) \left( x-{\mu }\right) }{{\beta }}}{2\left[ \left( x-{\mu }\right) \left( {\lambda }+1\right) -{\beta }{\theta }\right] ^2},\quad &{}x\le \mu ,\\ \dfrac{{\theta }\left( x-{\mu }+{\beta }(\theta +1)\right) \textrm{e}^{-\frac{x-{\mu }}{{\beta }}}}{\left( x-{\mu }+{\beta }{\theta }\right) ^2}\\ -\dfrac{{\theta }\left[ \left( x-{\mu }\right) \left( {\lambda }+1\right) +{\beta }({\theta }+1)\right] \textrm{e}^{-\frac{\left( x-{\mu }\right) \left( {\lambda }+1\right) }{{\beta }}}}{2\left[ \left( x-{\mu }\right) \left( {\lambda }+1\right) +{\beta }{\theta }\right] ^2} ,\quad &{}x> \mu , \end{array}\right. } \end{aligned}$$

(26)

where $x, \mu \in (-\infty ,\infty )$, $\beta , \theta >0$ and $\lambda \ge 0$, with (6) used as the conditional (reference) distribution. Figure 7 illustrates (26) for varying values of $\theta$, where it can be observed that the $SSEL_{I}$ distribution reduces to the $SL_{I}$ distribution (6) as $\theta \rightarrow \infty$.

Figure 17a in Appendix C illustrates the skewness bounded between (-2,2) and behaves similarly to the skewness of $SL_{I}$ when $\theta \rightarrow \infty$; it is evident that the kurtosis increases as $\theta \rightarrow 0$.

3.3.2 Skew shifted exponential type II distribution

Suppose the PDF in (13) is the reference distribution in (3), then we propose the skew shifted exponential Laplace type II (SSEL$_{II}$) distribution with PDF

$$\begin{aligned} \begin{aligned} g_{SSEL_{II}}(x;\mu ,\beta ,\theta ,\lambda )&=\frac{2\theta f_{L}(x;\mu ,\beta )}{\left( \frac{|x-\mu |}{\beta }+\theta \right) }\left( \frac{\textrm{E}_{X_3}\left[ \Phi \left( \frac{\sqrt{2}\lambda (X_3+1)(x-\mu )}{\beta }\right) \right] }{\left( \frac{|x-\mu |}{\beta }+\theta \right) }\right. \\&\quad \left. +\textrm{E}_{X_4}\left[ \Phi \left( \frac{\sqrt{2}\lambda (X_4+1)(x-\mu )}{\beta }\right) \right] \right) , \end{aligned} \end{aligned}$$

(27)

where $x, \mu , \lambda \in (-\infty ,\infty )$, $\beta , \theta >0$, $X_3\sim Gamma\left( 2,\frac{|x-\mu |}{\beta }+\theta \right)$ and $X_4 \sim Exp\left( \frac{|x-\mu |}{\beta }+\theta \right)$.

Figure 8 illustrates (27) for varying values of $\theta$, while the skewness and kurtosis are shown in Fig. 17b and 18b, respectively. These are interpretable in a similar manner as for the $SSEL_{I}$ distribution. It follows that (26) and (27) reduce to (21) and (22) respectively as $\theta \rightarrow \infty$. It follows from Fig. 18b that for small values of $\theta$, the kurtosis of the SSEL models is higher.

Fig. 8

$SSEL_{II}$ with PDF (27) for $\mu =0,\beta =1,\lambda =1$ and different $\theta$

3.4 Skew unimodal gamma Laplace distributions

As mixing distribution we consider the unimodal gamma (UG) distribution (Chen, 2000; Punzo, 2019) with PDF

$$\begin{aligned} h_{UG}(w;\theta )=\frac{w^{\frac{1}{\theta }}\textrm{e}^{-\frac{w}{\theta }}}{\theta ^{\frac{1}{\theta }+1}\Gamma \left( \frac{1}{\theta }+1\right) }, \quad w>0, \end{aligned}$$

(28)

where $\theta >0$ and $\Gamma (\cdot )$ denotes the gamma function. It follows that the kth moment of 1/W is

$$\begin{aligned} \textrm{E}\left( \frac{1}{W^k}\right) =\frac{\Gamma \left( \frac{1}{\theta }+1-k\right) }{\theta ^{k-1}\Gamma \left( \frac{1}{\theta }\right) } \end{aligned}$$

if $\theta <1/(k-1)$.

3.4.1 Skew unimodal gamma Laplace type I distribution

From (6) and (28) it follows that X has the skew unimodal gamma Laplace type I (SUGL$_{{I}}$) distribution with PDF

$$\begin{aligned} g_{SUGL_{I}}(x;\mu ,\beta ,\theta ,\lambda )= {\left\{ \begin{array}{ll} \frac{1}{2}(\theta +1)\beta ^{\frac{1}{\theta }+1}\left[ \beta -\theta \left( \lambda +1\right) (x-\mu )\right] ^{-\frac{1}{\theta }-2},\quad &{}x\le \mu ,\\ \\ (\theta +1)\beta ^{\frac{1}{\theta }+1}\left( \left[ \beta +\theta (x-\mu )\right] ^{-\frac{1}{\theta }-2}\right. \\ \left. -\frac{1}{2}\left[ \beta +\theta (\lambda +1)(x-\mu )\right] ^{-\frac{1}{\theta }-2}\right) ,\quad &{}x>\mu , \end{array}\right. } \end{aligned}$$

(29)

where $x, \mu \in (-\infty ,\infty )$, $\beta , \theta ,>0$ and $\lambda \ge 0$. Figure 9 illustrates the PDF (29).

Fig. 9

$SUGL_{I}$ with PDF (29) for $\mu =0,\beta =1,\lambda =1$ and different values of $\theta$

From Figs. 17c and 18c it is evident that the range of possible values of both the skewness and kurtosis of (29) are increasing functions of $\theta$ and behave in a similar manner to that of the $SL_{I}$ distribution when $\theta \rightarrow 0$.

3.4.2 Skew unimodal gamma Laplace type II distribution

Next, from (13) and (28), a random variable X has the skew unimodal gamma Laplace type II (SUGL$_{II}$) distribution with PDF

$$\begin{aligned} g_{SUGL_{II}}(x;\mu ,\beta ,\theta ,\lambda )=\frac{{\theta }+1}{\beta \theta ^{\frac{1}{\theta }+2}\left( \frac{1}{\theta }+\frac{|x-\mu |}{\beta }\right) ^{\frac{1}{\theta }+2}}\textrm{E}_{X_5}\left[ \Phi \left( \sqrt{2}\lambda X_5\left( \frac{x-\mu }{\beta }\right) \right) \right] , \end{aligned}$$

(30)

where $x, \mu , \lambda \in (-\infty ,\infty )$, $\beta , \theta >0$ and $X_5\sim Gamma\left( \frac{1}{\theta }+2,\frac{1}{\theta }+\frac{|x-\mu |}{\beta }\right)$. Figure 10 illustrates (30) for varying values of $\theta$, and Figs. 17d and 18d the corresponding skewness and kurtosis as a function of $\lambda$.

Fig. 10

$SUGL_{II}$ with PDF (30) for $\mu =0,\beta =1,\lambda =1$ and different values of $\theta$

3.5 Skew power-function Laplace distributions

Lastly, the power function (PF) distribution is considered as mixing distribution with PDF given as

$$\begin{aligned} h_{PF}(w;\theta )=\theta w^{\theta -1},\quad 0<w<1, \end{aligned}$$

(31)

where $\theta >0$ Ahsanullah and Kabir (1974). The kth moment of 1/W is

$$\begin{aligned} \textrm{E}\left( \frac{1}{W^k}\right) =\frac{\theta }{\theta -k}, \end{aligned}$$

which exists for $\theta >k$.

3.5.1 Skew power-function Laplace type I distribution

From (31) and (6), it follows that a random variable X has the skew power-function Laplace type I (SPFL$_{I}$) distribution with PDF given by

$$\begin{aligned} g_{SPFL_{I}}(x;\mu ,\beta ,\theta )={\left\{ \begin{array}{ll} \frac{\theta \left( \Gamma (\theta +1)-\Gamma \left( \theta +1,-\frac{(\lambda +1) (x-\mu )}{\beta }\right) \right) }{2 \beta \left( -\frac{(\lambda +1) (x-\mu )}{\beta }\right) ^{\theta +1} }, \quad &{}x\le \mu ,\\ \\ \frac{\beta ^\theta \theta }{(x-\mu )^{\theta +1}}\left[ \Gamma (\theta +1)-\Gamma \left( \theta +1,\frac{x-\mu }{\beta }\right) \right. \\ -\left. \frac{\left( \Gamma (\theta +1)-\Gamma \left( \theta +1,\frac{(\lambda +1)(x-\mu ) }{\beta }\right) \right) }{2(\lambda +1)^{\theta +1}}\right] ,\quad &{}x>\mu , \end{array}\right. } \end{aligned}$$

(32)

where $x, \mu \in (-\infty ,\infty )$, $\beta , \theta >0$, $\lambda \ge 0$, $\Gamma (\cdot ,\cdot )$ denotes the upper incomplete gamma function (Gradshteyn & Ryzhik, 2014). Figure 11 illustrates (32) for varying values of $\theta$. From Figs. 17e and 18e, it is evident that as $\theta \rightarrow \infty$, the skewness and kurtosis reduces to that of the $SL_{I}$ distribution with PDF (6). Conversely, the range of possible values of the skewness and kurtosis increase as $\theta \rightarrow 0$; $\theta \rightarrow \infty$ acts as a lower bound.

Fig. 11

$SPFL_{I}$ with PDF (32) for $\mu =0,\beta =1,\lambda =1$ and different values of $\theta$

3.5.2 Skew power-function Laplace type II distribution

From (13) and (31) a random variable X has the SPFL$_{II}$ distribution with PDF given by

$$\begin{aligned} g_{SPFL_{{II}}}(x;\mu ,\beta ,\theta _1,\theta _2,\lambda )&=\frac{\theta \beta ^\theta \gamma (\theta +1,\frac{|x-\mu |}{\beta })}{|x-\mu |^{\theta +1}}\textrm{E}_{X_6}\left[ \Phi \left( \sqrt{2}\lambda X_6\left( \frac{x-\mu }{\beta }\right) \right) \right] , \end{aligned}$$

(33)

where $x, \mu ,\lambda \in (-\infty ,\infty )$ and $\beta ,\theta >0$, $X_6\sim TGamma\left( \theta +1,\frac{\beta }{|x-\mu |},1\right)$. Note if Z has a truncated gamma distribution its PDF is given as

$$\begin{aligned} f(z;k,\theta ,a)=\frac{z^{k-1}\textrm{e}^{-\frac{z}{\theta }}}{\theta ^k\gamma \left( k,\frac{a}{\theta }\right) } \end{aligned}$$

where $z\in (0,a]$, $\kappa ,\theta , a>0$ and $\gamma (\cdot ,\cdot )$ denotes the lower incomplete gamma function (Gradshteyn & Ryzhik, 2014). This is denoted by $Z\sim TGamma(k,\theta ,a)$.

Figure 12 illustrates (33) for varying values of $\theta$ and Figs. 17f and 18f shows the corresponding skewness and kurtosis as a function of $\lambda$.

Fig. 12

$SPFL_{II}$ with PDF (33) for $\mu =0,\beta =1,\lambda =1$ and different values of $\theta$

4 Finite mixtures

In this section, the focus shifts to a finite mixture approach that is able to model multimodal data, while still being flexible enough to model skewness and heavy-tailed data. Finite mixture models provide a flexible framework for analysing a variety of data, with numerous applications, including classification, clustering, and data mining, image analysis, pattern recognition, latent class analysis, density estimation (Bishop & Nasrabadi, 2006; Frühwirth-Schnatter, 2006; McLachlan & Basford, 1988; McLachlan et al., 2019). According to Titterington et al. (1985), a broad motivation for using a finite mixture of univariate densities is that we assume that there are k underlying groups/components and that each observation belongs to one of the components. The aim is to infer the distribution for each component separately. The PDF of a k-component SLSM finite mixture is given in Definition 4.1.

Definition 4.1

The finite mixture model of k unimodal SLSM PDFs, where $g_{SLSM}(x;\mu _i,\beta _i,\varvec{\theta }_i,\lambda _i)$ is the unimodal PDF of the ith component with parameters $\mu _i,\beta _i,\varvec{\theta }_i,\lambda _i$ (as defined in Definition 2), is given as

$$\begin{aligned} m(x;\varvec{\psi })=\sum ^k_{j=1}\pi _jg_{SLSM}(x;\mu _j,\beta _j,\varvec{\theta }_j,\lambda _j), \quad -\infty<x<\infty , \end{aligned}$$

(34)

where $\pi _j \in (0,1]$ is the mixing proportion for the jth component and $\sum ^{k}_{j=1}\pi _j=1$, and $\varvec{\psi }=(\varvec{\pi }',\varvec{\mu }',\varvec{\beta }',\varvec{\theta }',\varvec{\lambda }')'$, with $\varvec{\pi }=(\pi _1,\dots ,\pi _k)'$, $\varvec{\mu }=(\mu _1,\dots ,\mu _k)'$, $\varvec{\beta }=(\beta _1,\dots ,\beta _k)'$, $\varvec{\theta }=(\varvec{\theta }_1',\dots , \varvec{\theta }_k')'$ and $\varvec{\lambda }=(\lambda _1,\dots ,\lambda _k)'$, contains all the parameters of the finite mixture.

Finite mixtures consisting of members of the SLSM models described in Sect. 3 are fitted to a real-world data set in Sect. 6.

5 Maximum likelihood estimation

The EM algorithm developed by Dempster et al. (1977) is based on finding the maximum likelihood estimate (MLE) of the parameters and weights of a distribution. A brief description of the EM algorithm follows: for the application of the EM algorithm, it is convenient to view the observed data, denoted by $x_i$, as incomplete. An unobserved, also known as latent, random variable is introduced. Let a vector of unknown parameters be denoted by $\varvec{\psi }$ and the complete data likelihood function, denoted by $L_{c}(\varvec{\psi })$. The EM algorithm seeks to find the MLE of the data likelihood function by iteratively applying two steps until convergence, namely the expectation and maximization step.

The expectation step requires the calculation of the conditional expectation of the complete-data log-likelihood function. For the $(r+1)$th iteration, this is given as

$$\begin{aligned} Q(\varvec{\psi }|\varvec{\psi }^{(r)})=\textrm{E}[\textrm{ln}L_{c}(\varvec{\psi })]. \end{aligned}$$

In the maximization step, the parameters are found that maximize $Q(\varvec{\psi }|\varvec{\psi }^{(r)})$, i.e.

$$\begin{aligned} \varvec{\psi }^{(r+1)}=\arg \max _{\varvec{\psi }}Q(\varvec{\psi }|\varvec{\psi }^{(r)}). \end{aligned}$$

A full description and further extensions of the EM algorithm can be found in McLachlan and Krishnan (2007).

The computational ease and availability of optimization routines in R software, make direct numerical maximization (DNM) a practical choice to obtain parameter estimates when the distributions are unimodal. See MacDonald (2014) and MacDonald (2021) for several examples to show the advantages of DNM over the EM algorithm. While estimates for the SSEL, SUGL and SPFL distributions in Sect. 3 can also be estimated by making use of the EM algorithm, we opted to use the DNM method to numerically optimize the parameter estimates using the optim() function in R R Core Team (2013), included in the stats package. A simulation study is conducted in Example 6.1 to investigate the parameter recovery of the DNM method.

The EM algorithm is further expanded for the $SBL_I$ and $SBL_{II}$ distributions with PDFs (21) and (22) in Sect. 5.1 as an illustration and in Appendix B for the finite mixture models consisting of the SLSM models since they are not unimodal.

5.1 EM algorithm for SBL distributions

If the latent variable is denoted by W, the complete data are given by $(x_1,w_1),\dots ,(x_i,w_i),\dots ,(x_n,w_n).$ It follows that the complete data likelihood function, $L_c(\mu ,\beta ,\theta _1,\theta _2,\lambda )$, can be factored into the product of the conditional PDFs of $X_i|w_i$ and the joint marginal PDFs of $W_i$

$$\begin{aligned} L_c(\mu ,\beta ,\theta _1,\theta _2,\lambda )=\prod _{i=1}^{n}f_{SL}(x_i;\mu ,\beta /w_i,\lambda )h_B(w_i;\theta _1,\theta _2), \end{aligned}$$

(35)

where $f_{SL}(\cdot )$ is given in either (6) or (13) and $h_B(\cdot )$ in (19). From (35), the complete-data log-likelihood function can be written as

$$\begin{aligned} l_c(\mu ,\beta ,\theta _1,\theta _2,\lambda )&=\sum _{i=1}^{n}\textrm{ln}\left[ f_{SL}(x_i;\mu ,\beta /w_i,\lambda )h_B(w_i;\theta _1,\theta _2)\right] . \end{aligned}$$

(36)

Consider the linear transformation of the missing variable W in (18)

$$\begin{aligned} V&=\frac{W-1/\theta _2}{1-1/\theta _2}\\&={\left\{ \begin{array}{ll} 1 \quad \text {with probability } \theta _1\\ 0 \quad \text {with probability } 1-\theta _1.\\ \end{array}\right. } \end{aligned}$$

In this case, $v_i$ acts as an indicator variable where $v_i=1$ if $x_i$ comes from the reference distribution and $v_i=0$ otherwise. The complete data are thus given by $(x_1,v_1),\dots ,(x_i,v_i),\dots ,(x_n,v_n)$ and the complete-data likelihood function in (35) can be rewritten as

$$\begin{aligned} L_c(\mu ,\beta ,\theta _1,\theta _2,\lambda )=\prod _{i=1}^{n}\left[ \theta _1f_{SL}(x_i;\mu ,\beta ,\lambda )\right] ^{v_i}\left[ (1-\theta _1)f_{SL}(x_i;\mu ,\beta \theta _2,\lambda )\right] ^{1-v_i} \end{aligned}$$

(37)

and the complete-data log likelihood function in (36) as

$$\begin{aligned} l_c(\mu ,\beta ,\theta _1,\theta _2,\lambda )&=\sum _{i=1}^{n}\left[ v_i\textrm{ln}\theta _1+v_i\textrm{ln}f_{SL}(x_i;\mu ,\beta ,\lambda )\right. \nonumber \\&\quad \left. +(1-v_i)\textrm{ln}(1-\theta _1) +(1-v_i)\textrm{ln}f_{SL}(x_i;\mu ,\beta \theta _2,\lambda )\right] \nonumber \\&=l_{1c}(\mu ,\beta ,\theta _2,\lambda )+l_{2c}(\theta _1) \end{aligned}$$

(38)

where

$$\begin{aligned} l_{1c}(\mu ,\beta ,\theta _2,\lambda )=\sum _{i=1}^{n}\left[ v_i\textrm{ln}f_{SL}(x_i;\mu ,\beta ,\lambda )+(1-v_i)\textrm{ln}f_{SL}(x_i;\mu ,\beta \theta _2,\lambda )\right] \end{aligned}$$

and

$$\begin{aligned} l_{2c}=\sum _{i=1}^{n}\left[ v_i\textrm{ln}\theta _1+(1-v_i)\textrm{ln}(1-\theta _1)\right] . \end{aligned}$$

In the expectation step, the conditional expectation of the complete-data log likelihood function given in (38), is denoted by

$$\begin{aligned} \begin{aligned}&Q(\mu ,\beta ,\theta _1,\theta _2,\lambda |{\mu }^{(r)},{\beta }^{(r)},{\theta _1}^{(r)},{\theta _2}^{(r)},{\lambda }^{(r)})\\&\quad = Q_1(\mu ,\beta ,\theta _2,\lambda ,|{\mu }^{(r)},{\beta }^{(r)},{\theta _1}^{(r)},{\theta _2}^{(r)},{\lambda }^{(r)})\\&\qquad +Q_2(\theta _1|{\mu }^{(r)},{\beta }^{(r)},{\theta _1}^{(r)},{\theta _2}^{(r)},{\lambda }^{(r)}) \end{aligned} \end{aligned}$$

(39)

for the $(r+1)th$ iteration, which is in the same order as (38). From (24), it follows that the expected a posteriori probability for $x_i$ to come from the reference distribution is given as

$$\begin{aligned} \begin{aligned} {\textrm{E}}(V_i|X_i=x_i)&=\frac{{\theta _1}^{(r)}g_{SL}(x_i;{\mu }^{(r)},{\beta }^{(r)},{\lambda }^{(r)})}{{\theta _1}^{(r)}g_{SL}(x_i;{\mu }^{(r)},{\beta }^{(r)},{\lambda }^{(r)})+(1-{\theta _1}^{(r)})g_{SL}(x_i;{\mu }^{(r)},{\beta }^{(r)}{\theta _2}^{(r)},{\lambda }^{(r)})}\\&=:{{v}_i}^{(r)}. \end{aligned} \end{aligned}$$

(40)

By substituting ${{v}_i}^{(r)}$ in (38), the expected complete log likelihood in (39) is obtained.

In the maximization step, the update for ${\theta _1}^{(r+1)}$ is calculated independently by maximizing

$Q_2(\theta _1|{\mu }^{(r)},{\beta }^{(r)},{\lambda }^{(r)},{\theta _1}^{(r)},{\theta _2}^{(r)})$ with respect to $\theta _1$. It follows that ${\hat{\theta }_1}^{(r+1)}=\frac{1}{n}\sum _{i=1}^{n}{{v}_i}^{(r)}$. Similarly, updates for $\mu ^{(r+1)},\beta ^{(r+1)},{\theta _2}^{(r+1)}$ and $\lambda ^{(r+1)}$ are calculated by numerically maximizing

$Q_1(\mu ,\beta ,\theta _2,\lambda ,|{\mu }^{(r)},{\beta }^{(r)},{\lambda }^{(r)},{\theta _1}^{(r)},{\theta _2}^{(r)})$.

An observation x is considered to come from the reference distribution if $v_i>0.5$. Such a point can be referred to as a good point and as a bad point otherwise. This can be equivalently defined in terms of discriminant functions

$$\begin{aligned} D_{good}(x;\mu ,\beta ,\theta _1,\lambda )=\theta _1g_{SL}(x;\mu ,\beta ,\lambda ) \end{aligned}$$

(41)

and

$$\begin{aligned} D_{bad}(x;\mu ,\beta ,\theta _1,\theta _2,\lambda )=(1-\theta _1)g_{SL}(x;\mu ,\beta \theta _2,\lambda ) \end{aligned}$$

(42)

so that x will be classified as good if

$$\begin{aligned} D_{good}(x;\mu ,\beta ,\theta _1,\lambda )>D_{bad}(x;\mu ,\beta ,\theta _1,\theta _2,\lambda ) \end{aligned}$$

and bad otherwise. Solving the intersection points of the discriminant functions in (41) and (42), delimits the good and bad regions.

5.2 Initialization of the estimation process

It is well known that both the EM algorithm and DNM suffer from locally optimal solutions and the final estimates are dependent on the initial starting values, as pointed out by Mahdavi et al. (2023). To address this, we suggest using the following as initial values

$$\begin{aligned} \mu ^{(0)}&=\text {median}(x),\\ \beta ^{(0)}&= \frac{1}{n}\sum _{i=1}^n\left| x_i-\mu ^{(0)}\right| ,\\ \lambda ^{(0)}&= \text {empirical skewness}(x). \end{aligned}$$

For $\varvec{\theta }$, we recommend initial values that make the SLSM model tend to the corresponding SL model. In the case of SBL$_{I}$ for example, we suggest initializing $\theta _1^{(0)}\rightarrow 1^-$ and $\theta _2^{(0)}\rightarrow 1^+$.

6 Application

In this section a simulation study is conducted to investigate the parameter recovery of the DNM described in Sect. 5. The SLSM distributions developed in Sect. 3 are then applied to real-world data sets, namely the bodily injury claims data set (Rempala & Derrig, 2005) and the refractive index of glass fragments. The SLSM are compared to the corresponding ALSM distributions (Punzo & Bagnato, 2022a) formed with the same mixing distributions, and to other flexible distributions: skew normal (SN) (Azzalini, 1985), SGN, skew t (ST) and skew generalised t (SGT) (Theodossiou, 1998) distribution. Finite mixtures consisting of the members of the SLSM distributions are fit to campaign finance scores that measure the ideology of donors to American political candidates. The Akaike information criterion (AIC) (Akaike, 1974) and the Bayesian information criterion (BIC) (Schwarz, 1978) are employed for model comparison and are ranked to aid the reader in comparing the performance of the different fitted models - in the spirit of Morris et al. (2019).

6.1 SUGL simulation study

As an illustration of the ability of the DNM approach to recover parameter estimates of the SLSM distributions, a simulation study on the $SUGL_{I}$ distribution is considered. Samples were generated using the sampling scheme described in Definition 3.1 for sample sizes of $n=100,200,500$. Each of these instances was repeated 500 times in order to determine and observe the bias, standard error and mean squared error (MSE) of the estimates. For the simulation we consider $\mu =0$, $\beta =2$, $\lambda =2$ and $\theta =0.5$. The empirical results are displayed in Table 1. As expected, the bias is consistently small and the MSE decreases as the sample size increases.

Table 1 Simulation results for generated SUGL$_{I}$ data

Similar studies can be performed for the other SLSM models. This example proves that DNM can be used successfully for estimating the parameters of the different models.

6.2 Bodily injury claims

The data set consists of 348 observations, i.e. claim amounts, given in thousands and is available in the CASdatasets package in R Dutang and Charpentier (2018). Insurance data are frequently skewed and leptokurtic (Ibragimov et al., 2015), once again emphasizing the need for flexible distributions. In analogy with Rempala and Derrig (2005), we considered the log of the claim amounts. From the descriptive statistics in Table 2 there is an indication that the data exhibit heavy-tail behaviour in the log of the claim amounts, as well as skewness. Furthermore, peakedness in the data is also evident from the histogram in Fig. 13a.

Table 2 Descriptive statistics of the log bodily injury claim amounts

Fig. 13

Histogram of log bodily injury claim amounts and SBL$_{I}$ quantile-quantile plot

Table 3 Results of fitted models to the log bodily injury claim amounts

Table 3 shows that both the AIC and BIC indicate that (21) fits the best to the data (represented by bold values). Furthermore, 3 members of the SLSM models presented in this paper claim the first three spots. The fitted PDF (21) and the corresponding conditional $SL_I$ distribution (13) are overlaid in Fig. 13a, while the quantile–quantile (Q–Q) $SBL_{I}$ is given in Fig. 13b. From the linearity of the points in the Q–Q plot, it is evident that the $SBL_{I}$ can be considered a valid candidate.

6.3 Forensic glass fragments

Various types of glass are made of different elements and have distinct refractive indices. The refractive index (RI) determines how much light is bent, or refracted, when entering a material and plays an important role in differentiating types of glass. The SLSM models are fit to the RI of 214 glass fragments that are available in the fgl dataset in the MASS package in R Ripley et al. (2013) (summary statistics reported in Table 4).

Table 5 shows that both the AIC and BIC indicate that the SSEL$_{II}$ (27) fits the data the best (represented by bold values), supported by the Q–Q plot. The fitted PDF (26) and the corresponding conditional SL$_{II}$ are superimposed in Fig. 14a.

Table 4 Descriptive statistics of the forensic glass fragments refractive index

Table 5 Results of fitted models to the forensic glass fragments refractive index

Fig. 14

Histogram of the refractive index of forensic glass fragments refractive index and SSEL$_{I}$ quantile-quantile plot

6.4 Measures of Donor Ideology

Ideology plays a central role in American politics, influencing the preferences and behaviours of political contributors. Generally, donors are more inclined to support candidates whose ideological positions align closely with their own. This phenomenon can be quantified using what are termed common-space campaign finance scores (CFscores), as described in Bonica (2014). These scores help estimate the ideal ideological point of donors. Data from the Database on Ideology, Money in Politics, and Elections (DIME): Public version 3.0 Bonica (2023) reveal notable patterns in the ideological distribution of political contributors across various industries. Some industries have donors that predominantly lean to the left, while others lean to the right. Historically, industries aligning with the Democratic Party have tended to support left-leaning policies, while those aligned with the Republican Party have favoured right-leaning ones.

Such industry-level ideological measures can shed light on the broader political behaviours of industries. For example, if we were to examine the CFscores of donors within the "pharmaceuticals" industry, we might gain insights into their general political inclinations. In order to better analyze and distinguish these patterns, we fit a SLSM finite mixture model with $k=2$ components. This approach allows for clearer differentiation between the left and right-leaning tendencies of the industries under observation. The AIC and BIC values of the fitted finite mixtures are shown in Table 6. From this table, it’s evident that the ALSM models outperformed our proposed models (represented by bold values). However, the SBL$_{II}$ model ranked second based on the AIC and fourth based on the BIC and the Q-Q plot further indicates that the SBL$_{II}$ remains a viable alternative model. It should be noted that the ALSM models discussed in the paper by Punzo and Bagnato (2022a) have not been previously examined within the framework of finite mixture models (Fig. 15).

Fig. 15

Histogram of CFscores and corresponding quantile–quantile plot of finite mixture of two SBL$_{II}$ PDFs

Table 6 Results of fitted mixtures with $k=2$ components to the CFscores of donors within the pharmaceutical industry

7 Final thoughts

7.1 Conclusion

Real data are often skewed and “contaminated" by outliers, highlighting the need for flexible models that are able to account for their unique characteristics. In this paper, a collection of flexible skew Laplace scale mixture (SLSM) distributions is developed by considering different skew Laplace candidates, formed with Azzalini’s method of introducing skewness to symmetric distributions, and also various convenient discrete and continuous mixing variables. The resulting distributions have closed-form probability distribution functions and are able to model data with heavy-tails, skewness and peakedness. The flexibility is further extended by developing finite mixture models that are able to model multimodal data. The maximum likelihood estimates are obtained via an expectation-maximization algorithm and direct optimization and compared via the AIC, BIC and the likelihood ratio test. The SLSM distributions represent valid alternatives to other flexible distributions, as shown in Sect. 6, where several of the proposed models outperform the ALSM developed in Punzo and Bagnato (2022a).

The novelty of the SLSM models is not limited to the illustrated distributions in this paper; see Kozubowski and Nadarajah (2010) for other unconsidered generalised Laplace distributions that can be considered as a conditional reference distribution. Similarly, other mixing distributions can be considered to further extend the collection of distributions. An example includes the reparameterised inverse Gaussian distribution introduced in Punzo (2019), with PDF

$$\begin{aligned} h(w,\theta )=\sqrt{\frac{3\theta +1}{2\pi \theta w^3}}\textrm{e}^{-\frac{(w-\sqrt{3\theta +1})^2}{2\theta w}}, \quad w>0 \end{aligned}$$

where $\theta >0$, although a multitude of other mixing distributions may be considered in future.

A Bayesian parameter estimation scheme is worth investigating as a valuable alternative to the EM algorithm in future work. By fitting mixtures of the shifted asymmetric Laplace distribution, Fang et al. (2023) illustrated that a Bayesian approach is particularly useful as it solves the “infinite likelihood problem” that might arise and thus produces better estimates in certain cases.

7.2 Future work

As a starting point for future work, a multivariate extension of the skew Bernoulli Laplace distribution is developed that is capable of modelling data when the dependence in the sample is non-negligible. Arslan (2010) proposed a p-dimensional multivatiate skew Laplace distribution with PDF

$$\begin{aligned} f_{MSL}(\varvec{x};\varvec{\mu },\varvec{\Sigma },\varvec{\gamma })=\frac{|\varvec{\Sigma }|^{-\frac{1}{2}}}{2^p\pi ^{(p-1)/2}\alpha \Gamma \left( \frac{p+1}{2}\right) }\textrm{e}^{-\alpha \sqrt{(\varvec{x}-\varvec{\mu })^T\varvec{\Sigma }^{-1}(\varvec{x}-\varvec{\mu })}+(\varvec{x}-\varvec{\mu })^T\varvec{\Sigma }^{-1}\varvec{\gamma }} \end{aligned}$$

(43)

where $\varvec{x}:p\times 1,\varvec{\mu }:p\times 1 \in \mathbb {R}^p, p\ge 1$, $\varvec{\Sigma }:p\times p$ is a positive definite matrix, $\varvec{\gamma }:p\times 1 \in \mathbb {R}^p$ is the skewness parameter and $\alpha =\sqrt{1+\varvec{\gamma }^T\varvec{\Sigma }^{-1}\varvec{\gamma }}$. This is denoted by $\varvec{X}\sim MSL_p(\varvec{\mu },\varvec{\Sigma }, \varvec{\gamma })$.

Definition 7.1

Let $\varvec{X}$ be a p-dimensional continuous random vector. The distribution of $\varvec{X}$ is in the multivariate SLSM class with location parameter $\varvec{\mu }$, dispersion matrix $\varvec{\Sigma }$, skewness parameter $\varvec{\gamma }$, and if there is a random variable $W\sim h(\cdot |\varvec{w})$, a univariate CDF indexed by the parameter vector $\varvec{w}$, such that $\varvec{X}|W=w\sim MSLSM_p\left( \varvec{\mu },\kappa (w)\varvec{\Sigma },\varvec{\gamma }\right)$ with PDF

$$\begin{aligned} f_{MSLSM}(\varvec{x};\varvec{\mu },\varvec{\Sigma },\varvec{\gamma },\varvec{w})=\int _{S_h}f_{MSL}(\varvec{x};\varvec{\mu },\kappa (w)\varvec{\Sigma },\varvec{\gamma })h(\varvec{w};\varvec{\theta })dw \end{aligned}$$

(44)

for all $\varvec{x},\varvec{\gamma }\in \mathbb {R}^p, \varvec{\Sigma }>0$ and some positive scale function $\kappa (w)$Punzo and Bagnato (2022b).

From (43) and Definition 7.1 and considering the Bernoulli as a mixing distribution, the multivariate skew Bernoulli Laplace distribution follows with PDF

$$\begin{aligned} f_{MSBL}(\varvec{x};\varvec{\mu },\varvec{\Sigma },\varvec{\gamma },\theta _1,\theta _2)&= \theta _1 f_{MSL}(\varvec{x};\varvec{\mu },\varvec{\Sigma },\varvec{\gamma }) + (1-\theta _1) f_{MSL}(\varvec{x};\varvec{\mu },\theta _2\varvec{\Sigma })\nonumber \\&=\frac{\theta _1|\varvec{\Sigma }|^{-\frac{1}{2}}}{2^p\pi ^{(p-1)/2}\alpha \Gamma \left( \frac{p+1}{2}\right) }\nonumber \\&\qquad \textrm{e}^{-\alpha \sqrt{(\varvec{x}-\varvec{\mu })^T\varvec{\Sigma }^{-1}(\varvec{x}-\varvec{\mu })}+(\varvec{x}-\varvec{\mu })^T\varvec{\Sigma }^{-1}\varvec{\gamma }}\nonumber \\&\quad +\frac{(1-\theta _1)|\theta _2\varvec{\Sigma }|^{-\frac{1}{2}}}{2^p\pi ^{(p-1)/2}\alpha \Gamma \left( \frac{p+1}{2}\right) }\nonumber \\&\qquad \textrm{e}^{-\alpha \sqrt{(\varvec{x}-\varvec{\mu })^T(\theta _2\varvec{\Sigma })^{-1}(\varvec{x}-\varvec{\mu })}+(\varvec{x}-\varvec{\mu })^T(\theta _2\varvec{\Sigma })^{-1}\varvec{\gamma }} \end{aligned}$$

(45)

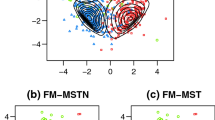
where $\varvec{x}:p\times 1, \varvec{\mu }:p\times 1 \in \mathbb {R}^p, p\ge 1$, $\varvec{\Sigma }:p\times p$ is a positive definite matrix, $\theta _1 \in (0,1)$ and $\theta _2>1$, $\varvec{\gamma }:p\times 1 \in \mathbb {R}^p$ is the skewness parameter and $\alpha =\sqrt{1+\varvec{\gamma }^T\varvec{\Sigma }^{-1}\varvec{\gamma }}$, denoted by $\varvec{X}\sim MSBL_p(\varvec{\mu },\varvec{\Sigma },\theta _1,\theta _2)$. Figure 16 illustrates (45) and (43) for $p=2$.

Fig. 16

Contour plots of (45) and (43) where $\varvec{\mu }=(0,0)^T$, $\varvec{\Sigma }=2\varvec{I}$, $\varvec{\gamma }=(- 0.5, 0.5)^T$, $\theta _1=0.6$ and $\theta _2=4$

It is clear that the MSBL distribution seems to be a promising starting point for future studies, while an investigation into multivariate extensions for other mixing distributions and their parameter estimation schemes, may also be considered. See Morris et al. (2019) for mixtures of multivariate contaminated shifted asymmetric Laplace distributions.

Appendices

$SBL_{I}$ moments

From (8), (17) and (20) it follows that

$$\begin{aligned}&\text {E}_{SBL_{{I}}}(X) =\beta \left( \theta _1+\left( 1-\theta _1\right) \theta _2\right) \left( 1-\frac{1}{(\lambda +1)^2}\right) +\mu ,\\ {}&\quad \text {Var}_{SBL_{{I}}}(X) =\beta ^2\left[ 2 \left( \theta _1+\left( 1-\theta _1\right) \theta _2^2\right) - \left( \theta _1+\left( 1-\theta _1\right) \theta _2\right) {}^2 \left( 1-\frac{1}{(\lambda -1)^2}\right) ^2\right] , \\ {}&\quad \text {Skewness}_{SBL_{{I}}}(X) =2\left( \left( \theta _1+\left( 1-\theta _1\right) \theta _2\right) {}^3 \left( 1-\frac{1}{(\lambda +1)^2}\right) ^3\right. \\ {}&\qquad \left. +3 \left( \left( 1-\theta _1\right) \theta _2^3+\theta _1\right) \left( 1-\frac{1}{(\lambda +1)^4}\right) \right. \\ {}&\qquad \left. -3 \left( \left( 1-\theta _1\right) \theta _2^2+\theta _1\right) \left( \theta _1+\left( 1-\theta _1\right) \theta _2\right) \left( 1-\frac{1}{(\lambda +1)^2}\right) \right) \\ {}&\quad \times \frac{1}{ \left( 2 \left( \left( 1-\theta _1\right) \theta _2^2+\theta _1\right) -\left( \theta _1+\left( 1-\theta _1\right) \theta _2\right) {}^2 \left( 1-\frac{1}{(\lambda +1)^2}\right) ^2\right) ^{3/2}},\\ {}&\quad \text {Kurtosis}_{SBL_{{I}}}(X) =-3 \left( \theta _1+\left( 1-\theta _1\right) \theta _2\right) {}^4 \left( 1-\frac{1}{(\lambda +1)^2}\right) ^4\\ {}&\quad +12 \left( \left( 1-\theta _1\right) \theta _2^2+\theta _1\right) \left( \theta _1+\left( 1-\theta _1\right) \theta _2\right) {}^2 \left( 1-\frac{1}{(\lambda +1)^2}\right) ^2\\ {}&\qquad -24 \left( \left( 1-\theta _1\right) \theta _2^3+\theta _1\right) \\ {}&\qquad \left( \theta _1+\left( 1-\theta _1\right) \theta _2\right) \left( 1-\frac{1}{(\lambda +1)^4}\right) \left( 1-\frac{1}{(\lambda +1)^2}\right) \\ {}&\qquad +24 \left( \left( 1-\theta _1\right) \theta _2^4{+}\theta _1\right) \\ {}&\times \frac{1}{\left( \theta _1{+} \left( 1{-}\theta _1\right) \theta _2\right) {}^4 \left( 1{-}\frac{1}{(\lambda {+}1)^2}\right) ^4{-}4 \left( \left( 1{-}\theta _1\right) \theta _2^2{+}\theta _1\right) \left( \theta _1{+}\left( 1{-}\theta _1\right) \theta _2\right) {}^2 \left( 1-\frac{1}{(\lambda {+}1)^2}\right) ^2}\\ {}&\qquad \qquad \qquad \qquad \qquad {{+}4 \left( \left( 1{-}\theta _1\right) \theta _2^2{+}\theta _1\right) {}^2}.\end{aligned}$$

EM algorithm for finite mixtures

Estimates for the finite mixtures described in Sect. 5 can be calculated by the EM algorithm. It follows that by denoting the latent variable as $\varvec{z}_i=(z_{i1},\dots ,z_{ik})$, which acts as an indicator vector, where $z_{ij}=1$ if $x_i$ comes for the jth component and $z_{ij}=0$ otherwise, the complete-data likelihood can be written as

$$\begin{aligned} L_c(\varvec{\psi })=\prod _{i=1}^{n}\prod _{j=1}^k\left[ \pi _jg_{SLSM}(x_i;\varvec{\theta }_j)\right] ^{z_{ij}} \end{aligned}$$

(46)

and from (46), the complete-data log likelihood as

$$\begin{aligned} l_c(\varvec{\psi })=l_{1c}(\varvec{\theta })+l_{2c}(\varvec{\pi }) \end{aligned}$$

(47)

where

$$\begin{aligned} l_{1c}(\varvec{\theta })=\sum _{i=1}^{n}\sum _{j=1}^{k}z_{ij}\textrm{ln}[g_{SLSM}(x_i;\varvec{\theta }_j)] \end{aligned}$$

and

$$\begin{aligned} l_{2c}(\varvec{\pi })=\sum _{i=1}^{n}\sum _{j=1}^{k}z_{ij}\textrm{ln}\pi _j. \end{aligned}$$

In order to calculate the conditional expectation of the complete-data log likelihood function

$$\begin{aligned} Q(\varvec{\theta },\varvec{\pi }|\varvec{\psi }^{(r)})&=Q_{1}(\varvec{\theta }|\varvec{\psi }^{(r)}) +Q_{2}(\varvec{\pi }|\varvec{\psi }^{(r)}) \end{aligned}$$

we need to substitute

$$\begin{aligned} \textrm{E}(Z_{ij}|x_i)&=\frac{{\pi }^{(r)}_jg_{SLSM}(x_i;\varvec{\theta }^{(r)}_j)}{m(\varvec{\psi }^{(r)})}\\&=:z_{ij}^{(r)} \end{aligned}$$

in (47). Thus, by maximizing $Q_2(\varvec{\pi }|\varvec{\psi }^{(r)})$ with respect to $\varvec{\pi }$, an update for ${\pi }_j$ is given as ${\hat{\pi }_j}^{(r+1)}=\frac{1}{n}\sum _{i=1}^{n}{{z}_{ij}^{(r)}}$, while updates for $\varvec{\theta }$ are estimated by numerically maximizing $Q_2(\varvec{\theta }|\varvec{\psi }^{(r)})$.

Skewness and kurtosis of SLSM models

See Figs. 17 and 18.

Fig. 17

Skewness of SLSM models as a function of $\lambda$

Fig. 18

Kurtosis of SLSM models as a function of $\lambda$