1 Introduction

Statistical learning and predictions are largely based on the tacit assumption of a correspondence between past and future observations. Whether there is a rational justification for this induction principle has been a long debated question, which can be traced back to the work of the renowned philosopher David Hume in the eighteenth century. In the twentieth century, de Finetti (1937) reformulates the problem in probabilistic terms: the symmetry between past and future can be postulated with an appropriate probabilistic framework through the concept of exchangeability, which requires the distribution of the observations to be invariant with respect to their order. More formally, a sequence \((X_n)_{n \ge 1}\) of observations on a Polish space \(\mathbb {X}\) is said to be exchangeable if for every \(N \in \mathbb {N}\), and for every permutation \(\pi \) of \(\{1,\dots ,N\}\),

$$\begin{aligned} (X_1,\dots , X_N) {\mathop {=}\limits ^{{\tiny {\textrm{d}}}}}(X_{\pi (1)},\dots , X_{\pi (N)}), \end{aligned}$$

where \({\mathop {=}\limits ^{{\tiny {\textrm{d}}}}}\) denotes the equality in distribution. Crucially, de Finetti proved that exchangeability is equivalent to conditional independence and identity in distribution, through the following representation theorem which goes under his name.

Theorem 1

(de Finetti Representation Theorem) A sequence \((X_n)_{n \ge 1}\) of random elements on \(\mathbb {X}\) is exchangeable if and only if there exists a probability law Q on the space \(\mathscr {P}_\mathbb {X}\) of probabilities on \(\mathbb {X}\) such that, for every \(N \in \mathbb {N}\) and any Borel sets \((A_1,\dots ,A_N)\),

$$\begin{aligned} \mathbb {P}(X_1 \in A_1,\dots , X_N \in A_N) = \int _{{\mathscr {P}}_\mathbb {X}} \prod _{i=1}^N P(A_i) \, Q(\textrm{d}P). \end{aligned}$$

Q is termed the de Finetti measure of \((X_n)_{n \ge 1}\).

The representation theorem was proved in full generality by Hewitt and Savage (1955), with compelling consequences in terms of both inference and prediction. First of all, it provides a neat justification of the Bayes–Laplace paradigm, that is, the use of a prior distribution on the model parameters for Bayesian inference. Indeed, one can rewrite the representation theorem in hierarchical form, so that for any exchangeable sequence \((X_n)_{n\ge 1}\) one can define a random probability \(\tilde{P}\) on \(\mathscr {P}_\mathbb {X}\) such that, for every \(n\in \mathbb {N}\),

$$\begin{aligned} X_i \mid \tilde{P}&{\mathop {\sim }\limits ^{{\tiny \textrm{iid}}}}\tilde{P} \qquad i=1,\dots ,n;\\ \tilde{P}&\sim Q. \end{aligned}$$

From this expression, it is apparent that the de Finetti measure Q may act as prior distribution, the latent parameter being the distribution of the data. After observing the values \(X^{(n)} = (X_1, \dots , X_n)\), one can perform Bayesian inference by finding the posterior distribution \(Q(\,\cdot \, \mid X^{(n)})\).

Moreover, de Finetti’s theorem can also be used as a technical tool for assigning explicit laws to exchangeable sequences and deriving predictive inference, the most important and fundamental kind of inductive inference according to Carnap (1950). Indeed, under the exchangeability assumption, the one-step predictions are conveniently evaluated as linear functions of the posterior distribution \(Q(\,\cdot \, \mid X^{(n)})\) as follows:

$$\begin{aligned} \mathbb {P}(X_{n+1} \in A \mid X^{(n)})= \int _{\mathscr {P}_\mathbb {X}} P(A) \, Q(\text {d}P \mid X^{(n)}), \end{aligned}$$

and similarly for m-step ahead predictions \(\mathbb {P}((X_{n+1}, \dots , X_{n+m}) \in A_m \mid X^{(n)})\).

Summing up, exchangeability guarantees an elegant and principled framework to perform inference and prediction on homogeneous observations. As for the flexibility of these models, it crucially depends on the support of the de Finetti measure Q on the space of probabilities \(\mathscr {P}_{\mathbb {X}}\). Though de Finetti had laid out the Bayesian framework in its full generality during the 1930s, for several decades, inference and predictions were confined to parametric models, that is, for priors Q that degenerate on a subclass of \(\mathscr {P}_{\mathbb {X}}\) indexed by a finite-dimensional parameter. Still in 1972, Dennis V. Lindley wrote that it is perhaps worth stopping to remark that the problem is a technical one; the Bayesian method embraces non-parametric problems but cannot solve them because the requisite tool is missing (Lindley, 1972). However, the times were ripe: Ferguson (1973) made the breakthrough with the definition of the Dirichlet process prior, which paved the way for the development of the field of Bayesian Nonparametrics (BNP). See also Ferguson (1974). The rest of this paper will outline some of the most notable uses of the Dirichlet process and highlight some effective generalizations. We start by introducing the Dirichlet process through its stick-breaking representation (Sethuraman, 1994), arguably its simplest construction though perhaps not most suitable to gain insight into its distributional properties.

Definition 1

A random probability \(\tilde{P} \sim DP (\theta , P^*)\) is distributed according to a Dirichlet process prior with concentration \(\theta >0\) and base probability \(P^* \in \mathscr {P}_\mathbb {X}\) if

$$\begin{aligned} \tilde{P} {\mathop {=}\limits ^{{\tiny {\textrm{d}}}}}\sum _{i \ge 1} \tilde{p}_i \delta _{Z_i}, \end{aligned}$$

where \(Z_i {\mathop {\sim }\limits ^{{\tiny \textrm{iid}}}}P^*\) are independent of \(\omega _i {\mathop {\sim }\limits ^{{\tiny \textrm{iid}}}}Beta (1,\theta )\), and \(\tilde{p}_i = \omega _i \prod _{j=1}^{i-1}(1- \omega _{j})\), with the convention \(\prod _{j=1}^{0}(1- \omega _{j})=1\).

For simplicity, we will throughout assume that \(P^*\) is non-atomic. Exhaustive accounts of the field can be found in the monographs (Hjort et al., 2010; Müller et al., 2015; Ghosal & van der Vaart, 2017).

2 Species discovery

In species sampling problems, a population of individuals is partitioned into different “types” or “species”, and each observation is a species label. Given an observed sample of size n, one of the main goals is predicting the number of new distinct species in a future sample of size m. There are two key elements of species sampling problems that make BNP models the natural choice: (i) since the scope of the notion of species is to group individual observations (according to some criterion of similarity), there should be a positive probability of ties among the data; (ii) since each new observation could potentially represent a new species, the model has to assign a positive probability to this event or, in other terms, incorporate a positive discovery probability at each sampling step. This BNP approach to species sampling was first laid out in Lijoi et al. (2007).

Let \(X^{(n)} = (X_1, \dots , X_n)\) be a vector of observed species labels. If one believes that the order with which the species are observed is irrelevant, assuming exchangeability is the natural choice leading to

$$\begin{aligned} X_1,\dots ,X_n \mid \tilde{P} {\mathop {\sim }\limits ^{{\tiny \textrm{iid}}}}\tilde{P}. \end{aligned}$$
(1)

In this modeling framework, it is quite natural to assume that \(\tilde{P}\) is discrete and defined as \(\tilde{P} = \sum _{i \ge 1} \tilde{p}_i \delta _{Z_i}\), where the \(\tilde{p}_j\)’s are the random species proportions in the population and the \(Z_j\)’s are the corresponding species labels such that \(Z_j{\mathop {\sim }\limits ^{{\tiny \textrm{iid}}}}P^*\) for some non–atomic base measure \(P^*\). These assumptions imply that ties may be recorded in \(X^{(n)}\) with positive probability, namely \(\mathbb P (X_i=X_j)>0\) for any \(i \ne j\). Henceforth, we will denote by \(K_n\) the total number of distinct species in the sample \(X^{(n)}\), by \(X_1^*,\dots ,X_{K_n}^*\) the unique values for the species, and by \(N_i\) the frequency of the i-th distinct species in order of appearance.

2.1 Dirichlet process

The task of learning the next species may be rephrased into finding the predictive distribution \(\mathbb P(X_{n+1} \mid X^{(n)})\). The species corresponding to the next observation \(X_{n+1}\) should have a positive probability of coinciding with the already discovered species but also a positive probability of being new. A natural probabilistic structure achieving these desiderata is obtained by taking a linear combination of one’s prior guess at the (marginal) distribution of the species labels \(P^*\) and the empirical measure. This results in a learning mechanism of the form

$$\begin{aligned} \mathbb {P}(X_{n+1} \in \cdot \mid X^{(n)})= & {} \mathbb {P}(X_{n+1} = \text {``new''} \mid X^{(n)}) \ P^*(\cdot ) \nonumber \\{} & {} + \mathbb {P}(X_{n+1} = \text {``old''}\mid X^{(n)}) \ \frac{1}{n} \sum _{i=1}^{K_n} N_i \delta _{X_i^*}(\cdot ). \end{aligned}$$
(2)

Now, if \(\tilde{P}\) is distributed according to a Dirichlet process prior (Definition 1), the corresponding predictive distributions replicate exactly (2) with

$$\begin{aligned} \mathbb {P}(X_{n+1} = \text {``new''} \mid X^{(n)}) = \frac{\theta }{\theta +n}; \quad \mathbb {P}(X_{n+1} = \text {``old''} \mid X^{(n)}) = \frac{n}{\theta +n}. \end{aligned}$$
(3)

Moreover, it can be proved (Regazzini, 1978; Lo, 1991) that the predictive distributions associated to an exchangeable sequence are a linear combination of \(P^*\) and the empirical measure \(\frac{1}{n} \sum _{i=1}^{K_n} N_i \delta _{X_i^*}\) if and only if the underlying \(\tilde{P}\) has a Dirichlet process distribution.

This predictive scheme, framed as a generative model, is known as the Blackwell–MacQueen generalized Pólya urn (Blackwell & MacQueen, 1973). Moreover, when focusing on the induced partition distribution, it reduces to the Chinese restaurant process, whose name originated from the following metaphor, attributed to L. Dubins and J. Pitman by D. Aldous. A sequence of customers arrives at a restaurant with \(X_i\) denoting the table of customer i. The first customer sits at one of the empty tables. The second customer sits at the same table (\(X_2 = X_1\)) with probability \(1/(\theta +1)\) and at a different table (\(X_2 = \text {``new''}\)) with probability \(1/(1+\theta )\), and so on. Thus, tables and species may be treated in the same way: the key feature they share is that they both determine a random partition of observations into clusters.

Let \(\Pi _k^n(n_1,\dots ,n_k)\) be the probability that a given sample \(X^{(n)}\) displays \(k \le n\) species with cardinalities \(n_1,\dots ,n_k\). Whenever \(\tilde{P}\) is an almost surely discrete distribution this can be characterized in terms of the de Finetti measure as

$$\begin{aligned} \Pi _k^n(n_1,\dots ,n_k) = {\mathbb {E}} \bigg ( \int _{\mathbb {X}^k_*} \prod _{i=1}^k \tilde{P}^{n_i}(\textrm{d}x_i) \bigg ), \end{aligned}$$
(4)

where \(\mathbb {X}^k_* = \{(x_1,\dots ,x_k) \in \mathbb {X}^k: x_i \ne x_j \text { for } i\ne j\}\), and it is referred to as the exchangeable partition probability function, a notion introduced by Pitman (1995). If \(\tilde{P}\) is sampled from a Dirichlet process this coincides with a variation of the popular Ewens sampling formula (Ewens, 1972; Antoniak, 1974), which plays a major role in population genetics and is given by

$$\begin{aligned} \Pi _k^n(n_1,\dots ,n_k) = \frac{\theta ^k}{(\theta )_n} \prod _{i=1}^k (n_i -1)!, \end{aligned}$$

where \((\theta )_n = \theta (\theta + 1)\cdots (\theta + n -1)\) denotes the n–th ascending factorial of \(\theta \) and we set \((\theta )_0 \equiv 1\). By summing (4) over all partitions of n elements into k groups, one obtains the probability of observing k distinct species in a sample of size n. Indeed,

$$\begin{aligned} \mathbb {P}(K_n = k) = \frac{\theta ^k}{(\theta )_{n}}\, \vert s(n,k)\vert , \end{aligned}$$

with \(\vert s(n,k) \vert \) the signless Stirling number of the first kind. From a modeling perspective, an important aspect is the growth rate of the number of distinct species \(K_n\) as n increases: under a Dirichlet process prior, \(K_n\) diverges with a logarithmic behavior. More specifically, as shown in Korwar and Hollander (1973), for \(n \rightarrow \infty \),

$$\begin{aligned} \frac{K_n}{\log n} {\mathop {\longrightarrow }\limits ^{\text{ a.s. }}} \theta . \end{aligned}$$

We refer to Pitman (2006), Mano (2018) and Yamato (2020) for further stimulating accounts.

2.2 Beyond the Dirichlet process

When modeling the probability of discovering a new species, one would expect this probability to depend explicitly on the number \(K_n\) of distinct species in the sample. More specifically, it is often desirable for the probability of discovering a new species to be monotonically increasing in \(K_n\), so that the probability of discovering a new species is higher if mostly distinct species have been recorded in the past, and vice versa. The Dirichlet process prior does not accommodate for this feature, as it is apparent from (3). However, other choices of the de Finetti measure allow for this modeling behavior: a popular instance is given by the two-parameter Poisson–Dirichlet process (Perman et al., 1992; Pitman, 1995; Pitman & Yor, 1997), also known as Pitman–Yor process. See Lijoi and Prünster (2010) and Müller et al. (2018) for reviews of the various classes of discrete random probability measures that share this property.

Definition 2

A random probability \(\tilde{P} \sim PY (\sigma , \theta , P^*)\) is distributed according to a Pitman–Yor process prior with discount \(\sigma \in [0,1)\), concentration \(\theta >-\sigma \), and diffuse base probability \(P^* \in \mathscr {P}_\mathbb {X}\) if

$$\begin{aligned} \tilde{P} {\mathop {=}\limits ^{{\tiny {\textrm{d}}}}}\sum _{i \ge 1} \tilde{p}_i \delta _{Z_i}, \end{aligned}$$

where \(Z_i {\mathop {\sim }\limits ^{{\tiny \textrm{iid}}}}P^*\) are independent of \(\omega _i {\mathop {\sim }\limits ^{{\tiny \textrm{ind}}}}Beta (1- \sigma , \theta + i \sigma )\), and \(\tilde{p}_i = \omega _i \prod _{j=1}^{i-1}(1- \omega _{j})\).

Clearly, the Dirichlet process represents a special case, corresponding to \(\sigma =0\). When \(\tilde{P} \sim PY (\theta , \sigma , P^*)\) is sampled from a Pitman–Yor process, the exchangeable partition probability function becomes

$$\begin{aligned} \Pi _k^n(n_1,\dots ,n_k) = \frac{\prod _{i=1}^{k-1}(\theta + i\sigma )}{(\theta + 1)_{n-1}} \prod _{i=1}^k (1 - \sigma )_{n_i - 1}. \end{aligned}$$

Moreover, the predictive distribution of a Pitman–Yor process satisfies

$$\begin{aligned} \mathbb {P}(X_{n+1} = \text {``new''} \mid X^{(n)}) = \frac{\theta + \sigma k}{\theta +n}, \end{aligned}$$

where k is the number of distinct species in the sample \(X^{(n)}\). The complete prediction scheme is of the form

$$\begin{aligned} \mathbb {P}(X_{n+1} \in \cdot \mid X^{(n)}) = \frac{\theta + \sigma k}{\theta +n} \ P^*(\cdot ) + \frac{n}{\theta +n} \ \frac{1}{n} \sum _{i=1}^{k} (N_i-\sigma ) \delta _{X_i^*}(\cdot ), \end{aligned}$$

which notably features a suitably weighted empirical measure. Depending on the value of \(\sigma \), this leads to a markedly different learning scheme, as highlighted in Fig. 1. Here, we compare the prediction of the number of new unique values \(K_m^{(n)}\) in an additional sample of size m, conditionally on \(X^{(n)}\). In particular, we consider the Bayesian nonparametric estimator for \(K_m^{(n)}\) derived in Favaro et al. (2009), that is

$$\begin{aligned} {\mathbb {E}}(K_m^{(n)} \mid X^{(n)}) = \left( k + \frac{\theta }{\sigma }\right) \left\{ \frac{(\theta + n + \sigma )_m}{(\theta + n)_m} - 1\right\} . \end{aligned}$$
(5)

We refer to Lijoi et al. (2007) and Favaro et al. (2009) for details. In the Dirichlet process case, as shown in Favaro et al. (2011), (5) reduces to

$$\begin{aligned} {\mathbb {E}}(K_m^{(n)} \mid X^{(n)}) =\sum _{i=1}^m \frac{\theta }{\theta +n+i-1}. \end{aligned}$$

A practical issue to face is the specification of the parameters \((\sigma ,\theta )\). A first convenient approach proposed in Lijoi et al. (2007) is based on empirical Bayes ideas. It consists in fixing \((\sigma ,\theta )\) to maximize the exchangeable partition probability function, so that in the Pitman–Yor case, we have

$$\begin{aligned} (\hat{\sigma }, \hat{\theta }) = \arg \max _{(\sigma ,\theta )} \left\{ \frac{\prod _{i=1}^{k-1}(\theta + i\sigma )}{(\theta + 1)_{n-1}} \prod _{i=1}^k (1 - \sigma )_{n_i - 1}\right\} . \end{aligned}$$

An alternative way of specifying \((\sigma ,\theta )\) is by placing a prior on it. However, as showcased in Lijoi et al. (2008), this often results in negligible differences for the estimates of \(K_m^{(n)}\) compared to the empirical Bayes approach, since in many practical scenarios the posterior distribution for \((\sigma ,\theta )\) is highly concentrated.

Fig. 1
figure 1

Species discovery: Bayesian nonparametric estimators \({\mathbb {E}}(K_m^{(n)} \mid X^{(n)})\) of the number of new distinct values \(K_m^{(n)}\) in an additional sample of size m, conditionally on the data \(X^{(n)}\), for a Dirichlet process (red line) and a Pitman–Yor process (blue line). The Good–Toulmin estimator (green line) is also displayed for comparison

Full size image

In order to illustrate the BNP methodology for species sampling problems we consider two real-world applications. First, we analyze a dataset of Holst (1981), which comprises \(n=204\) coins (obverse side) found in a hoard of ancient coins. They were classified according to different die types, which are the tools used to produce them and represent the “species” in this context: \(k=141\) distinct dies were recorded. The frequencies are conveniently summarized in terms of the number of “species” of a given size, i.e., \(r_i\) represents the number of species with frequency i, and we have \((r_1,r_2,r_3,r_4,r_5,r_6,r_7) = (102, 26, 8, 2, 1, 1, 1)\). The goal is to predict the number of new dies one may observe in a future hoard of coins. We adopt the BNP estimators \({\mathbb {E}}(K_m^{(n)} \mid X^{(n)})\) with empirical Bayes elicitation of \((\sigma ,\theta )\), which yields the parameter specifications \(\hat{\theta } = 200.65\) for the Dirichlet process and \((\hat{\sigma },\hat{\theta }) = (0.11, 172.48)\) for the Pitman–Yor process. The two BNP estimators are compared to the Good–Toulmin estimator (Good & Toulmin, 1956; Mao, 2004), which is one of the most popular frequentist estimators. It is well known that the Good–Toulmin estimator usually provides reliable predictions for \(m<n\), that is, if the additional sample over which predictions are made is not larger than the observed sample, whereas for values \(m > n\) it often shows an erratic behavior. All three estimators are depicted in Fig. 1a. The Dirichlet process and the Pitman–Yor process behave similarly. This is not surprising since the empirical Bayes estimate favors a low value for the discount parameter (\(\hat{\sigma } = 0.11\)), and we recall that the Pitman–Yor process reduces to the Dirichlet process if \(\sigma =0\). Moreover, we highlight that they both resemble the behavior of the Good–Toulmin estimator when m is smaller than the observed sample size. For larger values of m, the Good–Toulmin estimator becomes erratic, whereas this is not the case for the BNP estimators since they rely on principled probabilistic models.

Our second application concerns the genomic dataset FlavFr1: it comprises 1593 expressed sequence tags (ESTs) of a cDNA library obtained from the fruits of citrus clementina. These are categorized into 806 different genes with \(r_i = 561, 148, 37, 18, 6, 5, 12, 1, 1, 3, 1, 2\) for \(i\in \{1,\dots ,12\}\), and \(r_i = 3, 2, 1, 1, 1, 1, 1, 1\), for \(i\in \{14, 15, 16, 19, 22, 23, 58, 117 \}\). As before, we aim to predict the number of new genes in a future sample; the empirical Bayes specification yields \(\hat{\theta } = 651.05\) and \((\hat{\sigma },\hat{\theta }) = (0.63, 110.24)\) for the Dirichlet and the Pitman–Yor processes, respectively. The corresponding estimators together with the Good–Toulmin estimator are depicted in Fig. 1b. In this case, there are striking differences between the estimators obtained from the Dirichlet and the Pitman–Yor processes. This is due to the data favoring a large value for the discount parameter (\(\hat{\sigma } = 0.63\)), setting the Pitman–Yor case far apart from the Dirichlet process case (\(\hat{\sigma } = 0\)). This clearly showcases the usefulness of the additional flexibility of the Pitman–Yor process, which allows for polynomial growth rates controlled by the parameter \(\sigma \). Once again, the Good–Toulmin estimator diverges for large values of m. However, for moderately large values of m it nicely resembles the predictions of the Pitman–Yor estimator. This further underpins the need to go beyond the Dirichlet process in species sampling contexts. Further instances of applications requiring nonparametric priors with polynomial growth rate, or equivalently power law tail behavior, can be found in Hoshino (2001), Teh (2006), Caron (2012) and Caron and Fox (2017).

3 Mixture models

The Dirichlet and Pitman–Yor process priors are laws for almost surely discrete random probabilities. This implies that, when used as de Finetti measures, the induced exchangeable observations (1) will have a positive probability of being equal, i.e., \(\mathbb {P}(X_i = X_j)>0\) for every i, j. Thus, different models should be considered whenever the data do not display ties. A popular strategy is to model a random density function through a kernel mixture. Let f be a probability density kernel and \(\tilde{P}\) be an almost surely discrete random probability. The random probability density is then defined as

$$\begin{aligned} \tilde{f}(y) = \int _{\mathbb {X}} f(y \mid x) \tilde{P} (\textrm{d}x). \end{aligned}$$

Using the law \(Q_f\) of \(\tilde{f}\) as de Finetti measure, the law of induced exchangeable observations \((Y_i)_{i \ge 1}\) may be equivalently described in hierarchical form as

$$\begin{aligned} Y_i \mid X_i, \tilde{P}&{\mathop {\sim }\limits ^{{\tiny \textrm{ind}}}}f(\cdot \mid X_i) \qquad&i=1,\dots ,n; \\ X_i \mid \tilde{P}&{\mathop {\sim }\limits ^{{\tiny \textrm{iid}}}}\tilde{P} \qquad&i=1,\dots ,n; \\ \tilde{P}&\sim Q,&\end{aligned}$$

where the latent variable \(X_i\) represents the parameter of the probability density from which \(Y_i\) is sampled. Kernel mixtures over a Dirichlet process have been introduced in Lo (1984) and later extended to more general mixing measures, including the Pitman–Yor process (Ishwaran & James, 2001). See Müller and Quintana (2004), Barrios et al. (2013) and De Blasi et al. (2015) for reviews. Arguably, kernel mixtures over discrete random probabilities are the most popular Bayesian nonparametric models. This is because they allow one to perform two important statistical tasks at once: (i) flexible density estimation, which avoids parametric constraints and adapts to any data generating distribution; (ii) model-based clustering, which exempts from fixing the number of clusters a priori. Indeed, due to the discreteness of \(\tilde{P}\), any sample from the posterior distribution of the latent variables \(X_i\) given \(Y_{(n)}\) has \(K_n \in \{1,\dots , n\}\) distinct values. This automatically partitions the n observed data into \(K_n\) clusters, with two observations \(Y_i\) and \(Y_j\) belonging to the same cluster if they are sampled from the same mixture component, i.e., if \( f(\cdot \mid X_i) = f(\cdot \mid X_j)\) a posteriori.

Fig. 2
figure 2

Mixture models. Nonparametric density estimation using a synthetic dataset of \(n = 300\) observations from a mixture of Gaussians \(1/4\, \textrm{N}(-1, 1/4^2) + 1/2\, \textrm{N}(0, 1/4^2) + 1/4\, \textrm{N}(1, 1/4^2)\), under the Dirichlet process (red lines) and the Pitman–Yor process (blue lines)

Full size image

Different discrete nonparametric priors induce different distributions for the number of clusters \(K_n\). Given the important role played by \(K_n\) for the probabilistic clustering, when eliciting the prior this aspect should be taken into account. In the same way, the posterior distribution of \(\tilde{P}\) given the data \(Y^{(n)}\) will induce a posterior distribution \(\mathscr {L}(K_n \mid Y^{(n)})\), providing both point estimates and uncertainty quantification on the number of clusters in the data. In practice, posterior computations are customarily carried out using Markov Chain Monte Carlo, an avenue first explored in Escobar and West (1995). This is a highly non-trivial task, since it entails exploring the partition space. To address this issue, several computational methods have been proposed over the years. Another practical concern is the choice of the baseline distribution \(P^*\), which is known to have a significant impact on \(\mathscr {L}(K_n \mid Y^{(n)})\). See Richardson and Green (1997). However, this equally affects parametric and nonparametric specifications.

In Fig. 2, we consider synthetic data generated from a finite mixture of normal distributions with three components, and the estimates resulting from a normal mixture model with Dirichlet and Pitman–Yor process as mixing measures. We consider a highly miss-specified scenario, where the expected number of clusters a priori is about 34, significantly larger than the true number of mixing components (three). This leads to consider a Dirichlet process with \(\theta = 10\), whereas for the Pitman–Yor process infinite combinations of \(\sigma \) and \(\theta \) are possible: we set \(\sigma =0.6\) to highlight the role of \(\sigma \), and this results in \(\theta = 0.026\). In particular, the plot displays the prior and posterior distributions of the number of clusters in Fig. 2a, and the posterior densities in Fig. 2b. For both models, the posterior distribution moves away from the prior miss-specification. However, in the Pitman–Yor case, this correction is stronger leading to more accurate posterior inference on the number of clusters. The robustness of the clustering with respect to prior miss-specifications represents a highly appealing feature of Pitman–Yor process mixtures. In contrast, both models lead to highly accurate but essentially indistinguishable posterior densities. This is due to the lack of identifiability of the number of mixture components in a mixture density: one can always fit a mixture density with more components than needed.

4 Borrowing of information

In the previous sections, we focused on exchangeable models, which translate a notion of homogeneity in the data. Yet, there are many situations where this can be seen as a restrictive assumption. In de Finetti’s words (de Finetti, 1938) ‘But the case of exchangeability can only be considered as a limiting case: the case in which this “analogy" is, in a certain sense, absolute for all events under consideration’.More specifically, one may wish to generalize exchangeability to the case where data is collected under different experimental conditions, such that one retains homogeneity within each experiment though allowing for heterogeneity across different experiments. Typical examples include topic modeling, meta-analysis, two-sample problems, nonparametric regression, time-dependent data, and change point problems, to mention a few. A natural probabilistic framework that achieves this is partial exchangeability, as defined below. To simplify the notation, we focus on two groups of observations, though all the contents of this section may be easily extended to an arbitrary number of groups.

Definition 3

An array \((\varvec{X}_1, \varvec{X}_2) = (X_{1,j}, X_{2,j})_{j \ge 1}\) is partially exchangeable if for any \(N_1, N_2 \ge 1\), \(\pi \) permutation of \(\{1,\dots ,N_1\}\), and \(\phi \) permutation of \(\{1,\dots ,N_2\}\),

$$\begin{aligned} (X_{1,1},\ldots ,X_{1,N_1},X_{2,1},\ldots ,X_{2,N_2}){\mathop {=}\limits ^{{\tiny {\textrm{d}}}}}(X_{1,\pi (1)},\ldots ,X_{1,\pi (N_1)},X_{2,\phi (1)},\ldots ,X_{2,\phi (N_2)}). \end{aligned}$$

Partially exchangeable sequences may be characterized as conditionally independent through an extension of de Finetti’s representation theorem. Specifically, \((\varvec{X}_1, \varvec{X}_2)\) is partially exchangeable if and only if there exists a probability distribution Q on \(\mathscr {P}_{\mathbb {X}} \times \mathscr {P}_{\mathbb {X}}\) such that

$$\begin{aligned} {}&{} \mathbb {P} (X_{1,1}\in A_1, \ldots , X_{1,N_1}\in A_{N_1}, X_{2,1}\in B_1, \ldots , X_{2,N_2}\in B_{N_2}) \\{}&{} \quad =\int _{\mathscr {P}_{\mathbb {X}} \times \mathscr {P}_{\mathbb {X}}}\prod _{i=1}^{N_1} P_1(A_i)\, \prod _{j=1}^{N_2} P_2(B_j)\, Q(\text {d}P_1,\text {d}P_2). \end{aligned}$$

Equivalently, there exists a vector of dependent random probabilities \((\tilde{P}_1, \tilde{P}_2)\) such that

$$\begin{aligned} (X_{1,i}, X_{2,j}) \mid (\tilde{P}_1, \tilde{P}_2)&{\mathop {\sim }\limits ^{{\tiny \textrm{iid}}}}\tilde{P}_1 \times \tilde{P}_2 \qquad&\forall i,j \ge 1; \\ (\tilde{P}_1, \tilde{P}_2)&\sim Q. \end{aligned}$$

We observe that the dependence between random probabilities induces dependence between the sequences \(\varvec{X}_1, \varvec{X}_2\) of (exchangeable) observations, with two extreme scenarios: when \(\tilde{P}_1\) and \(\tilde{P}_2\) are independent, so are \(\varvec{X}_1\) and \(\varvec{X}_2\); when \(\tilde{P}_1 = \tilde{P}_2 = \tilde{P}\) almost surely, \(\varvec{X}_1, \varvec{X}_2\) are (fully) exchangeable, as it is clear by comparing the “degenerate" form of de Finetti’s representation theorem to the one for exchangeable sequences (1). Thus, we can interpret partial exchangeability as a dependence assumption on the observables that ranges from independence to exchangeability.

The use of partially exchangeable sequences for statistical purposes has been pioneered by Cifarelli and Regazzini (1978) and MacEachern (1999, 2000). To this end, one needs to build dependent random probability measures (see Quintana et al., 2022 for a recent review) with two key features in mind: (i) mathematical tractability, which corresponds to obtaining manageable representations for the posterior and/or the marginal structure, i.e., the partition distribution or the prediction rule; (ii) the ability to control the amount of dependence, since this is directly linked to the borrowing of information between the two groups: the more the dependence, the more information will be shared across the two groups. This is usually done by expressing the linear correlation between pairwise set-wise evaluations, \(\text {Cor}(\tilde{P}_1(A), \tilde{P}_2(A))\) for any Borel set A, and has been recently extended to an arbitrary number of groups by relying on the Wasserstein distance (Catalano et al., 2021a, b).

Fig. 3
figure 3

Borrowing of information: nonparametric density estimation using a Hierarchical Dirichlet process for two groups of synthetic observations with 15 and 200 data points, respectively

Full size image

There are many proposals in the literature that share both these features. We divide them into three categories: hierarchical structures (e.g., Teh, 2006; Teh & Jordan, 2010; Camerlenghi et al., 2017, 2019, 2021), nested structures (e.g., Rodríguez et al., 2008; Camerlenghi et al., 2019; Lijoi et al., 2023), and multivariate Lévy structures (e.g., Epifani & Lijoi, 2010; Lijoi et al., 2014a, b; Griffin & Leisen, 2017; Lau & Cripps, 2022).

Partial exchangeability represents the ideal probabilistic framework in many contexts. We showcase this by means of the hierarchical Dirichlet process mixture model (Teh et al., 2006), which is among the most popular and intuitive ways of introducing dependence between random probabilities and also enjoys attractive frequentist asymptotic properties (Catalano et al., 2022). We define \((\tilde{P}_1, \tilde{P}_2)\) to be distributed according to a hierarchical Dirichlet process prior if for \(\alpha , \alpha ^*>0\) and \(P^*\) a diffuse probability measure on \(\mathbb {X}\) such that

$$\begin{aligned} (\tilde{P}_1, \tilde{P}_2) \mid \tilde{P}_0&{\mathop {\sim }\limits ^{{\tiny \textrm{iid}}}}DP (\alpha , \tilde{P}_0);\\ \tilde{P}_0&\sim DP (\alpha ^*, P^*). \end{aligned}$$

We will use the notation \((\tilde{P}_1, \tilde{P}_2)\sim HDP (\alpha , \alpha ^*, P^*)\).

Different levels of dependence may be achieved by tuning the concentration hyperparameters \(\alpha , \alpha ^*>0\) of the HDP. The corresponding correlation structure is

$$\begin{aligned} Cor (\tilde{P}_1(A), \tilde{P}_2(A)) = \frac{\alpha + 1}{\alpha + 1 + \alpha ^*}, \end{aligned}$$

which remarkably does not depend on the set A nor on the base probability \(P^*\). Starting from a hierarchical Dirichlet process, one can use it to induce dependence between mixture densities in a natural way, that is,

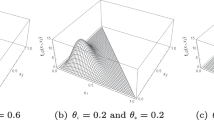
$$\begin{aligned} (Y_{1,i}, Y_{2,j}) \mid (X_{1,i}, X_{2,j}, \tilde{P}_1, \tilde{P}_2)&{\mathop {\sim }\limits ^{{\tiny \textrm{ind}}}}f(\cdot \mid X_{1,i}) \times f(\cdot \mid X_{2,j}) \qquad&\forall i,j \ge 1; \\ (X_{1,i}, X_{2,j}) \mid (\tilde{P}_1, \tilde{P}_2)&{\mathop {\sim }\limits ^{{\tiny \textrm{iid}}}}\tilde{P}_1 \times \tilde{P}_2 \qquad&\forall i,j \ge 1; \\ (\tilde{P}_1, \tilde{P}_2)&\sim HDP (\alpha , \alpha ^*, P^*).&\end{aligned}$$

To test the performance of the HDP in terms of borrowing of information we consider synthetic data generated from mixtures of three normal distributions. More specifically, the first group of \(n_1 = 15\) synthetic observations are iid from the mixture \(0.6\, \textrm{N}(-0.8, 0.2^2) + 0.3\, \textrm{N}(0, 0.2^2) + 0.1\, \textrm{N}(0.8, 0.2^2)\), whereas the second group of \(n_2 = 200\) observations are iid from the mixture \(0.575\, \textrm{N}(-0.8, 0.2^2) + 0.275\, \textrm{N}(0, 0.2^2) + 0.15\, \textrm{N}(0.8, 0.2^2)\). In other words, the two mixtures have the same scale and location parameters, but different probability weights. Moreover, the two groups of observations have markedly different sample sizes. As for the HDP model, we compare two different scenarios. We tune the parameters to achieve different values for the correlation, namely 0.09 and 0.91, corresponding to, respectively, weakly and highly dependent specifications. Among the infinite choices for \(\alpha \) and \(\alpha ^*\) that induce the aforementioned values for the correlation, in both cases we select those that lead to an overall prior expected number of clusters among the two groups approximately equal to 7.5. This allows for a fair comparison of the two models. The resulting parameters are \(\alpha =1\) and \(\alpha ^*=20\) for the weakly and \(\alpha =19\) and \(\alpha ^*=2\) highly dependent HPD. In Fig. 3 we display the corresponding mean posterior densities

$$\begin{aligned} {\mathbb {E}}\left( \int _{\mathbb {X}} f(y \mid x) \tilde{P}_j (\textrm{d}x) \bigg \vert \, Y_{1,1},\dots ,Y_{1,15}, Y_{2,1},\dots ,Y_{2,200}\right) . \end{aligned}$$

As in the exchangeable case, posterior computations are based on Markov Chain Monte Carlo, leveraging specialized algorithms such as Lijoi et al. (2020).

The plots in Fig. 3 highlight the crucial role of the specification of the dependence structure. In the case of an HDP with weak dependence (Fig. 3b), the data of the first group (left panel) are not sufficiently informative to discover the existence of a third mixture component. Conversely, when we impose a stronger dependence (Fig. 3c), the data of the first group can effectively borrow strength from the second, whose sample size is much larger and therefore contains more information. As a result, the correct number of mixture components is recovered, despite the limited sample size of the first group. Moreover, the borrowing of information is also apparent from the credible intervals: a larger borrowing of information greatly reduces the uncertainty around the point estimator for the first group.