Inference on high-dimensional mean vectors under the strongly spiked eigenvalue model

Abstract

In this paper, we discuss inference problems on high-dimensional mean vectors under the strongly spiked eigenvalue (SSE) model. First, we consider one-sample test. In order to avoid huge noise, we derive a new test statistic by using a data transformation technique. We show that the asymptotic normality can be established for the new test statistic. We give an asymptotic size and power of a new test procedure and investigate the performance theoretically and numerically. We apply the findings to the construction of confidence regions on the mean vector under the SSE model. We further discuss multi-sample problems under the SSE models. Finally, we demonstrate the new test procedure by using actual microarray data sets.

Introduction

In this paper, we consider statistical inference on mean vectors in the high-dimension, low-sample-size (HDLSS) context. Let ${\varvec{x}}_{1}, \ldots , {\varvec{x}}_{n}$ be a random sample of size $n (\ge 4)$ from a p-variate distribution with an unknown mean vector ${\varvec{\mu }}$ and unknown covariance matrix ${\varvec{\varSigma }}$. In the HDLSS context, the data dimension p is very high and n is much smaller than p. We define the eigen-decomposition of ${\varvec{\varSigma }}$ by ${\varvec{\varSigma }}={\varvec{H}}{\varvec{\varLambda }}{\varvec{H}}^T$, where ${\varvec{\varLambda }}=\hbox {diag}(\lambda _{1},\ldots ,\lambda _{p})$ is a diagonal matrix of eigenvalues, $\lambda _{1}\ge \cdots \ge \lambda _{p}\ge 0$, and ${\varvec{H}}=[{\varvec{h}}_{1},\ldots ,{\varvec{h}}_{p}]$ is an orthogonal matrix of the corresponding eigenvectors. We write the sample mean vector and the sample covariance matrix as ${\overline{{\varvec{x}}}}=\sum _{j=1}^{n}{{\varvec{x}}_{j}}/{n}$ and ${\varvec{S}}=\sum _{j=1}^{n}({\varvec{x}}_{j}-{\overline{{\varvec{x}}}})({\varvec{x}}_{j}-{\overline{{\varvec{x}}}})^T/(n-1)$.

In this paper, we discuss the one-sample test:

$$\begin{aligned} H_0:\ {\varvec{\mu }}={\varvec{\mu }}_0 \quad \hbox {vs.} \quad H_1:\ {\varvec{\mu }}\ne {\varvec{\mu }}_0, \end{aligned}$$

(1)

where ${\varvec{\mu }}_{0}$ is a candidate mean vector. We assume ${\varvec{\mu }}_0={\varvec{0}}$ without loss of generality. One should note that Hotelling’s $T^2$-statistic defined by

$$\begin{aligned} T^2=n^{-1}{\overline{{\varvec{x}}}}^T{\varvec{S}}^{-1}{\overline{{\varvec{x}}}} \end{aligned}$$

is not available because ${\varvec{S}}^{-1}$ does not exist in the HDLSS context. Dempster (1958, 1960) and Srivastava (2007) considered the test when ${\varvec{X}}$ is Gaussian. When ${\varvec{X}}$ is non-Gaussian, Bai and Saranadasa (1996) considered the test. They considered a test statistic defined by

$$\begin{aligned} T_{\mathrm{BS}}=\Vert {\overline{{\varvec{x}}}}\Vert ^2 -\text{ tr }({\varvec{S}})/n, \end{aligned}$$

(2)

where $\Vert \cdot \Vert$ denotes the Euclidean norm. Let $\varDelta =\Vert {\varvec{\mu }}\Vert ^2$. Note that $E(T_{\mathrm{BS}})=\varDelta$ and $\text{ Var }(T_{\mathrm{BS}})=K$, where $K=K_{1}+K_{2}$ having

$$\begin{aligned} K_{1}=2 \frac{\text{ tr }\left( {\varvec{\varSigma }}^2 \right) }{n(n-1)} \ \hbox { and } \ K_{2}=4\frac{{\varvec{\mu }}^T{\varvec{\varSigma }}{\varvec{\mu }}}{n }. \end{aligned}$$

Let us consider the following eigenvalue condition:

$$\begin{aligned} \frac{\lambda _{1}^2}{ \text{ tr }({\varvec{\varSigma }}^2)}\rightarrow 0 \ \hbox { as }p\rightarrow \infty . \end{aligned}$$

(3)

Let

$$\begin{aligned} m=\min \{p,n\}. \end{aligned}$$

Under (3), $H_0$ and some regularity conditions, Bai and Saranadasa (1996) and Aoshima and Yata (2015) showed the asymptotic normality as follows:

$$\begin{aligned} T_{\mathrm{BS}}/K_1^{1/2}\ \Rightarrow N(0,1) \hbox { as } m \rightarrow \infty . \end{aligned}$$

(4)

Here, "$\Rightarrow$" denotes the convergence in distribution and N(0, 1) denotes a random variable distributed as the standard normal distribution.

Aoshima and Yata (2018a) called the eigenvalue condition (3) the “non-strongly spiked eigenvalue (NSSE) model” and drew attention that high-dimensional data do not fit the NSSE model on several occasions. In order to overcome this inconvenience, Aoshima and Yata (2018a) proposed the “strongly spiked eigenvalue (SSE) model” defined by

$$\begin{aligned} \liminf _{p\rightarrow \infty }\left\{ \frac{\lambda _{1}^2}{\text{ tr }\left( {\varvec{\varSigma }}^2 \right) }\right\} >0 \end{aligned}$$

(5)

and gave a data transformation technique from the SSE model to the NSSE model.

Remark 1

When we consider a spiked model such as

$$\begin{aligned} \lambda _{r}=a_{r}p^{\alpha _{r}}\ (r=1,\ldots ,t)\quad \hbox {and}\quad \lambda _{r}=c_{r}\ (r=t+1,\ldots ,p) \end{aligned}$$

(6)

with positive and fixed constants, $a_{r}$s, $c_{r}$s and $\alpha _{r}$s, and a positive and fixed integer t. Note that the NSSE condition (3) is met when $\alpha _{1}<1/2$. On the other hand, the SSE condition (5) is met when $\alpha _{1}\ge 1/2$. We emphasize that high-dimensional data often have the SSE model. For instance, when we analyze a microarray data, we find several gene networks in which genes in the same network are highly correlated each other. The high correlation is one of the reasons why strongly spiked eigenvalues appear in high-dimensional data analysis.

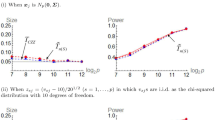
Let us show a toy example about the asymptotic null distribution of $T_{\mathrm{BS}}$ in (4). We set $p=2000$ and $n=90$. We assumed that ${\varvec{X}}$ is Gaussian as $N_{p}({\varvec{0}}, {\varvec{\varSigma }})$ under $H_0:\ {\varvec{\mu }}={\varvec{0}}$. We set ${\varvec{\varSigma }}= \hbox {diag}(p^{\alpha _{1}},p^{\alpha _{2}},1,\ldots ,1)$ and considered two cases:

$$\begin{aligned} \hbox {(i)}\ (\alpha _1,\alpha _2)=(1/3, 1/4) \quad \hbox {and} \quad \hbox {(ii)}\ (\alpha _1,\alpha _2)=(2/3, 1/2). \end{aligned}$$

Note that (i) is a NSSE model and (ii) is a SSE model. We generated independent pseudo-random observations for each case and calculated $T_{\mathrm{BS}}/K_{1}^{1/2}$ 1000 times. In Fig. 1, we gave histograms for (i) and (ii). One can observe that $T_{\mathrm{BS}}/K_{1}^{1/2}$ does not converge to N(0, 1) in case (ii).

Fig. 1

The histograms of $T_{\mathrm{BS}}/K_{1}^{1/2}$ for a NSSE model (i) and for a SSE model (ii) when $(p,n)=(2000,90)$. The solid line denotes the p.d.f. of N(0, 1)

It is necessary to develop a new test statistic instead of $T_{\mathrm{BS}}$ for the SSE model. Katayama et al. (2013) gave a test statistic and showed that it has an asymptotic null distribution as a $\chi ^2$-distribution when ${\varvec{X}}$ is Gaussian. When ${\varvec{X}}$ is non-Gaussian, Ishii et al. (2016) gave a different test statistic by using the noise reduction (NR) method due to Yata and Aoshima (2012) and provided an asymptotic non-null distribution to discuss the size and power when $p \rightarrow \infty$ while n is fixed. However, the performance of those test statistics is not always preferable because they are heavily influenced by strongly spiked eigenvalues and the variance of their statistics becomes very large because of the huge noise.

In this paper, we avoid the huge noise by using the data transformation technique and construct a new test procedure for the SSE model. The organization of this paper is as follows. In Sect. 2, we consider one-sample test and give a new test statistic by the data transformation. We show that the asymptotic normality can be established for the new test statistic. We give an asymptotic size and power of a new test procedure and investigate the performance theoretically and numerically. In Sect. 3, we apply the findings to the construction of confidence regions on the mean vector under the SSE model. In Sect. 4, we further discuss multi-sample problems under the SSE models. Finally, in Sect. 5, we demonstrate the new test procedure by using actual microarray data sets.

High-dimensional one-sample test by data transformation

In this section, we give a new test statistic by the data transformation and show that the asymptotic normality can be established for the new test statistic. We provide an asymptotic size and power of a new test procedure and investigate the performance theoretically and numerically.

Assumptions

We write the square root of ${\varvec{M}}$ as ${\varvec{M}}^{1/2}$ for any positive-semidefinite matrix ${\varvec{M}}$. Let

$$\begin{aligned} {\varvec{x}}_{l}={\varvec{H}}{\varvec{\varLambda }}^{1/2}{\varvec{z}}_{l}+{\varvec{\mu }}, \end{aligned}$$

where ${\varvec{z}}_{l}=(z_{1l},\ldots ,z_{pl})^T$ is considered as a sphered data vector having the zero mean vector and identity covariance matrix. Similar to Bai and Saranadasa (1996) and Chen and Qin (2010), we assume the following assumption as necessary:

• (A-i) $\displaystyle \limsup _{p\rightarrow \infty } E(z_{rl}^4)<\infty$ for all r, $E( z_{rl}^2z_{sl}^2)=E( z_{rl}^2)E(z_{sl}^2)=1$, $E( z_{rl}z_{sl}z_{tl})=0$ and $E( z_{rl} z_{sl}z_{tl}z_{ul})=0$ for all $r \ne s,t,u$.

When ${\varvec{x}}_l$s are Gaussian, (A-i) naturally holds. Let

$$\begin{aligned} \varPsi _{r} =\text{ tr }\left( {\varvec{\varSigma }}^2 \right) -\sum _{s=1}^{r-1}\lambda _{s}^2 = \sum _{s=r}^p\lambda _{s}^2\quad \hbox {for }r=1,\ldots ,p. \end{aligned}$$

Similar to Aoshima and Yata (2018a), we assume the following model:

• (A-ii) There exists a fixed integer $k\ (\ge 1)$ such that

  • (i) When $k\ge 2$, $\lambda _{1},\ldots ,\lambda _{k}$ are distinct in the sense that

    $$\begin{aligned} \liminf _{p\rightarrow \infty }(\lambda _{r}/\lambda _{s}-1)>0 \ \hbox { for } 1\le r<s\le k; \end{aligned}$$

  • (ii) $\lambda _{k}$ and $\lambda _{k+1}$ satisfy

    $$\begin{aligned} \liminf _{p\rightarrow \infty }\frac{\lambda _{k }^2}{\varPsi _{k} }>0 \ \ \hbox {and} \ \ \frac{\lambda _{k+1}^2}{ \varPsi _{k+1} }\rightarrow 0 \ \hbox { as } p\rightarrow \infty . \end{aligned}$$

Note that (A-ii) is one of the SSE models. For example, (A-ii) holds when the spiked model in (6) has the constants such that

$$\begin{aligned}&\alpha _{1}\ge \cdots \ge \alpha _{k}\ge 1/2>\alpha _{k+1}\ge \cdots \ge \alpha _{t} \ \hbox { and }\\&a_{r}\ne a_{s} \ \hbox { for } \ 1\le r< s\le k. \end{aligned}$$

Remark 2

For instance, one may consider a ($k+1$)-mixture model as a SSE model having k strongly spiked eigenvalues ($\alpha _k\ge 1/2$). See Sect. 5.1 in Aoshima and Yata (2018b) and Sect. 3 in Yata and Aoshima (2015) for the details.

Data transformation

According to Aoshima and Yata (2018a, b), we consider transforming the data from the SSE model to the NSSE model using the projection matrix

$$\begin{aligned} {\varvec{A}}={\varvec{I}}_p-\sum _{j=1}^{k}{\varvec{h}}_{j}{\varvec{h}}_{j}^T=\sum _{j=k+1}^{p}{\varvec{h}}_{j}{\varvec{h}}_{j}^T. \end{aligned}$$

We have that $E({\varvec{A}}{\varvec{x}}_j)={\varvec{A}}{\varvec{\mu }}\ (={\varvec{\mu }}_{*},\ \hbox {say})$ and

$$\begin{aligned} \text{ Var }({\varvec{A}}{\varvec{x}}_j)={{\varvec{A}}}{\varvec{\varSigma }}{{\varvec{A}}}=\sum _{j=k+1}^p\lambda _{j}{\varvec{h}}_{j}{\varvec{h}}_{j}^T\ (={\varvec{\varSigma }}_{*},\ \hbox {say}). \end{aligned}$$

Note that $\text{ tr }({\varvec{\varSigma }}_{*}^2)=\varPsi _{k+1}$ and $\lambda _{\max }({\varvec{\varSigma }}_{*})=\lambda _{k+1}$, where $\lambda _{\max }({\varvec{\varSigma }}_{*})$ denotes the largest eigenvalue of ${\varvec{\varSigma }}_{*}$. Then, it holds that

$$\begin{aligned} \lambda _{\max }^2({\varvec{\varSigma }}_{*})/\text{ tr }({\varvec{\varSigma }}_{*}^2)\rightarrow 0 \ \ \hbox {as }p\rightarrow \infty \hbox { under (A-ii)}. \end{aligned}$$

Thus, the transformed data has the NSSE model.

By using the transformed data, we consider the following quantity:

$$\begin{aligned} {T}_{\mathrm{DT}}& = \Vert {\varvec{A}}{\overline{{\varvec{x}}}} \Vert ^{2}-\frac{\text{ tr }({\varvec{A}}{\varvec{S}})}{n} =2 \frac{\sum _{ l<l' }^{n}{\varvec{x}}_{l}^T{\varvec{A}}{\varvec{x}}_{l'} }{n(n-1)}\\& = 2 \frac{\sum _{ l<l' }^{n}\big ({\varvec{x}}_{l}^T{\varvec{x}}_{l'}-\sum _{j=1}^k x_{jl}x_{jl'} \big )}{n(n-1)}, \end{aligned}$$

where

$$\begin{aligned} x_{jl}= {\varvec{h}}_j^T{\varvec{x}}_l \ \hbox { for all }j,l. \end{aligned}$$

Let $\varDelta _*=\Vert {\varvec{\mu }}_{*}\Vert ^2$. Note that $E({T}_{\mathrm{DT}})=\varDelta _*$ and $\text{ Var }({T}_{\mathrm{DT}})=K_*$, where $K_*=K_{1*}+K_{2*}$ having

$$\begin{aligned} K_{1*}=2 \frac{\text{ tr }({\varvec{\varSigma }}_{*}^2)}{n(n-1)} \ \hbox { and } \ K_{2*}=4\frac{{\varvec{\mu }}_{*}^T{\varvec{\varSigma }}_{*}{\varvec{\mu }}_{*}}{n }. \end{aligned}$$

Under (A-ii), we consider the following conditions as necessary:

• (A-iii) $\displaystyle \limsup _{m\rightarrow \infty }\frac{\varDelta _*^2}{K_{1*}}<\infty$;    (A-iv) $\displaystyle \frac{ K_{1*}}{\varDelta _*^2}\rightarrow 0$ as $m\rightarrow \infty$.

We note that (A-iii) is met under $H_0$ in (1). Also, note that $K_{2*}/K_{1*}=o(1)$ under (A-ii) and (A-iii), and $K_{2*}/\varDelta ^2=o(1)$ under (A-iv) from the facts that $K_{2*}\le 4 \varDelta _* \lambda _{k+1}/n=O( \varDelta _*K_{1*}^{1/2})$ and $\varDelta _* \lambda _{k+1}/n=o(K_{1*})$ under (A-ii) and (A-iii). Then, we have the following results.

Proposition 1

Assume (A-i) to (A-iii). Then, it holds that as $m\rightarrow \infty$

$$\begin{aligned} \frac{{T}_{\mathrm{DT}}-\varDelta _*}{K_*^{1/2}}= \frac{{T}_{\mathrm{DT}}-\varDelta _*}{K_{1*}^{1/2}}+o_P(1) \Rightarrow N(0,1). \end{aligned}$$

Proposition 2

Assume (A-ii) and (A-iv). Then, it holds that as $m\rightarrow \infty$

$$\begin{aligned} \frac{{T}_{\mathrm{DT}}}{\varDelta _*}=1+o_P(1). \end{aligned}$$

New test statistic and its asymptotic properties

Based on $T_{\mathrm{DT}}$, we define the test statistic as follows:

$$\begin{aligned} {\widehat{T}}_{\mathrm{DT}}&=2\frac{\sum _{l<l'}^{n}\Big ( {\varvec{x}}_{l}^T{\varvec{x}}_{l'}-\sum _{j=1}^{k} {\tilde{x}}_{jl}{\tilde{x}}_{jl'}\Big )}{n(n-1)} \nonumber \\&=\Vert {\overline{{\varvec{x}}}}\Vert ^2-\text{ tr }({\varvec{S}})/n-2\frac{\sum _{l<l'}^{n}\sum _{j=1}^{k} {\tilde{x}}_{jl}{\tilde{x}}_{jl'}}{n(n-1)}, \end{aligned}$$

(7)

where ${\tilde{x}}_{jl}$ is a certain estimator of $x_{jl}$. We give the definition of ${\tilde{x}}_{jl}$ in Appendix 1 since its derivation is somewhat technical. The number k in ${\widehat{T}}_{\mathrm{DT}}$ should be determined before the data transformation. See Appendix 1 about a choice of k.

We assume the following conditions when (A-ii) is met.

• (A-v) $\displaystyle \frac{\lambda _{1}^2}{n \text{ tr }({\varvec{\varSigma }}_*^2) }\rightarrow 0$ as $m\rightarrow \infty$;    (A-vi) $\displaystyle \liminf _{p\rightarrow \infty } \frac{\varDelta _*}{\varDelta }>0$ when $\varDelta \ne 0$.

Note that (A-vi) is a mild condition when p is much larger than k because $\varDelta _*=\varDelta -\sum _{j=1}^k ({\varvec{h}}_j^T{\varvec{\mu }})^2=\sum _{j=k+1}^p ({\varvec{h}}_j^T{\varvec{\mu }})^2$. Also, note that $\varDelta _*\ne 0$ when $\varDelta \ne 0$ under (A-vi). Then, we have the following results.

Theorem 1

Assume (A-i), (A-ii), (A-v) and (A-vi). It holds that

$$\begin{aligned} {\widehat{T}}_{\mathrm{DT}}-T_{\mathrm{DT}} =o_P( \max \{ K_{1*}^{1/2}, \varDelta _* \}) \ \hbox { as }m\rightarrow \infty . \end{aligned}$$

Furthermore, we also assume (A-iii). Then, it holds that

$$\begin{aligned} \frac{{\widehat{T}}_{\mathrm{DT}}-\varDelta _*}{K_*^{1/2}} =\frac{{\widehat{T}}_{\mathrm{DT}}-\varDelta _*}{K_{1*}^{1/2}}+o_P(1) \Rightarrow N(0,1) \ \hbox { as } m\rightarrow \infty . \end{aligned}$$

Corollary 1

Assume (A-i), (A-ii) and (A-iv) to (A-vi). Then, it holds that

$$\begin{aligned} \frac{{\widehat{T}}_{\mathrm{DT}}}{\varDelta _*}=1+o_P(1) \ \hbox { as }m\rightarrow \infty . \end{aligned}$$

From Theorem 1 and Lemma 1 in Appendix 1, under (A-i) to (A-iii), (A-v) and (A-vi), it holds that

$$\begin{aligned} \frac{{\widehat{T}}_{\mathrm{DT}}-\varDelta _*}{\widehat{K}_{1*}^{1/2}} \Rightarrow N(0,1) \ \hbox { as }m\rightarrow \infty , \end{aligned}$$

(8)

where $\widehat{K}_{1*}$ is given in Lemma 1 in Appendix 1. Thus, we can construct a test procedure of (1) by (8).

We checked the behavior of the asymptotic null distribution by using the toy example in (ii) of Fig. 1. We assumed $N_{p}({\varvec{0}}, {\varvec{\varSigma }})$ under $H_0:\ {\varvec{\mu }}={\varvec{0}}$. We set $p=2000$, $n=90$ and ${\varvec{\varSigma }}= \hbox {diag}(p^{\alpha _{1}},p^{\alpha _{2}},1,\ldots ,1)$ with $(\alpha _1,\alpha _2)=(2/3, 1/2)$. We calculated ${\widehat{T}}_{\mathrm{DT}}/\widehat{K}_{1*}^{1/2}$ 1000 times and constructed a histogram in Fig. 2. One can observe that ${\widehat{T}}_{\mathrm{DT}}/\widehat{K}_{1*}^{1/2}$ converges to N(0, 1) as expected theoretically.

Fig. 2

The histogram of ${\widehat{T}}_{\mathrm{DT}}/\widehat{K}_{1*}^{1/2}$ for a SSE model having $(\alpha _1,\alpha _2)=(2/3,1/2)$. The solid line denotes the p.d.f. of N(0, 1)

Test procedure for (1) by ${\widehat{T}}_{\mathrm{DT}}$ and its performance

We give a new test procedure for (1) by using ${\widehat{T}}_{\mathrm{DT}}$. For a given $\alpha \in (0,1/2)$, we test the hypothesis (1) by

$$\begin{aligned} \hbox {rejecting }H_0\Longleftrightarrow \frac{{\widehat{T}}_{\mathrm{DT}}}{\widehat{K}_{1*}^{1/2}}>z_{\alpha }, \end{aligned}$$

(9)

where $z_{\alpha }$ is a constant such that $P\{N(0,1)>z_{\alpha }\}=\alpha$. From Theorem 1, Corollary 1 and Lemma 1 in Appendix 1, we have the following results.

Theorem 2

Assume (A-i), (A-ii), (A-v) and (A-vi). The test procedure (9) holds that as $m\rightarrow \infty$

$$\begin{aligned} \hbox {Size}= \alpha +o(1)\quad \hbox {and}\quad &\hbox {Power} = \varPhi \bigg (\frac{ \varDelta _* }{K_*^{1/2}}-z_{\alpha }\Big (\frac{K_{1*}}{K_*} \Big )^{1/2} \bigg )+o(1), \end{aligned}$$

where $\varPhi (\cdot )$ denotes the c.d.f. of N(0, 1).

Corollary 2

Assume (A-i), (A-ii) and (A-iv) to (A-vi). Under $H_1$, the test procedure (9) holds that as $m\rightarrow \infty$

$$\begin{aligned} \hbox {Power}=1+o(1). \end{aligned}$$

Remark 3

The number k in ${\widehat{T}}_{\mathrm{DT}}/\widehat{K}_{1*}^{1/2}$ should be determined before the data transformation. See Appendix 1 about a choice of k.

We used computer simulations to study performances of the test procedures given by Bai and Saranadasa (1996), Katayama et al. (2013), Srivastava and Du (2008) and (9) with $k={\hat{k}}$ given in Appendix 1. Srivastava and Du (2008) proposed the following test statistic$:$

$$\begin{aligned} T_{\mathrm{SD}}=\frac{n{{\bar{{\varvec{x}}}}^T}{\varvec{D}}_S^{-1}{\bar{{\varvec{x}}}}-(n-1)p/(n-3)}{\sqrt{2\{ \text{ tr }({\varvec{R}}^2)-p^2/(n-1)\}c_{p,n}}}, \end{aligned}$$

(10)

where ${\varvec{D}}_S$ is the diagonal matrix having the diagonal elements of ${\varvec{S}}$, ${\varvec{R}}={\varvec{D}}_S^{-1/2}{\varvec{S}}{\varvec{D}}_S^{-1/2}$ and $c_{p,n}=1+\text{ tr }({\varvec{R}}^2)p^{-3/2}$. Katayama et al. (2013) dealt with $T_{\mathrm{SD}}$ under a strongly spiked eigenvalue model. They also gave asymptotic distributions of $T_{\mathrm{BS}}$ and $T_{\mathrm{SD}}$ as a chi-squared distribution. In this simulation, we used the test procedures given by Katayama et al. (2013) for $T_{\mathrm{BS}}$ and $T_{\mathrm{SD}}$ and denoted them by $\widetilde{T}_{\mathrm{BS}}$ and $\widetilde{T}_{\mathrm{SD}}$. We set ${\varvec{\mu }}={\varvec{0}}$ under $H_0$ in (1). We set $\alpha =0.05$. Let ${\varvec{\varOmega }}_{s}$ be a $s\times s$ matrix as ${\varvec{\varOmega }}_{s}=(0.3^{|i-j|^{1/3}})$. We considered three cases. For (i) and (ii), we set

$$\begin{aligned} {\varvec{\varSigma }}= \begin{pmatrix} {\varvec{\varGamma }}_{p_1} &{} {\varvec{O}}&{} {\varvec{O}}\\ {\varvec{O}}&{} {\varvec{\varGamma }}_{p_2} &{} {\varvec{O}}\\ {\varvec{O}}&{} {\varvec{O}}&{} {\varvec{\varOmega }}_{p-p_1-p_2} \end{pmatrix}, \end{aligned}$$

where ${\varvec{\varGamma }}_{s}=({\varvec{I}}_{s}+{\varvec{1}}_{s}{\varvec{1}}_{s}^{T})/2$, ${\varvec{1}}_{s}=(1,\ldots ,1)^T$ and ${\varvec{O}}$ is a zero matrix. As for ${\varvec{\varGamma }}_{s}$, note that the largest eigenvalue is $(s+1)/2$ and the other ones are 1 / 2.

• (i) ${\varvec{x}}_l$ is Gaussian, $N_{p}({\varvec{0}}, {\varvec{\varSigma }}),\ p=2^s\ (s=6,\ldots ,12)$. We set $n=2\lceil p^{1/2} \rceil$ and $(p_1,p_2)=(\lceil p^{2/3} \rceil , \lceil p^{1/2} \rceil )$, where $\lceil x \rceil$ denotes the smallest integer $\ge x$.

• (ii) ${\varvec{x}}_{l}={\varvec{H}}{\varvec{\varLambda }}^{1/2}(z_{1l},\ldots ,z_{pl})^T+{\varvec{\mu }}$, where ${\varvec{H}}$ and ${\varvec{\varLambda }}$ are given by ${\varvec{\varSigma }}={\varvec{H}}{\varvec{\varLambda }}{\varvec{H}}^T$ having $(p_1,p_2)=(\lceil p^{3/4} \rceil , \lceil p^{1/2} \rceil )$, and $z_{rl}=(v_{rl}-5)/{10}^{1/2}$ $(r=1,\ldots ,p)$ with $v_{rl}$s i.i.d. as the chi-squared distribution with 5 degrees of freedom. We set $n=50$ and $p=100s$ for $s=1,\ldots ,10$.

• (iii) ${\varvec{x}}_l$ is of a Gaussian mixture of $N_p({\varvec{\mu }}_1, {\varvec{\varOmega }}_{p})$ and $N_p({\varvec{\mu }}_2,{\varvec{\varOmega }}_{p})$ with a mixture proportion 1 / 2, where ${\varvec{\mu }}_1=(1,\ldots ,1,0,\ldots ,0)^T$ and ${\varvec{\mu }}_2=(-1,\ldots ,-1,0,\ldots ,0)^T$ whose first $p_1$ elements are 1 and $-1$. We set $n=10s\ (s=4,\ldots ,12)$, $p=1000$ and $p_1=\lceil p^{2/3} \rceil$. Note that ${\varvec{\varSigma }}={\varvec{\varOmega }}_{p}+({\varvec{\mu }}_1-{\varvec{\mu }}_2)({\varvec{\mu }}_1-{\varvec{\mu }}_2)^T/4$ and $\lambda _{1} \approx p^{2/3}$.

For (i) and (ii), (A-i) and (A-ii) with $k=2$ are met. For (iii), (A-ii) with $k=1$ is met while (A-i) is not met. See Sect. 6 in Yata and Aoshima (2010) for the details. Note that (A-v) is met for (i). As for the alternative hypothesis, we considered two cases:

• (a) ${\varvec{\mu }}=(1,1,1,0,\ldots ,0)^T$ whose first 3 elements are 1 and the remaining elements are 0; and

• (b) ${\varvec{\mu }}=(0,\ldots ,0,1,1,1)^T$ whose last 3 elements are 1 and the remaining elements are 0.

In each case of (i) to (iii), we checked the performance by 2000 replications. We defined $P_{r}=1\ (\hbox {or}\ 0)$ when $H_0$ was falsely rejected (or not) for $r=1,\ldots ,2000$, and defined ${\overline{\alpha }}=\sum _{r=1}^{2000}P_{r}/2000$ to estimate the size. We also defined $P_{r}=1\ (\hbox {or}\ 0)$ when $H_1$ was falsely rejected (or not) for $r=1,\ldots ,2000$, and defined $1-{\overline{\beta }}=1-\sum _{r=1}^{2000}P_{r}/2000$ to estimate the power for (a) and (b). Note that their standard deviations are less than 0.011. In Fig. 3, we plotted ${\overline{\alpha }}$ (the left panel) and $1-{\overline{\beta }}$ (the right upper panel for (a) and right lower panel for (b)) in each case of (i) to (iii). One can observe that ${\widehat{T}}_{\mathrm{DT}}$ gave preferable performances both for the size and power in (i) and (iii). ${\widehat{T}}_{\mathrm{DT}}$ gave a moderate performance for (ii); however, it seems that the sample size was not large enough to guarantee accuracy. $T_{\mathrm{BS}}$ and $T_{\mathrm{SD}}$ gave bad performances for the size and power. They are quite sensitive about the NSSE condition (3). On the other hand, $\widetilde{T}_{\mathrm{BS}}$ and $\widetilde{T}_{\mathrm{SD}}$ gave good performances for (i) to (iii) regarding the size, while they gave much worse performances regarding the power compared to ${\widehat{T}}_{\mathrm{DT}}$. This is probably because the variance of those statistics becomes very large since they are heavily influenced by strongly spiked eigenvalues. In fact, it holds that $\text{ Var }({T}_{\mathrm{DT}})/\text{ Var }({T}_{\mathrm{BS}})=K_*/K=o(1)$ for (i) to (iii). We emphasize that it is quite important to select a suitable test procedure depending on the eigenstructure. In conclusion, we recommend using ${\widehat{T}}_{\mathrm{DT}}$ when the data fits the SSE model.

Fig. 3

The performance of the test procedures given by Bai and Saranadasa (1996) (denoted by $T_{\mathrm{BS}}$), Srivastava and Du (2008) (denoted by $T_{\mathrm{SD}}$), Katayama et al. (2013) (denoted by $\widetilde{T}_{\mathrm{BS}}$ and $\widetilde{T}_{\mathrm{SD}}$) and (9) (denoted by ${\widehat{T}}_{\mathrm{DT}}$). The value of ${\overline{\alpha }}$ is denoted by the dashed line in the left panel, and the value of $1-{\overline{\beta }}$ is denoted by the dashed line in the right upper panel for (a) and in the right lower panel for (b) in each case of (i) to (iii). The solid line denotes the asymptotic power of ${\widehat{T}}_{\mathrm{DT}}$ given in Theorem 2

Applications

In this section, we give several applications of the findings in Sect. 2.

Confidence region for ${\varvec{\mu }}$

We first consider the following quantity:

$$\begin{aligned} T_{{\varvec{\mu }}}&=\Vert {\varvec{A}}({\overline{{\varvec{x}}}}-{\varvec{\mu }}) \Vert ^{2}-\text{ tr }({\varvec{A}}{\varvec{S}})/n\\&=\Vert {\overline{{\varvec{x}}}}-{\varvec{\mu }}\Vert ^{2} -\text{ tr }({\varvec{S}})/n-2\frac{\sum _{l<l'}^{n}\sum _{j=1}^{k} {{\varvec{h}}}_{j}^T({\varvec{x}}_{l}-{\varvec{\mu }}){{\varvec{h}}}_{j}^T({\varvec{x}}_{l'}-{\varvec{\mu }})}{n(n-1)}. \end{aligned}$$

Note that $E(T_{{\varvec{\mu }}})=0$ and $\text{ Var }(T_{{\varvec{\mu }}})=K_{1*}$. Then, from Proposition 1, we have the following result.

Proposition 3

Assume (A-i) and (A-ii). It holds that as $m\rightarrow \infty$

$$\begin{aligned} T_{{\varvec{\mu }}}/K_{1*}^{1/2} \Rightarrow N(0,1). \end{aligned}$$

Let

$$\begin{aligned} {\varvec{R}}&=\Big \{{\varvec{\mu }}\in \mathcal {R}^p: \ \text{ tr }({\varvec{A}}{\varvec{S}})/n-z_{\alpha /2}K_{1*}^{1/2} \le \Vert {\varvec{A}}({\overline{{\varvec{x}}}}-{\varvec{\mu }}) \Vert ^{2}\\&\qquad \qquad \qquad \qquad \le \text{ tr }({\varvec{A}}{\varvec{S}})/n +z_{\alpha /2}K_{1*}^{1/2} \Big \}. \end{aligned}$$

From Proposition 3 it holds that under (A-i) and (A-ii),

$$\begin{aligned} P({\varvec{\mu }}\in {\varvec{R}})= 1-\alpha +o(1)\ \hbox { as }m\rightarrow \infty . \end{aligned}$$

We note that $\text{ tr }({\varvec{A}}{\varvec{S}})/n=\text{ tr }({\varvec{\varSigma }}_*)/n+o_P(K_{1*}^{1/2})$ under (A-i) and (A-ii). Also, note that $z_{\alpha /2}K_{1*}^{1/2}=o(\text{ tr }({\varvec{\varSigma }}_*)/n)$ under (A-ii) from the fact that $\text{ tr }({\varvec{\varSigma }}_{*}^{2})/\{\text{ tr }({\varvec{\varSigma }}_{*})\}^2=o(1)$ as $p \rightarrow \infty$ under (A-ii). One can claim that $\text{ tr }({\varvec{A}}{\varvec{S}})/n-z_{\alpha /2}K_{1*}^{1/2}>0$ with probability tending to 1. Thus, ${\varvec{R}}$ indicates that ${\varvec{A}}{\varvec{\mu }}\ (={\varvec{\mu }}_*)$ is included in the region sandwiched by the two p-dimensional spheres with radii of $( \text{ tr }({\varvec{\varSigma }}_*)/n -z_{\alpha /2}K_{1*}^{1/2})^{1/2}$ and $( \text{ tr }({\varvec{\varSigma }}_*)/n +z_{\alpha /2}K_{1*}^{1/2})^{1/2}$ from the center ${\varvec{A}}{\overline{{\varvec{x}}}}$.

Now, we construct a confidence region for ${\varvec{\mu }}$ by estimating the eigenstructures. Let

$$\begin{aligned} \eta ({\varvec{\mu }})= 2\frac{\sum _{l<l'}^{n}\sum _{j=1}^{k} {\tilde{{\varvec{h}}}}_{jl}^T({\varvec{x}}_{l}-{\varvec{\mu }}){\tilde{{\varvec{h}}}}_{jl'}^T({\varvec{x}}_{l'}-{\varvec{\mu }})}{n(n-1)}, \end{aligned}$$

where ${\tilde{{\varvec{h}}}}_{jl}$s are given in Appendix 1. From (7) we consider the following quantity:

$$\begin{aligned} {\widehat{T}}_{{\varvec{\mu }}}=\Vert {\overline{{\varvec{x}}}}-{\varvec{\mu }}\Vert ^{2}-\text{ tr }({\varvec{S}})/n-\eta ({\varvec{\mu }}). \end{aligned}$$

By using Theorem 1, we have the following result.

Proposition 4

Assume (A-i), (A-ii) and (A-v). It holds that as $m\rightarrow \infty$

$$\begin{aligned} {\widehat{T}}_{{\varvec{\mu }}}-{T}_{{\varvec{\mu }}}=o_P(K_{1*}^{1/2}). \end{aligned}$$

Let

$$\begin{aligned} \widehat{{\varvec{R}}}&=\Big \{{\varvec{\mu }}\in \mathcal {R}^p: \ {\text{ tr }({\varvec{S}})}/{n} -z_{\alpha /2}\widehat{K}_{1*}^{1/2} \le \Vert {\overline{{\varvec{x}}}}-{\varvec{\mu }}\Vert ^{2}-\eta ({\varvec{\mu }}) \nonumber \\&\qquad \qquad \qquad \qquad \le \text{ tr }({\varvec{S}})/n +z_{\alpha /2}\widehat{K}_{1*}^{1/2} \Big \}. \end{aligned}$$

(11)

From Lemma 1 in Appendix 1, Propositions 3 and 4, it holds that under (A-i), (A-ii) and (A-v),

$$\begin{aligned} P({\varvec{\mu }}\in \widehat{{\varvec{R}}})= 1-\alpha +o(1)\ \hbox { as }m\rightarrow \infty . \end{aligned}$$

For example, if ${\varvec{0}}\in \widehat{{\varvec{R}}}$, we can consider ${\varvec{0}}$ as a likely candidate of ${\varvec{\mu }}$.

Remark 4

From Lemma 1 in Appendix 1, the length of the interval for $\Vert {\overline{{\varvec{x}}}}-{\varvec{\mu }}\Vert ^{2}-\eta ({\varvec{\mu }})$ in $\widehat{{\varvec{R}}}$ is $2 z_{\alpha /2}{K}_{1*}^{1/2}\{1+o_P(1)\}$. When $\text{ tr }({\varvec{\varSigma }}_*^2)=O(p)$ and $p^{1/2}/n=o(1)$, it holds that ${K}_{1*}=o(1)$ so that the length of the interval tends to 0.

Confidence lower bound for $\varDelta$

We construct a confidence lower bound for $\varDelta$ by

$$\begin{aligned} I_L=[\max \left\{ {\widehat{T}}_{\mathrm{DT}}-z_{\alpha }\widehat{K}_{1*}^{1/2},\ 0 \right\} ,\ \infty ), \end{aligned}$$

where $\alpha \in (0,1/2)$. By using Theorem 1 and Lemma 1, it holds that

$$\begin{aligned} P(\varDelta \in I_L)\ge 1-\alpha +o(1) \ \hbox { as }m\rightarrow \infty \end{aligned}$$

under (A-i) to (A-iii), (A-v) and (A-vi) from the fact that $\varDelta \ge \varDelta _*$. For example, one can apply $I_L$ to the high-dimensional discriminant analysis in which a lower bound for $\varDelta$ is the key to discuss misclassification rates of any classifier. See Sect. 4 in Aoshima and Yata (2011) and Sects. 3 and 4 in Aoshima and Yata (2014).

Estimation of $\varDelta$

We consider the following conditions when (A-ii) is met.

• (A-vii) $\displaystyle \frac{\lambda _{1}^2}{n^3 \varDelta ^2 }\rightarrow 0$ and $\displaystyle \frac{\lambda _1}{\lambda _k}=O(n^{1/2})$ as $m\rightarrow \infty$;

• (A-viii) $\varDelta _*/\varDelta \rightarrow 1$ as $p\rightarrow \infty$.

We note that the second condition “${\lambda _1}/{\lambda _k}=O(n^{1/2})$” in (A-vii) naturally holds when $k=1$. Also, note that (A-viii) is a mild condition when p is much larger than k because $\varDelta _*=\varDelta -\sum _{j=1}^k ({\varvec{h}}_j^T{\varvec{\mu }})^2=\sum _{j=k+1}^p ({\varvec{h}}_j^T{\varvec{\mu }})^2$.

We have the following result.

Theorem 3

Assume (A-i), (A-ii), (A-iv), (A-vii) and (A-viii). It holds that

$$\begin{aligned} \frac{{\widehat{T}}_{\mathrm{DT}}}{\varDelta }=1+o_P(1)\ \hbox { as } m\rightarrow \infty . \end{aligned}$$

One can estimate $\varDelta$ by ${\widehat{T}}_{\mathrm{DT}}$. On the other hand, by noting that $K_2\le 4 \varDelta \lambda _{1}/n \le 4 \varDelta K_{1}^{1/2}$, it holds that $\text{ Var }({T}_{\mathrm{BS}})/\varDelta ^2\rightarrow 0$ as $m\rightarrow \infty$ under

$$\begin{aligned} {K_1}/{\varDelta }\rightarrow 0 \ \hbox { as }m\rightarrow \infty . \end{aligned}$$

(12)

Hence, we have that

$$\begin{aligned} {T}_{\mathrm{BS}}/\varDelta =1+o_P(1). \end{aligned}$$

We note that (12) is equivalent to

$$\begin{aligned} \frac{\lambda _1^2}{n^2 \varDelta ^2 }\rightarrow 0 \ \hbox { as }m\rightarrow \infty \end{aligned}$$

under (A-ii). If $\lambda _1$ is quite large enough to claim $\varDelta /\lambda _1 \rightarrow 0$ as $p\rightarrow \infty$, the first condition in (A-vii) is much milder than (12). Thus, we recommend using ${\widehat{T}}_{\mathrm{DT}}$ as an estimation of $\varDelta$ under the SSE model. We demonstrate the estimation of $\varDelta$ by using a microarray data set in Sect. 5.2.

Multi-sample problems

Suppose we have independent and p-variate populations, $\pi _i,\ i=1,\ldots ,g$, having unknown mean vector ${\varvec{\mu }}_i$ and unknown covariance matrix ${\varvec{\varSigma }}_i$ for each $\pi _i$. We have i.i.d. observations, ${\varvec{x}}_{i1},\ldots ,{\varvec{x}}_{in_i}$, from each $\pi _i$. We assume $n_1=\min \{n_1,\ldots ,n_g\}$ without loss of generality.

Two-sample test with balanced samples

In this section, we set $g=2$ and consider the two-sample test:

$$\begin{aligned} H_0:{\varvec{\mu }}_{1} ={\varvec{\mu }}_2 \quad \hbox {vs.}\quad H_1:{\varvec{\mu }}_{1} \ne {\varvec{\mu }}_2. \end{aligned}$$

(13)

Aoshima and Yata (2018a) gave a two-sample test procedure under the SSE model by the data transformation technique. We consider testing (13) by using the one-sample test procedure (9) when the sample sizes are asymptotically balanced such that $n_1/n_2 \rightarrow 1$ as $n_1,n_2 \rightarrow \infty$.

Let

$$\begin{aligned} {\varvec{x}}_{j}={\varvec{x}}_{1j}-{\varvec{x}}_{2j} \ \hbox { for }j=1,\ldots ,n_1(=n, \hbox { say }), \end{aligned}$$

(14)

and let ${\varvec{\mu }}={\varvec{\mu }}_1-{\varvec{\mu }}_2$ and ${\varvec{\varSigma }}= {\varvec{\varSigma }}_1+{\varvec{\varSigma }}_2$. Note that ${\varvec{x}}_{j}$ has the SSE model in general if one of the $\pi _i$s has the SSE model. For example, if $\text{ tr }({\varvec{\varSigma }}_1^2)\ge \text{ tr }({\varvec{\varSigma }}_{2}^2)$ and $\liminf _{p\rightarrow \infty }\lambda _{\max }^{2}({\varvec{\varSigma }}_1)/\text{ tr }({\varvec{\varSigma }}_1^2)>0$, it holds that

$$\begin{aligned} \liminf _{p\rightarrow \infty }\frac{\lambda _{\max }^{2}({\varvec{\varSigma }})}{\text{ tr }\left( {\varvec{\varSigma }}^2 \right) }\ge \liminf _{p\rightarrow \infty } \frac{\lambda _{\max }^{2}({\varvec{\varSigma }}_1)}{4\text{ tr }({\varvec{\varSigma }}_1^2)}>0. \end{aligned}$$

Now, we consider using the test procedure (9) with ${\varvec{x}}_{j}$.

When we apply the test procedure (9) to (13), we do not use the remaining samples, ${\varvec{x}}_{2n_1+1},\ldots ,{\varvec{x}}_{2n_2}$. Let us check the influence of the remaining samples. Let ${\varvec{\varSigma }}_*={\varvec{\varSigma }}_{1*}+{\varvec{\varSigma }}_{2*}$. From Theorem 2, the asymptotic power is given by

$$\begin{aligned} \varPhi (\varDelta _*/K_*^{1/2}-z_{\alpha }K_{1*}^{1/2}/K_{*}^{1/2} ), \end{aligned}$$

where

$$\begin{aligned}&K_{1*}=2\text{ tr }({\varvec{\varSigma }}_*^2)/n^2=2\{\text{ tr }({\varvec{\varSigma }}_{1*}^2)+\text{ tr }({\varvec{\varSigma }}_{2*}^2) \}/n^2+4\text{ tr }({\varvec{\varSigma }}_{1*}{\varvec{\varSigma }}_{2*})/n^2 \\&\quad \hbox {and } K_{*}=K_{1*}+4\sum _{i=1}^2{\varvec{\mu }}_*^T{\varvec{\varSigma }}_{i*}{\varvec{\mu }}_*/n. \end{aligned}$$

In the balanced setting such as $n_1/n_2 \rightarrow 1$ when $n_1\rightarrow \infty$, the above asymptotic power is equivalent to that of the two-sample test procedure by Aoshima and Yata (2018a). See Theorem 6 in Aoshima and Yata (2018a). Thus, one may use the test procedure (9) when the sample sizes are balanced. We give a demonstration by using microarray data sets in Sections 5.1 and 5.2.

Multi-sample test for a linear function of mean vectors

In this section, we consider the following test for a linear function of mean vectors:

$$\begin{aligned} H_0:\ \sum _{i=1}^g b_i{\varvec{\mu }}_i={\varvec{0}}\quad \hbox {vs.} \quad H_1:\ \sum _{i=1}^g b_i{\varvec{\mu }}_i \ne {\varvec{0}}, \end{aligned}$$

(15)

where $b_i$s are known and nonzero scalars (not depending on p). We consider a transformation given by Bennett (1951) and Anderson (2003). Let

$$\begin{aligned} {\varvec{x}}_j = b_1{\varvec{x}}_{1j}+\sum _{i=2}^g b_i \sqrt{\frac{n_1}{n_i}}\left ( {\varvec{x}}_{ij}-\frac{1}{n_1}\sum _{j=1}^{n_1}{\varvec{x}}_{ij} + \frac{1}{\sqrt{n_1n_i}} \sum _{j'=1}^{n_i}{\varvec{x}}_{ij'} \right) \ \hbox { for }j=1,\ldots ,n_1. \end{aligned}$$

(16)

Then, it holds that

$$\begin{aligned} E({\varvec{x}}_j)=\sum _{i=1}^g b_i{\varvec{\mu }}_i\ \hbox { and } \ \text{ Var }({\varvec{x}}_j)=\sum _{i=1}^gb_i^2(n_1/n_i){\varvec{\varSigma }}_i. \end{aligned}$$

Now, we assume $\pi _i: N_p({\varvec{\mu }}_i,{\varvec{\varSigma }}_i)$ for $i=1,\ldots ,g$. Then, ${\varvec{x}}_1,\ldots ,{\varvec{x}}_{n_1}$ are i.i.d. as $N_p(\sum _{i=1}^g b_i{\varvec{\mu }}_i,\ \sum _{i=1}^gb_i^2(n_1/n_i){\varvec{\varSigma }}_i)$. Nishiyama et al. (2013) proposed a test procedure for (15) by the transformation (16) under a NSSE model. In this section, we consider testing (15) under the SSE model. Let $n=n_1$, ${\varvec{\mu }}=\sum _{i=1}^g b_i{\varvec{\mu }}_i$ and ${\varvec{\varSigma }}=\sum _{i=1}^gb_i^2(n_1/n_i){\varvec{\varSigma }}_i$. Note that ${\varvec{x}}_{j}$ has the SSE model in general if one of the $\pi _i$s has the SSE model. For example, if $\text{ tr }({\varvec{\varSigma }}_1^2)\ge \text{ tr }({\varvec{\varSigma }}_{i}^2)$ for $i\ge 2$ and $\liminf _{p\rightarrow \infty }\lambda _{\max }^{2}({\varvec{\varSigma }}_1)/\text{ tr }({\varvec{\varSigma }}_1^2)>0$, it holds that

$$\begin{aligned} \liminf _{p\rightarrow \infty }\frac{\lambda _{\max }^{2}({\varvec{\varSigma }})}{\text{ tr }\left( {\varvec{\varSigma }}^2 \right) }\ge \liminf _{p\rightarrow \infty } \frac{b_1^2 \lambda _{\max }^{2}({\varvec{\varSigma }}_1)}{ \left( \sum _{i=1}^g b_i^2\right) ^2 \text{ tr }({\varvec{\varSigma }}_1^2)}>0. \end{aligned}$$

One may apply the one-sample test procedure (9) with ${\varvec{x}}_{j}$ to (15). We give a demonstration using a microarray data set in Sect. 5.3.

It should be noted that the Gaussian assumption is required for the multi-sample test. We investigate robustness of our test procedure against the Gaussian assumption by some simulation studies. We set $g=4$, $b_i=1$, ${\varvec{\mu }}_i={\varvec{0}}$ and ${\varvec{\varSigma }}_i=c_i\hbox {diag}(p^{2/3},p^{1/3},1,\ldots ,1)$ for $i=1,\ldots ,4$, where $c_1=1$ and $c_2=c_3=c_4=2$. We considered three cases:

• (a) ${\varvec{x}}_{ij}, j=1,\ldots ,n_i$ are i.i.d. as $N_p({\varvec{\mu }}_i,{\varvec{\varSigma }}_i)$, where $n_1=\lceil p^{1/2} \rceil$, $p=2^s (s=6,\ldots ,12)$ and $n_i=2n_1\ (i=2,3,4)$;

• (b) ${\varvec{x}}_{ij}={\varvec{\varSigma }}_{i}^{1/2}(z_{1j(i)},\ldots ,z_{pj(i)})^T+{\varvec{\mu }}_i,\ j=1,\ldots ,n_i$, having $z_{rj(i)}=(v_{rj(i)}-\nu )/\sqrt{2\nu }$, where $v_{rj(i)}$s are i.i.d. as the chi-squared distribution with degrees of freedom $\nu =5s\ (s=1,\ldots ,7)$, and $n_1=50$ and $n_i=100\ (i=2,3,4)$;

• (c) ${\varvec{x}}_{ij}={\varvec{\varSigma }}_{i}^{1/2}(z_{1j(i)},\ldots ,z_{pj(i)})^T+{\varvec{\mu }}_i,\ j=1,\ldots ,n_i$, where $(z_{1j(i)},\ldots ,z_{pj(i)})^T$s are i.i.d. as p-variate t-distribution, $t_{p}({\varvec{I}}_{p},\nu )$, with mean zero, covariance matrix ${\varvec{I}}_{p}$ and degrees of freedom $\nu =5s\ (s=1,\ldots ,7)$, and $n_1=50$ and $n_i=100\ (i=2,3,4)$.

Case (a) corresponds to the cases (b) and (c) when $\nu \rightarrow \infty$.

In each case of (a) to (c), we checked the performance by 2000 replications. We defined $P_{r}=1\ (\hbox {or}\ 0)$ when $H_0$ in (15) was falsely rejected (or not) for $r=1,\ldots ,2000$, and defined ${\overline{\alpha }}=\sum _{r=1}^{2000}P_{r}/2000$ to estimate the size. In Fig. 4, we plotted ${\overline{\alpha }}$ for (a) in the left panel, for (b) in the right upper panel and for (c) in the right lower panel. As for (a), our test procedure gave a good performance when p is large as expected in theory. One can observe that our test procedure is robust in (b). On the other hand, our test procedure seems to be a little affected by a heavy tail distribution in (c).

Fig. 4

The value of ${\overline{\alpha }}$ for (a) to (c). We considered three cases$:$ (a) ${\varvec{x}}_{ij}, j=1,\ldots ,n_i$ are i.i.d. as $N_p({\varvec{0}},{\varvec{\varSigma }}_i)$ in the left panel; (b) ${\varvec{x}}_{ij}={\varvec{\varSigma }}_{i}^{1/2}(z_{1j(i)},\ldots ,z_{pj(i)})^T+{\varvec{\mu }}_i,\ j=1,\ldots ,n_i$, having $z_{rj(i)}=(v_{rj(i)}-\nu )/\sqrt{2\nu }$, where $v_{rj(i)}$s are i.i.d. as the chi-squared distribution with degrees of freedom $\nu$ in the right upper panel; and (c) ${\varvec{x}}_{ij}={\varvec{\varSigma }}_{i}^{1/2}(z_{1j(i)},\ldots ,z_{pj(i)})^T+{\varvec{\mu }}_i,\ j=1,\ldots ,n_i$, where $(z_{1j(i)},\ldots ,z_{pj(i)})^T$s are i.i.d. as $t_{p}({\varvec{I}}_{p},\nu )$ in the right lower panel

Data analysis

Two-sample test with balanced samples

We analyzed gene expression data by using the proposed test procedure (9). We used microarray data sets of prostate cancer with $12625 (=p)$ genes consisting of two classes: $\pi _1 :$ non-tumor ($50(=n_1)$ samples) and $\pi _2 :$ prostate cancer ($52(=n_2)$ samples). See Singh et al. (2002) for the details. The data set is available at Jeffery’s web page (URL: http://www.bioinf.ucd.ie/people/ian/). First, we checked (A-ii) by applying the method given in Sect. 5 of Aoshima and Yata (2018a) and confirmed that each class fits the SSE model. According to the test procedure by (9) with ${\hat{k}}$ given in Appendix 1, we tested (13) at significant level 0.05. We used the first $50(=n_2)$ samples of prostate cancer and constructed new data as ${\varvec{x}}_{j}={\varvec{x}}_{1j}-{\varvec{x}}_{2j},\ j=1,\ldots ,n_1$, where ${\varvec{x}}_{ij}$ denotes the jth sample in $\pi _i$.

In addition, we considered testing (13) when $H_0$ was true. For each $\pi _i$, we divided the samples into two parts, ${\varvec{x}}_{i1},\ldots ,{\varvec{x}}_{in_{i}/2}$ and ${\varvec{x}}_{in_{i}/2+1},\ldots ,{\varvec{x}}_{in_i}$ for $i=1,2$. We constructed new data as ${\varvec{x}}'_{ij}={\varvec{x}}_{ij}-{\varvec{x}}_{in_{i}/2+j},\ j=1,\ldots ,n_i/2$. Then, we applied the test procedure (9) in the same way.

The results are summarized in Table 1. One can observe that the test procedure (9) worked well when $H_0$ in (13) was true. On the other hand, the preceding test procedures ${T}_{\mathrm{BS}}$ in (2) and ${T}_{\mathrm{SD}}$ in (10) did not control the size.

Table 1 The values of three test statistics, ${\widehat{T}}_{\mathrm{DT}}/\widehat{K}_{1*}^{1/2}$, ${T}_{\mathrm{BS}}/\widehat{K}_{1}^{1/2}$ and ${T}_{\mathrm{SD}}$, where $\widehat{K}_{1}$ is a consistent estimator of $K_1$ given in Bai and Saranadasa (1996). We also gave the value of ${\hat{k}}$ used in ${\widehat{T}}_{\mathrm{DT}}$, where ${\hat{k}}$ is given in Appendix 1. We used the data sets from Singh et al. (2002) having $p=12625$

Two-sample test for matched samples

We considered applying the test procedure (9) to a microarray data set of matched samples. We used the colon adenocarcinomas data with $7457 (=p)$ genes given by Notterman et al. (2001). The data set includes the microarray data of $\pi _1$: adenocarcinomas cell and $\pi _2$: normal cell from $18 (=n)$ persons. Note that one cannot use a two-sample test procedure because the data sets do not satisfy the independency. The data set is available at Princeton university’s web page (URL: http://genomics-pubs.princeton.edu/oncology/). First, we confirmed that ${\varvec{x}}_{1j}-{\varvec{x}}_{2j},\ j=1,\ldots ,18$, fit the SSE model. We plotted the first 10 eigenvalues in Fig. 5. We used the test procedure (9) similarly to Sect.  5.1. Then, $H_0$ in (13) was rejected.

Next, we estimated $\varDelta$ using the two estimators given in Sect. 3.3. We had ${T}_{\mathrm{BS}}=3132.66$ and ${\widehat{T}}_{\mathrm{DT}}=2125.49$, so that the ratio was ${T}_{\mathrm{BS}}/{\widehat{T}}_{\mathrm{DT}}=1.47$. Note that our estimation ${\widehat{T}}_{\mathrm{DT}}$ has the consistency property. See Sect. 3.3 for the details. It seems that ${T}_{\mathrm{BS}}$ overestimated $\varDelta$ because of huge noise.

Fig. 5

The first 10 eigenvalues of the data set given by Notterman et al. (2001). We calculated the eigenvalues for ${\varvec{x}}_{1j}-{\varvec{x}}_{2j},\ j=1,\ldots ,18$

Multi-sample problem using confidence region

We considered applying the test procedure given in Sect. 4.2 to a microarray data set. We used malignant gliomas and oligodendrogliomas data sets having $12625 (=p)$ genes. See Nutt et al. (2003) for the details. We analyzed microarray data consisting of four classes: $\pi _1$: classic oligodendrogliomas (CO) ($7(=n_1)$ samples), $\pi _2$: nonclassic oligodendrogliomas (NO) ($15(=n_2)$ samples), $\pi _3$: classic glioblastoma (CG) ($14(=n_3)$ samples) and $\pi _4$: nonclassic glioblastoma (NG) ($14(=n_4)$ samples). We transformed the data by (16) and we had ${\hat{k}}=1$ for the transformed data. We constructed the confidence region by (11) for ${\varvec{\mu }}=({\varvec{\mu }}_{1}-{\varvec{\mu }}_{3})-({\varvec{\mu }}_{2}-{\varvec{\mu }}_{4})$. When ${\varvec{\mu }}={\varvec{0}}$, we had

$$\begin{aligned} \widehat{{\varvec{R}}}=\left\{ {\varvec{\mu }}\in \mathcal {R}^{p} | 1.83 \times 10^7\le \Vert {\overline{{\varvec{x}}}}\Vert ^2-\eta ({\varvec{0}}) \le 3.79\times 10^7\right\} . \end{aligned}$$

We calculated $\Vert {\overline{{\varvec{x}}}}\Vert ^2-\eta ({\varvec{0}})=3.29 \times 10^7$, so that ${\varvec{\mu }}={\varvec{0}}\in \widehat{{\varvec{R}}}$. Hence, we concluded that ${\varvec{\mu }}={\varvec{0}}$ is a candidate of ${\varvec{\mu }}=({\varvec{\mu }}_{1}-{\varvec{\mu }}_{3})-({\varvec{\mu }}_{2}-{\varvec{\mu }}_{4})$.

Appendices

Appendix 1

In this section, we give estimators for the parameters in our new test statistic, ${\widehat{T}}_{\mathrm{DT}}$, and discuss their asymptotic properties.

Estimation of ${x}_{jl}$

Let ${\varvec{X}}=[{\varvec{x}}_{1},\ldots ,{\varvec{x}}_{n}]$, $\overline{{\varvec{X}}}=[{\overline{{\varvec{x}}}},\ldots ,{\overline{{\varvec{x}}}}]$ and ${\varvec{P}}_{n}={\varvec{I}}_{n}-{\varvec{1}}_{n}{\varvec{1}}_{n}^T/n$, where ${\varvec{1}}_{n}=(1,\ldots ,1)^T$. Recall ${\varvec{S}}$ is the sample covariance matrix. One can write that ${\varvec{S}}=({\varvec{X}}-\overline{{\varvec{X}}})({\varvec{X}}-\overline{{\varvec{X}}})^T/(n-1)={\varvec{X}}{\varvec{P}}_{n}{\varvec{X}}^T/(n-1)$. Let us write the eigen-decomposition of ${\varvec{S}}$ as ${\varvec{S}}=\sum _{j=1}^{p}\hat{\lambda }_{j}\hat{{\varvec{h}}}_{j}\hat{{\varvec{h}}}_{j}^T$ having eigenvalues $\hat{\lambda }_{1}\ge \cdots \ge \hat{\lambda }_{p}\ge 0$ and the corresponding p-dimensional unit eigenvectors $\hat{{\varvec{h}}}_{1},\ldots ,\hat{{\varvec{h}}}_{p}$. We assume $P({\varvec{h}}_{j}^T\hat{{\varvec{h}}}_{j} \ge 0)=1$ for all j without loss of generality. We also define the following $n \times n$ dual sample covariance matrix$:$

$$\begin{aligned} {\varvec{S}}_{D}=(n-1)^{-1}{\varvec{P}}_{n}{\varvec{X}}{\varvec{X}}^T {\varvec{P}}_n =(n-1)^{-1}({\varvec{X}}-\overline{{\varvec{X}}})^T({\varvec{X}}-\overline{{\varvec{X}}}). \end{aligned}$$

Note that ${\varvec{S}}$ and ${\varvec{S}}_{D}$ share non-zero eigenvalues. Let us write the eigen-decomposition of ${\varvec{S}}_{D}$ as ${\varvec{S}}_{D}=\sum _{j=1}^{n-1}\hat{\lambda }_{j}\hat{{\varvec{u}}}_{j}\hat{{\varvec{u}}}_{j}^T$, where $\hat{{\varvec{u}}}_{j}=(\hat{u}_{j1},\ldots ,\hat{u}_{jn})^T$ denotes a n-dimensional unit eigenvector corresponding to $\hat{\lambda }_{j}$. In high-dimensional settings, we calculate $\hat{{\varvec{h}}}_{j}$ by using $\hat{{\varvec{u}}}_{j}$ as follows$:$

$$\begin{aligned} \hat{{\varvec{h}}}_{j}=\{(n-1)\hat{\lambda }_{j}\}^{-1/2}({\varvec{X}}-\overline{{\varvec{X}}}) \hat{{\varvec{u}}}_{j}. \end{aligned}$$

Note that ${\varvec{1}}_{n}^T {\varvec{S}}_D{\varvec{1}}_{n}=0$, so that ${\varvec{1}}_{n}^T\hat{{\varvec{u}}}_{j}=\sum _{l=1}^n\hat{u}_{jl}=0$ when $\hat{\lambda }_{j}>0$.

For high-dimensional data, the sample eigenvalues and eigenvectors get huge noise. See Jung and Marron (2009) and Shen et al. (2016) for the details. In order to remove the huge noise, Yata and Aoshima (2012) focused on a geometric representation of ${\varvec{S}}_{D}$ and proposed the NR method. If one applies the NR method, the $\lambda _{j}$s and ${\varvec{h}}_j$s are estimated by

$$\begin{aligned} {\tilde{\lambda }}_{j}= & {} \hat{\lambda }_{j}-\frac{\text{ tr }({\varvec{S}}_{D}) -\sum _{l=1}^j\hat{\lambda }_{l} }{n-1-j}\quad (j=1,\ldots ,n-2) \hbox { and } \end{aligned}$$

(17)

$$\begin{aligned} {\tilde{{\varvec{h}}}}_{j}= & {} \{(n-1){\tilde{\lambda }}_{j}\}^{-1/2} ({\varvec{X}}-\overline{{\varvec{X}}})\hat{{\varvec{u}}}_{j}\quad (j=1,\ldots ,n-2). \end{aligned}$$

(18)

Note that $P({\tilde{\lambda }}_j \ge 0)=1$ for $j=1,\ldots ,n-2$. We emphasize that ${\tilde{\lambda }}_{j}$s and ${\tilde{{\varvec{h}}}}_j$s have consistency properties under much milder conditions than $\hat{\lambda }_{j}$s and $\hat{{\varvec{h}}}_j$s. However, for the estimation of $x_{jl}={\varvec{x}}_{l}^T{{\varvec{h}}}_{j}$, Aoshima and Yata (2018a) showed that ${\varvec{x}}_{l}^T{\tilde{{\varvec{h}}}}_{j}$ involves a huge bias and gave a modification for all j, l by

$$\begin{aligned} {\tilde{{\varvec{h}}}}_{jl}=\Big (\frac{n-1}{n-2}\Big ) \frac{({\varvec{X}}-\overline{{\varvec{X}}}) \hat{{\varvec{u}}}_{jl} }{\{(n-1){\tilde{\lambda }}_{j}\}^{1/2}}=\frac{(n-1)^{1/2}({\varvec{X}}-\overline{{\varvec{X}}}) \hat{{\varvec{u}}}_{jl} }{(n-2){{\tilde{\lambda }}}_{j}^{1/2}}, \end{aligned}$$

where

$$\begin{aligned} \hat{{\varvec{u}}}_{jl}=(\hat{u}_{j1},\ldots ,\hat{u}_{jl-1},-\hat{u}_{jl}/(n-1), \hat{u}_{jl+1},\ldots ,\hat{u}_{jn})^T. \end{aligned}$$

Note that $\sum _{l=1}^{n}\hat{{\varvec{u}}}_{jl}/n_i=\{(n-2)/(n-1)\}\hat{{\varvec{u}}}_{j}$ and $\sum _{l=1}^{n}{\tilde{{\varvec{h}}}}_{jl}/n={\tilde{{\varvec{h}}}}_{j}$. Then, we estimate $x_{jl}$ by

$$\begin{aligned} {\tilde{x}}_{jl}={\varvec{x}}_{l}^T{\tilde{{\varvec{h}}}}_{jl} \ \hbox { for all }j,l. \end{aligned}$$

(19)

From Lemma B.1 in Aoshima and Yata (2018a), we have the following result.

Proposition 5

Assume (A-i) and (A-ii). It holds for $j=1,\ldots ,k$ that as $m \rightarrow \infty$

$$\begin{aligned} \sum _{l=1}^{n}\frac{({\tilde{x}}_{jl}-{x}_{jl})^2}{n \lambda _j}=O_P\Big ( \frac{\lambda _1^2/n+{\varvec{\mu }}^T {\varvec{\varSigma }}{\varvec{\mu }}}{\lambda _j^2}\Big ). \end{aligned}$$

Note that $\text{ Var }({x}_{jl})=\lambda _j$. If $\lambda _1^2/(n\lambda _j^2)=o(1)$, the normalized mean squared error in Proposition 5 tends to 0 under $H_0$ in (1). See Sect. 5.1 in Aoshima and Yata (2018a) for the details.

Estimation of $K_{1*}$

We use the CDM method given by Yata and Aoshima (2010) to estimate $K_{1*}$. Let $n_{(1)}=\lceil n/2 \rceil$ and $n_{(2)}=n-n_{(1)}$. Let ${\varvec{X}}_{1}=[{\varvec{x}}_{1},\ldots ,{\varvec{x}}_{n_{(1)}}]$ and ${\varvec{X}}_{2}=[{\varvec{x}}_{n_{(1)}+1},\ldots ,{\varvec{x}}_{n}]$. We define

$$\begin{aligned} {\varvec{S}}_{D(1)}=\{(n_{(1)}-1)(n_{(2)}-1)\}^{-1/2}({\varvec{X}}_{1} -\overline{{\varvec{X}}}_{1})^T({\varvec{X}}_{2}-\overline{{\varvec{X}}}_{2}), \end{aligned}$$

where $\overline{{\varvec{X}}}_{i}=[{\overline{{\varvec{x}}}}_{n(i)},\ldots ,{\overline{{\varvec{x}}}}_{n(i)}]$ with ${\overline{{\varvec{x}}}}_{n(1)}=\sum _{l=1}^{n_{(1)}}{\varvec{x}}_{l}/n_{(1)}$ and ${\overline{{\varvec{x}}}}_{n(2)}=\sum _{l=n_{(1)}+1}^{n}$ ${\varvec{x}}_{l}/n_{(2)}$. We estimate $\lambda _{j}$ by the j-th singular value, $\acute{\lambda }_{j}$, of ${\varvec{S}}_{D(1)}$, where

$$\begin{aligned} \acute{\lambda }_{1}\ge \cdots \ge \acute{\lambda }_{n_{(2)}-1}\ge 0. \end{aligned}$$

Yata and Aoshima (2010) showed that $\acute{\lambda }_{j}$ has several consistency properties for high-dimensional non-Gaussian data. Note that $E\{\text{ tr }({\varvec{S}}_{D(1)}{\varvec{S}}_{D(1)}^T)\}=\text{ tr }\left( {\varvec{\varSigma }}^2 \right)$. We estimate ${\varPsi }_{r}$ by $\widehat{\varPsi }_{1}=\text{ tr }({\varvec{S}}_{D(1)}{\varvec{S}}_{D(1)}^T)$ and

$$\begin{aligned} \widehat{\varPsi }_{r}=\text{ tr }({\varvec{S}}_{D(1)}{\varvec{S}}_{D(1)}^T) -\sum _{s=1}^{r-1}\acute{\lambda }_{s}^2\ \ \hbox {for }r=2,\ldots ,n_{(2)}-1. \end{aligned}$$

(20)

Note that $P(\widehat{\varPsi }_{r}\ge 0)=1$ for $r=1,\ldots ,n_{(2)}-1$. Then, Aoshima and Yata (2018a) gave the following result.

Lemma 1

(Aoshima and Yata 2018a) Assume (A-i) and (A-ii). Then, it holds that $\widehat{\varPsi }_{r}/{{\varPsi }_{r}}=1+o_P(1)$ as $m\rightarrow \infty$ for $r=1,\ldots ,k+1$.

Thus, we estimate $\text{ tr }({\varvec{\varSigma }}_*^2)$ by $\widehat{\varPsi }_{k+1}$. Let

$$\begin{aligned} \widehat{K}_{1*}=2\widehat{\varPsi }_{k+1}/\{n(n-1) \}. \end{aligned}$$

Then, from Lemma 1, under (A-i) and (A-ii), it holds that

$$\begin{aligned} \widehat{K}_{1*}/{K}_{1*}=1+o_P(1) \ \hbox { as }m\rightarrow \infty . \end{aligned}$$

Estimation of k

Recently, Jung et al. (2018) proposed a test of the number of spiked components for high-dimensional data. On the other hand, Aoshima and Yata (2018a) gave estimation of k in (A-ii) by using the CDM method. Let $\hat{\tau }_{r}=\widehat{\varPsi }_{r+1}/\widehat{\varPsi }_{r}\ (=1-\acute{\lambda }_{r}^2/\widehat{\varPsi }_{r})$ for all r, where $\widehat{\varPsi }_{r}$ given by (20). Note that $\hat{\tau }_{r}\in [0,1)$ for $\acute{\lambda }_{r}>0$. Then, Aoshima and Yata (2018a) gave the following results.

Proposition 6

(Aoshima and Yata 2018a) Assume (A-i) and (A-ii). It holds that as $m\rightarrow \infty$

$$\begin{aligned}&P(\hat{\tau }_{r}<1-c_r)\rightarrow 1 \ \ \hbox {with some fixed constant }c_r\in (0,1)\hbox { for }r=1,\ldots ,k;\\&\hat{\tau }_{k+1}=1+o_P(1). \end{aligned}$$

Proposition 7

(Aoshima and Yata 2018a) Assume (A-i), (A-ii) and (A-v). Assume also $\lambda _{k+1}^2/\varPsi _{k+1}=O(n^{-c})$ as $m\rightarrow \infty$ with some fixed constant $c>1/2$. It holds that as $m\rightarrow \infty$

$$\begin{aligned} P\Big (\hat{\tau }_{k+1}> \{1+(k+1)\gamma (n)\}^{-1} \Big ) \rightarrow 1, \end{aligned}$$

where $\gamma (n)$ is a function such that $\gamma (n)\rightarrow 0$ and $n^{1/2}\gamma (n)\rightarrow \infty$ as $n\rightarrow \infty$.

From Propositions 6 and 7, if one can assume the conditions in Proposition 7, one may consider k as the first integer $r\ (={\hat{k}}_{o},\ \hbox {say})$ such that

$$\begin{aligned} \hat{\tau }_{r+1}\{1+(r+1)\gamma (n)\}>1 \quad (r \ge 0). \end{aligned}$$

(21)

Then, it holds that $P({\hat{k}}_{o}=k)\rightarrow 1$ as $m\rightarrow \infty$. Note that $\widehat{\varPsi }_{n_{(2)}}=0$ from the fact that rank$({\varvec{S}}_{D(1)})\le n_{(2)}-1$. Finally, one may choose k as

$$\begin{aligned} {\hat{k}}=\min \{{\hat{k}}_{o},n_{(2)}-2\} \end{aligned}$$

in actual data analysis. According to Aoshima and Yata (2018a), we use $\gamma (n)=(n^{-1} \log {n})^{1/2}$ in (21). If ${\hat{k}}=0$, that is, the data is the NSSE model.

Appendix 2

Let $\psi _{r}=\lambda _1^2/(n^2\lambda _{r})+{\varvec{\mu }}^T{\varvec{\varSigma }}{\varvec{\mu }}/(n\lambda _{r})$ for $r=1,\ldots ,k$.

Proofs of Propositions 1 and 2

From the fact that $\lambda _{k+1}^2\le \text{ tr }({\varvec{\varSigma }}_*^2)$, we note that

$$\begin{aligned} K_{2*}&\le 4\varDelta _* \lambda _{k+1}/n =O( \varDelta _* K_{1*}^{1/2}). \end{aligned}$$

(22)

Then, under (A-iv), it holds that as $m\rightarrow \infty$

$$\begin{aligned} \text{ Var }(T_{\mathrm{DT}})/\varDelta _*^2=K_*/\varDelta _*^2\rightarrow 0. \end{aligned}$$

(23)

Thus, we can conclude the result of Proposition 2. On the other hand, from (22), under (A-ii) and (A-iii), it holds that $K_{2*}=o(K_{1*})$. Then, from Theorem 5 in Aoshima and Yata (2015), we can conclude the result of Proposition 1.

Proof of Theorem 1

From (S6.28) in Appendix B of Aoshima and Yata (2018a), we claim that for $r=1,\ldots ,k$,

$$\begin{aligned} \sum _{l<l'}^{n} \frac{ {\tilde{x}}_{rl} {\tilde{x}}_{rl'}-{x}_{rl} {x}_{rl'}}{n(n-1)} =O_P\Big \{\psi _{r}^{1/2}(\psi _{r}^{1/2}+\lambda _{r}^{1/2} /n^{1/2}+{\varvec{h}}_r^T{\varvec{\mu }})\Big \} \end{aligned}$$

(24)

as $m\rightarrow \infty$ under (A-i) and (A-ii). Here, by noting that $\text{ tr }({\varvec{\varSigma }}_*^2)/\lambda _k^2=O(1)$ and ${\varvec{\mu }}^T {\varvec{\varSigma }}{\varvec{\mu }}\le \varDelta \lambda _1$ we have that for $r=1,\ldots ,k$

$$\begin{aligned} \lambda _1^2/(n^2 \lambda _r)&=o(K_{1*}^{1/2});\quad {\varvec{\mu }}^T {\varvec{\varSigma }}{\varvec{\mu }}/(n \lambda _r)=O\{\varDelta _* \lambda _1/(n \lambda _r)\}=o(\varDelta _*); \\ \lambda _1^2/n^3&=o(K_{1*}); \ \hbox { and } \ {\varvec{\mu }}^T {\varvec{\varSigma }}{\varvec{\mu }}/n^2=O(\varDelta _* \lambda _1/n^2 )=o(\varDelta _* K_{1*}^{1/2}) \end{aligned}$$

under (A-ii), (A-v) and (A-vi), so that for $r=1,\ldots ,k$

$$\begin{aligned} \psi _{r}=o\big (\max \{K_{1*}^{1/2}, \varDelta _* \}\big ) \ \hbox { and } \ \psi _{r}^{1/2}\lambda _{r}^{1/2}/n^{1/2}=o\big (\max \{K_{1*}^{1/2}, \varDelta _* \}\big ). \end{aligned}$$

Also, note that $|{\varvec{h}}_r^T{\varvec{\mu }}|\le \varDelta ^{1/2}=O(\varDelta _{*}^{1/2})$ under (A-vi), so that for $r=1,\ldots ,k$

$$\begin{aligned} \psi _{r}^{1/2} {\varvec{h}}_r^T{\varvec{\mu }}=o\big (\max \{K_{1*}^{1/2}, \varDelta _* \}\big ). \end{aligned}$$

Thus, from (24) we can conclude the first result of Theorem 1. In addition, from the first result, it holds that

$$\begin{aligned} {\widehat{T}}_{\mathrm{DT}}=T_{\mathrm{DT}}+o_P( K_{1*}^{1/2} ) \end{aligned}$$

under (A-i) to (A-iii), (A-v) and (A-vi). Thus from Proposition 1, it concludes the second result of Theorem 1.

Proofs of Corollaries 1 and 2

From the first result of Theorem 1, it holds that

$$\begin{aligned} {\widehat{T}}_{\mathrm{DT}}/\varDelta _*={T}_{\mathrm{DT}}/\varDelta _*+o_P(1) \end{aligned}$$

under (A-i), (A-ii) and (A-iv) to (A-vi). Thus from Proposition 2, it concludes the result of Corollary 1. In addition, from Corollary 1 and Lemma 1, it holds

$$\begin{aligned} P\left( {\widehat{T}}_{\mathrm{DT}}/{\widehat{K}_{1*}^{1/2}}>z_{\alpha }\right) =P\left( {\widehat{T}}_{\mathrm{DT}}/{\varDelta _*}>z_{\alpha }{\widehat{K}_{1*}^{1/2}}/{\varDelta _*}\right) =P\{1+o_P(1)>o_P(1)\} \rightarrow 1 \end{aligned}$$

under (A-i), (A-ii) and (A-iv) to (A-vi). It concludes the result of Corollary 2.

Proof of Theorem 2

First, we consider the case when (A-iii) is met. We note that $K_*/K_{1*}\rightarrow 1$ as $m\rightarrow \infty$ under (A-ii) and (A-iii). Then, from Theorem 1 and Lemma 1, under (A-i) to (A-iii), (A-v) and (A-vi), we have that

$$\begin{aligned}&P\left( {\widehat{T}}_{\mathrm{DT}}/{\widehat{K}_{1*}^{1/2}}>z_{\alpha }\right) \nonumber \\&\quad =P\{ \left( {\widehat{T}}_{\mathrm{DT}}-\varDelta _*\right) /K_{*}^{1/2}> \left( z_{\alpha }{K}_{1*}^{1/2}-\varDelta _*\right) /K_*^{1/2}+o_P(1)\}\nonumber \\&\quad =\varPhi \{ \left( \varDelta _*-z_{\alpha }K_{1*}^{1/2}\right) /K_*^{1/2}\}+o(1) =\varPhi \left( {\varDelta }_*/{K_{1*}^{1/2}}-z_{\alpha }\right) +o(1). \end{aligned}$$

(25)

It concludes the result about Size in Theorem 2. On the other hand, under (A-iv), from (23), it holds that

$$\begin{aligned} \varPhi \{ \left( \varDelta _*-z_{\alpha }K_{1*}^{1/2}\right) /K_*^{1/2}\}=1+o(1). \end{aligned}$$

Hence, from (25) and Corollary 2, by considering a convergent subsequence of $\varDelta _*^2/K_{1*}$, we can conclude the result about Power in Theorem 2.

Proofs of Propositions 3 and 4

By noting that $E({\varvec{x}}_l-{\varvec{\mu }})={\varvec{0}}$ ($l=1,\ldots ,n$) and $\text{ Var }(T_{{\varvec{\mu }}})=K_{1*}$, the results are obtained straightforwardly from the results of Proposition 1 and Theorem 1.

Proof of Theorem 3

By noting that ${\varvec{\mu }}^T {\varvec{\varSigma }}{\varvec{\mu }}\le \varDelta \lambda _1$ we have that for $r=1,\ldots ,k$

$$\begin{aligned} \lambda _1^2/(n^2 \lambda _r)&=O(\lambda _1/n^{3/2})=o(\varDelta );\quad {\varvec{\mu }}^T {\varvec{\varSigma }}{\varvec{\mu }}/(n \lambda _r)=O\{\varDelta \lambda _1/(n \lambda _r)\}=o(\varDelta ); \\ \lambda _1^2/n^3&=o(\varDelta ^2 ); \ \hbox { and } \ {\varvec{\mu }}^T {\varvec{\varSigma }}{\varvec{\mu }}/n^2=O(\varDelta _* \lambda _1/n^2 )=o(\varDelta ^2) \end{aligned}$$

as $m\rightarrow \infty$ under (A-vii). Thus, from (24) it holds that

$$\begin{aligned} {\widehat{T}}_{\mathrm{DT}}/\varDelta =T_{\mathrm{DT}}/\varDelta +o_P(1) \end{aligned}$$

under (A-i), (A-ii) and (A-vii). Then, from Proposition 2, we can conclude the result of Theorem 3.

Proof of Proposition 5

From Lemma B.1 in Appendix B of Aoshima and Yata (2018a), under (A-i) and (A-ii), it holds for $j=1,\ldots ,k$ that as $m \rightarrow \infty$

$$\begin{aligned} \sum _{l=1}^{n}\frac{({\tilde{x}}_{jl}-{x}_{jl})^2}{n}=O_P(n\psi _{j}). \end{aligned}$$

Thus, we can conclude the result of Proposition 5.