Introduction

Person missingness is an enigmatic yet frequent phenomenon that can have negative consequences for the missing person, their relatives, and society. Older adults (e.g., those above 60 years old) may be vulnerable to going missing. Aging can negatively impact cognitive functions, such as attention, memory, and/or cognitive control [1,2,3]. Age also increases the risk for depression, cognitive impairment, or dementia [4]. For example, older adults in the early stages of dementia may go missing while wandering [5, 6], and at any stage of dementia can older adults be involved in one or more missing incidents [7]. In other cases, older adults with or without depressive symptoms might go ‘voluntarily’ missing to plan or commit suicide [8]. Furthermore, elder abuse, including social isolation, loneliness, or neglect [9] can also modify the risk of an older person going missing. The negative consequences on mental health or physical integrity [10] might also be more severe in older adults because they may become more disoriented in time, place, or even person while missing. Greater disorientation, in turn, decreases the probability of a missing older person being found or their being able to return home by themselves. In addition, chronic medical conditions requiring multiple medications are more prevalent in older adults [11], which in turn makes finding the missing older person even more imperative. Therefore, a better understanding of the factors that modify the probability of finding an older adult reported missing can shed light on the phenomenon of missingness in general but can also have practical implications for addressing the problem more effectively.

Numerous individual and environmental factors can modify the probability of finding a missing older adult [12], through the clues and guidance they offer to the missing case investigators [13] and/or to the missing older person (e.g., to help them return). For example, a missing person’s greater cognitive resources or tighter social bonds could increase the probability of their returning if they went unintentionally missing. Moreover, a more organized environmental context in which the missingness occurs might provide the investigator searching for the missing person with better clues (see, e.g., the experimental work of [14] for the role of spatial information in the search), while at the same time can help the missing person find their way back. Therefore, the present work aimed to predict the probability of a missing older person being found and identify the factors relevant for that prediction based on supervised machine learning models.

Machine learning is an artificial intelligence tool that allows a computer to infer the rules that are necessary to build predictions automatically [15, 16]. Machine learning classification tasks are a suitable tool [17, 18] for the study of complex social and psychological phenomena [19, 20], such as missing person cases. Previous work has utilized machine learning methods to investigate missing persons’ profiles or to predict the probability of finding them. Accordingly, pioneer work used data mining to draw rules to predict the outcome of missing person cases and thereby support the intuitions of police investigators involved in those cases [21]. Recent work has also proposed utilizing machine learning models during the missing person search (e.g., with face recognition [22] or feature-based multimodal data fusion [23]). Other methods are using data from global positioning system tracking devices to attempt to predict typical locations [24] or mobility patterns [25] of individuals with dementia, who may be at a higher risk of wandering and getting lost, but who are not yet missing.

A recent study with a sample of missing persons showed an adequate performance of models, such as K-nearest neighbors and decision trees, to predict whether a missing person is found alive vs. dead and whether a missing person is found (independent of whether alive or dead) vs. not found, respectively [26]. This previous study was based on data on missing persons of all ages reported missing in 2017. Another recent study on an overlapping sample used the Waikato environment for knowledge analysis and found profiles that link the causes of missingness (e.g., ‘voluntary’ missing vs. forced disappearance) to particular places and age groups [27]. However, despite the particular conditions and vulnerability of older adults, no study has, to the best of our knowledge, investigated the phenomenon of older adults who go missing in Colombia for reasons different from forced disappearance over the last 50 years.

In sum, the present study aimed to identify individual and environmental factors that predict whether a missing older adult will be found, using supervised machine learning algorithms. To do so, we used open data provided by the information system of the missing persons and cadavers network (Sistema de Información Red de Desaparecidos y Cadáveres, SIRDEC) of the national institute of legal medicine and forensic sciences of Colombia. Our specific goals were (i) to find the probability for a missing older person to be found, using classification algorithms and (ii) to identify which individual or environmental characteristics of missing persons contribute to that probability, using interpretative machine learning.

Materials and methods

Data

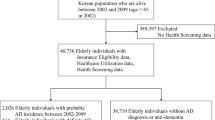
The present study used the open data provided by the SIRDEC of the Colombian National Institute of Forensic Medicine and Forensic Sciences (Instituto Nacional de Medicina Legal y Ciencias Forenses de Colombia) through the Open Data initiative of the Colombian government (Datos Abiertos Colombia), available on the website: (https://www.datos.gov.co/Justicia-y-Derecho/Desaparecidos-Colombia-hist-rico-a-os-1930-a-junio/8hqm-7fdt). Data were downloaded on August 5, 2021. The original version of the database included 162,401 entries (i.e., examples) of persons who went missing at any time in the period from 1930 to June 2021. The present study was conducted in three phases: (i) data cleaning and selection of relevant examples and features, (ii) descriptive analyses, and (iii) identification of models, model assessment, and interpretation.

Data and variable preparation

In the first phase, examples with null information on the variables Age (n = 202) and Date of missingness (n = 129) were excluded. This was done so for two reasons. First, to ensure that an example did correspond to an older adult and, second, to ensure the accuracy of the date of missingness. Examples whose cause of missingness was “allegedly forced disappearance” (n = 32,403) were further excluded based on the study's aim. The reason for doing so was that this cause makes it more difficult to find predictive patterns, as it depends on arguably more complex factors (e.g., social conflict and violence), external to the missing person. After this step, the following exclusion criteria were applied: age at the missingness below 60 years, current status “Found dead”, and country of missingness other than Colombia. These criteria left 7855 valid examples.

The predictor variables included were date and place of missingness—as ‘environmental’ or extrinsic variables—and age, sex, marital status, education level, and vulnerability factor—as ‘individual’ or intrinsic variables. Other variables initially available, such as ‘country of birth’ or ‘racial ancestry,’ were excluded because they had the same value across almost all included examples (i.e., “Colombia” and “mixed”, respectively) and were not deemed relevant in the current sample. In the last part of this phase, some of the variables were transformed for the model training step (Table 1), and a descriptive analysis was then conducted for each variable, to identify the data distribution, as well as missing values.

Table 1 Variable transformation
Full size table

Data preprocessing and modeling

The third phase comprised preprocessing and modeling. In the preprocessing, first, data were split into training and testing sets, using 80% (n = 6284) and 20% (n = 1571) of the data, respectively. Data were randomly split using the train_test_split function, stratifying by class (i.e., “Still missing” and “Found alive”). This step ensured that both training and testing data sets had the same class representation, as 65.8% (n = 5166) of the examples had a “Still missing” label and 34.2% (n = 2689) a “Found” label in the entire data frame. Next, missing values were imputed in both training and testing sets, using the corresponding mean of the numeric variables with missing values (i.e., Education and Municipality) in the training data. Likewise, missing values were imputed in both training and testing sets, using the corresponding mode of the categorical variables with missing values (i.e., Vulnerability and Relationship) in the training data. Imputation was done through the SimpleImputer function, fit in the training data, and then applied to both training and testing data sets.

Next, a simple, reference (or base) model, based (only) on the training data, was proposed. This rule-based model was simply used to judge the performance of the machine learning models. Additionally, numeric and categorical variables were transformed with standard scaling and one-hot encoding, respectively, to have only numeric features as input to the models. Similarly, the outcome variable was adjusted with the Label Encoder function. Again, variable adjustment was done fitting the training data only (i.e., to avoid data leakage) and was then applied to both (training and testing) data sets.

The class “Still missing” had almost twice the number of examples in the class “Found” (i.e., 65.8% vs. 34.2% in both the training and the testing data). Therefore, we trained the models on resampled data in the training set only as a means to avoid models being biased toward the majority class. A balanced (i.e., 50/50) distribution of classes in the training data was thus achieved through (a) synthetic minority oversampling technique (SMOTE) (ntrain(1) = ntrain(2) = 4133) and (b) under-sampling (ntrain(1) = ntrain(2) = 2151). For completeness and transparency, results are also presented using all training data available during model training (i.e., without resampling; Table 2).

Table 2 Mean performance in the testing data (with tenfold cross-validation) of the three best models with and without class imbalance fix (sorted based on Accuracy)
Full size table

In the modeling part, a global analysis of classification algorithms (Fig. S1) was first conducted with tenfold stratified cross-validation (outcome variable, “Found”: 0 = “no”, 1 = “yes”). Next, the three models with the highest accuracy scores (i.e., number of correct predictions/total number of predictions) for each resampling strategy were selected, from which their confusion matrices were examined. Other performance metrics, such as recall (i.e., identification of true positive cases out of all possible positive cases), precision (i.e., identification of true positive cases out of all cases identified as positive), the area under the curve (AUC) of the receiving operator characteristic (ROC) curve (i.e., ability to distinguish between positive and negative classes), and F1-score (i.e., harmonic mean weighting sensitivity and specificity), were also evaluated. The extraction of feature importance for the interpretation of model predictions was done with the SHapley Additive exPlanation (SHAP) values [28]. The three analytical phases were conducted in Python (v. 3.6) with the PyCaret (https://pycaret.org/) (v. 2.3.6) and Scikit Learn (v. 1.0.2) (https://scikit-learn.org/stable/) [29] libraries.

Data availability

The data and code on which the results of the present study are based are openly available and can be found at [https://osf.io/agz5e/].

Results

Descriptive statistics

The distribution of “Found” and “Still missing” examples across months and years is presented in Fig. 1. Overall, “Still missing” cases appear sparse before the year 1980, and “Found” cases appear sparse before 2000. Across the entire sample, the mean age of examples with “Found” status was 71.35 ± 8.36 years old (vs. 71.45 ± 9.91 years old of “Still missing”) (Fig. 2) and the mean education was 5.12 ± 3.53 years (vs. 4.85 ± 3.39 years of “Still missing”). Most of the examples were male (72.8% “Found” vs. 83% “Still missing”) and corresponded to cases of older adults with no evident vulnerability factor (74.3% “Found” vs. 71.7% “Still missing”) and with a current relationship (40.2% “Found” vs. 49.2% “Still missing”) at the time of the missingness report. Almost half of the missing cases happened in municipalities with a population below 1 million inhabitants, almost 36% occurred in the capital city alone (with approx. 8 million inhabitants), and a greater proportion of “Found” cases occurred in municipalities with a population above 2 million inhabitants (Fig. 3). The majority of cases were reported less than 5000 days ago (i.e., 14 years approx.), with this number being the upper bound for almost all cases with “Found” status (Fig. 4).

Fig. 1
figure 1

Strip plot of the per-class distribution across time. The month and year of the missingness report are shown for each class (i.e., ‘Found’ and ‘Still missing’) in the entire data frame

Full size image
Fig. 2
figure 2

Histogram of age (in years) by the missing status of the entire data frame (n = 7855). Age distribution was similar in both status groups. The light blue line above the histogram bars represents the empirical cumulative distribution function or the proportion of examples that are below each unique value in the data set

Full size image
Fig. 3
figure 3

Histogram of the municipality size (in million inhabitants) of the place where the missing case was reported to occur by missing status (“Still missing” or “Found”). The light blue line above the bars indicates the cumulative proportion of the examples with status “Found”: the greatest proportion of cases with status “Found” is observed in municipalities with a population above two million inhabitants

Full size image
Fig. 4
figure 4

Histogram of date of missingness (in number of days since the report until July 30, 2021) by missing status (“Still missing” or “Found”). The light blue line above the bars indicates the cumulative proportion of examples with the status “Found:” more than 90% of the cases with the status “Found” have a report date below 5000 days or 14 years approximately (i.e., went missing in 2007 or later). Note that this variable represents the temporal context of the missingness (i.e., the when) and not the actual duration of the missingness for the “Found” cases, which is not included in the data

Full size image

Base model

Following the insights of the descriptive analysis, a base model was formulated as the reference model. This model only served the purpose of allowing us to judge the performance of the machine learning models—but not to draw any conclusions. The base model was the mean of the elapsed timeFootnote 1 (in days) since the missingness report, which was the predictive rule for the outcome, i.e., whether the missing older person will be found. Note that we chose the mean time elapsed as the rule because of its simplicity and because it can easily be estimated from existing data. This rule (4474.8 days in the present data) was calculated in the training set only and then applied to the testing set, which yielded 63% accuracy (Table 2). Machine learning model performance was thus compared and judged against this ‘baseline’ 63% accuracy.

Machine learning models

The three ‘best’ models for each class imbalance fix strategy are listed in Table 2 (see Supplementary Table S1 for a report of all models’ metrics without using class imbalance fix during model training). The performance was similar among them in all metrics across training data resampling strategies (including no resampling). However, Recall was substantially improved when under-sampling was used in the training data. Both the gradient boosting classifier (GBC) and the light gradient boosting machine (LGBM) were among the best models, independent of whether or not class imbalance was fixed.

We examined in greater detail the GBC trained with undersampled training data, as both with SMOTE and without imbalance fix, the minority class (i.e., “Found”) was penalized in most metrics even in the most accurate models (see Supplementary Figs. S1 and S2). As can be observed in the confusion matrix (Fig. 5), 17% of the examples were false negatives (i.e., “Found” cases that were predicted to be “Still missing”), whereas 41% of the examples were false positives (i.e., “Still missing” cases that were predicted to be “Found”). The false-positive rate in particular represents a substantial improvement with respect to the reference or base model, in which this percentage was at the chance level (false positives) (Supplementary Fig. S3). Moreover, the AUC score increased by at least 7% with respect to the reference model in all of the best models across all resampling strategies (Table 2 and Fig. 6). The AUC was similar across the best machine learning models (i.e., 0.76–0.79; also see Supplementary Figs. S5 and S6 for comparison). Finally, the GBC model that used under-sampling of the training data showed a higher recall metric (i.e., 0.83) and a higher F1-score (i.e., 0.63) in the class “Found” (i.e., the class of interest; Supplementary Fig. S4) compared to both the LGBM model trained using SMOTE (Supplementary Fig. S2) (recall: 0.65; F1-score: 0.60) and the GBC model trained without resampling the training data (recall: 0.52; F1-score: 0.55; Supplementary Fig. S2).

Fig. 5
figure 5

Confusion matrix of the gradient boosting classifier model with undersampling of the training data. Classification scores are normalized per row. For the class “Found”, 83% of the cases are correctly classified, whereas 59% of the cases are correctly classified for the class “Still missing”

Full size image
Fig. 6
figure 6

Receiver Operating Characteristic (ROC) curve for the gradient boosting classifier (GBC). The true-positive rate is higher than the false-positive rate. The area under the curve (AUC) values were similar across machine learning models (shown in Table 2). The dotted black line represents a ‘dummy’ classifier with AUC = 0.50

Full size image

Relevant features for prediction in missing older person cases

The second goal of the present study was to identify the factors that determine whether an older adult who went missing in Colombia will be found later. Accordingly, we examined the feature importance, i.e., the relative feature contribution to the prediction in the GBC model (Fig. 7). The features identified were the number of days elapsed since the report of missingness, the size of the municipality (in number of inhabitants) where the missingness occurred, the missing person’s sex, and the age of the missing person at the time of the report. Some examples of the values of these variables as well as of the specific predictions in the testing data set can be observed in Supplementary Fig. S7.

Fig. 7
figure 7

Feature importance of the GBC model with under-sampled training data. The features used for the prediction are shown by relevance order on the y-axis and the SHAP (SHapley Additive exPlanations) values are shown on the x-axis, with negative values representing the label “Still missing” and, the positive values, the label “Found”. Every dot is an example of the training data set. The color scale codes for a particular example’s value: blue dots, low values; purple dots, intermediate values; red dots, high values

Full size image

To identify the features that contributed the most to model prediction, we examined the feature importance as a function of the SHapley Additive exPlanation (SHAP) values (Fig. 7) for the GBC model with under-sampled training data. A longer time elapsed (in days) since the missingness report, a small municipality (i.e., with a relatively lower population), being male, and more advanced age of the missing person were all associated with a decreased probability of a missing older adult to be found later.

Potential impact of societal changes over 90 years on missing person cases

While the majority (i.e., 83.8%) of our examples were reported missing in 2000 and later, our data spanned missing older person cases from 1930 to mid-2021 (Fig. 1). Many societal changes have occurred during these 90 years, and the incoming new technologies have certainly allowed improving the search, report, and recording of missing person cases. Therefore, post hoc, we restricted the examples to those of the past 20.5 years only (n = 6582; “Found:” 2638; “Still missing:” 3944), to reduce the potential impact of societal and technological changes in model training and performance. We thus repeated model training under-sampling the training data in line with that described in the previous two sections. Table 3 lists the most accurate models. In agreement with the ‘1930–2021’ data results, GBC outperformed the reference model in all metrics. The machine learning model metrics remained robust and were similar to those obtained without restricting the data to the most recent years (Table 2). In contrast, the rule-based model—heavily dependent on the elapsed time—notoriously decreased its performance. Finally, the feature importance was also comparable to that using the ‘1930–2021’ data (Fig. 8).

Table 3 Mean performance (with tenfold cross-validation) in the testing data (restricted to missingness in 2000 and later) of the models with the highest accuracy
Full size table
Fig. 8
figure 8

Feature importance of the GBC model in data with missingness in the year 2000 and later. The features used for the prediction are shown by relevance order on the y-axis and the SHAP (SHapley Additive exPlanations) values are shown on the x-axis, with negative values representing the label “Still missing” and, the positive values, the label “Found”. Note that the feature importance may slightly differ from that observed when the ‘1930–2021’ data are used for model training (Fig. 7). Every dot is an example of the training data set. The color scale codes for a particular example’s value: blue dots, low values; purple dots, intermediate values; red dots, high values

Full size image

Discussion

The present study sought to identify the individual and environmental factors that predict whether a missing older adult will be found, using supervised machine learning. Results showed that the best models for this purpose were those based on ensembles and, more specifically, on gradient boosting; in particular, light gradient boosting machine (LGBM) and gradient boosting classifier (GBC). The classification error of the machine learning models (i.e., between 28 and 32%) was below the level of error of a base model (i.e., 37%) that used the mean elapsed time (in days) since the missingness report in the training data as the prediction rule. This finding indicates that machine learning models can inform us about the factors predicting the outcome of missing older person cases while at the same time yielding a prediction for each individual case. The factors identified as crucial in predicting that a missing person will be later found were less time elapsed since the missingness report, a relatively medium-sized municipality where the missingness occurs, female sex, and a less advanced age of the missing person. The machine learning model performance was robust even when only data from the last 20.5 years were used for model training and testing. Together, the present findings provide insights into the complex social phenomenon of missingness in older adults and potentially bear practical implications.

The most accurate classification models in the current study were models based on decision tree ensembles, e.g., gradient boosting [30, 31] and Random Forest [32]. This result aligns well with previous reports [21, 26]. Nevertheless, the majority of classifiers (e.g., K-Neighbors, SVM with linear kernel, Linear Discriminant Analysis; also see Table S1) performed well on most metrics. Notable examples in the current study were the GBC and the LGBM, which had the highest performance metrics, independent of whether or not class imbalance was fixed during model training. GBC is, in simple terms, an iterative model ensemble, in which a new, weak model is each time trained taking into account the ensemble’s previously learned error (see, e.g. [33]). LGBM is a special implementation of the gradient boosting decision tree algorithm [34]. In the present study, a GBC model trained with balanced data through the undersampling of the dominant class (i.e., “Still missing”) allowed us to maximize the recall metric in both classes with respect to the reference model. This result implies that GBC reduced the false-positive rate (i.e., the prediction that a case is “Found” when, in reality, it is “Still missing”) from 50 to 41% compared to the reference model, as reflected in a greater AUC of the ROC curve (i.e., 79% of GBC vs. 69% of the reference model). In practical terms, this result means that our machine learning model can correctly predict at least one missing person case more in every ten cases, compared to a data-informed, mean-based model (Fig. 5 and Fig. S3).

To further put those results in perspective, first, without a model any reliable probability for the outcome of a missing older person case can hardly be generated—or such probability will solely be based on the intuition of the investigator of the missing case. Second, with the current reference, data-informed model, only the time elapsed since the missingness informs the prediction (i.e., above or below ~ 12 years). Here it is worth mentioning that our data-driven reference (or base) model is congruent with empirical reports on younger samples of forced disappearance in Colombia, with an average elapsed time of 13.38 ± 6.88 years [35]. Using the mean time elapsed since the missingness report as the rule implies that the reference model is mostly useful as an explanatory model but less useful as a predictive model, i.e., for the new cases—all of which will inherently have an elapsed time since the missingness below 12 years. Nevertheless, the value of the base model lies in that it provides a meaningful baseline to compare the machine learning models. Lastly, and in stark contrast to the previous two options, with the machine learning model identified in the current study, individual predictions can be generated on new missing person cases. This result represents a significant step toward providing robust, computationally based support [19] for the investigation of missing older person cases and for the study of person missingness as a social phenomenon from a quantitative, flexible approach [36]. In future, some efforts could be spent on training and testing more complex models, e.g., those based on neural networks. However, these models tend to perform suboptimally with tabular data [37] and may not generalize well [38].

Our study also identified the features that were critical for the missingness outcome prediction. As expected, both intrinsic and extrinsic factors proved crucial. Specifically, the missing person’s age, which relates to the person’s cognitive [1,2,3,4, 39] or global health [11] state, or the missing person’s sex, which relates to the reason for going missing [40] or the type of behaviors in which the person engages during the missingness, was important. Similarly, the date of missingness or the size of the municipality in which the missingness occurred was relevant, as they are indirectly associated with the structure and organization of the physical and social environment that surrounds the missingness. On the one hand, these temporal and place factors most probably reflect the societal change throughout the second half of the twentieth century and the beginning of the twenty-first century (e.g., in terms of infrastructure, technology, communications, population growth, and social organization). On the other hand, they may also reflect the increasing acknowledgment of missing persons as a common social problem and the corresponding enactment and refinement of the recording of and search for missing persons in Colombia. Overall, these results lend themselves to future human- and/or functionally grounded evaluations as another means of judging the performance [41] of the models identified in the present study.

Contrary to our expectations, other intrinsic factors did not seem to contribute significantly to the prediction. These factors were the vulnerability, relationship status, and education level of the missing older person. One possible explanation for these negative findings is the relatively low data variability in these features, in addition to the high proportion of values that were missing for them. Therefore, in future, quantifying these variables could help elucidate whether they do have an impact on the probability of finding the missing person. Particular examples in this regard are recording the number of people with whom the missing person was living; the number of vulnerability factors (e.g., medical, social, cognitive) of the missing person; the number of years of education of the missing person; the number of previous missing incidents, if any; or a ‘closeness’ degree depending on who reports the missingness.

Three dimensions of behavior can typify a missing adult person: dysfunctional (i.e., mental problems including dementia [7]), escape (i.e., people who decide or are driven to go missing to gain independence or flee from difficulties), and unintentional (i.e., under the influence of others or as a result of an accident or communication problem with those close to them) [42]. The typologies that most characterize older adults (i.e., age above 60 years) are dysfunctional and escape [42]. This particularity, coupled with the multiplicity of environmental circumstances associated with the missingness, implies that the consequences of missingness can impact not only the missing person but also those directly or indirectly related to them [43]. For example, in many cases, relatives find it difficult to mourn, even many years after their relative went missing [35]. In this context, the insights of the present study might have practical implications for both the task force dealing with missing person cases and the psychosocial work with the family of a missing older adult. In particular, greater societal awareness can be raised toward the missingness outcome of the oldest–old, especially men (e.g., by a wide implementation of identification and reorientation strategies, [44]). Similarly, targeted improvements can be pursued in the smaller municipalities in the missing person task forces. Furthermore, psychosocial professionals might utilize the outcome prediction in a specific case to make better data-informed decisions that help them tailor their counseling, e.g., by emphasizing the coping strategies that may be more relevant for that specific case.

The present findings ought to be considered taking some limitations into account. First, the present data were not collected for scientific research purposes, and, hence, do not include all theory-relevant details or depth in the information or might not be accurate. Second, there was a high number of missing values, which we handled through methods of simple imputation. Thus, there might be a certain degree of uncertainty in the predictions due to those aspects. Third, and as a consequence of that, the data were noisy and might not have allowed for better model performances. However, it is important to bear in mind that missing person cases are an inherently complex social phenomenon. More importantly, every percentage point gained with any given model translates into one missing person case that is predicted correctly, which ultimately justifies the model’s use and further improvement. Finally, future studies should determine whether the present findings and conclusions generalize also to missing person cases involving younger adults or children or in which there was forced disappearance or the outcome was fatal, or to missing older person cases in other countries. Nevertheless, despite its limitations, the current study yielded insights for a better understanding of the factors that predict that a missing older adult in Colombia will be later found and set a precedent in terms of artificial intelligence algorithms that can be suitable for addressing the problem of outcome prediction in cases of missing older adults.

Conclusion

The present study identified the individual (such as age and sex) and environmental (such as elapsed time and place size of the missingness) factors that predict whether a missing older adult will be found, using a supervised machine learning model based on ensembles. The present findings suggest that there are intrinsic and extrinsic factors at play, all of which can influence the outcome prediction. These factors are the missing person’s cognitive state before or during the missingness, the type of behaviors in which the person engages during the missingness, and the structure and organization of the physical and social environment that surrounds the missingness. Additionally, this machine learning model not only reduced the reference, data-informed model error by 5% and increased the positive rate discrimination (i.e., AUC-ROC curve) by 10%, but it did also enable us to generate individual predictions for new, unseen cases. Overall, the present work bears practical implications for missing older person cases, as it can help inform the decision of the professionals involved in both the search for missing older persons and the psychosocial work to support the missing person’s relatives.