Introduction

Research using big data has been conducted from the viewpoints of “Volume,” where the amount of data is too large to be handled by conventional tools, “Variety,” where the types of data and the formats used to handle them vary, and “Velocity,” where data are generated and updated frequently [1]. As social science research advances, it has become clear that big data research poses the following major problems. The data characteristics of “Incompleteness,” which implies often lacking the data needed for research, and “Nonrepresentative,” which does not reflect a random sample from the population, have been pointed out by sociologist M. J. Salganik of Princeton University [2]. These very critical issues are at the heart of big data science. To solve these issues, this paper proposes a method to interpolate the non-random missing values in commercial financial statements’ big data.

From around 2012, national statistics offices and international organizations began to consider the use of big data in official statistics [3]. In recent years, various works have pointed out the need to develop interpolation and resampling techniques to fill in missing data to ensure the accuracy of big data in handling official statistics [4,5,6,7,8]. The major interpolation techniques include the \(k-\)means method of finding and replicating similar samples without missing data [9], the method of finding and interpolating relationships between elements using matrix decomposition, such as principal component analysis [10], and the method of Bayesian estimation of missing values [11, 12]. For the interpolation of big data, a method applying a decision tree is often adopted from the viewpoint of calculation cost [13, 14]. In addition, a report by the German Statistical Office indicated that, in recent years, clustering has become the most common use of machine learning in official statistics and that interpolation of missing data has become the second most common use, in which the use of extended decision trees is a promising technique for interpolating missing data [15].

In this paper, we focus on the world’s largest commercial dataset on firm finance, ORBIS by Bureau van Dijk [16], which is widely used in various researchers and government agencies. Bureau van Dijk has contracted with data vendors around the world to collect the last 10 years of corporate information held by each vendor, combines these sources in the same format, and sells the resulting product. The latest ORBIS contains financial data of approximately 400  million listed and unlisted firms from around the world, and the number of firms included in the database continues to grow with each edition. However, although the coverage of large-scale firms is high in the balance sheets (BS) and profit and loss statements (P/L) published in ORBIS, it has been found that the actual coverage depends on the firms’ sizes, countries, years, and key financial items, and that data coverage tends to increase over time [6]. This is because the main users of ORBIS are institutional investors who are not interested in old data, small-scale firms, or minor financial items. This causes “Incompleteness” and a “Nonrepresentative” nature of big data [2].

ORBIS is frequently used by various researchers to understand global economic trends and the role of policies across firms within and across countries[17,18,19,20,21,22,23]. However, the OECD report cautions that we should be aware of missing data when using ORBIS [6]. For example, in the field of Econophysics, which analyzes corporate financial information of hundreds of millions of firms worldwide, researchers frequently use ORBIS to investigate the functional form of firm-size distribution, such as operating revenue, number of employees, assets, and profit of the firms in each country. However, the completeness of data is assumed implicitly, and the effect of non-random missing data on the functional type is not sufficiently considered [24,25,26].

A previous study showed that the overall firm-size distributions of number of employees and receipts in dollars follow Zipf’s law (a power law with an exponent of \(-1\)), using United States Census data, which is considered exhaustive [27]. To a lesser extent, it is important to realize that all data, large and small, should be included in the analysis when discussing the scale to which Zipf’s law will hold, which can be done by analyzing firm-size variables in Portugal, Austria, and France, where full data are available [28]. As stated above, various works have demonstrated that there is a significant difference in firm-size distribution between the total data and all available data, including missing data. However, the interpolation of missing data is difficult in light of Zipf’s law. Because the distribution in a large-scale range obeys Zipf’s law, the mean and variance of the variables diverge when we integrate it to infinity [29]. Therefore, it is difficult to correctly estimate the mean square error, the mean absolute error, and the coefficient of determination used in the machine learning model. Because firm sizes often take zero or negative values, logarithmic transformations are not always possible. Net income is operating revenue minus costs, therefore it can be negative when the latter exceeds the former. And inactive firms have zero operating revenue.

To solve this problem, we use the prediction error of the financial item converted by the inverse hyperbolic function as the evaluation function [30]. Using CatBoost [31], we interpolate non-random missing values of financial items with high accuracy without breaking Zipf’s law. Furthermore, it should be noted that Zipf’s law breaks down due to the missing data in financial items within the range normally considered to be mid-scale firms. In this learning, the missing information of the explanatory variable itself is useful for predicting the objective variable. Our method learns about non-random situations in which missions occur, and at the same time predicts missing data by regression.

In this paper, we find that the rate of missing data varies depending on the country and the type and size of financial items. Accordingly, we interpolate non-random missing financial values from the previous- and/or next-year values of the same financial item, the values of the other financial items, and the conditions of missing data using CatBoost. We confirm the effectiveness of this method by predicting non-missing financial values as objective variables and comparing them with true values. To justify this approach, we assume that the probability of missing an objective variable is the same if the explanatory variables are identical. In the data interpolated by this method, we confirm that the range of firm-size variables in which Zipf’s law is established becomes wider than before interpolation.

The structure of this paper is as follows. "Data" describes a dataset for machine learning as well as the object of analysis in this paper. It is important that the time course of the missing data rate and the missing data rate by financial item for the same year show non-randomness, depending on the country, financial item, and firm size. In addition, the missing data rate of the value of a financial item is highly dependent on the missing value of the financial item in the previous or next year. "Method" describes the machine learning models used in this paper. First, we use an inverse hyperbolic function to convert the value of a financial item as a target variable. Then, we explain two types of models for interpolating missing values according to the two types of conditions surrounding missing objective variables using CatBoost. "Results" describes the verification of the accuracies and stabilities of the models and the properties of the firm-size variables in which non-random missing values are interpolated. Here, we introduce a method to interpolate non-random missing values by combining these two models. Finally, "Conclusions" summarizes this paper and describes future issues.

Data

This paper discusses the extent to which missing corporate financial data can be interpolated by machine learning using BS and P/L for all firms in ORBIS 2020 and 2016 editions. We also discuss how the firm-size distribution, which has not been sufficiently observed due to missing data, can be corrected. Tables 1 and 2 show the number of major financial items by country in 2017 for 10 representative countries (USA, China, United Kingdom, Japan, Portugal, Russia, Brazil, Colombia, Morocco, and India), where ORBIS lists a large number of firms with financial information and relatively high operating revenue compared to the other financial items.

First, "Missing data rate over time" describes the time variation of the missing data rate. In "Missing data rate by financial item", we discuss the differences in missing data rates among financial items for the same year.

Table 1 Number of firms with primary financial statements in 2017 from all countries, as well as the United States (US), China (CN), Japan (JP), United Kingdom (GB), and Portugal (PT)
Full size table
Table 2 Number of firms with primary financial statements in 2017 from all countries, as well as Russia (RU), Brazil (BR), Colombia (CO), Morocco (MA), and India (IN)
Full size table

Missing data rate over time

In this section, we observe how the ratios of the number of firms with operating revenue (OR) in 2013 and 2019 to that in 2017 depend on the size of OR in 2017, taking Japan, Portugal, Colombia, and Morocco as examples, which have typical characteristics in the missing data rate in the time direction from Tables 1 and 2.

Figure 1 shows how the ratio of the number of firms with OR in 2013 to that in 2017 depends on the size of OR in 2017. Specifically, the smaller the size of OR in 2017, the smaller the number of firms with OR in 2013. This trend is particularly pronounced in Japan among these four countries. The other countries have similar trends but different rates of decline, as shown in Fig. 1. It also shows that firms in Japan with OR of less than 10 million dollars in 2013 are extremely deficient compared to 2017. This corresponds to the breaking down of Zipf’s law for the 2013 OR-size distribution at 10  million dollars, as described in Firm-size distribution with interpolated missing values.

In addition, the following characteristics are observed in the size dependency of the ratio of the number of firms with OR in 2019 to that in 2017. In Morocco, the OR of small-scale firms in 2017 was barely recorded in 2019. The larger the size of OR in 2017, the greater the proportion recorded. This observation means that the OR of Moroccan firms for 2019 is being collected. Data are initially collected from large-scale firms that are important and easy for making collections.

Fig. 1
figure 1

Relationship between the ratio of the number of firms with 2013 operating revenue (OR) to that with 2017 OR and 2017 OR size

Full size image

Missing data rate by financial item

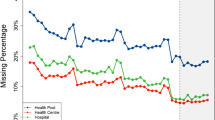
We examine how the ratio of the number of firms with the number of employees (NE), tangible fixed assets (TFA), and net income (NI) to that with operating revenue (OR) in 2017 depends on the size of OR in the same year. Here, we take Japan, Portugal, Colombia, and Morocco as examples, which have typical characteristics in their missing data rates due to the differences in financial items from Tables 1 and 2. These are important financial items for a firm’s productivity. The ratio of the number of firms with OR and NE (Fig.  2a), as well as the number of firms with OR and TFA (Fig. 2b), to that with OR depends on the size of OR.

Figure 2a shows that, in Colombia and Morocco, most of the firms for which OR are recorded are missing NE. Furthermore, the data on NE in Colombia are larger than those in Morocco (Table 1). Of these 150,000 firms, only around 20,000 include OR. On the other hand, most Portuguese firms with OR ranging from \(10 ^ 2\) to \(10 ^ 5\) thousands of dollars have NE. In Japan, the smaller the size of OR, the higher the missing rate of NE.

Figure 2b shows that, in Portugal and Morocco, most firms with OR also include TFA, and that the missing data ratio increases by as much as 20% when OR is less than \(10 ^ 2\) or greater than \(10 ^ 5\) thousands of dollars. In Japan and Colombia, the smaller the size of OR, the higher the missing rate of TFA.

Similar properties to NE and TFA are observed for NI. The following characteristics are observed in the ratio of the number of firms with OR and NI to that with OR. In Portugal, Colombia, and Morocco, most firms with OR include NI. In Japan, the smaller the size of OR, the higher the missing ratio of NI. As described above, the missing ratio for each financial item in the same year varies depending on the country, the type of financial item, and the firm size.

Fig. 2
figure 2

a Relationship between the ratio of the number of firms with OR & NE to that with OR and the size of OR. b Relationship between the ratio of the number of firms with OR & TFA to that with OR and the size of OR

Full size image

Method

In this paper, we construct two models that predict the value of financial items in the middle of three consecutive years for all firms in all countries listed in ORBIS. The variables are the 14 or 13 financial statements listed in Tables 1 and 2 for the consecutive 3-year period, standard industrial classification (SIC) code, and country code. Specifically, we adopt CatBoost, which can use the information of missing data themselves for interpolation.

CatBoost

CatBoost is an extension of supervised machine learning with decision trees. In the regression analysis using the decision tree [32], the multidimensional space of the explanatory variables is divided by the decision trees, and a regression model is constructed to predict representative values such as the average value of the objective variables in each divided area. In this case, the learning is performed so that a loss function such as the square sum of errors of the training data is minimized. Disadvantages of regression analysis using decision trees include the followings: it has low prediction accuracy, overlearning is likely to occur, and the prediction model changes significantly (low robustness) by setting hyperparameters that adjust the learning algorithm, such as maximum depth of tree.

To compensate for these shortcomings of the decision tree, ensemble learning, which combines decision trees, was devised. In ensemble learning, decision trees (single weak learners) which have been separately learned are fused to improve prediction ability for unlearned data. Ensemble learning consists of two methods: bagging and boosting.

In bagging, decision trees (weak discriminators) with low prediction accuracy are combined, and prediction is performed by a majority vote or an average value. A typical library that uses bagging is RandomForest [33]. RandomForest still has the following shortcomings: overlearning is likely to occur, and the prediction accuracy becomes low when the training data is small.

Boosting is a learning method in which a weak discriminator is gradually updated into a strong discriminator. In Gradient boosting, which is one of the most promising methods, when the weak discriminator is updated, the error up to the N-th is reduced by \((N + 1)\)-th by using the differential gradient. Typical algorithms that use gradient boosting include XGBoost, LingtGBM, and CatBoost [34, 35, 38,39,40].

XGBoost is an early learning method using gradient boosting. While RandomForest’s accuracy and overlearning problems are greatly improved, XGBoost runs slower than other algorithms. LightGBM greatly improves the execution speed of XGBoost with a decision tree algorithm based on histograms. In the LightGBM, the calculation time for hyperparameter tuning can be secured by improving the execution speed, but the following problems remain: the prediction accuracy lowers when there are many categorical variables. CatBoost is an algorithm that improves on the problems with categorical data variables in LightGBM. The CatBoost algorithm has three features: efficient preprocessing of categorical variables (Ordered Target Statistics), learning by randomly changing the order of training data (Ordered Boosting), and use of binary symmetric decision tree as weak discriminator (one decision tree). As a result, CatBoost does not reduce prediction accuracy even if there are many categorical variables.

Because the data we deal with includes categorical variables for countries, we adopted CatBoost’s algorithm. We used the official CatBoost Python package [41]. In learning, we used default values for each hyperparameter: RMES as loss function, maximum number of trees at 1,000, depth of tree at 6, and learning rate at 0.226236001.

Creating an objective variable

It is empirically known that the distribution of financial variables follows Zipf’s law around the top 1/4 percent [36, 37]. In such a power-law distribution with an exponent of \(-1\), when an integral up to infinity is considered, the mean and variance diverge, and it is impossible to calculate a statistic using them. If it is forced, the statistics depend strongly on outliers (tail of the distribution). Financial items are not only positive. Values in P/L can have zero or negative values. Negative values also follow Zipf’s law in the large-scale range.

To deal with firm financial data having such properties, this paper considers the amount \(z _ I ^ k\) converted by an inverse hyperbolic function as an objective variable of CatBoost as follows [30]:

$$\begin{aligned} z_I^k=\sinh ^{-1} \frac{y_I^k}{\sigma _y} = \log \left( \frac{y_I^k}{\sigma _y} +\sqrt{ \left( \frac{y_I^k}{\sigma _y} \right) ^2+1} \right) ~, \end{aligned}$$
(1)

where \(y _ I ^ k\) is the value of the financial item I to be predicted for the firm k and \(\sigma _ y\) is the value of y in the top \(25\%\). \(z _ I ^ k\) can be approximated as \(\log ( 2 y_I^k/\sigma _y )\) in the range \(y _ I ^ k \gg \sigma _ y > 0\) and as \(- \log 2 |y _ I ^ k/ \sigma _ y |\) in the range \(y_I^k \ll -\sigma _y<0\). Thus, the variable \(z _ I ^ k\) can smoothly describe positive and negative large-scale and other ranges at equal intervals.

The quantity \(z _ I ^ k\) converted by the inverse hyperbolic function is close to a two-sided exponential distribution. Thus, \(z _ I ^ k\) is a very manageable variable in CatBoost where the mean and variance are included in the loss function to estimate the parameter. Conversely, if we try to minimize the value of the loss function using \(y _ I ^ k\) instead of \(z _ I ^ k\) as the objective variable, only a very small percentage of errors in the large positive or negative ranges that follow Zipf’s law will affect the value of the loss function, creating a model that can predict only certain large-scale ranges. To avoid this problem, in this paper, the variable transformed by the inverse hyperbolic function is used as the objective variable.

Description of missing value interpolation model

In this section, we consider the following missing value interpolation model with CatBoost, which predicts the objective variable introduced in "CatBoost" as follows:

$$\begin{aligned} z_{t,I}^k&=f(y_{t-1,1}^k,y_{t,1}^k, y_{t+1,1}^k; y_{t-1,2}^k,y_{t,2,}^k, y_{t+1,2}^k; \cdots ; \\ \nonumber & y_{t-1,I}^k, y_{t+1,I}^k; \cdots ; y_{t-1,n}^k,y_{t,n}^k, y_{t+1,n}^k ;x_1^k, \cdots , x_m^k )~. \end{aligned}$$
(2)

Here, f is a CatBoost evaluation function. The explanatory variable \(y _ {t, i} ^ k\) is the numerical value of the financial item i of t year of a firm k, and n is the number of financial items to be used for the explanatory variable. \(y _ {t, I} ^ k\) does not exist on the right side, and Eq. (2) predicts it by converting \(z _ {t, I} ^ k\) using Eq. (1). The explanatory variable \(x _ j ^ k\) is the j-th attribute of a firm k, such as a time-independent number or category, and m is the number. In this paper, we consider \(x _ j ^ k\) as the main industry of a firm k (4-digit SIC code [42]) and a dummy variable of the country where the firm k is located (204 countries with financial values in ORBIS). The reason why the SIC code is considered an industry is that a similar industry has been assigned a number that is close to a four-digit code.

As described in "CatBoost", the explanatory variable \(y _ {t, i} ^ k\) is characterized by the divergence of statistical quantities such as the average value and variance in the large positive and negative scale ranges. Furthermore, \(y _ {t, i} ^ k\) is often missing. CatBoost, a nonparametric method of classifying explanatory variables under various conditions and regressing objective variables, is compatible with \(y _ {t, i} ^ k\), which has these properties.

Handling of explanatory variables when missing values are present

As discussed in "Data", smaller firms are more likely to miss financial values. In order for the model to learn this feature, if the value of the explanatory variable is missing, a numerical number that the financial value cannot take is inserted into the explanatory variable \((y_{t,i}^k= -1,000,000,000,000)\).

In predicting \(y _ {t, I} ^ k\) from the objective variable \(z _ {t, I} ^ k\), there are two typical patterns of how explanatory variables can be missing. In one, there is at least one of the explanatory variables \(y ^ k _ {t -1, I}\) and \(y ^ k _ {t + 1, I}\). On the other, they are both missing. In the learning of the model, the prediction is performed for \(y _ {t, I} ^ k\), where a value actually exists, and the parameter is adjusted so that the difference between the predicted value and the true value becomes minimum. Note that when \(y _ {t, I} ^ k\) is present, there is often at least one of \(y ^ k _ {t -1, I}\) and \(y ^ k _ {t + 1, I}\). Moreover, there is a very strong correlation between the t year value \(y _ {t, I} ^ k\) and the \((t \pm 1)\) year value \(y ^ k _ {t \pm 1, I}\) of the same financial item I [36]. Therefore, most of the learning with the model introduced in the previous section uses \(y ^ k _ {t \pm 1, I}\) to predict \(y _ {t, I} ^ k\).

In practice, however, when \(y _ {t, I} ^ k\) does not exist, in most cases neither \(y ^ k _ {t -1, I}\) nor \(y ^ k _ {t + 1, I}\) exists. As an effective model for this case, we introduce a new model that omits \(y ^ k _ {t \pm 1, I}\) from the right side of Eq. (2) and predicts \(y _ {t, I} ^ k\) using only other financial items (\(y _ {t -1, i \ne I} ^ k\), \(y _ {t, i \ne I} ^ k\), \(y _ {t + 1, i \ne I} ^ k\)).

In summary, this paper uses the following two models according to the missing state of the explanatory variables \(y _ {t \pm 1, I} ^ k\). If \(y _ {t -1, I} ^ k\) or/and \(y _ {t + 1, I} ^ k\) exists, we interpolate \(y ^ k _ {t, I}\) from 3 years’ \(n = 14\) financial items minus 1 for the objective variable. This is referred to as Model 1. If both \(y ^ k _ {t -1, I}\) and \(y ^ k _ {t + 1, I}\) are missing, we interpolate \(y ^ k _ {t, I}\) from 3 years’ \(n = 13\) financial items, excluding I. This is referred to as Model 2.

Results

In this section, we first evaluate the accuracy of the two missing value interpolation models introduced in "Method". Next, the temporal stability of model parameters is discussed using importance. Finally, using a dataset with interpolated missing values, we show how defects break Zipf’s law.

Accuracy evaluation of non-random missing value interpolation models

Prediction accuracy of missing values

In Model 1, 41 explanatory variables are adopted for the 3 years’ 14 financial items minus 1 of the objective variable. In Model 2, there are 39 explanatory variables for 13 financial items over 3 years.

Objective variables are set for each of the firm’s key financial items representing productivity: operating revenue (OR), number of employees (NE), tangible fixed assets (TFA), and net income (NI). We evaluated the accuracy of the value predicted (although it actually exists) by the contribution ratio \(R ^ 2\) in comparison to the actual value transformed by the inverse hyperbolic function. Table 3 compares the contributions of Models 1 and 2 to these 4 objective variables in 2017 by training data used to estimate model parameters and test data not used to estimate model parameters for all firms whose financial items are listed in ORBIS (Tables 1 and 2) and for firms from 10 representative countries. Training and test data were generated by randomly dividing the learning data into \(80\%: 20\%\) portions.

Table 3 shows that both Models 1 and 2 can often predict the four objective variables with high accuracy. In particular, since the value of each financial item has a very strong correlation with the values of the same financial item in the previous year and in the following year, Model 1, which uses these values for prediction, shows a higher prediction accuracy than Model 2. However, as described in "Comparison with a simple method" below, since there are few cases in which Model 1 can be used for interpolation processing of missing values, the high prediction accuracy of Model 2 is important. In both Models 1 and 2, the prediction accuracy is not so different between training data and test data. This indicates that no overlearning occurs in these two models.

Table 3 Comparison of Estimated Accuracy between Training Data and (/) Test Data in 2017
Full size table

Number of non-missing items and prediction accuracy

This section describes how the prediction accuracy shown in Table 3 varies with the number of non-missing values in the explanatory variables. Since we confirmed that overlearning is sufficiently suppressed in "Prediction accuracy of missing values", the prediction accuracy was evaluated by combining training data and test data. Model 1 is an easy-to-understand prediction in which the value of the same financial item as the objective variable for the previous or next year determines most of the prediction accuracy, and it is therefore omitted here. As mentioned earlier, in Model 2, there are 39 explanatory variables for 3 years of 13 financial items. We used Model 2 to predict the value of each financial item for all firms that include at least one of the 4 financial items (OR, NE, TFA, and NI) in 2017.

Figure 3 shows how the prediction accuracy of the values of these 4 financial items changes when the number of non-missing explanatory variables changes from 1 to 39, regardless of the kind of item. The prediction accuracy for the four financial items increases dramatically with an increasing number of explanatory variables up to about nine. The reason for this is considered as follows. If there are no more than nine non-missing explanatory variables, the majority is a firm that reports only primary financial items. Since the main financial items are strongly correlated with OR, NE, TFA, and NI, these characteristics appear in the prediction accuracy when there are nine or fewer items. On the other hand, when there are 10 or more explanatory variables with no missing data, the prediction accuracy for these 4 financial items monotonically increases depending on the number of non-missing values. If there are more than 10 non-missing explanatory variables, the majority will be those firms that partially report non-key financial items. Such financial items do not correlate well with OR, NE, TFA, and NI on their own, and their multiple uses improves their prediction accuracy.

Fig. 3
figure 3

Relationship between the accuracy of four financial items (operating revenue (OR), number of employees (NE), tangible fixed assets (TFA), net income (NI)) in Model 2 and the number of non-missing explanatory variables

Full size image

Firm-size dependence of prediction accuracy

Firm size ranges from local micro firms to global giants. This section examines the dependency of predictive accuracy on firm size. Figure 4a, b show the prediction accuracy for OR of Models 1 and 2. Figure 4c, d show the prediction accuracy for NI of Models 1 and 2. In each figure, the horizontal axis represents the actual value, and the vertical axis represents the median and average of the predicted values by each model. The error bar represents the fourth quantile. Each value is converted by an inverse hyperbolic function.

Figure 4a, b show that both Models 1 and 2 can predict OR with high accuracy regardless of OR size. While small- and mid-scale firms account for the majority of the training data, each model is also well trained in predicting OR for large-scale firms.

Next, we discuss the accuracy of NI predictions. Figures 4c, d show that Model 1 can predict positive NI with high accuracy regardless of NI size. On the other hand, Model 2 shows that the accuracy decreases depending on the NI size, and the predicted value is lower than the actual value. Both Models 1 and 2 show that the accuracy of negative NI decreases depending on NI size. Large negative NIs often result from unforeseen extraordinary losses such as natural disasters. Because it is difficult to predict such temporary losses from these explanatory variables, it is likely that the accuracy of predicting negative NI is lower than that of predicting positive NI.

Fig. 4
figure 4

Accuracy of predicting operating revenue (OR) and net income (NI) by size using Models 1 and 2 (\(\sigma = 1,024,000\) dollars in (a) and (b) and \(\sigma =64,000\) dollars in (c) and (d))

Full size image

Accuracy of reproducing firm-size distribution with predicted values

As shown in the previous sections, the predicted values by Models 1 and 2 include errors. Here, we show that the prediction error does not affect the functional form of the firm-size cumulative distribution. In this paper, the cumulative distribution is defined as the integrated probability density function from x to \(\infty\).

Figure 5a is a comparison of the actual and predicted OR distributions for Japanese firms in 2017 by Model 1. For both OR and NI, the distributions reproduced by the predicted values closely match the actual distributions, indicating that the interpolation of the missing data by Model 1 does not distort the actual distributions.

Figure 5b is a comparison of these two variables in Model 2. As with Model 1 in Fig. 5a, the distribution of OR is faithfully reproduced by the predicted values. On the other hand, in the case of NI, the power-law distribution in the upper range shifts to the lower left overall. This corresponds to the lower NI predicted by Model 2 overall, as shown in "Firm-size dependence of prediction accuracy". However, it is possible to reproduce Zipf’s law in the large-scale range of NI distribution, even with the most inaccurate Model 2 estimates in Table 3. That is, in both Models 1 and 2, the interpolation processing of the missing data by the predicted values does not distort the shape of the distribution of the actual values.

Fig. 5
figure 5

Cumulative distributions of actual and predicted values from Models 1 and 2 for operating revenue (OR) and positive net income (NI) for Japanese firms in 2017

Full size image

Comparison with a simple method

We compared the number of firms with interpolatable financial values between the interpolation using the models we proposed and the simple interpolation method described below. Furthermore, we compared the accuracy of a simple interpolation method and the comparable Model 1.

Simple interpolation method: For financial item I, the following conditions 1, 2, and 3 are used to interpolate the missing value in preference to 1.

  1. 1.

    If there is no value for t year and there are values for \((t + 1)\) year and \((t -1)\) year, the average value interpolates the value for t year.

  2. 2.

    If there is no value for t year and there is a value for \((t + 1)\) year, the value interpolates the value for t year.

  3. 3.

    If there is no value for t year and there is a value for \((t - 1)\) year, the value interpolates the value for t year.

The conditions under which the simple interpolation method can be used to interpolate missing values are the same as the conditions under which Model 1 is used. Model 2 is used when both \((t + 1)\) year and \((t -1)\) year values are missing. Therefore, by combining the interpolation by Models 1 and 2, the number of firms having the interpolatable missing value is greatly increased compared with the simple interpolation method.

The number of Japanese firms listed by ORBIS in 2017 was 5, 150, 662. Table 4 shows the number of firms for which OR, NE, TFA, and NI are included, and this table further shows the number of firms with missing values for financial items that can be interpolated by a simple method or by Model 1 as well as the numbers of those that can be interpolated by combining Models 1 and 2. In addition, Table 4 shows that the number of firms that can be interpolated by Models 1 and 2 is two to six times larger than the simple method in terms of OR, NE, TFA, and NI. In particular, the introduction of Model 2, which interpolates over other financial items without the \((t + 1)\) year and \((t -1)\) year values, has overwhelmingly increased the number of firms that can be interpolated.

Table 4 Number of Japanese firms that are missing the values of financial items that can be interpolated in 2017
Full size table

Table  5 compares the interpolation accuracy between the simple method and Model 1. We confirm that the interpolation accuracy of Model 1 is higher than that of the simple method for all four financial items.

Table 5 Comparison of accuracy (\(R ^ 2\)) when it can be interpolated by a simple method or Model 1 in 2017 in Japan
Full size table

Temporal stability of the interpolation models

In this Firm-size dependence of prediction accuracyion, the temporal stability of model parameters is discussed by observing the importance of explanatory variables in the model for each year. Since the explanatory variable’s importance in Model 1 becomes an obvious result in which the explanatory variables \((t -1)\) year and \((t + 1)\) year corresponding to the objective variable I have a total value of around \(70\%\), we observed the annual change in importance while focusing on Model 2. We measured the importance of Model 2 to estimate the missing operating revenue (OR) as follows. First, we built Model 2 for each year from \(t = 2012\) to 2019 year using ORBIS 2020 edition. Second, we built Model 2 for each year from \(t = 2008\) to 2011 year using ORBIS 2016 edition. After these steps, we summed the \((t -1)\), t, and \((t + 1)\) year importances of the same financial item. Figure 6 shows the importance of the dummy variable for the countries averaged over all years, listed from the top 15 countries. The error bar represents the standard deviation due to the difference in years. Figure 6 shows that the country importance is low and that this model is generally useful without country information.

Fig. 6
figure 6

Importance of the country dummy variable averaged over all years (horizontal axis is country code [43])

Full size image

Figure 7 shows the annual change in the sum of the country importances (Countries) and all other explanatory variables’ importances from 2008 to 2018. The high importance of net income (NI) in OR predictions is due to the fact that NI is calculated by subtracting expenditures from OR. Furthermore, the high importance of the number of employees (NE) is due to the causality of labor productivity, in which NE generates OR. Figure 7 shows that importance is relatively stable for all explanatory variables. This suggests that the relationship between financial items changes slowly over the years. Thus, models built in one year can be used in other years with some degree of accuracy.

Fig. 7
figure 7

Annual changes in the sum of the country dummy variable’s importances (Countries) and importances of all other explanatory variables (see Tables 1 or 2 for abbreviations)

Full size image

Firm-size distribution with interpolated missing values

Finally, by observing the firm-size distribution in the financial data set with interpolated missing values, we clarify the distortion that the missing values have been `given to the firm-size distribution. In this section, data are first interpolated by Model 1, and when it is not available, the data are interpolated by Model 2. This is the interpolation method proposed in this paper.

To clarify the distribution distortion caused by the missing data in the time direction, Fig. 8a shows how the cumulative distributions of the operating revenues (OR) of Japanese firms recorded in ORBIS for 2017 and 2013 are changed by the interpolation method. To clarify the distribution distortion caused by the difference in financial items in the same year, Fig. 8b shows how the cumulative distribution of OR and tangible fixed assets (TFA) of Portuguese firms in 2017 changes as a result of interpolation using our method.

From Tables 1 and 4, the OR of Japanese and Portuguese firms in 2017 showed less deficit than those of other years and other financial items, and the change due to interpolation was small. On the other hand, as shown in Fig. 1a, the percentage of missing data in financial items increases as we go back to the past, particularly among small- and mid-scale firms. Figure 8a shows the state in which missing data in the time direction are interpolated by our method, particularly in small- and mid-scale ranges. Specifically, we observed that the cumulative distribution of OR in 2013 approaches that in 2017 as the scale decreases due to the interpolation.

Next, as shown in Fig. 2, even in the same year, missing data in other financial items were more frequent among small- and mid-scale firms compared to OR. Figure 8b shows that missing data due to differences in financial items are being interpolated, particularly in small- and mid-scale ranges. Specifically, we observed that the cumulative distribution of TFA in 2017 approaches that of OR as the size decreases.

In these examples, we confirmed that the power-law range of the cumulative distribution of past OR and TFA in the same year was expanded, and the lower limit of the transition to the log-normal distribution was lowered to the small-scale range. In other words, it became clear that the missing data of financial items, which occurs in the time direction and in the financial item direction, broke Zipf’s law in the mid-scale range of the firm-size distribution.

Fig. 8
figure 8

a Cumulative distributions of original operating revenue (OR) of Japanese firms in 2017 and 2013 and those of interpolated OR by our method. b Cumulative distributions of original OR and tangible fixed assets (TFA) of Portuguese firms in 2017 and those of interpolated OR and TFA by our method (in each figure, dashed line is the power law of an exponent \(-1\) (Zipf’s law))

Full size image

Conclusions

In this paper, we proposed a method to interpolate non-random missing values in financial statements’ big data using CatBoost. We focused on the world’s largest commercial database, ORBIS, and observed the rate of missing data in the time direction and the rate by financial items in the same year, and we found that the rate of missing data varies depending on the country, the type and size of financial items, and the year. These results indicate that the missing data themselves are useful as information for interpolating the missing values.

We constructed a model that incorporates this information on missing data and interpolates the missing value by regression as follows. The values of a financial item for three consecutive years are used as explanatory variables, and the value of a financial item for the middle year is predicted as an objective variable. We proposed two models, depending on whether there was at least one prior-year or next-year value of the financial item of the predicted value or, on the other hand, both were missing. The first model dealt with 41 explanatory variables in 3 years’ 14 financial items subtracting 1 as the objective variable, and the second model dealt with 39 explanatory variables in 3 years’ 13 financial items.

We measured the prediction accuracy of the missing values for each model and compared the distribution of data replicated by each model with that of the original data. In both cases, we confirmed that the accuracy of the model predictions was high, and that the shape of the original distribution was maintained even if the prediction values contained errors. We then compared the number of missing data that could be interpolated by each model or a simple interpolation method and found that the number for the two models was two to six times larger than that for the simple method. We also compared the prediction accuracy and confirmed the temporal stability of the interpolation model. It is important to note that, to justify these models, we assume that the probability of missing the objective variable is the same if the explanatory variables are all the same.

Finally, we combined the two models, giving priority to the first model. We used this method to interpolate the missing values likely to appear in the past and those likely to appear in financial items other than operating revenue. As a result, we confirmed that the power-law range of the cumulative distribution of past operating revenue and tangible fixed assets in the same year was expanded, and the lower limit of the transition to the log-normal distribution was lowered to the small-scale range. In previous studies, it has often been argued that the shape of a firm-size distribution depends on its financial items. This study showed that this may be due to missing data. This analysis also means that data must be interpolated to discuss the temporal variation of the cumulative distribution.

Compared to the total number of firms in ORBIS, there are far fewer firms that have at least one financial value. There are probably many firms that have no actual activities but are registered. It is a future issue to predict the firm-size distribution of firms that have actual activities but do not contain any financial values from macroeconomic statistics such as GDP.

It’s also interesting to note that in the process of CatBoost, debtors contribute significantly to the importance of operating revenue predictions. Does debt have a more positive impact on a firm’s productivity than assets? The stability of causality between financial items is also a future issue.