Macroscopic fundamental diagram in simple street networks

Abstract

Macroscopic fundamental diagrams (MFDs) on simple street networks are studied analytically and numerically. We consider nonlinear circuit model that consists of road elements with piecewise linear fundamental diagram. We find that MFDs of the model are discontinuous and sawtooth like. Meanwhile, simulations of optimal velocity model on the same street networks yield continuous MFDs, that are observed in real urban traffic.

Introduction

Traffic flow has attracted the interest of statistical physicists in these decades [1, 2]. Free-way traffic, or one-dimensional traffic flow, has been mainly studied in the field [1,2,3,4]. Meanwhile, there are some studies about urban traffic; one of the most famous models is the so-called Biham–Middleton–Levine model [2, 5]. This model is an extension of the Rule 184 cellular automaton to two-dimensional systems, and it is found that there are three phases of traffic, that is, free-flowing, jammed, and intermediate phases. However, these models are too simplified to compare observations with actual urban traffic.

Recently, the so-called macroscopic fundamental diagram (MFD) draws great attention in studies of urban traffic [6]. MFD is a reproducible unimodal relation between vehicle density and vehicle flow rate averaged over a total urban traffic network. It is very interesting because it might enable rough predictions of large-scale urban traffic. Although some observations [6] and simulations [6, 7] argued the existence of MFD, a mechanism of obtaining MFD is not well understood.

For this purpose, we study two models of urban traffic in simple street networks. In “Nonlinear circuit model”, we discuss MFDs in the case of the nonlinear circuit model that we proposed recently [8,9,10]. Moreover, we discuss simulation results of the so-called optimal velocity model [11] in “Optimal velocity model”. Finally, we summarize our works in “Summary”.

Nonlinear circuit model

In this section, we consider the nonlinear circuit model to study MFDs. This model is recently proposed by some of the authors [8,9,10].

Fig. 1

Schematic picture of street networks that are considered in this work. Each directed edge means street, and a vertex is an intersection connecting all streets. The network shown in this figure has four streets ($N=4$)

Model

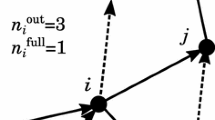
As a model of urban traffic, we consider directed graphs with 1 vertex and N edges as shown in Fig. 1. It is interpreted that a vertex and edges $i = 1, \ldots , N$ are an intersection and streets with the same length, respectively. By ignoring spatial structures of vehicle groups, traffic on each street i is characterized only by two scalar quantities, that is, vehicle density $0 \le \rho _i \le 1$ and flow rate $q_i \equiv q(\rho _i)$, $0 \le q_i \le 1$. Here, $q(\rho )$ is a fundamental diagram (FD) defined on every street i;

$$\begin{aligned} q(\rho ) = {\left\{ \begin{array}{ll} v \rho &{} \text {if} \, \rho < \rho _{\mathrm {p}} \equiv 1/v, \\ w(1-\rho ) &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

(1)

as shown in Fig. 2, where $v > 0$ is maximal speed for each street, and w satisfies $w = (1-\rho _\mathrm {p})^{-1} = (1-1/v)^{-1}$. A street with $\rho < \rho _\mathrm {p}$ and one with $\rho > \rho _\mathrm {p}$ are called free and jammed, respectively. Moreover, a street with $\rho = 1$ is especially called completely jammed. Note that length and time in this work are dimensionless using maximal values of vehicle density and flow rate on each street.

Fig. 2

Schematic picture of fundamental diagram on each street. Now, we set $\rho _\mathrm {p} = 0.3$ as an example. See text (especially Eq. (1)) for details

Assuming equal distribution of vehicle density to outgoing streets at the intersection, dynamical equations of vehicle density are given by

$$\begin{aligned} \dfrac{\mathrm {d} \rho _i}{\mathrm {d} t} = {\left\{ \begin{array}{ll} \dfrac{1}{N-n} {\sum }_{j=1}^N q(\rho _j) - q(\rho _i) &{} \text {if} \, \rho _i < 1, \\ 0 &{} \text {otherwise}, \end{array}\right. } \end{aligned}$$

(2)

where n is the number of completely jammed streets. Here, the first term and second one in the r.h.s. of Eq. (2) represent incoming flow from the intersection to a street i and outgoing flow from the intersection of a street i, respectively. Note that if there are completely jammed streets, vehicles that are not in completely jammed streets are assumed not to enter completely jammed streets. Therefore, we set the coefficient of the first term in r.h.s of Eq. (2) as above.

Previous studies

There are previous studies related to our model shown in “Model”.

Daganzo and his coworkers studied the nonlinear circuit model with $N=2$ [12]. Instead of Eq. (2), they discuss the case that the dynamical equation is given by

$$\begin{aligned} \dfrac{\mathrm {d} \rho _i}{\mathrm {d} t} = {\left\{ \begin{array}{ll} \dfrac{1}{2} {\sum }_{j=1}^2 q(\rho _j) - q(\rho _i) &{} \text {if} \, \rho _1< 1 \, \text {and} \, \rho _2 < 1, \\ 0 &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

(3)

Considering the linear stability around ${\dot{\rho }}_i = 0$ or $q_1 = q_2 = \mathrm {const.}$, they found the system with $\rho _1 < \rho _\mathrm {p}$ and $\rho _2 > \rho _\mathrm {p}$ is stable for $\rho _\mathrm {p}< {\bar{\rho }} (= (\rho _1 + \rho _2)/2) < 1/2$. Therefore, MFD ${\bar{q}}_\mathrm {D}({\bar{\rho }})$ is continuous and given by

$$\begin{aligned} {\bar{q}}_\mathrm {D}({\bar{\rho }}) = {\left\{ \begin{array}{ll} v{\bar{\rho }} &{} \text {if} \, {\bar{\rho }}< \rho _\mathrm {p} = \dfrac{1}{v}, \\ \dfrac{2v}{2-v} \biggl ({\bar{\rho }} - \dfrac{1}{2}\biggr ) &{} \text {if} \, \dfrac{1}{v}< {\bar{\rho }} < \dfrac{1}{2}, \\ 0 &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

(4)

Meanwhile, Ezaki and his coworkers extended the model to arbitrary strongly connected directed graphs [13, 14]. Note that FD $q(\rho )$ in their model is parabola like and symmetric, that is, $\rho _\mathrm {p} = 1/2$. Using the linear stability analysis around $\rho _i = \mathrm {const.}$, they found the system with $\rho _i > 1/2$ is linearly unstable, and MFD ${\bar{q}}_\mathrm {E}({\bar{\rho }})$ is discontinuous at ${\bar{\rho }} (= \sum _i \rho _i / N) = 1/2$;

$$\begin{aligned} {\bar{q}}_\mathrm {E}({\bar{\rho }}) = {\left\{ \begin{array}{ll} q({\bar{\rho }}) &{} \text {if} \, {\bar{\rho }} < \rho _\mathrm {p} = \dfrac{1}{2}, \\ q(1) &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

(5)

Why they conclude different MFDs? Actually, both of the works have some problems. In the case of Daganzo’s study [12], the system size is too small. Meanwhile, in the case of Ezaki’s study [13], symmetric FD would cause problems. If we consider Daganzo’s model with symmetric FD, MFD becomes discontinuous because Eq. (4) becomes

$$\begin{aligned} {\bar{q}}_\mathrm {D}({\bar{\rho }}) = {\left\{ \begin{array}{ll} v{\bar{\rho }} &{} \text {if} \, {\bar{\rho }} < \rho _\mathrm {p} = \dfrac{1}{2}, \\ 0 &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

(6)

Moreover, their fixed point $\rho _i = \mathrm {const.}$ is also problematic because this assumption dismisses a state with $\rho _1 < \rho _\mathrm {p}$ and $\rho _\mathrm {p}< \rho _2 < 1/2$, which exists in Daganzo’s results.

As described above, some of the authors proposed this model recently [10]. In that study, they solved the model numericaly in the case of grid street networks, and they discussed discontinuous MFD. In this study, we consider simpler networks. It enables analytical study for the nonlinear circuit models.

Linear stability analysis

Assume n streets are completely jammed $\rho _i = 1$ and m streets are not completely but still jammed $\rho _\mathrm {p}< \rho _i < 1$. Without loss of generality, we order indices such that first $[N-(n+m)]$ streets are free, next m streets are jammed, and the other n streets are completely jammed. If we write $\rho _i(t) = \rho ^*_i + \epsilon _i(t)$, where $\rho ^*_i$ is a time-independent fixed point (${\dot{\rho }}^*_i=0$), that is,

$$\begin{aligned} q(\rho ^*_i) = {\left\{ \begin{array}{ll} q^* &{} \text {if} \, 1 \le i \le N-n, \\ 0 &{} \text {otherwise}, \end{array}\right. } \end{aligned}$$

(7)

Eq. (2) can be linearized around $\rho _i = \rho ^*_i$ such as

$$\begin{aligned} \dfrac{\mathrm {d} \mathbf {\epsilon }}{\mathrm {d} t}&= \dfrac{v}{{\tilde{N}}} \begin{pmatrix} -{\hat{N}} &{} 1 &{} \cdots &{} 1 &{} -\omega &{} -\omega &{} \cdots &{} -\omega \\ 1 &{} -{\hat{N}} &{} \cdots &{} 1 &{} -\omega &{} -\omega &{} \cdots &{} -\omega \\ \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots &{} \vdots &{} &{} \vdots \\ 1 &{} 1 &{} \cdots &{} -{\hat{N}} &{} -\omega &{} -\omega &{} \cdots &{} -\omega \\ 1 &{} 1 &{} \cdots &{} 1 &{} {\hat{N}}\omega &{} -\omega &{} \cdots &{} -\omega \\ 1 &{} 1 &{} \cdots &{} 1 &{} -\omega &{} {\hat{N}}\omega &{} \cdots &{} -\omega \\ \vdots &{} \vdots &{} &{} \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ 1 &{} 1 &{} \cdots &{} 1 &{} -\omega &{} -\omega &{} \cdots &{} {\hat{N}}\omega \end{pmatrix} \mathbf {\epsilon } \nonumber \\&= \dfrac{v}{{\tilde{N}}} A \mathbf {\epsilon }, \end{aligned}$$

(8)

where ${\tilde{N}} = N-n$, ${\hat{N}} = {\tilde{N}}-1$, $\omega =w/v=(v-1)^{-1}$, and $\mathbf {\epsilon } = {}^t(\epsilon _1, \ldots , \epsilon _{{\tilde{N}}})$. Note that the first ${\tilde{N}}-m$ columns and the other m columns correspond to free and jammed streets, respectively. We can discuss linear stability of the fixed point $\rho _i(t) = \rho ^*_i$, if we consider sign of the largest eigenvalue of a matrix A.

If $m = 0$, the characteristic polynomial of A is

$$\begin{aligned}&\begin{vmatrix} -{\hat{N}}-\lambda&1&\cdots&1 \\ 1&-{\hat{N}}-\lambda&\cdots&1 \\ \vdots&\vdots&\ddots&\vdots \\ 1&1&\cdots&-{\hat{N}}-\lambda \end{vmatrix} \nonumber \\&\quad = \begin{vmatrix} \alpha&-\alpha&&&\\&\alpha&-\alpha&&\\&&\ddots&\ddots&\\&&&\alpha&-\alpha \\ 1&1&\cdots&1&\alpha +1 \end{vmatrix} \nonumber \\&\quad = ({\tilde{N}}-1) \alpha ^{{\tilde{N}}-1} + (\alpha +1) \alpha ^{{\tilde{N}}-1} \nonumber \\&\quad = -\lambda \alpha ^{{\tilde{N}}-1} \nonumber \\&\quad = 0, \end{aligned}$$

(9)

where $\alpha = -{\tilde{N}}-\lambda$. Therefore, eigenvalues satisfy

$$\begin{aligned} \lambda = 0, -{\tilde{N}}, \end{aligned}$$

(10)

which means the fixed point $\rho _i(t) = \rho ^*_i$ is linearly stable.

If $m \ge 1$, the characteristic polynomial of A is

$$\begin{aligned}&\begin{vmatrix} -{\hat{N}}-\lambda&1&\cdots&1&-\omega&-\omega&\cdots&-\omega \\ 1&-{\hat{N}}-\lambda&\cdots&1&-\omega&-\omega&\cdots&-\omega \\ \vdots&\vdots&\ddots&\vdots&\vdots&\vdots&&\vdots \\ 1&1&\cdots&-{\hat{N}}-\lambda&-\omega&-\omega&\cdots&-\omega \\ 1&1&\cdots&1&{\hat{N}}\omega -\lambda&-\omega&\cdots&-\omega \\ 1&1&\cdots&1&-\omega&{\hat{N}}\omega -\lambda&\cdots&-\omega \\ \vdots&\vdots&&\vdots&\vdots&\vdots&\ddots&\vdots \\ 1&1&\cdots&1&-\omega&-\omega&\cdots&{\hat{N}}\omega -\lambda \end{vmatrix} \nonumber \\&\quad = \begin{vmatrix} \alpha&-\alpha&&&&&&&&\\&\alpha&-\alpha&&&&&&&\\&&\ddots&\ddots&&&&&&\\&&&\alpha&-\alpha&&&&&\\&&&&\alpha&-\beta&&&&\\&&&&&\beta&-\beta&&&\\&&&&&&\beta&-\beta&&\\&&&&&&&\ddots&\ddots&\\&&&&&&&&\beta&-\beta \\ 1&1&1&\cdots&1&-\omega&-\omega&\cdots&-\omega&\beta -\omega \end{vmatrix} \nonumber \\&\quad = ({\tilde{N}}-m) \alpha ^{{\tilde{N}}-m-1} \beta ^m + (m-1) (-\omega ) \alpha ^{{\tilde{N}}-m} \beta ^{m-1} \nonumber \\&\qquad + (\beta -\omega ) \alpha ^{{\tilde{N}}-m} \beta ^{m-1} \nonumber \\&\quad = -\alpha ^{{\tilde{N}}-m-1} \beta ^{m-1} [({\tilde{N}}-m) \beta - (m-1) \omega \alpha + (\beta -\omega ) \alpha ] \nonumber \\&\quad = 0, \end{aligned}$$

(11)

where $\alpha = -{\tilde{N}}-\lambda$ and $\beta = {\tilde{N}}\omega -\lambda$. In the case of $m \ge 2$, some of eigenvalues satisfy $\lambda = (N-n)\omega > 0$, that is, the fixed point $\rho _i(t) = \rho ^*_i$ is always linearly unstable. Meanwhile, if $m = 1$, eigenvalues satisfy $\lambda = -{\tilde{N}}$ or

$$\begin{aligned} ({\tilde{N}}-1) \beta + (\beta -\omega ) \alpha = 0. \end{aligned}$$

(12)

Solutions of Eq. (12) are

$$\begin{aligned} \lambda = 0, -[1 - ({\tilde{N}}-1) \omega ]. \end{aligned}$$

(13)

Therefore, in the case of $m = 1$, the condition of linear stability is $\omega \le ({\tilde{N}}-1)^{-1}$, that is,

$$\begin{aligned} v \ge {\tilde{N}},\ \rho _\mathrm {p} \le \dfrac{1}{{\tilde{N}}}. \end{aligned}$$

(14)

This means that the fixed point $\rho _i(t) = \rho ^*_i$ is linearly unstable as $N \rightarrow \infty$.

Macroscopic fundamental diagram

According to the results in “Linear stability analysis”, we discuss MFDs in this model.

Here, we consider the case n streets are completely jammed and the time-independent fixed point $\rho _i(t) = \rho ^*_i$ is linearly stable. In the case of $N-n>v$, all of the $(N-n)$ streets are free, that is, $\rho ^*_i = \rho _\mathrm {f}$ and $q^*_i = v \rho _\mathrm {f}$ for those streets. Therefore, the average vehicle density becomes

$$\begin{aligned} {\bar{\rho }} = \dfrac{(N-n)\rho _\mathrm {f}+n}{N}, \end{aligned}$$

(15)

and MFD ${\bar{q}}_N({\bar{\rho }})$ satisfies

$$\begin{aligned} {\bar{q}}_N({\bar{\rho }}) = \dfrac{(N-n)v\rho _\mathrm {f}}{N} = \dfrac{(N-n)v}{N} \dfrac{N{\bar{\rho }}-n}{N-n} = v \biggl ({\bar{\rho }} - \dfrac{n}{N}\biggr ). \end{aligned}$$

(16)

Meanwhile, the fixed point is linearly stable for $N-n \le v$ if, at least, $(N-n-1)$ streets are free. If all of $(N-n)$ streets are free, that is, $n/N \le {\bar{\rho }} \le [(N-n)v^{-1}+n]/N$, MFD is again given by Eq. (16). Hereafter, we consider the case that $(N-n-1)$ streets are free and the other street is jammed.

If we write vehicle density of free streets by $\rho ^*_i = \rho _\mathrm {f}$, their flow rate is $q^*_i = v\rho _\mathrm {f}$. Because flow rates of jammed street and free streets are the same, vehicle density of jammed street is $\rho ^*_i = 1-(v/w)\rho _\mathrm {f} = 1-(v-1)\rho _\mathrm {f}$, and the average vehicle density satisfies

$$\begin{aligned} {\bar{\rho }} = \dfrac{(N-n-1)\rho _\mathrm {f} + [1-(v-1)\rho _\mathrm {f}] + n}{N} = \dfrac{(N-n-v)\rho _\mathrm {f} + n + 1}{N}. \end{aligned}$$

(17)

Therefore, MFD ${\bar{q}}_N({\bar{\rho }})$ in this case is

$$\begin{aligned} {\bar{q}}_N({\bar{\rho }})&= \dfrac{(N-n)v\rho _\mathrm {f}}{N} = \dfrac{(N-n)v}{N} \dfrac{N{\bar{\rho }}-n-1}{N-n-v} \nonumber \\&= -\dfrac{(N-n)v}{v-(N-n)} \biggl ({\bar{\rho }} - \dfrac{n+1}{N}\biggr ) \end{aligned}$$

(18)

In summary, MFD of this nonlinear circuit model is given by

$$\begin{aligned} {\bar{q}}_N({\bar{\rho }})&= \sum _{n=0}^{N-1} {\bar{q}}_{N,n}({\bar{\rho }}), \end{aligned}$$

(19)

$$\begin{aligned} {\bar{q}}_{N,n}({\bar{\rho }})&= {\left\{ \begin{array}{ll} v \biggl ({\bar{\rho }} - \dfrac{n}{N}\biggr ) &{} \text {if} \, \max \biggl \{\rho _{n-1}, \dfrac{n}{N}\biggr \} \le {\bar{\rho }}< \rho _n, \\ -\dfrac{(N-n)v}{v-(N-n)} \biggl ({\bar{\rho }} - \dfrac{n+1}{N}\biggr ) &{} \text {if} \, \rho _n \le {\bar{\rho }} < \dfrac{n+1}{N}, \\ 0 &{} \text {otherwise}, \end{array}\right. } \end{aligned}$$

(20)

where

$$\begin{aligned} \rho _n = \dfrac{1}{v} + \dfrac{n}{N} \biggl (1-\dfrac{1}{v}\biggr ),\ \rho _{-1} = 0. \end{aligned}$$

(21)

Figure 3 shows the results for $v = 10/3$. As shown in this figure, MFD contains N peaks, and it is discontinuous for large N. This discontinuity corresponds to the fact that one of the streets in the system becomes completely jammed. It is also shown that MFD becomes similar to FD of each street for large N. Actually, the following theorem can be proved:

Fig. 3

Macroscopic fundamental diagram in the nonlinear circuit model in the case of $v = 10/3$, or $\rho _\mathrm {p} = 0.3$. This is given by Eqs. (19) and (20). Bold line is fundamental diagram of each street, which is give by Eq. (1)

Theorem 1

Here, we consider street network with one intersection and N streets, whose fundamental diagram is$q(\rho )$. Let us denote the macroscopic fundamental diagram in the nonlinear circuit model as${\bar{q}}_N({\bar{\rho }})$, sequence of functions$\{{\bar{q}}_N\}_N$ are convergent uniformly to the fundamental diagram q.

Proof

First, we obtain $q({\bar{\rho }}) - {\bar{q}}_{N,0}({\bar{\rho }}) = 0$ for $0 \le {\bar{\rho }} < \rho _0 = 1/v$.

Next, for $n \ge 1$ and ${\bar{\rho }} \in L_{N,n} = [\max \{\rho _{n-1}, n/N\}, \rho _n)$, we get

$$\begin{aligned} q({\bar{\rho }})-{\bar{q}}_{N,n}({\bar{\rho }})&= \dfrac{v}{v-1} (1-{\bar{\rho }}) - v\biggl ({\bar{\rho }}-\dfrac{n}{N}\biggr ) \nonumber \\&= -\dfrac{v^2}{v-1} {\bar{\rho }} +\dfrac{v}{v-1} + v\dfrac{n}{N}. \end{aligned}$$

(22)

Because this is monotonically decreasing as increasing ${\bar{\rho }}$, we obtain

$$\begin{aligned} \sup _{{\bar{\rho }} \in L_{N,n}} \{q({\bar{\rho }})-{\bar{q}}_{N,n}({\bar{\rho }})\} = {\left\{ \begin{array}{ll} \dfrac{v}{N} &{} \text {if} \, \rho _{n-1} > \dfrac{n}{N}, \\ \dfrac{v}{v-1} \biggl (1-\dfrac{n}{N}\biggr ) &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

(23)

For any n, $\rho _{n-1} > n/N$ does always hold if we select an integer N such that $N > n-1+v$. Therefore, we conclude

$$\begin{aligned} \lim _{N\rightarrow \infty } \sup _{{\bar{\rho }} \in L_{N,n}} \{q({\bar{\rho }})-{\bar{q}}_{N,n}({\bar{\rho }})\} = \lim _{N \rightarrow \infty } \dfrac{v}{N} = 0. \end{aligned}$$

(24)

Moreover, for any n, $\rho _n > (n+1)/N$ does always hold if we select an integer N such that $N > n+v$. Therefore, $R_{N,n} = \bigl [\rho _n, (n+1)/N\bigr )$ goes to a null set as $N \rightarrow \infty$.

Summarizing, we obtain

$$\begin{aligned}&\lim _{N\rightarrow \infty } \sup _{0\le {\bar{\rho }} \le 1} \{q({\bar{\rho }})-{\bar{q}}_N({\bar{\rho }})\} \nonumber \\&\quad = \lim _{N\rightarrow \infty } \max _n \sup _{{\bar{\rho }} \in L_{N,n} \cup R_{N,n}} \{q({\bar{\rho }}) - {\bar{q}}_{N,n}({\bar{\rho }})\} \nonumber \\&\quad = 0 \end{aligned}$$

(25)

and we conclude that $\{{\bar{q}}_N\}_N$ converges to q uniformly. $\square$

Optimal velocity model

The nonlinear circuit model dicussed in “Nonlinear circuit model” might be criticized that it is too simple to discuss real urban traffic. Therefore, we perform simulations using the optimal velocity (OV) model [15, 16] to consider MFD in more realistic urban traffic [11].

Model

We consider street network with N streets with length L, as shown in Fig. 1. Each street is assumed to have single lane and be unidirectional. We label $n_i$ vehicles on a street i from the latter to the former such as $k=1, 2, \ldots , n_i$. If $x_{ik}$ is position of a vehicle k in a street i, the equation of motion of each vehicle is given by

$$\begin{aligned} \ddot{x}_{ik} = a[U(x_{i,k+1}-x_{ik})-{\dot{x}}_{ik}], \end{aligned}$$

(26)

where a is a constant sensitivity and U(b) is a so-called OV function

$$\begin{aligned} U(b) = \tanh (b-2) + \tanh 2. \end{aligned}$$

(27)

For the top vehicle $k = n_i$ in a street i, the next street that the vehicle transfers is randomly determined, and distance to the end vehicle in the next street, $x_{j,1} + (L - x_{i, n_i})$, is given as an argument of the OV function. Note that we set the distance as infinity if there is no vehicle in the next street.

The case $N=1$ is a single-lane OV model with periodic boundary condition. This has been studied very much numerically and analytically [3, 15,16,17]. The fixed point $x_{1, k} = {\bar{b}} k + U({\bar{b}}) t + \mathrm {const.}$ with ${\bar{b}} = L/n_1$ is known to be linearly unstable if

$$\begin{aligned} a < 2U'({\bar{b}}) = \dfrac{2}{\cosh ^2({\bar{b}}-2)} = \dfrac{2}{\cosh ^2(\rho ^{-1}-2)}, \end{aligned}$$

(28)

that is,

$$\begin{aligned} \Biggl [ 2 + \log \left( \sqrt{\dfrac{2}{a}} + \sqrt{\dfrac{2}{a} - 1} \right) \Biggr ]^{-1}< \rho < \Biggl [ 2 + \log \left( \sqrt{\dfrac{2}{a}} - \sqrt{\dfrac{2}{a} - 1} \right) \Biggr ]^{-1}. \end{aligned}$$

(29)

The weakly nonlinear analysis around the fixed point gives the Korteweg-de-Vries (KdV) equation and the modified KdV equation with perturbation terms [17].

We perform simulations for the OV model in the N-street network. The 4-th order Runge–Kutta scheme is used to solve Eq. (26) with time step ${\varDelta }t = 10^{-3}$. The length of each street is set $L=100$. As initial conditions, the number of vehicles on each street is given by $n_i = \rho L$, where $\rho$ is the average vehicle density, the distance between consecutive vehicles are the same $x_{i,k+1}-x_{ik} = 1/\rho$, and velocity is given by ${\dot{x}}_{ik} = U(1/\rho ) + \delta v_{ik}$, where $\delta v_{ik}$ is a uniformly distributed random number satisfying $-0.15 \le \delta v_{ik} < 0.15$.

Macroscopic fundamental diagram

MFD of the OV model is shown in Fig. 4. The horizontal axis is the average vehicle density $\rho$, and the vertical axis shows the average flow rate $q = N^{-1} \sum _{i=1}^N \sum _{k=1}^{n_i} {\dot{x}}_{ik}/L$ in a steady state. In Fig. 4, we show results for $N=1$, 2, 4, and $a = 1, 1.2$. Note that the number of samples for each data is only one.

Fig. 4

Macroscopic fundamental diagram in the optimal velocity model. Solid points and empty points are the cases $a = 1.0$ and 1.2, respectively. Black, red, and blue points mean $N=1$, 2, and 4, respectively

This result is different from that of the nonlinear circuit model very much. First, the transition between the free-flow phase and the jammed phase is continuous. It is well known that (M)FD of the OV model with periodic boundary condition has an inverse-$\lambda$ shape, and the transition is discontinuous. However, for $N=2,4$, the transition is continuous as shown in Fig. 4.

Next, it should be mentioned that the transition densities between free-flow phase and jammed phase are not the same, if we compare FD and MFD. In the case of the nonlinear circuit model, the transition density $\rho = \rho _\mathrm {p}$ does not change even if N is increased, as shown in Fig. 3. However, Fig. 4 shows the transition densities for $N=2$ and 4 are less than that for $N=1$. Note that we have another phase transition at higher density in the OV models, and this transition densities for $N=2,4$ are greater than that for $N=1$.

Moreover, it is interesting that the average flow rates in jammed phase for $N=2,4$ are almost constant and less than that for $N=1$. This behavior is reported in the study of cellular automaton models [18, 19]. Note that MFD in the nonlinear circuit model has multiple peaks. It is not strange that MFD in this OV model does not have such multiple peaks because jammed streets do not become completely jammed in this model.

Summary

In this study, we discuss macroscopic fundamental diagram (MFD) in simple street networks to understand MFDs observed in real urban traffic. While MFD in the nonlinear circuit model is discontinuous, MFD in the OV model is continuous. The reason of discontinuous MFD in the nonlinear circuit model is decrement of the number of streets to be able to enter vehicles at the intersection. Because vehicles can enter jammed streets even if their vehicle density is very high, this is a possibility to explain thes continuous MFD in the OV model. We would study to change the rule of vehicle transfers at an intersection in near future.

Moreover, in our previous work, it is found that MFD of the nonlinear circuit model becomes discontinuous in the case of grid street network [10]. Therefore, it would be interesting to study MFD of the OV model in more complicated street networks.