Introduction

Computational fluid dynamic (CFD) calculations have become increasingly important for obtaining insight into characteristics of flow reactors in particular, which are difficult to obtain experimentally. One of these characteristics is the mixing of fluids, which was addressed for both static mixing elements and more complex systems such as bubble columns [1, 2]. Additionally, CFD allows to predict heat transfer and the outcome of reactions in chemical applications. This has made CFD useful for the description of the operation of larger industrial equipment as well as microscale reactors [3,4,5,6]. The advance in computational power during recent decades allowed to apply CFD to more complex reaction systems, such as (free radical) polymerization in non-ideal reactors. CFD and polymerization kinetics were thus coupled to give a description of common polymerizations, like those of styrene or ethylene [7,8,9]. These investigations have usually been performed for commercially available reactors, in form of CSTRs or interdigital micromixers, but also for some proprietary reactor designs [7, 9, 10].

The method of moments is often used for a kinetic description as it gives access to the most important properties of the polymerization, i.e. molar masses and conversion, while not necessitating the consideration of every polymer chain, keeping computational expense low. Recent research aimed at overcoming the inherent loss of information that comes along with using the method of moments, trying to establish a full molar mass distribution through iterative surrogate model methods. Also fluidized bed reactors and suspension polymerizations have been modelled [11,12,13].

The production of poly-n-butyl acrylate in a free radical polymerization has seen a steady interest in the context of modeling. It is a polymer with a continuously growing market, it is e.g. useful as dispersant for paints or as adhesive. The kinetics of the polymerization of n-butyl acrylate were intensively studied to show that a full description of the system is quite challenging on account of the complex reaction network. In addition to the classical FRP reaction steps of initiation, propagation and termination of radical chains, various transfer reactions are to be considered which lead to a branched polymer structure [14, 15]. These include transfer to monomer by hydrogen abstraction and transfer to the polymer through inter- and intramolecular pathways [16, 17]. The resulting mid-chain radicals can lead to short- and long-chain branches. The mid-chain radicals can also undergo a β-scission reaction, resulting in the formation of macromonomers [18]. Transfer reactions to the solvent in solution polymerization can also occur, respectively to added chain transfer agents [19, 20]. Full consideration of these systems have only recently become feasible, as more quantitative information on the system has become available [21, 22]. An integration of the kinetics into a CFD description has not been achieved, neither has such a model been validated against experimental values.

CFD simulation is of particular interest when considering novel reactor geometries, as they cannot yet be described by the semi-empirical equations that are often available for classic heat exchangers, batch reactors or CSTRs. Tailor made reactors have become readily accessible by additive manufacturing tools. Additive manufacturing has seen an extension of application over the last years, as various types of 3D printers in both “do-it-yourself” and industrial scale have become more affordable and give parts of satisfactory qualities [23].

A variety of structures has since been produced for micro- and millifluidic devices [24, 25]. Microfluidic devices are commonly produced by stereolithography or by selective laser sintering (SLS), as these methods give chemically and mechanically robust structures with a decent print resolution [26]. The fused deposition modeling (FDM) method of 3D-printing is cheap and easy to use, although the print precision does not reach the level of the previously mentioned methods. In this method, heated polymer is extruded through a nozzle and deposited in layers. This allows to use the wide array of thermoplastic (crystalline) materials, such as PLA, PVA, Nylon and also PP [23]. FDM has been used for both fluidic connectors and reactors for a number of low molecular chemical reactions [25, 27,28,29].

Additive manufacturing of reactors in combination with CFD simulations have been a useful tool to evaluate and optimize mixing and flow through milli and microfluidic reactors, to reduce material waste in the prototyping stage by gaining insight into flow behavior before printing and testing the design [30,31,32]. The purpose of this study is to design a smart reactor for the kinetically challenging system of BA solution polymerization by the combination of CFD and additive manufacturing. Thus, a 3D printable reactor containing static mixing elements is derived comprising polymerization kinetics for n-butyl acrylate and fluid flow calculations. CFD calculations were first performed to evaluate flow reactors of varying geometries regarding the achieved mixing. The residence time of the derived and a reference reactor were both simulated and determined experimentally. The method of moments was used to combine polymerization kinetics and flow calculations. Free radical polymerizations were carried out in the 3D printed reactor and experimental molecular weights and conversions were compared to the model to judge the accuracy of the implemented approach.

Reactor geometry

The reactors considered in this work have a common basic structure, an example is shown in Fig. 1. It is comprised of an inlet section, vertical pipe, pipe bend with degassing adapter, vertical pipe and outlet section. Two SMX element mixing stacks rest on 3 holding fins in the pipe to enable manufacturing of the mixing elements by fused deposition modeling. Inlet, outlet and upper piping bend are held at identical sizes, resulting in an inner volume of 48.4624 ml (inlet and outlet with holding fins each 6.5327 ml, upper bend 35.297 ml), while the length of the vertical pipe was varied to accommodate the mixing elements, leading to Eq. (1) for the total reactor volume.

$$ {V}_{reactor}/ ml=48.4624+6.1472\ {N}_L+3.1968\ {N}_S $$
(1)
Fig. 1
figure 1

Cut model of the reactor containing 6 large SMX elements per side

Full size image

Inlet and outlet possess an inner piping diameter of 6 mm to enable connecting to piping by compression fittings. The vertical pipe section containing the mixing elements and the upper bend have an inner diameter of 25 mm. The SMX elements used here (Fig. 2) have a plate angle of 45°, a plate width of 25/6 mm, a horizontal plate distance of 50/7 mm (center-to-center) and a plate thickness of 0.8 mm. Small elements have a height of 7.1429 mm, large ones a height of 14.286 mm. A stable surface for 3D-printing is ensured in the elements by strips of material, 0.3 mm in height on either side, which compensate for sagging of the plates during the manufacturing process and supply an even surface for the next element to adhere to. Every second SMX element is rotated by 90° along the center axis of the pipe. Models were set up for NS = 4–12 and NL = 0, NS = 0 and NL = 3–7.

Fig. 2
figure 2

SMX-elements used a small element, isometric view; b small element, side view; c large element, isometric view. d large element, side view

Full size image

Two reactors were printed, one containing 6 large mixing elements and a simple tubular reactor without mixing elements and an inner volume of 175.7 ml. They were printed using the FDM method, taking about 70 h. Polypropylene was chosen as material, because of its temperature stability and chemical resistancy. Popular FDM filaments from polylactide or polyamide have a lower resistance to solvents, especially against ethyl acetate used in this study. Also, reaction temperatures of up to 100 °C are tolerable.

Reactor modeling

General formulation

The laminar flow in the fluid domain of the reactors is described by Eq. (2) to (4).

$$\rho \frac{\partial \mathbf{u}}{\partial t}+\rho \left(\mathbf{u}\cdot \nabla \right)\mathbf{u}=\nabla \cdot \left(-p\mathbf{I}+\mathbf{K}\right)+\mathbf{F}+\rho \text{g}$$
(2)
$$\rho \nabla \cdot \left(\mathbf{u}\right)=0$$
(3)
$$ \mathbf{K}=\mu \left(\nabla \mathbf{u}+{\left(\nabla \mathbf{u}\right)}^{\mathrm{T}}\right) $$
(4)

Equation 1 to 3 can be solved under certain boundary conditions, e.g. those which describe the inlet (Eq. (5) to Eq. (7)), the outlet Eq. (8) and the no-slip condition that is assumed at the inner reactor walls (Eq. (9)).

$$\mathbf{u}\cdot \mathbf{t}=0$$
(5)
$$ \dot{V}=\frac{V_{reactor}}{\uptau} $$
(6)
$$ \left(-p\mathbf{I}+\mathbf{K}\right)\mathbf{n}=-{\mathrm{p}}_{\mathrm{inlet}}\mathbf{n} $$
(7)
$$\left(-p\mathbf{I}+\mathbf{K}\right)=0$$
(8)
$$\mathbf{u}=0$$
(9)

The transport of a species i in the convective flow field of the reactor is described by Eq. (10), with the inlet boundary condition given by Eq. (11).

$$ \frac{\partial \left({c}_i\right)}{\partial t}+\mathbf{u}\cdotp \nabla {\mathbf{c}}_{\mathbf{i}}=\nabla \cdotp \left({\mathrm{D}}_{\mathrm{i}}\nabla {\mathrm{c}}_{\mathrm{i}}\right)+{\mathrm{R}}_{\mathrm{i}} $$
(10)
$${c}_{i}={c}_{0,i}$$
(11)

The boundary condition for wall and outlet are mathematically identical for the species transport and are given by Eq. (12). The difference between outlet and wall is captured due to the fact that the outlet possesses convective flow, while the wall does not (see Eq. (9)).

$$ \mathbf{n}\cdotp {\mathrm{D}}_i\nabla {c}_i=0 $$
(12)

The reactor used in experiment was submerged in a water bath. This necessitates the modeling of heat transport by conduction and convection in the fluid, as well as heat transport by conduction through the reactor. The heat transport in the fluid domain and the reactor can be described through Eq. (13).

$$ \rho {C}_p\frac{\partial (T)}{\partial t}+\uprho {C}_p\mathbf{u}\cdotp \nabla \mathrm{T}=\nabla \left(\lambda \nabla \mathrm{T}\right) $$
(13)

Equation 13 can be solved through the boundary conditions given by Eqs. (14) to (16), where Eq. (17) pertains to the temperature at the inlet, Eq. (14) the temperature of the outer walls of the reactor structure and Eq. (16) to the outlet.

$$T={T}_{0,inlet}$$
(14)
$${T}_{walls,outside}={T}_{0,bath}$$
(15)
$$ \mathbf{n}\cdotp \lambda \nabla \mathrm{T}=0 $$
(16)

To solve Eqs. (2), (10) and (13) with the given boundary conditions computational fluid dynamics (CFD) software was used. CFD software solves the differential equations given above by numerical methods with the finite element and volume averaging methods. The reactor geometry and numerical model were built and solved with the commercial software COMSOL Multiphysics® 5.4. Calculations were performed on a computing cluster, under the Ubuntu 18.04.5 LTS operating system, using four Intel(R) Xeon(R) Gold 6130 CPUs with 1547 GB of available memory. The number of mesh elements used in the calculations, as well as the degrees of freedom of the calculations and simulation times are given in the supporting information. The simulations performed to evaluate mixing allow qualitative comparisons of the investigated reactor types, but no quantitative statements. The mesh chosen for the polymerization reaction shows very small remaining numerical errors, so that quantitative analysis is possible. A detailed discussion of numerical diffusion and mesh independence can be found in the SI.

Mixing

The mixing created by the SMX elements was modeled for stationary solutions \(\left(\frac{\partial }{\partial t}=0\right)\) for the flow of an ideal incompressible fluid with a density of ρ = 1000 kg/m3, a viscosity of µ = 100 Pa∙s and a hydraulic residence time of τ = 10 min. The concentration field of a tracer species originating in one half of the inlet was calculated by modifying the boundary condition in Eq. (11) to:

$$c_{i,0,x<0}=0,\;c_{i,0,x>0}=20\frac{mol}{m^3}$$
(17)

where x = 0 is the center of the inlet.

The diffusion coefficient for this tracer species was set to Di =1∙10− 10 m2/s. The effect of the mixing elements and the degree of segregation (DoS) was quantified as first introduced by Danckwerts [33].

$$DoS=\frac{\sqrt{\overline{\left(c-\overline c\right)}^2}}{\overline c}=\frac{\sigma_c}{\overline c}$$
(18)

The DoS was evaluated at the inlet and outlet of the reactor, and before and after each element throughout the mixer sections of the reactors. Planar faces were inserted before, after and in between elements to enable the evaluations. A graphical representation of the evaluated surfaces for a reactor containing 6 large SMX mixing elements is given in the supporting information.

Residence time

Experimental residence time measurements were performed as step measurements using distilled water and a potassium chloride solution of the concentration cKCl = 20 mol/m3. Two calculation steps were used to encompass this in the simulation. Equations (2), (3) and (10) were solved in a time independent fashion with the initial concentrations throughout the reactor and on the inlet boundary \({c}_{0,\text{K}\text{C}\text{l}}=0\) mol/m3. The viscosity was assumed to be identical to that of water at 293.15 K, while the density was given by Eq. (19). This served to provide an initial flow field for the time dependent calculation.

$$\rho ={\rho }_{{H}_{2}O}\left(293.15 K\right)+{c}_{KCl}{M}_{KCl}$$
(19)

In the second step, the same equations were solved in a time dependent calculation, with an inlet concentration of cKCl = 20 mol/m3. The diffusion coefficient of KCl was set to DKCl = 1.89∙10− 9 m2/s [34].

Polymerization

The polymerization of butyl acrylate was modeled by simultaneously solving Eqs. (2), (3), (10) and (13) for the steady state \(\left(\frac{\partial }{\partial t}=0\right)\) in a continuous flow reactor including 6 large SMX mixing elements. Information about the conversion and the molar masses resulting in the polymerization of n-butyl acrylate was acquired by modeling the transport and reaction of low molecular species and transport and reaction of polymer radicals and dead chains up to the second moment. The considered low molecular species were monomers, CTA, solvent, initiator, and initiator radicals. The moments were modeled for polymer chains, secondary polymer radicals, tertiary radicals received through backbiting and tertiary radicals received through transfer to polymer. The full kinetic scheme used in terms of reaction rates Ri is given in the supporting information. Reaction rate coefficients were described by Arrhenius-expressions (Eq. (20)), using the coefficients given in Table 1. They were taken from literature as indicated and analogously to [21], \({k}_{\beta -\text{s}\text{c}\text{i}\text{s}\text{s}\text{i}\text{o}\text{n}}^{\text{t}}\)and \({k}_{\text{b}\text{a}\text{c}\text{k}\text{b}\text{i}\text{t}\text{i}\text{n}\text{g} }^{\text{s}}\) were adjusted within the error tolerance given by [35] to improve the model predictive power with regard to the molar masses. Constant factors necessary for the transfer reaction and the initiator efficiency are given in Table 2.

$$k={A}_{0}\cdot {\text{e}}^{-\frac{{E}_{a}}{\text{R}T}}$$
(20)
Table 1 Collision factors and activation energies used for the modeling of polymerizations
Full size table
Table 2 Constant factors used for polymerization simulations
Full size table

The boundary conditions used for the temperatures of the reactors were \({T}_{0,inlet}=318.15 \text{K}\) and \({T}_{0,bath}=333.15 \text{K}\).

Concentrations at the inlet were assumed to be zero for all species and moments apart from solvent, monomer, initiator and CTA, which are defined by Eq. (21), where wi corresponds to the weight fraction used in the experiments as given in Table 3.

$${\text{c}}_{i}=\frac{{w}_{i}{\rho }_{\text{m}\text{i}\text{x}}}{{M}_{i}}$$
(21)
Table 3 Mass fractions of monomer, solvent, chain transfer agent and initiating agent used in the continuous polymerizations
Full size table

Density, heat capacity and thermal conductivity of the mixture were approximated from temperature dependent literature values of the components[43,44,45,46,47,48]. The thermal conductivity of PBA was assumed to have a constant value of 0.19 W/m/K. Mixture viscosity was fitted to experimental values determined for this system previously[21]. The temperature dependent heat capacity, density and heat conductivity of the polypropylene reactor were interpolated from literature values[49]. The parameters and equations used for this are given in the supporting information.

Diffusion coefficients of the species and moments were assumed to take the value of D = 1∙10− 9 m2/s, which is significantly higher than usual experimental values for polymers in solution[50,51,52,53]. Diffusion coefficients for the solvents, polymers and initiator are dependent on temperature, viscosity, polymer chain length and composition of the solution. Consequently, they cannot be modelled easily if no literature values are available as is the case for diffusion in this system. Lower values of the diffusion coefficient are known to significantly increase the dispersity in the simulations if perfect mixing cannot be assumed[9]. The heat of polymerization was not considered as may be taken from Eq. (13). This simplification is valid if the generation of heat is not of prior interest and for low monomer concentrations and low conversions as investigated in this study.

The number and weight averaged molar masses in the method of moments can be calculated from the zeroth to second moment of the polymer P0- P2 and the monomer molar mass MBA, leading to Eq. (22) for Mn, Eq. (23) for Mw and Eq. 24 for the dispersity of the polymer.

$$M_{\text{n}}=\frac{P_1}{P_0}\cdot M_{\text{B}\text{A}}$$
(22)
$$M_{\text{w}}=\frac{P_2}{P_1}\cdot M_{\text{B}\text{A}}$$
(23)
$$Đ=\frac{{M}_{\text{w}}}{{M}_{\text{n}}}=\frac{{P}_{2}{P}_{0}}{{{P}_{1}}^{2}}$$
(24)

Experimental section

3D printing

The reactors used within this study were designed with the CAD geometry kernel of COMSOL Multiphysics® 5.4 and then sliced with the Slicing software Cura 4.6.1. They were printed using portable 3D printers (Ultimaker 2 Extended + and Ultimaker 3) with PP filaments (2.85 mm, PPPrints). They were printed with a nozzle temperature of 240 °C, bed temperature of 60 °C (60 °C for the first 5 layers), nozzle diameter of 0.4 mm, layer height of 0.075 mm, line width 0.38 mm, material flow of 130 % and print speed of 17 mm/s. The reactors were printed on TESA tesapack Crystal Clear band attached to a glass surface. Printing time was 67 h for the reactor without mixing elements and 74 h for the reactor with mixing elements.

Polymerization of butyl acrylate

n-butyl acrylate (BASF), ethyl acetate (BCD Chemie GmbH), isopropyl alcohol (BCD Chemie GmbH), p-Methoxyphenol (Sigma Aldrich) and 2,2’-Azobis(2,4-dimethylvaleronitril) (V65, FUJIFILM Wako Chemicals Europe GmbH) where used as received. Continuous polymerizations were carried out in a 122.1 ml polypropylene reactor produced via additive manufacturing, which contained 12 SMX mixing elements (6 per side). For the polymerizations, 4 fluids (BA, EA, 1:1 IPA/EA, 1:99 V65/EA) were pumped into the reactor by Prominent gamma/X GMXa 1604 and 1601 metering pumps at flow rates balanced to reach both a total flow of 12.21 ml/min and the mass fractions of the components given in Table 3. The pumps were controlled by the software LabVIEW 17.0f2 and the intensity of the mass flow out of the storage was checked via scales of the types Precisa BJ 6100D and Mettler Toledo Viper PS 35.

All fluids except the initiating agent solution were premixed by a Kenics-mixer and preheated to 60 °C. Both the preheated mixture and the initiating agent solution were routed into the reactor, which was placed in a 60 °C water bath. Temperatures were measured at reactor inlet and outlet by type K thermocouples. Reactions were run for 35 min, with samples taken after 30 and 35 min. Further polymerization after sampling was prevented by adding MEHQ and cooling.

Polymer analysis

NMR spectra were recorded for each polymer sample on a Bruker Avance Ultrashield-400 spectrometer in CDCl3 at room temperature using the solvent peak as reference The relative integrals of methyl protons of MEHQ and vinylic protons of n-butyl acrylate were used to determine remaining monomer content. Gravimetric measurements of the solid content were performed on a CEM Smart Systems 5 moisture analyzer using about 1 ml of each polymer sample.

Molecular weights were obtained by SEC (PLGel MIXED-B column (10 μm, 300 × 7.5 mm), Schambeck RI 2000 detector, and a Flom Intelligent pump AI-12) in tetrahydrofuran as eluent at a flow rate of 1 ml/min and an injection volume of 20 µl. The molecular weight distributions were evaluated using the software Chromatographica V1.1.25. Monodisperse PS standards (Polymer Standards Service GmbH) were used for calibration and the measured values were referenced against these standards and rescaled by an internal standard for poly-butyl acrylate.

Residence time measurements

Residence times for an unmixed tube reactor (V = 175.6 ml) and the reactor containing 6 mixing elements (V = 122.1 ml) were determined by conduction measurements. The conductivity was measured at the inlet and outlet by WTW TetraCon DU/T Flow-through conductivity cells. Fluids were pumped at a flow rate equal to one tenth of the reactor volume per minute by a Prominent gamma/X GMXa 1604 metering pump. The pump was controlled by the software LabVIEW 17.0f2 and the intensity of the mass flow out of the storage vessel was checked via scales of the type Precisa BJ 6100D. Initially, distilled water was pumped through the reactors for 15 min to allow for the flow to reach a steady state. The inlet was then switched over to a 0.02 M solution of potassium chloride. Conductivity values were measured until the conductivity at the outlet was constant.

Results and discussion

Modeling of mixing efficiency

The choice of reactor geometry for butyl acrylate polymerizations with respect to the mixing by a varying number of two sizes of SMX elements was made after mapping the performance in CFD calculations as described earlier. This is a crucial matter as the outcome of polymerizations are highly susceptible to fluctuations in both concentrations and temperature.

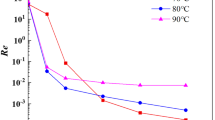
The degree of segregation in relation to hydraulic residence time for pipe reactors containing small and large mixing elements is shown in Fig. 3a and b, respectively. The region without points corresponds to the upper turn section of the reactor with no mixing. The degree of segregation decreases near exponentially when smaller SMX elements are used (Fig. 3a). Each of these elements reduces the DoS on average to 78.8 % of the preceding value. As expected, the reactors containing more mixing elements reach a lower total DoS. Additionally, the increased reactor volume at a constant hydraulic residence time leads to increased time efficiency of the mixing, as more elements are passed in the same time span. The mixing effect of the large elements (Fig. 3b) is less uniform than of the smaller ones, with the DoS in each of the first four elements being reduced to between 19.4 and 72.0 %, but the mixing overall is significantly improved. On average, in reactors with 3–5 large mixing elements the DoS is reduced to 44.3 % of the previous value in each element. In reactors containing 6 or more large elements per side, the DoS begins to level off in the second stack of mixing, leading to a total average reduction to 56.1 % of the DoS per element. If only the first stack of mixing elements is considered, the average reduction values for all reactors lie between 46.5 % and 44.0 %. An average DoS of 3.31∙10− 2 is reached after two mixing elements, while it takes about between 9 and 10 of the smaller elements to reach similar values.

Fig. 3
figure 3

Degree of Segregation at 100 Pa∙s in reactors containing different mixing sections in relation to the hydraulic residence time. a reactors containing small elements. b reactors containing large elements

Full size image

The superior but less uniform mixing indicated for the larger SMX elements may be understood by considering the concentration profiles at different heights (Fig. 4). When passing through smaller SMX elements (Fig. 4a-e), the interfaces between areas of low and high concentrations become stretched by the first element, as expected. In subsequent elements however, it becomes apparent that the scale of the stretching along the reactor radius is not sufficient, as a significant portion of the fluid near the wall stays relatively unmixed. This leads to areas with concentrations 70 % higher than average even after the fluid has passed 4 mixing elements (Fig. 4e). Flow through larger mixing elements shows a similar profile of stretching after the first element (Fig. 4f) but interfaces are stretched throughout the entire reactor. The following two elements induce a more complete mixing, with no areas higher than 40 % above the average concentration remaining after the third element.

Fig. 4
figure 4

Effect of mixing elements on concentration: a profile before entering mixed section, after b, 1 small element, c 2 small elements, d 3 small elements, e 4 small elements, f 1 large element, g 2 large elements and h 3 large elements

Full size image

It is necessary to initially achieve both fast and complete mixing for a uniform polymerization and also to transport heat effectively through the reactor in later phases. Heat transport in a laminar mixed fluid is dominated by convection and this will coincide with mass transport. The large elements are preferable for an efficient dispersal of heat from the walls and throughout the reactor. The polymerization of BA is to be performed with external heating through the wall and the reactor temperature should be as uniform as possible. Therefore, a reactor with 6 large mixing elements was chosen to be printed and used in polymerization experiments.

Modeling and experimental determination of residence time behavior

The action of the mixing elements included in the design with regard to the residence time behavior of the reactors was mapped in a concentration step experiment for both an unmixed tube reactor and the reactor containing the 6 large mixing elements. The cumulative distribution function and distribution density function of a simple tube reactor show a rapid increase in concentration after a residence time of 300 s of experiment (Fig. 5a and b). The cumulative distribution function shows that the bulk of the tracer has passed through the reactor after 450 s. Almost no tailing was observed in the experimental residence time. The early onset at 300 s is expected due to the laminar flow behavior, which leads to a core velocity twice as high as the average velocity of the cross section. At the same time tailing would be expected due to slower velocity in boundary region of the tube. Thus, the experimentally observed behavior indicates a significant bypass flow in the reactor. The simulation shows a similar signal arising at 294 s, indicating a similar bypass flow and in contrast to the experiment a taper in the distribution functions, a typical sign for the slow filling of a dead zone. The average residence time in the experiments was 339.3 s, while the numerical simulation yielded a value of 596 s.

Fig. 5
figure 5

Experimental and simulated residence time distributions of a simple 3D-printed tube reactor. a Cumulative distribution function, b Distribution density function

Full size image

The tracer concentration in the reactor containing 6 large mixing elements per mixing section at the outlet begins increasing after 342 s in experiment and after 360 s in the simulation, which is a reasonable agreement (Fig. 6a and b). The presence of mixing elements in the reactor significantly broadens the distribution density function of both simulation and experiment, implying a reduction of the bypass flow. As before, the simulation shows a more pronounced tailing than the experiment. The simulated average residence time was 493.9 s, while the numerical simulation yielded a value of 711.3 s.

Fig. 6
figure 6

Experimental and simulated residence time distributions of a 3D-printed reactor with 6 large SMX mixing elements per mixing section. a Cumulative distribution function, b Distribution density function

Full size image

The computational model is able to capture the early response of the reactors to a concentration step in an acceptable way. The peak of the experimental and simulated distribution density function coincide well in both reactors. Both experiment and simulation show the increase of the average residence time with the addition of mixing elements.

The tailing that is predicted by the CFD calculation is not observed in experiment. This suggests that the dead volume in the reactor is not effectively filled during the experiment although measurements were performed up to four hours (equivalent to 24 hydraulic residence times). The dead volume in the reactor could be visualized in a residence time experiment with blue dyestuff added to the tracer fluid (the reactor is operated vertically). Comparing the image of this experiment after a time of 300 s with the simulation leads to the conclusion of high accordance between experiment and simulation (Fig. 7). It is apparent, that the flow in the upper reactor turn is not uniform, leading to the bypass flow surmised for both reactor geometries.

Fig. 7
figure 7

Upper reactor turn during residence time measurement. a Image of experiment with added dyestuff. b Simulated concentration profile after 300 s

Full size image

Initial calculations disregarded the change in density and the resulting gravitational effect given by Eq. (19), as the relative difference in density is less than 0.2 %, but these calculations were unable to capture the non-uniformity in the reactor bend. For comparison these calculations are also pictured in Figs. 5 and 6. For both reactors the initial signal onset and the maximum of the distribution density function are shifted to higher residence times, when compared to both experiment and simulations considering the density change.

The simulated concentration profile in the reactor (Fig. 7) shows a transitional area above the area of high concentration, where upward solute transport occurs mainly by diffusion. This diffusion leads to a slow filling of the upper volume, leading to the tailing effect in the calculations.

It is possible that this effect is overestimated in the simulation due to numerical diffusion in the reactor bend.

Polymerization of n-butyl acrylate: experimental and theoretical results

Solution polymerizations of BA in EA in the reactor containing 6 large mixing elements were carried out to assess the accuracy of the model. Monomer weight fractions were varied from 20 to 40 wt% at a chain transfer agent (isopropyl alcohol) weight fraction of 10 wt%. Additionally, the amount of the chain transfer agent was varied between 0 and 10 wt% for a monomer weight fraction of 40 wt% (Table 3).

The monomer conversions predicted for a reactor containing the 6 large SMX elements per mixing section at varying monomer weight are of medium quality (Fig. 8). The mathematical model overestimates conversion significantly at low initial monomer weight fractions. The increase in conversion with the monomer concentration in particular is overestimated. An acceptable coincidence is reached for monomer fractions higher than 30 %. Thus, at a monomer weight fraction of 0.4 the predicted and actual values of 49.96 % and 48.12 % / 41.90 % (by microwave gravimetry and NMR, respectively) are quite close together.

Fig. 8
figure 8

Monomer conversion of n-butyl acrylate in relation to monomer content at a CTA weight fraction of 0.1

Full size image

The too high predicted conversions at low monomer concentrations indicate that the model is not accounting for all relevant parameters. The radical concentration apparently is too high, the rate of the start reaction \({r}_{s}={2fk}_{d}\left[I\right]\) overestimated. An impact of membrane pumps on initial mixing or a medium dependent cage effect would be a good guess, \(f\) being a function of the amount and type of solvent used in the polyreaction. In the simulations, such effects are not specifically modeled and the initiator efficiency is assumed to be constant at \(f\) of 0.5. In addition the unknown diffusion constants of involved species as well as the numerical diffusion might increase f artificially by spreading the initiator radicals and compensating local monomer deficiencies. The kinetic parameters were taken from literature and not modified for the shown simulations. The result of the simulation in that regard are surprisingly good, given the complexity of the system, where tertiary radicals play a significant role in the consumption of monomer and the termination of chains.

The molecular weights of the resulting polymer (Fig. 9a) predicted by simulation are in reasonable agreement with experimental results. They again show a similar but stronger trend of the molar masses increasing with the initial monomer content for simulation and experiment, respectively. The experimental value of Mn is between 30.92 % and 20.97 % higher than the simulated one for the monomer weight fractions from 0.20 to 0.30. When a monomer weight fraction of 0.35 is reached however, the experimental molar masses reach a maximum and decrease when the monomer content is increased further. This is not mirrored by the simulation, leading to an inversion of the relation observed at lower monomer weight fractions, with the experimental number averaged molar masses now 9.10 % lower than the predicted ones. Also here, the parameter of the model needs adjustment over the straight forward taken values from the literature, here probably with regard to the rate of the transfer reactions.

Fig. 9
figure 9

Polymer characteristics at varying BA weight fractions. a Number and weight average molar mass by GPC. b Dispersities predicted by the calculations and determined in experiment

Full size image

The dispersities show good agreement between experimental and simulated trends (Fig. 9b). The calculated dispersities increase steadily with the amount of monomer, at around 2.3 % per 5.0 wt% fraction of monomer. The experimental values increase similarly, but are between 3.50 % and 5.14 % lower. This low deviation together with the values already shown for the molar masses demonstrate an acceptable first principle coupling between CFD and the BA kinetic model.

Neither simulation nor experiment show a clear trend of increasing or decreasing conversion in the presence of IPA as CTA (Fig. 10). This is in accordance with expectation as the CTA would only transfer a radical, and should not significantly influence the amount of radicals present. In fact, simulations show almost no change in conversion (< 1 %). The experimental conversions on the other hand show some fluctuations. The fluctuations may be within experimental error. Note that the conversion at determination of conversion by NMR and microgravimetry differ, but trends are consistently reproduced. Again, a too low conversion is found in regard to the calculations, possibly for the same reasons of a too low rate of start of polymerization.

Fig. 10
figure 10

Monomer conversion of n-butyl acrylate in relation to CTA content at a monomer weight fraction of 0.4

Full size image

The molar mass decreases when the weight fraction of CTA in the reaction is higher, as more transfer reactions take place (Fig. 11a). The data of experiment and simulation are almost identical for IPA weight fractions higher than 5 wt%. At lower amounts of CTA in the reaction, the predicted values start diverging from the experimentally determined ones. The overestimation of the number average molar mass in the simulation for example, increases from 9.10 % at wIPA = 0.1 to 18.7 % at wBA = 0.05 and finally 59.20 % at wIPA = 0. The weight averaged molar masses diverge in a similar fashion, with the overestimation ranging from 13.71 % at wIPA = 0.1 to 62.10 % at wIPA = 0.

Fig. 11
figure 11

Polymer characteristics at varying CTA weight fractions. a Number and weight average molar mass. b Dispersities predicted by the calculations and determined in experiments

Full size image

The dispersities of the polymer show an almost identical behavior for both simulation and experiment, decreasing in a nearly exponential fashion with the amount of CTA utilized (Fig. 11b). As already seen for the polymerizations with increasing monomer weight fractions (Fig. 9b), the computation somewhat overestimates the dispersity. The experimental values are therefore between 4.93 % and 13.16 % lower than the expected ones.

Concluding remarks

The scope of this study was to optimize a flow reactor for the continuous solution polymerization of n-butyl acrylate. This reaction system is complex on account of the manifold transfer reactions and requires good mixing. A 3D-printable reactor was chosen with modular geometry, giving the option to adjust its mixing characteristics. CFD calculations were performed to evaluate mixing in the various reactor geometries. Intensive mixing at the desired flow velocities, while keeping optimal printability lead to the choice of SMX elements, which had a height to diameter quotient of 4/7 with a horizontal plate distance of 50/7 mm. A reactor containing 6 of these elements was printed from polypropylene filament. The application of 3D printing enabled the specially tailored reactor to be fabricated fast and cheaply in 74 h and at a material cost of 10.99 € (6.58 € per 100 g of filament).

Residence times were calculated employing CFD calculations and compared to experimentally measured ones. Quantitative agreement was good. Bypass flows could be significantly reduced by the introduced SMX mixing elements. Using ink and the semi-transparent 3D-printed reactor a dead volume in the bend could be visualized experimentally. This finding could be used to refine the CFD model with respect to varying densities so that the agreement between model and simulation could be significantly improved.

A kinetic model for the free radical polymerization of BA was incorporated into the CFD model. It could be coupled to the optimized geometry and was used to predict conversion as well as number and weight average molecular weight and dispersities for various reaction conditions. Then, the corresponding polymerizations were performed in flow and the results could be used to validate the model. While discrepancies are observed, the overall agreement is satisfactory. Especially when taking into account the complexity of the BA polymerization and the purely predictive nature of the implemented model (no parameters were fitted), the model performs well. Thus, it is expected to serve as a basis for further investigations as well as optimizations.

Finally, this work demonstrates the power of coupling CFD calculations with complex reaction kinetics to improve reactor geometries even for systems as challenging as the polymerization of BA. When this approach was further combined with additive manufacturing for the reactor, very fast, cheap and effective optimization cycles can be realized.