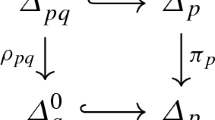On the Computation of the Cohomological Invariants of Bott–Samelson Resolutions of Schubert Varieties

Abstract

Let $X\subseteq G/\mathcal {B}$ be a Schubert variety in a flag manifold and let $\pi : \tilde{X} \rightarrow X$ be a Bott–Samelson resolution of X. In this paper, we prove an effective version of the decomposition theorem for the derived pushforward $R \pi _{*} \mathbb {Q}_{\tilde{X}}$. As a by-product, we obtain recursive procedure to extract Kazhdan–Lusztig polynomials from the polynomials introduced by Deodhar [7], which does not require prior knowledge of a minimal set. We also observe that any family of equivariant resolutions of Schubert varieties allows to define a new basis in the Hecke algebra and we show a way to compute the transition matrix, from the Kazhdan–Lusztig basis to the new one.

1 Introduction

This work is a sort of appendix to [7]. In such a paper, Vinay Deodhar introduces a statistic, called defect, on the subexpressions of a given reduced expression of an element of a Coxeter group W (see also [2, Section 6.3.17]). Specifically, let $w\in W$ be an element of length l(w) and let

$$\begin{aligned} w=s_1 \dots s_l, \quad l=l(w) \end{aligned}$$

be a reduced expression of w. A subexpression $\sigma =(\sigma _0, \dots , \sigma _l)$ is a sequence of Coxeter group elements, such that

$$\begin{aligned} \sigma _{j-1}^{-1}\sigma _j \in \{id, s_j\}, \quad \text {for all} \quad 1\le j \le l. \end{aligned}$$

Let $\mathcal {S}$ be the set such sequences for the given reduced expression and let

$$\begin{aligned} \pi (\sigma ):= \sigma _l, \quad \text {if} \quad \sigma =(\sigma _0, \dots , \sigma _l)\in \mathcal {S}. \end{aligned}$$

For any subexpression $\sigma =(\sigma _0, \dots , \sigma _l)\in \mathcal {S}$, Deodhar defines the defect of $\sigma$ by

$$\begin{aligned} d(\sigma ):= \# \{1\le j \le l \mid \sigma _{j-1}^{-1}s_j < \sigma _{j-1} \}. \end{aligned}$$

If one fixes a reduced expression for all $w\in W$ and consider $v\in W$, such that $v\le w$ in the Bruhat order, then one can use the defect to define the following polynomial:

$$\begin{aligned} Q_{w, v}:= \sum _{\sigma \in \mathcal {S}, \, \pi (\sigma )=v}q^{d(\sigma )} \in \mathbb {Z}[q]. \end{aligned}$$

(1.1)

In [7], Deodhar proves that the Kazhdan–Lusztig polynomial $P_{w, v}$ admit a description as subsum of (1.1). More precisely, he gives a recursive algorithm for computing a minimal set $E_{min}\subseteq \mathcal {S}$, such that

$$\begin{aligned} P_{w, v}:= \sum _{\sigma \in E_{min}, \, \pi (\sigma )=v}q^{d(\sigma )} \in \mathbb {Z}[q], \end{aligned}$$

(1.2)

for any pair $w, v\in W$, $v\le w$. What is more, in [7], one can find a new basis of the Hecke algebra of W that is defined starting from the polynomials (1.1).

The main aim of this paper is to give a recursive procedure to extract Kazhdan–Lusztig polynomials $P_{w, \, v}$ from polynomials $Q_{w, \, v}$, without going through the computation of the minimal set $E_{min}\subseteq \mathcal {S}$; in the case, W is the Weyl group of a semisimple connected algebraic group over $\mathbb {C}$. Instead, our approach is based on an effective version of the Beilinson–Bernstein–Deligne–Gabber decomposition theorem (BBDG for short) for the Bott–Samelson resolution. As a by-product of our analysis, we provide a recursive procedure to compute the change-of-basis matrix, from the Kazhdan–Lusztig basis of the Hecke algebra to the basis defined in [7].

The starting point of our analysis is Proposition 3.9 of [7], where the author shows that, when W is the Weyl group of a semisimple connected algebraic group, the polynomial (1.1) has a nice geometric interpretation as Poincaré polynomial of a suitable fiber of the Bott–Samelson resolution of the Schubert variety X(w) [see Sect. 2 for a short review of some standard definitions and notations concerning Schubert varieties]. More precisely, if we denote by G an algebraic group with Weyl group W and Borel subgroup $\mathcal {B}$, then to the chosen reduced expression $w=s_1 \dots s_l$, it is also associated the Bott–Samelson resolution

$$\begin{aligned} \pi _{w}: \tilde{X} (w) \rightarrow X(w). \end{aligned}$$

The smooth variety $\tilde{X} (w)$ is defined as the subvariety of $(G/\mathcal {B})^l$ consisting of l-tuples $(g_1\mathcal {B}, \dots , g_l\mathcal {B})$, such that

$$\begin{aligned} g_{i-1}^{-1}g_i\in \overline{\mathcal {B}s_i \mathcal {B}}, \quad 1\le i \le l\quad (\text {by convention}, \,\,g_0=1), \end{aligned}$$

and $\pi _w$ is the projection on the last factor. The polynomial (1.1) is the Poincaré polynomial of the fiber of $\pi _w$ over the cell $\Omega _v\subset X(w)$ associated with v:

$$\begin{aligned} Q_{w, \, v}= \sum _i \dim H^{2i}(\pi _w^{-1}(x))q^i, \quad \forall x\in \Omega (v). \end{aligned}$$

(1.3)

Our approach for extracting the Kazhdan–Lusztig polynomials from the polynomials defined in (1.1) is to prove an effective version of the BBDG decomposition theorem for the Bott-Samelson resolution and, more generally, for any equivariant resolution of a Schubert variety (in [10, 12], and [3] partial results in this direction were previously obtained). Specifically, let $D_{c}^{b}(X)$ be the derived category of bounded complexes of constructible $\mathbb {Q}$-vector sheaves on a Schubert variety $X\subseteq G/\mathcal {B}$. The decomposition theorem, applied to an equivariant resolution $\pi :\tilde{X} \rightarrow X$, states that the derived direct image $R \pi _{*} \mathbb {Q}_{\tilde{X}} [ \dim X ]$ splits in $D_{c}^{b}(X)$ as a direct sum of shifts of irreducible perverse sheaves on X. By [6, § 1.5], we have a non-canonical decomposition

$$\begin{aligned} R \pi _{*} \mathbb {Q}_{\tilde{X}} [ \dim X] \cong \bigoplus _{i \in \mathbb {Z}} \bigoplus _{j \in \mathbb {N}} IC(L_{ij}) [-i], \end{aligned}$$

(1.4)

where the summands are shifted intersection cohomology complexes of the semisimple local systems $L_{ij}$, each of which is supported on a suitable locally closed stratum of codimension j, usually called a support of the decomposition. The summand supported in the general point is precisely the intersection cohomology of X. The supports appearing in the splitting (1.4) and the local systems $L_{ij}$ are, generally, rather mysterious objects when $j \ge 1$.

Quite luckily, in our case, a crucial simplification arises because all the local systems $L_{ij}$ appearing in the decomposition (1.4) are trivial by an easy argument that is explained in Proposition 3.2. As a consequence, we have

$$\begin{aligned} R \pi _{*} \mathbb {Q}_{\tilde{X}} [ \dim X] \cong \bigoplus _{X(v)\subseteq X} \bigoplus _{\alpha \in \mathbb {Z}} IC_{X(v)}^{\oplus s_{v, \alpha }} [- \alpha ], \end{aligned}$$

(1.5)

for suitable multiplicities $s_{v, \alpha }$. In a completely similar way, for any equivariant resolution $\pi _w: \tilde{X}(w) \rightarrow X(w)$, we have a splitting

$$\begin{aligned} (R \pi _w) _{*} \mathbb {Q}_{\tilde{X}(w)} [ \dim X(w)] \cong \bigoplus _{X(v)\subseteq X(w)} \bigoplus _{\alpha \in \mathbb {Z}} IC_{X(v)}^{\oplus s_{v, \alpha }^w} [- \alpha ]. \end{aligned}$$

Hence, we can define a Laurent polynomial recording the contribution to the decomposition theorem for $\pi _w$, with support X(v)

$$\begin{aligned} D_{w, v} (t) := \sum _{\alpha \in \mathbb {Z}} s_{v, \alpha }^{w} \cdot t^{\alpha }\in \mathbb {Z}[t, t^{-1}], \end{aligned}$$

for every pair (v, w) in W, such that $v\le w$.

Now, assume to have fixed an equivariant resolution $\pi _w: \tilde{X}(w) \rightarrow X(w)$ for every Schubert variety X(w) and assume that the cohomology of the fibers of $\pi _w$ vanishes in odd degrees (this property is satisfied by any reasonable resolution of Schubert varieties). Similarly, as in (1.3), define the analogue Deodhar’s polynomial $Q_{w, v}$ as the Poincaré polynomial of the fibers of $\pi _w$ over the cell $\Omega (v)$. The main results contained in this paper can be summarized as follows:

• a) we set up an iterative procedure that allows to compute both the Kazhdan–Lusztig polynomials $P_{w, v}$ and the Laurent polynomials $D_{w, v}$ starting from Deodhar’s polynomials $Q_{w, v}$;

• b) we observe that the polynomials $Q_{w, v}$ allow to construct a new basis $\{B_w \mid w\in W\}$ of the Hecke algebra;

• c) we prove that the transition matrix, from the Kazhdan–Lusztig basis to the new basis $\{B_w \mid w\in W\}$, can be easily deduced from the Laurent polynomials $D_{w, v}$ and does not require prior knowledge of the transition matrix from the Kazhdan–Lusztig basis to the standard one (compare with Remark 5.2).

2 Notations and basic facts

In this section, we review some basic facts concerning Buhat decomposition, Schubert varieties, and combinatorics of subexpressions that are needed in the following.

• (i) Let G be a semisimple connected algebraic group over $\mathbb {C}$. Let $\mathcal {T}$ and $\mathcal {B}$ be a maximal torus and a Borel subgroup of G, respectively. Denote by W be the Weyl group of G. If we consider

  $$\begin{aligned} \{e_w \mid \,\, w\in W\}\subset G/\mathcal {B}, \end{aligned}$$

  the set of fixed points for the torus action on $G/\mathcal {B}$, then we have the Bruhat decomposition of $G/\mathcal {B}$, i.e., the disjoint union of Bruhat cells

  $$\begin{aligned}G/\mathcal {B}= \bigsqcup _{w\in W}\Omega (w), \quad \Omega (w):=\mathcal {B}e_w.\end{aligned}$$

  For every $w\in W$, the Schubert variety associated with w is defined as the Zariski closure of the corresponding Bruhat cell

  $$\begin{aligned} X(w):= \overline{\Omega (w)}. \end{aligned}$$

• (ii) There is a partial order on the Weyl group W determined by the decomposition above. Specifically, for $w_1, w_2\in W$, we have

  $$\begin{aligned} w_1\ge w_2 \quad \Leftrightarrow \quad X(w_1) \supseteq X(w_2). \end{aligned}$$

  Furthermore, we have

  $$\begin{aligned} X(w)= \bigcup _{v \le w}\Omega (v). \end{aligned}$$

  We borrow from Deodhar’s paper [7] some crucial definitions concerning the combinatorics of subexpressions of a reduced word in a Coxeter group.

Definition 2.1

[7, Def. 2.1–2.2]

• (1) Let $w\in W$ be an element of length l(w) and let

  $$\begin{aligned} w=s_1 \dots s_l, \quad l=l(w) \end{aligned}$$

  be a reduced expression of w. A subexpression $\sigma =(\sigma _0, \dots , \sigma _l)$ is a sequence of Weyl group elements, such that $\sigma _0=id$ and

  $$\begin{aligned} \sigma _{j-1}^{-1}\sigma _j \in \{id, s_j\}, \quad \text {for all} \quad 1\le j \le l. \end{aligned}$$

  For any reduced word r, let $\mathcal {S} _r$ be the set of reduced expressions of r and let

  $$\begin{aligned} \pi (\sigma ):= \sigma _l, \quad \text {if} \quad \sigma =(\sigma _0, \dots , \sigma _l)\in \mathcal {S} _r. \end{aligned}$$

• (2) For any $\sigma =(\sigma _0, \dots , \sigma _l)\in \mathcal {S} _r$, define the defect of $\sigma$ by

  $$\begin{aligned} d(\sigma ):= \# \{1\le j \le l \mid \sigma _{j-1}s_j < \sigma _{j-1} \}. \end{aligned}$$

If $v\le w$, we let

$$\begin{aligned} Q_{w, v}:= \sum _{\sigma \in \mathcal {S}_r, \,\pi (\sigma )=v}q^{d(\sigma )} \in \mathbb {Z}[q]. \end{aligned}$$

(2.1)

From now on, we assume that we have chosen a reduced expression for all$w\in W$, and hence, (2.1) provides a polynomial $Q_{w, v}\in \mathbb {Z}[q]$ for any pair (w, v), such that $v\le w$.

As explained in [7, Proposition 3.9], the polynomial above has a nice geometric interpretation as Poincaré polynomial of the Bott–Samelson resolution. We recall that to each reduced expression $w=s_1 \dots s_l,$ it is also associated the Bott–Samelson resolution

$$\begin{aligned} \pi _{w}: \tilde{X} (w) \rightarrow X(w). \end{aligned}$$

The smooth variety $\tilde{X} (w)$ is defined as the subvariety of $(G/\mathcal {B})^l$ consisting of l-tuples $(g_1\mathcal {B}, \dots , g_l\mathcal {B})$, such that

$$\begin{aligned} g_{i-1}^{-1}g_i\in \overline{\mathcal {B}s_i\mathcal {B}}, \quad 1\le i \le l\quad (\text {by convention}, \,\,g_0=1), \end{aligned}$$

and $\pi _w$ is the projection on the last factor. It is clear that $\pi _w$ is equivariant under the action of the Borel subgroup $\mathcal {B}$.

By [7, Proposition 3.9], (2.1) is the Poincaré polynomial of the fiber of $\pi _w$ over the cell $\Omega (v)\subset X(w)$

$$\begin{aligned} Q_{w, v}= \sum _i \dim H^{2i}(\pi _{w}^{-1}(x))q^i, \quad \forall x\in \Omega (v). \end{aligned}$$

(2.2)

3 The Decomposition Theorem

Formula (2.2) and Deodhar’s paper suggest that there should be a closed relationship between the Poincaré polynomials of the stalk cohomology of the complex $R \pi _{*} \mathbb {Q}_{\tilde{X}(w)}$ and the Kazhdan–Lusztig polynomials. The most important result concerning the complex $R \pi _{*} \mathbb {Q}_{\tilde{X}(w)}$ and, in general, concerning the topology of proper algebraic map is the decomposition theorem of Beilinson, Bernstein, Deligne, and Gabber, which we now recall.

In what follows, we shall work cohomology with $\mathbb {Q}$-coefficients and the self-dual perversity $\mathfrak {p}$ (see [1, §2.1], and [14, p. 79]).

Theorem 3.1

(Decomposition theorem[6, 1.6.1]) Let $f: X \rightarrow Y$ be a proper map of complex algebraic varieties. In $D_{c}^{b}(Y)$, the derived category of bounded complexes of constructible $\mathbb {Q}$-vector sheaves on Y, there is a non-canonical isomorphism

$$\begin{aligned} Rf_{*} IC_{X} \cong \bigoplus _{\alpha \in \mathbb {Z}}{}^{\mathfrak {p}}{}{\mathcal {H}}^{\alpha }(Rf_{*} IC_{X}) \left[ - \alpha \right] . \end{aligned}$$

(3.1)

Furthermore, the perverse sheaves ${}^{\mathfrak {p}}{}{\mathcal {H}}^{\alpha }(Rf_{*} IC_{X})$ are semisimple, i.e., there is a decomposition into finitely many disjoint locally closed and nonsingular subvarieties $Y = \coprod S_{\beta }$ and a canonical decomposition into a direct sum of intersection complexes

$$\begin{aligned} {}^{\mathfrak {p}}{}{\mathcal {H}}^{\alpha }(Rf_{*} IC_{X}) \cong \bigoplus _{\beta } IC_{\overline{S_{\beta }}}(L_{\alpha , S_{\beta }}), \end{aligned}$$

(3.2)

where $L_{\alpha , S_{\beta }}$ denote suitable semisimple local systems defined on $S_{\beta }$.

Combining (3.1) and (3.2), we have

$$\begin{aligned} Rf_{*} IC_{X} \cong \bigoplus _{\alpha \in \mathbb {Z}} {}^{\mathfrak {p}}{}{\mathcal {H}}^{\alpha }(Rf_{*} IC_{X}) [- \alpha ] \cong \bigoplus _{\alpha \in \mathbb {Z}} \bigoplus _{\beta } IC_{\overline{S_{\beta }}}(L_{\alpha , S_{\beta }}) [- \alpha ], \end{aligned}$$

(3.3)

which can be written in the form

$$\begin{aligned} Rf_{*} IC_{X} \cong \bigoplus _{\alpha \in \mathbb {Z}} {}^{\mathfrak {p}}{}{\mathcal {H}}^{\alpha }(Rf_{*} IC_{X}) [- \alpha ] \cong \bigoplus _{\alpha \in \mathbb {Z}} \bigoplus _{\beta } {}^{\mathfrak {p}}{}{\mathcal {H}}^{\alpha }(Rf_{*} IC_{X})_{\overline{S_{\beta }}} [- \alpha ], \end{aligned}$$

where ${}^{\mathfrak {p}}{}{\mathcal {H}}^{\alpha }(Rf_{*} IC_{X})_{\overline{S_{\beta }}}:= IC_{\overline{S_{\beta }}}(L_{\alpha , S_{\beta }})$, and where the closed subsets $\overline{S_{\beta }}$ are called supports of f (see [16, Definition 9.3.41]). In the literature, one can find different approaches to the Decomposition Theorem (see [1, 6, 17, 18]), which is a very general result but also rather implicit. On the other hand, there are many special cases for which the Decomposition Theorem admits a simplified and explicit approach. One of these is the case of varieties with isolated singularities. For instance, in the work [11], a simplified approach to the Decomposition Theorem for varieties with isolated singularities is developed, in connection with the existence of a natural Gysin morphism, as defined in [8, Definition 2.3] (see also [9] for other applications of the Decomposition Theorem to the Noether–Lefschetz Theory).

As remarked before, the Bott–Samelson resolution

$$\begin{aligned} \pi _{w}: \tilde{X} (w) \rightarrow X(w) \end{aligned}$$

is equivariant under the action of the Borel subgroup $\mathcal {B}$, and hence, $\pi _{w}$ is stratified according to the Bruhat decomposition

$$\begin{aligned} X(w) = \bigsqcup _{v\le w} \Omega (v). \end{aligned}$$

In this case, the supports of the decomposition theorem applied to the resolution $\pi _w$ are the Schubert subvarieties

$$\begin{aligned} X(v)=\overline{\Omega }(v), \qquad v \le w. \end{aligned}$$

Furthermore, all local systems appearing in the decomposition theorem are trivial, since the isotropy subgroup of each orbit $\Omega (v)$ is connected [15, Remark 11.6.2].

We include in the following proposition a proof of these facts, although they are probably well-known (compare, e.g., with [5, Theorem 2.2.7 and equation (2.1)]), in the attempt of making the present paper reasonably self-contained and also because the simple argument is very close to the rest of the paper.

Proposition 3.2

Let $\pi : \tilde{X} \rightarrow X$ be an equivariant resolution of a Schubert variety $X=X(w)$ of dimension l. In the derived category $D_{c}^{b}(X)$, we have a splitting

$$\begin{aligned} R \pi _{*} (\mathbb {Q}_{\tilde{X}}) [l] = \bigoplus _{v \le w} \bigoplus _{\alpha \in \mathbb {Z}} IC_{X(v)}^{ \oplus s_{v, \alpha }} [- \alpha ], \end{aligned}$$

for suitable multiplicities $s_{v, \alpha }$. In other words, the supports of the decomposition theorem applied to the resolution $\pi$ are the Schubert varieties contained in X and all local systems are trivial.

Proof

Let $l:=l(w)$, fix r, such that $-1\le r\le l$ and define the following decreasing sequence of open sets of X:

$$\begin{aligned} \ \mathcal {U}_r:= X(w)\backslash \bigsqcup _{v\le w, \, l(v)\le r} \Omega (v). \end{aligned}$$

Clearly we have $\mathcal {U}_l= \emptyset$ , $\mathcal {U}_{-1}=X$. We are going to prove, by decreasing induction on r, that

$$\begin{aligned} R \pi _{*} (\mathbb {Q}_{\tilde{X}}) [l] \mid _{\mathcal {U}_r}= \bigoplus _{v \le w,\, r<l(v)} \bigoplus _{\alpha \in \mathbb {Z}} IC_{X(v)}^{ \oplus s_{v, \alpha }} [- \alpha ]\mid _{\mathcal {U}_r}, \end{aligned}$$

(3.4)

for suitable multiplicities $s_{v, \alpha }$. Since $\mathcal {U}_{l-1}=\Omega :=\Omega (w)$ and since $\pi$ is an isomorphism over $\Omega$, we have

$$\begin{aligned} R \pi _{*} \mathbb {Q}_{\tilde{X}} [l] \mid _{\Omega }\cong \mathbb {Q}_{\Omega } [l]; \end{aligned}$$

hence, the base step follows from the well-known isomorphism:

$$\begin{aligned} \mathbb {Q}_{\Omega } [l] \cong IC_{X}\mid _{\Omega } \end{aligned}$$

(compare, e.g., with [16, Definition 6.3.1]). As for the inductive step, let

$$\begin{aligned} \mathcal {D}:= \bigsqcup _{v \le w,\, r=l(v)}\Omega (v). \end{aligned}$$

By induction, we have

$$\begin{aligned} R \pi _{*} (\mathbb {Q}_{\tilde{X}}) [l] \mid _{\mathcal {U}_{r}}= \bigoplus _{v \le w,\, r<l(v)} \bigoplus _{\alpha \in \mathbb {Z}} IC_{X(v)}^{ \oplus s_{v, \alpha }} [- \alpha ]\mid _{\mathcal {U}_{r}}; \end{aligned}$$

hence, we deduce

$$\begin{aligned} R \pi _{*} (\mathbb {Q}_{\tilde{X}}) [l] \mid _{\mathcal {U}_{r-1}}= \mathcal {L}\mid _{\mathcal {D}} \oplus \bigoplus _{v \le w,\, r<l(v)} \bigoplus _{\alpha \in \mathbb {Z}} IC_{X(v)}^{ \oplus s_{v, \alpha }} [- \alpha ]\mid _{\mathcal {U}_{r-1}}, \end{aligned}$$

(3.5)

where $\mathcal {L}$ gathers all the summands supported in $\mathcal {U}_r^*=\bigsqcup _{v \le w,\, l(v)\le r}\Omega (v)$

$$\begin{aligned} \mathcal {L}:= \bigoplus _{\alpha \in \mathbb {Z}} \bigoplus _{S\subseteq \mathcal {U}_r^*} {}^{\mathfrak {p}}{}{\mathcal {H}}^{\alpha }(R \pi _{*} (\mathbb {Q}_{\tilde{X}}) [l] )_{S} [- \alpha ]. \end{aligned}$$

In the previous formula, the summand ${}^{\mathfrak {p}}{}{\mathcal {H}}^{\alpha }(R \pi _{*} (\mathbb {Q}_{\tilde{X}}) [l] )_{S}$ denotes the S component of ${}^{\mathfrak {p}}{}{\mathcal {H}}^{\alpha }(R \pi _{*} (\mathbb {Q}_{\tilde{X}}) [l] )$ in the decomposition by supports [4, Section 1.1]. By proper base change, we also have

$$\begin{aligned} R \pi _{*} (\mathbb {Q}_{\tilde{X}}) [l] \mid _{\mathcal {D}}= \mathcal {L}\mid _{\mathcal {D}} \oplus \bigoplus _{v \le w,\, r<l(v)} \bigoplus _{\alpha \in \mathbb {Z}} IC_{X(v)}^{ \oplus s_{v, \alpha }} [- \alpha ]\mid _{\mathcal {D}}. \end{aligned}$$

(3.6)

Since $\pi : \tilde{X} \rightarrow X$ is equivariant and $\mathcal {D}$ is a disjoint union of B-orbits, the dimension of the cohomology stalk $\mathcal {H}^i R \pi _{*} (\mathbb {Q}_{\tilde{X}}) [l]_x$ is independent of $x\in \mathcal {D}$, for all i. The same holds true also for all $IC_{X(v)} [- \alpha ]\mid _{\mathcal {D}}$. Then (3.6) shows that the dimension of the cohomology stalk $\mathcal {H}^i \mathcal {L}_x$ is independent of $x\in \mathcal {D}$, for all i. Thus, $\mathcal {L}\mid _{\mathcal {D}}$ is a direct sum of shifted local systems, because, by [6, Remark 1.5.1], the perverse cohomology sheaves ${}^{\mathfrak {p}}{}{\mathcal {H}}^{i}(\mathcal {L}\mid _{\mathcal {D}})$ concide, up to a shift, with the ordinary cohomology

$$\begin{aligned} {}^{\mathfrak {p}}{}{\mathcal {H}}^{i}(\mathcal {L}\mid _{\mathcal {D}})\cong \mathcal {H}^{i-r}\mathcal {L}\mid _{\mathcal {D}}[r],\quad \forall i. \end{aligned}$$

We are done, because $\mathcal {D}= \bigsqcup _{v \le w,\, r=l(v)}\Omega (v)$ is a disjoint union of affine spaces of dimension r (compare, e.g., with [15, Theorem 9.9.5 (i)]), so any local system on $\mathcal {D}$ is trivial and (3.4) follows for the restriction to the open set $\mathcal {U}_{r-1}$. $\square$

4 A Consequence of the Decomposition Theorem

In this section, we assume to have fixed an equivariant resolution $\pi _{w}: \tilde{X} (w) \rightarrow X(w),$ for any Schubert variety X(w), $w\in W$. As a consequence of Proposition 3.2, the decomposition theorem for $\pi _w$ can be stated as

$$\begin{aligned} (R \pi _w) _{*} \mathbb {Q}_{\tilde{X}(w)} [l(w)] = \bigoplus _{v \le w} \bigoplus _{\alpha \in \mathbb {Z}} IC_{X(v)}^{ \oplus s_{v, \alpha }^{w}} [- \alpha ], \end{aligned}$$

(4.1)

for suitable multiplicities $s_{v, \alpha }^w$, where recall that $l(w) = \dim X(w)$.

Notations 4.1

For any pair (v, w) of permutations such that $v \le w$, let

$$\begin{aligned} D_{w, v} (t) := \sum _{\alpha \in \mathbb {Z}} s_{v, \alpha }^{w} \cdot t^{\alpha } \in \mathbb {Z}[t, t^{-1}] \end{aligned}$$

(4.2)

be the Laurent polynomial recording the contribution to the decomposition theorem (4.1) coming from support X(v). Let moreover

$$\begin{aligned} F_{w, v} (t) := \sum _{\alpha \in \mathbb {Z}} f_{w, v}^{l(w)+\alpha } t^{\alpha } \in \mathbb {Z}[t, t^{-1}], \quad f_{w, v}^{i} := \dim H^{i}(\pi _w^{-1}(x)), \,\,\,x\in \Omega (v) \end{aligned}$$

(4.3)

be the shifted Poincaré polynomial of the fibers of $\pi _w$ over $\Omega (v)$.

Remark 4.2

Let X(w) be a Schubert variety and let $\Omega (v)\subseteq X(w)$ be a Schubert cell. It is well known the dimensions of the stalks $\mathcal {H}^{\alpha }(IC_{X(w)})_{x}$ do not depend on $x\in \Omega (v)$.

The Laurent polynomial encoding the dimensions of the stalks $\mathcal {H}^{\alpha }(IC_{\mathcal {S}_{\tau }}^{\bullet })_{x}$ is the shifted Kazhdan–Lusztig polynomial

$$\begin{aligned} H_{w, v}(t) := \sum _{\alpha \in \mathbb {Z}} h_{w, v}^{\alpha } t^{\alpha }, \quad h_{w, v}^{\alpha } := \dim \mathcal {H}^{\alpha }(IC_{X(w)})_{x}, \,\,\, x \in \Omega (v). \end{aligned}$$

Recall that we have

$$\begin{aligned} P_{w, v}(q)= q^{\frac{l(w)}{2}}H_{w, v}(\sqrt{q}), \end{aligned}$$

(4.4)

where $P_{w, v}(q)$ is the corresponding Kazhdan–Lusztig polynomial (1.2) (compare, e.g., with [2, Theorem 6.1.11]).

Before stating the main result of this section, let us introduce the truncation U and symmetrizing S operators

$$\begin{aligned}&U: \sum _{\alpha \in \mathbb {Z}} a_{\alpha } t^{\alpha } \in \mathbb {Z}[t, t^{-1}] \mapsto \sum _{\alpha \ge 0} a_{\alpha } t^{\alpha }\in \mathbb {Z}[t];\\&S: \sum _{\alpha \ge 0} a_{\alpha } t^{\alpha }\in \mathbb {Z}[t] \mapsto a_{0} + \sum _{\alpha > 0} a_{\alpha } (t^{\alpha } + t^{- \alpha }) \in \mathbb {Z}[t, t^{-1}]. \end{aligned}$$

Theorem 4.3

With notations as above, let $u\le w$ in W. Then, we have the following recursive formulae for the computation of the Laurent polynomials $D_{w, u}$ and the shifted Kazhdan–Lusztig polynomials $H_{w, u}$:

$$\begin{aligned} {\left\{ \begin{array}{ll} D_{w, u} = S \circ U(R_{w, u})\\ H_{w, u} = t^{-l(u)}(R_{w, u} - D_{w, u}), \end{array}\right. } \end{aligned}$$

where

$$\begin{aligned} R_{w, u} := t^{l(u)} \left( F_{w, u} - \sum _{u< v < w} D_{w, v} \cdot H_{v, u} \right) . \end{aligned}$$

Proof

For the sake of simplicity, in the proof, we set $\pi : \tilde{X} \rightarrow X$ instead of

$\pi _w: \tilde{X} (w)\rightarrow X(w)$. By Proposition 3.2, we have

$$\begin{aligned} R \pi _{*} \mathbb {Q}_{\tilde{X}} [l] = \bigoplus _{v \le w} \bigoplus _{\alpha \in \mathbb {Z}} IC_{X(v)}^{ \oplus s_{v, \alpha }^{w}} [- \alpha ]. \end{aligned}$$

(4.5)

Consider a cell $\Omega (u)\subset X$, take the stalk cohomology at $x\in \Omega (u)$ and recall (4.2) and (4.3). From (4.5), we infer

$$\begin{aligned} F_{w, u}(t)= & {} \sum _{u\le v \le w} D_{w, v}(t) \cdot H_{v, u}(t)\nonumber \\= & {} D_{w, w}(t) \cdot H_{w, u}(t)+ D_{w, u}(t) \cdot H_{u, u}(t)\nonumber \\{} & {} + \sum _{u< v < w} D_{w, v}(t) \cdot H_{v, u}(t). \end{aligned}$$

(4.6)

Since the resolution $\pi : \tilde{X} \rightarrow X$ is equivariant, it must be an isomorphism over $\Omega (w)$ and we have $D_{w, w}(t) =1$ (recall (4.1) and (4.2)). Furthermore, from the well-known isomorphism $IC_{X(u)}|_{\Omega (u)} \cong \mathbb {Q}_{\Omega (u)}[l(u)]$ (compare, e.g., with [16, Definition 6.3.1]) we deduce $H_{u, u}(t)=t^{-l(u)}$. Hence, from (4.6), we get

$$\begin{aligned} F_{w, u}(t)= H_{w, u}(t)+ t^{-l(u)}\cdot D_{w, u}(t) + \sum _{u< v < w} D_{w, v}(t) \cdot H_{v, u}(t). \end{aligned}$$

(4.7)

The last equality can be written as

$$\begin{aligned} D_{w, u}(t)= & {} t^{l(u)}\cdot \left( F_{w, u}(t) - \sum _{u< v < w} D_{w, v}(t) \cdot H_{v, u}(t)\right) - t^{l(u)} \cdot H_{w,u}(t)\\= & {} R_{w, u} - t^{l(u)} \cdot H_{w, u}(t). \end{aligned}$$

The support conditions for perverse sheaves imply that $t^{l(u)} \cdot H_{w, u}(t)$ is concentrated in negative degrees (see [6, p. 552, equation 12]), and thus

$$\begin{aligned} U(D_{w, u}(t)) = U(R_{w, u}(t)). \end{aligned}$$

Finally, the Laurent polynomials $D_{w, u}(t)$ are symmetric because of Hard–Lefschetz theorem (see [6, Theorem 1.6.3]), that is to say

$$\begin{aligned} D_{w, u}(t)= D_{w, u}(t^{-1}). \end{aligned}$$

Therefore, we have

$$\begin{aligned} {\left\{ \begin{array}{ll} D_{w, u}(t) = S \circ U(R_{w, u}(t))\\ H_{w, u}(t) = t^{-l(u)}(R_{w, u}(t)-D_{w, u}(t)), \end{array}\right. } \end{aligned}$$

(4.8)

and the statement follows. $\square$

By (4.4), the last theorem provides an iterative procedure to compute Kazhdan–Lusztig polynomials $P_{w, v}$ from Poincaré polynomials $Q_{w, v}$. To this end, let us introduce the following operators:

$$\begin{aligned} U_{\beta }&: \sum _{\alpha \ge 0} c_{\alpha } t^{\alpha } \in \mathbb {Z} \left[ t \right] \mapsto \sum _{\alpha \ge \beta } c_{\alpha } t^{\alpha } \in \mathbb {Z} \left[ t \right] , \hspace{0.33em} \forall \beta \ge 0.\\ \end{aligned}$$

Next statement follows from Theorem 4.3 and collects all informations we obtained until now.

Corollary 4.4

Assume to have fixed an equivariant resolution $\pi _{w}: \tilde{X} (w) \rightarrow X(w),$ for any Schubert variety X(w), $w\in W$. For any pair w, u in W such that $u\le w$, let $\tilde{F}_{w, u}$ be the Poincaré polynomials of the fiber $\pi _w^{-1}(x)$, $\forall x\in \Omega (u)$. Then, we have the following recursive formulae:

$$\begin{aligned} {\left\{ \begin{array}{ll} \tilde{D}_{w, u} = t^{l(w)-l(u)} \circ S \circ t^{l(u)-l(w)} \circ U_{l(w)-l(u)}(\tilde{R}_{w, u})\\ \tilde{H}_{w, u} = \tilde{R}_{w, u} -\tilde{D}_{w, u}, \end{array}\right. } \end{aligned}$$

where

$$\begin{aligned} \tilde{D}_{w, u}:= t^{l(w)-l(u)} D_{w, u}, \quad \tilde{H}_{w, u}:= t^{l(w)} H_{w, u}, \quad \tilde{R}_{w, u} := \tilde{F}_{w, u} - \sum _{u< v < w} \tilde{D}_{w, v} \cdot \tilde{H}_{v, u}. \end{aligned}$$

Proof

From (4.3) we find $\tilde{F}_{w, u}=t^{l(w)}F_{w, u}$. Thus, we have

$$\begin{aligned}{} & {} \tilde{R}_{w, u}:= \tilde{F}_{w, u} - \sum _{u< v< w} \tilde{D}_{w, v} \cdot \tilde{H}_{v, u}= t^{l(w)} F_{w, u} \\{} & {} \qquad \quad \quad \quad - \sum _{u< v < w} t^{l(w)-l(u)}D_{w, v} \cdot t^{l(v)} H_{v, u}=t^{l(w)-l(v)} R_{w, u}, \end{aligned}$$

and the statement straightforwardly follows just combining Theorem 4.3 with

$$\begin{aligned} t^{l(u)-l(w)} \circ U_{l(w)-l(u)}\circ t^{l(w)-l(v)}= U_0. \end{aligned}$$

$\square$

Remark 4.5

By (4.4), we have

$$\begin{aligned} P_{w, v}(q)= q^{\frac{l(w)}{2}}H_{w, v}(\sqrt{q})=\tilde{H}_{w, v}(\sqrt{q}); \end{aligned}$$

hence, previous corollary provides an iterative procedure that allows to compute both the Kazhdan–Lusztig polynomials $P_{w, v}$ and the Laurent polynomials $D_{w, v}$.

5 Bases for the Hecke Algebra

As in the previous section, we assume to have fixed an equivariant resolution $\pi _{w}$ for any Schubert variety X(w), $w\in W$ and we assume in addition that the cohomology of the fibers of $\pi _w$ vanishes in odd degrees (this property is satisfied by any reasonable resolution of Schubert varieties). As a consequence, we have that the coefficients of the polynomials $\tilde{F}_{w, v}$ vanish in odd degree. Furthermore, from the relations

$$\begin{aligned} {\left\{ \begin{array}{ll} \tilde{D}_{w, u} = t^{l(w)-l(u)} \circ S \circ t^{l(u)-l(w)} \circ U_{l(w)-l(u)}(\tilde{R}_{w, u})\\ \tilde{R}_{w, u} := \tilde{F}_{w, u} - \sum _{u< v < w} \tilde{D}_{w, v} \cdot \tilde{H}_{v, u} \end{array}\right. } \end{aligned}$$

one deduces immediately that the same holds true for the polynomials $\tilde{D}_{w, v}$. We define

$$\begin{aligned} Q_{w, v}(q)=\tilde{F}_{w, v}(\sqrt{q}) \in \mathbb {Z}[q], \end{aligned}$$

(5.1)

$$\begin{aligned} S_{w, v}(q)=\tilde{D}_{w, v}(\sqrt{q}) \in \mathbb {Z}[q], \end{aligned}$$

(5.2)

for all $v, w \in W$ such that $v\le w$. Our aim in this section is to define a new basis for the Hecke algebra by means of the polynomials $Q_{w, v}(q)$. We start by recalling the definition of Hecke algebra.

Let $\mathcal {H}$ be the Hecke algebra of W, i.e., the algebra over $\mathbb {Z}[q^{\frac{1}{2}}, q^{-\frac{1}{2}}]$ with basis elements $\{T_w\mid \,\, w\in W \}$ and relations [2, Sec. 6.1]

$$\begin{aligned} {\left\{ \begin{array}{ll} T_{s_i}T_w=T_{s_iw} \quad \text {if} \quad l(s_iw)>l(w),\\ T_{s_i} T_{s_i}=(q-1) T_{s_i}+q T_{id}. \end{array}\right. } \end{aligned}$$

The Hecke algebra is also equipped with the Kazhdan–Lusztig basis $\{C_w\mid \,\, w\in W \}$, where

$$\begin{aligned} C_w= T_w + \sum _{v<w}P_{w, v}T_v, \end{aligned}$$

(5.3)

where $P_{w, v}\in \mathbb {Z}[q]$ are the Kazhdan–Lusztig polynomials.

Theorem 5.1

For any $w\in W$, let

$$\begin{aligned} B_w= T_w + \sum _{v<w}Q_{w, v}T_v\in \mathcal {H}. \end{aligned}$$

The polynomials $S_{w, v}(q)\in \mathbb {Z}[q]$ are the coefficients of $B_w$ with respect to the Kazhdan–Lusztig basis

$$\begin{aligned} B_w= C_w + \sum _{v<w}S_{w, v}C_v\in \mathcal {H}. \end{aligned}$$

Proof

From (4.7) and recalling $\tilde{F}_{w, u}=t^{l(w)}F_{w, u}$, we get

$$\begin{aligned} \tilde{F}_{w, u}=t^{l(w)}F_{w, u}= \sum _{u\le v \le w} t^{l(w)-l(v)}D_{w, v} \cdot t^{l(v)}H_{v, u}= \sum _{u\le v \le w} \tilde{D}_{w, v} \cdot \tilde{H}_{v, u}, \end{aligned}$$

(5.4)

where we have taken into account 4.4. Combining 4.5 with (5.1) and (5.2) and evaluating in $t=\sqrt{q}$ the last equality, we get

$$\begin{aligned} Q_{w, u} = \sum _{u\le v \le w} S_{w, v}\cdot P_{v, u}\in \mathbb {Z}[q]. \end{aligned}$$

(5.5)

Since the resolution $\pi : \tilde{X} \rightarrow X$ is equivariant, it must be an isomorphism over $\Omega (w)$, so we have $Q_{w, w}=1$ and

$$\begin{aligned} B_w= T_w + \sum _{u<w}Q_{w, u}T_u= \sum _{u\le w}Q_{w, u}T_u{} & {} =\sum _{u\le w}\left( \sum _{u\le v \le w} S_{w, v}\cdot P_{v, u}\right) T_u\\{} & {} =\sum _{v\le w}S_{w, v}\left( \sum _{u\le v } P_{v, u}T_u \right) . \end{aligned}$$

Again, since $\pi _w$ an isomorphism over $\Omega (w)$ and we have $D_{w, w}= S_{w, w}=1$ (recall (4.1) and (4.2)) and the last sum can be written as

$$\begin{aligned} \sum _{u\le w } P_{w, u}T_u+ \sum _{v< w}S_{w, v}\left( \sum _{u\le v } P_{v, u}T_u \right) \end{aligned}$$

that coincides with

$$\begin{aligned} C_w + \sum _{v<w}S_{w, v}C_v \end{aligned}$$

in view of (5.3). $\square$

Remark 5.2

Theorem above shows that the transition matrix, from the Kazhdan–Lusztig basis $\{C_w \mid w\in W\}$ to the new one $\{B_w \mid w\in W\}$, is triangular with coefficients $S_{w, v}\in \mathbb {Z}[q]$. In this work, we have set up an iterative procedure that allows the computation of such a matrix and which does not require prior knowledge of the transition matrix from the Kazhdan–Lusztig basis to the standard one $\{T_w \mid w\in W\}$.

6 Some Applications

In this section, we give some applications of our previous results to explicit formulas and computations of Kazhdan–Lusztig polynomials for the symmetric group $S_4$.

• 1) Fix $w:= s_2s_3s_2$. From the definition (2.1), it is very easy to deduce that $Q_{w, s_2}=1+q$. Indeed, the set of subexpressions of w ending with $s_2$ is $\{(id, id, id, s_2), (id, s_2, s_2, s_2)\}$, whose corresponding defects are

  $$\begin{aligned} {\left\{ \begin{array}{ll} d((id, id, id, s_2))=0\\ d((id, s_2, s_2, s_2))=1. \end{array}\right. } \end{aligned}$$

  Similarly, the set of subexpressions of w ending with id is $\{(id, id, id, id), (id, s_2, s_2, id)\}$, and the corresponding defects are

  $$\begin{aligned} {\left\{ \begin{array}{ll} d((id, id, id, id))=0\\ d((id, s_2, s_2, id))=1; \end{array}\right. } \end{aligned}$$

  hence, $Q_{w, id}=1+q$. With a similar but somewhat tedious check, one can verify that $Q_{w, v}=1$ in all other cases where $v\le w$. Taking into account of formulas (5.1), we get $\tilde{F} _{w, s_2}=\tilde{F} _{w, id}=1+t^2$ and $\tilde{F}_{w, v}=1$, respectively. By Corollary 4.4, we conclude that $\tilde{D} _{w, s_2}=t^2$ and that $\tilde{D}_{w, v}=0$ in all other cases where $v\le w$. Combining 4.4 with (4.1) and (4.2), we find an explicit form for the decomposition theorem applied to the resolution $\pi :=\pi _w$

  $$\begin{aligned} R \pi _{*} \mathbb {Q}_{\tilde{X}(w)} [3] \cong IC_{X(w)}\oplus IC_{X(s_2)}. \end{aligned}$$

  Moreover, by Corollary 4.4 and Remark 4.5, we find that $P_{w, v}=1$ in all cases, in accordance with the tables of Kazhdan–Lusztig polynomials, which can be found, e.g., in Mark Goresky’s web page [13]. Then, the last isomorphism becomes

  $$\begin{aligned} R \pi _{*} \mathbb {Q}_{\tilde{X}(w)} \cong \mathbb {Q}_{X(w)}\oplus \mathbb {Q}_{X(s_2)}[-2]. \end{aligned}$$

  With a very similar procedure, one can easily prove the following isomorphism:

  $$\begin{aligned} R \pi _{*} \mathbb {Q}_{\tilde{X}(s_1s_2s_1)} \cong \mathbb {Q}_{X(s_1s_2s_1)}\oplus \mathbb {Q}_{X(s_1)}[-2]. \end{aligned}$$

• 2) $w:= s_2s_1s_3s_2$. Similarly as above, from the definition (2.1), one may deduce that $Q_{w, s_2}=1+q$. Indeed, the subexpressions of w ending with $s_2$ are $(id, id, id, id, s_2)$ and $(id, s_2, s_2, s_2, s_2)$, and the corresponding defects are

  $$\begin{aligned} {\left\{ \begin{array}{ll} d((id, id, id, id, s_2))=0\\ d((id, s_2, s_2, s_2, s_2))=1. \end{array}\right. }. \end{aligned}$$

  Similarly, one deduces that $Q_{w, id}=1+q$ and that $Q_{w, v}=1$ in all other cases where $v\le w$, and hence, $\tilde{F} _{w, s_2}=\tilde{F} _{w, id}=1+t^2$ and $\tilde{F}_{w, v}=1$, respectively. By Corollary 4.4, we get $\tilde{D}_{w, v}=D_{w, v} =0$ in all cases. Therefore, the decomposition theorem applied to the resolution $\pi :=\pi _w$ gives

  $$\begin{aligned} R \pi _{*} \mathbb {Q}_{\tilde{X}(w)} [4] \cong IC_{X(w)}, \end{aligned}$$

  consistently with the fact that, as can easily be verified, the resolution is small. Finally, by Corollary 4.4 and Remark 4.5, we find the Kazhdan–Lusztig polynomial of the singular locus

  $$\begin{aligned} P_{w, s_2}=1+q, \end{aligned}$$

  in accordance with item 19 of Mark Goresky’s table [13] for the Weyl group of type A3.

• 3) $w:= s_1s_2s_3s_2s_1$. In this case, we have $\tilde{F} _{w, s_1s_2s_1}=\tilde{F} _{w, s_1s_2}=\tilde{F} _{w, s_2s_1}=\tilde{F} _{w, s_1s_3} =1+t^2$ and $\tilde{F}_{w, v}=1$ in all other cases where $v\le w$ and $l(v)\ge 2$. By Corollary 4.4, we deduce

  $$\begin{aligned}{} & {} \tilde{D} _{w, s_1s_2s_1}= t^{2} \circ S \circ t^{2} \circ U_{2}( 1+t^2 )=t^2, \\{} & {} \tilde{D} _{w, s_1s_2}= t^{3} \circ S \circ t^{3} \circ U_{3}( 1+t^2 - \tilde{D} _{w, s_1s_2s_1})=t^{3} \circ S \circ t^{3} \circ U_{3}( 1)=0,\\{} & {} \tilde{D} _{w, s_2s_1}= t^{3} \circ S \circ t^{3} \circ U_{3}( 1+t^2 - \tilde{D} _{w, s_1s_2s_1})=t^{3} \circ S \circ t^{3} \circ U_{3}( 1)=0,\\{} & {} \tilde{D} _{w, s_1s_3}= t^{3} \circ S \circ t^{3} \circ U_{3}( 1+t^2)=0. \end{aligned}$$

  By Corollary 4.4 and Remark 4.5, we find the following Kazhdan–Lusztig polynomials:

  $$\begin{aligned} P _{w, s_1s_2s_1}=P _{w, s_1s_2}=P _{w, s_2s_1}=1, \quad P _{w, s_1s_3}=1+q, \end{aligned}$$

  in accordance with the tables of Kazhdan–Lusztig polynomials. We conclude with the computation of the Kazhdan–Lusztig polynomial $P _{w, s_1}.$ The set of subexpressions of w ending with $s_1$ is

  $$\begin{aligned}{} & {} \{(id,id, id, id, id, s_1), (id, s_1, s_1, s_1, s_1, s_1), (id,id, s_2, s_2, id, s_1),\\{} & {} (id, s_1, s_1s_2, s_1s_2, s_1, s_1)\}, \end{aligned}$$

  and the corresponding defects are

  $$\begin{aligned} {\left\{ \begin{array}{ll} d((id,id, id, id, id, s_1))=0\\ d((id, s_1, s_1, s_1, s_1, s_1))=1 \\ d((id,id, s_2, s_2, id, s_1))=1 \\ d((id, s_1, s_1s_2, s_1s_2, s_1, s_1))=2. \end{array}\right. }. \end{aligned}$$

  We find $\tilde{F} _{w, s_1}= 1+ 2t^2 + t^4,$ and Corollary 4.4 implies

  $$\begin{aligned} \tilde{R} _{w, s_1}=1+ 2t^2 + t^4- \tilde{D} _{w, s_1s_2s_1}=1+ t^2 + t^4, \quad \tilde{D} _{w, s_1}=t^4, \quad \tilde{H} _{w, s_1}=1+t^2. \end{aligned}$$

  From Remark 4.5, we find $P _{w, s_1}=1+q$, in accordance with the tables of Kazhdan–Lusztig polynomials.