Inclusion Properties of the Triangular Ratio Metric Balls

Abstract

Inclusion properties are studied for balls of the triangular ratio metric, the hyperbolic metric, the $j^*$-metric, and the distance ratio metric defined in the unit ball domain. Several sharp results are proven and a conjecture about the relation between triangular ratio metric balls and hyperbolic balls is given. An algorithm is also built for drawing triangular ratio circles or three-dimensional spheres.

1 Introduction

In the field of geometric function theory, the study focuses on different geometrical properties of several types of functions, including for instance conformal [1], quasiconformal [16], and quasiregular mappings [13]. It is often useful to construct a metric space to investigate behaviour of metrics under these mappings to understand better how they distort distances. Especially, the hyperbolic metric is an important subject of study [3, 5, 17] because of its conformal invariance, sensitivity to boundary variation, monotonicity with respect to domain, and intricate features of hyperbolic geometry [5, p. 191–192]. Numerous generalizations of the hyperbolic metric, called hyperbolic type metrics, have also been defined to create geometrical systems sharing some of these properties, including the way the hyperbolic metric measures distances between two points x, y in a domain G by taking into account their position with respect to the boundary $\partial G$ of the domain [5, 8, 14].

For a domain $G\subsetneq \mathbb {R}^n$, one of the hyperbolic type metrics is the triangular ratio metric $s_G:G\times G\rightarrow [0,1],$ [2, (1.1), p. 683]

$$\begin{aligned} s_G(x,y)=\frac{|x-y|}{\inf _{z\in \partial G}(|x-z|+|z-y|)}, \end{aligned}$$

(1.1)

which was originally introduced by P. Hästö in 2002 [8]. This metric has been studied much [2, 4, 6, 12,13,14,15,16] because, despite its relatively simple definition, computing the value of the infimum in the denominator is a non-trivial task in the case where the domain G is, for instance, the unit ball $\mathbb {B}^n$. In fact, if $G=\mathbb {B}^3$ and the boundary of this domain is a spherical mirror, the extremal point z coincides with the point that the light ray sent from the point x must hit to reflect into the point y and, because of this relation to optics, the problem has a very long history explained in [4].

Given the point x in a domain $G\subsetneq \mathbb {R}^n$ and some radius $0<t<1$, the x-centered triangular ratio metric ball with this radius t is defined as $B_s(x,t)=\{y\in G\text { }|\text { }s_G(x,y)<t\}$. To study the different mappings, it is often useful to know what is the largest ball $B_d(x,r_0)$ defined with some other metric d that is included in the triangular ratio metric ball $B_s(x,t)$ or the smallest ball $B_d(x,r_1)$ containing the ball $B_s(x,t)$. This type of an inclusion question has been recently studied for the triangular metric by Hokuni et al. [9] in such cases where the domain G is the upper half-space or the punctured real space, and Klén and Vuorinen have also researched the inclusion properties of several hyperbolic metrics other than the triangular ratio metric in the unit ball [11] and other domains [10].

In this article we continue the earlier research by studying the inclusion properties of the balls of the triangular ratio metric defined in the unit ball. In Sect. 3, we focus on triangular ratio metric balls in terms of the Euclidean geometry, give the sharp inclusion result between triangular ratio metric and Euclidean balls, and also offer an algorithm for drawing triangular ratio metric circles or three-dimensional spheres. In Sect. 4, we study the ball inclusions for the triangular ratio metric and two other hyperbolic type metrics called the distance ratio metric and the $j^*$-metric, find an explicit formula for $j^*$-metric balls and also prove one earlier conjecture from [9]. Finally, in Sect. 5, we research the connection between triangular ratio metric balls and hyperbolic balls.

2 Preliminaries

An n-dimensional Euclidean ball with center $x\in \mathbb {R}^n$ and radius $r>0$ is denoted by $B^n(x,r)$, its closure by $\overline{B}^n(x,r)$ and its sphere by $S^{n-1}(x,r)$. For the unit ball and sphere, the simplified notations $\mathbb {B}^n$ and $S^{n-1}$ are used. The notation L(x, y) means a Euclidean line through points $x,y\in \mathbb {R}^n$. For any point x in a domain $G\subsetneq \mathbb {R}^n$, $d_G(x)$ denotes the Euclidean distance from x to the boundary $\partial G$ by $d_G(x)=\inf \{|x-z|\text { }|\text { }z\in \partial G\}$. Trivially $d_G(x)=1-|x|$ when $G=\mathbb {B}^n$. For $x\in \mathbb {R}^2$, let $\overline{x}$ be the complex conjugate of x. For three points $x,y,z\in \mathbb {R}^n$, let be the magnitude of the angle between the vector from y to x and the vector from y to z and denote the origin with the letter o in these angle notations.

The hyperbolic metric can be computed in the unit ball with the following formula [5, (4.16), p. 55]

$$\begin{aligned} \text {sh}^2\frac{\rho _{\mathbb {B}^n}(x,y)}{2}&=\frac{|x-y|^2}{(1-|x|^2)(1-|y|^2)},\quad x,y\in \mathbb {B}^n, \end{aligned}$$

(2.1)

the distance ratio metric $j_G:G\times G\rightarrow [0,\infty )$ in any domain $G\subsetneq \mathbb {R}^n$ is defined as [2, p. 685],

$$\begin{aligned} j_G(x,y)=\log \left( 1+\frac{|x-y|}{\min \{d_G(x),d_G(y)\}}\right) , \end{aligned}$$

(2.2)

and the $j^*$-metric $j^*_G:G\times G\rightarrow [0,1],$ has the definition [7, 2.2, p. 1123 & Lemma 2.1, p. 1124]

$$\begin{aligned} j^*_G(x,y)=\textrm{th}\frac{j_G(x,y)}{2}=\frac{|x-y|}{|x-y|+2\min \{d_G(x),d_G(y)\}}, \end{aligned}$$

(2.3)

In (2.1), sh denotes the hyperbolic sine. Similarly, the hyperbolic cosine and tangent are denoted here by ch and th, and the inverse hyperbolic functions are arsh, arch, and arth, while $\textrm{acos}$ is the arccosine function. For any hyperbolic type metric d defined in a domain $G\subsetneq \mathbb {R}^n$, $x\in G$, and $r>0$, the n-dimensional ball is $B_d(x,r)=\{y\in G\text { }|\text { }d(x,y)<r\}$ and its sphere is $S_d(x,r)$.

Lemma 2.1

[5, (4.20) p. 56] For $G=\mathbb {B}^n$, the equality $B_\rho (x,R)=B^n(y,h)$ holds, if

$$\begin{aligned} y=\frac{x(1-k^2)}{1-|x|^2k^2},\quad \text {and}\quad h=\frac{(1-|x|^2)k}{1-|x|^2k^2} \quad \text {and}\quad k=\textrm{th}\frac{R}{2}. \end{aligned}$$

The inclusion result between the hyperbolic and the distance ratio metric is known in the case of the unit ball.

Theorem 2.2

[11, Thm 3.1, p. 31 & Cor. 3.3, p. 33] For $x\in G=\mathbb {B}^n$ and $R>0$, $B_j(x,K_0)\subseteq B_\rho (x,R)\subseteq B_j(x,K_1)$ if and only if

$$\begin{aligned}&0< K_0\le \max \left\{ \log \left( 1+(1+|x|)\textrm{sh}\left( \frac{R}{2}\right) \right) , \log \left( 1+(1-|x|)\frac{e^R-1}{2}\right) \right\} \quad \text {and}\\&K_1\ge \log \left( 1+(1+|x|)\frac{e^R-1}{2}\right) , \end{aligned}$$

and, for $x\in G=\mathbb {B}^n$ and $K>0$, $B_\rho (x,R_0)\subseteq B_j(x,K)\subseteq B_\rho (x,R_1)$ if and only if

$$\begin{aligned}&0<R_0\le \log \left( 1+\frac{2(e^K-1)}{1+|x|}\right) \quad \text {and} \\&R_1\ge \min \left\{ 2\textrm{arsh}\frac{e^K-1}{1+|x|},\log \left( \frac{2e^K-1-|x|}{1-|x|}\right) \right\} . \end{aligned}$$

The following inequality holds between the triangular ratio metric and the $j^*$-metric.

Theorem 2.3

[7, Lemma 2.1, p. 1124; Lemma 2.2, p. 1125; Lemma 2.8 & Thm 2.9(1), p. 1129] For a domain $G\subsetneq \mathbb {R}^n$, the inequality $j^*_G(x,y)\le s_G(x,y)\le 2j^*_G(x,y)$ holds for all $x,y\in G$ and, if G is convex, then $s_G(x,y)\le \sqrt{2}j^*_G(x,y)$.

There are a few results that help to find the triangular ratio distance in the unit ball.

Theorem 2.4

[4, p. 138] For all $x,y\in \mathbb {B}^n$, the infimum $\inf _{z\in S^{n-1}}(|x-z|+|z-y|)$ is found with such a point $z\in S^{n-1}$ that the line L(0, z) bisects the angle between the lines L(x, z) and L(z, y).

Lemma 2.5

[5, 11.2.1(1) p. 205] For all $x,y\in \mathbb {B}^n$,

$$\begin{aligned} s_{\mathbb {B}^n}(x,y)\le \frac{|x-y|}{2-|x+y|}, \end{aligned}$$

where the equality holds if and only if the points x, y are collinear with the origin.

Theorem 2.6

[6, Thm 3.1, p. 276] If $x\in \mathbb {B}^2$ with $\min \{\textrm{Re}(x),\textrm{Im}(x)\}>0$, then

$$\begin{aligned} s_{\mathbb {B}^2}(x,\overline{x})&=|x|\text { if }|x-\frac{1}{2}|>\frac{1}{2},\\ s_{\mathbb {B}^2}(x,\overline{x})&=\frac{\textrm{Im}(x)}{\sqrt{(1-\textrm{Re}(x))^2+\textrm{Im}(x)^2}}\le |x|\text { otherwise.} \end{aligned}$$

3 Triangular Ratio Metric Balls in Euclidean Geometry

If triangular metric balls defined in $G=\mathbb {B}^n$ are origin-centered, they are equivalent to Euclidean balls, as stated by the following lemma. However, if $x\ne 0$, expressing the triangular ratio metric ball $B_s(x,t)$ for $0<t<1$ in terms of Euclidean geometry becomes considerably more difficult, but with the help Lemma 2.5 and Theorem 2.6, we can prove Lemmas 3.2 and 3.3 that reveal certain points always contained in the sphere $S_s(x,t)$.

Lemma 3.1

For $G=\mathbb {B}^n$ and $0<t<1$, the origin-centered triangular ratio metric ball $B_s(0,t)$ equals the Euclidean ball $B^n(0,2t/(1+t))$.

Proof

Trivially, $y\in B_s(0,t)$ if and only if $s_{\mathbb {B}^n}(y,0)=|y|/(2-|y|)<t$ or, equivalently, $|y|<2t/(1+t)$.

Fig. 1

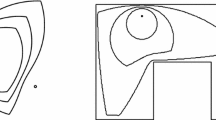
The intersection points $y_0$ and $y_1$ of Lemma 3.2 for the triangular ratio metric circle $S_s(x,t)$ and the line L(0, x) in the domain $G=\mathbb {B}^2$, when $x=0.3+0.7i$ and $t=0.5$

Next, we will find the intersection points of the triangular ratio metric sphere $S_s(x,t)$ and the line L(0, x) that can be also seen in Fig. 1.

Lemma 3.2

For $G=\mathbb {B}^n$, $x\in \mathbb {B}^n{\setminus }\{0\}$ and $0<t<1$, the triangular ratio metric sphere $S_s(x,t)$ intersects with the line L(0, x) at the points

$$\begin{aligned} y_0=x+\frac{2tx(1-|x|)}{|x|(1+t)}\quad \text {and}\quad y_1=x-\frac{2tx}{|x|}\min \left\{ \frac{1-|x|}{1-t},\frac{1+|x|}{1+t}\right\} . \end{aligned}$$

Proof

Any point $y\in L(0,x)$ can be written as $y=x+rx/|x|$ with $r\in \mathbb {R}$. Since the points x, y, 0 are collinear, by Lemma 2.5,

$$\begin{aligned} s_{\mathbb {B}^n}(x,y)&=\frac{|x-y|}{2-|x+y|}=\frac{|r|}{2-|2|x|+r|}\\&= {\left\{ \begin{array}{ll} -|r|/(2+2|x|-|r|)\text { if }r<-2|x|,\\ |r|/(2-2|x|+|r|)\text { if }-2|x|\le r<0,\text { or}\\ |r|/(2-2|x|-|r|)\text { if }r\ge 0. \end{array}\right. } \end{aligned}$$

For $s_{\mathbb {B}^n}(x,y)=t$, we can solve

$$\begin{aligned} r={\left\{ \begin{array}{ll} -2t(1+|x|)/(1+t)\text { if }t>|x|\text { and }r<0,\\ -2t(1-|x|)/(1-t)\text { if }t\le |x|\text { and }r<0,\text { or}\\ 2t(1-|x|)/(1+t)\text { if }r>0. \end{array}\right. } \end{aligned}$$

Clearly, one intersection point is found with $r<0$ and the other one with $r>0$ and, since $(1-|x|)/(1-t)\le (1+|x|)/(1+t)$ is equivalent to $t\le |x|$, r can be written as a minimum expression so that substituting these values of r in $y=x+rx/|x|$ proves the lemma.

Lemma 3.3

For $G=\mathbb {B}^2$, $x\in \mathbb {B}^2{\setminus }\{0\}$ and $0<t\le |x|$, the triangular ratio metric circle $S_s(x,t)$ and the Euclidean circle $S^1(0,|x|)$ intersect at points

$$\begin{aligned} x(2c^2-1+2c\sqrt{1-c^2}i)^{\pm 1}\quad \text {with}\quad c=\frac{t^2+\sqrt{(1-t^2)(|x|^2-t^2)}}{|x|}, \end{aligned}$$

and, if $t>|x|$, the triangular ratio metric disk $B_s(x,t)$ contains the Euclidean circle $S^1(0,|x|)$.

Proof

Let $x=|x|e^{ki}$ and $y=|x|e^{(k\pm 2u)i}$ with $0\le k<2\pi$, $0<u<\pi /2$. By Theorem 2.6 and the fact that triangular ratio metric is invariant under rotations around the origin,

$$\begin{aligned} s_{\mathbb {B}^2}(x,y)=\frac{|x|\sin (u)}{\sqrt{(1-|x|\cos (u))^2+|x|^2\sin (u)}}\le |x|\quad \text {if}\quad ||x|e^{ui}-\frac{1}{2}|\le \frac{1}{2}. \end{aligned}$$

Since $||x|e^{ui}-1/2|=\sqrt{|x|^2-|x|\cos (u)+1/4}$, the condition above holds if and only if $\cos (u)\ge |x|$ and, since $0<u<\pi /2$, we need to have $|x|\le \cos (u)<1$.

By the quadratic formula, we can solve that,

$$\begin{aligned} t&=\frac{|x|\sin (u)}{\sqrt{(1-|x|\cos (u))^2+|x|^2\sin (u)}}\quad \Leftrightarrow \quad t^2=\frac{|x|^2(1-\cos ^2(u))}{1+|x|^2-2|x|\cos (u)}\\&\Leftrightarrow \quad |x|^2\cos ^2(u)-2t^2|x|\cos (u)+t^2+t^2|x|^2-|x|^2=0\\&\Leftrightarrow \quad \cos (u)=\frac{t^2\pm \sqrt{(1-t^2)(|x|^2-t^2)}}{|x|}. \end{aligned}$$

Above, the sign ± needs to be a plus sign. This is because

$$\begin{aligned} \frac{t^2-\sqrt{(1-t^2)(|x|^2-t^2)}}{|x|}\ge |x| \quad \Leftrightarrow \quad |x|^2-t^2\le -\sqrt{(1-t^2)(|x|^2-t^2)}, \end{aligned}$$

where the difference is $|x|^2-t^2$ non-negative for $t\le |x|$. Thus, the root with a minus sign fulfills the condition $|x|<\cos (u)<1$ if and only if $t=|x|$ and, in this special case, it is equal to the root with a plus sign. In turn,

$$\begin{aligned} |x|&\le \frac{t^2+\sqrt{(1-t^2)(|x|^2-t^2)}}{|x|}<1\\&\Leftrightarrow \quad |x|^2-t^2\le \sqrt{(1-t^2)(|x|^2-t^2)} \quad \text {and}\quad \sqrt{(1-t^2)(|x|^2-t^2)}<|x|-t^2\\&\Leftrightarrow \quad |x|^2\le 1 \quad \text {and}\quad 0<(1-|x|)^2, \end{aligned}$$

which holds for all $x\in \mathbb {B}^2{\setminus }\{0\}$ and $0<t\le |x|$.

Consequently, we have

$$\begin{aligned} \cos (u)=\frac{t^2+\sqrt{(1-t^2)(|x|^2-t^2)}}{|x|}, \end{aligned}$$

and the points $y=|x|e^{(k\pm 2u)i}$ can be written as $x(e^{ui})^{\pm 1}$, where

$$\begin{aligned} e^{2ui}&=\cos (2u)+\sin (2u)i=2\cos ^2(u)-1+2\sin (u)\cos (u)i\\&=2\cos ^2(u)-1+2\cos (u)\sqrt{1-\cos ^2(u)}i. \end{aligned}$$

Let us yet prove the rest of the lemma. For all such points $x,y\in \mathbb {B}^2$ that $|y|=|x|$, the inequality $s_{\mathbb {B}^2}(x,y)\le |x|$ holds because, if x, y are collinear with the origin, then by Lemma 2.5

$$\begin{aligned} s_{\mathbb {B}^2}(x,y)=\frac{|x|+|y|}{2-||x|-|y||}=|x|, \end{aligned}$$

and otherwise this inequality can be directly seen from Theorem 2.6. Therefore, if $t>|x|$, $s_{\mathbb {B}^n}(x,y)<t$ for all $x\in \mathbb {B}^2{\setminus }\{0\}$ and $y\in S^1(0,|x|)$.

Lemmas 3.2 and 3.3 can be used to prove that certain inclusion results are sharp, as done also in the following theorem.

Theorem 3.4

For $x\in G=\mathbb {B}^n$ and $0<t<1$, $B^n(x,r_0)\subseteq B_s(x,t)\subseteq B^n(x,r_1)$ if and only if

$$\begin{aligned} 0<r_0\le \frac{2t(1-|x|)}{1+t} \quad \text {and}\quad r_1\ge \min \left\{ \frac{2t(1-|x|)}{1-t},\frac{2t(1+|x|)}{1+t}\right\} \end{aligned}$$

Proof

For all $y\in \mathbb {B}^n(x,r_0)$ with $r_0$ as above, it follows from the fact that $B^n(x,1-|x|)\subseteq \mathbb {B}^n$ that

$$\begin{aligned} s_{\mathbb {B}^n}(x,y)\le s_{B^n(x,1-|x|)}(x,y)=\frac{|x-y|}{2-2|x|-|x-y|}<\frac{r_0}{2-2|x|-r_0}\le t. \end{aligned}$$

Consequently, for all $y\in \mathbb {B}^n(x,r_0)$, the triangular ratio distance between x and y is less than t so $B^n(x,r_0)\subseteq B_s(x,t)$. Note that the upper limit of $r_0$ is also sharp. Namely, if the radius $r_0$ would be any greater than $2t(1-|x|)/(1+t)$, the ball $\mathbb {B}^n(x,r_0)$ would contain the point $y_0\in S_s(x,t)$ of Lemma 3.2 and this point is trivially outside of the ball $B_s(x,t)$.

For all $y\in \mathbb {B}^n{\setminus }\overline{B}^n(x,r_1)$ where $r_1$ is as in the theorem, it follows from the fact that $\mathbb {B}^n\subseteq B^n(x,1+|x|){\setminus }\{x/|x|\}$ that

$$\begin{aligned} s_{\mathbb {B}^n}(x,y)&\ge s_{B^n(x,1+|x|){\setminus }\{x/|x|\}}(x,y) \ge \max \{s_{\mathbb {R}^n{\setminus }\{x/|x|\}}(x,y),s_{B^n(x,1+|x|)}(x,y)\}\\&=\max \left\{ \frac{|x-y|}{1-|x|+|x/|x|-y|},\frac{|x-y|}{2+2|x|-|x-y|}\right\} \\&\ge \max \left\{ \frac{|x-y|}{2-2|x|+|x-y|},\frac{|x-y|}{2+2|x|-|x-y|}\right\} \\&>\max \left\{ \frac{r_1}{2-2|x|+r_1},\frac{r_1}{2+2|x|-r_1}\right\} \ge s, \end{aligned}$$

so $B_s(x,t)\cap (\mathbb {B}^n{\setminus }\overline{B}^n(x,r_1))=\varnothing$. However, since $B_s(x,t)\subseteq \mathbb {B}^n$, this proves that $B_s(x,t)\subseteq B^n(x,r_1)$. It follows from this inclusion that $|x-y_1|\le r_1$ for the point $y_1\in S_s(x,t)$ of Lemma 3.2, which shows that the lower limit of $r_1$ in this theorem is sharp.

Note that it is not possible find such a Euclidean ball $B^n(x,r)$ for the triangular ratio metric ball $B_s(x,t)$ that $B_s(x,t)\subseteq B^n(x,r)\subsetneq \mathbb {B}^n$ if the conditions of the following lemma do not hold.

Lemma 3.5

For $x\in G=\mathbb {B}^n$ and $0<t<1$, the smallest Euclidean ball centered at x and containing the triangular ratio metric ball $B_s(x,t)$ is included in the unit ball if and only if either $t<1/3$ and $t\le |x|$, or $|x|<1/3$ and $|x|<t<(1-|x|)/(1+3|x|)$.

Proof

Let $B^n(x,r)$ be the smallest Euclidean ball centered at x and containing $B_s(x,t)$. It is in the unit disk if and only if $|x|+r<1$. If $t\le |x|$, $r=2t(1-|x|)/(1-t)$ here by Theorem 3.4, and $|x|+2t(1-|x|)/(1-t)<1$ is equivalent to $t<1/3$. If $t>|x|$, $r=2t(1+|x|)/(1+t)$ by Theorem 3.4, and $|x|+2t(1+|x|)/(1+t)<1$ if and only if $t<(1-|x|)/(1+3|x|)$. The conditions $t>|x|$ and $t<(1-|x|)/(1+3|x|)$ can both hold only if $|x|<(1-|x|)/(1+3|x|)$, which is equivalent to $3|x|^2+2|x|-1<0$. The equation $3|x|^2+2|x|-1=0$ has roots $|x|=-1$ and $|x|=1/3$ and, since |x| is non-negative, $3|x|^2+2|x|-1<0$ holds with $|x|<1/3$.

The following theorem is used to create an algorithm for drawing triangular ratio circles.

Theorem 3.6

For $x\in \mathbb {B}^2{\setminus }\{0\}$, $0<t<1$, and $u\in [0,\pi ]$, fix $z=xe^{ui}/|x|$. If

$$\begin{aligned} t<|x|\quad \text {and}\quad \frac{t^2-\sqrt{(1-t^2)(|x|^2-t^2)}}{|x|}<\cos (u)<\frac{t^2+\sqrt{(1-t^2)(|x|^2-t^2)}}{|x|}, \end{aligned}$$

there is no such point $y\in \mathbb {B}^2$ for which the equality

$$\begin{aligned} t=\frac{|x-y|}{|x-z|+|z-y|} \end{aligned}$$

would hold and L(0, z) would bisect the angle between L(x, z) and L(y, z). Otherwise, a point $y\in \mathbb {B}^2$ fulfills both of these conditions if and only if

$$\begin{aligned} y&=z(1-he^{-vi})\quad \text {with}\quad v=\textrm{acos}\left( \frac{1-|x|\cos (u)}{|x-z|}\right) \in [0,\pi /2]\quad \text {and}\\ h&=\frac{|x-z|(t^2+\cos (2v)\pm 2\cos (v)\sqrt{t^2-\sin ^2(v)})}{1-t^2}\in (0,2\cos (v)). \end{aligned}$$

Proof

Fix t, x, u, and z as in the lemma. Note that . Now,

$$\begin{aligned} |x-z|=||x|-e^{ui}|=\sqrt{1+|x|^2-2|x|\cos (u)}. \end{aligned}$$

Let . By the cosine formula,

$$\begin{aligned} \cos (v)=\frac{1+|x-z|^2-|x|^2}{2|x-z|}=\frac{1-|x|\cos (u)}{|x-z|}. \end{aligned}$$

For $y\in \mathbb {B}^2$, L(0, z) bisects the angle between L(x, z) and L(y, z), if and only if but $y\notin L(x,z)$ unless $v=0$. See Fig. 2. Consequently, we can write

$$\begin{aligned} y&=z+h(-z)e^{-vi}=z(1-he^{-vi}) \end{aligned}$$

for some $h\in \mathbb {R}$. The condition $y\in \mathbb {B}^2$ is equivalent to

$$\begin{aligned} |y|&=|1-he^{vi}|=\sqrt{1+h^2-2h\cos (v)}<1 \quad \Leftrightarrow \quad h(h-2\cos (v))<0\\&\Leftrightarrow \quad 0<h<2\cos (v). \end{aligned}$$

Fig. 2

For $x=0.5i$, $t=0.5$, $u=\pi /5$, and $z=xe^{ui}/|x|$, a point y found with Theorem 3.6 so that $t=|x-y|/(|x-z|+|z-y|)$ and the line L(0, z) bisects the angle between the lines L(x, z) and L(y, z)

Suppose then that $t=|x-y|/(|x-z|+|z-y|)$. By using trigonometric identities $\cos (2v)=2\cos ^2(v)-1$ and $\cos ^2(v)+\sin ^2(v)=1$, we will have

$$\begin{aligned} t&=\frac{|x-y|}{|x-z|+|z-y|} =\frac{\sqrt{h^2+|x-z|^2-2h|x-z|\cos (2v)}}{|x-z|+h}\\&\Leftrightarrow \quad (1-t^2)h^2-2|x-z|(t^2+\cos (2v))h+(1-t^2)|x-z|^2=0\\&\Leftrightarrow \quad h=\frac{2|x-z|(t^2+\cos (2v))\pm \sqrt{4|x-z|^2(t^2+\cos (2v))^2-4|x-z|^2(1-t^2)^2}}{2(1-t^2)}\\&=\frac{|x-z|(t^2+\cos (2v)\pm \sqrt{\cos ^2(2v)+2t^2(\cos (2v)+1)-1})}{1-t^2}\\&=\frac{|x-z|(t^2+\cos (2v)\pm 2\cos (v) \sqrt{t^2-\sin ^2(v)})}{1-t^2} \end{aligned}$$

The roots above are real numbers if and only if

$$\begin{aligned} t^2&\ge \sin ^2(v)=1-\cos ^2(v)=1-\frac{(1-|x|\cos (u))^2}{|x-z|^2} =\frac{|x|^2(1-\cos ^2(u))}{1+|x|^2-2|x|\cos (u)}\\&\Leftrightarrow \quad |x|^2\cos ^2(u)-2t^2|x|\cos (u)+t^2+t^2|x|^2-|x|^2\ge 0. \end{aligned}$$

If $t\ge |x|$, the inequality above holds for all $\cos (u)$. If $t<|x|$, we can solve that

$$\begin{aligned}&|x|^2\cos ^2(u)-2t^2|x|\cos (u)+t^2+t^2|x|^2-|x|^2\\&\quad =0\Leftrightarrow \cos (u)=\frac{t^2+\sqrt{(1-t^2)(|x|^2-t^2)}}{|x|} \end{aligned}$$

and we need to choose

$$\begin{aligned} \cos (u)\le \frac{t^2-\sqrt{(1-t^2)(|x|^2-t^2)}}{|x|}\quad \text {or}\quad \cos (u)\ge \frac{t^2+\sqrt{(1-t^2)(|x|^2-t^2)}}{|x|} \end{aligned}$$

for h to be well-defined. The proof is now finished.

Note that even if $x,y\in \mathbb {B}^2$ and $z\in S^1$ so that L(0, z) bisects the angle between the lines L(x, z) and L(y, z), this does not necessarily mean that

$$\begin{aligned} s_{\mathbb {B}^2}(x,y)=\frac{|x-y|}{|x-z|+|z-y|}. \end{aligned}$$

(3.1)

However, if this equality holds for some $x,y\in \mathbb {B}^2$ and $z\in S^1$, then L(0, z) must bisect the angle between the lines L(x, z) and L(y, z) by Theorem 2.4. In other words, when given $x\in \mathbb {B}^2$ and $u\in [0,\pi ]$, Theorem 3.6 can be only used to find potential candidates for such points $y\in \mathbb {B}^2$ that the equality (3.1) holds with the point $z=e^{ui}$. This is also the idea behind the following algorithm, which finds efficiently such points y that belong to the circle $S_s(x,t)$. This algorithm has been used to create most of the images of this article, including Fig. 3 that shows how the radius t affects the shape of the triangular ratio metric circles.

Fig. 3

The triangular ratio metric circles $S_s(x,t)$ for the radii $t=0.1,0.3,0.5,0.7$, when the center x is 0.6 and the domain G is the unit disk $\mathbb {B}^2$

3.1 Algorithm for Drawing Triangular Ratio Circles in the Unit Disk

The following instructions can be used to write an algorithm that plots the triangular ratio circle $S_s(x,t)$ in the domain $G=\mathbb {B}^2$ when the user gives the center $x\in \mathbb {B}^2$ and the radius $0<t<1$ as an input.

• 1. If $x=0$, plot the Euclidean circle $S^1(x,2t/(1+t))$ and stop after that.

• 2. Otherwise, initialize a vector Y, fix for instance $N=10,000$ and $\epsilon =10^{-5}$, and define the functions

  $$\begin{aligned} z(u)&=\frac{x}{|x|}e^{ui},\quad v(u)=\textrm{acos}\left( \frac{1-|x|\cos (u)}{|x-z(u)|}\right) \\ h_0(u)&=\frac{|x-z(u)|(t^2+\cos (2v(u))-2\cos (v(u))\sqrt{t^2-\sin ^2(v(u))})}{1-t^2},\quad \text {and}\\ h_1(u)&=\frac{|x-z(u)|(t^2+\cos (2v(u))+2\cos (v(u))\sqrt{t^2-\sin ^2(v(u))})}{1-t^2}. \end{aligned}$$

• 3. If $t\ge |x|$, create a vector U containing N values from the interval $[0,\pi ]$ and, if $t<|x|$ instead, choose the N values of the vector U from the set

  $$\begin{aligned} \left[ 0,\textrm{acos}\left( \frac{t^2+\sqrt{(1-t^2)(|x|^2-t^2)}}{|x|}\right) \!\right] \!\cup \!\left[ \textrm{acos}\left( \frac{t^2-\sqrt{(1-t^2)(|x|^2-t^2)}}{|x|}\right) ,\pi \!\right] . \end{aligned}$$

• 4. For each value $u\in U$, compute $h_0(u)$ and $h_1(u)$, add the point $z(u)(1-h_0(u)e^{-v(u)i})$ to the vector Y if $0<h_0(u)<2\cos (v(u))$ and, similarly, add the point $z(u)(1-h_1(u)e^{-v(u)i})$ to the vector Y if $0<h_1(u)<2\cos (v(u))$.

• 5. Then for each value $y\in Y$, compute the triangular ratio distance $s_{\mathbb {B}^2}(x,y)$ by using for instance the algorithm [2, Algorithm 2.5, p. 686] and remove this value y from Y if $|s_{\mathbb {B}^2}(x,y)-t|>\epsilon$.

• 6. For each remaining element $y\in Y$ to the vector Y, add the value $x\overline{y}/\overline{x}$ to the vector Y because this is a reflection of y over the line L(0, x) by [5, B.11, p. 460] and the triangular ratio metric is invariant under reflection.

• 7. Organize all the values $y\in Y$ so that the complex argument of the difference $y-x$ increases monotonically on $[0,2\pi )$ as the one lists the elements of the vector Y and plot the triangular ratio circle $S_s(x,t)$ by connecting the organized points of Y.

For $x\in G=\mathbb {B}^3$ and $0<t<1$, the three-dimensional triangular ratio sphere $S_s(x,t)$ can be drawn by using the algorithm above to plot the two-dimensional circle $S_s(x,t)$ in any two-dimensional plane containing both x and the origin, and then plot the three-dimensional sphere by rotating this circle around either the line L(0, x) or any line that contains the origin if $x=0$.

4 Triangular Ratio Metric and $j^*$-Metric Balls

Unlike for triangular ratio metric balls, an explicit expression can be found for any $j^*$-metric sphere $S_{j^*}(x,k)$ in terms of Euclidean geometry in the domain $G=\mathbb {B}^n$, and the results of Theorem 4.1 and Corollary 4.2 can be used to create an algorithm drawing $j^*$-metric spheres in the unit disk or ball.

Theorem 4.1

For $x\in \mathbb {B}^n{\setminus }\{0\}$ and $0<k<1$, the sphere $S_\Upsilon (x,k)$ defined with the function

$$\begin{aligned} \Upsilon _{\mathbb {B}^n}(x,y)=\frac{|x-y|}{|x-y|+2-2|y|} \end{aligned}$$

in the domain $\mathbb {B}^n{\setminus }\{0\}$ is

where

$$\begin{aligned} l_0(u)&=\frac{4k^2-(1-k)^2|x|\cos (u)-(1-k)\sqrt{4k^2(1+|x|^2-2|x| \cos (u))-(1-k)^2|x|^2\sin ^2(u)}}{3k^2+2k-1},\\ l_1(u)&=\frac{4k^2-(1-k)^2|x|\cos (u)+(1-k)\sqrt{4k^2(1+|x|^2-2|x| \cos (u))-(1-k)^2|x|^2\sin ^2(u)}}{3k^2+2k-1}. \end{aligned}$$

Proof

For $y\in \mathbb {B}^n{\setminus }\{0\}$, let . By the cosine formula,

$$\begin{aligned} |x-y|=\sqrt{|x|^2+|y|^2-2|x||y|\cos (u)}. \end{aligned}$$

Consequently,

$$\begin{aligned} \Upsilon _{\mathbb {B}^n}(x,y)&=\frac{\sqrt{|x|^2+|y|^2-2|x||y|\cos (u)}}{\sqrt{|x|^2+|y|^2-2|x||y|\cos (u)}+2(1-|y|)}=k\\&\Leftrightarrow (1-k)\sqrt{|x|^2+|y|^2-2|x||y|\cos (u)}=2k(1-|y|)\\&\Leftrightarrow (3k^2+2k-1)|y|^2-2(4k^2-2(1-k)^2|x|\cos (u))|y|\\&\quad +4k^2-(1-k)^2|x|^2=0. \end{aligned}$$

Thus, for $0<k<1$, $\Upsilon _{\mathbb {B}^n}(x,y)=k$ if and only if $f(|y|)=0$, where

$$\begin{aligned} f(q)=(3k^2+2k-1)q^2-2(4k^2-2(1-k)^2|x|\cos (u))q+4k^2-(1-k)^2|x|^2. \end{aligned}$$

For $k\ne 1/3$, f is a quadratic polynomial.

Let $l_0(u)$ and $l_1(u)$ be the roots of f as in the theorem. To verify if $\Upsilon _{\mathbb {B}^n}(x,y)=k$, we need to know whether the roots $l_0(u)$ and $l_1(u)$ are real numbers and, if so, to find if $l_0(u)$ or $l_1(u)$ belongs to the open interval (0, 1). Note that

$$\begin{aligned} l_0(u)\cdot l_1(u)=\frac{(1-k)^2(2k/(1-k)+|x|)(2k/(1-k)-|x|)}{3(k+1)(k-1/3)}. \end{aligned}$$

We can calculate that

$$\begin{aligned} f(0)&=4k^2-(1-k)^2|x|^2=(1-k)^2(2k/(1-k)+|x|)(2k/(1-k)-|x|),\\ f(1)&=-(1-k)^2(|x|^2-2|x|\cos (u)+1)<0. \end{aligned}$$

The discriminant of f is $(1-k)^2g(\cos (u))$, where

$$\begin{aligned} g(r)=(1-k)^2|x|^2r^2-8k^2|x|r+4k^2(1+|x|^2)-(1-k)^2|x|^2 \end{aligned}$$

is a quadratic polynomial. The equation $f(q)=0$ has real roots if and only if $g(\cos (u))\ge 0$. The discriminant of g is

$$\begin{aligned} \Delta (|x|,k)&=4|x|^2(3k^2+2k-1)(4k^2-|x|^2(1-k^2))\\&=12|x|^2(k+1)(2k+|x|(1-k))(2k-|x|(1-k))\left( k-\frac{1}{3}\right) . \end{aligned}$$

We see that $\Delta (|x|,k)$ has the same sign as $(k-1/3)(2k-|x|(1-k))$. Denote the roots of g by $c_0$ and $c_1$ so that

$$\begin{aligned} c_0&=\frac{4k^2-\sqrt{(3k^2+2k-1)(4k^2-|x|^2(1-k)^2)}}{|x|(1-k)^2},\\ c_1&=\frac{4k^2+\sqrt{(3k^2+2k-1)(4k^2-|x|^2(1-k)^2)}}{|x|(1-k)^2}. \end{aligned}$$

There are five possible cases, as listed below.

Case 1: If $k=1/3$, we can solve that $\Upsilon _{\mathbb {B}^n}(x,y)=k$ holds if and only if $|y|=(1-|x|^2)/(2(1-|x|\cos (u)))$.

Case 2: Consider then the case where $k>1/3$. It follows that $2k-|x|(1-k)>0$ since $|x|<1$ and $1-k>0$ imply $2k-|x|(1-k)>3k-1>0$. Consequently, $\Delta (|x|,k)$ so the roots $c_0$ and $c_1$ of the equation $g(r)=0$ are real and distinct.

Case 3: Suppose then that $k<1/3$ and $|x|<2k/(1-k)$. Now, $\Delta (|x|,k)<0$ and $g(r)>0$ whenever r is a real number. In particular, $g(\cos (u))>0$. The roots $l_0(u)$ and $l_1(u)$ are real and distinct. Moreover, $l_1(u)<0<l_0(u)$. It follows that $f(|y|)=0$ is satisfied if and only if $|y|=l_0(u)$. Since $3k^2+2k-1<0$ and $f(1)<0$, we see that $l_0(u)<1$. Consequently, $|y|=l_0(u)$ gives a unique solution for every angle u.

Case 4: Assume that $k<1/3$ and $|x|=2k/(1-k)$. We have

$$\begin{aligned} f(q)=q(3k^2+2k-1)\left( q-\frac{4k(1-k)}{3k^2+2k-1} \left( \frac{2k}{1-k}-\cos (u)\right) \right) . \end{aligned}$$

If $\cos (u)\le 2k/(1-k)$, then $f(|y|)<0$ for all $y\in \mathbb {R}^n{\setminus }\{0\}$ and we cannot find a solution. If $2k/(1-k)<\cos (u)<1$, then $f(|y|)=0$ with $y\in \mathbb {R}^n{\setminus }\{0\}$ if and only if

$$\begin{aligned} |y|=\frac{4k(1-k)}{3k^2+2k-1}\left( \frac{2k}{1-k}-\cos (u)\right) . \end{aligned}$$

If |y| is as above, then $|y|<1$ for every angle u as

$$\begin{aligned} \frac{4k(1-k)}{3k^2+2k-1}\left( \frac{2k}{1-k}-\cos (u)\right)<1 \quad \Leftrightarrow \quad \cos (u)<\frac{5k^2-2k+1}{4k(1-k)} \end{aligned}$$

where $(5k^2-2k+1)/(4k(1-k))>1$.

Case 5: If $k<1/3$ and $|x|>2k/(1-k)$ instead, then $\Delta (|x|,k)>0$, from which it follows that the roots $c_0$ and $c_1$ are real and distinct.

In both cases 2 and 5, the real distinct roots of $l_0(u)$ and $l_1(u)$ of the equation $f(q)=0$ satisfy $l_0(u)\cdot l_1(u)>0$ and

$$\begin{aligned} l_0(u)+l_1(u)=\frac{4k^2-(1-k)^2|x|\cos (u)}{3k^2+2k-1}. \end{aligned}$$

In Case 2, $4k^2-(1-k)^2|x|\cos (u)\ge 3k^2+2k-1>1$ and it follows that both roots $l_0(u)$ and $l_1(u)$ are positive. Since $f(1)<0$, we can conclude that $0<l_0(u)<1<l_1(u)$. Therefore, $f(|y|)=0$ for $y\in \mathbb {B}^n$ if and only if $|y|=l_0(u)$.

In Case 5, we have $f(0)<0$ and $f(1)<0$. Because of this, 0 and 1 are outside of the interval determined by $l_1(u)<l_0(u)$. If $4k^2-2(1-k)^2|x|\cos (u)<0$, then $0<l_1(u)<l_0(u)<1$ and $f(|y|)=0$ with $y\in \mathbb {B}^n$ if and only if $|y|\in \{l_0(u),l_1(u)\}$. If $4k^2-2(1-k)^2|x|\cos (u)>0$, then $l_1(u)<l_0(u)<0$ and the equation $f(|y|)=0$ has no solution with $y\in \mathbb {B}^n$.

The theorem follows now. $\square$

The result of the following corollary can be better understood by looking at Fig. 4.

Fig. 4

For $x=0.3+0.3i$ and $k=0.3$, the Euclidean circles $S^1(0,|x|)$ and $S^1(x,2k(1-|x|)/(1-k))$ as dotted line, the circle $S_\Upsilon (x,k)$ defined with the function $\Upsilon _{\mathbb {B}^2}(x,y)$ of Theorem 4.1 as dashed line, and the $j^*$-metric circle $S_{j^*}(x,k)$ as solid line in the domain $G=\mathbb {B}^2$

Corollary 4.2

For $x\in G=\mathbb {B}^n$ and $0<k<1$,

$$\begin{aligned}&S_{j^*}(x,k)=S^{n-1}(0,2k/(1+k))\quad \text {if}\quad x=0,\quad \text {and otherwise}\\&S_{j^*}(x,k)= \left( S^{n-1}\left( x,\frac{2k(1-|x|)}{1-k}\right) \cap \overline{B}^n(0,|x|)\right) \cup (S_\Upsilon (x,k){\setminus }\overline{B}^n(0,|x|)), \end{aligned}$$

where $S_\Upsilon (x,k)$ is as in Theorem 4.1.

Proof

The first part of the corollary follows directly from Lemma 3.1 because $j^*_{\mathbb {B}^n}(y,0)=s_{\mathbb {B}^n}(y,0)$ for all $y\in \mathbb {B}^n$.

Suppose below that $x\ne 0$ and denote $r=|x-y|$. Consider first the part of the $j^*$-metric sphere $S_{j^*}(x,k)$ in the closure of the Euclidean metric ball $B^n(0,|x|)$. For all $y\in \overline{B}^n(0,|x|)$, $|y|\le |x|$ and $j^*_{\mathbb {B}^n}(x,y)=r/(r+2-2|x|)=k$ holds if and only if $r=2k(1-|x|)/(1-k)$. Consequently,

$$\begin{aligned} S_{j^*}(x,k)\cap \overline{B}^n(0,|x|)=S^{n-1}\left( x,\frac{2k(1-|x|)}{1-k}\right) \cap \overline{B}^n(0,|x|). \end{aligned}$$

If $|y|>|x|$, then the distance $j^*(x,y)$ is equivalent to the value $\Upsilon _{\mathbb {B}^n}(x,y)$ of the function introduced in Theorem 4.1, so

$$\begin{aligned} S_{j^*}(x,k){\setminus }\overline{B}^n(0,|x|)=S_\Upsilon (x,k){\setminus }\overline{B}^n(0,|x|), \end{aligned}$$

and the corollary follows. $\square$

Remark 4.3

Note that Corollary 4.2 can be used to find the balls in the distance ratio metric, too, given $j_{\mathbb {B}^n}(x,y)=\textrm{th}(j^*_{\mathbb {B}^n}(x,y)/2)$.

Lemma 4.4

For $x\in G=\mathbb {B}^n$ and $0<r<1-|x|$, $B_{j^*}(x,k_0)\subseteq B^n(x,r)\subseteq B_{j^*}(x,k_1)$ if and only if

$$\begin{aligned} 0<k_0\le \frac{r}{2-|r-2|x||} \quad \text {and}\quad k_1\ge \frac{r}{2-2|x|-r}. \end{aligned}$$

Proof

The $j^*$-metric ball $B_{j^*}(x,k_0)$ is included in the Euclidean ball $B^n(x,r)$ if and only if $k_0\le j^*_{\mathbb {B}^n}(x,y)$ for all $y\in S^{n-1}(x,r)$, and $B_{j^*}(x,k_1)$ contains $B^n(x,r)$ if and only if $j^*_{\mathbb {B}^n}(x,y)\le k_1$ for $y\in S^{n-1}(x,r)$. For all $y\in S^{n-1}(x,r)$,

$$\begin{aligned} j^*_{\mathbb {B}^n}(x,y)=\frac{r}{r+2-2\max \{|x|,\sqrt{r^2+|x|^2-2r|x|\cos (u)}\}}, \end{aligned}$$

where or, if $x=0$, with $z=1$. Clearly, the minimum value of the distance $j^*_{\mathbb {B}^n}(x,y)$ with respect to $y\in S^{n-1}(x,r)$ is

$$\begin{aligned} \frac{r}{r+2-2\max \{|x|,||x|-r|\}} ={\left\{ \begin{array}{ll} r/(r+2-2|x|)\text { if }r\le 2|x|,\\ r/(r+2-2(r-|x|))\text { if }r>2|x| \end{array}\right. } \end{aligned}$$

and the maximum value $r/(2-2|x|-r)$, from which the lemma follows. $\square$

Corollary 4.5

For $x\in G=\mathbb {B}^n$ and $0<k<1$, $B^n(x,r_0)\subseteq B_{j^*}(x,k)\subseteq B^n(x,r_1)$ if and only if

$$\begin{aligned} 0<r_0\le \frac{2k(1-|x|)}{1+k}\quad \text {and}\quad r_1\ge \min \left\{ \frac{2k(1-|x|)}{1-k},\frac{2k(1+|x|)}{1+k}\right\} \end{aligned}$$

Proof

Follows from Lemma 4.4. $\square$

The following inequality helps to formulate a result about the ball inclusion between the triangular ratio metric and the $j^*$-metric.

Corollary 4.6

For any domain $G\subsetneq \mathbb {R}^n$ and all $x,y\in G$,

$$\begin{aligned} s_G(x,y)\ge \frac{j^*_G(x,y)}{1-j^*_G(x,y)}. \end{aligned}$$

Proof

By [7, Lemma 2.1, p. 1124]

$$\begin{aligned} s_G(x,y)\le \frac{e^{j_G(x,y)}-1}{2}=\frac{e^{2\textrm{arth}(j^*_G(x,y))}-1}{2}=\frac{j^*_G(x,y)}{1-j^*_G(x,y)}. \end{aligned}$$

$\square$

Lemma 4.7

For any domain $G\subsetneq \mathbb {R}^n$, $x\in G$, and $0<t<1$,

$$\begin{aligned} B_{j^*}\left( x,t/(1+t)\right) \subseteq B_s(x,t)\subseteq B_{j^*}(x,t), \end{aligned}$$

where the latter inclusion above is sharp for all possible choices of a domain G, and the former inclusion can be replaced with

$$\begin{aligned} B_{j^*}\left( x,t/\min \{(1+t),\sqrt{2}\}\right) \subseteq B_s(x,t) \end{aligned}$$

if G is convex.

Proof

The inequality of Corollary 4.6 is equivalent to $j^*_G(x,y)\le s_G(x,y)/(1+s_G(x,y))$ and, by Theorem 2.3, the inequality $j^*_G(x,y)\le s_G(x,y)$ holds for all $x,y\in G$. It now follows that

$$\begin{aligned} B_{j^*}(x,t/(1+t))&=\{y\in \mathbb {B}^n|j^*_{\mathbb {B}^n}(x,y)<t/(1+t)\} \subseteq \{y\in \mathbb {B}^n|s_{\mathbb {B}^n}(x,y)<t\}\\&=B_s(x,t)\subseteq B_{j^*}(x,t). \end{aligned}$$

To show the inclusion $B_s(x,t)\subseteq B_{j^*}(x,t)$ is sharp, fix $x\in G$, $z\in S^{n-1}(x,d_G(x))\cap \partial G$, and $y=x+2t(z-x)/(1+t)$ and note that

$$\begin{aligned} s_G(x,y) =\frac{|x-y|}{|x-z|+|z-y|} =t =\frac{|x-y|}{|x-y|+2\min \{d_G(x),d_G(y)\}} =j^*_G(x,y). \end{aligned}$$

The last part of the lemma follows from Theorem 2.3. $\square$

Given $j^*_G(x,y)=\textrm{th}(j_G(x,y)/2)$, the $j^*$-metric in the former result can be easily replaced with the distance ratio metric.

Corollary 4.8

For any domain $G\subsetneq \mathbb {R}^n$, $x\in G$, and $0<t<1$,

$$\begin{aligned} B_j(x,\log (1+2t))\subseteq B_s(x,t)\subseteq B_j(x,\log ((1+t)/(1-t))), \end{aligned}$$

where latter inclusion above is sharp for all possible choices of a domain G and the former inclusion can be replaced with

$$\begin{aligned} B_j\left( x,\max \left\{ \log \left( \frac{t+\sqrt{2}}{\sqrt{2}-t}\right) ,\log (1+2t)\right\} \right) \subseteq B_s(x,t) \end{aligned}$$

if G is convex.

Proof

Follows from Lemma 4.7 and the formula (2.3). $\square$

Remark 4.9

Corollary 4.8 proves an earlier conjecture in [9, Conj. 7.7, p. 122], and also improves the constant in the first of this conjecture.

As noted already in Lemma 3.5, there is not always a Euclidean ball that is included in the unit ball, contains another ball defined with some hyperbolic type metric, and has the same center as the other ball, the following lemma offers a non-x-centered Euclidean ball that contains the balls $B_s(x,t)$ and $B_{j^*}(x,t)$ and is included in the unit ball if $t\ge |x|$.

Lemma 4.10

For $G=\mathbb {B}^n$, $x\in \mathbb {B}^n{\setminus }\{0\}$, and $|x|\le t<1$, $B_s(x,t)\subseteq B_{j^*}(x,t)\subseteq B^n(q,r)\subsetneq \mathbb {B}^n$ if

$$\begin{aligned} q=x-\frac{2tx}{1+t} \quad \text {and}\quad r=\frac{2t}{1+t} \end{aligned}$$

and $B^n(q,r)$ here is the smallest Euclidean ball containing the ball $B_s(x,t)$.

Proof

By Lemma 4.7, $B_s(x,t)\subseteq B_{j^*}(x,t)$. Let $y_0$ and $y_1$ be the intersection points in $S_s(x,t)\cap L(0,x)$ found in Lemma 3.2. Since $t\ge |x|$,

$$\begin{aligned} y_0=x+\frac{2tx(1-|x|)}{|x|(1+t)}\quad \text {and}\quad y_1=x-\frac{2tx(1+|x|)}{|x|(1+t)} \end{aligned}$$

and it can be easily verified that $q=(y_0-y_1)/2$ and $r=|q-y_0|/2$. Consequently, $B^n(q,r)\subsetneq \mathbb {B}^n$ because $|q|+r=|y_0|<1$. Let us now prove that $B_{j^*}(x,t)\subseteq B^n(q,r)$ by showing that, for all $y\in S^{n-1}(q,r)$,

$$\begin{aligned} j^*_{\mathbb {B}^n}(x,y)=\left( 1+\frac{2(1-\max \{|x|,|y|\})}{|x-y|}\right) ^{-1}>t \quad \Leftrightarrow \quad \frac{1-\max \{|x|,|y|\}}{|x-y|}<\frac{1-t}{2t} \end{aligned}$$

If since q is between the origin and the point x. By cosine formula,

$$\begin{aligned}&|y|=\sqrt{|q|^2+r^2+2r|q|\cos (u)}=\frac{1}{1+t}\sqrt{|x|(1-t)^2+4t^2+4t(1-t)|x|\cos (u)},\\&|x-y|=\sqrt{|x-q|^2+r^2-2r|x-q|\cos (u)}=\frac{2t}{1+t}\sqrt{1+|x|^2-2|x|\cos (u)}. \end{aligned}$$

Clearly, the distances |x|, |y|, and $|x-y|$ are all increasing with respect to |x| and therefore

$$\begin{aligned}&\frac{1-\max \{|x|,|y|\}}{|x-y|}\\&\quad =\frac{1+t-\max \{(1+t)|x|,\sqrt{|x|(1-t)^2+4t^2+4t(1-t)|x|\cos (u)}\}}{2t\sqrt{1+|x|^2-2|x|\cos (u)}}\\&\quad <\frac{1+t-\max \{(1+t)\cdot 0,\sqrt{0\cdot (1-t)^2+4t^2+4t(1-t)\cdot 0\cdot \cos (u)}\}}{2t\sqrt{1+0^2-2\cdot 0\cdot \cos (u)}} =\frac{1-t}{2t}. \end{aligned}$$

Thus, the inclusion of the lemma holds and, since $y_0,y_1\in S_s(x,t)$ and $|y_0-y_1|=2r$, there is no such Euclidean ball with smaller radius than r that contains $B_s(x,t)$. $\square$

Remark 4.11

If $G=\mathbb {B}^n$, $x\in \mathbb {B}^n{\setminus }\{0\}$, and $0<t<|x|$ and $q=(y_0-y_1)/2$ and $r=|q-y_0|/2$ for the points $y_0,y_1$ of Lemma 3.2, the inclusion $B_s(x,t)\subseteq B^n(q,r)\subsetneq \mathbb {B}^n$ holds but $B_{j^*}(x,t)\nsubseteq B^n(q,r)$ according to computer tests.

5 Triangular Ratio Metric Balls in Hyperbolic Geometry

Since the hyperbolic metric is conformally invariant unlike the $j^*$-metric or the triangular ratio metric, it is useful to have some ball inclusion results between the hyperbolic metric and these two metrics.

Corollary 5.1

For $x\in G=\mathbb {B}^n$ and $R>0$, $B_{j^*}(x,k_0)\subseteq B_\rho (x,R)\subseteq B_{j^*}(x,k_1)$ if and only if

$$\begin{aligned}&0<k_0\le \max \left\{ \frac{(1+|x|)\textrm{sh}(R/2)}{2+(1+|x|)\textrm{sh}(R/2)},\frac{(1-|x|)(e^R-1)}{3+e^R-|x|(e^R-1)}\right\} \quad \text {and}\\&k_1\ge \frac{(1+|x|)(e^R-1)}{3+e^R+|x|(e^R-1)}, \end{aligned}$$

and, for $x\in G=\mathbb {B}^n$ and $0<k<1$, $B_\rho (x,R_0)\subseteq B_{j^*}(x,k)\subseteq B_\rho (x,R_1)$ if and only if

$$\begin{aligned}&0<R_0\le \log \left( 1+\frac{4k}{(1-k)(1+|x|)}\right) \quad \text {and}\\&R_1\ge \min \left\{ 2\textrm{arsh}\left( \frac{2k}{(1-k)(1+|x|)}\right) ,\log \left( 1+\frac{4k}{(1-k)(1-|x|)}\right) \right\} . \end{aligned}$$

Proof

Follows from Theorem 2.2 and the formula (2.3). $\square$

The next result is very trivial but needed to check that other results hold in the special case $x=0$.

Lemma 5.2

For $G=\mathbb {B}^n$ and $0<t<1$, $B_s(0,s)=B_\rho (0,\log ((1+3t)/(1-t)))$.

Proof

By formula (2.1) and Lemma 3.1,

$$\begin{aligned} \rho _{\mathbb {B}^n}(y,0) =2\textrm{arsh}\left( \frac{|y|}{\sqrt{1-|y|^2}}\right) =2\textrm{arsh}\left( \frac{2t}{\sqrt{(1-t)(1+3t)}}\right) =\log \left( \frac{1+3t}{1-t}\right) . \end{aligned}$$

$\square$

Recall that, if $G=\mathbb {B}^n$, we have explicit formulas for two points $y_0,y_1\in S_s(x,t)$ with any $x\in \mathbb {B}^n{\setminus }\{0\}$ and $0<t<1$ by Lemma 3.2, from which follows that we can create upper and lower bounds for the radii in the inclusion of the triangular ratio metric balls and hyperbolic balls.

Lemma 5.3

For $x\in G=\mathbb {B}^n$ and $R>0$, $B_s(x,t_0)\subseteq B_\rho (x,R)\subseteq B_s(x,t_1)$ can hold only if

$$\begin{aligned}&0<t_0\le \frac{\textrm{th}(R/2)(1-|x|^2)}{2(1-|x|\textrm{th}(R/2))-|2|x|-\textrm{th}(R/2)(1+|x|^2)|} \quad \text {and}\\&t_1\ge \frac{(1+|x|)(e^R-1)}{3+e^R+|x|(e^R-1)}, \end{aligned}$$

and, for $x\in G=\mathbb {B}^n$ and $0<t<1$, $B_\rho (x,R_0)\subseteq B_s(x,t)\subseteq B_\rho (x,R_1)$ can hold only if

$$\begin{aligned}&0<R_0\le \log \left( 1+\frac{4t}{(1-t)(1+|x|)}\right) \quad \text {and}\quad R_1\ge 2\textrm{arsh}\left( \frac{2t}{\sqrt{l(t,|x|)}}\right) , \quad \text {where}\\&l(t,|x|)=\max \{(1+t)(1+|x|)(1-3t+|x|(1+t)),\\&\quad \quad \quad \quad \quad \quad \quad (1-t)(1-|x|)(1+3t-|x|(1-t))\}. \end{aligned}$$

Proof

Let us first consider the latter part of the result. Suppose first that $x\in \mathbb {B}^n{\setminus }\{0\}$. If $y_0,y_1\in S_s(x,t)$ are as in Lemma 3.2,

$$\begin{aligned}&\rho _{\mathbb {B}^n}(x,y_0) =\log \left( 1+\frac{4t}{(1-t)(1+|x|)}\right) ,\\&\rho _{\mathbb {B}^n}(x,y_1) =2\textrm{arsh}\left( \frac{2t}{\sqrt{(1+t)(1+|x|)(1-3t+|x|(1+t))}}\right) \quad \text {if}\quad t<|x|,\\&\rho _{\mathbb {B}^n}(x,y_1) =\log \left( 1+\frac{4t}{(1-t)(1-|x|)}\right) \quad \text {if}\quad t\ge |x|. \end{aligned}$$

Clearly, $B_\rho (x,R_0)\subseteq B_s(x,t)\subseteq B_\rho (x,R_1)$ can only hold if $R_0\le \rho _{\mathbb {B}^n}(x,y_0)$ and $R_1\ge \rho _{\mathbb {B}^n}(x,y_1)$. Note that, since

$$\begin{aligned} \left( 1+\frac{4t}{(1-t)(1-|x|)}\right) =2\textrm{arsh}\left( \frac{2t}{\sqrt{(1-t)(1-|x|)(1+3t-|x|(1-t))}}\right) , \end{aligned}$$

the distance $\rho _{\mathbb {B}^n}(x,y_1)$ can be written as $2\textrm{arsh}(2t/\sqrt{l(t,|x|})$ where l(t, |x|) is as in the lemma. Because these bounds of $R_0$ and $R_1$ hold also in the special case $x=0$ by Lemma 5.2, the latter part of the result follows.

Now, we can solve that

$$\begin{aligned} R\le \log \left( 1+\frac{4t}{(1-t)(1+|x|)}\right) \quad \Leftrightarrow \quad t\ge \frac{(1+|x|)(e^R-1)}{3+e^R+|x|(e^R-1)}, \end{aligned}$$

which proves the lower bound of $t_1$.

For $x\in \mathbb {B}^n{\setminus }\{0\}$, suppose that $R=\rho _{\mathbb {B}^n}(x,y_1)$ with $y_1$ as in Lemma 3.2 for $0<t<1$. Now, the circles $S_\rho (x,R)$ and $S_s(x,t)$ intersect at the point $y_1$. Since $y_1=S_\rho (x,R)\cap L(0,x)\cap B(0,|x|)$, it follows from Lemma 2.1 that

$$\begin{aligned} y_1=\frac{x(1-\textrm{th}^2(R/2))}{1-|x|^2\textrm{th}^2(R/2)}-\frac{x(1-|x|^2)\textrm{th}(R/2)}{|x|(1-|x|^2\textrm{th}^2(R/2))}=\frac{x(|x|-\textrm{th}(R/2))}{|x|(1-|x|^2\textrm{th}^2(R/2))}. \end{aligned}$$

By Lemma 2.5, we have

$$\begin{aligned} t=s_{\mathbb {B}^n}(x,y_1)=\frac{\textrm{th}(R/2)(1-|x|^2)}{2(1-|x|\textrm{th}(R/2))-|2|x|-\textrm{th}(R/2)(1+|x|^2)|}. \end{aligned}$$

Thus, the upper bound of $t_0$ follows, too. $\square$

The next result follows directly from Corollary 5.1 and, while all of its bounds might not be sharp, we know by Lemma 5.3 and its proof that the upper bound of $t_0$ and the lower bound of $R_1$ below are the best ones possible in the case $t\ge |x|$.

Corollary 5.4

For $x\in G=\mathbb {B}^n$ and $R>0$, $B_s(x,t_0)\subseteq B_\rho (x,R)\subseteq B_s(x,t_1)$ if

$$\begin{aligned}&0<t_0\le \max \left\{ \frac{(1+|x|)\textrm{sh}(R/2)}{2+(1+|x|)\textrm{sh}(R/2)},\frac{(1-|x|)(e^R-1)}{3+e^R-|x|(e^R-1)}\right\} \quad \text {and}\\&t_1\ge \left\{ \frac{\sqrt{2}(1+|x|)(e^R-1)}{3+e^R+|x|(e^R-1)},\frac{(1+|x|)(e^R-1)}{4}\right\} , \end{aligned}$$

and, for $x\in G=\mathbb {B}^n$ and $0<t<1$, $B_\rho (x,R_0)\subseteq B_s(x,t)\subseteq B_\rho (x,R_1)$ if

$$\begin{aligned}&0<R_0\le \log \left( 1+\frac{4k}{(1-k)(1+|x|)}\right) \quad \text {with}\quad k=\frac{t}{\min \{(1+t),\sqrt{2}\}}\quad \text {and}\\&R_1\ge \min \left\{ 2\textrm{arsh}\left( \frac{2t}{(1-t)(1+|x|)}\right) ,\log \left( 1+\frac{4t}{(1-t)(1-|x|)}\right) \right\} . \end{aligned}$$

Proof

Follows from Lemma 4.7 and Corollary 5.1. $\square$

Computer tests suggest that the following conjecture holds and, by comparing it to Lemma 5.3 and Corollary 5.4, we see that, to prove this result, it is enough to show that the inclusion $B_\rho (x,R_0)\subseteq B_s(x,t)$ holds for $0<t<1$ and the inclusion $B_s(x,t)\subseteq B_\rho (x,R_1)$ for $0<t<|x|$.

Conjecture 5.5

For $x\in G=\mathbb {B}^n$ and $R>0$, $B_s(x,t_0)\subseteq B_\rho (x,R)\subseteq B_s(x,t_1)$ if and only if

$$\begin{aligned}&0<t_0\le \frac{\textrm{th}(R/2)(1-|x|^2)}{2(1-|x|\textrm{th}(R/2))-|2|x|-\textrm{th}(R/2)(1+|x|^2)|} \quad \text {and}\\&t_1\ge \frac{(1+|x|)(e^R-1)}{3+e^R+|x|(e^R-1)}, \end{aligned}$$

and, for $x\in G=\mathbb {B}^n$ and $0<t<1$, $B_\rho (x,R_0)\subseteq B_s(x,t)\subseteq B_\rho (x,R_1)$ if and only if

$$\begin{aligned}&0<R_0\le \log \left( 1+\frac{4t}{(1-t)(1+|x|)}\right) \quad \text {and}\quad R_1\ge 2\textrm{arsh}\left( \frac{2t}{\sqrt{l(t,|x|)}}\right) , \quad \text {where}\\&l(t,|x|)=\max \{(1+t)(1+|x|)(1-3t+|x|(1+t)),\\&\quad \quad \quad \quad \quad \quad \quad (1-t)(1-|x|)(1+3t-|x|(1-t))\}. \end{aligned}$$

Fig. 5

The triangular ratio metric circle $S_s(x,t)$ for $G=\mathbb {B}^2$, $x=0.3+0.45i$ and $t=0.5$ as solid line and the hyperbolic circles $S_\rho (x,R_0)$ and $S_\rho (x,R_1)$ as dotted line, when $R_0$ is as large as possible and $R_1$ as small as possible within the bounds of Conjecture 5.5

Figure 5 depicts the sharp inclusion of a triangular ratio metric balls and two hyperbolic metric balls found with Conjecture 5.5.