1 Introduction

The concept of semi-exponential operators was first discussed by Tyliba and Wachnicki [14], who introduced semi-exponential extension of the Szász–Mirakyan and Weierstrass operators. Later, Herzog [11] captured semi-exponential Post–Widder operators for \(\beta , \lambda >0\), \(x\in I:=[0,+\infty )\) and \(f\in C(I)\) (the space of real-valued continuous functions defined on the interval I) as follows:

$$\begin{aligned} (P_\lambda ^\beta f)(x)=\frac{\lambda }{x^\lambda \exp (\beta x)}\int _0^\infty \frac{\left( \frac{\lambda y}{\beta }\right) ^{(\lambda -1)/2}I_{\lambda -1}(2\sqrt{\lambda \beta y})}{\exp (\lambda y/x)} f(y)\textrm{d}y, \ \ \end{aligned}$$
(1.1)

where

$$\begin{aligned} I_{\lambda -1}:=\sum _{j=0}^\infty \frac{z^{2j+\lambda -1}}{j!\varGamma (j+\lambda )2^{2j+\lambda -1}} \end{aligned}$$

represents the modified form of Bessel function of first kind. Moreover, we denote by \(C_B(I)\) the class of bounded continuous functions on I and we consider the sup-norm for \(f\in C_B(I)\), as

$$\begin{aligned} \vert \vert f\vert \vert =\sup \{\vert f(x)\vert :x\in I\}. \end{aligned}$$

Alternatively, (1.1) can be written as

$$\begin{aligned} (P_\lambda ^\beta f)(x)= & {} \int _0^\infty k_\lambda ^\beta (x,t)f(t)\textrm{d}t, \end{aligned}$$

where the kernel

$$\begin{aligned} k_\lambda ^\beta (x,t)=\frac{\lambda ^\lambda }{x^\lambda e^{\beta x}}\sum _{k=0}^\infty \frac{\left( \lambda \beta \right) ^k}{k!\varGamma (\lambda +k)} e^{-\lambda t/x} t^{\lambda +k-1} \end{aligned}$$

satisfies the partial differential equation

$$\begin{aligned} \frac{\partial }{\partial x}k_\lambda ^\beta (x,t)=\left[ \frac{\lambda (t-x)}{x^2}-\beta \right] k_\lambda ^\beta (x,t), \end{aligned}$$
(1.2)

which is the required condition for \(P_\lambda ^\beta \) to be of semi-exponential type operator. Also, for specific value \(\beta =0\), we get the Post–Widder operators [12, (3.9)] defined by

$$\begin{aligned} (P_\lambda f)(x)=\frac{\lambda ^\lambda }{x^\lambda } \frac{1}{\varGamma (\lambda )}\int _0^\infty e^{-\lambda y/x} y^{\lambda -1} f(y)\textrm{d}y. \end{aligned}$$
(1.3)

Abel et al. [2] and Gupta and Milovanović [9] introduced all remaining semi-exponential operators from available exponential-type operators. In a very recent paper [6], some more general form of exponential-type operators was introduced and discussed. Also, we refer the readers to the recent related work [10, 13].

In this paper, we shall investigate the difference between two operators which is an active area of research in the recent years. For example, in papers [3, 7, 8], the differences amongst operators having the same/different basis under summation are estimated. It is pointed out here that in case of the Post–Widder operators, the difference with other operators is not analogous due to the purely integral term of the operators, but for the semi-exponential Post–Widder operators, one can find the difference with other operators. We also consider composition of such operators with some other operators to capture some other operators. Also, some modification of \(P_\lambda ^\beta \) is proposed here which preserves the linear functions.

2 Difference and Composition

In this section, we deal with the difference between \(P_\lambda ^\beta \) to the general Baskakov operators and some Kantorovich variants. We shall apply some estimates from paper [7] and [8]. Also, we indicate some composition estimates.

First, we write the operators (1.1) in an alternative form as

$$\begin{aligned} (P_\lambda ^\beta f)(x)= & {} \sum _{k=0}^\infty s_k(\beta x)J_{\lambda ,k}(f), \end{aligned}$$

where \(s_k(\beta x)=\frac{e^{-\beta x}\left( x\beta \right) ^k}{k!}\) and

$$\begin{aligned} J_{\lambda ,k}(f)=\frac{1}{\varGamma (\lambda +k)}\int _0^\infty e^{-u} u^{\lambda +k-1}f\left( \frac{xu}{\lambda }\right) \textrm{d}u. \end{aligned}$$

Remark 2.1

By simple computation, we have

$$\begin{aligned} J_{\lambda ,k}(e_r)=\frac{1}{\varGamma (\lambda +k)}\int _0^\infty e^{-u} u^{\lambda +r+k-1}\frac{x^r}{\lambda ^r}\textrm{d}u=\frac{x^r}{\lambda ^r}\frac{\varGamma (\lambda +r+k)}{\varGamma (\lambda +k)}. \end{aligned}$$

In particular

$$\begin{aligned} b_{J_{\lambda ,k}}=J_{\lambda ,k}(e_1)=\frac{1}{\varGamma (\lambda +k)}\int _0^\infty e^{-u} u^{\lambda +k-1}\frac{xu}{\lambda }\textrm{d}u=\frac{x}{\lambda }(\lambda +k). \end{aligned}$$

Also, using above, we have

$$\begin{aligned} \mu _2^{J_{\lambda ,k}}= & {} J_{\lambda ,k}(e_1-b_{J_{\lambda ,k}}e_0)^2=\sum _{i=0}^2 {2\atopwithdelims ()i} (-1)^iJ_{\lambda ,k}(e_{2-i})[b_{J_{\lambda ,k}}]^i\\= & {} \frac{x^2}{\lambda ^2}(\lambda +k+1)(\lambda +k)-\frac{x^2}{\lambda ^2}(\lambda +k)^2=\frac{x^2}{\lambda ^2}(\lambda +k). \\ \mu _3^{J_{\lambda ,k}}= & {} J_{\lambda ,k}(e_1-b_{J_{\lambda ,k}}e_0)^3=\sum _{i=0}^3 {3\atopwithdelims ()i} (-1)^iJ_{\lambda ,k}(e_{3-i})[b_{J_{\lambda ,k}}]^i\\= & {} \frac{x^3}{\lambda ^3}(\lambda +k+2)(\lambda +k+1)(\lambda +k)\\{} & {} -3\frac{x^3}{\lambda ^3}(\lambda +k+1)(\lambda +k)^2+2\frac{x^3}{\lambda ^3}(\lambda +k)^3\\= & {} 2\frac{x^3}{\lambda ^3}(\lambda +k) \end{aligned}$$

and

$$\begin{aligned} \mu _4^{J_{\lambda ,k}}= & {} J_{\lambda ,k}(e_1-b_{J_{\lambda ,k}}e_0)^4=\sum _{i=0}^4 {4\atopwithdelims ()i} (-1)^iJ_{\lambda ,k}(e_{4-i})[b_{J_{\lambda ,k}}]^i\\= & {} \frac{x^4}{\lambda ^4}(\lambda +k+3)(\lambda +k+2)(\lambda +k+1)(\lambda +k)\\{} & {} -4\frac{x^4}{\lambda ^4}(\lambda +k+2)(\lambda +k+1)(\lambda +k)^2\\{} & {} +6\frac{x^4}{\lambda ^4}(\lambda +k+1)(\lambda +k)^3-3\frac{x^4}{\lambda ^4}(\lambda +k)^4\\= & {} \frac{x^4}{\lambda ^4}[3(\lambda +k)+6]. \end{aligned}$$

The general Baskakov type operators for \(x\in I\) are defined as

$$\begin{aligned} (B^c_\lambda f)(x) = \sum _{k=0}^\infty a^c_{\lambda ,k}(x)F_{\lambda ,k}(f), \end{aligned}$$
(2.1)

where

$$\begin{aligned} a^c_{\lambda ,k}(x)=\frac{(-x)^k}{k!} \phi _{c,\lambda }^{(k)}(x), \ \ F_{\lambda ,k}(f)=f\left( \frac{k}{\lambda }\right) . \end{aligned}$$

and \(\phi _{c,\lambda }(x)=(1+cx)^{-\lambda /c}, c\ge 0.\)

In particular if \(c=1\), \(\phi _{1,\lambda }(x)=(1+x)^{-\lambda }\) in this case, we get the Baskakov operators, and if \(c=0\), \(\phi _{0,\lambda }(x)=e^{-\lambda x}\) is a limit for \(c\rightarrow 0^+\) and we obtain the Szász–Mirakyan operators.

Remark 2.2

By simple computation in (2.1), we have

$$\begin{aligned} b_{F_{\lambda ,k}}=F_{\lambda ,k}(e_1)=\frac{k}{\lambda }, \ \ \mu _r^{F_{\lambda ,k}}:= F_{\lambda ,k}(e_1-b_{F_{\lambda ,k}}e_0)^r=0, r=1,2,\ldots \end{aligned}$$

Applying [7, Theorem 2.1], we get the estimation of \(P_\lambda ^\beta \) and \(B^c_\lambda \).

The Kantorovich version of the Szász–Mirakyan operators is defined by

$$\begin{aligned} (K_\lambda f)(x) = \sum _{k=0}^\infty s_k(\lambda x)H_{\lambda ,k}(f), \end{aligned}$$
(2.2)

where \(s_k(\lambda x)=e^{-\lambda x}\frac{(\lambda x)^k}{k!}\), and \(H_{\lambda ,k}(f)=\lambda \int _{k/\lambda }^{(k+1)/\lambda } f(t)\textrm{d}t\).

Remark 2.3

Following the computation given in [8] for (2.2), we have:

$$\begin{aligned} b_{H_{\lambda ,k}}=H_{\lambda ,k}(e_1)=\frac{k}{\lambda }+\frac{1}{2\lambda }, \ \ \mu _2^{H_{\lambda ,k}}=\frac{1}{12 \lambda ^2}, \mu _3^{H_{\lambda ,k}}=0, \mu _4^{H_{\lambda ,k}}=\frac{1}{80 \lambda ^4}. \end{aligned}$$

2.1 Difference with Discrete Operator

In the following two theorems, we find the difference between semi-exponential Post–Widder operators and the generalized Baskakov type operators.

Theorem 2.4

If D(I) be the set of all functions in C(I) for which the two operators \(P_\lambda ^\beta ,B^c_\lambda \in C(I)\) are defined and \(f^{\prime \prime }\in C_{B}(I)\), then

$$\begin{aligned} \vert ((P_\lambda ^\beta -B^c_\lambda )f)(x)\vert\le & {} \left( \frac{x^2}{2\lambda }+\frac{x^3 \beta }{2\lambda ^2}\right) \vert \vert f^{\prime \prime }\vert \vert +2\omega \left( f,\sqrt{\frac{x(1+cx)}{\lambda }}\right) \\ {}{} & {} +2\omega \left( f,\frac{x^{3/2}\sqrt{\beta }(x \beta +1)^{1/2}}{\lambda }\right) , \end{aligned}$$

for \(c=0\) and \(c=1\), we obtain the difference of semi Post–Widder operators with Szász–Mirakyan and Baskakov operators, respectively.

Proof

Applying Remarks 2.1 and 2.2 to the aforementioned theorem, we have

$$\begin{aligned} \vert ((P_\lambda ^\beta -B^c_\lambda )f)(x)\vert \le e_{\lambda ,\beta }(x) \vert \vert f^{\prime \prime }\vert \vert +2\omega \left( f,\delta _1\right) +2\omega \left( f,\delta _2\right) , \end{aligned}$$

where

$$\begin{aligned} e_{\lambda ,\beta }(x)= & {} \frac{1}{2}\displaystyle \sum _{k=0}^\infty \left( a^c_{\lambda ,k}(x)\mu _2^{F_{\lambda ,k}}+s_{k}(\beta x)\mu _2^{J_{\lambda ,k}}\right) \\= & {} \frac{1}{2}\displaystyle \sum _{k=0}^\infty s_{k}(\beta x)\frac{x^2}{\lambda ^2}(\lambda +k)=\frac{x^2}{2\lambda }+\frac{x^3 \beta }{2\lambda ^2}, \\ \delta _1(x)= & {} \left( \displaystyle \sum _{k=0}^\infty a^c_{\lambda ,k}(x)\left( b_{F_{\lambda ,k}}-x\right) ^2\right) ^{1/2}\\= & {} \left( \displaystyle \sum _{k=0}^\infty a^c_{\lambda ,k}(x)\left( \frac{k}{\lambda }-x\right) ^2\right) ^{1/2}=\sqrt{\frac{x(1+cx)}{\lambda }} \end{aligned}$$

and

$$\begin{aligned} \delta _{2,\beta }(x)= & {} \left( \displaystyle \sum _{k=0}^\infty s_{k}(\beta x)\left( b_{J_{\lambda ,k}}-x\right) ^2\right) ^{1/2}\\= & {} \left( \displaystyle \sum _{k=0}^\infty s_{k}(\beta x)\left( \frac{x}{\lambda }(\lambda +k)-x\right) ^2\right) ^{1/2}=\left( \frac{x^2}{\lambda ^2}\displaystyle \sum _{k=0}^\infty s_{k}(\beta x)k^2\right) ^{1/2}\\= & {} \frac{x^{3/2}\sqrt{\beta (x \beta +1)}}{\lambda }. \end{aligned}$$

This completes the proof. \(\square \)

Theorem 2.5

If D(I) be the set of all functions in C(I) for which the two operators \(P_\lambda ^\beta ,B^c_\lambda \in C(I)\) are defined with \(f^{(i)}\in C_{B}(I), i=2,3,4\), then

$$\begin{aligned} \vert ((P_\lambda ^\beta -B^c_\lambda )f)(x)\vert\le & {} \left( \frac{x^4}{8\lambda ^3}+\frac{x^4}{4\lambda ^4}+\frac{x^5\beta }{8\lambda ^4}\right) \vert \vert f^{iv}\vert \vert +\left( \frac{x^3}{3\lambda ^2}+\frac{x^4\beta }{3\lambda ^3}\right) \vert \vert f^{\prime \prime \prime }\vert \vert \\{} & {} +\left( \frac{x^2}{2\lambda } +\frac{x^3\beta }{2\lambda ^2}\right) \vert \vert f^{\prime \prime }\vert \vert \\ {}{} & {} +2\omega \left( f,\sqrt{\frac{x(1+cx)}{\lambda }}\right) +2\omega \left( f,\frac{x^{3/2}\sqrt{\beta }(x \beta +1)^{1/2}}{\lambda }\right) , \end{aligned}$$

for \(c=0\) and \(c=1\), we obtain the difference of semi-exponential Post–Widder operators with the Szász–Mirakyan and the Baskakov operators, respectively.

Proof

Following [8, Theorem 2] and using Remarks 2.1 and 2.2, we have

$$\begin{aligned} \vert ((P_\lambda ^\beta -B^c_\lambda )f)(x)\vert\le & {} e_{\lambda ,\beta }^1(x) \vert \vert f^{iv}\vert \vert +e_{\lambda ,\beta }^2(x) \vert \vert f^{\prime \prime \prime }\vert \vert +e_{\lambda ,\beta }^3(x) \vert \vert f^{\prime \prime }\vert \vert \\{} & {} +2\omega \left( f,\delta _1\right) +2\omega \left( f,\delta _2\right) ,\\ e_{\lambda ,\beta }^1(x)= & {} \frac{1}{4!}\displaystyle \sum _{k=0}^\infty ( a^c_{\lambda ,k}(x) \mu _4^{F_{\lambda ,k}}+s_{k}(\beta x) \mu _4^{J_{\lambda ,k}})\\= & {} \frac{1}{24}\displaystyle \sum _{k=0}^\infty s_{k}(\beta x)\mu _4^{J_{\lambda ,k}}=\frac{x^4}{8\lambda ^4}\displaystyle \sum _{k=0}^\infty s_{k}(\beta x)(\lambda +k+2)\\= & {} \frac{(\lambda +2)x^4}{8\lambda ^4}+\frac{x^5\beta }{8\lambda ^4}\\ e_{\lambda ,\beta }^2(x)= & {} \frac{1}{3!}\left| \displaystyle \sum _{k=0}^\infty a^c_{\lambda ,k}(x)\mu _3^{F_{\lambda ,k}} -\displaystyle \sum _{k=0}^\infty s_{k}(\beta x)\mu _3^{J_{\lambda ,k}}\right| \\= & {} \frac{1}{6}\displaystyle \sum _{k=0}^\infty s_{k}(\beta x)\mu _3^{J_{\lambda ,k}}\\= & {} \frac{x^3}{3\lambda ^3}\displaystyle \sum _{k=0}^\infty s_{k}(\beta x)(\lambda +k)=\frac{x^3}{3\lambda ^2}+\frac{x^4\beta }{3\lambda ^3}. \end{aligned}$$

Finally

$$\begin{aligned} e_{\lambda ,\beta }^3(x)= & {} \frac{1}{2!}\left| \displaystyle \sum _{k=0}^\infty a^c_{\lambda ,k}(x)\mu _2^{F_{\lambda ,k}}-\displaystyle \sum _{k=0}^\infty s_{k}(\beta x) \mu _2^{J_{\lambda ,k}}\right| \\= & {} \frac{1}{2}\displaystyle \sum _{k=0}^\infty s_{k}(\beta x) \mu _2^{J_{\lambda ,k}}=\frac{x^2}{2\lambda }+\frac{x^3 \beta }{2\lambda ^2}. \end{aligned}$$

The estimates of \(\delta _1\) and \(\delta _2\) can be obtained as in Theorem 2.4. Collecting the above estimates, the result follows. \(\square \)

2.2 Difference with Integral Operator

In the following two theorems, we provide the difference of semi-exponential Post–Widder operators with the generalized Szász–Kantorovich operators.

Theorem 2.6

If D(I) be the set of all functions in C(I) for which the two operators \(P_\lambda ^\beta ,K_\lambda \in C(I)\) hold with \(f^{\prime \prime }\in C_{B}(I)\), then

$$\begin{aligned} \vert ((P_\lambda ^\beta -K_\lambda )f)(x)\vert\le & {} \left( \frac{1}{24\lambda ^2}+\frac{x^2}{2\lambda }+\frac{x^3 \beta }{2\lambda ^2}\right) \vert \vert f^{\prime \prime }\vert \vert +2\omega \left( f,\frac{\sqrt{4 \lambda x+1}}{2\lambda }\right) \\ {}{} & {} +2\omega \left( f,\frac{x^{3/2}\sqrt{\beta }(x \beta +1)^{1/2}}{\lambda }\right) . \end{aligned}$$

Proof

Applying Remarks 2.3 and 2.1 to the aforementioned theorem, we have

$$\begin{aligned} \vert ((P_\lambda ^\beta -K_\lambda )f)(x)\vert \le d_{\lambda ,\beta }(x) \vert \vert f^{\prime \prime }\vert \vert +2\omega \left( f,\widehat{\delta }_1\right) +2\omega \left( f,\widehat{\delta }_2\right) , \end{aligned}$$

where

$$\begin{aligned} d_{\lambda ,\beta }(x)= & {} \frac{1}{2}\displaystyle \sum _{k=0}^\infty \left( s_{k}(\lambda x)\mu _2^{H_{\lambda ,k}}+s_{k}(\beta x)\mu _2^{J_{\lambda ,k}}\right) \\= & {} \frac{1}{24\lambda ^2}+\frac{x^2}{2\lambda }+\frac{x^3 \beta }{2\lambda ^2},\\ \widehat{\delta }_1(x)= & {} \left( \displaystyle \sum _{k=0}^\infty s_{k}(\lambda x)\left( b_{H_{\lambda ,k}}-x\right) ^2\right) ^{1/2}\\= & {} \left( \displaystyle \sum _{k=0}^\infty s_{k}(\lambda x)\left( \frac{k}{\lambda }+\frac{1}{2\lambda }-x\right) ^2\right) ^{1/2}=\frac{\sqrt{4 \lambda x+1}}{2\lambda } \end{aligned}$$

and

$$\begin{aligned} \widehat{\delta }_{2,\beta }(x)= & {} \left( \displaystyle \sum _{k=0}^\infty s_{k}(\beta x)\left( b_{J_{\lambda ,k}}-x\right) ^2\right) ^{1/2}\\= & {} \frac{x^{3/2}\sqrt{\beta (x \beta +1)}}{\lambda }. \end{aligned}$$

This completes the proof. \(\square \)

Theorem 2.7

If D(I) be the set of all functions in C(I) for which the two operators \(P_\lambda ^\beta ,K_\lambda \in C(I)\) are defined with \(f^{(i)}\in C_{B}(I), i=2,3,4\), then

$$\begin{aligned} \vert ((P_\lambda ^\beta -K_\lambda )f)(x)\vert\le & {} \left( \frac{1}{1920 \lambda ^4}+\frac{(\lambda +2)x^4}{8\lambda ^4}+\frac{x^5\beta }{8\lambda ^4}\right) \vert \vert f^{iv}\vert \vert \\{} & {} +\left( \frac{x^3}{3\lambda ^2} +\frac{x^4\beta }{3\lambda ^3}\right) \vert \vert f^{\prime \prime \prime }\vert \vert \\ {}{} & {} +\left( \frac{1}{24\lambda ^2}+\frac{x^2}{2\lambda }+\frac{x^3 \beta }{2\lambda ^2}\right) \vert \vert f^{\prime \prime }\vert \vert \\{} & {} +2\omega \left( f,\frac{\sqrt{4 \lambda x+1}}{2\lambda }\right) \\ {}{} & {} +2\omega \left( f,\frac{x^{3/2}\sqrt{\beta }(x \beta +1)^{1/2}}{\lambda }\right) . \end{aligned}$$

Proof

Following [8, Theorem 2] and using Remarks 2.1 and 2.2, we have:

$$\begin{aligned} \vert ((P_\lambda ^\beta -K_\lambda )f)(x)\vert\le & {} d_{\lambda ,\beta }^1(x) \vert \vert f^{iv}\vert \vert +d_{\lambda ,\beta }^2(x) \vert \vert f^{\prime \prime \prime }\vert \vert +d_{\lambda ,\beta }^3(x) \vert \vert f^{\prime \prime }\vert \vert \\ {}{} & {} +2\omega \left( f,\widehat{\delta }_1\right) +2\omega \left( f,\widehat{\delta }_2\right) ,\\ d_{\lambda ,\beta }^1(x)= & {} \frac{1}{4!}\displaystyle \sum _{k=0}^\infty ( s_{k}(\lambda x) \mu _4^{H_{\lambda ,k}}+s_{k}(\beta x) \mu _4^{J_{\lambda ,k}})\\= & {} \frac{1}{1920 \lambda ^4}+\frac{(\lambda +2)x^4}{8\lambda ^4}+\frac{x^5\beta }{8\lambda ^4}\\ d_{\lambda ,\beta }^2(x)= & {} \frac{1}{3!}\left| \displaystyle \sum _{k=0}^\infty s_{k}(\lambda x)\mu _3^{H_{\lambda ,k}} -\displaystyle \sum _{k=0}^\infty s_{k}(\beta x)\mu _3^{J_{\lambda ,k}}\right| \\= & {} \frac{x^3}{3\lambda ^2}+\frac{x^4\beta }{3\lambda ^3}. \end{aligned}$$

Next

$$\begin{aligned} d_{\lambda ,\beta }^3(x)= & {} \frac{1}{2!}\left| \displaystyle \sum _{k=0}^\infty s_{k}(\lambda x)\mu _2^{H_{\lambda ,k}}-\displaystyle \sum _{k=0}^\infty s_{k}(\beta x) \mu _2^{J_{\lambda ,k}}\right| \\\le & {} \frac{1}{24\lambda ^2}+\frac{x^2}{2\lambda }+\frac{x^3 \beta }{2\lambda ^2}. \end{aligned}$$

The estimates of \(\widehat{\delta }_1\) and \(\widehat{\delta }_2\) can be obtained as in Theorem 2.6. Collecting the above estimates, the result follows. \(\square \)

2.3 Composition

Proposition 2.8

Composition of semi-exponential Post–Widder and the Szász–Mirakyan operators provides the new operator

$$\begin{aligned} (O_\lambda f)(x)=\frac{1}{ e^{\beta x}}\sum _{s=0}^\infty \sum _{m=s}^\infty \frac{\beta ^{m-s}(\lambda +m-s)_s}{(m-s)!s!}\frac{x^m}{(1 +x)^{\lambda +m}}f\left( \frac{s}{\lambda }\right) , \end{aligned}$$

which may be considered as representation of semi-exponential Baskakov operator, slightly different from [2]. If \(\beta =0\), then \(m=s\) and we get the Baskakov operators.

Proof

By definition

$$\begin{aligned} ((P_\lambda ^\beta \circ S_\lambda ) f)(x)= & {} \frac{\lambda ^\lambda }{x^\lambda e^{\beta x}}\sum _{s=0}^\infty \sum _{k=0}^\infty \frac{\left( \lambda \beta \right) ^k}{k!\varGamma (\lambda +k)}f\left( \frac{s}{\lambda }\right) \\{} & {} \times \int _0^\infty e^{-\lambda t/x} t^{\lambda +k-1}e^{-\lambda t}\frac{(\lambda t)^s}{s!}\textrm{d}t\\= & {} \frac{\lambda ^\lambda }{x^\lambda e^{\beta x}}\sum _{s=0}^\infty \sum _{k=0}^\infty \frac{\left( \lambda \beta \right) ^k\lambda ^s}{k!s!\varGamma (\lambda +k)}f\left( \frac{s}{\lambda }\right) \\{} & {} \times \int _0^\infty e^{-t(\lambda +\lambda /x)} t^{\lambda +k+s-1}\textrm{d}t\\= & {} \frac{\lambda ^\lambda }{x^\lambda e^{\beta x}}\sum _{s=0}^\infty \sum _{k=0}^\infty \frac{\left( \lambda \beta \right) ^k\lambda ^s}{k!s!\varGamma (\lambda +k)(\lambda +\lambda /x)^{\lambda +k+s}}f\left( \frac{s}{\lambda }\right) \\{} & {} \times \int _0^\infty e^{-u} u^{\lambda +k+s-1}\textrm{d}u\\= & {} \frac{1}{ e^{\beta x}}\sum _{s=0}^\infty \sum _{k=0}^\infty \frac{\beta ^k\varGamma (\lambda +k+s)x^{k+s}}{k!s!\varGamma (\lambda +k)(1 +x)^{\lambda +k+s}}f\left( \frac{s}{\lambda }\right) \\= & {} \frac{1}{ e^{\beta x}}\sum _{s=0}^\infty \sum _{k=0}^\infty \frac{\beta ^k(\lambda +k)_sx^{k+s}}{k!s!(1 +x)^{\lambda +k+s}}f\left( \frac{s}{\lambda }\right) . \end{aligned}$$

This completes the proof. \(\square \)

Proposition 2.9

The composition of Post–Widder operators and the Szász–Kantorovich operators provides the Baskakov–Kantorovich operators (see [1])

$$\begin{aligned} (P_{\lambda }\circ K_\lambda )(x)=\lambda \sum _{k=0}^\infty a^1_{\lambda ,k}(x)\int _{k/\lambda }^{(k+1)/\lambda }f(y)\textrm{d}y, \end{aligned}$$

where \(a^1_{\lambda ,k}(x)=\sum _{k=0}^\infty {\lambda +k-1\atopwithdelims ()k}\frac{x^k}{(1+x)^{\lambda +k}}\) is defined in (2.1).

Proof

We can write

$$\begin{aligned} ((P_{\lambda }\circ K_\lambda )f)(x)= & {} \sum _{k=0}^\infty \frac{\lambda ^\lambda }{x^\lambda } \frac{1}{\varGamma (\lambda )}\int _0^\infty e^{-\lambda t/x} t^{\lambda -1} e^{-\lambda t}\frac{(\lambda t)^k}{k!}H_{\lambda ,k}(f)\textrm{d}t\\= & {} \frac{\lambda ^\lambda }{x^\lambda } \frac{1}{\varGamma (\lambda )}\sum _{k=0}^\infty \frac{\lambda ^k}{k!}H_{\lambda ,k}(f)\int _0^\infty e^{-(\frac{\lambda }{x}+\lambda )t}t^{\lambda +k-1} \textrm{d}t\\= & {} \frac{\lambda ^\lambda }{x^\lambda } \frac{1}{\varGamma (\lambda )}\sum _{k=0}^\infty \frac{\lambda ^k}{k!}H_{\lambda ,k}(f)\frac{x^{\lambda +k}}{(\lambda +\lambda x)^{\lambda +k}}\int _0^\infty e^{-u}u^{\lambda +k-1} \textrm{d}u\\= & {} \sum _{k=0}^\infty v_{\lambda ,k}(x)H_{\lambda ,k}(f). \end{aligned}$$

This completes the proof of the proposition. \(\square \)

3 Modified Semi-exponential Post–Widder Operators

Let us consider the following modified form of the semi-exponential Post–Widder operators:

$$\begin{aligned} (\widehat{P}_\lambda ^\beta f)(x)=\frac{\lambda ^\lambda }{(v_{\lambda }^{\beta }(x))^\lambda e^{\beta v_{\lambda }^{\beta }(x)}}\sum _{k=0}^\infty \frac{\left( \lambda \beta \right) ^k}{k!\varGamma (\lambda +k)}\int _0^\infty e^{-\lambda t/v_{\lambda }^{\beta }(x)} t^{\lambda +k-1} f(t)\textrm{d}t, \end{aligned}$$

where

$$\begin{aligned} v_{\lambda }^{\beta }(x)=\frac{-\lambda +\sqrt{\lambda ^2+4\lambda \beta x}}{2\beta }, \beta \ne 0. \end{aligned}$$

For \(\lambda >4\beta x\), we may write

$$\begin{aligned} v_{\lambda }^{\beta }(x)= & {} \frac{-\lambda +\sqrt{\lambda ^2+4\lambda \beta x}}{2\beta }\\= & {} \frac{1}{2\beta }\left[ -\lambda +\lambda \left( 1+\frac{4\beta x}{\lambda }\right) ^{1/2}\right] \\= & {} \frac{1}{2\beta }\left[ -\lambda +\lambda \left( 1+\frac{2\beta x}{\lambda }-\frac{2\beta ^2x^2}{\lambda ^2}+\frac{4\beta ^3x^3}{\lambda ^3}-\frac{10\beta ^4x^4}{\lambda ^4}+\cdots \right) \right] \\= & {} \left[ x-\frac{\beta x^2}{\lambda }+\frac{2\beta ^2x^3}{\lambda ^2}-\frac{5\beta ^3x^4}{\lambda ^3}+\cdots \right] . \end{aligned}$$

Also, we can calculate

$$\begin{aligned} \lim _{\beta \rightarrow 0}v_{\lambda }^{\beta }(x)= & {} x\\ \lim _{\lambda \rightarrow \infty }v_{\lambda }^{\beta }(x)= & {} x. \end{aligned}$$

We observe that the operators \((\widehat{P}_\lambda ^\beta f)(x)=(P_{\lambda }^{\beta }f)(v_{\lambda }^{\beta }(x))\) preserve constants and linear functions, but we do not capture the exact Post–Widder operators (1.3). Also, these operators are neither exponential nor semi-exponential type operators as, for these operators, condition (1.2) is not satisfied for \(\beta \ge 0\).

Lemma 3.1

The moment producing function of \((\widehat{P}_\lambda ^\beta f)(x)\) for A in some neighborhood of zero is given as

$$\begin{aligned} (\widehat{P}_\lambda ^\beta e^{At})(x)= & {} \frac{\lambda ^\lambda }{(\lambda -A v_{\lambda }^{\beta }(x))^\lambda }\exp \left( \frac{A[v_{\lambda }^{\beta }(x)]^2\beta }{\lambda -A v_{\lambda }^{\beta }(x)} \right) . \end{aligned}$$

In particular with \(e_s(x)=x^s\), we have the representation

$$\begin{aligned} (\widehat{P}_\lambda ^\beta e_0)(x)= & {} 1\\ (\widehat{P}_\lambda ^\beta e_1)(x)= & {} x\\ (\widehat{P}_\lambda ^\beta e_2)(x)= & {} x^2+\frac{\sqrt{4\lambda \beta x+\lambda ^2}}{\lambda \beta }x-\frac{2x}{\beta }+\frac{\sqrt{4\lambda \beta x+\lambda ^2}}{2 \beta ^2}-\frac{\lambda }{2\beta ^2}\\ (\widehat{P}_\lambda ^\beta e_3)(x)= & {} x^3+\frac{3\sqrt{4\lambda \beta x+\lambda ^2}}{\lambda \beta }x^2-\frac{6}{\beta }x^2+\frac{6}{\lambda \beta }x^2+\frac{3\sqrt{4\lambda \beta x+\lambda ^2}}{2{\beta }^2}x\\{} & {} -\frac{5\sqrt{4\lambda \beta x+\lambda ^2}}{\lambda {\beta }^2}x+\frac{9}{{\beta }^2}x-\frac{3\lambda }{2{\beta }^2}x-\frac{2\sqrt{4\lambda \beta x+\lambda ^2}}{{\beta }^3}+\frac{2\lambda }{{\beta }^3}\\ (\widehat{P}_\lambda ^\beta e_4)(x)= & {} x^4+\frac{6\sqrt{4\lambda \beta x+\lambda ^2}}{\lambda \beta }x^3-\frac{12}{\beta }x^3+\frac{36}{\lambda \beta }x^3+\frac{3\sqrt{4\lambda \beta x+\lambda ^2}}{{\beta }^2}x^2\\{} & {} -\frac{32\sqrt{4\lambda \beta x+\lambda ^2}}{\lambda {\beta }^2}x^2+\frac{12\sqrt{4\lambda \beta x+\lambda ^2}}{{\lambda }^2{\beta }^2}x^2+\frac{63}{{\beta }^2}x^2-\frac{54}{\lambda {\beta }^2}x^2\\{} & {} -\frac{3\lambda }{{\beta }^2}x^2-\frac{17\sqrt{4\lambda \beta x+\lambda ^2}}{{\beta }^3}x+\frac{30\sqrt{4\lambda \beta x+\lambda ^2}}{\lambda {\beta }^3}x-\frac{48}{{\beta }^3}x+\frac{20\lambda }{{\beta }^3}x\\{} & {} -\frac{3\lambda \sqrt{4\lambda \beta x+\lambda ^2}}{2{\beta }^4}-\frac{9\lambda }{{\beta }^4}+\frac{3{\lambda }^2}{2{\beta }^4}. \end{aligned}$$

Proof

By the definition of the operators \(\widehat{P}_\lambda ^\beta \), we have

$$\begin{aligned} (\widehat{P}_\lambda ^\beta e^{At})(x)= & {} \frac{\lambda ^\lambda }{[v_{\lambda }^{\beta }(x)]^\lambda e^{\beta v_{\lambda }^{\beta }(x)}}\sum _{k=0}^\infty \frac{\left( \lambda \beta \right) ^k}{k!\varGamma (\lambda +k)}\int _0^\infty e^{-(\lambda -A v_{\lambda }^{\beta }(x))t/v_{\lambda }^{\beta }(x)} t^{\lambda +k-1}\textrm{d}t\\= & {} \frac{\lambda ^\lambda }{(\lambda -A v_{\lambda }^{\beta }(x))^\lambda }e^{-\beta v_{\lambda }^{\beta }(x)}\sum _{k=0}^\infty \frac{\left( \frac{\lambda \beta v_{\lambda }^{\beta }(x)}{\lambda -A v_{\lambda }^{\beta }(x)} \right) ^k}{k!}\\= & {} \frac{\lambda ^\lambda }{(\lambda -A v_{\lambda }^{\beta }(x))^\lambda }\exp \left( \frac{A[v_{\lambda }^{\beta }(x)]^2\beta }{\lambda -A v_{\lambda }^{\beta }(x)} \right) . \end{aligned}$$

Using the following connection between moments and moment generating function:

$$\begin{aligned} (\widehat{P}_\lambda ^\beta e_m)(x)= & {} \left[ \frac{\partial ^m}{\partial A^m}\frac{\lambda ^\lambda }{(\lambda -A v_{\lambda }^{\beta }(x))^\lambda }\exp \left( \frac{A[v_{\lambda }^{\beta }(x)]^2\beta }{\lambda -A v_{\lambda }^{\beta }(x)} \right) \right] _{A=0}, \end{aligned}$$

we may get the moments by simple computation. \(\square \)

Lemma 3.2

If \(\mu _{\lambda ,m}^\beta (x)=(\widehat{P}_{\lambda }^{\beta }(e_1-xe_0)^m)(x)\), then we have

$$\begin{aligned} \mu _{\lambda ,0}^\beta (x)= & {} 1\\ \mu _{\lambda ,1}^\beta (x)= & {} 0\\ \mu _{\lambda ,2}^\beta (x)= & {} \frac{x\sqrt{4\lambda \beta x+\lambda ^2}}{\lambda \beta }-\frac{2x}{\beta }+\frac{\sqrt{4\lambda \beta x+\lambda ^2}}{2 \beta ^2}-\frac{\lambda }{2\beta ^2}\\ \mu _{\lambda ,3}^\beta (x)= & {} \frac{6 x^2}{\beta \lambda }-\frac{5 x \sqrt{4\lambda \beta x+\lambda ^2}}{\beta ^2 \lambda }+\frac{9 x}{\beta ^2}-\frac{2 \sqrt{4\lambda \beta x+\lambda ^2}}{\beta ^3}+\frac{2 \lambda }{\beta ^3}\\ \mu _{\lambda ,4}^\beta (x)= & {} \frac{12 x^3}{\beta \lambda } -\frac{12 x^2 \sqrt{4\lambda \beta x+\lambda ^2}}{\beta ^2 \lambda }+\frac{12 x^2\sqrt{4\lambda \beta x+\lambda ^2}}{\beta ^2 \lambda ^2}+\frac{27 x^2}{\beta ^2}-\frac{54 x^2}{\beta ^2 \lambda }\\{} & {} +\frac{9\sqrt{4\lambda \beta x+\lambda ^2}}{\beta ^4}-\frac{9 x \sqrt{4\lambda \beta x+\lambda ^2}}{\beta ^3}+\frac{30 x \sqrt{4\lambda \beta x+\lambda ^2}}{\beta ^3 n}\\{} & {} +\frac{12 \lambda x}{\beta ^3}-\frac{48 x}{\beta ^3} -\frac{3 \lambda \sqrt{4\lambda \beta x+\lambda ^2}}{2 \beta ^4}+\frac{3 \lambda ^2}{2 \beta ^4}-\frac{9 \lambda }{\beta ^4}. \end{aligned}$$

3.1 Weighted Convergence

According to [5], we consider the following spaces:

$$\begin{aligned} B_{e_2}\left( I \right) =\left\{ f:{I}\rightarrow {I}:\left| f\left( x\right) \right| \le M_{f}(1+e_2(x)) \right\} , \end{aligned}$$

where the constant \(M_{f}\) depends on f,

$$\begin{aligned} C_{ e_2}\left( {R^+} \right) =B_{e_2 }\left( {I} \right) \cap C\left( {I} \right) , \end{aligned}$$

and

$$\begin{aligned} C_{e_2 }^{*}\left( {I} \right) =\left\{ f\in C_{e_2}\left( {I} \right) :\lim \limits _{x \rightarrow \infty }\frac{ f\left( x\right) }{1+e_2 \left( x\right) } \text{ exists } \text{ and } \text{ it } \text{ is } \text{ finite } \right\} . \end{aligned}$$

If the space \(B_{e_2}\left( {I} \right) \) is yielded with the norm \(\left\| .\right\| _{e_2 }\) defined by

$$\begin{aligned} \left\| f\right\| _{e_2 }=\sup \limits _{x\in {R^+} }\frac{\left| f\left( x\right) \right| }{1+e_2(x) }, \end{aligned}$$

then the same norm is considered in both of the spaces defined above.

The aim of the section is to achieve approximating theorems including Voronovskaya-type result in the aforementioned spaces.

Theorem A

[5] Let \(\left( A_{n}\right) _{n\ge 1}\) be a sequence of linear positive operators mapping \(C_{e_2 }\left( {I} \right) \) into \(B_{e_2 }\left( {I} \right) \). If

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }\left\| A_{n}e_{v}-e_{v}\right\| _{e_2}=0, v=0,1,2, \end{aligned}$$

then, for \(f\in C_{e_2 }^{*}\left( {I} \right) \), we have

$$\begin{aligned} \lim _{n\rightarrow \infty }\left\| A_{n}f-f\right\| _{e_2 }=0. \end{aligned}$$

Now, we apply the theorem to our operators.

Theorem 3.3

Let \(f\in C_{e_2}^{*}\left( {I}\right) \), then the following holds true:

$$\begin{aligned} \lim \limits _{\lambda \rightarrow \infty }\left\| \widehat{P}_{\lambda }^{\beta }f-f\right\| _{e_2 }=0. \end{aligned}$$

Proof

As we mentioned above, we shall examine the assumptions of Theorem A, applying them to the operators \(\widehat{P}_{\lambda }^{\beta }\). According to Lemma 3.1, for the operators \( \widehat{P}_{\lambda }^{\beta }\) on \(C_{e_2}\left( {I} \right) \), the result holds true for \(v=0,1\). Next, for \(v=2\), we obtain

$$\begin{aligned} \left\| \widehat{P}_{\lambda }^{\beta }e_{2}-e_{2}\right\| _{e_2 }= & {} \sup \limits _{x\in {I} }\frac{\left| \left( \widehat{ P}_{\lambda }^{\beta }e_{2}\right) \left( x\right) -x^{2}\right| }{1+x^{2}} \\= & {} \sup \limits _{x\in {I} }\frac{\left| \frac{x\sqrt{4\lambda \beta x+\lambda ^2}}{\lambda \beta }-\frac{2x}{\beta }+\frac{\sqrt{4\lambda \beta x+\lambda ^2}}{2 \beta ^2}-\frac{\lambda }{2\beta ^2}\right| }{1+x^{2}}. \end{aligned}$$

We have to prove that the above expression tends to zero as \(\lambda \rightarrow \infty \).

First, we notice that for \(z\in {I}\) and \(\lambda >0\), we have \((z+\lambda )^2\ge (2z+\lambda )\lambda \). Now, we substitute \(z=2\beta x\) which is no-negative by our assumptions, and we get

$$\begin{aligned} (2\beta x+\lambda )^2\ge \lambda (4\beta x+\lambda ). \end{aligned}$$

Multiplying by \(\lambda (4\beta x+\lambda ) >0\) we have

$$\begin{aligned} (\lambda ^2+4\lambda \beta x)(2\beta x+\lambda )^2\ge \lambda ^2(4\beta x+\lambda )^2. \end{aligned}$$

Due to monotonicity of the square root, we achieve the following estimation:

$$\begin{aligned} \sqrt{4\lambda \beta x+\lambda ^2}(2\beta x+\lambda )\ge \lambda (4\beta x+\lambda ), \end{aligned}$$

which is equivalent to the inequality

$$\begin{aligned} \frac{x\sqrt{4\lambda \beta x+\lambda ^2}}{\lambda \beta }-\frac{2x}{\beta }+\frac{\sqrt{4\lambda \beta x+\lambda ^2}}{2 \beta ^2}-\frac{\lambda }{2\beta ^2}\ge 0. \end{aligned}$$

Now, we proceed to the estimation from above. For \(u\ge -1\) and \(r\in [0,1]\), we have Bernoulli’s inequality as follows:

$$\begin{aligned} (1+u)^r\le 1+ru. \end{aligned}$$

Substituting \(u=\frac{4\beta x}{\lambda }\) and \(r=\frac{1}{2}\), we get

$$\begin{aligned} \left( 1+\frac{4\beta x}{\lambda }\right) ^{\frac{1}{2}}\le 1+\frac{2\beta x}{\lambda } \end{aligned}$$
(3.1)

for \(x\ge 0, \beta >0\) and \(\lambda >0\). Now, using (3.1), we can estimate the following expression:

$$\begin{aligned}{} & {} \frac{x\sqrt{4\lambda \beta x+\lambda ^2}}{\lambda \beta }-\frac{2x}{\beta }+\frac{\sqrt{4\lambda \beta x+\lambda ^2}}{2 \beta ^2}-\frac{\lambda }{2\beta ^2}\\{} & {} \quad =\frac{x}{\beta }\left( 1+\frac{4\beta x}{\lambda }\right) ^{1/2}-\frac{2x}{\beta }+\frac{\lambda }{2\beta ^2}\left( \left( 1+\frac{4\beta x}{\lambda }\right) ^{1/2}-1\right) \le \frac{2x^2}{\lambda }. \end{aligned}$$

Hence, we get the estimation

$$\begin{aligned} 0\le \frac{\frac{x\sqrt{4\lambda \beta x+\lambda ^2}}{\lambda \beta }-\frac{2x}{\beta }+\frac{\sqrt{4\lambda \beta x+\lambda ^2}}{2 \beta ^2}-\frac{\lambda }{2\beta ^2}}{1+x^{2}}\le \frac{2}{\lambda }, \end{aligned}$$

which proves our assertion. \(\square \)

Theorem 3.4

Let f and \(f^{\prime \prime }\) belong to \(C_{e_2 }^{*}\left( {I} \right) \), then, for \(x\in {I} \) and \(\lambda >4\beta x\), one has

$$\begin{aligned}{} & {} \left| \lambda \left[ \left( \widehat{P}_{\lambda }^{\beta }f\right) \left( x\right) -f\left( x\right) \right] - \frac{x^2}{2}\left( 1-\frac{\beta ^2 x^2}{\lambda ^2}-\cdots \right) f^{\prime \prime }\left( x\right) \right| \\{} & {} \quad \le 2\lambda \omega \left( f^{\prime \prime },\frac{1}{\sqrt{\lambda }}\right) \left[ \mu _{\lambda ,2}^{\beta }\left( x\right) +\lambda {\mu _{\lambda ,4}^{\beta }\left( x\right) }\right] , \end{aligned}$$

where \(\omega \) is the classical modulus of continuity.

Proof

By Taylor’s expansion and applying the operator \(\widehat{P}_{\lambda }^{\beta }\), we can write that

$$\begin{aligned}{} & {} \left| \left( \widehat{P}_{\lambda }^{\beta }f\right) \left( x\right) -f\left( x\right) -( \widehat{P}_{\lambda }^{\beta }(e_1-xe_0)) \left( x\right) f^{\prime }\left( x\right) -\frac{( \widehat{P}_{\lambda }^{\beta }(e_1-xe_0)^2) \left( x\right) }{2} f^{\prime \prime }\left( x\right) \right| \\{} & {} \quad =\left| \left( \widehat{P}_{\lambda }^{\beta }h\left( t,x\right) \left( t-x\right) ^{2}\right) \left( x\right) \right| , \end{aligned}$$

where \(h\left( t,x\right) :=\frac{f^{\prime \prime }\left( \xi \right) -f^{\prime \prime }\left( x\right) }{2},\) and \(\xi \) lying between x and t. Thus, using Lemma 3.2 for \(\lambda >4\beta x\) and arguing as follows:

$$\begin{aligned} ( \widehat{P}_{\lambda }^{\beta }(e_1-x e_0)^2) \left( x\right)= & {} \frac{x\sqrt{4\lambda \beta x+\lambda ^2}}{\lambda \beta }-\frac{2x}{\beta }+\frac{\sqrt{4\lambda \beta x+\lambda ^2}}{2 \beta ^2}-\frac{\lambda }{2\beta ^2}\\= & {} \frac{x}{\beta }\left( 1+\frac{4\beta x}{\lambda }\right) ^{1/2}-\frac{2x}{\beta }+\frac{\lambda }{2\beta ^2}\left( 1+\frac{4\beta x}{\lambda }\right) ^{1/2}-\frac{\lambda }{2\beta ^2}\\= & {} \frac{x}{\beta }\left( 1+\frac{2\beta x}{\lambda }-\frac{2\beta ^2 x^2}{\lambda ^2}+\frac{4 \beta ^3 x^3}{\lambda ^3}-\frac{10 \beta ^4x^4}{\lambda ^4}+\cdots \right) -\frac{2x}{\beta }\\ {}{} & {} +\frac{\lambda }{2\beta ^2}\left( \frac{2\beta x}{\lambda }-\frac{2\beta ^2 x^2}{\lambda ^2}+\frac{4 \beta ^3 x^3}{\lambda ^3}-\frac{10 \beta ^4x^4}{\lambda ^4}+\cdots \right) \\= & {} \frac{x}{\beta }\left( -1+\frac{2\beta x}{\lambda }-\frac{2\beta ^2 x^2}{\lambda ^2}+\frac{4 \beta ^3 x^3}{\lambda ^3}-\frac{10 \beta ^4x^4}{\lambda ^4}+\cdots \right) \\ {}{} & {} +\frac{\lambda }{2\beta ^2}\left( \frac{2\beta x}{\lambda }-\frac{2\beta ^2 x^2}{\lambda ^2}+\frac{4 \beta ^3 x^3}{\lambda ^3}-\frac{10 \beta ^4x^4}{\lambda ^4}+\cdots \right) \\= & {} \frac{x^2}{\lambda }\left( 1-\frac{\beta ^2 x^2}{\lambda ^2}-\cdots \right) , \end{aligned}$$

we get

$$\begin{aligned}{} & {} \left| \lambda \left[ \left( \widehat{P}_{\lambda }^{\beta }f\right) \left( x\right) -f\left( x\right) \right] -\frac{x^2}{2}\left( 1-\frac{\beta ^2 x^2}{\lambda ^2}-\cdots \right) f^{\prime \prime }\left( x\right) \right| \\{} & {} \quad =\left| \lambda \left( \widehat{P}_{\lambda }^{\beta }h\left( t,x\right) \left( t-x\right) ^{2}\right) \left( x\right) \right| . \end{aligned}$$

Using the classical modulus of continuity, we get

$$\begin{aligned} \lambda \left( \widehat{P}_{\lambda }^{\beta }\left| h\left( t,x\right) \right| \left( t-x\right) ^{2}\right) \left( x\right)\le & {} 2\lambda \omega \left( f^{\prime \prime },\delta \right) \biggl [ \mu _{\lambda ,2}^{\beta }\left( x\right) +\frac{ {\mu _{\lambda ,4}^{\beta }\left( x\right) }}{\delta ^{2}}\biggr ]. \end{aligned}$$

Considering \(\delta =\lambda ^{-1/2}\), we obtain the required result. \(\square \)

Corollary 3.5

Let f and \(f^{\prime \prime }\in C_{e_2 }^{*}\left( {I} \right) \), then, for \(x\in {I} \), we have

$$\begin{aligned} \lim _{\lambda \rightarrow \infty } \lambda \left[ \left( \widehat{P}_{\lambda }^{\beta }f\right) \left( x\right) -f\left( x\right) \right] =x^2\frac{f^{\prime \prime }\left( x\right) }{2}. \end{aligned}$$

While, for the original operators, we have

$$\begin{aligned} \lim _{\lambda \rightarrow \infty }\lambda \left[ \left( {P}_{\lambda }^{\beta }f\right) \left( x\right) -f\left( x\right) \right] =\beta x^2 f^\prime (x)+x^2\frac{f^{\prime \prime }\left( x\right) }{2}. \end{aligned}$$

Theorem 3.6

For \(f\in C_B(I)\), there exists a constant \(C_1>0\), such that

$$\begin{aligned} \vert (\widehat{P}_\lambda ^\beta f)(x)-f(x)\vert\le & {} C_1\omega _2\biggl (f,\frac{x}{\sqrt{\lambda }}\left( 1-\frac{\beta ^2 x^2}{\lambda ^2}-\cdots \right) ^{1/2}\biggr ). \end{aligned}$$

Proof

Let \(h\in C_B^2(I)\) and \(x, \, t \in I.\) By Taylor’s expansion, we have

$$\begin{aligned} h(t) = h(x)+(t-x) \ h^\prime (x)+\int \limits _{x}^{t}(t-u) \ h^{\prime \prime }(u) \ \textrm{d}u. \end{aligned}$$

Hence, arguing as in Theorem 3.4, we have

$$\begin{aligned} \vert (\widehat{P}_\lambda ^\beta h)(x)-h(x)\vert= & {} \bigg ((\widehat{P}_\lambda ^\beta \bigg \vert \int _{x}^{t}(t-u) \ h^{\prime \prime }(u) \ \textrm{d}u\bigg \vert )(x)\bigg ) \\\le & {} (\widehat{P}_\lambda ^\beta (e_1-xe_0)^2)(x) \ \vert \vert h^{\prime \prime }\vert \vert \\= & {} \frac{x^2}{\lambda }\left( 1-\frac{\beta ^2 x^2}{\lambda ^2}-\cdots \right) \vert \vert h^{\prime \prime }\vert \vert . \end{aligned}$$

Due to constants preservation of \(\widehat{P}_\lambda ^\beta \), we have

$$\begin{aligned} \vert (\widehat{P}_\lambda ^\beta f)(x)\vert \le \vert \vert f\vert \vert . \end{aligned}$$

Therefore

$$\begin{aligned} \vert (\widehat{P}_\lambda ^\beta f)(x)-f(x)\vert\le & {} \vert (\widehat{P}_\lambda ^\beta (f-h))(x)-(f-h)(x)\vert +\vert (\widehat{P}_\lambda ^\beta h)(x)-h(x)\vert \\\le & {} 2 \vert \vert f-h\vert \vert + \frac{x^2}{\lambda }\left( 1-\frac{\beta ^2 x^2}{\lambda ^2}-\cdots \right) \vert \vert h^{\prime \prime }\vert \vert . \end{aligned}$$

Considering infimum over all \(h\in C_B^2(I)\), and using the inequality between K-functional and second-order moduli property given in [4], we obtain the assertion. \(\square \)

4 Graphical Representation

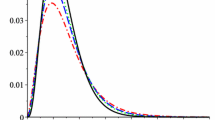
In this section, we use the Mathematica software to visualize the convergence of our operators. For \(t\in [0,20]\subset I\), we deal with the function \(f(t)=t^2+e^{-t}\) which belongs to the space \(C_{e_2}^{*}\left( {I}\right) \). Figure  performs six terms of the sequence of operators \(\widehat{P}_\lambda ^\beta \), for \(\lambda = 1,5,10,20,50,100\) and \(\beta =1\).

Fig. 1
figure 1

From the top \(\widehat{P}_{1}^{1}\), \(\widehat{P}_{5}^{1}\), \(\widehat{P}_{10}^{1}\), \(\widehat{P}_{20}^{1}\), \(\widehat{P}_{50}^{1}\), \(\widehat{P}_{100}^{1}\), f

Full size image

In Fig. , we enlarge the plots that we have above.

Fig. 2
figure 2

From the top \(\widehat{P}_{1}^{1}\), \(\widehat{P}_{5}^{1}\), \(\widehat{P}_{10}^{1}\), \(\widehat{P}_{20}^{1}\), \(\widehat{P}_{50}^{1}\), \(\widehat{P}_{100}^{1}\), f

Full size image

In Fig. , we can see the comparison between the convergence of the classical Post–Widder operators \(P_{\lambda }\), the semi-exponential Post–Widder operators \(P_{\lambda }^{\beta }\), and the modified semi-exponential Post–Widder operators \(\widehat{P}_\lambda ^\beta \). We propose the graphs of the following operators: \(P_5\), \(P_5^1\), \(\widehat{P}_5^1\) and the function f for \(x\in [0,20]\).

Fig. 3
figure 3

From the top \(P_{5}^{1}\), \(P_{5}\), \(\widehat{P}_{5}^{1}\), f

Full size image

The last picture demonstrates the approximation error for the operators \(\widehat{P}_5^1\), \(\widehat{P}_{50}^1\), \(\widehat{P}_{100}^1\). Observe that the difference \(d_{\lambda }(f)=\widehat{P}_{\lambda }^{\beta }(f)-f\) tends to 0 as \(\lambda \rightarrow +\infty \). In Fig. , we have the difference for \(\beta =1\) and \(\lambda =1,5,50\).

Fig. 4
figure 4

From the top \(d_{1}\), \(d_{5}\), \(d_{50}\)

Full size image