Partial Order in Matrix Nearrings

Abstract

Let N be a zero-symmetric (right) nearring with identity. We introduce a partial order in the matrix nearring corresponding to the partial order (defined by Pilz in Near-rings: the theory and its applications, North Holland, Amsterdam, 1983) in N. A positive cone in a matrix nearring is defined and a characterization theorem is obtained. For a convex ideal I in N, we prove that the corresponding ideal ${I^*}$ is convex in $M_n(N)$, and conversely, if I is convex in $M_n(N)$, then ${I_{*}}$ is convex in N. Consequently, we establish an order-preserving isomorphism between the p.o. quotient matrix nearrings $M_n(N)/{I^*}$ and $M_n(N')/{(I')^*}$ where I and $I'$ are the convex ideals of p.o. nearrings N and $N'$, respectively. Finally, we prove some properties of Archimedean ordering in matrix nearrings corresponding to those in nearrings.

1 Introduction

The notion of partial order in algebraic systems such such as groups, rings, and modules is known [6, 19]. However, the notion of partially ordered nearring (in short, p.o. nearring) was defined by Pilz [9, 10]. Some developments in the ideal theory of partially ordered nearrings and lattice ordered nearrings were found in [17, 18]. The purpose of this paper is to introduce and study the matrix nearrings over partial order nearrings. Matrix nearrings over arbitrary nearrings were introduced in Meldrum & Van der Walt [11], where several results about the correspondence between the two-sided ideals in the base nearring N and those in the matrix nearring $M_n(N)$ were proved. Later, remarkable developments in matrix nearrings over arbitrary nearrings were due to Meldrum and Meyer [12], Meyer [13, 15]. Meldrum and Meyer [12] have shown the existence of an arbitrary large lattice of ideals in the matrix nearring corresponding to an ideal in the base nearring N. More concepts in the ideal theory of matrix nearrings are due to [1, 3, 4]. Van der Walt [20, 21] studied the relationship between the modules over a nearring N, and those in modules over a matrix nearring $M_n(N)$. We refer to Bhavanari and Kuncham [2], Kuncham et al. [8], and Pilz [10] for fundamental notations and literature on nearrings. Further, we refer to Meldrum and Van der Walt [11], Meyer [14, 16], and Ke [7] for the comprehensive literature on matrix nearrings.

In Sect. 2, we provide the basic definitions and results in p.o. nearrings and matrix nearrings, while in Sect. 3, the positive cone is defined in the matrix nearring and obtain a characterization theorem. In Sect. 4, the convex ideal in the matrix nearring corresponding to a convex ideal in the base nearring N is introduced. Further, it is proved that if I is a convex ideal of N, then the corresponding ideal $I^{*}$ is convex in $M_n(N)$; conversely, it is shown that for a convex ideal I in $M_n(N)$, $I_{*}$ is convex in the base nearring N. Consequently, an order-preserving isomorphism between the matrix nearrings $M_n(N)/{I^*}$ and $M_n(N')/{(I')^*}$ where I and $I'$ are the convex ideals of N and $N'$, respectively, is established. In the final section, we deal with the Archimedean order in a matrix nearring corresponding to the Archimedean order in N.

2 Preliminaries

An algebraic structure $(N,+,\cdot )$ is called a (right) nearring if: (i) $(N, +)$ is a group (not necessarily abelian); (ii) $(N, \cdot )$ is a semigroup; and (iii) $(a+ b)c = ac + bc$ for all $a, b, c\in N$. Obviously, if $(N,+,\cdot )$ is a right nearring, then $0a = 0$ and $(-a)b = -ab$, for all $a,~b\in N$, but in general $a0\ne 0$ for some $a\in N$. If $a0=0$, for all $a\in N$, then N is called zero-symmetric, and is denoted as $N=N_0.$ Moreover, $n_0$ denotes the zero-symmetric part of the element $n\in N$. If $aa'=a$, or $a0=a$, for all $a,a'\in N$, then N is called a constant nearring, denoted as $N=N_c$. We use ‘$\Leftrightarrow$ or iff’ to denote ‘if and only if’.

A nearring N is called a partially ordered (abbr. p.o.) nearring (Pilz [10]) if $(N, +)$ is a partially ordered group under a relation ‘$\le$’, and for any $a,b,c\in N$,

• (i) $a\le b, c\ge 0$ implies $ca\le cb ,$

• (ii) $a\le b, c\ge 0$ implies $ac\le bc$.

The case, if $0\le a$ and $a\ne 0$ is denoted as $0<a$.

If the partial order is a full order (or total order) [5], then the nearring is said to be a fully ordered (f.o.) (or a totally ordered) nearring. An element $a\in N$ is called positive if $a\ge 0$, and $N^{+}=\{a\in N ~|~a\ge 0\}$, is called the positive cone. If P is the positive cone of a p.o. nearring N, then P satisfies: (i) $P\cap -P=\{0\}$, (ii) $x+P=P+x$, for all $x\in N$, (iii) $P+P\subseteq P$, (iv) $P\cdot P\subseteq P$. Conversely, if $P\subseteq N$ satisfies the above conditions, then the relation ‘$\le$’ defined by $a\le b\Leftrightarrow b-a\in P$ is a partial order on N, for which P is a positive cone. Let N, $N'$ be nearrings ordered by the positive cones P and $P'$ respectively. A map $f:N\rightarrow N'$ is said to be an order-preserving homomorphism (or isomorphism, denoted by $\backsimeq _{o}$) if (i) f is homomorphism (or isomorphism); (ii) $f(P)\subseteq P'$. A subset T of an ordered nearring N is called convex if for all $t_1,t_2\in T$, and $n\in N$, $t_1\le n\le t_2$, imply $n\in T$. A partial order on an additive group N is called Archimedean, if for every pair a, b in $N^{+}$, $na\nleq b$ for all $n\in \mathbb {Z}^{+}$ implies $a=0$. A p.o. nearring is Archimedean, if $(N, +)$ is an Archimedean group. If N is not Archimedean, then there exists a pair (a, b) of $N^2$ with $k|a|<|b|$ for all $k\in \mathbb {N}$. In this case, we say that a is small with respect to b, denoted by $a\ll b$. For an ordered nearring N,  an element $n\in N$ is said to be nearly constant, if $n_0\ll N_c^{*}$ where $N_c^{*}=N_{c}{\setminus }\lbrace 0\rbrace .$

For a zero-symmetric right nearring N with identity 1,  let $N^{n}$ denote the direct sum of n copies of $(N,+)$. The elements of $N^{n}$ are thought of as column vectors and written as $\langle r_1,\ldots ,r_n\rangle$. The symbols $i_{j}$ and $\pi _{j}$ will denote the $i^{th}$ coordinate injection and $j^{th}$ coordinate projection functions respectively. The nearring of $n\times n$-matrices over N, denoted by $M_n{(N)}$, is defined to be the subnearring of $M(N^{n})$, generated by the set of functions {$f_{ij}^{r}:N^{n}\rightarrow N^{n}~|~r\in N,1\le i,j\le n$} where $f_{ij}^{r}\langle r_1,r_2,\ldots ,r_n\rangle :=\langle s_1,s_2,\ldots ,s_n\rangle$ with $s_i=rr_j$ and $s_k=0$ if $k\ne i$. The elements of $M_{n}(N)$ will be referred to as $n\times n$-matrices over N. The zero matrix in $M_n(N)$ is denoted by $\mathbf {\overline{0}}=0_{M_n(N)}$.

Any matrix A can be represented as an expression involving only the $f_{ij}^{r}$. The length of such an expression is the number of $f_{ij}^{r}$ therein. The weight w(A) of A is the length of an expression of minimal length for A. Clearly, if A is represented by an expression of length $w(A)\ge 2$, then from this expression we can find representations for A as either $A=B+C$ or $A=BC$, where $w(B),w(C)<w(A)$.

3 Positive Cone in a Matrix Nearring

Definition 3.1

Let N be a partially ordered nearring with 1.

• (i) For any $A,B \in M_{n}(N),$ we define

  

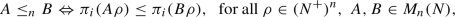
  $~\text {and}~ \text { for all}~1\le i\le n.$

• (ii) $M_{n}(N)$ is said to be a p.o. matrix nearring if $~\le _{n}$ defined in (i) is a partial order and satisfies the monotone properties of addition and multiplication in $M_{n}(N)$.

Lemma 3.2

If N is a p.o. nearring with 1, then the relation in Definition 3.1 on $M_n(N)$, is a p.o. relation and hence $M_n(N)$ is a p.o. matrix nearring.

Proof

We show that $\le _{n}$ is a p.o. relation on $M_n(N)$. Since $\pi _{i}(A\rho )\le \pi _{i}(A\rho )$, for all $A\in M_{n}(N)$, $\rho \in (N^{+})^{n}$, $1\le i\le n$, we have $A\le _{n}A$, so $\le _{n}$ is reflexive. To see $\le _{n}$ is anti-symmetric, suppose $A\le _{n}B$, and $B\le _{n}A$. Then, $\pi _{i}(A\rho )\le \pi _{i}(B\rho )$, and $\pi _{i}(B\rho )\le \pi _{i}(A\rho )$ for all $A,B\in M_{n}(N)$, $\rho \in (N^{+})^{n}$, $1\le i\le n$. Since $\le$ is anti-symmetric on N, we get $\pi _{i}(A\rho )=\pi _{i}(B\rho )$ for all $\rho \in (N^{+})^{n}$, $1\le i\le n$. Therefore, $A=B$. Suppose $A\le _{n}B$, and $B\le _{n}C$. Then, $\pi _{i}(A\rho )\le \pi _{i}(B\rho )$, and $\pi _{i}(B\rho )\le \pi _{i}(C\rho )$ for all $A,B,C\in M_{n}(N)$, $\rho \in (N^{+})^{n}$, $1\le i\le n$. Since $\le$ is transitive on N, we get $\pi _{i}(A\rho )\le \pi _{i}(C\rho )$ for all $\rho \in (N^{+})^{n}$, $1\le i\le n$, shows that $A\le _{n}C$. Next, to see the monotonicity in $M_{n}(N)$, assume that $A\le _{n}B$ and $\mathbf {\overline{0}}\le _{n}C$. That is, $\pi _{i}(A\rho )\le \pi _{i}(B\rho )$, and $\pi _i(0\rho )\le \pi _i(C\rho )$, for all $i\in \{1,2,\ldots , n\}$ and $\rho \in (N^{+})^n$. Now,

Therefore, $A+C \le _{n} B+C.$

Further,

$$\begin{aligned} \pi _i((AC)\rho )&= \pi _i(A(C\rho ))\\&\le \pi _i(B(C\rho )),~ \text {since }N \text { is p.o. nearring and }C\rho \in (N^{+})^n\\&=\pi _i((BC)\rho ). \end{aligned}$$

Therefore, $AC \le _{n} BC.$

Definition 3.3

The positive cone $\mathcal {P}_{M_{n}{(N)}}$ (or simply $\mathcal {P}$) of $M_{n}(N)$ is defined as

$$\begin{aligned} \mathcal {P}=\Big \lbrace A\in M_{n}{(N)}~|~ A\ge _{n} \mathbf {\overline{0}} \Big \rbrace , \end{aligned}$$

and the negative cone is,

$$\begin{aligned} \mathcal {-P}=\Big \lbrace A\in M_{n}{(N)}~|~ A\le _{n} \mathbf {\overline{0}} \Big \rbrace , \end{aligned}$$

where $\mathbf {\overline{0}}$ is the zero matrix in $M_n(N)$.

Now, we prove a characterization for a positive cone in $M_n(N)$.

Theorem 3.4

Let N be a p.o. nearring, and let $M_{n}(N)$ be its p.o. matrix nearring with positive cone $\mathcal {P}.$ Then,

• (1) $\mathcal {P}+\mathcal {P}=\mathcal {P};$

• (2) $\mathcal {P}\cap \left( -\mathcal {P}\right) =\{\mathbf {\overline{0}}\};$

• (3) $\mathcal {P} \mathcal {P} \subseteq \mathcal {P};$

• (4) $A+\mathcal {P}-A \subseteq \mathcal {P}$ for all $A \in M_{n}(N).$

Conversely, for every subset P of a matrix nearring $M_n(N)$ fulfilling (1)–(4), we get an ordered matrix nearring $(M_n(N),\le _{P})$, where $\le _{P}$ is defined by $A\le _{P}B\Leftrightarrow B-A\in P$.

Proof

Assume that $\mathcal {P}$ is a positive cone in $M_n(N)$.

• (1) Let $A,B\in \mathcal {P}$. Then, $A\ge _{n} \mathbf {\overline{0}}$ and $B\ge _{n} \mathbf {\overline{0}}$. Now, $\mathbf {\overline{0}}\le _{n} A\le _{n} A+B$ (by monotonicity), implies $A+B\in \mathcal {P}$. Therefore, $\mathcal {P}+\mathcal {P}\subseteq \mathcal {P}$. On the other hand, if $A\in \mathcal {P}$, then $A=A+\mathbf {\overline{0}}\in \mathcal {P}+\mathcal {P}$. Therefore, $\mathcal {P}\subseteq \mathcal {P}+\mathcal {P}$.

• (2) As $\mathcal {-P}=\{A\in M_n(N)|~A\le _{n}\mathbf {\overline{0}}\}$, we get $\mathcal {P}\cap \mathcal {-P}=\{\mathbf {\overline{0}}\}$.

• (3) Let $I\in M_n(N)$, $A\in \mathcal {P}$. Then, since $A\ge _{n} \mathbf {\overline{0}}$ and by monotone property, $I+A\ge _{n} I$, implies $I+A-I\ge _{n} \mathbf {\overline{0}}$, which shows that $I+A-I\in \mathcal {P}$.

• (4) Let $A,B\in \mathcal {P}$. Then, by monotonicity in $M_n(N)$, $AB\ge _{n} \mathbf {\overline{0}}$. Hence, $\mathcal {P}\mathcal {P}\subseteq \mathcal {P}$. The Converse follows from Lemma 3.2 where $P=N^{+}$, the set of positive elements in N.

Since every non-trivially ordered nearring is infinite by ( [10], Proposition 9.127), we consider the matrix nearring to be of infinite order.

Lemma 3.5

[11] We provide some properties of matrix calculations. For all $r,s,t,r_i$ $(1\le i\le n)\in N$, and $1\le i,j,k,l\le n,$

• 1. $f_{ij}^r+f_{ij}^s=f_{ij}^{r+s}$;

• 2. $f_{ij}^r+f_{kl}^s=f_{kl}^s+f_{ij}^r$, if $i\ne k$;

• 3. $f_{ij}^rf_{kl}^s=\left\{ \begin{array}{ll} f_{il}^{rs}, &{}\text {if~} j=k;\\ f_{il}^{r0}, &{}\text {if~} j\ne k. \end{array} \right.$

Example 3.6

Let $\left( N,+,\cdot \right)$ be a f.o. nearring, and $\nonumber x \cdot a = \left\{ \begin{array}{ll} -x, &{} \hbox {if }a<0 \\ 0, &{} \hbox {if }a=0\\ x, &{} \hbox {if }a>0 \end{array} \right.$, for all $x,a\in N$. Then, $M_{n}(N)$ is a p.o. matrix nearring, with

$$\begin{aligned} f_{ij}^{r} \cdot f_{kl}^{s} = \left\{ \begin{array}{ll} f_{il}^{-r}, &{} \hbox {if }s<0 \\ \mathbf {\overline{0}}, &{} \hbox {if } s=0 ,\\ f_{il}^{r}, &{} \hbox {if }s>0 \end{array} \right. \end{aligned}$$

for all $r,s\in N$, $1\le i,j=k,l\le n$.

(i) For simplicity, we verify for weight 1. Let $a\le b$ in N. Then, for any $\rho =\langle x_{1}, x_{2},\ldots ,x_{n}\rangle \in (N^{+})^{n}$, and for $A=f_{ij}^{a}$, $B=f_{ij}^{b}$ it follows that

$$\begin{aligned} \pi _{i}(A\rho )=\pi _{i}(f_{ij}^{a}\langle x_{1}, x_{2},\ldots ,x_{n}\rangle )&=\pi _{i}(\langle 0,0,\ldots ,\underbrace{ax_{j}}_{i^{th}},\ldots ,0\rangle )\\&=ax_{j}\\&\le bx_{j}~~(\text {since}~ a\le b~\text {and}~x_{j}\ge 0)\\&=\pi _{i}(\langle 0,0,\ldots ,\underbrace{bx_{j}}_{i^{th}},\ldots ,0\rangle )\\&=\pi _{i}(f_{ij}^{b}\langle x_{1}, x_{2},\ldots ,x_{n}\rangle )\\&=\pi _{i}(B\rho ). \end{aligned}$$

Therefore, $f_{ij}^{a}\le _{n} f_{ij}^{b}$.

(ii) Let $A=f_{ij}^{r_{1}},~B=f_{ij}^{r_{2}},~C=f_{ij}^{s} \in M_{n}(N), \mathbf {\overline{0}}<_{n}f_{ij}^{s}$ and $f_{ij}^{r_{1}}\le _{n} f_{ij}^{r_{2}}.$ Then,

$A+C= f_{ij}^{r_{1}}+f_{ij}^{s}=f_{ij}^{r_{1}+s}\le _{n} f_{ij}^{r_{2}+s}=f_{ij}^{r_{2}}+f_{ij}^{s}=B+C ,$ and

$C+A= f_{ij}^{s}+f_{ij}^{r_{1}}=f_{ij}^{s+r_{1}}\le _{n} f_{ij}^{s+r_{2}}=f_{ij}^{s}+f_{ij}^{r_{2}}=C+B.$

Therefore, ‘$+$’ is monotone.

(iii) Let $r_{1}<0<r_{2}$ and $s>0 .$ Let $A=f_{ij}^{r_{1}},~B=f_{ij}^{r_{2}},~C=f_{kl}^{s} \in M_{n}(N)$. Then, $AC= f_{ij}^{r_{1}}\cdot f_{kl}^{s}=f_{il}^{r_{1}s}=f_{il}^{r_{1}}$ and $BC= f_{ij}^{r_{2}}\cdot f_{kl}^{s}=f_{il}^{r_{2}s}=f_{il}^{r_{2}}.$ Since $r_{1}<r_{2}$, we have $f_{il}^{r_{1}}<_{n} f_{il}^{r_{2}}$ implies $AC <_{n} BC.$ On the other hand, $CA= f_{kl}^{s}\cdot f_{ij}^{r_{1}}= f_{kj}^{sr_{1}}=f_{kj}^{-s}$ and $CA= f_{kl}^{s}\cdot f_{ij}^{r_{2}}= f_{kj}^{sr_{2}}=f_{kj}^{s}.$ Since $-s<s,$ we have $f_{kj}^{-s}<_{n}f_{kj}^{s}$, which implies that $CA<_{n}CB.$ Therefore, ‘$\cdot$’ is monotone.

Hence, $M_{n}(N)$ is a p.o. matrix nearring.

Remark 3.7

$M_n(N)$ is not f.o. in general, even if N is f.o. For example take $N=(\mathbb {Z},+,\cdot )$. Then, N is f.o., that is, $a\le b$ or $b\le a$, for all $a, b\in N$. But $M_n(\mathbb {Z})$ is not f.o., for let $A=f_{12}^{1}$ and $B=f_{21}^{1}$, we have $A\langle 1,1 \rangle =\langle 1,0\rangle$ and $B\langle 1,1 \rangle =\langle 0,1\rangle$. Clearly, $\langle 1,0\rangle \nleq _{n}\langle 0,1\rangle$ and $\langle 0,1\rangle \nleq _{n}\langle 1,0\rangle$.

4 Convex Ideal in a Matrix Nearring

Definition 4.1

An ideal I of $M_{n}(N)$ is said to be convex, if for any $A_{1},A_{2}\in I,$ and $B \in M_{n}(N)$ with $A_{1}\le _{n} B \le _{n} A_{2}$ imply $B\in I,$ that is, $\pi _{i}(A_1\rho )\le \pi _{i}(B\rho ) \le \pi _{i}(A_2\rho )$, for all $\rho \in (N^{+})^{n}$, $1\le i\le n$, imply $B\in I$.

Proposition 4.2

[11] If I is a two-sided ideal of N, then $I^{*}=(I^{n}:N^{n})=\{A\in \mathbb {M}_{n}(N)|A\rho \in I^{n}~\textit{for all}~\rho \in N^{n}\}$, is a two-sided ideal of $\mathbb {M}_{n}(N)$.

Lemma 4.3

If I is a two-sided convex ideal of N,  then $I^{*}$ is a two-sided convex ideal in $M_{n}(N).$

Proof

Let I be a two-sided convex ideal of N. In view of Proposition 4.2, it is enough to show the convexity of $I^{*}$. Let $A_{1},A_{2}\in I^{*}$ and $B \in M_{n}(N)$ such that $A_{1}\le _{n} B \le _{n} A_{2}.$ We prove that $B\in I^{*}$. Since $A_1,A_2\in I^{*}$, we have $A_1\rho \in I^{n}$ and $A_2\rho \in I^{n}$ for all $\rho \in (N^{+})^{n}$. Let $A_1\rho =\langle a_1,\ldots ,a_n \rangle \in I^{n}$, $B\rho =\langle b_1,\ldots ,b_n\rangle$ and $A_2\rho =\langle a_1^{'},\ldots ,a_n^{'} \rangle \in I^{n}$. Then, $\pi _{i}\langle a_1,\ldots ,a_n \rangle \le \pi _{i}\langle b_1,\ldots ,b_n \rangle \le \pi _{i}\langle a_1^{'},\ldots ,a_n^{'} \rangle$, implies $a_i\le b_{i}\le a_{i}^{'}$, for all $i\in \{1,2,\ldots ,n\}$. Since $a_i,~a_i^{'}\in I$ and I is convex, we get $b_{i}\in I$, for all $i\in \{1,2,\ldots ,n\}$. Therefore, $B\rho \in I^{n}$, implies $B\in I^{*}$. Hence, $I^{*}$ is convex.

Example 4.4

Consider the nearring $N=\mathbb {Z}_{2}\times \mathbb {Z}$ (where $\mathbb {Z}$ is the set of all integers), operations are defined component wise. Define ‘$\le$’ on N as $(a,b)\le (c,d)\Leftrightarrow (a=c~\text {and}~b<d)$ or $(a<c,~b<d)$. Then, ‘$\le$’ is a partial order on N, and hence N is a p.o. nearring. The ideals are $I_1=\{0\}\times \mathbb {Z}$, $I_2=\mathbb {Z}_{2}\times \{0\}$. Clearly $I_1$ is convex in N. Now, write the matrix nearring

$$\begin{aligned} M_n(\mathbb {Z}_2\times \mathbb {Z})=\Big \langle \{f_{ij}^{(a,b)}|(a,b)\in \mathbb {Z}_{2}\times \mathbb {Z}, 1\le i,j\le n\}\Big \rangle . \end{aligned}$$

Then, $I_1^{*}=\Big \langle \{f_{ij}^{(a,b)}|(a,b)\in I_1, 1\le i,j\le n\}\Big \rangle ,$ is a convex ideal in $M_n(\mathbb {Z}_2\times \mathbb {Z})$.

Theorem 4.5

[12] For an ideal I of N, $I^{+}=\langle \{f_{ij}^{a}|a\in I,1\le i,j\le n\}\rangle$ is an ideal of $M_{n}(N)$.

Proposition 4.6

If I is a two-sided convex ideal of N,  then $I^{+}$ is a two-sided convex ideal in $M_{n}(N).$

Proof

Let I be a convex ideal of N. Then, by Theorem 4.5, $I^{+}$ is an ideal of $M_{n}(N).$ To show, $I^{+}$ is convex in $M_{n}(N),$ let $f_{ij}^{a_{1}}, f_{ij}^{a_{2}}\in I^{+}$ and $f_{ij}^{b}\in M_{n}(N)$ such that $f_{ij}^{a_{1}}\le _{n} f_{ij}^{b}\le _{n} f_{ij}^{a_{2}},$ for some $a_1,a_2,b\in N$, $1\le i,j\le n$. Then, $\pi _{i}(f_{ij}^{a_{1}}\rho ) \le \pi _{i}(f_{ij}^{b}\rho ) \le \pi _{i}(f_{ij}^{a_{2}}\rho )$ for all $\rho \in (N^{+})^{n}.$ In particular, $\pi _{i}(f_{ij}^{a_{1}}\langle 1,1,\ldots ,1\rangle ) \le \pi _{i}(f_{ij}^{b}\langle 1,1,\ldots ,1\rangle ) \le \pi _{i}( f_{ij}^{a_{2}}\langle 1,1,\ldots ,1\rangle )$, where $\langle 1,1,\ldots ,1\rangle \in (N^{+})^{n}.$ This implies, which shows that $a_{1}\le b \le a_{2}$. Since $f_{ij}^{a_{1}}, f_{ij}^{a_{2}}\in I^{+},$ it follows that $a_{1}, a_{2}\in I.$ Now, since I is convex, we have $b \in I.$ Therefore, $f_{ij}^{b}\in I^{+}$, which proves that $I^{+}$ is convex in $M_{n}(N).$

Proposition 4.7

[11] If I is a two-sided ideal of $M_{n}(N)$, then $I_{*}=\{x\in N|x\in \text {Im}(\pi _{j}A)~\text {for some}~A\in I~\text {and}~j,1\le j\le n\}$ is a two-sided ideal N.

Corollary 4.8

[11] If I is a two-sided ideal of $M_{n}(N)$, then $a\in I_{*}$ iff $f_{ij}^{a}\in I$, for all $1\le i,j\le n$.

Lemma 4.9

If I is a two-sided convex ideal of $M_{n}(N)$ then $I_{*}$ is a two-sided convex ideal in N.

Proof

Let I be a convex ideal of $M_{n}(N).$ Then, by Proposition 4.7, $I_{*}$ is an ideal of N. To prove $I_{*}$ is convex in N,  let $a,b \in I_{*}$ and $r\in N$ such that $a\le r \le b.$ Then, by Corollary 4.8, $f_{ij}^{a},f_{ij}^{b}\in I$. Now, we show that $f_{ij}^{a}\le _{n} f_{ij}^{r}\le _{n} f_{ij}^{b}.$ Let $\rho =\langle x_1,\ldots ,x_n\rangle \in (N^{+})^{n}$,

$$\begin{aligned} \pi _{i}(f_{ij}^{a}\rho )&=\pi _{i}(f_{ij}^{a}\langle x_{1}, x_{2},\ldots ,x_{n}\rangle )\\&=\pi _{i}(\langle 0,0,\ldots ,\underbrace{ax_{j}}_{i^{th} },\ldots ,0\rangle )\\&\le \pi _{i}(\langle 0,0,\ldots ,\underbrace{rx_{j}}_{i^{th}},\ldots ,0\rangle ) ~(\text {by monotonicity}, \text {as}~ a\le r, x_j\ge 0)\\&=\pi _{i}(f_{ij}^{r}\langle x_{1}, x_{2},\ldots ,x_{n}\rangle )\\&=\pi _{i}(f_{ij}^{r}\rho ) \end{aligned}$$

implies that $f_{ij}^{a}\le _{n} f_{ij}^{r}.$ Other way,

$$\begin{aligned} \pi _{i}(f_{ij}^{r}\rho )&=\pi _{i}(f_{ij}^{r}\langle x_{1}, x_{2},\ldots ,x_{n}\rangle )\\&=\pi _{i}(\langle 0,0,\ldots ,\underbrace{rx_{j}}_{i^{th} },\ldots ,0\rangle )\\&\le \pi _{i}(\langle 0,0,\ldots ,\underbrace{bx_{j}}_{i^{th}},\ldots ,0\rangle ) ~(\text {by monotonicity}, \text {as}~ r\le b, x_j\ge 0)\\&=\pi _{i}(f_{ij}^{b}\langle x_{1}, x_{2},\ldots ,x_{n}\rangle )\\&=\pi _{i}(f_{ij}^{b}\rho ) \end{aligned}$$

implies that $f_{ij}^{r}\le _{n} f_{ij}^{b}.$ Therefore, $f_{ij}^{a}\le _{n} f_{ij}^{r}\le _{n} f_{ij}^{b}.$ Since I is convex in $M_{n}(N),$ we get $f_{ij}^{r}\in I$ and by Corollary 4.8, $r \in I_{*}$, showing that $I_{*}$ is convex in N.

Definition 4.10

[22] An $n\times n$-matrix A over a nearring N is said to be $\sigma$-generated if it can be expressed as a sum of elements $f_{ij}^{r}$, $r\in N$, $1\le i,j\le n$. $M_{n}(N)$ is said to be $\sigma$-generated if every $n\times n$-matrix A over N is $\sigma$-generated. N is said to be $\sigma$-generated if $M_{n}(N)$ is $\sigma$-generated for every $n\ge 1$.

Let $E_n(N)$ be set of matrix expressions. The matrix represented by $U\in E_{n}(N)$ is denoted by $\mu (U)$. The depth of an expression is a unique number d(U), $U\in E_{n}(N)$, assigned as follows: (i) $d(f_{ij}^{r})=0$, (ii) $d(U+V)=max(d(U),d(V))$, (iii) $d(UV)=d(U)+d(V)+1$. Let N and $N'$ be two nearrings and $h:N\rightarrow N'$, $h(r)=r'$ be a nearring epimorphism. Consider the mapping $\theta :E_n(N)\rightarrow E_n(N')$, where $\theta (E)=E'$ is the expression derived from $E\in E_n(N)$ by replacing every $f_{ij}^{r}$ in E by $f_{ij}^{r'}$. Then, $\theta$ is onto and $\theta (E+F)=\theta (E)+\theta (F)$, $\theta (EF)=\theta (E)\theta (F)$ for all $E,F\in E_n(N)$. We define $\psi :M_n(N)\rightarrow M_n(N')$, by $\psi (A)=\mu (\theta (E))$, where $A=\mu (E)$. $M_{n}(N)$ is $\sigma$-generated if every $n\times n$-matrix A over N has an expression $U\in E_{n}(N)$ such that $\mu (U)=A$ and $d(U)=0$.

Lemma 4.11

Let N and $N'$ be p.o. $\sigma$-generated nearrings. If $h:N\rightarrow N^{'}$ is an order-preserving map, then the map $\psi :M_{n}(N)\rightarrow M_{n}(N^{'})$ is also order-preserving.

Proof

Let $M_{n}(N)$ and $M_{n}(N^{'})$ be two p.o. matrix nearrings with positive cones $\mathcal {P}$ and $\mathcal {P}'$ respectively. Define $\psi :M_{n}(N)\rightarrow M_{n}(N^{'})$ by $\psi (I)=\mu (E^{'})$ where $I=\mu (E)$ as in [22]. To show $\psi \left( \mathcal {P}\right) \subseteq \mathcal {P}',$ let $A\in \psi \left( \mathcal {P}\right)$. Then, $A=\psi (B)$, for some $B\in \mathcal {P}$. That is, $A=\psi (B)=\mu (E_1')$, where $B=\mu (E_1)$. Now, we apply induction on $d(E_1)$.

Case-(i): $d(E_1)=0$. Since N is $\sigma$-generated, by definition, $M_{n}(N)$ is $\sigma$-generated, for all $n\ge 1$. Hence, B has an expression $E_1\in E_{n}(N)$ such that $B=\mu (E_1)$ and $d(E_1)=0$. Let $E_1=f_{ij}^{r}$, where $r\in N^{+}$. Now, $A=\mu (E_1')=\mu (f_{ij}^{r'})\in \mathcal {P}$, where $r'\in (N')^{+}$. Hence, $\psi (\mathcal {P})\subseteq {\mathcal {P}}'$. Assume that the result is true for $d(E_1)< t$, for all $E_1\in E_{n}(N)$.

Case-(ii): $d(E_1)=t>0$. Then, $E_1=U+V$ or $E_1=UV$, where $U,V\in E_n(N)$ and $d(U), d(V)<t$.

Subcase-(i): $E_1=U+V$. Then, $A=\psi (B)=\mu (E_1')=\mu (U'+V')=\mu (U')+\mu (V')\in \mathcal {P'}+\mathcal {P'}= \mathcal {P'}$, by Theorem 3.4(1). Therefore, $\psi (\mathcal {P})\subseteq \mathcal {P'}$.

Subcase-(ii): $E_1=UV$. Then, $A=\psi (B)=\mu (E_1')=\mu (U'V')=\mu (U')\mu (V')\in \mathcal {P'}\mathcal {P'}\subseteq \mathcal {P'}$, by Theorem 3.4(3). Therefore, $\psi (\mathcal {P})\subseteq \mathcal {P'}$.

Theorem 4.12

Let $h:N\rightarrow N^{'}$ be an order-preserving homomorphism, where N and $N'$ are $\sigma$-generated p.o. nearrings, such that $ker ~h =I$ is convex. Then, $I^{*}$ is the kernel of the order-preserving homomorphism $\psi :M_{n}(N)\rightarrow M_{n}(N^{'})$, which is convex.

Proof

Since I is a convex ideal of N, by Lemma 4.3, we have $I^{*}$ is convex ideal in $M_{n}(N)$. Also, since h is an order-preserving homomorphism, by Lemma 4.11, $\psi$ is order-preserving homomorphism. It remains to show that $I^{*}=ker ~\psi$. Now,

$$\begin{aligned} A\in ker~\psi&\Leftrightarrow \psi (A)=(\overline{\mathbf {0}})'\\&\Leftrightarrow \psi (A)\rho '=(\overline{\mathbf {0}})',~\text {for all}~ \rho '\in (N')^{n}\\&\Leftrightarrow \mu (E')\rho '=(\overline{\mathbf {0}})'\\&\Leftrightarrow \pi _{i}\mu (E')\rho '=0_{N'}\\&\Leftrightarrow h\pi _{i}\mu (E)\rho =0_{N},~\text {by }([22], \text {Lemma 3.1})\\&\Leftrightarrow \pi _{i}\mu (E)\rho \in ker~ h=I\\&\Leftrightarrow \pi _{i}\mu (E)\rho \in I,~\text {for all}~i,~1\le i\le n\\&\Leftrightarrow \mu (E)\rho \in I^{n}\\&\Leftrightarrow A\rho \in I^{n}, ~\text {for all}~\rho \in N^{n}\\&\Leftrightarrow A\in I^{*}. \end{aligned}$$

Therefore, $I^{*}=ker~ \psi$.

Proposition 4.13

Let I be a convex ideal of a p.o. nearring N. Then, for any $A,B\in M_n(N)$, $A+I^{*} \le _{n}^{*} B+I^{*}$ if $A \le _{n} B+C,$ for some $C \in I^{*}$.

Proof

We show $\le _{n}^{*}$ is well defined. Let $A+I^{*}, B+I^{*}\in M_n(N)/I^{*}$ such that $A+I^{*} \le _{n}^{*} B+I^{*}.$ Let $A+I^{*}= A_{1}+I^{*}$ and $B+I^{*}=B_{1}+I^{*}.$ Then, we note that $A-A_{1}\in I^{*}$ and $B-B_{1}\in I^{*}$, implies $(A-A_{1})\rho \in I^{n}$ and $(B-B_{1})\rho \in I^{n}$ for all $\rho \in N^{n}.$ Therefore, $(A-A_{1})\rho =C_{1}\rho$ and $(B-B_{1})\rho =C_{2}\rho$ for some $C_{1},C_{2}\in M_{n}(N).$ That is, $A\rho -A_{1}\rho =C_{1}\rho$ and $B\rho -B_{1}\rho =C_{2}\rho ,$ which implies $A\rho =C_{1}\rho +A_{1}\rho$ and $B\rho =C_{2}\rho +B_{1}\rho .$ Now,

$$\begin{aligned} \pi _{i}(C_{1}\rho +A_{1}\rho )&=\pi _{i}(A\rho )\\&\le \pi _{i}((B+C)\rho )\\&=\pi _{i}(B\rho +C\rho )\\&=\pi _{i}\left( C_{2}\rho +B_{1}\rho +C\rho \right) . \end{aligned}$$

Thus, $\pi _{i}(C_{1}\rho ) +\pi _{i}(A_{1}\rho )\le \pi _{i}(C_{2}\rho )+\pi _{i}(B_{1}\rho )+\pi _{i}(C\rho )$, implies

$$\begin{aligned} \pi _{i}(A_{1}\rho )&\le -\pi _{i}(C_{1}\rho )+ \pi _{i}(C_{2}\rho )+\pi _{i}(B_{1}\rho )+\pi _{i}(C\rho )\\&=\pi _{i}(D\rho )+\pi _{i}(B_{1}\rho )+\pi _{i}(C\rho ),~\text {where } \pi _{i}(D\rho )\\&=-\pi _{i}(C_{1}\rho )+ \pi _{i}(C_{2}\rho )\in I\\&=\pi _{i}(B_{1}\rho )+\pi _{i}(E\rho ),~\text {where }\pi _{i}(E\rho )\in I\\&=\pi _{i}(B_{1}\rho +E\rho )\\&=\pi _{i}((B_{1}+E)\rho ), \end{aligned}$$

for all $\rho \in (N^{+})^{n}$, for all i, $1\le i\le n$.

This shows that $A_1\le _{n}B_1+E$, where $E\in I^{*}$. Hence, $A_1+I^{*}\le _{n}^{*}B_1+I^{*}$.

Clearly, since $\le _{n}$ is a partial order relation, we have $\le _{n}^{*}$ is also a partial order relation. Now, we show the monotonicity.

(i) Let $A+I^{*}, B+I^{*}\in M_n(N)/I^{*}$ such that $A+I^{*} \le _{n}^{*} B+I^{*}.$ Then, $A\le B+D$, for some $D\in I^{*}$, implies $\pi _{i}(A\rho )\le \pi _{i}((B+D)\rho )=\pi _{i}(B\rho )+\pi _{i}(D\rho )$, for all $\rho \in (N^{+})^{n}$, for all i. Now, by monotonicity in N, $\pi _{i}(A\rho )+\pi _{i}(C\rho )\le \pi _{i}(B\rho )+\pi _{i}(D\rho )+\pi _{i}(C\rho )$, for some $\pi _{i}(C\rho )\in N$. Then,

$$\begin{aligned} \pi _{i}((A+C)\rho )&=\pi _{i}(A\rho )+\pi _{i}(C\rho )\\&\le \pi _{i}(B\rho )+\pi _{i}(D\rho )+\pi _{i}(C\rho )\\&=\pi _{i}(B\rho )+\pi _{i}(C\rho )+\pi _{i}(D_1\rho ),~\text {where }\pi _{i}(D_1\rho )\in I\\&=\pi _{i}((B+C)\rho )+\pi _{i}(D_1\rho ), \end{aligned}$$

for all i, $1\le i\le n$.

This shows that $A+C\le _{n}(B+C)+D_1$, where $D_1\in I^{*}$. Hence $(A+C)+I^{*}\le _{n}^{*}(B+C)+I^{*}$. Similarly, $(C+A)+I^{*}\le _{n}^{*}(C+B)+I^{*}$.

(ii) Let $A+I^{*}, B+I^{*}\in M_n(N)/I^{*}$ such that $A+I^{*} \le _{n}^{*} B+I^{*}.$ Then, $A\le B+D$, for some $D\in I^{*}$, implies $\pi _{i}(A\rho )\le \pi _{i}((B+D)\rho )=\pi _{i}(B\rho )+\pi _{i}(D\rho )$, for all $\rho \in (N^{+})^{n}$, for all i. Now, by monotonicity in N, $\pi _{i}(A\rho )\pi _{i}(C\rho )\le \left( \pi _{i}(B\rho )+\pi _{i}(D\rho )\right) \pi _{i}(C\rho )$, for some $\pi _{i}(C\rho )\in N$. Then,

$$\begin{aligned} \pi _{i}((A C)\rho )=\pi _{i}(A\rho )\pi _{i}(C\rho )&\le \pi _{i}(B\rho ) \pi _{i}(C\rho )+\pi _{i}(D\rho )\pi _{i}(C\rho )\\&=\pi _{i}((B C)\rho )+\pi _{i}((D C)\rho )\\&=\pi _{i}((B C+D C)\rho ), \end{aligned}$$

for all i, $1\le i\le n$.

This shows that $A C\le _{n}B C+D C$, where $DC\in I^{*}$, as $I^{*}$ is a right ideal of N. Hence $(A C)+I^{*}\le _{n}^{*}(B C)+I^{*}$. Similarly, $(C A)+I^{*}\le _{n}^{*}(C B)+I^{*}$. Therefore, $M_n(N)/I^{*}$ is a p.o. matrix nearring.

Lemma 4.14

[20] If A is an ideal of N, then $~~M_{n}\left( N/ A\right) \backsimeq M_{n}(N)/ A^{*}$.

Theorem 4.15

Let N, $N'$ be p.o. $\sigma$-generated nearrings and let $h:N \rightarrow N^{'}$ be an order-preserving epimorphism with positive cones P and $P^{'}$ respectively such that for every convex ideal $I^{'}$ of $N^{'},$ $h^{-1}(I^{'})=I$ is convex, with $N/ I\backsimeq _{\circ } N^{'}/ I^{'}.$ Then, there exists an order-preserving epimorphism $\phi :M_{n}(N)\rightarrow M_{n}(N^{'})$, such that if $(I^{'})^{*}$ is convex in $M_{n}(N^{'})$, then $\phi ^{-1}((I^{'})^{*})=I^{*}$ is convex in $M_{n}(N)$, and $M_{n}(N)/ I^{*}\backsimeq _{\circ } M_{n}(N^{'})/(I^{'})^{*}.$

Proof

Define $\phi :M_{n}(N)\rightarrow M_{n}(N^{'})$ by $\phi (A)=A^{'}$. Let $(I^{'})^{*}$ be a convex ideal of $M_{n}(N^{'}).$ To show $I^{*}$ is convex in $M_{n}(N),$ let $A,B \in I^{*}$ and $C \in M_{n}(N)$ such that $A\le _{n} C \le _{n} B.$ Then, there exist $A^{'},B^{'}\in (I^{'})^{*}$ such that $A=\phi ^{-1}(A^{'}), B=\phi ^{-1}(B^{'}).$ Now, $\phi ^{-1}(A^{'})\le _{n} C \le _{n}\phi ^{-1}(B^{'}),$ implies $\phi \left( \phi ^{-1}(A^{'})\right) \le _{n} \phi \left( C\right) \le _{n} \phi \left( \phi ^{-1}(B^{'})\right) ,$ by Lemma 4.11. That is, $A^{'}\le _{n} \phi \left( C\right) \le _{n} B^{'}.$ Since $(I^{'})^{*}$ is convex and $\phi (C) \in M_{n}(N^{'}),$ we get $\phi (C)\in (I^{'})^{*},$ which implies $C \in \phi ^{-1}(I^{'})^{*}=I^{*}.$ Therefore, $I^{*}$ is convex in $M_{n}(N).$ Next we show that $M_{n}(N)/ I^{*}\backsimeq _{\circ } M_{n}(N^{'})/(I^{'})^{*}.$ Since I is an ideal of N, by Lemma 4.14, $M_{n}\left( N/ I\right) \backsimeq M_{n}(N)/ I^{*}$, similarly, if $I^{'}$ is an ideal of $N^{'},$ then $M_{n}(N^{'}/ I^{'})\backsimeq M_{n}(N^{'})/ (I^{'})^{*}$. Again since, $N/ I\backsimeq _{\circ }N^{'}/ I^{'},$ by Theorem 4.11, it follows that $M_{n}\left( N/ I\right) \backsimeq _{\circ } M_{n}(N^{'}/ I^{'}).$ Therefore, $M_{n}(N)/ I^{*}\backsimeq _{\circ } M_{n}(N^{'})/(I^{'})^{*}.$

5 Archimedean Order in Matrix Nearring

Definition 5.1

An ordered matrix nearing $M_{n}(N)$ is called Archimedean if $(M_{n}(N),+)$ is Archimedean. That is, for any $A,B \in \mathcal {P},~ kA\le _{n} B$ for all $k\in \mathbb {Z}^{+},$ implies $A=\overline{\mathbf{0 }}.$

Corollary 5.2

[11] N is abelian iff $M_n(N)$ is abelian.

Proposition 5.3

If N is f.o. Archimedean, then $M_{n}(N)$ is f.o. Archimedean and $M_{n}(N)$ is abelian.

Proof

Suppose N is f.o. Archimedean. First, we show that $(N,+)$ is abelian.

Case (i): Let $a \in N$ such that $a>0$ and $0\le x <a$ implies $x=0~~\cdots (*)$, say. We have for each $b\in N,$ there exist $n\in \mathbb {Z}^{+}$ such that $na \le b<(n+1)a.$ This implies that $0\le -na+b <a.$ Now, by assumption $(*)$, we have $-na+b=0, b=na.$

Case (ii): Assume that no such ‘a’ exists as in Case (i). For every $x\in N,0<x,$ we find $y \in N$ such that $0<y<x.$ Suppose that $2(x-y)\nleq x .$ Since N is f.o., $2(x-y)\ge x .$ That is, $(x-y)+(x-y)\ge x ,$ implies that $-x+x-y+x-y\ge 0 .$ Therefore, $-y+x\ge y ,$ and so $x\ge 2y.$ Hence, $2y\le x$ or $2(x-y)\le x.$ Thus, to each $x>0,$ there exists $z \in N$ such that $0<z<x$ and $2z\le x.$ Assume that $a,b \in N^{+}$ with $a+b \ne b+a.$ Suppose $a+b > b+a.$ Put $x=a+b-a-b>0 .$ Let $z\in N$ such that $0<z<x$ and $2z\le x.$ Since N is Archimedean, there exists $m,n\in \mathbb {Z}^{+}$ satisfying $mz\le a <(m+1)z$ and $nz\le b <(n+1)z .$ This implies that

$$\begin{aligned} mz+nz\le a+b<(m+1)z+(n+1)z~~\cdots (1) . \end{aligned}$$

In addition, $-(m+1)z<-a\le -mz$ and $-(n+1)z<-b\le -nz ,$ imply that

$$\begin{aligned} -(m+1)z-(n+1)z<-a-b\le -mz-nz~~\cdots (2) . \end{aligned}$$

Adding (1) and (2) we get,

$$\begin{aligned} mz+nz-(m+1)z-(n+1)z<x<(m+1)z+(n+1)z-mz-nz , \end{aligned}$$

implies that

$$\begin{aligned} \left[ m+n-(m+1)-(n+1)\right] z<x<\left[ (m+1)+(n+1)-m-n\right] z . \end{aligned}$$

Therefore, $-2z<x<2z$, hence, $x<2z,$ a contradiction to $2z\le x.$ Therefore, $a+b=b+a.$ Hence $(N,+)$ is abelian. Now, by Corollary 5.2, it follows that $\left( M_{n}(N),+\right)$ is abelian. Next we prove that $M_{n}(N)$ is Archimedean ordered. Suppose $\mathbf {\overline{0}}\le _{n} A,\mathbf {\overline{0}}\le _{n} B$, $kA\le _{n} B$ for all $k\in \mathbb {Z}^{+}.$ To show $A=\mathbf {\overline{0}},$ let $A=f_{ij}^{r}$ and $B=f_{ij}^{s}.$ Now, $kf_{ij}^{r}\le _{n} f_{ij}^{s},$ implies that $\pi _{i}(kf_{ij}^{r}\rho )\le \pi _{i}(f_{ij}^{s}\rho ),$ for all $\rho \in (N^{+})^{n}, 1\le i\le n$.

That is,

$$\begin{aligned} \pi _{i}\left( \underbrace{\left( f_{ij}^{r}+f_{ij}^{r}+\cdots +f_{ij}^{r}\right) }_{ k \text { times}} \rho \right) \le \pi _{i}( f_{ij}^{s}\rho ),~ \text {for all}~ \rho \in (N^{+})^{n}. \end{aligned}$$

In particular,

$$\begin{aligned} \pi _{i}( f_{ij}^{kr}\langle 1,1,\ldots ,1\rangle ) \le \pi _{i}( f_{ij}^{s}\langle 1,1,\ldots ,1\rangle ) . \end{aligned}$$

Therefore, , and hence, $kr \le s$ for all $k \in \mathbb {Z}^{+}.$ Since N is Archimedean, we get $r=0.$ Now,

$$\begin{aligned} f_{ij}^{r}\langle a_{1},a_{2},\ldots ,a_{n} \rangle&=\langle 0,0,\ldots ,\underbrace{ra_{j}}_{i^{th}},\ldots ,0\rangle \\&=\langle 0,0,\ldots ,\underbrace{0a_{j}}_{i^{th}},\ldots ,0\rangle \\&=\langle 0,0,\ldots ,0\rangle =f_{ij}^{0}\langle a_{1},a_{2},\ldots ,a_{n} \rangle \end{aligned}$$

for all $\langle a_{1},a_{2},\ldots ,a_{n} \rangle \in N^{n}.$ Hence, $f_{ij}^{r}=\mathbf {\overline{0}}.$ Therefore, $M_{n}(N)$ is Archimedean.

The following definition is analogous to ([10], Definition 9.140).

Definition 5.4

If $M_{n}(N)$ is not Archimedean, then for any $A,B \in M_{n}(N),$ A is small with respect to B,  if

$$\begin{aligned} k|A|=\underbrace{\left( |A|+|A|+\cdots +|A|\right) }_\text { k times}<_{n}|B|, ~\text {for all}~ k\in \mathbb {Z}^{+}, \end{aligned}$$

where $|A|=\text {max}~(A,-A)$. That is, $A\le _{n}-A$ or $-A\le _{n}A$.

Definition 5.5

$A\in M_{n}(N)$ is nearly constant if and only if $A_{0}\ll _{n}\left[ \left( M_{n}(N)\right) _{c}\right] ^{*}.$

Lemma 5.6

[11] r is constant in N iff $f_{ij}^{r}$ is constant in $\mathbb {M}_n{(N)}$.

Proposition 5.7

Let N be f.o. and $N_{c}\ne \lbrace 0\rbrace .$ If $r\in N$ is nearly constant in N, then $f_{ij}^{r}$ is nearly constant in $M_{n}(N).$

Proof

Suppose $r\in N$ is nearly constant. Then, $r_{0}\ll N_{c}^{*}$ and $k|r_{0}|<b$ for all $b \in N_{c}^{*}.$ Now, $\underbrace{\left( |r_{0}|+|r_{0}|+\cdots +|r_{0}|\right) }_\text { k times} <b$ implies that $kr_{0}<b$ or $-kr_{0}<b.$

Suppose $kr_{0}<b.$ To show $f_{ij}^{kr_{0}}<_{n}f_{ij}^{b},$ let $\rho = \langle a_{1},a_{2},\ldots ,a_{n} \rangle \in N^{n}.$ Now,

Therefore, $f_{ij}^{kr_{0}}<_{n}f_{ij}^{b}.$ In a similar way, we get $f_{ij}^{-kr_{0}}<_{n}f_{ij}^{b}.$ Now, $f_{ij}^{kr_{0}}<_{n}f_{ij}^{b}$ or $f_{ij}^{-kr_{0}}<_{n}f_{ij}^{b},$ it follows that $f_{ij}^{k|r_{0}|}<_{n}f_{ij}^{b}.$ Now, we show $f_{ij}^{b}\in \left[ \left( M_{n}(N)\right) _{c}\right] ^{*}.$ Since b is constant in N, by Lemma 5.6, $f_{ij}^{b}$ is constant in $M_{n}(N).$ Since $b\ne 0,$ if $f_{ij}^{b}= \overline{0},$ then $f_{ij}^{b}\langle a_{1},a_{2},\ldots ,a_{n} \rangle =\overline{0}$ for all $\langle a_{1},a_{2},\ldots ,a_{n} \rangle \in N^{n}.$ Now, , implies $b=0,$ a contradiction. Therefore, $f_{ij}^{b}\in \left[ \left( M_{n}(N)\right) _{c}\right] ^{*},$ implies $f_{ij}^{k|r_{0}|}<_{n}f_{ij}^{b}$ for all $f_{ij}^{b}\in \left[ \left( M_{n}(N)\right) _{c}\right] ^{*}.$ Hence, $f_{ij}^{r}$ is nearly constant in $M_{n}(N).$

6 Conclusion

There are enormous developments in the study of partial order in algebraic systems such as groups, rings, and modules. In this paper, we have extended the notion of partial order to the matrix nearrings wherein its base nearring is partially ordered with identity. Convexity is one of the significant properties in p.o. nearrings; accordingly, we have defined the convex ideal of a matrix nearring corresponding to a convex ideal in a p.o. nearring. We have established some properties and isomorphism theorems of convex ideals of p.o. matrix nearrings. One can extend the study to the ideal theory of lattice ordered concepts in matrix nearrings corresponding to the existing ideal theory of lattice ordered nearrings.