Introduction

Multiple approaches to conducting STEM investigations have appeared in the literature, with various frameworks advanced (e.g., Bryan et al., 2015; English, 2017; Guzey et al., 2017; Roehrig, Dare, Ellis, & Ring-Walen, 2021). Selecting an appropriate framework to suit specific learning goals continues to be a challenge, with many schools preferring to remain with siloed STEM learning. However, as Li (Feb. 2017) emphasized, such a siloed approach leaves students to integrate their own learning in preparation for future, interdisciplinary problem solving. Previous studies have indicated that students do not spontaneously link knowledge and processes from different disciplines (e.g., Pearson, 2017); rather, these interdisciplinary connections need to be made explicit.

One of the enduring challenges in integrated STEM education is maintaining the integrity of disciplinary content. This is especially the case for mathematics, which is frequently “watered down” or even ignored in STEM investigations (English, 2017; Larson, 2017; National Council of Supervisors of Mathematics & the National Council of Teachers of Mathematics, 2019). Yet, mathematics is fundamental to interdisciplinary STEM experiences, providing the tools to quantify a science activity, analyze engineering designs, and model large sets of data (Mayes, 2019; Roehrig et al., 2021). Even quantitative reasoning in the STEM disciplines is given little credit, despite its importance in conceptualizing a situation in terms of quantities and the relationships among the quantities (Mayes, 2019; Thompson & Carlson, 2017). Unfortunately, quantitative reasoning “is often misrepresented, underdeveloped, and ignored in STEM classrooms” (Mayes, 2019, p. 113).

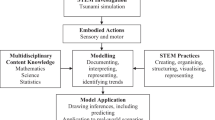
In the STEM investigation reported here, mathematics and science shared a reciprocal relationship (Panorkou & Germia, 2021)—mathematics was enriched through the science context of viscosity and science was enriched through the quantitative modeling of the flow-time data. Quantitative reasoning formed the integrative link. Adopting Mayes and Myers’ (2014) definition, quantitative reasoning incorporates the application of both mathematics and statistics in a meaningful, interdisciplinary investigation within a real-world context. As a comprehensive construct, quantitative reasoning may be viewed as progressing from the act of quantifying, to quantitative interpretation, and then to quantitative modeling (Mayes, 2016). The “quantitative act” incorporates determining attributes of variables to measure within a real-world science context, with the attribute having a unit measure (Mayes, 2016, p. 182). This quantitative act enables movement from context to quantifying (e.g., measuring lava flow times), to interpreting the quantities, and to building quantitative models. Quantitative reasoning is thus a powerful tool in integrating the STEM disciplines, especially in activities where mathematics and science each play a key role.

In the present investigation, students applied quantitative reasoning in exploring the flow times of three simulated lavas of different viscosities down the slope of a hand-made volcano (https://www.teachengineering.org). After modeling the lava flow times for 6 km down the volcano slope, students used their models to predict the times for villagers to evacuate if they resided 10 km down the volcano. Three research questions were of interest: (1) How did students structure and represent their data in model creation? (2) How did students apply their knowledge of viscosity in identifying variation and covariation displayed in their models? (3) How was quantitative reasoning applied in making predictions from their models?

Quantitative Modeling

It is well established that models and modeling can provide rich tools for fostering integrated and real-world STEM experiences, providing opportunities for students to express and develop disciplinary understandings across the STEM fields, to apply different ways of thinking, and to make decisions in the face of uncertainty (Baker & Galanti, 2017; Hallström & Schönborn, 2019; Hjalmarson et al., 2020). As such, models can be integrated within STEM investigations at different developmental points in students’ learning, but are yet to be utilized fully in the elementary curriculum.

Numerous definitions and frameworks for models and modeling abound in the literature, with a good proportion referring to the secondary years. Some of the most frequently cited models include those of Blomhøj and Jensen (2003) and Blum and Leiß (2007), which represent idealized behavior in the sense that it is assumed students proceed smoothly from a real-world problem through to an abstract mathematical model (Haines & Crouch, 2010). Several studies have shown this is not always the case, with students continually returning to the real-world problem and its context (e.g., Doerr, 2007; Lesh et al., 2013). In addressing elementary students’ quantitative reasoning and modeling in the present STEM investigation, I drew on the work of Brady et al. (2015) and Mayes (2014), given that their research provided scope for different levels of development. For the present study, models are systems that describe, explain, construct, modify, or predict a series of experiences (Brady et al., 2015). Quantitative modeling is considered a component of these systems, and incorporates both mathematics and science domains (Mayes & Myers, 2014). Adopting Mayes and Myers’ (2014) perspectives, quantitative modeling refers to the “ability to create representations to explain a phenomenon and to revise them based on fit to reality” (p. 16). As depicted in Fig. 1, quantitative reasoning is a major component in each phase of the investigation, including interpreting the problem and its context, structuring and representing data, and building and applying models.

Fig. 1
figure 1

Quantitative reasoning and quantitative modeling

Full size image

Interpreting Problem and Context

Quantitative reasoning activities are context dependent (Mayes, 2019). The importance of context in working with data, and in modeling in particular, has been well documented—conclusions only become meaningful when they are interpreted in light of the context in which they were generated (Zapata-Cardona, 2018). For modeling problems, problem interpretation draws on both disciplinary content and general knowledge, which can both enhance and detract from an investigation (Gil & Ben-Zvi, 2011; Groth, 2019). Identifying an appropriate context in designing STEM investigations can present challenges when students “have ways of thinking about particular combinations of topic, context, and task that are difficult to foresee” (e.g., assuming that data trends follow the shape of a volcano; Lehrer & Schauble, 2021). Problem context, however, is often ignored as emphasis is placed on abstractions and statistical procedures (Gil & Ben-Zvi, 2011; Langrall et al., 2011; Makar & Allmond, 2018; Rubin, 2020). Modeling can help avoid this over-emphasis on abstractions and procedures, as the required contextual knowledge incorporates not only key features of the problem but also the STEM disciplinary knowledge.

Organizing, Structuring, and Representing Data

It is well documented that our students require statistical foundations if they are to become critical consumers of information, where a lack of or misuse of data can impact public emotions in the absence of evidence-based facts (e.g., Engel, 2017; Engledowl & Weiland, online, 2021; Finzer, 2013). The foundations of data handling need to begin early, yet as Konold et al. (2015) pointed out, there is insufficient research on how students organize and structure data. In their study of middle school students’ approaches to data structuring, Konold et al. (2015) identified the use of tables as the most common approach, with the tables varying in the extent of “completion” (inclusion of core attributes or variables) and “binding” involving gathering of information into cases (i.e., “a physical record of one repetition of a repeatable observational process”, p. 191). Structuring data is essential to students’ creation of models as systems of representation (Lehrer & Schauble, 2007, 2017).

In contrast to their usually narrow classroom experiences, young students display flexibility and inventiveness in creating a range of data structures and representations that have not been taught and/or go beyond what is “traditionally accepted” (English, 2010; Hutchison et al., 2000; Lehrer & Schauble, 2007). Despite the importance of student choice in structuring and representing data, such opportunities have not been as prolific as desired (Cengiz & Grant, 2009; Hutchison et al., 2000; Lehrer & Schauble, 2007). As is often the case, children’s competence in transforming data structures into various representational forms is underestimated; rather, the focus is often on their difficulties in constructing and interpreting a standard set of instructed representations (diSessa & Sherin, 2000; English, 2014; Garcia & Cox, 2010). In particular, children’s meta-representational competence has been overlooked in many studies of early statistics. That is, their capabilities in constructing and productively using a wide range of representations, as well as critiquing and refining representations, have been largely ignored.

diSessa and Sherin’s (2000) research has unveiled representational abilities that are not likely to emerge in studies examining adult-created representations. Capitalizing on these abilities is frequently absent in the classroom, despite their importance in establishing foundational concepts (Fielding-Wells, 2018). When students apply their disciplinary understanding in constructing and representing data in relation to a specific inquiry, they are better able to appreciate the phenomenon in question through their efforts in quantifying it (Lehrer & Schauble, 2004). The application of quantitative reasoning in discerning data patterns paves the way for detecting variation and covariation.

Discerning Data Patterns: Variation and Covariation

Understanding variation in data, which includes determining and justifying reasons for this variation, has received some research in the younger grades (e.g., English, 2014; Franklin et al., 2005; Makar, 2018); however, narrow curricula have reduced the required attention, especially in evidence-based reasoning (Siverling et al., 2021).

Covariation, which is complex for both students and adults, is usually reserved for the secondary school and college levels (e.g., Gil & Gibbs, 2017; Thompson & Carlson, 2017). There are numerous perspectives on covariation including Thompson and Carlson’s (2017) notion of envisioning covariation as “ways of thinking in reasoning” (p. 423); covariation is conceptualized in terms of how individual quantities vary and then how two or more quantities varying simultaneously. Pertinent here is the Covariation Framework of Carlson, et al. (2002), who viewed covariational reasoning as the “cognitive activities involved in coordinating two varying quantities while attending to the ways in which they change in relation to each other” (p. 357). Designed to assess students’ covariational reasoning development, the Framework comprises five levels, namely, coordinating: 1. the value of one variable with changes in the other; 2. the direction of change; 3. the amount of change; 4. the average rate of change; and 5. the instantaneous rate of change.

For this study, covariation is viewed as an association between two variables (e.g., viscosity and time to reach a specified point), where one explores the variability of the individual variables, identifies the shape and strength of the relationship, and explains and generalizes the relationship (Gil & Gibbs, 2017; Watkins et al., 2004). Of interest in the present study was how the students would view the variability in the lava flow times and rates of flow, and the association/s they would identify between lava viscosities and the times taken to reach a designated point.

Covariational reasoning is underrepresented in the elementary and middle schools, with students afforded insufficient opportunities to experience variability in a range of contexts (English & Watson, 2016). Gravemeijer (2000), for example, investigated eighth-grade students’ perceptions of “local” variation (individual points in the data) and “global/aggregate” variation (general trend in bivariate data), and found that students had difficulty in distinguishing between the local and global views of bivariate data; he thus recommended a focus on exploring and comparing univariate data first. Panorkou and Germia’s (2021) study of gravitational force showed how covariational reasoning can support the reciprocal relationship between mathematics and science. Sixth-grade students reasoned about the change in the magnitudes and values of mass, distance, and gravity as they changed simultaneously, as well as their multiplicative change as they varied in relation to each other. The investigation developed students’ understanding of the distance between two objects and their masses as factors that influence gravity. Their construction of mathematical relationships between these quantities enabled them to explore gravity in more depth than it is typically taught. Despite these few studies, there appears limited research on younger students’ covariational reasoning, yet its foundations need to be established before formal study in secondary school and beyond (Panorkou & Maloney, 2020).

Using Models to make Predictions

An important aspect of quantitative modeling is interpretation, where models are used to discover trends and make predictions, with respect to both mathematics and scientific phenomena. As highlighted by Mayes and Myers (2014), using models in this way is central to becoming a “citizen scientist,” who can make informed decisions about issues that are affecting their communities (p. 16).

The generalizability feature of modeling enables key disciplinary and interdisciplinary structures to be applied across multiple contexts (Doerr et al., 2017), as well as informal inferences to be drawn that extend beyond the data. Drawing informal inferences is considered a major component of modeling and entails the application of quantitative reasoning and disciplinary knowledge in detecting variation, making predictions and hypotheses, and exploring and forming decisions involving uncertainty (English, 2016; Lehrer, 2011; Makar, 2016; Makar & Allmond, 2018; Makar & Rubin, 2009). Incorporating informal inference within a modeling pedagogy is considered a more complete approach to learning by developing coherence in foundational statistical ideas (Kazak et al., 2018; Makar & Rubin, 2018).

Although informal inference has received increased attention in recent years, it is still underrepresented in the elementary grades even though young students can detect variation in their everyday experiences and readily make predictions in their daily lives (Doerr et al., 2017; Makar & Rubin, 2009). Given that informal inference is a foundational component of statistical literacy and a precursor to formal inference (Lehrer, 2011; Makar, 2016; Makar et al., 2011), it is of concern that many curricula ignore or downplay informal inferential reasoning as important learning in the elementary grades. This lack of early attention, in contrast to the secondary years and adult population, results in poor foundations for older students who frequently apply statistical methods without understanding or appreciating why, when, or how these are applied sensibly to a range of contexts (Garfield et al., 2008; Groth, 2019).

Method

Research Design

The investigation reported here was part of a larger study, which was longitudinal in nature and conducted across third- through sixth-grade. The present fifth-grade investigation was designed to align with the teachers’ mathematics and science programs for that grade. The investigation was developed in consultation with the classroom teachers, and subsequently revised and refined with their feedback on successive drafts.

Participants

Two classes of fifth-grade students, representing the entire cohort (43 students in total; mean age = 10.6 years) participated in the present investigation. The study was conducted in an all-girls school in a middle socioeconomic suburb in a capital Australian city. As the school had participated in previous engineering education programs we had conducted, they were keen to be a part of the present study. The teachers were well-qualified and experienced in their profession, having taught across a number of elementary grades.

In the first 2 years of the study, the students had undertaken STEM investigations with a focus on foundational concepts and processes from statistics, probability, mathematics, science, and engineering. They had explored viscosity with their teacher as part of their science curriculum prior to undertaking the investigation.

Lava Flow Investigation Procedures

The investigation was implemented across two half-days in each of the two classes, for a total duration of 7 h 40 min. The teachers were supplied with detailed booklets that included the objectives of the investigation, background information on volcanoes including video clips, the disciplinary content being addressed, the activity materials supplied, and instructions for conducting the activity. Meetings were also held with the teachers before and after implementation, to explain the disciplinary content and procedures, and to obtain their feedback on the implementation and students’ progress. Together with the teacher, the research assistant and I observed the classroom implementation and the students’ actions, and where appropriate, answered any queries on procedures, but we did not interfere with their deliberations or with their recording and representations. At appropriate times, as we wandered around the classroom, we asked “how” and “why” questions to give us further insights into the students’ thinking, but we did not directly influence their actions or their model creations. The teachers did not guide the students in their creation of representations; rather, they moved around the room observing their progress and responding to the students’ comments such as the one who stated she would create “a triple bar graph.” The teacher asked, “How would that work?” and listened to the explanation.

The teachers initially demonstrated how to set up the materials, including the volcano cone, the syringes for pouring the liquids, and a split-lap timer (http://www.timeme.com/split-lap-timer.htm). The students were encouraged to undertake the investigation in their groups, as instructed in their workbooks. They were free to design their own forms of data recording and representations. As one student mentioned, “I like doing STEM cause I really like making the um, the stuff and I like finding out how it’s mathematically correct … and learning new things, I don’t usually learn at school … so, we learn how to do graphs and stuff but we don’t know how to like, like put the data on, so we usually in my maths class … we usually use Excel to make a nice graph, but doing them by hand is a lot more fun because it tests yourself.”

The teacher and students first explored volcanoes and lava flow, the history of some well-known volcanoes, and the roles of volcanologists and environmental engineers in monitoring volcanoes and predicting eruptions (e.g., see “TeachEngineering” https://www.teachengineering.org/lessons/view/cub_natdis_lesson04). The volcano context with lava flows was selected because it linked effectively with the students’ prior study of the viscosity of liquids, that is, how rapidly a liquid will flow down an inclined plane (liquids with high viscosity flow very slowly, while those with low viscosity flow more rapidly). A knowledge of viscosity is important in understanding time scales of lava flows, their velocities, the power of their volcanic eruptions, and the hazards associated with different forms of volcanic activity (Edwards et al., 2006).

In line with Mayes’ (2016) “quantitative act” involving progressing from context interpretation to quantifying, students applied their knowledge of liquids and viscosity as they collected measurements on the flow times of three “lavas” for 6 km down the slope of a cone volcano (marked by 6 beacons, each beacon representing 1 km; Fig. 2). Hair conditioner was used to simulate the three lavas of varying viscosities. Each lava was made using 10 mL of conditioner and varying quantities of water. Lava 1, the most viscous, comprised 2 mL of water, while lava 2 was less viscous with 5 mL of water, and lava 3, the least viscous with 10 mL of water. A sample data collection appears in Table 1, with the data showing the covariation between lava viscosity and time taken to travel down the volcano. Although volume, viscosity, and slope affect the surface area that lava covers, we did not place a major focus on these additional factors, although we did question the students on the effect of a volcanic slope.

Fig. 2
figure 2

Cone construction for volcano

Full size image
Table 1 Sample data collection
Full size table

Student groups constructed their volcanoes from nets of a polar grid to form a cone shape (Fig. 2). All groups received the same polar grid and followed instructions for assembling it. The cones were marked with concentric lines around the cone’s surface and a colored apex/crater marked where the liquids were to be poured with a syringe. The students recorded the numbers 1 to 6 on successive lines to indicate the distance, in kilometers, from the top of the cone down to the volcano’s base. The distance between each line was to represent 1 km, with an imaginary “emergency beacon” positioned at each of these 1-km intervals. The teachers reminded the students of their previous work on scale, asked them why the use of a scale was needed for the investigation, and how the scale represented the distances down each beacon to the volcano’s base.

Using a split-lap timer, the students measured the time it took for each lava to reach each emergency beacon down the volcano, as well as an overall time for the lava to reach the village at the base of the volcano. Prior to data collection, considerable classroom discussion took place on the time measurement units that would be obtained, with a focus on whether minutes and seconds would be realistic measures of actual lava flow times. On recalling what they had learned from viewing and discussing the video clips, the students concluded that these measures would not be appropriate for the given context. It was decided to let one minute represent one hour and one second, 1 min. Students explained that lava takes a lot longer to flow down the slope of a volcano, with several factors impacting on flow times. Factors such as the steepness of the volcano and the presence of debris were not taken into account in the actual investigation, however.

In the second component of the investigation, students adopted the role of a volcanologist and were to use the models they had created from the first part of the investigation to predict evacuation times for a newly discovered remote village in Peru, which was at the base of a 10-km volcano. Students were to prepare a report for the “Peru Emergency Evacuation Team” documenting: (a) the time predicted for each lava to flow to the 10-km point, and evidence to support their predictions; (b) how certain they were of their predictions; and (c) factors that might affect their predictions. Reports were presented subsequently to their class peers.

Students were supplied with their own workbooks where they individually recorded their responses, including their data structuring and representations, and responded to the questions asked in the workbook. Although students conducted the actual pouring of the liquids in a group situation, they recorded their own responses for each component of the investigation. There was considerable variation in the responses of group members, with some individual students having more than one attempt in their responses (e.g., completing a bar graph but then switching to a different graph for their final representation). The workbooks were an important component of the data collection corpus and also served to scaffold “complex learning” by giving structure to the investigation and problematizing the disciplinary content and practices (Reiser, 2004, p. 273).

Data Collection and Analysis

Several forms of data collection were undertaken including audio- and video-recordings of small group interactions as students completed the investigation, as well as whole-class discussions. Two groups in each class (referred to here as focal groups) were chosen for video-recording and were used to illustrate in greater depth some of the responses and interactions in undertaking the investigation. These focal groups comprised three or four students, who could converse and work together, and were of mixed achievement levels. The teacher advised on the identification of students who met these criteria.

In answering the three main research questions (RQ), the data analyses focused on students’ data structuring and representation (for RQ1), their application of viscosity knowledge in detecting variation and covariation in their models (RQ2), and their quantitative reasoning in using their models to make predictions (RQ3). All students’ individual responses were recorded in their own workbooks. The responses were coded using deductive coding (Miles et al., 2019) and then analyzed using frequency distributions. The senior research assistant, who was experienced in data coding, commenced the coding of the workbook responses using content analysis to generate a range of codes. We then both undertook separate coding to refine the coding schemes. Any discrepancies were identified and were subsequently modified through further data checking including reviewing students’ workbook responses and transcripts of their class presentations. For example, in the coding of how students used their models to predict the times for the lavas to flow 10 km down the volcano slope, there was initial difficulty in deciding on the coding of eight students because of their changes in model use or a lack of clarity in their recorded responses. Mutual agreement was readily reached on further reviews of all the data sources.

Students’ data structures and representations (RQ1) were coded using aspects of Konold et al. (2015) system for analysis of students’ structuring of cases (one case being a “record of one repetition of a repeatable observational process”, pp. 194–195) The number and type of structures and representations were noted, together with the inclusion of variables and annotations (e.g., measurement units, “beacon times” and “total times,” differences in times, conversions from seconds to minutes).

With regard to RQ2, students’ application of viscosity knowledge in detecting variation and covariation, data were coded according to students’ detection of the variability in the lava flow times and in rates of flow, and the association/s they identified between lava viscosities and the times taken to reach a designated point (in line with Gil & Gibbs, 2017; Watkins et al., 2004).

Coding of students’ explanations of how their representations showed covariation between lava flow times and viscosity included whether they referenced specific components (e.g., height of the bars, the difference in height of the bars, or the slope or angle of the lines), and whether their explanation related the component to viscosity or different lava flow times or rates of flow (e.g., “It shows the variations by comparing them because taller bars are slower than smaller bars, that Lava 1 had the smallest bars, so it had the least viscosity and lava 2 had the tallest bars, so it had the most viscosity.”).

For RQ3, how students applied quantitative reasoning in making predictions from their models, data were analyzed in terms of aspects of Mayes’ (2016) progression, specifically, quantitative interpretation and quantitative modeling. Consideration was also given to whether students identified the nature and strength of the covariation between lava viscosity and flow times, and how they explained and generalized this relationship in making their predictions (Gil & Gibbs, 2017; Watkins et al., 2004).

As previously noted, the transcripts of the focal groups served to illustrate in greater depth some of the students’ responses and interactions in responding to the workbook questions. The transcripts were analyzed qualitatively, adopting the form of iterative refinement cycles for in-depth evidence of students’ learning (Lesh & Lehrer, 2000). Through repeated viewing of the transcripts, examples of focal group students’ responses illustrating aspects of the research questions were identified (e.g., students’ discussions on how covariation was displayed in their models).

Results

Q1. Students’ data structuring and representations

All students favored a table format in recording their data, reflecting Konold et al.’s (2015) “flat table” format (Fig. 3), where the rows of the table comprise cases and the columns contain a variable or attribute (pp. 194–195). Students’ tables displayed differences in the inclusion of core attributes or variables, with some students attempting to include all variables (time, lava number, beacon number, distance) by incorporating them within rows or columns. There were also differences in the number of tables the students used to record their data, with the majority of students (83%) using just one table (Fig. 3), while the remainder used three tables, one for each lava. The use of three tables could have served to simplify the recording, or alternatively, the lava types were seen as distinct entities rather than variations in solution viscosity.

Fig. 3
figure 3

Use of flat tables to record lava times

Full size image

As an illustration of students’ deliberations in recording and structuring their data, an excerpt from one of the focal groups is provided below. The group was cognizant of the need to record first prior to representing the data, and subsequently created one table:

Elise: Remember you’ve got to show 3 different lavas.

Bettina: Oh! So I’ll do Lava 1, Lava 2, Lava 3, and split times … Or maybe we can do a graph instead of a table?

Elise: No … first you need a way to record your data.

Bettina: So then you write Lava 1, Lava 2 and Lava 3 (indicating 3 column headings in the one table).

Elise: So, then you do like a little extra column (for recording beacon numbers).

Stephanie: Yes, cause then you can record the times (in the table).

Students generated a number of representations, with vertical bar graphs the most common (Table 2). These graphs displayed the time variable on one axis (the y-axis for vertical bar graphs, x-axis for horizontal bar graphs) and either beacon numbers (denoting distance) or lava type (denoting viscosity) on the other axis (the x-axis for vertical bar graphs, y-axis for horizontal axis). Line graphs were less popular, with approximately 20% of students generating these.

Table 2 Representations constructed (n = 43*, 1 student absent)
Full size table

It is interesting to note the distribution of bar graphs created, with stacked bar graphs appearing as frequently as the remaining bar graph forms. Students’ stacked bar graphs comprised a bar for each lava type, with sub-bars designating beacons 1–6 as illustrated in Fig. 4. Such a graph may be regarded as more compact than the other two forms and can facilitate comparison of the lava types’ duration of flow (Casey et al., 2019), but can also be more difficult to interpret because of the number of variables indicated on a single bar.

Fig. 4
figure 4

Sample of a stacked bar graph

Full size image

The graphs displayed in Figs. 5 and 6 may be referred to as ordered case value bar graphs (Konold & Higgins, 2002) or as series comparison graphs (Moritz, 2004). Figure 5 shows six bars for each lava type on the x-axis, with each set of bars ordered by beacon number (with beacon number denoting distance traveled). For these representations, ordering is considered important in assisting the scanning of values to offer a global summary, and may also serve as a way of reducing the complexity of bivariate data (Moritz, 2004). The representation displayed in Fig. 5 is interesting in that the student applied quantitative reasoning in determining time differences between beacons.

Fig. 5
figure 5

Use of ordered case value bar graph. Note. B1–B6 refer to beacons passed. Time (in minutes) to reach each beacon is indicated at the top of each bar. Time differences from one beacon to the next are displayed for lava 1 but are incomplete for the remaining lavas

Full size image
Fig. 6
figure 6

Second type of ordered case value bar graph

Full size image

The next example (Fig. 6) is similar in display to Fig. 5 but comprises three bars designating the lava types for each beacon (1 km distance) on the x-axis and time on the y-axis. A representation of this form may also be regarded as a means to reduce the complexity of the bivariate data. The example in Fig. 6 can be viewed both locally (i.e., each set of lava types with the flow times for each lava showing a decline as each beacon is passed), and globally (across all bars), where there is an increase in flow times across all beacons. As such, this representation may be viewed as leading towards the line graph.

Line graphs, which the students had not been formally taught, were generated by 9 students, two of whom completed a bar graph as well. The bar graphs displayed the flow times for each of the three lava types for each beacon (as in Fig. 5). Students who did line graphs preferred to do these by hand (as illustrated in Fig. 7), with only three using Excel.

Fig. 7
figure 7

Hand-drawn line graph

Full size image

Students’ group interactions on their representational choices revealed their awareness of different graph forms and their reasons behind their decisions. For example, in deciding on a line graph, one focal group commented: “They’re [referring to another group] doing theirs on Excel?” A group member responded, “We’re going to do ours the harder way … we are going to be old fashioned and use good old pencil and paper.” “And a ruler.” Another group debated the types of graphs that would be most appropriate for representing their data, including line graphs. Maryanne, for example, maintained that a “line graph would work because we have 3 different colours and then let’s say the middle of it, it goes up to 13 min at Station 1 (Beacon 1), then it goes down to 2 …, then it goes up again to 13 min to 14 min at Station 2 (Beacon 2) and it continues like that and that is why a line graph would work. It would be so much easier than everything else.” Others preferred a bar graph for ease of comparison “You could do a bar graph and put them up and compare which one … flowed the fastest.” Another suggestion to create “a line graph but in the shape of a volcano” (activity context) was rejected by the group members as inappropriate for representing the data.

Students’ application of meta-representational competence (diSessa & Sherrin, 2000) was evident in their responses to the workbook question that asked how they might improve their representation to better show their data and trends in the data. Sixty-three percent of all students (n = 42) noted that they would enhance the overall display to facilitate data interpretation and comparison, and/or increase accuracy. Twenty-one percent referred explicitly to improving core components of their representations such as marking the height of the bars more accurately, or better delineating the x- and y-axes. A few students mentioned doing more tests to increase the accuracy of the data, while a couple of students suggested doing a different type of representation or restructuring their existing bar graph.

RQ2. Students’ application of viscosity knowledge in identifying variation and covariation

In response to the workbook question asking how viscosity affects the lava flow, the majority of students could apply their knowledge of viscosity in explaining lava flow times, suggesting they were aware of the covariation between viscosity and flow time (Table 3).

Table 3 How viscosity affects lava flow (n = 42; 1 absent)
Full size table

Students who did not elaborate on how viscosity affects lava flow gave responses such as, “The thicker the lava, the longer it takes to reach the bottom of the volcano.” Such responses align with the first two levels of Carlson and et al.’s (2002) Covariation Framework, namely, coordinating the value of one variable with changes in the other, and the direction of change. That is, an increase in lava viscosity is associated with an increase in time to reach a beacon.

Responses that included accompanying explanations, however, could be considered to be reaching level 3 of the Covariation Framework. That is, they not only clearly displayed the first two levels but also indicated the amount of change. Furthermore, they linked viscosity with flow rates as well as with flow times. Responses include “The lower the viscosity the faster the lava will flow down the volcano, so the higher the viscosity the slower it will go because of its resistance to flowing,” and “If a liquid has a high viscosity than (then) it won’t flow as well so it will take longer to reach the bottom. Lava 1, it has a high viscosity. If a liquid has a low viscosity than (then) it will flow faster. Lava 2 and Lava 3 have a lower viscosity than Lava 1 because it took lava 1 1 h 2 min to reach the village but in lava 2 it took 51 min and in lava 3 it only took 25 min.”

Almost half of the students could identify relevant components of their representations that showed covariation between lava flow times and viscosity, but only 24% of students offered detailed explanations specifically highlighting the covariation (Table 4).

Table 4 How representation shows covariation between viscosity and lava flow times (n = 42;1 absent)
Full size table

Responses of the last type in Table 4 suggest that these students were taking a more global view of the data (Gravemeijer, 2000), that is, they were looking at trends across the three lavas.

RQ3. Students’ application of quantitative reasoning in making predictions

The quantitative reasoning students applied in making predictions from their models displayed a range of mathematical and statistical approaches, together with a knowledge of viscosity (cf. Mayes & Myers, 2014). Adopting Mayes’ (2019) perspectives, it is conjectured that the students’ quantitative reasoning entailed both quantitative interpretation and quantitative literacy. That is, quantitative interpretation was evident as the students used their models to determine trends and make predictions (e.g., identifying patterns in the time differences between existing beacons), while quantitative literacy was displayed as the students applied fundamental mathematical and statistical concepts (e.g., modes and means) to compare, manipulate, and draw conclusions. Some of the students displayed more sophisticated quantitative reasoning than anticipated, such as maximizing times for the villagers to escape, as described below. The forms of quantitative reasoning the students displayed were not taught; rather, the students developed these independently as they interpreted their modeling of their data. Six forms of quantitative reasoning were noted:

Doubling

Sixteen percent of student responses (n = 43, 2 absent, 2 students displayed two approaches) doubled the time taken to reach the 5-km beacon. Some of these students simply read the times they had recorded for the 5-km beacon and doubled these times, while others calculated the time difference between each beacon (i.e., 0 – 1 km, 1 – 2 km etc.) up to the 5-km beacon, added these times, and then doubled the total.

Decomposing

This second approach was similar to the first, except 10 km was decomposed into 4 km and 6 km to determine the total time for each lava to reach a 10-km point. That is, the time to reach the 4 km beacon was added to the time to reach the 6 km beacon for each lava (23% of responses). Some students determined these times by calculating, for each lava, the time differences between each beacon and then adding the 4-km and 6-km totals.

Maximizing Times

A few students (7% of responses) maximized their times for the villages to escape by recording the time differences between each beacon, selecting the smallest difference, and then multiplying this difference by 10. One student explained why she chose the smallest difference, namely, “… what I did for my method is that I counted how many minutes it took the lava to flow past each beacon and just in case the lava goes faster, I chose the smallest number and I times it by ten because there is [sic] 10 beacons. I chose the smallest number because I have to make sure everyone in the village is safe.”

The student’s documentation appears in Fig. 8.

Fig. 8
figure 8

Maximizing times

Full size image

Determining Mode and Mean Times

The most common response calculated the mode and mean times between beacons (42% of responses). This involved finding the mode or the mean of the time differences between beacons to the 6 km point and then multiplying the result by 10, or finding the mode or the mean of the time differences between beacons to the 6 km point, multiplying the result by four and adding this to the time taken to reach the 6 km beacon.

Identifying a Pattern

A few students (12% of responses) identified a pattern in the time differences between existing beacons (e.g., “big jump, no jump, small jump, big jump, no jump, small jump” …) and repeated this pattern of differences until a 10-km point was reached. Alternatively, students used their identified pattern to estimate the time differences between beacons if they were extended to 10 km.

Below is an example of a student explaining her model to her peers and how she applied both the second and fifth approaches above:

Today we have discovered that the volcano near you could erupt any minute! I have done an experiment on a volcano 6 km high. We had three different samples of different Lavas. Lava 1, Lava 2 and Lava 3. Since your volcano is 10 km high, I have predicted on how much time you have to evacuate everyone. First I wrote up how much time it took after 1 km. Then I discovered how long it took to travel between them [beacons]. After that, I added how long it took for each one to come down 6 km and 4 more other top numbers. When I was trying to find the time it will take, I discovered a pattern. Some jumps between them were small and some were big. I also discovered that sometimes there were no jumps. I took the time from 6 km and 4 more numbers that were after the lava passed 1 km. I am certain of my prediction, because at the end I did a rough check to make sure that they are at least 20 minutes more. My predictions are: Lava 1 = 79 minutesLava 2 = 172 minutes Lava 3 = 38 minutes. So if I were you, I would try to evacuate everyone in 38 min.

In the next example, the student included reference to a mode time but primarily adopted the second approach above. Science disciplinary knowledge was incorporated in her approach.

I am to believe that the new village in Peru is in danger of a volcanic eruption. We know this for we have been monitoring the magna chamber and we have found that the pressure has been rising. Sadly, we don’t know the consistency of lava. Here are our most likely predictions. For the thickest lava we have estimated 1.2 hours for the lava to reach the village. Also the fastest was estimated as only 30 minutes but a median of both would be only 1 hour. We found our ideas on these estimates by using research on another volcanic eruption. This volcano was only 6 km high and each km a beacon would go off. We counted the minutes between beacons. So to estimate the possible time for evacuation we looked for the shortest amount of time for a beacon to go off then we timesed [sic] it by 10. Hopefully, there is time to evacuate.

Certainty of Predictions

In reporting the certainty of their predictions, students referred to their modeling, their knowledge of viscosity, and the problem context in identifying variables that could have an impact. Reference to viscosity and lava flow rates, the dimensions of the volcano (e.g., “incline of the volcano”), and environmental factors were made. For example, one student indicated “We chose the most common number [difference] and we multiplied it by 10 so we could work out the most likely average, although how steep the mountain is and the viscosity of the lava, or type of lava, type of mountain or how rocky it is or even the weather could change that…” Another student stated she was “… 60% sure this is true although the type of lava or how steep the mountain is could affect the speed of the lava flow. It could also be affected by the viscosity.” Errors occurring in conducting the experiment and in performing the calculations were also cited, for example, “I believe that I am 95% percent correct because of the differences when people applied the lava. Their calculations could be incorrect too.”

Discussion

The ability to apply mathematics within a real-world context is at the core of quantitative reasoning, which, in turn, is a key component of STEM integration (Mayes, 2019). As the application of mathematics and statistics in a real-world context, quantitative reasoning formed the integrative link in the present investigation, with mathematics and science sharing a reciprocal relationship (Panorkou & Germia, 2021). Unfortunately, quantitative reasoning is not given due credit for its significant role in STEM integration, despite its increasing importance in today’s world where quantitative modeling and interpretation play major roles (Mayes, 2019).

Three research questions were of interest in the present study, namely, how students structured and represented their data in model creation, how they applied their knowledge of viscosity in identifying variation and covariation displayed in their models, and how they applied quantitative reasoning in making predictions from their models.

Students’ Development of Quantitative Models

Organizing and Structuring Data

With the freedom to approach model creation in their own way, students displayed an overall level of competence beyond curriculum expectations (cf. Lesh & Zawojewski, 2007).

Not surprisingly, students created “flat tables,” where rows of their table comprised cases and the columns contained a variable or attribute (Konold et al., 2015, pp. 194–195). There were unexpected differences, however, in the number of tables a few students used in recording their data—the majority of students used just one table for recording and structuring their data, while a few used three tables, one for each lava. Whether students used three tables to reduce the complexity of their data structuring or whether they viewed the lava types as distinct entities rather than an aggregate, requires further research. Nevertheless, the use of three tables could be regarded as a “stepping stone” to consolidating all three lava forms within the one table. Giving children the freedom to choose their own forms of data recording and data structuring can reveal insights into their quantitative reasoning that might otherwise go unnoticed.

Other differences included the extent of table completion (Konold et al., 2015), that is, the inclusion of core attributes or variables. Some students attempted to include all variables (time, lava number, beacon number, distance) by incorporating them within rows or columns. This varied display of completeness might not only indicate students’ attempts to include as much information as possible but also their intention to model their investigation more accurately (cf., Konold et al., 2015). Such approaches to incorporating all variable labels might be viewed as a stepping stone to “hierarchical tables” (Konold et al., 2015), where relationships among cases (e.g., beacon numbers and distances) are placed in a nested spatial arrangement (e.g., beacon numbers with distances underneath).

Representing Data

Students’ preference for representing their data in bar graph formats was evident, as typically noted in the literature and commonly displayed in textbooks (Batanero et al., 2018). The number of stacked bar graphs, however, was not anticipated given that these were not included in the students’ curriculum. Interpreting these graphs is not easy, as students have to deal with two variables for each bar, such as lava type (viscosity) and beacons passed (distance); it is thus not surprising that stacked bar graphs are infrequently featured in studies of young students’ representations (e.g., Leavy et al., 2018; Moritz, 2004). Yet, this study has indicated that young children are capable of more advanced representations than we give them credit for, reflecting di Sessa and Sherin’s (2000) work on meta-representational competence.

Identifying Variation and Covariation in Quantitative Models

Models comprising ordered case value graphs and line graphs appeared to facilitate the detection and interpretation of covariation between lava viscosity and flow times. All students ordered their cases by one of the variables, with ordering a key feature in enabling the scanning of values to obtain a global summary (Konold, 2002). Although line graphs may be regarded as displaying bivariate data more effectively, those displaying ordered case values may also facilitate reasoning about covariate data (Moritz, 2004). As such, they may be viewed as natural progressions towards line graph models. On the other hand, as Groth (2019) indicates, case value bars can sometimes be less effective in displaying certain distributional features, in contrast to those where aggregated data appear more compact (e.g., line graph). Questioning students on how they could improve their representations to facilitate data interpretation could be a step in advancing their progression towards more compact quantitative models.

The ability to generate more sophisticated representations, however, does not always mean that students can detect aggregates and their characteristics (Groth, 2019). Students had some difficulty in explicating a global view of covariation. It appeared that they could identify the variation in the viscosity or time separately, but identifying how their models displayed covariation between the two proved more problematic. Nevertheless, students’ ability to link their knowledge of viscosity with lava flow times suggests at least an implicit understanding of covariation, which they could readily describe verbally.

Applying Quantitative Reasoning in making Predictions

An analysis of the students’ reasoning in making their predictions suggested they were applying both quantitative interpretation and quantitative literacy (Mayes, 2019), together with their understanding of viscosity and their contextual knowledge of volcanoes. Students’ diverse applications of quantitative reasoning were not anticipated, especially since they were not given any particular directions. Likewise, students displayed multiple ways of reporting the certainty of their predictions, making reference to viscosity and lava flow rates, the dimensions of the volcano (e.g., “incline of the volcano”), and environmental factors. Students’ allowance of additional time for unanticipated real-world conditions further indicates the impact of the investigative context on the students’ responses.

In reflecting on the students’ reasoning in making predictions, it is interesting to consider Johnson et al. (2016) notion of a reflexive relationship between quantitative reasoning and quantitative literacy. Viewing quantitative literacy as resulting from quantitative reasoning, Johnson et al. argued that subsequent quantitative literacy enables further quantitative reasoning. An alternative conjecture on the students’ reasoning could thus be that the quantitative literacy they had developed from the previous components of the investigation facilitated further quantitative reasoning as they looked for ways to predict times for 10 km.

Of interest is whether students’ knowledge of viscosity was strengthened during their investigation. Although this aspect was not specifically tested, analysis of the focal group transcripts suggests this could have been a possibility, where some students applied their knowledge of viscosity to the heating and cooling of real-world lava. For example, one student explained, “Some things that might affect my prediction…is the steepness of the hill because if the hill is steeper the lava will flow faster. The temperature is also a big factor that will impact on the speed because when lava cools down it’s viscosity changes and it gets a lot thicker so it will take longer to flow.”

Limitations

A number of limitations to this study should be noted. First, the students were from a single-gender, non-state school and were thus non-representative of the broader population of students. The inclusion of a cross-section of students would enrich the present findings and enhance the analytic generalization of the theoretical framework (Yin, 1994). Applying the framework to incorporate other STEM disciplines, such as engineering, would also contribute to its theoretical transferability (Maxwell, 2005). Engineering, for example, has substantial scope for applying modeling (English & King, 2015; Moore et al., 2014). Second, it could be argued that the use of hair conditioner is not an appropriate material for simulating the viscosity of lava, which cools and solidifies as it flows, often slowing in the process. Although the students appeared to accept this simulation, it is worth discussing this aspect with the students beforehand. Third, follow-up investigations in which students determine the measures and measurements they undertake could reveal further insights into their quantitative modeling developments. Finally, consideration of ways in which the theoretical framework and the activity can inform teachers’ reflections on, and development of, their pedagogical knowledge and skills in implementing STEM investigations would add to the study.

Concluding Points

This study has revealed how fifth-grade students can successfully undertake a STEM investigation involving quantitative reasoning, including quantitative modeling and interpretation, areas that are underrepresented in many curricula. Opportunities for elementary school students to construct their own quantitative models are not frequent, nor are their experiences with different forms of quantitative reasoning, especially when standard textbooks are used (Jones et al., 2015).

Students’ responses support claims that statistics should begin earlier than recommended in the Common Core State Standards (mathematics). As Groth (2019) argued, “…the deep understanding of the content described in the Grade 6 standards is likely to occupy a much greater timespan than generally anticipated or available” (Groth, 2019, p. 32). Indeed, experiences with STEM investigations involving quantitative reasoning should commence in kindergarten and continue across the grades through to graduate school. As Martinez and Lalonde (2020) emphasized, attitudes towards statistics and mathematics are formed early, so it is critical that we provide elementary grade students with positive and meaningful experiences.

Although the present investigation was constrained partly by specific measures being given (e.g., distances between beacons), students nevertheless had the flexibility to construct their own quantitative models. Given that students were not directed on how to structure and represent their data, or how to apply quantitative reasoning, it is conjectured that modeling encourages flexible learning and adaptive expertise (English & Watson, 2018; McKenna, 2014, p. 232). Such expertise is reflected in the generation of new knowledge (often beyond students’ grade level), which can be subsequently applied to related investigations. Within these investigations, students should be encouraged to describe how they were using their STEM knowledge bases and how these facilitated their learning during the activity.

Since commencing the project, the students had been encouraged to generate their own paths to solution, within the parameters of each investigation. The teacher’s role has been one of facilitating, stimulating, and questioning, not directing. As Roehrig et al., (2021) emphasized:

Integrated STEM education requires that students are afforded the opportunity to determine their own solution paths. Teacher proscribed directions will result in a single design solution, and integrated STEM education calls for the possibility of multiple possible solutions to a problem. The open-ended nature [of] these integrated tasks requires careful facilitation from teachers, helping students to understand the STEM practices in which they are engaging and reflecting on their process (p. 4).