1 Introduction

Fire severity represents the magnitude of the ecological changes produced by a fire across all vegetation layers in an ecosystem, as opposed to fire intensity, which measures the energy released by a fire (sensu [73]). Conventionally, fire severity has been estimated from direct observations on the burnt ground by assessing canopy and stem scorch, plant mortality and soil loss [75]. However, in the last few decades, there has been increased access to remotely-sensed data (multispectral satellite images) suitable for assessing fire severity [38, 144, 166]. Multispectral images show changes in the reflectance of burnt areas, and these can be used to understand environmental drivers that influence fire severity [90, 164].

Fire severity is influenced by local and regional environmental drivers that interact at various spatio-temporal scales. For example, rainforests produce abundant aboveground biomass but, because they mostly remain wet, they only undergo high-severity fires after protracted drought [11, 27]. In contrast, ecosystems such as dry forests and savannas have enough aboveground biomass and recurrent dry periods to burn at varying fire severities [17, 117]. In addition, weather influences fire severity from a seasonal to an hourly scale through changes in humidity, precipitation, temperature and wind [18, 83]. For instance, in south-east Australia, vegetation begins to dry throughout late spring and early summer, while hot days with strong, north-westerly gusts are frequent, which, in the presence of ignitions, can lead to high-severity fires that spread rapidly [28]. Furthermore, fire severity is affected by environmental drivers that are temporally stable, such as topography [45].

Most studies of drivers of fire severity that have used satellite images have been limited in scale and centred on a single fire [82, 154, 164], a small set of fires occurring over a short timespan [6, 106, 155] or a fixed vegetation type, usually forests [35, 155]. The few studies that have focused on multiple fires have tended to consider the influence of a small number of environmental drivers on fire severity, commonly climate, topography, vegetation and weather [100, 106, 111, 114]. Moreover, few studies have investigated the drivers of fire severity in prescribed burns across forested and non-forested vegetation [6, 30, 154, 162].

The temperate Australian island of Tasmania, and especially western Tasmania, is an important study system for the response of vegetation to fire (Fig. 1a–c) [68, 171]. Fire is the only significant source of disturbance across western Tasmania and creates landscapes consisting of complex, small-scale mosaics of fire-adapted and fire-sensitive plant communities [49, 97]. Such spatial variation of post-fire landscapes, also influenced by different lengths of fire intervals, is known as pyrodiversity [99]. In western Tasmania, this pyrodiversity is partly driven by lightning fires, which have become the primary source of ignitions since the 2000s [142]. Although it is uncertain whether lightning has increased in western Tasmania in the last few decades, there remains evidence that lightning-ignited fires and total area burnt are increasing [16, 142]. Another feature of the pyrodiversity of western Tasmania is anthropogenic fires, including accidental ignitions and prescribed burning, which creates barriers to or reduces the spread and severity of wildfires [51, 78]. Indeed, Tasmania is a unique ecological system for pyrogeographical studies because of its multi-dimensional fire regimes and complex landscapes with various vegetation types.

Fig. 1
figure 1

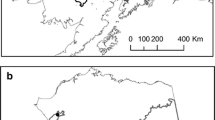
The study area in western Tasmania. (a) All 127 fires classified by aggregated vegetation (forested or treeless) in the Tarkine and the Tasmanian Wilderness World Heritage Area (TWWHA). The two fires shown in panels (d) and (e) are highlighted. (b) Major vegetation types. (c) Mean annual precipitation (mm) and elevation (m above mean sea level). (d, e) Examples of ΔNBR computed using Landsat images (left), and the redigitised fire boundaries by aggregated vegetation (right). (d) Mount Castor wildfire and (e) Dempster Plains North prescribed burn

Full size image

This study aimed at identifying the main environmental drivers (predictor variables) of fire severity of wildfires and prescribed burns, in forested and treeless vegetation, in western Tasmania. We used multispectral Landsat (Land Satellite, United States Earth Observation program; [85]) images to estimate, through a spectral index (Delta Normalised Burn Ratio; [75]), the severity of a 25-year sample of fires. We then used these data to answer the questions: (1) what are the most important environmental drivers that affect fire severity?, and (2) can we validate with remote sensing that forest wildfires are generally more severe than prescribed burns? To date, it has been challenging to answer these questions in western Tasmania using satellite images because of the high frequency of clouds [138]. Our study is novel in that we determined the relative importance of a range of potential environmental drivers of fire severity across forested and treeless vegetation, for a sample containing wildfires and prescribed burns, in a region where clear satellite images are scarce.

2 Methods

2.1 Environmental Context of the Study Area, and Predictor Variables

The study area includes the Tasmanian Wilderness World Heritage Area in western Tasmania, plus the adjacent Tarkine region in north-west Tasmania (Fig. 1a) [8, 9]. This area contains one of the largest undeveloped temperate landscapes in the Southern Hemisphere [172] and is predominantly reserved, although it also contains significant areas of commercial forestry [7]. The region is mountainous and has a cool and wet climate, with approximately 80% more precipitation in winter (June–August) than in summer (December–February) [12, 13]. The contemporary climate of the region is strongly shaped by the interaction of westerly cyclonic winds and the rugged terrain of the island [49], leading to pronounced climate gradients, with mean annual precipitation ranging from slightly over 1000 mm in north-west Tasmania to over 3500 mm in montane areas of the central west (Fig. 1c; Figure S1) [13]. Short heatwaves during the summer and dry lightning can create conditions favourable for fire [50].

The combination of varied climate, geology and topography, and the practice of prescribed burning, is reflected in a complex mosaic of plant communities, including fire-adapted eucalypt forests and sedgelands, and pyrophobic cool-temperate rainforests and wetlands (Fig. 1b) [128]. Another important feature of western Tasmania is the abundance of organic soils, epitomised by moorlands dominated by tussock-forming sedges, especially the highly pyrogenic Gymnoschoenus sphaerocephalus, or buttongrass [69]. Sphagnum bogs are present but uncommon [165]. Buttongrass moorlands remain a priority in prescribed burning in western Tasmania due to their high flammability and rapid growth after rain [98]. Fire management is a prominent issue in the region, especially since the 2016 fire season, where lightning fires propagated quickly and damaged permanently fire-sensitive plant communities and Aboriginal heritage sites [124].

Considering the environmental characteristics and pyrodiversity of western Tasmania, and our knowledge of fire ecology, we identified a priori 42 ecologically relevant predictor variables that could influence fire severity in the study area. Our predictor variables were classified into four groups: six fire-related attribute variables, 19 bioclimatic variables, six fire-weather variables and 11 environmental and topographic variables (Table 1; Table S2).

Table 1 Predictor variables used in the Random Forests analyses. “Round” indicates whether the predictor was selected as important in the three rounds of Random Forests: F is forested and T is treeless. The predictors selected in the third round of Random Forests are highlighted in bold. Acronyms and abbreviations: The LIST is The Land Information System Tasmania; BARRA is the Bureau of Meteorology Atmospheric high-resolution Regional Reanalysis for Australia [143]; DEM is the 25-m Digital Elevation Model of Tasmania [149]; DPIPWE is the Tasmanian Department of Primary Industries, Water and Environment; FFDI is Forest Fire Danger Index; WorldClim 2 is WorldClim Global Climate Data version 2 [47]
Full size table

The bioclimatic raster variables, from the WorldClim Global Climate dataset, are the variable averages for 1970–2000 [47], while the fire-weather raster variables, from the Bureau of Meteorology Atmospheric high-resolution Regional Reanalysis for Australia [143], are for the years 1990–2019. For the fire-weather variables, for each month from 1990 to 2016 and each pixel, we calculated the mean, mean maximum and mean minimum Forest Fire Danger Index (FFDI) and soil moisture [95]. Most rasters from all groups of variables had a small number of pixels with missing data, either inherited from the original raster data sources, or created during the rasterisation of vector layers to help increase processing speed later in the sampling process. Hence, we applied a three-by-three neighbourhood focal to all rasters to impute missing values using the focal function (mean) from the raster R package (version 3.3.13; [64]).

2.2 Fire History and Fire Selection

We used the Tasmanian fire history dataset [37] to select the boundaries of all prescribed burns and wildfires (ignition cause different than prescribed) in the study area. This dataset was limited because it did not provide fire end dates and did not contain fire isochrones (lines that show the growth of the fires throughout time). Fire perimeters in the fire history dataset were collected by a variety of means, including aerial photographic interpretation, and active aerial and on-ground surveys, and may be of varying accuracy, so efforts were made to refine these perimeters to actual burnt area as detected by satellite (see below). The study area is remote, with few roads, so suppression effort is low and most boundaries represent natural meteorological and topographical boundaries, rather than firefighting control lines. In the Tasmanian Wilderness World Heritage Area, we selected fires ≥ 100 ha from 2000 to 2016 because, due to the unavailability of more frequent overpasses afforded by Landsat 7, the quality of available satellite images before the 2000s was poor, with frequent clouds, cloud shadows and haze. Conversely, for the Tarkine, due to the larger number of fires, we selected fires ≥ 1000 ha from 1990 to 2016. We excluded fires in the Tarkine from before the 1990s due to the scarcity of Landsat images before this time.

Next, we used the EarthExplorer online database (EROS 2017–2020) to search and download multispectral Landsat images (30-m pixel resolution) of the selected fires. For each fire, we endeavoured to find the best available pre- and post-fire image, as close as possible in time to the ignition date, but ensuring that, at the time when the post-fire image was taken, the fire had finished burning (fire scar in the image matched or partially matched the fire boundary). It was important to select post-fire images soon after the fire to capture the fire scar with the maximum accuracy before vegetation regrowth or recovery begins (initial assessment sensu [75]), although it was often only possible to select post-fire images after or during the next growing season (extended assessment sensu [75]). Besides, to minimise seasonal (e.g. albedo) and phenological (e.g. tree flowering, leaf shedding) effects, pre- and post-fire images from the same time of year (e.g. summer) were preferred, although not necessarily from the same time of year as the fire ignition date (Table S1) [25]. This meant that, sometimes, we selected a pre- or post-fire image further back or later in time, respectively, from the fire ignition date, so both images were cloud-free and from the same season. Also, we verified that no other fires occurred within the fire boundary between the fire ignition date and the post-fire image date.

After excluding fires with unsuitable Landsat images (e.g. images with clouds, haze and detector failures; [158]), the sample consisted of 127 fires, comprising 112 different Landsat images from four Landsat scenes (path-row: 91–89, 91–90, 92–88 and 92–89) [2] and spanning three Landsat satellite missions: Landsat 5 Thematic Mapper (1984–2013), Landsat 7 Enhanced Thematic Mapper Plus (1999–ongoing), and Landsat 8 Operational Land Imager and Thermal Infrared Sensor (2013–ongoing) [159]. These 127 fires covered a burnt area of approximately 474,000 ha (Fig. 1a; Table S1). Most of the vegetation burnt was treeless (308,000 ha), followed by forests (150,000 ha) and other minor vegetation types (16,000 ha), such as agricultural, highland and saltmarsh. Overall, 45% of the fires were wildfires (392,000 ha) and 55% were prescribed burns (82,000 ha) (Fig. 1d; Table S1). About 54% of the fires occurred in the dry season (October–March), while 46% occurred in the cool season (April–September). Of the fires in the dry season, 45% were wildfires. In contrast, of the fires in the cool season, 97% were prescribed burns (Table S1).

The mean times between the pre-fire images and fire ignitions dates, pre- and post-fire images dates and fire ignitions and post-fire images dates were, respectively, 19.5 months ± 15.6 months (standard deviation), 27.9 months ± 17.4 months, and 8.4 months ± 5.4 months. About 20% and 80% of the post-fire images occurred, respectively, within 3 and 12 months of the fire (Figure S2), and about 40% and 60% of the fires were, respectively, initial and extended assessments. The extended assessment is approximate because the post-fire images could be from either any time during the next growing season (early, middle or late) or past the next growing season, so it is not possible to know with certainty whether initial recovery and delayed mortality was already present in the case of early or middle growing season (see discussion in [75]).

All Landsat images downloaded from EarthExplorer had been corrected geometrically (pixel coordinates matched the correct place on Earth according to the specific projection) and radiometrically (brightness intensity calibrated across the scene) [174]. The two types of radiometric correction applied to the Landsat images were Terrain Precision Correction, and Systematic Terrain Correction (only one image) [157]. To minimise residual bias in the images, we applied a topographic correction via the topocorr function from the landsat R package (version 1.1.0; [58]). The topographic arguments of this function (aspect and slope) were calculated from a 25-m Digital Elevation Model of Tasmania [149] using the terrain function from the raster R package (version 3.3.13), and the radiometric arguments (sun azimuth and sun elevation) were in the metadata file of each Landsat image. Due to the lack of local wind or progressive fire isochrons for our fires, we could not discriminate down-slope and up-slope spread based on the direction of fire spread; rather, slope was treated as a general topographic control variable.

After correcting all images topographically, we assessed the quality of pixels using the quality assessment raster band provided with each Landsat image [160]. First, we applied a filter in each quality assessment band to select pixels with a quality > 0, that is, pixels of lower quality as a result of clouds, cloud shadows, haze and stripes of missing data (only in Landsat 7 images due to a failure of the Scan Line Corrector; [158]). Second, we applied a five-by-five neighbourhood focal to the lower-quality pixels, using the focal function (mean) from the raster R package (version 3.3.13), to aggregate the pixels within the specified neighbourhood. Last, we polygonised the aggregated lower-quality pixels and created a layer of polygons for each quality assessment raster band.

2.3 Delta Normalised Burn Ratio

For each fire, we computed fire severity using a dimensionless spectral index known as the Delta Normalised Burn Ratio (ΔNBR), which is the difference between the pre- and post-fire Normalised Burn Ratio (NBR) [53]. NBR is calculated using the near-infrared (NIR: 760–900 nm) and shortwave-infrared 2 (SWIR2: 2000–2400 nm) bands of the electromagnetic spectrum, applying the following raster operation: NBR = (NIR − SWIR2) / (NRI + SWIR2) [67]. Commonly, ΔNBR is preferred to NBR because it provides greater contrast between burnt and unburnt vegetation [38, 75]. Other advantages of ΔNBR, compared with other spectral indices of fire severity (e.g. Delta Normalised Difference Vegetation Index), are its stronger correlation with fire severity measured in the field [39, 67], and its higher discriminatory power to differentiate between burnt and unburnt areas [41, 57], although this discriminatory power is normally greater in forests than in treeless vegetation [4, 163, 178]. Other studies have estimated remotely-sensed fire severity using a relativised form of ΔNBR, which estimates the amount of vegetation killed by the fire in relation to the total pre-fire vegetation [105, 115]. In contrast to this relativised ΔNBR, ΔNBR measures the absolute change in green, healthy vegetation caused by the fire, which we think is a better indicator of the ecological damage, across all vegetation layers, produced by a fire [67, 73].

2.4 New Fire Boundaries, and Random Sampling Points

We manually corrected the boundary of each fire in QGIS (version 3.10.6; [125]) using the post-fire images because it was mostly possible to visually distinguish burnt from unburnt vegetation in these images, although this was more evident in treeless than in forested vegetation. Forested vegetation where fire severity might have been extremely low (e.g. burnt patches on the ground layer) was unlikely to have been observed in the post-fire images; thus, we would have considered it unburnt and, therefore, excluded it from the corrected fire boundaries. Also, we removed areas from the fire boundaries that corresponded with waterbodies and watercourses, according to the Tasmanian hydrographic area dataset [152], because they may have a spectral signature similar to that of burnt areas [109]. Finally, we removed from the fire boundaries the polygons created from the quality assessment raster bands, and clipped all fire boundaries to the Tasmanian coastline [55]. This refinement of the fire boundaries reduced the total burnt area by 10% (Table S1).

Next, we used random sampling to evaluate ΔNBR within the corrected fire boundaries. First, to minimise the effects of spatial autocorrelation, the number of sampling points to sample per fire was calculated as: number of sampling points (rounded up to the nearest integer) = area of corrected fire boundary (m2) / pixel area (900 m2). Then, using the st_sample function (type = “random”) from the sf R package (version 0.9.5; [119]), we randomly generated this number of sampling points per fire and extracted the corresponding ΔNBRs of the sampling points via the extract function from the raster R package (version 3.3.13). We produced two variograms per fire, one with an exponential family and another with a spherical family [101], using the variogram function from the gstat R package (version 2.0.6; [118]). For each variogram, we calculated the range (the distance at which the variogram levels off) and the residual sum of squares. Last, for each fire, we chose the range of the variogram with the lowest residual sum of squares, as recommended by Burrough (1995) [22].

To further curtail the effects of spatial autocorrelation, and both over- and under-sampling, the process of randomly generating sampling points within each corrected fire boundary, extracting their ΔNBRs, producing two variograms per fire (exponential and spherical families) and choosing, for each fire, the range of the variogram with the lowest residual sum of squares, was repeated 100 times, resulting in 100 ranges per fire. Finally, we averaged the 100 ranges of each fire and recalculated the new number of sampling points to sample per fire as: new number of sampling points (rounded up to the nearest integer) = area of corrected fire boundary (m2) / square of the averaged range (m2). This produced 42,092 sampling points to sample within the 127 corrected fire boundaries.

2.5 Sampling of Predictor Variables and ΔNBR

We randomly generated the number of sampling points per fire within the corrected fire boundaries and extracted the corresponding values of ΔNBR and the 42 predictor variables. However, fire type, fire type of previous fire, and time since previous fire were obtained directly from the fire history dataset [37]. In addition, as the fire history dataset did not have fire isochrones showing the progression of the fires across space and time, each sampling point was assigned the mean, mean maximum and mean minimum FFDI and soil moisture of the month of the year of the fire ignition date, reflecting prevailing conditions of the month of the year when the fire began, rather than hour-to-hour weather of fire progression [111]. Regarding land tenure, because the boundary of the Tasmanian Wilderness World Heritage Area was extended in June 2013, sampling points from fires with an ignition date prior to the boundary extension were assigned the land tenure from the latest tenure dataset available before the extension, whereas sampling points after June 2013 received the land tenure from the 2015 dataset [151, 153]. In all, this sampling process produced a dataset with 42,092 records and 44 columns (fire id, ΔNBR and the 42 predictors).

To account for variability in our data, and following the process described in the previous paragraph, we generated 100 datasets with 42,092 records and 44 columns each. In all datasets, we only kept records with the following five vegetation types: buttongrass, wetland and peatland; dry eucalypt forest; rainforest; scrub, heathland and coastal; and wet eucalypt forest [152]. We eliminated records with soil types of vertosol or unknown because we could not reclassify them into one of the four major groups of soil types, namely dermosol, kandosol, organosol and tenosol (Table 1) [148]. The elimination of these records that did not meet our vegetation and soil type criteria accounted for, approximately, 3.5% of records per dataset. Due to the limited length of the fire history dataset, there were records without a fire type of previous fire and time since previous fire. For these records, the fire type of previous fire was set to unknown, and the date of previous fire to 1900-01-01.

2.6 Selecting Predictor Variables Through Random Forests

Given the large number of predictor variables selected a priori, we undertook a two-step process to identify a smaller subset of predictors. First, we randomly chose four datasets and produced correlation matrices between predictors. In each of the four datasets, we calculated the Pearson’s correlation coefficient between all pairs of quantitative, continuous predictors via the rcorr function from the Hmisc R package (version 4.4.1; [62]) (Table S4). Similarly, we calculated the Cramér’s V coefficient for all pairs of categorical predictors via the cramersV function from the lsr R package (version 0.5; [110]) (Table S5). Correlation matrices across the four datasets showed similar correlation coefficients between pairs of predictors. Hence, we selected 22 predictors for the first round of Random Forests (Fig. 2), supported by our knowledge of the ecological significance of these predictors in fire ecology, as follows: six fire-related attribute variables, six bioclimatic variables, four fire-weather variables, and six environmental and topographic variables (Table 1).

Fig. 2
figure 2

Variable selection through three successive rounds of Random Forests (RF). In each round, the RF models were constructed using the number of predictor variables indicated inside the arrows (asterisk), and the most important predictors were selected (number sign). Predictors were ranked according to aggregated vegetation (F for forested and T for treeless), and two measures of variable importance: impurity corrected (IC) and permutation (P). Prediction accuracy of the RF ensembles was assessed in each round based on the root mean square error and mean absolute error, averaged across 50 pairs of testing and training datasets. The four highest-ranked predictors from the third round of RF were used to conduct the generalised additive mixed models (GAMMs)

Full size image

The second step to reduce the number of predictor variables was to use Random Forests, a machine-learning classifier [19, 32]. Random Forests is a strong classifier because it minimises overfitting, accepts quantitative and categorical predictors and allows for non-linear relationships between the predictors and the response variable [20]. In the Random Forests ensembles, consisting of many regression trees, it is possible to rank predictors by importance, reflecting their contribution to predicting the response variable. We used two measures of variable importance to rank the predictors: impurity corrected and permutation. Higher values of both measures indicate a higher contribution of the predictor to predicting the response variable [14]. In all regression trees, the number of predictors to split at each node was kept at the default value (square root of the number of predictors rounded down) because this value typically provides optimal performance [34]. The number of trees to grow per ensemble was 2000 because larger ensembles yielded negligible changes in the out of bag error and R2. Regression trees were constructed with sampling without replacement and through recursive partitioning [135]. All Random Forests analyses were undertaken with the ranger R package (version 0.12.1; [173]).

To better understand the relationships between the 22 predictor variables and the response variable (ΔNBR), we produced, for three of the datasets, one-way and two-way partial dependence plots of Random Forests models containing these 22 predictors, using the partial function from the pdp R package (version 0.7.0; [60]). One-way partial dependence plots indicated overfitting of a few predictors, such as distance to roads, distance to rivers/lakes, and mean FFDI. To curtail overfitting in subsequent Random Forests analyses, the two numerical predictors, distance to roads and distance to rivers/lakes, were converted into two categorical predictors: distances < 1 km were classified as near, while distances ≥ 1 km were classified as distant (Table 1). In the two-way partial dependence plots, there was no evidence of interactions between the bioclimatic and fire-weather predictors. Finally, we partitioned each dataset into two aggregated vegetation types (forested and treeless) because ΔNBR typically performs better in forests [163, 178]. Forested vegetation included dry and wet eucalypt forests and rainforests, whereas treeless vegetation comprised buttongrass, wetland and peatland, and scrub, heathland and coastal [152].

From an average of 40,601 records per dataset (± 32 standard deviation), 25% were forested and 75% treeless (Table S3). For forested records, 49% were wet eucalypt forest, 33% were dry eucalypt forest, and 18% were rainforest. For treeless records, 79% were buttongrass, wetland and peatland, and 21% were scrub, heathland and coastal. Considering the type of fire, 93% of forested records were wildfires and 7% were prescribed burns, while 65% of treeless records were wildfires and 35% were prescribed burns. In all five vegetation types, across wildfires and prescribed burns, except prescribed burns in rainforests, the protected tenure contained the most records, followed by forestry and non-protected. When considering tenure by aggregated vegetation, 59% and 78% of records were protected, respectively, in forested and treeless vegetation; 39% (forested) and 19% (treeless) were forestry; and 2% (forested) and 3% (treeless) were non-protected (Table S3).

The Random Forests analyses consisted of three successive rounds of Random Forests (Fig. 2) [34]. In each round, we input the 100 datasets, with each dataset partitioned by aggregated vegetation, but with fewer predictor variables than in the preceding round, except for the first round, which contained all 22 predictors. In each round and for each dataset, we ranked the predictors according to the two measures of variable importance. We then averaged the importance values of each predictor across the 100 datasets. In the first round of Random Forests, we chose the 11 most important predictors out of the 22 and used them as the predictors in the second round. In the second round of Random Forests, we chose the six most important predictors, which were the predictors in the third round. Finally, we selected the four highest-ranked predictors from the third round of Random Forests for the statistical analysis (Fig. 2). Residuals of the Random Forests models, containing these four predictors, computed via the predict function of the ranger R package (version 0.12.1), were normally distributed, showing no indication of spatial clustering (Figure S3).

To appraise the most suitable number of predictor variables of ΔNBR, we implemented cross-validation [20, 29]. The 100 datasets were randomly split into 50 pairs of training and testing datasets (Fig. 2). Within each pair, we used one of the datasets (training dataset), split by aggregated vegetation, to fit Random Forests models (impurity corrected and permutation) containing the 22, 11, six, four and three most important predictors. We used the second dataset (testing dataset) within each pair to test the Random Forests models fitted with the training dataset. In each pair, the prediction accuracy of the Random Forests models fitted with the training dataset and tested with the testing dataset was evaluated by the root mean square error (RMSE) and the mean absolute error (MAE). RMSE and MAE measure the agreement between paired observations consisted of the predicted and observed values, and are expressed in the units of the response variable [24, 167]. Last, we averaged the values of RMSE and MAE across the 50 pairs according to the number of predictors (22, 11, six, four and three), the two measures of variable importance (impurity corrected and permutation), and aggregated vegetation (forested and treeless). We selected four predictors for the statistical analysis because there were small changes in RMSE and MAE when using Random Forests with 22, 11, six and four predictors, but a larger loss in prediction accuracy when using three predictors (Table S6).

2.7 Statistical Analysis Using Generalised Additive Mixed Models

We used generalised additive mixed models (GAMMs) to statistically test the relationship between ΔNBR and the four highest-ranked predictor variables from the third round of Random Forests (Fig. 2). The benefit of generalised additive models over generalised linear models is that generalised additive models can model non-linear relationships between a response variable and a set of predictors [63, 175]. We used GAMMs rather than standard generalised additive models to account for the effect of individual fires [120]. We applied a thin-plate regression spline as the wiggliness penalty function for the smoothing terms [121]. The basis dimension of each smoothing term was 100, except for time since previous fire, which was 10, because increasing the basis dimensions beyond these values yielded small changes in the effective degrees of freedom, indicating little effect on the shape of the smooth [170]. All models were fitted using the bam function from the mgcv R package (version 1.8.31; [169]).

We used model selection to find the best-performing model, in each dataset, in a five-model candidate set. We preserved all datasets partitioned by aggregated vegetation, so the statistical analysis was consistent with the Random Forests analyses. The null model was the intercept-only model, while the base model contained a smoothing term for each of the four highest-ranked predictor variables from the third round of Random Forests, and both models had “fire id” as a random smoothing term [120]. Other models included extra predictors: spatial contained a smoothing term for spatial variation (easting and northing coordinates of the sampling point to further control for spatial autocorrelation), and categorical included three categorical predictors, as follows: fire type (wildfire or prescribed burn), land tenure (forestry, non-protected or protected) and the non-aggregated vegetation. The global model was the base + spatial + categorical + topography, with topography consisting of three predictors: northness and slope as linear regressions, and topographic position index as a thin-plate regression spline.

In each dataset, the five models were ranked by the Akaike’s Information Criterion (AIC), calculated with the AIC function from the stats R package (version 4.0.2; [126]). The best-performing model in the candidate set was the model with the lowest AIC. We calculated the delta AIC (ΔAIC), which represents the difference in AIC between the model and the best-performing model (accorded ΔAIC = 0). As the results of model selection were similar across all datasets, we averaged the AICs, explained deviances and ΔAICs of each model across the 100 candidate sets. Following Burnham and Anderson (2002) [21], we considered models with an averaged ΔAIC < 2 as statistically supported.

We produced partial dependency plots, by aggregated vegetation, for each of the predictor variables of the global model. First, we fitted the global model in each dataset, using the ggpredict function from the ggeffects R package (version 0.15.1; [96]), to generate ΔNBR predictions (modelled ΔNBR hereafter) for each of the predictors included in the model. Next, for each quantitative, continuous predictor, we averaged the modelled ΔNBRs across the predictions of the 100 global models and applied a cubic smoothing spline to the averaged modelled ΔNBRs via the smooth.spline function from the stats R package (version 4.0.2). For categorical predictors, we computed the mean of the modelled ΔNBRs for each category of the predictor across the predictions of the 100 global models. Here, we tested for statistical differences (P-value < 0.05) among the categories of the predictor via the non-parametric Kruskal–Wallis test by ranks (kruskal.test function from the stats R package; version 4.0.2), followed by post hoc means comparisons through the Bonferroni method (pairw.kw function from the asbio R package; version 1.6–7; [3]). For all predictors, we calculated the 95% confidence intervals from the global model predictions, and averaged the lower and upper limits of the 95% confidence intervals across the 100 models.

3 Results

3.1 Selecting Predictor Variables Through Random Forests

In both forested and treeless vegetation, precipitation of the driest quarter, mean minimum monthly soil moisture, and time since previous fire were among the four most important predictor variables selected in the third round of Random Forests (Fig. 2; Table 1). Mean annual precipitation was an important predictor in forests, whereas temperature seasonality (standard deviation) was important in treeless vegetation. Cross-validation indicated little loss of prediction accuracy of the Random Forests models containing the four most important predictors (forested: 0.155 RMSE and 0.113 MAE; treeless: 0.119 RMSE and 0.085 MAE), compared to models with the 22 predictors (forested: 0.147 RMSE and 0.110 MAE; treeless: 0.117 RMSE and 0.085 MAE) (Table S6).

3.2 Statistical Analysis Using Generalised Additive Mixed Models

The global model had the best support across all datasets in treeless vegetation (mean ΔAIC = 0), and in all but four of the 100 candidate sets of GAMMs in forested vegetation (mean ΔAIC = 0.8, range: 0–37) (Table 2). In each of the four exceptions, the base + spatial + categorical model was the best-fitting model, but the improved fit over the global model was small (mean ΔAIC < 2). Therefore, we selected the global model as the best-performing model for both forested and treeless vegetation.

Table 2 Means of ΔAICs (range in parentheses) and deviance explained for the candidate sets of GAMMs, according to aggregated vegetation, across the 100 datasets. The preferred model is shown in bold. The null model is the intercept-only model. The base model contains a smoothing term for each of the most important predictor variables from the third round of Random Forests. Other models include extra predictors: spatial contains a smoothing term for spatial variation, and categorical includes three categorical predictors (fire type, land tenure and non-aggregated vegetation). The global model consists of the base + spatial + categorical model plus three topographic predictors (northness, slope and topographic position index). All models include a random effect for “fire id”. Note that the base + spatial + categorical model outperformed the global model in forested vegetation in four datasets, but the mean ΔAIC was less than 2
Full size table

Overall, we achieved a good sampling coverage of the four most important predictor variables of the global GAMM (Figure S4b–f; Figure S5a–h) across the 100 datasets, with time since previous fire presenting the highest difference in interquartile ranges between forested and treeless vegetation (Figure S4f) due to lack of ΔNBR values between 40 and 90 years (Figure S5g–h). Modelled ΔNBR (predicted ΔNBRs from the global GAMM) was negatively associated with mean annual precipitation in forested vegetation, with modelled ΔNBR < 0.44 above 2000 mm per annum, and > 1.1 below 1000 mm (Fig. 3a). Modelled ΔNBR increased with precipitation of the driest quarter in forested and treeless vegetation up to approximately 400 mm (Fig. 3c–d). There was a slight upward trend in modelled ΔNBR as time since previous fire increased up to 35 years (Fig. 3g–h). Modelled ΔNBR showed flat trends in temperature seasonality in treeless vegetation (Fig. 3b), and mean minimum monthly soil moisture in both forested and treeless vegetation (Fig. 3e–f). These predictors (temperature seasonality and mean minimum monthly soil moisture) were important in the Random Forests analyses because they explained a proportion of the variance not captured by other predictors, so removing them reduced model fit. Low sampling coverage affected the predictions for some regions of most predictors, notably for high values of precipitation-related variables (Fig. 3a, c–d; Figure S5a, c–d).

Fig. 3
figure 3

Partial dependence plots for important predictor variables of modelled ΔNBR in forested and treeless vegetation, based on the global GAMM. The solid black lines in plots (a–h) represent cubic smoothing splines on the mean of the ΔNBR predictions, while the grey-shaded areas show mean 95% confidence intervals. Plots (i–k) show mean modelled ΔNBR with 95% confidence intervals. Plots on the left (a, c, e, g) correspond to forests, while plots on the right (b, d, f, h) are for treeless vegetation. Plots (i–k) refer to both forests (black circles) and treeless vegetation (open squares). Different letters on the top right of the error bars (i–k) indicate significant differences between groups (P-value < 0.05) using a post hoc Bonferroni method applied after the Kruskal–Wallis test by ranks. See Figure S4 in the supplementary material for the partial dependence plots of the three topographic variables. Acronyms: DEF is dry eucalypt forest; WEF is wet eucalypt forest; R is rainforest; BWP is buttongrass, wetland and peatland; and SHC is scrub, heathland and coastal

Full size image

Sampled values of the topographic predictor variables across the 100 datasets showed a large range of variability (large interquartile range) in northness for forested and treeless vegetation, while the topographic position index had a low range of variability, and slope had some more variability, but was left-skewed (Figure S4g–i; Figure S5i–n). Regarding modelled ΔNBR, northness had a flat trend in forested and treeless vegetation (Figure S6a–b). However, modelled ΔNBR was predicted to slightly decrease as slope increased in forested vegetation, and to increase as slope increased in treeless vegetation (Figure S6 c–d). Topographic position index influenced modelled ΔNBR in flat areas (0 m) in forested and treeless vegetation, but the response was unstable for topographic position indices < −5 m or  > 5 m (Figure S6e–f).

For non-aggregated vegetation, sampled ΔNBRs across the 100 datasets showed similar ranges of variability, with dry eucalypt forests having the smallest interquartile range of all five vegetation types (Figure S4j). Dry and wet eucalypt forests presented the highest modelled ΔNBRs (0.61 ± 0.14 standard error of the mean and 0.58 ± 0.14, respectively) of all five vegetation types, and there was no statistical difference between these two vegetation types (Fig. 3k). In contrast, modelled ΔNBR of rainforests (0.53 ± 0.14) was statistically different from the other two forest types. In treeless vegetation, modelled ΔNBR of scrub, heathland and coastal (0.56 ± 0.08) was not statistically different to modelled ΔNBR of buttongrass, wetland and peatland (0.53 ± 0.08). Furthermore, there were no statistical differences in modelled ΔNBR between wet eucalypt forests and scrub, heathland and coastal, and among rainforest and the two treeless vegetation types (Fig. 3k).

In fire type, sampled ΔNBRs had similar interquartile ranges in forested and treeless vegetation across the 100 datasets regardless of the type of fire, although there was higher variability in treeless prescribed burns than in the other three groups (Figure S4k). For wildfires, modelled ΔNBR and prediction uncertainty (95% confidence interval) was higher in forests (0.61 ± 0.14) than in treeless vegetation (0.53 ± 0.08), with this difference being statistically different (Fig. 3i). In contrast, prescribed burns in treeless vegetation had higher modelled ΔNBR, but lower uncertainty (0.45 ± 0.09), than prescribed burns in forests (0.42 ± 0.15), and this difference was statistically different. Modelled ΔNBR was statistically different between wildfires and prescribed burns in forests, but not between wildfires and prescribed burns in treeless vegetation (Fig. 3i).

Land tenure was the categorical predictor variable that showed, across all its groups, the largest variability in the interquartile ranges of sampled ΔNBRs for all 100 datasets. This variability was small for forestry in both forested and treeless vegetation, and in non-protected forests, but larger in the other three groups (non-protected treeless, protected forested and protected treeless) (Figure S4l). Within both forested and treeless vegetation, modelled ΔNBR was statistically different between the forestry (forested: 0.61 ± 0.14; treeless: 0.53 ± 0.08) and protected (forested: 0.66 ± 0.14; treeless: 0.57 ± 0.07) tenures, but not between the forestry and non-protected (forested: 0.62 ± 0.14; treeless: 0.56 ± 0.07) tenures, and the non-protected and protected tenures.

4 Discussion

In this study, we have developed a methodological approach to rigorously select, and statistically test, predictor variables with ecological meaning in predicting fire severity estimated from remotely-sensed data. This approach provides predictions in a complex pyrogeographical system, covering 25 years of fire records, across forested and treeless landscapes.

4.1 Methodological Approach

Our methodological approach was developed to account for several of the major challenges of using remotely-sensed fire severity data, including spatial autocorrelation and multi-dimensional environmental drivers that interact at various spatio-temporal scales [29, 30]. We implemented Random Forests to select a smaller set of predictor variables, and fitted these models 100 times in each round of Random Forests to account for spatial autocorrelation and control the complex interactions between predictors (Fig. 2) [81]. Our Random Forests models appear to have been effective, given that variable importance rankings were similar across the 100 datasets, and the small loss of prediction accuracy when downsizing the number of predictors from 22 to four (Table S6).

To allow for the loss of a few important predictor variables in the Random Forests analyses (Fig. 2), we created a base GAMM using the four highest-ranked predictors from the third round of Random Forests, and added other likely predictors. The substantial fit improvement of the global GAMM validates this approach (Table 2). In particular, the strong effects of incorporating “fire id” as a random effect to control for inter-fire differences and local-scale effects supports the value of GAMMs over Random Forests [120]. Nonetheless, our GAMM models have not been designed for prediction in other ecosystems because it may not be possible to provide a comparable random effect for individual fires. In this study, we were interested in the ecological conclusions of the statistical analysis using GAMMs, rather than generating predictive models to apply across all ecosystems, because each ecosystem has specific ecological features that need to be considered when implementing and interpreting statistical models.

The strengths of our methodological approach are twofold. First, by using Random Forests, it is possible to obtain insights into the relative importance of interacting predictor variables [29], instead of selecting a priori a set of predictors for statistical analysis or implementing stepwise selection. Second, by using GAMMs and model selection, we can test the statistical relationships among predictors and improve model fit [81]. In addition, as the approach is semi-automatic, we can use existing knowledge of fire ecology to ensure that the outputs at each step of the approach are ecologically meaningful [127], and repeat any steps by modifying input variables in the Random Forests analyses and/or increasing model complexity in the candidate sets of GAMMs (Fig. 2; Table 2).

Future studies in fire severity that may follow our methodological approach would benefit from field validation. Here, we did not undertake field validation because of the sample size (127 fires), the remoteness of the study region, and the long time elapsed since most fires happened. Given this lack of field data, we chose a spectral index highly correlated with fire severity in the field and with a greater discriminatory power between burnt and unburnt vegetation than other spectral indices [39, 57]. Importantly, by partitioning our datasets into forested and treeless vegetation, we increased the accuracy of our analyses, since ΔNBR normally performs better in forested than in treeless vegetation [178]. Nevertheless, future studies could select a few distinguished fires (e.g. recent large wildfires and prescribed burns) to assess fire severity in the field (e.g. through the Composite Burn Index; [75]), and then calibrate the field fire severities with the remotely-sensed fire severity [111]. The benefits of determining ΔNBR ranges that correlate to field severity classes are that the results could be relevant to ecosystems with similar pyrogeographical features to western Tasmania.

4.2 Climate Variables and Time Since Previous Fire

The stronger relationships among predictor variables in treeless vegetation (deviance explained = 0.68) than in forests (0.54) in the global GAMM contrasts with previous studies that reported lower performance of ΔNBR in non-forested vegetation (Table 2) [4, 137, 140]. To ensure maximum accuracy of ΔNBR, especially in treeless areas, we searched multispectral pre- and post-fire satellite images as close as possible in time to the fire event and spanning the same season of the year [25]. These considerations are important when studying treeless communities, such as the Tasmanian buttongrass moorlands, where regrowth happens rapidly after fire if there is a wet period shortly thereafter [69].

Our results showed that precipitation-related variables were important drivers of fire severity in forested and treeless vegetation (Fig. 3a, c–d). In forests, higher levels of mean annual precipitation had a negative effect on modelled ΔNBR (Fig. 3a), which may be related to the role of annual precipitation in controlling ecosystem productivity [117]. Therefore, biomass connectivity and density may have been important in driving fire severity in our study area [134, 136]. Although previous research found that increases in annual precipitation led to high-severity surface and canopy fires through higher rates of horizontal and vertical biomass build-up [28, 84], annual precipitation may also have a negative relationship with fire danger indices in regions that lack regular dry periods that permit fire [122]. Another reason for the negative relationship between mean annual precipitation and modelled ΔNBR may be the positive association between annual precipitation and soil moisture, since wetter areas require more extreme weather conditions for fire ignition [5, 17]. For instance, Dimitrakopoulos et al. (2011) [36] showed that a year with normal annual precipitation in Mediterranean coniferous forests had > 48% low fire-danger days and < 88% extreme fire-danger days than a dry year (< 70% precipitation). The 25-year fire record in this study might have had few catastrophic fire days that could have originated fires of high intensity and severity [16, 71].

The negative relationship between modelled ΔNBR and mean annual precipitation in forests of western Tasmania (Fig. 3a) may reflect a dichotomy between the region’s mild and wet climate, but relatively frequent extreme weather conditions, such as dry lightning and short heatwaves [142]. Increased mean annual precipitation in the study region could be associated possibly with a trend towards denser, closed-canopy forests that require rare and extreme weather or severe drought to achieve fire intensities that would result in high-severity fires [131]. Future climate scenarios predict an increase in extreme weather conditions in Tasmania [50], so there will be a higher risk of large-scale and severe fires that may compromise the survival of fire-sensitive communities. For example, the palaeoendemic, slow-growing conifer Athrotaxis cupressoides, which persists in cool and wet refugia in western Tasmania, underwent a severe interval squeeze (68% adult mortality) as a result of fires from dry lightning in 2016 [15]. Other global climate modelling for the twenty-first century has shown that fluctuations in total annual precipitation in ecosystems of intermediate productivity, such as those found in western Tasmania, will be the main driver of ecosystem flammability and fire regimes [10, 116, 141].

The positive relationship between precipitation of the driest quarter, representing mean summer precipitation in this system, and modelled ΔNBR in both forested and treeless vegetation (Fig. 3c–d) may reflect greater plant productivity due to wet summers. Wetter summers can lead to horizontal and vertical biomass build-up, which may burn in hot days later in the summer [59, 88]. However, areas with high-average summer precipitation may still undergo episodic drought with high-severity fires [123, 156], a true case for western Tasmania [49, 171]. It is possible that, in ecosystems of intermediate productivity, a preceding wet summer may translate into higher fire risk in successive summers due to biomass build-up [56, 161]. Other studies worldwide have reported that such ecosystems are more affected by precipitation variability during the dry season than during the cool season [108, 113, 177] because cool seasons are not normally water-limited, contrarily to dry seasons, where precipitation increases lead to higher plant productivity and, therefore, more biomass available for burning [59, 89, 139].

A potential interaction between precipitation and temperature may explain why temperature seasonality was important in treeless vegetation (Fig. 3b). Treeless communities in our study region were mostly located in near-coastal areas (Fig. 1a–b), which are less affected by temperature fluctuation due to the modulating effect of the ocean. Consequently, lower fluctuations between minimum and maximum temperatures throughout the year may render plants longer growing periods, in opposition to areas with less thermally equable climates, where the lower temperatures of the cool season inhibit bud break and plant growth [80, 168].

Time since previous fire influenced fire severity in forested and treeless vegetation, with modelled ΔNBR continuing to increase to approximately 35 years after fire (Fig. 3g–h). This increase may be linked to the accumulation of finer biomass during fire-free periods, which becomes available for burning under adverse weather conditions, such as drought, high temperature, lightning, low humidity and wind [17]. These results align with previous studies that suggested that time since previous fire could be more important in the first years after a fire, while biomass is thinner and the understorey is regenerating [65, 92, 146]. Similar findings that highlighted the positive relationship between time since previous fire and fire severity have been reported in chaparral-dominated shrublands, fynbos, Australian heathlands, and Mediterranean forests of maritime pines [42, 74, 86, 176].

4.3 Relevance to Fire Management and Climate Change

Our research demonstrates that a multi-decadal satellite record can be successfully used to study fire severity in complex landscapes with a rich fire history. However, a caveat of this study was the coarse temporal resolution of the FFDI and soil moisture variables. Because we did not have fire isochrones, we did not know the day and time that each sampling point within the fire burnt, so we assigned to all sampling points within a fire the averaged FFDI and soil moisture of the month of the year of the fire ignition date. These averaged values of FFDI and soil moisture reflected the prevailing weather conditions of the month of the year when the fire began, rather than the specific weather conditions of the time of the day when the sampling point burnt. Specific weather conditions are important because most fires have outbursts that burn most of the area [31, 70, 91]. Given the importance of fire isochrones to better match fire severity to the local conditions when the fire burnt [45, 111], fire agencies would need to digitise fire isochrones to allow for better predictive modelling of fire severity. Furthermore, records on firefighting activities, including the timing and location of control lines and aerial waterbombing drops, are useful in fire severity analyses because the burnt area, fire intensity and fire severity may have been influenced by the firefighting efforts [43, 164].

The lower modelled ΔNBR in prescribed burns than in forest wildfires (Fig. 3i) was expected because prescribed burning uses low-intensity burns, which are attained by avoiding dry and hot weather conditions, to reduce biomass build-up, hence reducing fire hazards [46]. Nevertheless, the higher modelled ΔNBR of prescribed burns in treeless vegetation than in forests may be an artefact of the limited capacity of satellite images to capture reflectance changes of the understorey layer in forests. This layer is typically the part of the forest that burns during prescribed burning, but it is hindered by the tree canopies [93, 107]. In addition, the similar modelled ΔNBR of wildfires and prescribed burns in treeless vegetation may relate to the fewer layers available for burning in treeless communities, thus limiting fire severity [88, 117].

Modelled ΔNBR was higher in protected forests than in commercial forests, but not statistically different from modelled ΔNBR in non-protected forests (Fig. 3j), reflecting the greater continuity and density of aboveground biomass in forests [117]. By contrast, the similar modelled ΔNBR of protected and non-protected treeless areas was anticipated (Fig. 3j), because treeless vegetation burns more homogeneously due to biomass connectivity [72, 103]. Prescribed burning of treeless areas within protected forests can be an efficient management tool to reduce the occurrence and spread of future high-severity fires [77, 104, 162]. As an example, strict fire suppression policies led to large-scale, destructive wildfires in the Yellowstone National Park in 1988 [133]. This recommendation of burning treeless areas within forests to create mosaics of fuel structures is supported by previous experimental research [51, 66, 132] and simulation modelling [52, 77, 78]. Specifically, King et al. (2013) [79] underlined the effectiveness of prescribed burning in reducing unplanned fires and area burnt by large fires in south-west Tasmania, given the role of prescribed burns in fragmenting biomass connectivity.

Climate modelling for the twenty-first century projects a decrease in summer precipitation and an increase in winter precipitation in south-east Australia [33, 44], coupled with changes in frontal cyclones [129]. This modelling suggests a 69% increase in the number of days of dangerous fire weather in western Tasmania by the end of the twenty-first century [48, 50], possibly leading to more large-scale, high-severity wildfires [1, 94, 112]. Furthermore, climate modelling shows that the canonical driver of precipitation variability in Australia, El Niño–Southern Oscillation [112, 130], is predicted to become more severe than other climate systems, such as the Indian Ocean Dipole and the Southern Annular Mode, with extreme dry events associated with El Niño followed by greater favourable conditions for extreme wet weather associated with La Niña [23, 61, 76]. The increase in drought and fire days means that the weather window to apply prescribed burning will shorten in the future [26, 87]. Consequently, fire severity data collected during prescribed burning operations is important because it can help identify areas where prescribed burning would be more efficient.

5 Conclusions

Western Tasmania represents an interesting pyrogeographical model for studies in fire ecology due to its pyrodiversity and the potential impacts of climate change on wet ecosystems. The methodological approach developed here can be reproduced in other ecosystems to understand the drivers of fire severity. Our results showed that precipitation-related variables were the main drivers of fire severity in forested and treeless vegetation in western Tasmania. Importantly, our findings confirm previous base knowledge of the drivers of fire severity [28, 54, 102, 145]. However, additional studies would benefit from field validation, fine-scale fire weather, and fire progression data. Prescribed burns had lower remotely-sensed fire severity than forest wildfires, which supports that prescribed burning is suitable for reducing the connectivity and density of available biomass. In this study, we establish links between fire severity and both climate and weather, across a topographically and ecologically diverse ecosystem, over an extended time series of fires, and provide a framework to better understand the interactions between fire severity and prescribed burning under climate change.