Parallel virus machines

Abstract

Within the branch of Natural Computing, several models or types of computation arise, some of them are well-established such as neural networks, evolutionary computing or membrane computing, while others have yet to be studied and developed. One such model is virus machines, which draws inspiration from the replication and transmission mechanisms of viruses. This model has been successfully applied to mathematical problems, supported by its robust formal structure and the verification of various parallel virus machines. Parallelism has been one of the milestones in several branches of Natural Computing. This paper presents a novel extension: parallel virus machines. Furthermore, several semantics are studied to fix possible ambiguities related to this new variant. Finally, a comparison with well-established neural-like systems, called spiking neural P systems, is discussed.

1 Introduction

Natural Computing [1, 2] is a field of unconventional computation which focuses on computing models inspired by what occurs in nature and also simulates different natural structures.

Since the beginning of mankind, the world has been affected by viruses, major pandemics such as influenza [3], smallpox [4], and more recently, COVID19 [5] have caused not only biologists but also all types of people to become aware of viruses and the great impact they can have.

This basic biological entity has demonstrated its global impact, with intriguing characteristics that can be explored through computational methods. These include its dependency on a host for replication, the mechanisms of replication and transmission [6], and its significant mutation rate. For more biological aspects, we refer to Refs. [7, 8].

A novel computational model inspired by this biological structure has been created: virus machines [9]. In this computing paradigm, viruses move and replicate between hosts through channels controlled by an instruction graph. It has shown to be an interesting point of view to attack mathematical problems; in Ref. [10], the authors designed VMs to compute pairing functions, and its proper verification was mathematically proved; moreover, cryptosystems based on the prime factorization problem were attacked by means of virus machines in Ref. [11]. Finally, in Ref. [12], the authors define several examples of virus machines in the generating, computing, and recognizing mode; the last mode also opens the field of creating a novel theoretical complexity theory through virus machines.

In addition, its universality was also proved in different ways: by generating Diophantine sets [13], by computing partial recursive functions [14], or by simulating register machines [15].

In this work, we seek to improve the time efficiency of this computing paradigm by defining the syntax of a novel extension called parallel virus machines, then we discuss possible semantics associated with this extension, showing advantages and weaknesses of each chosen semantics. Finally, a comparison with other distributed parallel computing models, called spiking neural P systems, is made with a determination in the semantics associated.

This paper is structured as follows: first, the concept of basic virus machines is outlined, followed by an exploration of the new extension of parallel virus machines. Subsequently, various clarifications and ambiguities are examined in relation to the new potential semantics. Finally, a determination of the semantics with a comparison to other Natural Computing systems, called spiking neural P systems, is made, and some conclusions are drawn to conclude the paper.

2 Basic virus machines

This new computing model, which takes its cue from the way viruses are spread and replicated between hosts, was first presented in Ref. [15]. Subsequently, the structure of this model is formally outlined.

Definition 2.1

A virus machine (VM, for short) of degree (a, b), $a,b \ge 1$, is defined as the following tuple $\Pi =(\Gamma , H, I , D_H,D_I,G_C, n_1, \dots ,n_a, i_1,h_{out})$, where:

• $\Gamma =\{v\}$ is the singleton alphabet:

• $H=\{h_1,\dots ,h_a\}$ and $I=\{i_1,\dots ,i_b\}$ are ordered sets such that $v \notin H \cup I$, $H \cap I=\emptyset$ and $h_{out} \notin I \cup \{v\}$: either $h_{out} \in H$ or $h_{out} \notin H$ (in this case, $h_{out}$ represents the environment and it is denoted by $h_0)$;

• $D_H=(H \cup \{h_{out}\},E_H, w_H)$ is a weighted directed graph (WDG for short), where $E_H \subseteq H \times (H \cup \{ h_{out} \})$ such that $(h,h) \notin E_H$, for each $h \in H$, out-degree$(h_{out})=$ 0, and $w_H$ is a mapping from $E_H$ onto $\mathbb {N}\setminus \{0\}$;

• $D_I=(I,E_I,w_I)$ is a WDG, where $E_I \subseteq I \times I$, $w_I$ is a mapping from $E_I$ onto $\mathbb {N}{\setminus } \{0\}$ and the out-degree of each node is less than or equal to 2;

• $G_C=(V_C,E_C)$ is an undirected bipartite graph, where $V_C= I \cup E_H$, being $\{I, E_H\}$ the partition associated with it, in addition each edge connect an element from I with, at most, an arc from $E_H$;

• $i_1 \in I$ and $n_j \in \mathbb {N}$, for each j, $1 \le j \le p$, where $\mathbb {N}$ is the set of natural numbers.

Formally, a virus machine $\Pi =(\Gamma , H, I , D_H,D_I,G_C, n_1, \dots ,n_a, i_1,h_{out})$ of degree (a, b), is a tuple that can be viewed as an ordered set of a hosts labeled as $h_1,\dots ,h_a$, where each host $h_j$ initially contains $n_j$ viruses, and an ordered set of b control instruction units labeled with $i_1,\dots ,i_b\in I$. In this work, $h_{out}\notin H$ and it represents the output region, useally denoted by $h_0$. In this work, it will represent the environment. The arcs $(h_s, h_{s'})$, where $s \ne s'$, of the weighted directed graph $D_H$ represent transmission channels through which viruses can transmit from one host $h_s \in H$ to another host or region $h_{s'}\in H \cup \{h_{0}\}$. The computation of a virus machine starts with the activation of the instruction $i_1$. At any moment, at most one instruction $i_j$ is activated: if $i_j$ is attached to the channel $(h_s,h_{s'})$ (arc in $G_C$ with weight $w_{s,s'}$) and is activated at instant t, then it is opened and a virus will be transmitted and replicated $w_{s,s'}$ times from $h_s$ to $h_{s'}$, so one virus is consumed at $h_s$, and $w_{s,s'}$ viruses reach $h_{s'}$. By default, every channel is closed.

The arcs in the directed graph $D_I$ represent instruction paths, and they are associated with a weight. Finally, the undirected bipartite graph $G_C$ represents the instruction-channel relation by which an edge $\{i_j, (h_s,h_{s'})\}$ indicates a control between instruction $i_j$ and channel $(h_s,h_{s'})$.

Graphically, an example of a virus machine of degree (4, 6), can be seen in Fig. 1. Each host is drawn as a rectangle and each instruction is represented as a blue circle. The directed arrows are assigned with a weight (or weight 1 if not marked). Instruction-channel arcs are represented as dotted red lines.

Fig. 1

An example of Virus Machine

The semantics associated with the computing model is now described. A configuration $\mathcal{C}_t$ at an instant t of a virus machine is a tuple $(x_{1,t}, \dots ,x_{a,t}, u_t, x_{0,t})$ where $x_{0,t}, x_{1,t}, \dots ,x_{p,t}$ are natural numbers (representing the number of viruses within the environment $h_0$ and the hosts $h_1, \ldots , h_a$, respectively), and $u_t \in I \cup \{ \, \# \, \}$, being $\# \notin H \cup \{ h_0\} \cup I$. If $u_t \in I$, then $u_t$ will be activated in step $t+1$; otherwise, if $u_t=\#$, then no instruction will be activated. The initial configuration of the system $\Pi =(\Gamma , H, I , D_H,D_I,G_C, n_1, \dots ,n_a, i_1, h_{out})$ is $\mathcal{C}_0=( n_1, \dots ,n_a, i_1,0)$. A configuration $\mathcal {C}_t=( x_{1,t}, \dots ,x_{p,t}, u_t, x_{0,t})$ is a halting configuration if and only if $u_t=\#$. We say that a non-halting configuration $\mathcal {C}_t=( x_{1,t}, \dots ,x_{a,t}, u_t,x_{0,t})$ yields configuration $\mathcal {C}_{t+1}=( x_{1,t+1}, \dots ,x_{a,t+1}, u_{t+1},x_{0,t+1})$ in one transition step if we can pass from $\mathcal {C}_t$ to $\mathcal {C}_{t+1}$ in the following form.

• (a) Assume that the control instruction unit $u_t$ is attached to a channel $(h_s,h_{s'})$. If $x_{s,t} \ge 1$, then $x_{s,t+1}=x_{s,t}-1$ and $x_{s',t+1}=x_{s',t}+w_{s,s'}$, if $x_{s,t} =0$ then $x_{s,t+1}=x_{s,t}$ and $x_{s',t+1}=x_{s',t}$. If $u_t$ is not connected to any channel, then there is no transmission of viruses.

• (b) The object $u_{t+1} \in I \cup \{ \# \}$ is obtained depending on the out-degree of $u_t$ as follows:

  • If out-$degree (u_t)=2$ and $(u_t,u_{t'}) \in E_I$, $(u_t, u_{t''} ) \in E_I$, where $t' \ne t''$, then the following holds: (i) if $u_t$ is not attached to any channel, then $u_{t+1}$ will be either $u_{t'}$ or $u_{t''}$, selected in a non-deterministic way; (ii) if $u _t$ is attached to a channel $(h_s,h_{s'})$ and $a_{s,t} \ge 1$, then $u_{t+1}$ is max$\{w_{t,t'},w_{t,t''}\}$, otherwise $u_{t+1}$ is min$\{w_{t,t'},w_{t,t''}\}$. When $w_{t,t'}=w_{t,t''}$, either $u_{t+1}=u_{t'}$ or $u_{t+1}=u_{t''}$ is selected non-deterministically.

  • If out-$degree (u_t)=1$, then $u_{t+1}=u_{t'}$, being $(u_t,u_{t'}) \in E_I$.

  • If out-$degree (u_t)=0$ then $u_{t+1}=\#$, and $\mathcal{C}_{t+1}$ is a halting configuration.

A computation of a virus machine is a sequence of configurations such that: (a) the first term is the initial configuration $\mathcal{C}_0$ of the system; (b) for each $n \ge 2$, the nth term of the sequence is obtained from the previous term in one transition step; and (c) if it is a halting computation (the sequence is finite), then the last term is a halting configuration.

Remark 2.2

Virus machines are sequential devices; that is, at most one control instruction unit is activated in any instant, and hence at most one transmission channel will be opened.

Definition 2.3

A virus machine with input, of degree $(a,b,r), a \ge 1, b \ge 1, r \ge 1,$ is a tuple $\Pi =(\Gamma , H, H_r, I , D_H,D_I,G_C, n_1, \dots ,n_a, i_1,h_{out}),$ where:

• $(\Gamma , H, I, D_H,D_I,G_C, n_1, \dots ,n_a, i_1,h_{out})$ is a Virus Machine of degree (a, b).

• $H_r= \{h_{s_1}, \dots ,h_{s_r}\} \subseteq H$ is the ordered set of r input hosts and $h_{out} \notin H_r$.

If $\Pi$ is a virus machine with input of degree (a, b, r) and $(\alpha _1, \dots , \alpha _r) \in \mathbb {N}^r$, the initial configuration of $\Pi$ with input $(\alpha _1, \dots , \alpha _r)$ is $( n_1, \dots , n_{s_1}+\alpha _1, \dots , n_{s_r}+\alpha _r, \dots , n_a, i_t, 0)$, denoted by $\Pi + (\alpha _1,\dots , \alpha _r)$ proceeds as stated before. The result of a halting computation is the number of viruses sent to the output region (the environment) during that computation.

Next, virus machines providing function computing devices are introduced.

Definition 2.4

We say that a partial function $f : \mathbb {N}^k \rightarrow \mathbb {N}$, $k\ge 1$, is computed by a virus machine $\Pi$ with k input hosts, if for each $(x_1, \dots ,x_k ) \in \mathbb {N}^k$, we have:

• If $(x_1, \dots ,x_k ) \in \text {dom}(f)$ and $f(x_1, \dots ,x_k )=z$, then every computation of $\Pi + (x_1, \dots ,x_k )$ is a halting computation and the result is z.

• If $(x_1, \dots ,x_k ) \in \mathbb {N}\setminus \text {dom}(f)$, then every computation of $\Pi + (x_1, \dots ,x_k )$ is a non-halting computation.

3 Parallel virus machines

Given the sequential nature of virus machines, the obtained devices are not as powerful in terms of efficiency, since at most one instruction can be executed at each time step. In this sense, the possibility of executing more than one instruction in each computational step is a good approach to include some kind of parallelism in this model. In this section, the syntax and semantics of this model are defined, and possible ambiguities arising from the selected semantics are discussed.

Definition 3.1

A parallel virus machine (PVM) of degree (a, b), $a,b \ge 1$ is a tuple $\Pi =(\Gamma , H, I , D_H,D_I,G_C, n_1, \dots ,n_a, I_0,h_{out})$, where:

• Now $I_0 \subset I$, is the nonempty set of initial instructions;

• For each $i_j\in I_0$, we have that $\Pi _j = (\Gamma , H, I , D_H,D_I,G_C, n_1, \dots ,n_a, i_j,h_{out})$, is a virus machine.

The syntax of this model is very similar to the syntax of basic virus machines. Regarding the semantics associated with this extension, a configuration $\mathcal {C}_t$ of a given time t of a PVM is defined as a tuple $(x_{1,t},\dots , x_{p,t},I_t,e_t)$ where $x_{1,t},\dots , x_{a,t},e_t$ are natural numbers and $I_t\subseteq I\cup \{\#\}$. If $I_t = \{\#\}$, then $\mathcal {C}_t$ is a halting configuration; otherwise, the initial configuration is $\mathcal{C}_0=(n_1, \dots ,n_a, I_0,0)$.

The next configuration $C_{t+1} = (x_{1,t+1},\dots ,x_{a,t+1},I_{t+1},e_{t+1})$ will be defined as, for each $j\in \{1,\dots ,p\}$, $x_{j,t+1} = (x_{j,t} {\mathop {-}\limits ^{\bullet }}m_j) + m'_j$, where $m_j$ depends on the number of channels opened at that moment whose origin is the host $h_j$, and $m'_j$ depends on the sum of all viruses that reach that host $h_j$. Similarly to basic virus machines, all channels are closed unless an instruction from the set $I_t$ is attached to it. The following set of instructions $I_{t+1}$ will be defined as

$$\begin{aligned} I_{t+1} = \{s(i)\ |\ i\in I_t\}, \end{aligned}$$

where s(i) represents the following instruction from the instruction $i \in I_t$ according to the semantics associated. Despite several possible semantics that will be studied in the following section, the main idea is to generalize the basic virus machines; in the sense, if $|I_t| = 1$, then the computation of the machine is the same as in the vanilla version. That is, for each instruction $i\in I_t$, attached to a channel $(h_j,h_k)\in E$, and if:

• $x_{j,t}>0$, then one virus is consumed from host $h_j$ and sent to $h_k$ and replicated $w_H(h_j,h_k)$ times. If there is virus transmission, then the next instruction s(i) follows the highest weight path in the instruction graph.

• $x_{j,t}=0$, then there is no virus transmission through that channel, and the next instruction s(i) follows the path of least weight.

In case the highest/least path is not unique, then it is chosen non-deterministically.

The way in which the output of the system is understood in this extension remains equal to the basic model.

Despite the fact that some clarifications and possible ambiguities will be solved in the following section, let us first see an explicit example to clarify the mentioned semantics.

3.1 Example: addition function

Let $\Pi _{add}$ be the PVM with input of degree (2, 3, 2), visually described in Fig. 2, computing the addition function of two natural numbers $f(n_1,n_2) = n_1+n_2$. The computation of the machine is as follows, the initial configuration is $C_0 = (n_1,n_2,\{i_1,i_2\},0)$, instructions $i_1$ and $i_2$ open the channel $(h_1,h_0)$ and $(h_2,h_0)$, respectively, then a virus is consumed in hosts $h_1$ and $h_2$ and the highest weight path is followed in both instructions, leading to the following configuration $C_1 = (n_1-1,n_2-1,\{i_1,i_2\},1+1)$, this process will be repeated until one of both hosts is empty, without losing generalization; suppose that $n_1\le n_2$, then the computation is as follows:

$$\begin{aligned} \begin{aligned} C_{n_1}&= (n_1-n_1,n_2-n_1,\{i_1,i_2\},n_1+n_1),\\ C_{n_1+1}&= (0,n_2-n_1-1,\{i_3,i_2\},n_1+n_1+1),\\&\vdots \\ C_{n_1+(n_2-n_1)}&= (0,n_2-n_2,\{\#,i_2\},n_1+n_2),\\ C_{n_2+1}&= (0,0,\{\#,i_3\},n_1+n_2),\\ C_{n_2+2}&= (0,0,\{\#\},n_1+n_2), \end{aligned} \end{aligned}$$

Thus, the machine stops after $n_2+2$ steps and returns $n_1+n_2$, that is, the result of the addition function.

Fig. 2

The PVM $\Pi _{add}$ with $I_0 =\{i_1,i_2\}$

4 Clarifications and ambiguities

Although the extension may seem straightforward, it leads to a number of special cases or ambiguities that need to be clarified or defined. In the following, these cases and the possible decisions are presented, and some consequences of each decision are considered.

4.1 Channel coincidence

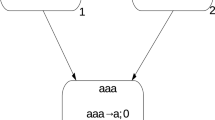
One of the possible incongruities or cases to be clarified in this extension is when two or more instructions that are activated in the same computation step are connected to the same channel, a visual example is illustrated in Fig. 3 where the set of initial instructions is $I_0 = \{i_1,i_2\}$.

Fig. 3

Ambiguity example 4.1

The question that arises is the following. How many viruses are consumed in each computation step? An answer could be that as many viruses are consumed as the number of active instructions that open that channel at that instant. (for example, in Fig. 3, two viruses would be consumed), but in the semantics of basic machines, the action that an instruction performs is simply to open channels, and if a channel is open, a virus can pass through it and replicate in that channel. If several instructions are active at the same time and associated to the same channel, the channel will be opened, and, following the basic machine semantics, the next instructions will follow the path of greater or lesser weight depending on whether the starting host contains a virus or not, respectively (if it is not unique, the path is non-deterministically chosen).

For the example mentioned in Fig. 3, the computation would be:

$$\begin{aligned} \begin{aligned} C_0&= (2,\{i_1,i_2\},0), \\ C_1&= (1,\{i_1,i_2\},1), \\ C_2&= (0,\{i_1,i_2\},2), \\ C_3&= (0,\{i_3\},2), \\ C_4&= (0,\{\#\},2), \end{aligned} \end{aligned}$$

where it can be easily seen that no acceleration of the computation or virus creation has occurred.

4.2 Coincidence in channel start host

On the other hand, we could also have the case where two or more instructions are associated with different channels but with the same starting host.

For this case, it is interesting to consider different semantics and study their advantages and disadvantages. In this work, two of them are considered.

4.2.1 Scenario 1

All associated channels are opened, so if there is a sufficient number of viruses on the host, one virus passes through each channel.

Now, what happens if the number of open channels is greater than the number of viruses contained in the host? For this case, a non-deterministic choice is made as to which channels the viruses pass through, i.e., if n is the number of viruses contained in a host h at an instant t and the number of channels outgoing from that host h opened at that instant are m with $m>n$, then n of these channels are chosen non-deterministically to pass a virus through each channel (with its corresponding replication).

Here arises another decision to be made in terms of semantics: in the above case, what happens to the instructions associated with the channels that have not passed any virus? There can be two options for this case:

• As no virus has passed through this channel, the path of least weight is followed.

• Having a virus in the starting host, the highest weight path is followed.

Actually, as we have defined the semantics previously, the first option seems to be closer to the basic semantics, but the difference between the two does not cause drastic changes in the model.

An advantage in this semantics is that the model now has another non-determinism option and not only the one purely associated with the instructions, which can be an advantage when thinking about PVMs in generating natural number sets. For example, a PVM that generates the arithmetic progression $\{n\cdot i\, i\ \ge 1\}$ is shown in Fig. 4 that enhances the time efficiency in linear time (3i steps to generate $n\cdot i$) and does not use the previous non-deterministic behavior of basic virus machines.

Fig. 4

A PVM generating $\{n\cdot i\ : i\ \ge 1\}$

A sketch of formal verification is established; let us suppose that the number $n\cdot i$ is generated, the following formula is verified:

$$\begin{aligned} \phi (k) \equiv C_{3k}=(1,0,\{i_1,i_2\}, n\cdot k), \ 0\le k \le i-1 \end{aligned}$$

Proving by induction, the case $k=0$ is trivial; for the inductive step, suppose the formula for $0\le k < i-1$, and prove that it is verified for $k+1$. By induction hypothesis, we have:

$$\begin{aligned} \begin{aligned} \phi (k) \equiv C_{3k}&=(1,0,\{i_1,i_2\}, n\cdot k), \\ C_{3k+1}&=(0,2,\{i_3,i_5\}, n\cdot k), \text { choose } i_2\\ C_{3k+2}&=(1,1,\{i_4,i_6\}, n\cdot k), \\ C_{3k+3}&=(1,0,\{i_1,i_2\}, n\cdot k + n), \end{aligned} \end{aligned}$$

Since $\phi (k)$ is true for all $0\le k\le i-1$, in particular it is true for $\phi (i-1)$:

$$\begin{aligned} \begin{aligned} \phi (i-1) \equiv C_{3(i-1)}&=(1,0,\{i_1,i_2\}, n\cdot (i-1)), \\&\text { choose } i_7\\ C_{3(i-1)+1}&=(0,0,\{i_7\}, n\cdot (i-1)+n), \\ C_{3(i-1)+2}&=(0,0,\{\#\}, n\cdot i), \end{aligned} \end{aligned}$$

Thus, in the $3i-1$ steps, the machine halts and returns $n\cdot i$.

For the other perspective, if we notice that we are only sending n viruses to the environment or zero at each instant, then the output can only be a multiple of n.

We also can take advantage of the non-determinism of instructions. Let us show an example by generating the powers of two $\{2^i \ : i\ge 1\}$, as we can see in Fig. 5. The machine is based on the following equality $\sum \nolimits _{j=0}^k 2^j = 2^{k+1} -1$.

Fig. 5

A PVM generating $\{2^i\ : i\ \ge 1\}$

For formal verification, we can take into account that deleting the node $i_{19}$ (which will lead to the halting configuration) of the instruction graph follows to three connected components: (i) the first one is $\{i_1,i_{16},i_{17},i_{18}\}$ such that it decides if the loop halts or not, (ii) the second one is $\{i_2,i_4,i_5,\dots ,i_9\}$ which generates powers of two in $h_4$, and (iii) the last one $\{i_3,i_{10},i_{11},\dots ,i_{15}\}$ which sends to the environment those powers of two calculated in the previous loop.

The design of this machine hides a new technique for the design of this new extension that we will talk about later: the “initiators”.

Finally, we conclude this subsection by seeing that the non-determinism from instructions is directly related to this semantics. In the example presented in Figs. 6 and 7, we can observe that both cases $i_2$ and $i_3$ will be chosen non-deterministically.

Fig. 6

Instructions non-determinism behavior

Fig. 7

A PVM that simulates the instructions non-determinism behavior

4.2.2 Scenario 2

Only one virus is consumed from the starting host, regardless of the number of channels open at that instant, and for each channel, one virus is handled. With this semantic, we are gaining some power in terms of achieving a higher number of viruses in a single transition step.

For example, we can make n copies of a number x in parallel in x transition steps, as we can see in Fig. 8.

Fig. 8

A PVM copying x viruses in n hosts

As in the previous section, the generating mode can be interesting to study, now we get a bit better efficiency in generating the arithmetic progression, as we can see in Fig. 9.

Fig. 9

A PVM generating $\{n\cdot i\ : i\ge 1\}$

Suppose that $n\cdot i$ is generated for $i\ge 2$, (the case where $i=1$ is almost trivial), then the following formula holds:

$$\begin{aligned} \phi (k)\equiv \mathcal {C}_{1+k}= (1,1,\{i_4,i_5,i_6\},n\cdot k), \ 0\le k \le i-2 \end{aligned}$$

If $\phi (k)$ is true for every k with $0\le k \le i-2$, in particular $\phi (i-2)$ is verified:

$$\begin{aligned} \begin{aligned} \mathcal {C}_{1+i-2}&= (1,1,\{i_4,i_5,i_6\},n\cdot (i-2)), \\&\text { choose } i_7\\ \mathcal {C}_{1+i-1}&= (1,1,\{i_5,i_6,i_7\},n\cdot (i-1)),\\ \mathcal {C}_{1+i}&= (0,2,\{i_5,i_6\},n\cdot i), \\ \mathcal {C}_{2+i}&= (0,2,\{i_7\},n\cdot i), \\ \mathcal {C}_{3+i}&= (0,2,\#,n\cdot i), \end{aligned} \end{aligned}$$

Thus, the PVM halts in $3+i$ steps and returns $n\cdot i$.

On the other hand, we are sending only multiples of n; hence; the other implication is true.

Ultimately, we can also achieve an improved computational time efficiency for computing functions, such as the function $f(x,y) = x\cdot y$. Let us examine a PVM that performs this computation (Fig. 10).

Fig. 10

A PVM that computes $f(x,y) = x\cdot y$

For $y>0$, the following invariant holds:

$$\begin{aligned} \phi (k) \equiv \left\{ \begin{array}{l} C_{\beta _k} = (x\cdot k, y-k, x,0,k,\{i_{7},i_{8}\},0), \\ 1\le k\le y, \quad k\text { odd,} \\ C_{\beta _k} = (x\cdot k, y-k, x,0,k,\{i_{11},i_{12}\},0), \\ 1\le k\le y, \quad k\text { even,} \end{array}\right. \end{aligned}$$

where $\beta _k = 1 + k\cdot x + 2(k-1)$. In particular, $\phi (y)$ is true, which leads to the next halting configuration:

$$\begin{aligned} \mathcal {C}_{\beta _y + x\cdot y + 3} = (0,0,x,0,y,\#,x\cdot y), \end{aligned}$$

That is, the machine halts in $2x\cdot y + 2y + 2$ steps (the basic VM halts in $3x\cdot y + 3y + 2$ steps in [10]) and returns $x\cdot y$.

In addition, compared to basic virus machines, some efficiency can be increased by a PVM $\Pi _{dif}$ of degree (3, 5, 2) that computes the reduced difference function $f(x,y) = x{\mathop {-}\limits ^{\bullet }}y$, visually represented in Fig. 11. For a given input $(x,y)\in \mathbb {N}^2$, the machine $\Pi _{sub}+(x,y)$ halts in $\max (x,y)+3$ transition steps with the halting configuration $\mathcal {C}_{(\max (x,y)+3)}=(0,0,x+y,\#,x{\mathop {-}\limits ^{\bullet }}y)$. Compared to the basic model, in Ref. [10], the authors presented a VM of degree (3, 4, 2), computing the same function in $x+y+2$ steps for the case $x>y$.

Fig. 11

The PVM $\Pi _{dif}$, computing the reduced difference

4.3 Decision

When comparing both scenarios, it is evident that the preferable choice is to proceed with the semantics defined in Scenario 1. Although Scenario 2 offers improved efficiency, the magnitude of this improvement is not significant enough to warrant selecting it over Scenario 1. Moreover, Scenario 1 is better suited for handling non-determinism and is considered a more seamless extension to the basic model.

4.4 Limitations

In this subsection, we will discuss some limitations of this extension (or generalization) of basic virus machines. Even if it seems to provide a large amount of computational power, only some calculi can be improved with this method.

4.4.1 Parallelism can only decrease

One of the main limitations of this model, regardless of the semantics associated with it, is that parallelism can only be decreased or maintained but never increased; that is, the number of instructions of a set of active instructions $I_t$ is always greater than or equal to the number of instructions of a set of active instructions $I_{t+1}$ obtained by applying the instructions from $I_t$. A further extension of the model that increases the parallelism could be interesting, but in this chapter, we will continue to focus on this parallel extension and a possible solution of this issue.

Let us suppose that we have several tasks $\{L_1,\dots ,L_k\}$ computed by a set of virus machines $\{\Pi _1,\dots ,\Pi _k\}$, respectively, and that we want to carry out those tasks in parallel, so we will need at least k initial instructions. For that, a “initiator” instruction that is activated initially and remains activated until some change is made in parallel (in the host associated). An idea of this can be seen in Fig. 12, where instruction $i_1$ will be activated until one virus is sent to $h_1$. Continuing this idea, we can generalize it to the case discussed above, as we can see in Fig. 13, where several instructions ensure that all the other tasks start in parallel.

Fig. 12

PVM initiator

Fig. 13

PVM that initialize tasks $\{L_1,\dots ,L_k\}$ in parallel

This seems to be a solution to this problem; nevertheless, there is another big issue to deal with.

4.4.2 Low information from instructions

A further limitation, in addition to the scope of the model, is that the instructions have limited information about the overall state of the machine (as the instructions in Turing Machines) as each instruction works independently. Note that when an instruction is activated, the subsequent instruction is only dependent on the number of viruses in a single host, specifically, on whether it is empty or not.

This issue brings with it a number of parallelism problems that need to be alleviated. Let us suppose that several (sub)machines have been initialized to solve an explicit problem (using a brute force search technique, for example) and then one of them solves the problem, at that instant the other (sub)machines should halt, but we do not know the state of the others. Some possible solutions could be as follows:

• XOR key. This holds the idea from Fig. 12, by the moment when one of the (sub)machines solves the problem, then a check if another one has reached it previously, if not, return the result and then start “killing” the other (sub)machines; this structure can be visualized in Fig. 14. This process of “killing” should be ad-hoc for each specific problem and cannot be generalized, unless new extensions or semantics are added. This idea has been thoroughly developed in Ref. [16].

• New halting criteria. This would solve the problem that, if the task is finished but other instructions are still activated, this should be solved machine-by-machine unless a new halting criteria would be defined: Once one virus is sent to the environment, as soon as no more viruses are sent to the environment, the machine will halt in the following step.

• Death instructions. Another solution could be the addition of a new kind of instructions associated with hosts that, once activated, kill the host and all the channels associated with it.

Fig. 14

PVMs $\Pi _1,\dots , \Pi _k$ which attack the same problem joint

5 Discussion with SNP systems

In this section, a comparison with spiking neural P systems (for short SNP) [17], a well-established Natural Computing model inspired by spikes between neurons, is discussed. Despite the computation process and the semantics different from virus machines, it is interesting to compare both memory units: the neurons from SNP systems and the hosts in virus machines, as both are the memory units of their respective computing models and, even more, both present a relatively similar parallelism behavior, as the authors proposed in Ref. [18].

In the foundational paper on the SNP systems [17], authors demonstrated that each arithmetic progression $\{n\cdot i\ |\ i\ge 1\}$ with $n\ge 3$ can be generated by a SNP system with 2n neurons; nevertheless, in parallel virus machines, we have proved in this paper that it can be generated with only 2 hosts for each n for both scenarios.

Moreover, in the same work, in Ref. [17], they presented an SNP system generating the set $\{2^n \ |\ n\ge 2\}$ using 18 neurons; in this work, we presented a PVM generating the same set with only 5 hosts.

This advantage in the memory units, also shown in Table 1, is because of the instruction graph; it gives more control to the parallelism behavior, so less “parallelism problems” arise.

Table 1 Comparison between SNP systems and the proposed model

6 Conclusion

In this work, we provide an extension of VM: parallel virus machines are studied as a first approach to parallelism. Several semantics are studied to fix all different ambiguities or clarifications of the model. In addition, possible solutions to parallelism problems are presented and studied. However, many problems remain to be solved in the search for a substantial improvement in efficiency:

• Adding a “channel parallelism” behavior, in the sense that one instruction can open more than one channel at the same time.

• The singleton alphabet seems to be another limitation; working with different kinds of virus seems to have another good scope.

• Host replication, inspired by cellular mitosis, gained exponential space in polynomial time similarly to other natural computing models.

• More bio-inspired ingredients such as virus mutation, dead hosts, etc.

More over, this paper opens the field of research of parallel virus machines attacking harder problems with better efficiency and also taking advantage of the parallelism behavior, for example, for image processing applications, time series forecasting, etc.