1 Introduction

Chemical reaction schemes, particularly those found in living organisms, appear to represent invisible networks. Identification of individual reactions mainly results from observation of measurable molecular interactions which reveals potentially involved substrates on the one hand and catalysts as well as products on the other hand [17]. Whenever specific substances seem to be related to each other within a couple of reproducible experiments, it is assumed that there exists a chemical reaction. Fluorescence markers attached to substances under study in concert with highly developed screening techniques and manifold fine-grained weighing, tests, and visualisations can substantiate hypotheses towards proved assumptions. This comes along with a growing knowledge about single reactions, pathways, and finally entire reaction schemes suitable to fulfil certain tasks. Comprehensive collections and repositories of reaction schemes have been reported up to now [15, 26]. Most of them concern aspects of metabolism, cell signalling, or gene expression [5]. When retrieving public data bases, it stands out that reaction schemes are commonly managed in a static manner. The topology of a reaction network is typically represented by an invariable, inherently unmodifiable structure.

For small and medium-sized reaction networks, a static topology seems to be in accordance with a reliable function and successful operation [21]. In most cases, those networks result from a highly conserved genotype. Even small changes within the network structure can often cause tremendous malfunctions or a complete loss of functionality. From an evolutionary point of view, emergence of corresponding networks previously required an advantageous interplay of numerous mutational effects whose probability in total keeps at a realistic stage. Seldomly, a reaction network evolved in this way, is comprising more than approximately 100 distinct reactions and a similar number of involved chemical species [15]. The network as a whole typically acts as a module, a functional unit of associated chemical reactions forming a static hypergraph structure.

Interestingly, the situation becomes completely different when considering complex networks composed of several modules. Here, a static reaction structure has been more and more replaced by a dynamical exchange of chemically interacting modules. While each module in its inner structure remains intact, the connectivity among modules tends to vary. Modules interact via shared chemical species. From the standpoint of an external observer, an initial set of modules forms a purposive overall reaction network structure which in turn comes into operation. Initiated by specific trigger signals or environmental stimuli, certain modules become deactivated while others are incorporated over time. In consequence, the topology of the corresponding overall reaction scheme undergoes some modifications. Having in mind that trigger signals or environmental stimuli might deviate from pure chemical parameters it becomes obvious that an organism or a complex biological system cannot sufficiently be captured by one static reaction system but more likely by a (spatio)temporal sequence of dynamically re-assembled network structures instead.

An illustrative example in this context is given by photosynthesis [16, 31]. Some reactions based on chlorophyll as one of the substrates run if and only if light—whose intensity exceeds a detection threshold—affects the underlying system in terms of environmental stimulus. So-called light reactions start their activity by completing the production of fructose, a storage medium of chemical energy. In the absence of brightness, so-called dark reactions persist for accumulation and standby preparation of organic material for later consumption within light reactions. This behavioural scenario implies at least two types of modules: one module contains light-dependent reactions whereas other module(s) subsume reactions independent of light. For a detailed trace of the entire photosynthesis’ systems behaviour, we need the temporal course of light intensity and spectrum along with detection thresholds and all involved modules, each of them expressed by a network of reactions together with appropriate kinetic issues. Light intensity within a relevant range of absorbed wavelengths (below and above “green”) acts as a conditional trigger for re-assembly of the module connectivity. In case of darkness, module(s) composed of light-dependent reactions become disconnected and hence deactivated while vice versa during penetration of light these modules are parts of the overall system.

Aspects of photosynthesis have been modelled using P systems. In [24] and [25], the model is restricted to light reactions neglecting the influence of dark reactions. Instead, the aspect of photoinhibition is focused on. Non photochemical quenching (NPQ), another aspect of photosynthesis, has been modelled using a metabolic P system [18, 22]. A probabilistic approach to photosynthesis interaction in cyanobacteria is described in [4, 30]. Here, the relation of photosynthesis to respiration has been figured out. Surveys are given in [6, 23]. Complementing these contributions, systems biology provides mechanistic modelling approaches [2, 32]. The significance and contribution of our work is a consistent model which integrates several, partially different reaction networks (light and dark reactions) and toggling between them by trigger signals. So, we obtain an integrative model for simulation considering varying reaction schemes over time.

A main advantage of P systems in comparison to pure ordinary differential equations lies in its ability for coping with dynamical structures [27, 29], for instance by active membranes. A large number of P systems is dedicated to describe dynamics of intramolecular or intracellular spatial structures, for instance by formalisation of a (complex) molecule by a character string [10, 12, 27]. Then, a multiset is employed in order to denote a reactive pool of molecules while a pair of multisets encodes a chemical reaction [28]. Term rewriting mechanisms allow for emulation of performed reactions over time and/or transduction or diffusion of molecules through a spatial structure of delimiting membranes [11]. Complementing the original notion and intention of P systems, we adopt multisets and rewriting for expression of dynamical modular structures based on a multiset of available modules.

A deterministic P module on its own is a static construct consisting of three components: a list of input signal identifiers, a list of output signal identifiers, and a formal description of reaction system’s temporal behaviour. Most repositories utilise ordinary differential equations for that, especially in case of multiple particle systems founded in metabolism or low-molecular biochemistry. Ordinary differential equations (ODEs) derived from underlying reaction kinetics are an established and practically approved formalisation for the purpose to trace species concentrations over time. Additional equations reflecting other potential parameters like temperature can complement the system’s description together with initial concentrations. Using a reliable and stable numerical solver (like adaptive Runge-Kutta), the concentration courses over time can be estimated and mapped into absolute particle numbers for all considered types of molecules and at all relevant points in time. Chemical concentrations are one form of signals able to be operated by a module. Other forms are for instance environmental temperature, light intensity, or electrical voltage. As far as the influence of those signals on the module’s behaviour is well-defined by arithmetic equations or numerically solvable differential equations, we obtain a suitable behavioural specification of the module under study. In other words, a module deterministically maps temporal input signal courses into temporal output signal courses taking into consideration internal parameters in terms of a “memory”.

Beyond modules on their own, the main focus of attention is laid to dynamical composition and decomposition of modules towards formalisation of more complex system’s behaviour. To this end, we introduce an extended concept of our P Meta Framework presented in [13] and exemplified by biological clock systems in [8]. A P Meta Framework is a collection of interacting deterministic P modules. The P modules might be connected, disconnected, or modified while the entire system is in operation. In addition to the primary version of P Meta Frameworks, we allow modifications of the module connectivity also subject to conditional trigger signals. This feature permits a higher flexibility in formalisation of measurable system’s properties which can be helpful to bring in silico-simulations closer to experimental observations. Furthermore, a compact but expressive formalism is provided to manage dynamical topologies of reaction network structures. The underlying concept resembles an event-based programming language: A program is composed of a final set of instructions. Each instruction contains a specific condition (a Boolean term based on evaluation of conditional trigger signals) followed by a corresponding action. An action could be the connection of two dedicated modules including coupling of shared species and supply of affected signal values. Other actions incorporate disconnection of modules, coupling/decoupling of additional species, module exchange, or module reset. The sequence of instructions defines individual priorities in order to prevent ambiguities. The P Meta Framework is intended to combine an easy-to-use approach for specification of polymorphic processes with a formalism aiming at a future implementation using Python [20], which is preferred due to its comprehensive scientific libraries along with a formally intuitive and powerful syntactical setting.

Section 2 familiarises the reader with the P Meta Framework in detail followed by a demonstrative case study. Therefore, we address photosynthesis of plants in Sect. 3. In the case study, dynamical composition of underlying modules plays a major role in understanding, traceability, and effective in-silico simulation towards practical approaches with benefit in systems biology.

2 P Meta Framework for dynamical composition of reaction schemes

In [9], we introduced the term of deterministic P modules complementary to other forms and in accordance with the notion of modules in systems biology. Each deterministic P module represents a container encapsulating an explicit specification of the dynamical behaviour of a reaction unit using a deterministic scheme like ODE-based reaction kinetics or explicit transfer functions. In addition to the inherent dynamical behaviour, a deterministic P module defines its interface by dedicated input and output signals (like species concentrations, temperature, light intensity) whose temporal courses reflect the data managed by the reaction unit. Interacting deterministic P modules communicate via shared molecular species. We define a deterministic P module by a triple

$$\begin{aligned} <\text {module name}>= (\mathrm {In}, \mathrm {Out}, \square ), \end{aligned}$$

where \(\mathrm {In} = (I_1, \ldots , I_i)\) indicates a finite enumerative list of input signal identifiers, \(\mathrm {Out} = (O_1, \ldots , O_o)\) a finite enumerative list of output signal identifiers, and \(\square\) the underlying system specification processing the input signals and producing the output signals with or without usage of auxiliary inherent signals not mentioned in the interface. Each signal is assumed to represent a real-valued temporal course, hence a specific function \(\sigma : {\mathbb {R}}_{\ge 0} \longrightarrow {\mathbb {R}}\) (\({\mathbb {R}}_{\ge 0}\): non-negative real numbers).

The system specification given in \(\square\) can be exclusively composed of arithmetic equations in an explicit manner. Typically, the specification is described implicitly instead, for instance resulting in ordinary differential equations. In case of ODEs, the deterministic P module makes use of a numerical ODE solver, preferably Runge-Kutta methods. Their advantage lies in the adaptive discretisation of time steps for numerical integration which allows a direct transformation into a term-rewriting scheme based on multisets according to the notion of membrane computing. Adaptability means that the duration of a time step remains variable. In case of heavily changing species concentration, the time step will be set to small values. In contrast, slight variations of species concentrations imply larger time steps. In this way, numerical imprecisions can be diminished in comparison to other techniques. For technical details, we refer the reader to [3]. In brief, the ODE system becomes adaptively discretised in progression of simulation time. For each point in time considered so far, the absolute number of molecules for each species derived from the concentration is estimated and released for output signal courses if required. The process of numerical ODE solution in conjunction with determination of absolute molecule numbers for discrete points in time can be perceived in terms of running a membrane system as introduced in [28]. The precision of inherent signal values captured by \(\square\) might be much higher than those of output values, especially integer particle numbers. Utilisation of an advanced internal precision during signal processing prevents the system from premature numerical blurring.

In line with the intention of systems biology stating that a complex (bio)chemical system is dynamically composed of functional units, so-called modules, we extend the formalism of P Meta Framework introduced in [13]. A P Meta Framework is able to describe a dynamical assembly of deterministic P modules towards more complex systems following the idea of an environmentally and/or genotypically controlled program. A P Meta Framework is a construct

$$\begin{aligned} \Pi _{\square \uparrow \downarrow } = (M, P), \end{aligned}$$

where M denotes a finite multiset of deterministic P modules with finite cardinality while the finite enumeration P keeps the executable program composed by a number of instructions affecting the interplay of underlying modules in M. The entirety of deterministic P modules expressed by the support of M can be interpreted as the genetic potential of highly conserved reaction units. The multiplicities of modules (having several copies of a module at hand) reflect the limitation of resources available for module composition. Having in mind that the gene expression capacity is restricted, the number of modules maintained simultaneously should also be delimited. Nevertheless, the individual multiplicities might vary among different modules.

When initiating \(\Pi _{\square \uparrow \downarrow }\), a corresponding directed graph

$$\begin{aligned} G = (V, E), \end{aligned}$$

is created that formalises the current connectivity structure of interacting deterministic P modules. All available modules on their own instantiate the nodes of G. There are no connections between them before executing the program P:

$$\begin{aligned} V& := {} \left\{ m[i] \,\, | \,\, m \in \mathrm {supp}(M) \,\, \wedge \,\, i \in \{1, \ldots , M(m)\}\right\} \\ E& := {} \emptyset . \end{aligned}$$

The indexing of all instances (copies) m[i] constituted from a module m allows a unique identification necessary for an appropriate matching of nodes addressed by program instructions.

Directed edges between nodes of G symbolise the connectivity of module instances. Let \(a = (a_{\mathrm {In}}, a_{\mathrm {Out}}, a_\square ) \in \mathrm {supp}(M)\) and \(b = (b_{\mathrm {In}}, b_{\mathrm {Out}}, b_\square ) \in \mathrm {supp}(M)\) be two module instances derived from M. An edge \((a,b,R_{a\rightarrow b}) \in E\) denotes a connection from a to b where dedicated output species of a act as input species of b. To this end, each edge comes with a binary relation \(R_{a \rightarrow b} \subseteq a_{\mathrm {Out}} \times b_{\mathrm {In}}\) in which the mapping of a’s output species onto b’s input species is given. \(R_{a\rightarrow b}\) is handled in an injective manner since one output species is allowed to cover several downstream input species, but each input species must be supplied by at most one upstream output species. More formally, we require: \(\forall x,z \in X\) and \(\forall y \in Y \,\, : \,\, (x,y) \in R \,\, \wedge \,\, (z,y) \in R \,\, \Rightarrow \,\, x=z\) where \(R \subseteq X \times Y\) stands for \(R_{a\rightarrow b}\).

Attention must be paid to the composition of deterministic P modules to keep signal semantics and quantitative signal values along with signal identifiers consistent when migrating from one module to another. Along with connecting two modules by shared species, downstream input signal values are taken (copied) from corresponding upstream output signal values according to the underlying binary relation. Supply of an input signal value by coupling on an output signal value overwrites a potential explicitly given initial input signal value.

The instructions of the program P capture the dynamics of our P Meta Framework \(\Pi _{\square \uparrow \downarrow }\) in (re-)assembly of its module instances. The underlying graph G becomes updated whenever an instruction from P is executed. To bring the individual instructions into a temporal order, we assume a global clock whose progression is expressed by a non-negative real-valued variable t marking points in time. We arrange five types of instructions called ModuleConnect, ModuleDisconnect, ModuleExchange, ModuleReset, SpeciesShare, and SpeciesUnshare.

Each instruction in P is opened by an evaluable Boolean term c composed of comparison results Cond among conditional triggers. Syntactically, valid Boolean terms c can be defined in an inductive manner. Each comparison result (Cond) constitutes c. Let c be a valid Boolean term, then also (c or (Cond)), ((Cond) or c), (c and (Cond)), ((Cond) and c), and (not c). Each comparison result Cond takes into account two signal values available in the entirety of modules. Additionally, a time stamp t supplied by the global clock can be employed. For comparison, the standard operators \({\texttt {<}}\), \({\texttt {>}}\), \({\texttt {<=}}\), \({\texttt {>=|}}\), \({\texttt {==}}\), and \({\texttt {!=}}\) are available. As an example, let a Kelvin temperature T and two chemical species concentrations [A] and B be defined. Then \({\texttt {+(((T>= 300) or ([A] < [B])) and (t > 5))+}}\) is sufficient as a Boolean term c. At each discretised point in time, all Boolean terms found in P are evaluated. For those of them having true as result, the subsequently defined action as second part of the instruction is executed.

Let \(a = (a_\downarrow , a_\uparrow , a_\square ) \in \mathrm {supp}(M)\) and \(b = (b_\downarrow , b_\uparrow , b_\square ) \in \mathrm {supp}(M)\) be two module instances derived from M:

\(c \, : \, \texttt {ModuleConnect}(a \rightarrow b, R_{a\rightarrow b})\)

Connects some or all of module a’s output species to represent b’s input species by sharing species identifiers according to the injective binary relation \(R_{a\rightarrow b} \subseteq a_\uparrow \times b_\downarrow\). Edge update scheme: \(E := E \cup \{(a,b,R_{a\rightarrow b})\}\)

\(c \, : \, \texttt {ModuleDisconnect}(a \leftrightarrow b)\)

Completely disconnects modules a and b by annihilating all cross-modular species sharings. This comes along with removing \(R_{a\rightarrow b}\) as well as \(R_{b\rightarrow a}\), respectively. Edge update scheme: \(E := E \setminus \{(a,b,R_{a\rightarrow b})\} \setminus \{(b,a,R_{b\rightarrow a})\}\)

\(c \, : \, \texttt {ModuleExchange}(a, b, R_\downarrow , R_\uparrow )\)

Replaces module a by module b iff both modules comprise the same number of input species and the same number of output species. Either bijective functions \(R_\downarrow \subseteq a_\downarrow \times b_\downarrow\) and \(R_\uparrow \subseteq a_\uparrow \times b_\uparrow\) formalise the renaming of species identifiers for input \((\downarrow )\) and output \((\uparrow )\). Edge update scheme: \(E := E \cup \{(b,x,R_\uparrow (R_{a \rightarrow x})) \,\, | \,\, (a,x,R_{a \rightarrow x})\} \setminus \,\, \{(a,x,R_{a \rightarrow x})\}\cup \,\, \{(x,b,R_\downarrow (R_{x \rightarrow a})) \,\, | \,\, (x,a,R_{x \rightarrow a})\} \setminus \,\, \{(x,a,R_{x\rightarrow a})\} \,\, \forall x \in V \setminus \{a,b\}\)

\(c \, : \, \texttt {ModuleReset}(a)\)

Sets all internal signal values (except input signals) of module a to the initialisation values without any changes of E

\(c \, : \, \texttt {SpeciesShare}(a \rightarrow b, \alpha = \beta )\)

Unifies the output species identifier \(\alpha \in a_\uparrow\) with the input species identifier \(\beta \in b_\downarrow\) if \(R_{a\rightarrow b}\) remains injective. The edge update scheme replaces \(R_{a\rightarrow b}\) within \((a,b,R_{a\rightarrow b})\) by \(R_{a\rightarrow b} \cup \{(\alpha , \beta )\}\).

\(c \, : \, \texttt {SpeciesUnshare}(a \rightarrow b, \alpha \, \natural \, \beta )\)

Annihilates the cross-modular sharing of species identifier \(\alpha \in a_\uparrow\) with the input species identifier \(\beta \in b_\downarrow\). The edge update scheme replaces \(R_{a\rightarrow b}\) within \((a,b,R_{a\rightarrow b})\) by \(R_{a\rightarrow b} \setminus \{(\alpha , \beta )\}\)

The evolution of a P Meta Framework \(\Pi _{\square \uparrow \downarrow } = (M,P)\) is expressed by the dynamically varying graph structure reflected in V and E along with all signal courses available in the individual modules subsumed by M. The program P exclusively composed of instructions of the aforementioned form iteratively tests all conditions at every discretised point in time. Except ModuleReset, the actions are resistant against repeated execution in case of unchanged evaluation results of relevant Boolean terms c over evolution time.

3 Photosynthesis

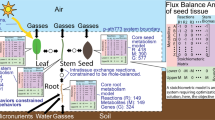
Photosynthesis is a biochemical process found in plants, algae and some bacteria able to make accessible absorbing light energy for production of fructose, a six carbon sugar (\(\mathrm {C}_6\mathrm {H}_{12}\mathrm {O}_6\)). Fructose can store a large amount of chemical energy and serves as a major supplier for maintenance of manifold essential life functions. Photosynthesis that occurs in plants consumes water (\(\mathrm {H}_2\mathrm {O}\)) and carbon dioxide (\(\mathrm {CO}_2\)) by release of oxygen (\(\mathrm {O}_2\)) as by-product. Here, chlorophyll is the crucial substance in order to drive the process which is organised in several interwoven reaction cascades and cycles. Located within green pigments and chloroplasts, chlorophyll appears as reticular \(\mathrm {Mg}^{2+}\)-centered macromolecule available in several closely related forms.

Fig. 1
figure 1

Schematic representation of photosynthesis by simplified reactions gathered from [7]

Full size image

Entering photons stimulate electrons residing within the chlorophyll to reach an increased energy level by movement onto a higher orbital. So, in the presence of light chlorophyll becomes transformed into chlorophyll with excited electrons. These electrons, typically 24 at a time, are released in order to fuel the Calvin cycle for subsequent fructose production. The remaining chlorophyll with electron gaps is restored into its original form by closing the chlorophyll-based cycle. To this end, a simultaneous photolysis dissociates water into free electrons, protons, and oxygen. While the oxygen is directly released to the environment, the protons (\(\mathrm {H}^{+}\)) contribute to obtain nicotinamide adenine dinucleotide phosphate in reduced form (\(\mathrm {NADPH}_2\) for short) from unmodified \(\mathrm {NADP}\). The \(\mathrm {NADPH}_2\) acts as an intermediate energy supplier within the light-independent Calvin cycle. Here, ribulose (\(\mathrm {C}_5\mathrm {H}_{10}\mathrm {O}_5\)) is converted into 3-phosphoglyceric acid (\(\mathrm {C}_3\mathrm {H}_7\mathrm {O}_7P\)), \(\mathrm {PGA}\) for short, under consumption of \(\mathrm {CO}_2\). Resulting \(\mathrm {PGA}\) in turn becomes transformed into glyceraldehyde 3-phosphate (\(\mathrm {C}_3\mathrm {H}_7\mathrm {O}_6P\)), G3P for short, for which \(\mathrm {NADPH}_2\) and adenosine triphosphate (\(\mathrm {ATP}\)) is needed. Some G3P molecules leave the Calvin cycle by formation of fructose. The rest of G3P renews ribulose completing the cycle. To this end, numerous auxiliary substances like \(\mathrm {ATP}\), adenosine diphosphate (\(\mathrm {ADP}\)), and phosphoric acid (\(\mathrm {H}_3\mathrm {PO}_4\)) are involved. See Fig. 1 for a simplified overall photosynthesis reaction scheme.

Within the sphere of membrane computing, aspects of photosynthesis has been modelled for exemplification of some concepts like metabolic P systems for non-photochemical quenching [22] and probabilistic P systems in [1] for anoxygenic photosynthesis processes in some bacteria.

We utilise photosynthesis to demonstrate dynamical composition and decomposition of modules within the P Meta Framework. To this end, two deterministic P modules need to be identified and defined first. One of these incorporates all reactions that require light to occur. In our simplified reaction system, excitation of chlorophyll exclusively constitutes a module named \(<\!\!\text {CphyllExcit}\!\!>\). Light intensity L, chlorophyll concentration [C], and an auxiliary signal CE, all over time, act as input signal identifiers while the concentration of excited chlorophyll marks the output. In a first approximation, we restrict ourselves to mass-action kinetics for capturing the kinetic reactions behaviour to avoid coping with parameters heavily to fit in a verifiable way. Hence, stoichiometry as well as reaction rates were adopted from [19].

$$\begin{aligned}&{<\!\!\text {CphyllExcit}\!\!> \,\, = \,\, (([C], L, CE), ([C_E]), \square )\, \hbox {with} \,\square \,\hbox { from ODE}}\\&\quad \dot{[C_E]} = L \cdot k_1 \cdot [C] + CE\\&\quad k_1 = 0.4, [C_E](0) = 0. \end{aligned}$$

Another deterministic P module called \(<\!\!\text {PhoSynLtIndep}\!\!>\) collects all light-independent reactions including the Calvin cycle. Although a simplified photosynthesis reaction system is applied, a total number of 7 reactions sums up. Some of them comprise numerous substrates and products complemented by large stoichiometric factors due to the organic nature of the underlying metabolism. Since \(\mathrm {H}_2\mathrm {O}\) and \(\mathrm {CO}_2\) are consumed permanently, we choose constant (fixed) concentrations here.

$$\begin{aligned}<\!\!\text {PhoSynLtIndep}\!\!> \,\, &= \,\, (([C_E]), ([C], [F], CE), \square )\\&\qquad \hbox { with } \square \hbox { from ODEs }\\ \dot{[C]} &= k_4 \cdot [C_G] \cdot [E]^{4} - k_1 \cdot [C]\\ CE &= - k_2 \cdot [C_E] \cdot [H]^{4} \cdot [\mathrm {NADP}]^{2} \cdot [\mathrm {ADP}]^{2} \cdot \\&\qquad [H_3PO_4]^{2}\\ \dot{[C_G]} &= - k_4 \cdot [C_G] \cdot [E]^{4} + k_2 \cdot [C_E] \cdot [H]^{4} \cdot \\&\qquad [\mathrm {NADP}]^{2} \cdot [\mathrm {ADP}]^{2} \cdot [\mathrm {H}_3\mathrm {PO}_4]^{2}\\ \dot{[E]} &= -4 \cdot k_4 \cdot [C_G] \cdot [E]^{4} + 4 \cdot k_3 \cdot [H_2O]^{2}\\ \dot{[H]} &= 4 \cdot k_3 \cdot [\mathrm {H}_2\mathrm {O}]^{2} - 4 \cdot k_2 \cdot [C_E] \cdot [H]^{4} \\&\qquad \cdot [\mathrm {NADP}]^{2} \cdot [\mathrm {ADP}]^{2} \cdot [\mathrm {H}_3\mathrm {PO}_4]^{2}\\ \dot{[\mathrm {O}_2]} &= k_3 \cdot [\mathrm {H}_2\mathrm {O}]^{2}\\ \dot{[\mathrm {NADP}]} &= 2 \cdot k_6 \cdot [\mathrm {PGA}]^{2} \cdot [\mathrm {NADPH}_2]^{2} \cdot [\mathrm {ATP}]\\&\quad -2 \cdot k_2 \cdot [C_E] \cdot [\mathrm {H}]^{4} \cdot [\mathrm {NADP}]^{2} \cdot [\mathrm {ADP}]^{2} \cdot [\mathrm {H}_3\mathrm {PO}_4]^{2}\\ \dot{[\mathrm {NADPH}_2]} &= -2 \cdot k_6 \cdot [\mathrm {PGA}]^{2} \cdot [\mathrm {NADPH}_2]^{2} \cdot [\mathrm {ATP}]\\&\quad +2 \cdot k_2 \cdot [C_E] \cdot [H]^{4} \cdot [\mathrm {NADP}]^{2} \cdot [\mathrm {ADP}]^{2} \cdot [\mathrm {H}_3\mathrm {PO}_4]^{2}\\ \dot{[\mathrm {ADP}]} &= k_8 \cdot [G3P]^{2} \cdot [\mathrm {ATP}]\\&\quad + k_6 \cdot [\mathrm {PGA}]^{2} \cdot [{NADPH}_2]^{2} \cdot [\mathrm {ATP]}\\&\quad -2 \cdot k_2 \cdot [C_E] \cdot [H]^{4} \cdot [\mathrm {NADP}]^{2} \cdot [\mathrm {ADP}]^{2} \cdot [\mathrm {H}_3\mathrm {PO}_4]^{2}\\ \dot{[H_3PO_4]} &= k_8 \cdot [G3P]^{2} \cdot [\mathrm {ATP}]\\&\quad +k_6 \cdot [\mathrm {PGA]}^{2} \cdot [\mathrm {NADPH}_2]^{2} \cdot [\mathrm {ATP}]\\&\quad -2 \cdot k_2 \cdot [C_E] \cdot [H]^{4} \cdot [\mathrm {NADP}]^{2} \cdot [\mathrm {ADP}]^{2} \cdot [\mathrm {H}_3\mathrm {PO}_4]^{2}\\ \dot{[\mathrm {ATP}]} &= - k_8 \cdot [G3P]^{2} \cdot [\mathrm {ATP}]\\&\quad - k_6 \cdot [\mathrm {PGA}]^{2} \cdot [\mathrm {NADPH}_2]^{2} \cdot [\mathrm {ATP}]\\&\quad +2 \cdot k_2 \cdot [C_E] \cdot [H]^{4} \cdot [\mathrm {NADP}]^{2} \cdot [\mathrm {ADP}]^{2} \cdot [\mathrm {H}_3\mathrm {PO}_4]^{2}\\ \dot{[R]} &= k_8 \cdot [G3P]^{2} \cdot [\mathrm {ATP}]\\&\,\,\quad - k_5 \cdot [R] \cdot [\mathrm {CO}_2], \end{aligned}$$
$$\begin{aligned} \dot{[\mathrm {PGA}]} & = -2 \cdot k_6 \cdot [\mathrm {PGA}]^{2} \cdot [\mathrm {NADPH}_2]^{2} \cdot [\mathrm {ATP}]\\& \quad \,\, +2 \cdot k_5 \cdot [R] \cdot [\mathrm {CO}_2]\\ \dot{[G3P]} & = -2 \cdot k_8 \cdot [G3P]^{2} \cdot [\mathrm {ATP}] - 2 \cdot k_7 \cdot [G3P]^{2}\\ &\quad \,\,+4 \cdot k_6 \cdot [\mathrm {PGA}]^{2} \cdot [\mathrm {NADPH}_2]^{2} \cdot [\mathrm {ATP}]\\ \dot{[F]} & = k_7 \cdot [G3P]^{2}\\ [\mathrm {H}_2\mathrm {O}] &= 12\\ [\mathrm {CO}_2] & = 6\\ k_1 & = 0.4, k_2 = 0.4, k_3 = 0.008, k_4 = 0.4,\\ k_5 & = 0.1, k_6 = 0.1, k_7 = 0.1, k_8 = 0.1,\\ [C](0) & = 10, [C_G](0) = 0, [E](0) = 0,\\ [H](0) & = 0, [O_2](0) = 0,\\ [\mathrm {NADP}](0) & = 12, [\mathrm {NADPH}_2](0) \\ &= 0, [\mathrm {ADP}](0) = 24, [\mathrm {H}_3\mathrm {PO}_4](0) = 6,\\ [\mathrm {ATP}](0) & = 0, [R](0) = 0, [\mathrm {PGA}](0)\\ & = 0, [G3P](0) = 10, [F](0) = 0. \end{aligned}$$

Having both deterministic P modules at hand, we can now specify its dynamical interplay by the P Meta Framework \(\Pi _{\clubsuit }\). Its specification includes the multiset M for capturing the available modules and their delimiting multiplicities. Here, at most one copy of \(<\!\!\text {CphyllExcit}\!\!>\) and one copy of \(<\!\!\text {PhoSynLtIndep}\!\!>\) is sufficient. The component P contains the program for dynamical re-assembly of modules. We arrange two instructions corresponding to high and low intensity of light. Assuming that the light intensity is provided by a course altering between 0 (dark) and 1 (bright), we can connect both modules as soon as light intensity exceeds the (arbitrarily chosen) threshold of 0.5. As soon as light intensity sinks below 0.5, both modules become immediately disconnected. Linkage of modules is expressed by shared species or shared signals mentioned in the binary relation assigned to ModuleConnect.

$$\begin{aligned} \Pi _{\clubsuit } &= (M, P) \quad \text {with}\\ M &= \{(\text {CphyllExcit}, 1),\\&\quad (\text {PhoSynLtIndep}, 1)\}\\ P &= \{\texttt {(L\!>\!0.5)} \, : \, \texttt {ModuleConnect}(\text {PhoSynLtIndep[1]} \rightarrow \\&\quad \text {CphyllExcit[1]},\\&\quad \{([C],[C]), (CE, CE)\}),\\&\quad \texttt {(L\!<\!0.5)} \, : \, \texttt {ModuleDisconnect}(\text {PhoSynLtIndep[1]} \leftrightarrow \\&\qquad \text {CphyllExcit[1]}). \} \end{aligned}$$

Now, the overall systems behaviour can be obtained by evolving \(\Pi _{\clubsuit }\) over time together with a freely selectable course of L. Figure 2 exhibits a typical outcome. Here, accumulation of fructose F is depicted for 36 h with repeated alteration between brightness and darkness after 12 h each. After a transient phase, production of fructose proceeds almost linear up to the first module disconnection. During the initial phase of suddenly prevailing darkness, fructose production can still continue. Along with gradual exhaustion of necessary substrates, fructose concentration asymptotically runs towards a steady state. With availability of light and after an appropriate delay, fructose production starts again. Due to a marginally shifted adjustment of G3P, ribulose R, and \(\mathrm {PGA}\) concentration balancing, fructose production runs with slightly reduced yield.

Fig. 2
figure 2

Simulated accumulation of produced fructose [F] dependent on penetration with light over time. Along with altering light intensity, modules become connected or disconnected, respectively

Full size image

Please note that signal courses under study might have points of discontinuity (sharp bends) when progression of signal values follows modified equations.

4 Conclusions

The P Meta Framework opens an alternative way to formalise dynamical reaction network topologies. Our approach is based on a program whose instructions are handled in an event-based manner. Conditional triggers initiate actions affecting the underlying reaction network structure. This concept combines a compact and expressive formulation of structural dynamics with the ability for efficient practical implementation. Continuatively, re-assembly of pre-defined reaction network modules on the fly appears to be a promising strategy to achieve complex systems capable of new or extended functionality. Inspired by biological evolution at a granularity of highly conserved genetic ensembles, our P Meta Framework provides a tool for control and systematic conduction of corresponding studies. Simulations for the photosynthesis case study were carried out using Copasi [14]. Sources are available from the author upon request. Future work will focus on a consistent software implementation using Python which enables a higher flexibility in systems specification.