A computational study on efficient yield surface calibrations using a crystal plasticity spectral solver

Abstract

A computational framework is presented, capable of calculating virtual loads using the spectral solver in the DAMASK software for crystal plasticity simulations in desired stress directions. Calculations are used for the calibration of yield surfaces. The required spatial resolution is assessed based on a comparison with the previously published crystal plasticity finite-element method (CPFEM) and experimental results for three different aluminum alloys (AA1050, AA3103O, and AA3103H18) with 1000 and 2500 grains in a representative volume element. The results of the crystal plasticity fast Fourier transform (CPFFT) method agree well with CPFEM. The elongated grain morphology of the AA3103H18 alloy was found to have a small effect on predicted anisotropy. An analysis was made of how many tests are required for proper calibration of the Yld2004-18p orthotropic yield surface. It was found that 32 virtual tests, along either uniformly distributed strain rate or stress directions but obeying the orthotropic symmetry of the Yld2004-18p yield surface, make a good compromise between accuracy and computation time. Randomly chosen directions have a significantly larger error and require more virtual tests for a similarly good calibration of the yield surface. Since a preselected set of strain–rate directions does not require extra iterations, it is the preferred choice for the calibration of the full stress-based Yld2004-18p.

1 Introduction

The crystal plasticity theory is used for modelling the mechanisms of plastic deformation of metals at the microscale level. The increased capacity of modern computers enables full-field crystal plasticity calculations of small structures. For larger structures, detailed calculations are not possible with existing technology. However, full-field crystal plasticity calculations can be used to perform virtual experiments to calibrate continuum-scale models. This can efficiently be done considering a small representative volume element (RVE) and periodic boundary conditions. This is mainly the case a spectral solver can deal with, but then it is also very fast.

Metals and metallic alloys are crystalline materials for which plastic deformation most often may occur by slip on planes and in crystallographic directions, i.e., slip systems. Plastic deformation may also involve twinning or grain boundary sliding, but these mechanisms are not considered in the present work here. The crystallographic texture in sheet metals, i.e., the statistical distribution of the grain orientations, develops during thermo-mechanical processing and is the primary source of plastic anisotropy, calculated by crystal plasticity simulations.

Analytical yield functions are employed at the component scale to describe polycrystalline materials’ anisotropy in the continuum plasticity framework because of their high performance and feasible implementation. Since Hill's quadratic anisotropic yield function (Hill 1948), increasingly complex formulations have been proposed (Aretz and Barlat 2013; Banabic et al. 2003; Barlat et al. 2007; Bron and Besson 2004; Cazacu et al. 2006; Karafillis and Boyce 1993; Soare 2022). These are linear transformation-based yield functions with an exponent that can be related to a material crystal structure. In most calibrations, the yield surface exponent is put equal to 6 for bcc and 8 for fcc structures, based on earlier calibrations, where the full constraint Taylor model was applied (Barlat 1987). However, recent CPFEM calculations suggest smaller exponents (Zhang et al. 2019). A precise calibration of the yield–surface exponent requires a high number of tests.

For calibrating the parameters of the material models, carefully chosen experimental tests are required for proper calibration (Lademo et al. 1999). Due to technical and cost limitations, it is only possible to perform a limited number of experimental tests on a sheet material, and often only tensile tests are performed in various plate directions. To utilize the improved flexibility and accuracy of the complex yield surfaces, time-consuming, expensive, and in some cases, very complex experiments are required, i.e., when out-of-plane properties of sheet metals are needed. No commonly accepted standards are established for choosing which experiments to include and how to include them in calibration procedures. The simulation results heavily rely on the quality of the parameter calibration, whereas most stress or strain paths are very challenging to probe by physical experiments, virtual experiments by crystal plasticity simulations can be performed in any direction in the stress or strain–rate space, enabling robust and efficient calibration of the complex yield functions.

The simplest and fastest crystal plasticity models are aggregate Taylor type of statistical models. A review of most of these Taylor types of models is found in Manik and Holmedal (2014). Recent comparisons of aggregate Taylor type of models, also with comparison to CPFEM, have been made by (Zhang et al. 2014, 2015). These aggregate Taylor types of models have successfully been applied to generate virtual experiments for calibrating yield surfaces. An example is (Plunkett et al. 2007, 2006), who employed VPSC model for calibration of yield surfaces. Grytten et al. (2008), who calculated the parameters of Yld2004-18p and pointed out the necessity of more advanced CP models in such approaches. A recent example is the work by Engler and Aretz (2021), who performed virtual tests by the VPSC model for calibration of the Yld2011-27p yield surface applied for deep-drawing simulations of aluminum alloys., and Coppieters et al. (2019) who calibrated the Yld2000-2d and Hills quadratic yield surface for deep-drawing simulations of a steel plate.

With improved computer capacity, CPFEM simulations have been enabled for calibrating yield surfaces based on virtual experiments calculated using representative volume elements, e.g., (Hama et al. 2021; Yoshida et al. 2021), or small samples, e.g., (Zecevic et al. 2021). CPFEM allows accounting for grain morphology, internal stresses due to grain interactions, and grain misorientation distribution. Virtual experiments by CPFEM have successfully been taken into use to calibrate continuum plasticity yield surfaces (Esmaeilpour et al. 2018; Inal et al. 2010; Liu et al. 2019; Liu and Pang 2021; Saai et al. 2013; Sun et al. 2021a, 2021b; Zhang et al. 2014, 2015).

As an alternative to CPFEM, the crystal plasticity Fast Fourier Transform (CPFFT) method (de Geus et al. 2017; Eisenlohr et al. 2013; Isavand and Assempour 2021; Lebensohn et al. 2012; Liu et al. 2010; Lucarini et al. 2022; Lucarini and Segurado 2019a, 2019b; Rovinelli et al. 2020; Shanthraj et al. 2015) has much higher computational efficiency and spatial resolution than CPFEM (Liu et al. 2010; Lucarini et al. 2022; Lucarini and Segurado 2019b; Rovinelli et al. 2020). However, the simulations are limited to periodic boundary conditions and cuboid simulation geometries (de Geus et al. 2017). Hence, this method is ideally suited for virtual experiments that are simulated on representative volume elements (Han et al. 2020; Liu et al. 2020; Liu and Pang 2021; Zhang et al. 2016).

By high-resolution CPFFT simulations using the DAMASK code, Zhang et al. (2016) calibrated the initial yield surfaces described by Yld91, Yld2000-2D, Yld2004-18p, and Yld2004-27p yield functions. They used 125 randomly generated virtual load cases. It was suggested that an optimization of the location of these yield–stress points, similar to earlier works with aggregate Taylor-type models (Gawad et al. 2015; Grytten et al. 2008; Rabahallah et al. 2009; Zhang et al. 2014, 2015) would further improve the quality of the yield–surface calibrations. Liu and Pang (2021) and Liu et al. (2020) applied this multiscale-modeling scheme to minimize the earing of deep drawing. Han et al. (2020) considered virtual tensile tests in 0°, 15°, 30°, 45°, 60°, 75°, and 90° directions relative to the rolling direction, a balanced biaxial tensile test in the RD-TD plane, 45° tensile tests in the TD-ND and ND-RD plane, and simple shear tests in the TD-ND and ND-RD planes to calibrate the Yld2004-18p yield surface. Furthermore, the DAMASK code was run for each integration point in a FEM calculation of deep drawing, with updated calibration of the yield surface at locally accumulated plastic strain increments of 0.05.

Continuum-plasticity models applied in FEM software are based on either a yield surface or alternatively a surface in the dual strain–rate space that separates elastic and plastic behaviors. The most common approach is to use a yield surface formulated in the stress space. Virtual experiments are then required for selected stress directions. Unlike the aggregate models, which are computationally faster, the detailed CPFEM or CPFFT calculations of the virtual experiments are time-consuming, and the number of tests must be kept limited. Furthermore, to enable future industrial standardization of the selection of stress or strain–rate directions to be probed for an optimal test, it is required that simulations of specified stress directions are enabled. Also, this is convenient for plotting a certain section of an anisotropic yield surface. The stress or strain–rate path in the DAMASK open-source CPFFT (Roters et al. 2019) can be prescribed according to certain mixed boundary conditions. However, pure stress paths along a specified stress direction cannot be prescribed in the DAMASK software used here. The recent development of this technology is reported by (Kabel et al. 2016) and Lucarini and Segurado (2019a), based on a variational algorithm for finite strains, but this is not implemented in the DAMASK software.

Therefore, in this work, an iterative approach is developed for applying the DAMASK software for calculating yield points for exact desired stress orientations. The spectral solvers have a very high spectral order of spatial discretization as long as the simulated field is sufficiently smooth. The Gibbs oscillations (Gottlieb et al. 2011) at the discontinuities across grain boundaries are reduced using the forward–backward numerical algorithm that is implemented in DAMASK as an option (Roters et al. 2019; Willot 2015). To assess the spatial resolution and the influence of texture and grain morphology in the spectral calculations, the anisotropic behaviors of AA1050 and AA3103 aluminum alloys in both cold-rolled and annealed conditions are calculated and compared with earlier reported CPFEM and experimental results (Zhang et al. 2014, 2015).

In continuum plasticity theories with linear elasticity, both the velocity gradient and the direction of the deviatoric stress can simultaneously be kept constant during proportional loading in the elastic region load toward the yield surface. This is not the case in crystal plasticity simulations in the elastoplastic transition, where the plasticity is gradually occurring in an increasing fraction of the grains. The load path here may become non-proportional. In crystal plasticity simulations, or in experiments, the yield points on the yield surface identified at a given plastic work, correspond to a plastic probing strain, e.g., 0.2%. One must choose either the stress direction or the velocity gradient to be kept constant during the tests. If the stress direction is constant, the velocity gradient will change during the test and vice versa. Hence, the yield surface identified by these two choices may result in a slightly different shape, in particular with large work hardening. This is a choice to be made in the definition of the yield surface, but the resulting yield surfaces at these small plastic strains are expected to be almost identical. The DAMASK software does not have an option to keep the stress direction constant during loading. Hence, it was decided in the current work to choose the alternative where velocity gradient is kept constant along the strain paths required to probe the yield surface.

With a spatial resolution chosen based on these results, the Yld2004-18p orthotropic yield surface is calibrated to selected material parameter sets. The calibration results with a random selection of either stress directions or strain rates are compared to selecting a uniform distribution of either stress directions or strain rates, obeying orthotropic symmetry and centro-symmetry. For each stress direction, this amounts to eight symmetric variants. When given as argument for Yld2004-18p, all these eight stress variants will give exactly the same equivalent stress. Hence, only one of them needs to be calculated, but all of them are part of the uniform distribution of stress directions. While a random selection of strain rate directions is the most common method used in the literature, a uniform selection of strain rate directions should be expected to give a better calibration with less variation from calibration to calibration. As compared to calibrating to a set of selected stress directions, a set of strain rates, with either uniformly or randomly distributed directions, will give a higher density of stress points in regions with higher curvatures of the yield surface. Computations of stress points in prescribed stress directions have a higher computational cost due to the involvement of an iterative procedure. For plates, however, virtual tests for calibration of a plane–stress yield surface by prescribing strain rates will result in non-zero out-of-the-plane stress components unless the texture and grain morphology strictly obey an orthotropic symmetry. This is the case only in the statistical sense for crystal plasticity simulations, and the approximation becomes better for larger, more costly systems to simulate, involving more grains. Virtual simulations of tests are used to study the required distribution type and the number of virtual tests for good calibrations.

2 Crystal plasticity model

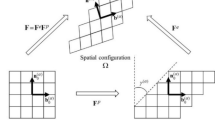
A brief description of the governing equations is given here. Details about the spectral solver and the equations implemented in the DAMASK software are referred to (Eisenlohr et al. 2013; Roters et al. 2019). The total deformation gradient is multiplicatively decomposed into elastic and plastic parts as

$${\varvec{F}}={{\varvec{F}}}_{e}\cdot {{\varvec{F}}}_{p}$$

(1)

where ${{\varvec{F}}}_{e}$ is elastic distortion and rigid-body rotation of the crystal lattice and ${{\varvec{F}}}_{p}$ indicates the plastic shear deformation because of slip in specific crystalline planes and directions. The plastic velocity gradient ${{\varvec{L}}}_{p}$ is described as

$${{\varvec{L}}}_{p}={\dot{{\varvec{F}}}}_{p}\cdot {{\varvec{F}}}_{p}^{-1}=\sum\limits_{\alpha =1}^{N}{\dot{\gamma }}^{\alpha }{s}_{0}^{\alpha }\otimes {n}_{0}^{\alpha }$$

(2)

where in the crystal coordinate system, ${\dot{\gamma }}^{\alpha }$ is the shear rate on the ${\alpha }^{th}$ slip system denoted by two-unit vectors ${n}_{0}^{\alpha }$ (slip plane normal) and ${s}_{0}^{\alpha }$ (slip direction). $N$ refers to the number of slip systems. The plastic flow on a slip system is defined via a rate-dependent flow rule as

$${\dot{\gamma }}^{\alpha }={\dot{\gamma }}_{0}{\left|\frac{{\tau }^{\alpha }}{{g}^{\alpha }}\right|}^{1/m}\mathrm{sgn}\left({\tau }^{\alpha }\right)$$

(3)

where ${\dot{\gamma }}_{0}$ indicates a reference shear rate, ${\tau }^{\alpha }$ denotes the resolved shear stress, $m$ is the instantaneous strain–rate sensitivity, and ${g}^{\alpha }$ evolves through the plastic deformation of single grains (where $\alpha =1,\dots ,12$, are prescribed for the 12 $\left\{111\right\}\langle \overline{1 }10\rangle$ fcc slip systems) via,

$${\dot{g}}^{\alpha }=\sum_a{h}_{0}\left(1-\frac{{g}^{\alpha }}{{g}_{\infty }}\right){q}_{\alpha \beta }|{\dot{\gamma }}^{\alpha }|,\quad g(0)=g_0$$

(4)

Here ${g}_{\infty }$ is the saturation stress, ${h}_{0}$ is the reference self-hardening coefficient and ${q}_{\alpha \beta }$ controls the latent hardening of non-coplanar slips, i.e. ${q}_{\alpha \beta }=q_{NCP}$ when $\alpha$ and $\beta$ labels non-coplanar slip systems, while $q_{\alpha \beta}=1$ for coplanar combinations of $\alpha$ and $\beta$.

Figure 1 shows a flow diagram for the algorithm used in the current computational framework for probing yield surfaces. In the first stage, the geometry and the texture are generated as inputs for DAMASK using the Dream3D software (Groeber and Jackson 2014). The parameters for the evolution of the critical resolved shear stresses are calibrated based on the stress–strain curve of an experimental tensile test in the reference direction, i.e., the rolling direction (RD).

Fig. 1

Flow chart showing the algorithm of the present computational framework

Two strategies are used for choosing a loading mode for the RVE simulation. Either a constant strain rate, $\mathbf{D}$, or a constant Cauchy stress direction, ${{\varvec{\sigma}}}^{\mathrm{aim}}$ with $\Vert {{\varvec{\sigma}}}^{\mathrm{aim}}\Vert =1$, is prescribed. For small strains, $\dot{{\varvec{F}}}\approx {\varvec{D}}$, hence, without loss of generality, the deformation of the RVE is controlled by prescribing a symmetric $\dot{{\varvec{F}}}$, which is available as a standard option in DAMASK.

However, the possibility of loading an RVE along a prescribed stress direction is not implemented in DAMASK. To do this, first, an initial guess of $\dot{{\varvec{F}}}$ with ${\Vert \dot{{\varvec{F}}}\Vert =\dot{F}}^{\mathrm{aim}}$ and the time $t$ for the desired stress point to be reached are made. Based on these guesses, the Cauchy stress, ${\varvec{\sigma}}$, and the corresponding plastic work ${W}_{p}$ are calculated in a post-processing step from the results of the DAMASK simulation.

Eight residuals are defined, i.e., for the prescribed stress direction, ${{\varvec{\sigma}}}^{\mathrm{aim}},$ for the prescribed total strain rate, ${\dot{F}}^{\mathrm{aim}}$, and for the prescribed plastic work, ${W}_{p}^{\mathrm{aim}}$, as:

$$\begin{gathered} \left| {\sigma_{ij} - k\sigma_{ij}^{{{\text{aim}}}} } \right| < \varepsilon \hfill \\ \left| {\frac{{\left\| {\dot{\varvec{F}}} \right\|}}{{\dot{F}^{{{\text{aim}}}} }} - 1} \right|< \varepsilon \hfill \\ \left| {\frac{{W_{p} }}{{W_{p}^{{{\text{aim}}}} }} - 1} \right| < \varepsilon \hfill \\ \end{gathered}$$

(5)

A multiplier $k$ is applied for the mathematical prescription of the stress direction. Given this set of 8 nonlinear equations and 8 unknowns, Powell’s method is used to find a solution vector ${\varvec{x}}$, defined as the six components of a symmetric $\dot{{\varvec{F}}}$, a multiplier $k$ and the time of the simulation $t$.

$${\varvec{x}}=\left[{\dot{F}}_{11},{\dot{F}}_{22}, {\dot{F}}_{33},{\dot{F}}_{12},{\dot{F}}_{23},{\dot{F}}_{13},k,t\right]$$

(6)

Improved guesses are now made for ${\varvec{x}}$, using the nonlinear solver Minpack (Moré et al. 1980; Powell 1968).

During each iteration, a new simulation is performed by DAMASK, taking the deformation gradient rate $\dot{{\varvec{F}}}$ and the time $t$ as inputs and returning the first Piola stress,${\varvec{P}}$, and the plastic velocity gradient,${{\varvec{L}}}_{p}$. The Cauchy stress, ${\varvec{\sigma}}={J}^{-1}{\varvec{F}}\cdot {\varvec{P}}$ and the plastic work, ${W}_{p}= \int {{\varvec{\sigma}}\boldsymbol{ }:{\varvec{D}}}_{p}dt,$ are determined, where${{\varvec{D}}}_{p}=({\boldsymbol{ }{\varvec{L}}}_{p}+{{\varvec{L}}}_{p}^{\mathrm{T}})/2$.

Once the residuals for these eight equations become smaller than $\varepsilon ={10}^{-6}$, the calculated Cauchy stress is selected as an acceptable result, which specifies the correct yield point.

In this work, strain rate ${\dot{F}}^{\mathrm{aim}}={10}^{-3}$ was applied for all the simulations, unless otherwise specified.

To have better efficiency and stability during yield point calculations, the algorithm was first applied to a 16 × 16 × 16 resolution, which takes a relatively short computational time, while at the same time maintaining a sufficiently fine mesh to resolve all grains in the calculation. After that, the solution from the 16 × 16 × 16 was given to the 32 × 32 × 32 resolution as an initial field, and the solution from 32 × 32 × 32 was given to 64 × 64 × 64, and so on. This helps reduce the number of iterations and lowers the simulation time in total.

3 Simulated cases

Three cases were chosen to investigate how fine resolution is required when using the spectral DAMASK solver. Then, one of these cases was further used to investigate how many and which distribution of virtual tests are required for a good calibration of an orthotropic yield surface.

Using the DAMASK software with its spectral solver, a comparison to earlier CPFEM simulation results and experiments (Zhang et al. 2014, 2015) was conducted as part of this work. The work-hardening model implemented in DAMASK is slightly different from the one applied in these previous works. To enable direct comparisons with the previous calculations, the parameters in Eq. (4) were adjusted to the experimental stress–strain curves of the AA3103H18, AA3103O, and AA1050 alloys, taken from Zhang et al. (Zhang et al. 2014, 2015). The cold-rolled AA3103H18 alloy had elongated grains and a typical rolling texture, while after annealing, the AA3103O was recrystallized with a weak texture (Zhang et al. 2014). The AA1050 alloy was in a recrystallized state with equiaxed grains and a strong cube texture (Zhang et al. 2015). In this study, the Euler angles and number of the grains are taken from (Zhang et al. 2014, 2015), but the underlying microstructure is not exactly the same. For example, the grains shape and grain neighbors are different. The material parameters are given in Table 1, and the plotted stress–strain curves for 32 × 32 × 32 resolution are compared to the CPFEM curves in Fig. 2. Note that the hardening model used in this study (Eq. 4) has only one hardening parameter and is different from the model used in (Zhang et al. 2015), where they have used a two-parameter hardening model. Considering the stress–strain curves in Fig. 2, it is seen that, at smaller strains, there is an almost perfect agreement between CPFFT and CPFEM, while it deviates increasingly with increased strains. Considering the weak coupling between isotropic work hardening and stress anisotropy in crystal plasticity simulations and the limited strain range of interest in this study, a very small difference is expected from the difference in the hardening behaviors. A strain rate of 0.1 s^–1 was used in the calibration of AA1050 and AA3103O and a strain rate of 0.015 s^–1 was used in the calibration of AA3103H18.

Table 1 Material properties of AA1050, AA3103H18, and AA3103O alloys

Fig. 2

Comparison of earlier CPFEM and new CPFFT calibrations of stress–strain curves in RD with a strain rate of 0.107 s⁻¹, 0.0152 s⁻¹ and 0.1 ${s}^{-1}$ for a the AA1050 (Zhang et al. 2015), b AA3103H18 and c AA3103O (Zhang et al. 2014), respectively, as predicted by the spectral simulations and the earlier CPFEM simulations

In this paper, tensile tests in various plate directions are considered and specified by an angle $\alpha$, determining the stress direction as compared to RD, i.e., varying from ${\sigma }_{xx} \left(\alpha =0^\circ \right)$ in RD to ${\sigma }_{yy} \left(\alpha =90^\circ \right)$ in the transverse direction (TD).

Regarding the tensile tests that were simulated by CPFEM and measured (Zhang et al. 2015), the total tensile deformation, the critical plastic strain or plastic work at which the yield stress was measured, and the considered range of plastic strain for calculations of the r values (the Lankford coefficient) are given in Table 2. To simulate tensile tests in various plate directions, the boundary conditions and the mesh were kept fixed while all grains were rotated around the normal direction. By doing this, the current reference system changes to (${\varphi }_{1}-\alpha ,\Phi , {\varphi }_{2})$ where $\alpha$ denotes the angle between RD and the tensile axis. Here, $\alpha$ varies between RD and TD in intervals of $15^\circ$, and 7 virtual tensile tests are simulated. An alternative approach would be to impose stress directions for different in-plane directions, but here, the idea is to compare our calculated results by the FFT solver with the CPFEM and experimental results that were reported by (Zhang et al. 2014; Zhang et al. 2015), where they have employed the “texture rotation” method, so we take the same approach.

Table 2 Description of extracted data in tensile tests

3.1 Representative volume elements

The DREAM.3D (Groeber and Jackson 2014) microstructural software analysis package was used to generate the RVEs with 5 different resolutions for each alloy; two of the resolutions for each alloy are shown in Fig. 3. RVEs containing 2500 grains were generated for the AA3103H18 alloy, while RVE's with 1000 grains were generated for AA3103O and AA1050. The resolution varies from 16 × 16 × 16 to 256 × 256 × 256 Fourier points. While the resolution of the modeled structure changes, the geometry, the grain orientations, and the grain structure are kept the same within the chosen resolution.

Fig. 3

RVEs for AA1050, AA3103O and AA3103H18 alloys, exemplified with two different resolutions, 32 × 32 × 32 and 256 × 256 × 256 resolution

For AA3103H18 (elongated grains) and AA3103O (recrystallized) alloys, the aspect ratios of grains were set to be 25:5:1 and 2.5:2:1, respectively. It should be mentioned that for AA3103H18 alloy, the ND length is smaller than other two lengths, but so is the grain ratio in that dimension. So, the resolution is kept consistent in all three axes.

In the case of AA3103H18, simulations were not carried out for the orientations between RD and TD. In this specific case, the strongly elongated forms of the grains cannot be accurately depicted using the 'texture rotation' technique employed in this study. Also the AA3103O alloys consist of elongated grains. Still, since the grains in this case are only moderately elongated in the plate plane (2.5:2), other directions than RD $(\alpha =0)$ and TD $(\alpha =90^\circ )$ were also simulated using the same mesh, but rotating the grains as described above. This only introduces a very small error at the other angles $\alpha$.

4 Results

4.1 Tensile test simulations to assess the required spatial resolution

Virtual tensile tests for AA1050, AA3103H18, and AA3103O alloys were simulated with the five different spatial resolutions and compared with the earlier results from CPFEM and experiments. The yield stresses are normalized with the corresponding values of resolutions 128 × 128 × 128 and 64 × 64 × 64 for the AA3103 and AA1050 alloys, respectively.

In Fig. 4a, normalized yield stresses of the AA1050 alloy are plotted for seven rolling directions. In Fig. 4b, r values for the AA1050 alloy are plotted for the same seven rolling directions. CPFFT and CPFEM give similar results for this alloy, where the most significant differences between the two methods are 1.2% for the normalized yield stress and 5.8% for the r values in 45° and 75° directions, respectively.

Fig. 4

Normalized yield stress and r values for AA1050 (a, b) and AA3103O (c, d) as a function of the angle $\alpha$ with the rolling directions. Results are given for 16 × 16 × 16, 32 × 32 × 32, 64 × 64 × 64 and 128 × 128 × 128 resolutions. In the cases where the results with the two highest resolutions were indistinguishable, the 128 × 128 × 128 resolution is not shown. For AA1050, the results are calculated at a plastic work of 0.2 MPa and strain rate of 0.107 ${s}^{-1}$ and for the AA3103O alloy the results are calculated at 0.5% plastic strain and with a strain rate of 0.1 s⁻¹ * (Zhang et al. 2014, 2015)

Figure 4c and d indicate tensile test results for the AA3103O alloy. It is noted that, especially for the tensile directions closest to the transverse direction, the normalized yield stresses calculated by DAMASK are closer to the experiments than the CPFEM predictions. On the other hand, considering the r values, there is a close agreement between CPFFT and CPFEM results.

To analyze the effect of the grain shape on the anisotropy, an additional grain geometry was generated for the AA3103H18 alloy using the Dream 3D software. This case had equiaxed grains instead of elongated grains, while the texture was kept the same as before. The normalized yield stresses and r values are shown in Fig. 5 for a 32 × 32 × 32 resolution, along with the results from CPFEM and experiments for rolling and transverse directions. In the transverse direction, the differences between elongated and equi-axed grains are 7% and 0.8% for r values and normalized yield stresses, respectively. In the rolling direction, the r values for elongated grains and equi-axed are 7% different.

Fig. 5

Variations of the normalized yield stress (a) and the r value (b) with the tensile direction angle $\alpha$, for the AA3103H18 with elongated grains. Predictions by FFT, CPFEM and experiments (Zhang et al. 2014) are compared. Equi-axed grains are meshed for all directions, while elongated grains are simulated only for the RD and TD directions. The FTT results are obtained by a 32 × 32 × 32 resolution. The results are calculated at plastic strain of 0.5% and with a strain rate of 0.0152 s⁻¹ * (Zhang et al. 2014, 2015)

In general, the calculated distribution of normalized yield stresses by the spectral solver is equally close or closer to the experiments than those by CPFEM, while the r values are very similar. Even the coarsest mesh with 16 × 16 × 16 Fourier points provides acceptable results for most of the rolling directions considered here.

4.2 Yield surface predictions

Calculated yield–surface sections of the cold-rolled (H18 temper), and the cold-rolled and annealed (O-temper) AA3103 alloy, respectively, are shown in Fig. 6 for three different resolutions with CPFFT and compared with the earlier CPFEM results by Zhang et al. In the following figures, S shows the deviatoric stress. All resolutions are finer than 32 × 32 × 32 and show very similar results. Considering Fig. 6a, one can see that there is a small difference between CPFFT and CPFEM for the yield surfaces calculated for the case of AA3103H18 with the elongated grains. For the more equi-axed grains in the recrystallized AA3103O in Fig. 6b, there is a good agreement between the yield surfaces derived by these two numerical methods.

Fig. 6

The yield surface in the first quadrant of the ${S}_{11}-{S}_{22}$ section for AA3103H18 (a) and AA3103O (b). The indicated resolutions for the FFT simulations are compared to the CPFEM simulations (Zhang et al. 2014) and with a strain rate of 0.0152 s⁻¹

Phenomenological yield surfaces can be calibrated from a sufficiently high number of calculated yield points, all in the π plane with hydrostatic pressure equal to zero. The hydrostatic pressure is not expected to influence the yield surface calibration. A set of required calibration points can be calculated by the computational framework using the DAMASK software for prescribed stress or strain–rate directions in the corresponding 5-dimensional spaces. In both cases, these directions can be chosen either randomly or uniformly.

To compare the calibrations to the different sets of directions, the Yld2004-18p yield surface was calibrated to calculated stress points for the AA3103H18 alloy with the elongated grains. Sets of either 16, 32, 64, or 125 either randomly or orthotropic distributed directions were calculated, where each yield point was taken at constant plastic work. In Fig. 7, yield surfaces for AA3103 in O and H18 temper are calibrated to 16 and 125 stress points and plotted and compared with selected yield–stress points calculated by DAMASK and the computational framework at uniformly distributed yield–stress directions in the ${\mathrm{S}}_{11}-{\mathrm{S}}_{22}$ plane. There is a significant difference between the yield surfaces that are calibrated with 16 stress directions and the dense set of calculated yield–stress points by the computational framework. The yield surface calibrated with 125 points, however, fits quite accurately.

Fig. 7

Comparison for the AA3103H18 alloy of the Yld2004-18p yield surface with calibrations to a N = 16, and b N = 125 yield–stress points. Corresponding DAMASK simulation results in the ${S}_{11}-{S}_{22}$ section are shown for selected shear stresses (${S}_{12}=0, 50, 75 \, \mathrm{and}\, 100\, \mathrm{MPa}.$), as a dense population of yield–stress points calculated by the present virtual lab

To provide a precise comparison, two large sets of yield–stress points were calculated as a reference. One set contained 208 yield–stress points with uniformly distributed orthotropic directions in the deviatoric stress space, and the other set included 72 yield–stress points uniformly distributed orthotropic directions in the stress space for the case of the plane–stress condition. The error is estimated as the average of the ${L}_{2}$ norm of the difference between these calculated yield–stress points and the corresponding prediction by the calibrated yield surface in the same stress direction.

To analyze the sensitivity of yield surface calibrations to different sets of random directions, four distinct random-direction distributions were tested for the sets of 16 and 32 stress and strain–rate directions. The corresponding four different errors measured are all indicated in Fig. 8. A significant spread is seen from time to time, where the error is in the range from 1.2% to 3.1% for 16 strain–rate directions, 0.68%–3.1% for 16 stress directions, 0.58%–1.05% for 32 strain–rate directions and 0.62%–1.1% for 32 stress directions.

Fig. 8

The Yld2004-18p yield surface is calibrated to $N=$ 16, 23, 64, and 125 yield–stress points, calculated by prescribing either stress or strain–rate directions that are chosen either randomly or uniformly, obeying orthotropic symmetry. The calibration error is estimated as the difference between the crystal plasticity calculation and the Yld2004-18p yield surface prediction for the same stress direction, where the total error is the average of the L₂ norms of these differences. a The error is calculated as the average of 208 yield–stress points in the 5D deviatoric stress space. b The error is calculated as the average of 72 yield–stress points in the 3D deviatoric plane–stress space, for which the plane–stress version of the calibrated Yld2004-18p yield surface (with 12 independent parameters) is calibrated

In Fig. 8a, errors are plotted and compared for the 5D stress cases, for different numbers of calibrated stress or strain–rate directions, with either random or orthotropic distributions. It is obvious that the use of only 16 stress points in the calibration provides large unacceptable errors, regardless of the choice of calibration directions. For 32 points, both calibrations with orthotropic stress and with orthotropic strain–rate directions give a much smaller error of $0.55\%$. However, the calibrations to random stress or strain–rate directions still have relatively higher errors of $0.6\%-1.1\%$. For calibrations using 64 yield–stress points, both the distribution of orthotropic stress and strain–rate directions and the random distribution of stress directions provide an acceptable error of $0.48\%$, while the calibration to random strain–rate directions gives a larger error of $0.55\%$. For 125 points, regardless of the set of calibration directions, the error is 0.47%.

Since the S₁₁–S₂₂–S₁₂ plane–stress space is of particular importance, i.e., considering plates, a study of the errors was made, considering stress directions restricted to this sub-stress space, i.e., the important cases of the plane–stress condition. When strain–rate directions are used for the calibration of plane–stress conditions, one must ensure that the texture is orthotropic and inspect that the stress of other components is zero or small. This was approximately guaranteed for the textures tested here. To ensure a fully orthotropic texture, additional grains with the rotations of each measured grain into all its orthorhombic symmetric variants would be required. However, this would increase the number of grains in the RVE significantly and was not done.

In Fig. 8b, the calibration errors are plotted for the different calibrations. It is seen that all cases with only 16 points have high errors. The calibration with 32 stress directions with an orthotropic stress direction distribution provides a lower error of 0.69% compared to the calibration with 32 strain–rate directions, which had an error of 1.24%. The two variants of calibrations to 32 random directions have significantly higher errors than this, while all calibrations to 64 and 125 directions result in errors below 1%.

To investigate the influence of the synthesized grain morphology by the DREAM.3D software, ten different RVEs were created independently and simulated. In Fig. 9, resulting yield–surface sections are plotted for these geometries. The texture, i.e., the list of grain orientations, was kept the same for all these simulations.

Fig. 9

The ${S}_{11}-{S}_{22} y$ ield-surface section calculated by the virtual lab for ten distinct geometries with identical texture, 2500 grains and 32 × 32 × 32 resolution for the case of AA3103H18 alloy

Although CPFFT simulations are much faster than CPFEM, they still require a significant amount of computer capacity for the highest resolutions of 128 and 256 and require sufficient internal memory (RAM) of the computer. Because of memory limitations, it was impossible to start simulations for the 256 × 256 × 256 resolutions on a stationary personal computer (PC) with 32 GB of RAM. Simulation times of a 10.7% tensile test on the PC and a supercomputer were compared for 32 × 32 × 32, 64 × 64 × 64, and 128 × 128 × 128 resolutions. The simulations on the supercomputer were run on 4 nodes, 8 tasks per node, and 5 CPU (Intel^® Xeon^® Gold 6148 Processor 27.5 M Cache, 2.40 GHz) cores per task. The supercomputer was provided by the NTNU IDUN/EPIC computing cluster, while the PC had an Intel Core i7-8700 @ 3.2 GHz × 12 processors. It was seen that the simulations on the supercomputer are 30 times faster than on the PC.

5 Discussion

In this work, two distinct approaches were considered. Either, prescribing $\dot{{\varvec{F}}}$, which is possible in the DAMASK code, or run is an iterative algorithm, allowing a stress state specified by a stress direction and a prescribed plastic work to be calculated. This is convenient, as it allows calculations of tensile tests and yield points in specified yield–surface sections. The DAMASK software offers a mixed boundary condition in terms of combinations of the first Piola–Kirchhoff stress and the rate-of-deformation gradient tensor, which generally cannot be used for this purpose.

The algorithm was applied first for calculations of an RVE for three different alloys, with different textures and with different grain morphologies. CPFEM simulations for the three alloys have been published earlier (Zhang et al. 2014, 2015) and enable a comparison between the DAMASK spectral solver and earlier published CPFEM simulations as well as experimental results. However, the main topic here was to investigate how fine mesh is required for the spectral calculations of these representative cases, for which the calculation with the finest mesh can serve as the reference solution.

Unlike the finite-element method formulations in the FEM codes compared here, which have a low second-order spatial accuracy, a spectral method is a global approach for solving the partial differential equations with an exponential spatial convergence for smooth functions. In the DAMASK code applied here, this methodology requires periodic boundary conditions and a Cartesian grid with constant spacing, which allows the use of the fast Fourier transform, providing very fast calculations for the grid with a power-of-two number of points in each direction. Recently, some studies were reported using the spectral method for non-periodic boundary conditions (Gélébart 2020) and irregular grids for discretizing microstructures (Zecevic et al. 2022). The method is suitable for calculating RVEs and, therefore, ideal for multiscale approaches. However, the RVE contains many grains, and each grain boundary is a discontinuity, which lowers the spatial accuracy of the spectral method, where use of composite voxel helps with this (Kabel et al. 2015). Discontinuities also give rise to the Gibbs oscillations phenomenon in a spectral series expansion (Gottlieb et al. 2011). However, the algorithm applied in the DAMASK solver is modified to minimize this error (Roters et al. 2019; Willot 2015), which will efficiently reduce the related errors. Hence, a few grid points per grain might be sufficient for spatial resolution.

A grid with 16 × 16 × 16 points provides 4096 points. For the case of 1000 grains, this is about 4 points per grain, i.e., 1.58 and 1.18 points per length in each direction in each grain, for the case of 1000 and 2500 grains, correspondingly. This is the absolute minimum resolution required for the considered RVEs. The results for tensile tests in various plate directions show that while the dependency of the tensile direction is captured well by the 16 × 16 × 16 points resolution, the tensile stress, i.e., the Taylor factor, is either a bit too high or low, within about one percent. Interestingly, the investigation by Zhang et al. (2019) found that when the resolution is too low, the Taylor factor decreases with increased resolution. However, the DAMASK results with 16 × 16 × 16 points do not show systematically higher Taylor factors, indicating that the spatial resolution is not too low. Instead, it is reasonable to assume that the spatial complexity of the solution is high but that the correct solution is not precisely found due to the solution being disturbed by the presence of all the discontinuities at the grain boundaries. A resolution of 32 × 32 × 32 points, on the other hand, with 8 times as many points per grain and more than 3 points per length in each grain for the case of 1000 grains, provides a similar solution as with the higher resolutions and can be used for the RVEs investigated with 1000 and with 2500 grains.

For the tensile test simulation results in Fig. 4c and d, it is seen that there is a significant difference between experimental and simulated r values. Therefore, to examine the validity of the boundary conditions of the CPFFT solver as compared to the experiments, two distinct boundary conditions were imposed for the loading—one with zero shear stress and one with zero shear strain, corresponding to clamped ends of the tensile specimen, which was the case for the tensile tests. However, both conditions resulted in the same r values. Hence, comparing the CPFEM and CPFFT results, it can be concluded that the variation between these two numerical methods is not as large as the difference between the simulations and the tensile tests.

For the yield–surface calibration, the effect of the number of yield points by specifying a random or orthotropic uniform distribution of stress or strain–rate directions in the 5D space is investigated in this work. By choosing 125 points, regardless of the chosen distribution, the error is very low. However, high computational costs can be reduced by performing simulations of yield–stress points for fewer directions. For the calibration to 32 or 64 yield–stress points, the influence of the distribution of probed directions becomes significant. With a uniform distribution, obeying the orthotropic symmetry, either in stress or strain rate space, an acceptable error ($\approx 0.5\%$) was achieved with only 32 points.

Interestingly, a uniform distribution of strain–rate directions provided a similarly good fit as with the uniform stress directions. Since the strain–rate directions could be simulated without further iterations, the strain–rate approach will be computationally less costly. Utilizing a uniformly distributed set of directions is more effective than a random arrangement. It could be argued that employing a non-uniform adaptive distribution of points on the yield surface might yield even better results. One approach could involve initiating with a basic layout and subsequently adding extra points in regions displaying significant curvature, which might end up in better results. Although in this paper that approach is not investigated, it can be an interesting topic for future research.

The spectral method is much faster than CPFEM but can also be expensive if refined resolutions, such as 128 × 128 × 128, are needed. A certain number of points are required for a good spatial resolution, which again depends on how many grains are considered in the simulation. In the current investigations, good accuracy was achieved with the 32 × 32 × 32 resolution, corresponding to about 13 points per grain for the case of 2500 grains. Assuming the same minimum number of points per grain is required, the 64 × 64 × 64 grid should be sufficient for about 20,000 grains of uniform size. This might be a reasonable rule of thumb. However, one should keep in mind that if, for example, a bimodal distribution of small and large grains is considered, the small grains would require a high resolution.

In principle it should be possible to implement a prescribed stress direction more directly and deeper into the DAMASK code, but that goes beyond the scope of the work reported her. Hence, the iterative algorithm that makes it possible to find the yield stress in one specified stress direction comes with an extra cost compared to the prescribed strain–rate tensor. However, time is saved by first calculating a 16 × 16 × 16 grid solution to provide an excellent first guess. This calculation is an order of magnitude faster and reduces the number of costly 32 × 32 × 32 grid iterations to a few. Still, the extra cost must be justified. For a calibration of the Yld2004-18p orthotropic yield surface, a uniform selection of 32 strain–rate directions gives equally good results as a uniform distribution of stress directions for an overall calibration and will be a preferred choice.

However, in some cases, the possibility of plotting and analyzing specific yield–surface sections is of interest. In particular, the case of plane stress, with only three non-zero stress components, is of common interest. In such cases, one should expect that the texture should ideally obey orthotropic symmetry. Hence, in simulations of plate-deformation modes, these components will ideally turn out to be small. However, in many cases, a non-perfect orthotropic selection of grain orientations may cause significant deviations from the plane–stress condition. To make these stress components precisely equal to zero, one would have to rotate each grain into all its orthorhombic symmetric orientations and include all rotation variants in the crystal plasticity simulation. However, the number of grains in the DAMASK simulation is restricted to keep the computing time low. Hence, the iteration procedure is safe and convenient for precise calibration or plotting of a plane–stress yield surface and might often be required.

6 Conclusion

A framework is presented, allowing CPFFT calculations for prescribed stress directions. It is tested by comparison to experiments and CPFEM calculations earlier reported for plate materials.

• High grid resolutions, up to 256 × 256 × 256, were calculated as a reference, but a 32 × 32 × 32 grid resolution is enough for analyzing the considered RVEs, both for the cases with 1000 and for the case with 2500 grains that were tested. Hence, with the DAMASK software, one can simulate virtual experiments with an RVE containing about 1000 grains on a personal computer without needing a supercomputer.

• Two different grain geometries were generated for AA3103H18, one with equi-axed grains and the other with strongly elongated grains. By comparing the r values and normalized yield stresses for these two cases, it can be concluded that there is a difference for these two-grain morphologies, but it is not very large.

• The calibration of 32 virtual tests, chosen from a uniform distribution of orthotropic strain–rate directions, provides a very good calibration of the Yld2004-18p yield surface. Choosing a virtual test from a uniform distribution of stress directions instead gives equally good results but is more costly. The simpler approach of randomly chosen directions in either strain–rate or stress directions is not recommended, as it gives larger errors with a larger error spread.

These outcomes indicate that the framework based on the DAMASK crystal plasticity solver can effectively generate virtual tests to calibrate yield–stress points for a continuum yield surface. Guidelines are provided here for the required grid resolution, how many virtual tests are required, and how to choose their loading modes.