Introduction

In 2016, the City of Toronto reported 76 fatal traffic collisions that resulted in 78 individual fatalities. This peak year prompted increased efforts by law enforcement to target and reduce the number of fatalities resulting from traffic collisions, with special attention being paid to the numbers of pedestrian and cyclist deaths from these incidents. In the City of Toronto, public concern over traffic collisions is evidenced by initiatives such as the Vision Zero Plan (City of Toronto 2017), a municipal data-driven strategy for reducing traffic-related fatalities. At the core of such initiatives is the all-important task of identifying priority areas where the risk of traffic fatalities is highest. The identification of high-risk locales aids law enforcement officials in assigning resources where they might have the greatest impact in reducing fatalities.

This study employs a ‘near-miss’ model to forecast locations of fatal collisions in one recent year based on the distribution of non-fatal collisions in the 4 years prior. The aim of this paper is to demonstrate a simple, easily reproducible methodology for police and transportation organizations to optimize resource allocation. The method is similar to what has been done for knife murders in London (UK), with almost identical distributions of fatalities based on prior non-fatal incidents (Massey et al. 2019).

Forecasting locations of rare events

Spatial forecasting tools are built on the premise that even rare events follow predictable patterns. This premise is clearly established with the concentration of most crimes in a tiny fraction of micro-places in virtually any community (Sherman et al. 1989; Weisburd 2015). Crime is an iterative process, with criminals often committing the same types of crime at the same time in the same geographical locations (Koss 2015). Yet other events also occur in spatial patterns, from disease to airplane crashes to automobile collisions.

Two types of place-based forecasting models are most commonly used in research to predict crime locations: the near-repeat model and risk terrain modelling (RTM). This study applies the near-repeat model to the forecasting of fatal vehicle crashes.

Near-repeat forecasting

Any near-repeat model of crime suggests that it may spread throughout a local environment at the micro-level, much like an infectious disease. Such models predict that once a particular location is afflicted by an event, the statistical likelihood of repeat events within that location and the close surrounding environment increases significantly. When a home has been burglarized, for example, the near-repeat model predicts that this home as well as the homes surrounding it will be at a greater risk (statistically speaking) of future burglaries within the next week relative to a home that has not been burglarized. Using near-repeat models, Townsley et al. (2003) demonstrated that a greater number of burglary event pairs in Queensland, Australia, were clustered within a distance of 200 m and 2 months than would be expected on the basis of chance. A similar near-repeat burglary pattern was also found in Merseyside, UK, at distances of 400 m in 2 months (Johnson and Bowers 2004). The Johnson et al. (2007) analysis of data from 10 separate cities from five different countries (Australia, Netherlands, New Zealand, UK, and USA) revealed that near-repeat burglary patterns were ubiquitous. The results showed that near-repeat burglary patterns were consistent across all studied locations; burglary point pairs were clustered within distances of about 100 m and 2 weeks (Johnson et al. 2007). Finally, a near-repeat analysis conducted using burglary and theft from motor vehicles (TFMV) data from Bournemouth, UK, found a near-repeat pattern for both the burglary events (400 m and 6 weeks) and TFMV events (400 m and 6 weeks) separately, but a modified analysis that examined burglary and TFMV simultaneously failed to find any evidence of a bivariate space–time concentration (Johnson et al. 2009).

Rare events and near-misses

Forecasting the occurrence of rare events is a particularly difficult task. However, “the most fundamental starting point for predicting most kinds of rare events is near-misses of those events” (Massey et al. 2019: 3). A ‘near-miss’ is an event where no significant harm occurs despite the event almost coming to past. Systems for reporting near misses, ‘close calls’, or ‘sentinel events’ have been institutionalised in aviation, nuclear power technology, petrochemical processing, steel production, military operations, and air transportation (Barach and Small 2000). In healthcare, incident reporting systems for medical near-misses supplement the limited data available from mandatory reporting systems focused on preventable deaths and serious injuries (Gambino and Mallon 1991).

There is ample evidence for violent but non-fatal events predicting the much rarer occurrences of fatal violence. Mohler (2014) demonstrated that long-term patterns of prior assaults can be used to forecast homicides across spatial units. In a shorter time frame, Massey et al. (2019) examined how accurately the locations of knife homicides in London can be forecasted in 1 year based on the spatial distribution of non-fatal knife-related assaults in the preceding year. The Massey analysis found that 69% of all knife-enabled homicides took place in 1.4% of all lower super output areas (LSOAs) in London, a standard category for micro-areas. Furthermore, by using the near-miss methodology, they found that areas with the highest numbers of non-fatal knife assaults were 1400% more likely to have a knife-related homicide than the ‘coldest’ LSOAs. Non-fatal knife assaults can therefore be used as a reliable basis by which to forecast knife homicides.

Research question

The research question for this study is

How accurately can all recorded locations of 44 fatal vehicle collisions in one year (2012) be forecast across 1403 hexagonal tessellations within Toronto, based upon 1482 non-fatal collisions in the preceding four years (2008 through 2011)?

As a related technical comparison into an alternative method of forecasting, a brief appendix to this study addresses a related question: Is the utility of the near-miss model the result of a larger surface area or the higher forecasting value of non-fatal collisions?

The main research question seeks to determine how well the locations of fatal collisions can be forecasted based on non-fatal collisions. Our focus is purposely limited to fatal collisions and near-misses because they have risen most rapidly in recent years in Toronto. They are also a homogenous group that offers more reliability in forecasting than the full diversity of all traffic incidents. While many other predictors could ultimately contribute to a forecasting model, we limit the present analysis so that a wide audience can understand how a purely objective criteria can be used for targeting police resources to save lives.

The second research question seeks to address the efficacy of near-miss forecasting relative to an alternative forecasting model.

Data

For the purposes of this study, a near-miss event is defined as a vehicular collision that did not result in a fatality, but was otherwise reported to have major, minor, minimal, or no injuries. A total of 1482 non-fatal traffic collisions in 2008 through 2011 and 44 fatal traffic collisions from 2012 were aggregated across 1403 micro-areas called ‘hexagonal tessellations’ to create Periods 1 and 2, respectively. By sorting each hexagonal tessellation into different categories of risk, the study was able to use Period 1 coding to forecast Period 2 fatal collisions in Period 2. The Period 1 and Period 2 categories were coded according to whether a micro-area had 0, 1, 2, 3, 4, 5, or 6 or more non-fatal traffic collisions in Period 1. The 44 fatal collisions in Period 2 were then assigned to each of the 43 areas in which they occurred, with only one micro-area having two fatalities while the rest had one and only one fatal collision. The Period 1 counts omitted the 173 fatal collisions during Period 1. They would have added 12% more prior collisions to the prediction data. Yet they would not have counted as ‘near-misses’ for the purposes of this model. Others applying this research design in other cities may wish to include all collisions in Period 1, both non-fatal and fatal, to predict fatal collisions in Period 2.

These data were acquired from the Toronto Police Service’s Public Safety Data Portal. Specifically, the Killed and Seriously Injured (KSI) dataset was used to produce the fatal and non-fatal collisions that acted as input data for the near-miss model. A selection of these data was extracted from the original database to construct a new, tabulated record of every single recorded fatality for the period 2008–2012 (using sequential, financial year periods). When these data were first acquired, there was a row for each victim of a collision where an individual was killed or seriously injured. The unit of analysis was a collision event, rather than the number of victims per event. Each event was therefore classified with binary coding as either fatal or non-fatal. Each recorded incident had affixed to it the corresponding latitude and longitude; all fatalities and non-fatalities were successfully geocoded.

Methods

Geographic units of analysis: Hexagonal tessellation

Unlike the Massey et al. (2019) study of homicides in London, the present analysis did not adapt existing geographical units of analysis. Our method provided an original set of geographical divisions of the city that covered its entire surface, in order to improve the accuracy of the forecasting. This method employs custom-generated ‘hexagonal tessellations’ of the City of Toronto, originally identified for this study.

The concept of a hexagon is an elementary pillar of Euclidian geometry: a figure on a flat surface plane with six straight sides and angles. Developments in digital analysis now allow anyone to design their own borders of urban areas with different numbers of hexagons of widely varying sizes. Rather than accepting the limitations of areas drawn for historic reasons of administrative data collection, analysts can deploy computer programs to break down a city into equal-sized hexagons—but with a range of possible sizes. Those options, in turn, allow the analyses to be sensitive to the needs of operational decision-making, including the allocation of scarce resources to work in different micro-areas.

In this analysis, we subdivided the City of Toronto into 1403 hexagons by using the method of ‘tessellation’, in which an arrangement of shapes is closely fitted together in a repeated pattern without gaps or overlapping. Given the size of Toronto as 630.20 km2, the 1403 hexagonal micro-areas used in this study are the approximate equivalent of 449 m2, of four and one-half football fields square. The point, however, is that square shapes pose analytic challenges that can be ameliorated by the use of six-sided micro-areas.

The reasons for preferring six-sided areas are two-fold: (1) mitigating the ‘border issue’ and (2) reducing variance in surface area.

Edge or border effects

Summing up various types of crimes within an administrative zone is a staple of crime analysis. It is often useful for law enforcement to place crimes in their respective police administrative zones for resource deployment and visualization purposes. However, a possible methodological flaw of this approach is the ‘border issue’ (Zhang et al. 2012).

The border issue in cities is that crimes such as collisions and break and enter tend to occur almost exclusively on streets. Using administrative boundaries to locate such events tends to cluster them at the borders. This is further exacerbated by the fact that most administrative and census-based boundaries are bounded or created using streets. When first beginning the analysis, we attempted to utilize Statistics Canada’s ‘dissemination areas’. However, this was quickly abandoned as the majority of collision events fell on the borders or edges of areas, creating a considerable classification problem. The use of a custom hexagonal layer addresses the border issue by creating sub-areas that are GIS-generated and capture variation in collisions while minimizing classification problems.

Size matters

Traditional or census-based administrative zones (such as LSOAs in the UK or Dissemination Areas in the Canada) are usually created to represent an equal number of households. Downtown areas with a high population density have a much smaller surface area than more rural or suburban areas with smaller population densities. This variance in surface area is based on a factor that has little to do with the phenomenon being studied. Furthermore, the presence of large area polygons can negatively impact the examination of crime events. This is primarily due to smaller spatial units providing greater granularity than large administrative zones.

If one assumes even a small level of environmental and criminal heterogeneity, then using large units can obscure important differences within areas. On the other hand, units that are at too small risk leaves the analyst with too few cases in each, resulting in a ‘small number’ problem. The question then is how small a geographic unit can be before the drawbacks outweigh the benefits (Oberwittler and Wikstrom 2009). Through an iterative process, we determined that 500-m long hexagons were the most efficient.

Specificity and sensitivity in crime forecasting

The gold standard for evaluating a clinical test is a joint examination of the test’s ability to correctly identify both positive and negative cases. To test the accuracy of our near-miss model, we assess the ‘specificity’ (true negative rate) and ‘sensitivity’ (true positive rate) of the model’s forecasts. These two concepts are derived from the four basic outcomes of any prediction: true positives, true negatives, false positives, and false negatives.

True positives are outcomes in which the model correctly predicts the positive case: one in which something did happen as predicted. In this context, the true positives are hexagonal tessellations that had a traffic fatality in Period 2 with 1 or more non-fatal collisions in Period 1. Similarly, true negatives are events that were predicted not to occur and did not. In contrast, false positives are outcomes where the model incorrectly predicts a fatal accident when one did not happen in the period predicted (year two). Similarly, false negatives are events that were predicted not to occur, but they did. Here, false negatives are hexagonal tessellations that had a traffic fatality in Period 2 despite being predicted to not occur based on non-fatal collisions in Period 1.

Also known as the ‘true positive’ rate, sensitivity measures how often a model generates a correct positive prediction based on the condition it is testing for.

$$ \mathrm{Sensitivity}=\left(\frac{\mathrm{True}\ \mathrm{positives}}{\mathrm{True}\ \mathrm{positives}+\mathrm{False}\ \mathrm{positives}}\right)\mathrm{x}\ 100 $$

Similarly, specificity, or the ‘true negative’ rate, measures the how often a model generates a correct negative prediction.

$$ \mathrm{Specificity}=\left(\frac{\mathrm{True}\ \mathrm{negatives}}{\mathrm{True}\ \mathrm{negatives}+\mathrm{False}\ \mathrm{negatives}}\right)\mathrm{x}\ 100 $$

Sensitivity and specificity are expressed as percentages ranging between 0 and 100%. The false positive and false negative rates are therefore the mathematical inverses of the true positive and true negative rates, respectively. As such, if the sensitivity of a model is 85%, the false positive rate is 15%. Similarly, if the specificity of the model is 73%, the false negative rate is 27%. In a perfect forecasting model, both the sensitivity and the specificity would be 100%. However, in practice, forecasting usually confronts an inverse relationship between true positives and true negatives: the higher the true positive rate, the lower the true negative rate and vice versa. Selecting an appropriate model requires finding an acceptable balance between the two rates.

Limitations

A limitation of this study is the type of event selected for examination. Collisions, by definition, involve vehicles and their interaction within an environment. Those areas that do not have roads cannot (usually) have collisions. While the use of hexagonal zones might ameliorate other spatial problems, they could also serve to distort the results. This is because there are hexagonal zones in the study that likely contain no roads at all. These could encapsulate areas such as parks and other green space, bodies of water, and large buildings. Therefore, there are hexagonal zones in the dataset where the probability of a collision is approaching zero. On the other hand, this method provides far greater precision in the identification of clusters of collisions on arterial roads.

Findings

Within the study period (2008 through 2012) (Figs. 1, 2, and 3), there were 2108 unique collisions recorded in the City of Toronto. Of these, 10.3% (217) were fatal, while 89.7% (1891) were non-fatal. Two-thirds (66.3%) of all collisions in Toronto took place on major arterial roads. The percentage is nearly identical for fatal collisions. This is not particularly surprising given the busyness of arterial roads.

Fig. 1
figure 1

Fatal and non-fatal collisions, 2008–2018

Full size image
Fig. 2
figure 2

Fatal and non-fatal collisions, 2008–2012

Full size image
Fig. 3
figure 3

Fatal and non-fatal collisions by hexagonal tessellations, 2008–2012

Full size image

Near-miss forecasting counts

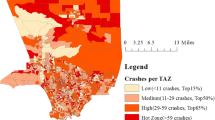
Based on the figures in Table 1, 70.5% of fatal collisions in Period 2 took place in a hexagonal tessellation that had at least one non-fatal collision in Period 1. The number of hexagonal tessellations that had 1 or more non-fatal collisions in Period 1 was 659, or 47% of all hexagonal spatial units. If one focused only on those hexagonal areas that had 2 or more non-fatal collisions in Period 1, this would target the areas where 50% of the fatal collisions in Period 2 took place in an that area constituting only 25% of all hexagons. It must be noted, however, that 29.5% of fatal collisions in Period 2 took place in hexagonal tessellations without a single non-fatal collision in the 4 years of Period 1.

Table 1 Prevalence of hexagons with fatal collisions in Period 2 by frequency of non-fatal collisions in Period 1
Full size table

Figure 4 presents probabilities for fatal collisions by the number of tessellations with a given number of non-fatal collisions. Indeed, we observe a very similar relationship to the one found in Massey et al. (2019). Specifically, the results indicate that there is a demonstrable increase in the risk for a fatal collision in Period 2 based on the number of non-fatal collisions that have taken place in those hexagonal tessellations in Period 1. If the categories for 2, 3, and 4 non-fatal collisions are combined, the relationship is steady: the more near-miss collisions that occur in a category of hexagons, the greater the likelihood of a collision fatality. In hexagonal tessellations that had zero non-fatal collisions during Period 1, only 1.7% of them had a fatal collision in Period 2. This increases to 3% for those with 1 non-fatal collision, 5.1% for those with 2 to 4 non-fatal collisions, and 15% for those with 6 or more non-fatal collisions during Period 1.

Fig. 4
figure 4

Percent of hexagons with Period 2 fatal collisions by frequency of Period 1 non-fatal collisions

Full size image

Of the hexagonal tessellations with the lowest risk (those lacking any non-fatal collisions during Period 1), only 1.7% reported a fatal collision during the 2012 target year. On the opposite end, the highest risk zones (those with 6 or more non-fatal collisions during Period 1) had a 15% chance of a fatal collision in Period 2. This means that the category of tessellations with 6 or more non-fatal collisions in Period 1 had a risk of fatal collision in Period 2 that was 8.7 times higher than the lowest risk zones. While this number may appear trivial in absolute terms, it can nonetheless be an important tool for distinguishing between zones. Indeed, in making decisions about how best to deploy increasingly scarce police resources for enforcement, knowing that certain areas have a risk that is almost 770% greater than all other areas combined is valuable information. This is made even more noteworthy given that these highest risk zones constitute less than 2% of all hexagonal tessellations.

Sensitivity and specificity by risk thresholds

Table 2 presents five targeting strategies for police commanders based on the risk probability of a collision fatality. Each row represents a near-miss targeting strategy, offering both the sensitivity and specificity of the strategy as well as the percentages of hexagons targeted (effort) and potential fatalities prevented (efficiency). Similar to Massey et al. (2018), we find no major difference in specificity between targeting the highest risk hexagons and the lowest risk hexagons. However, the sensitivity of the targeting strategies increases as the risk of a collision fatality increases.

Table 2 Sensitivity, specificity, effort, and efficiency per targeting model
Full size table

Nevertheless, the resource allocation requirements and potential harm reduction impact of each strategy differ. To this extent, while targeting hexagonal zones with a 15% risk of a Period 2 collision fatality would be the most accurate strategy based on its sensitivity, this strategy would target only 2% of hexagons and prevent (at most) only 9% of collision fatalities—leaving 91% of the micro-locations as false negatives. In contrast, targeting hexagonal zones with a 1.7% risk of a Period 2 collision fatality is not particularly feasible as it would require Toronto police to allocate resources equally to all hexagonal zones: the entire city.

Table 2 also reveals a compromise strategy, by which it may be prudent to target resources on hexagons with a 5.1% risk of a Period 2 collision fatality (Fig. 5). While the sensitivity is only 6%, resources would be allocated to 25% of hexagonal zones and would potentially reduce collision fatalities by 50%. Depending on the effectiveness and costs of any intervention efforts, this may be the most cost-efficient spatial targeting strategy for reducing vehicle collision deaths.

Fig. 5
figure 5

Areas targeted vs. potential fatal collisions prevented at 5.1% annualized risk of a fatal collision

Full size image

Conclusion

This study demonstrates the use of near-miss forecasting as a tool for identifying and targeting high-risk spatial units for collision fatalities. To this extent, collisions that did not result in a fatality in the recent past can help to forecast where fatal collisions are most likely to occur in the near future. Crime analysts need not rely solely on dense statistical models or algorithms whose operation can be understood by data scientists or model builders. These computations can be done by arithmetic alone, once the hexagonal boundaries are programmed to sort all collisions by hexagon.

For crime and traffic analysts and their employers, near-miss forecasting represents are easy-to-understand and easy-to-implement tool with high capacity for accurately targeting high-harm locations. This analysis has shown that this method can forecast fatal collision risk with known rates of error, including specificity and sensitivity.

When it comes to crime targeting strategies, little transparency is available about the overall accuracy, cost, and impact of forecasting models. One benefit of a near-miss forecasting model is its transparency. Based on our model, police commanders have a variety of targeting options to choose from in combatting fatal collisions. More importantly, however, police commanders are made aware of the various benefits and drawbacks of each strategy, distinguishing between the accuracy, effort, and efficiency. To this extent, the near-miss model ensures that the allocation of police resources is led by risk forecasts, which takes into account the maximum preventative impact of each deployment pattern.

In broad strategic terms, police leaders might opt for a utilitarian option where resources are deployed to zones with both the highest risk and specificity. However, resources might be better spent on a more all-encompassing deployment strategy where hexagonal zones with middling risk probabilities are targeted. This ensures that a wide swath of hexagonal zones is covered, with a higher total number of collision fatalities being prevented. Such patrols do currently take place but are often deployed across whole areas for short, isolated periods.

In a way that is similar to the study by Massey et al. (2019), this study forms a basis for an automated digital policing system. To this extent, should non-fatal traffic collisions occur in a hexagonal zone on a consistent basis over the course of 6 months, for example, a high level of risk for the hexagonal zone could be declared. Intensive policing, at least in the interim, could lead to greater reductions in both prospective fatal collisions and future non-fatal collisions. If a digital analysis shows that after several months, or even weeks or days, the risk of a non-fatal collisions has decreased, the resources invested in preventing these incidents in that zone could be reallocated to other zones with comparable risk probabilities.

Technical appendix

Upon examining these results, a sceptical observer might rightly note that any forecasting value gained from the near-miss method is acquired by increasing the surface area or number of hexagonal tessellations classified as having a non-fatal collision in Period 1. Indeed, the number of hexagons ‘covered’ by using non-fatal collisions is significantly larger than what would be accomplished using only fatal collisions from the previous year. This is due to the fact that there are, on average, 6.7 times as many non-fatal collisions as there are fatal collisions within a given year. As such, by increasing the surface area of hexagons where a non-fatal collision took place in Period 1, successful forecasting could be the result of simply increasing the forecasting surface area rather than a useful model.

To measure the methodological efficacy of near-miss forecasting, we conducted same N comparisons against forecasting models based on fatalities and randomly generated data points. To be clear, the number of hexagons ‘covered’ by using non-fatal collisions is significantly larger than what would be accomplished by using only fatal collisions from the previous year. This is because there are, on average, 6.7 times as many non-fatal collisions as there are fatal collisions within a given year (between 2008 and 2018). As such, by increasing the surface area of hexagons where a non-fatal collision took place in Period 1, successful forecasting could be the result of simply increasing the forecasting surface area rather than a methodologically robust model.

If this is true, it cannot be said that using non-fatal collisions for Period 1 provides any greater forecasting value than using the same number of collision fatalities or randomly generated points. In order to address this issue, it is useful to conduct a comparison of the forecasting success for fatal vs non-fatal points when both have the same number of points. As such, forecasting for 2012 was conducted once again using two datasets, 150 non-fatal collisions and 150 fatal collisions. Given the small number of fatal collisions per year, the set of 150 fatal collisions extends from December 2011 to the end of June 2018. This constitutes a very broad, multi-year temporal range. On the other hand, the 150 non-fatal collisions used for this test only constitute 3 months of non-fatal collisions for the 2011 year.

To assess the accuracy of these forecasting models, we examine the sensitivity of the model as well as the Global Moran’s I. The Moran I measures the autocorrelation of a spatial feature class (Li et al. 2007). In short, it measures how similar a feature class is to those surrounding it. If objects are attracted (or repelled) by each other, it means that the observations are not independent.

Using the same number of input variables for fatal collisions, non-fatal collisions, and randomly generated points, it is evident that non-fatal collisions have the highest forecasting success (see Table 3). Indeed, non-fatal collisions yielded a true positive rate of 25%, while fatal collisions had a sensitivity of 18%. This represents a 7% improvement when using non-fatal collisions even when controlling for the size of the input dataset. As expected, randomly generated points had the lowest true positive rate. However, it is surprising that even randomly generated points recorded a sensitivity of 14%. This could possibly be attributed to the spatially dispersed nature of collisions relative to other crimes.

Table 3 Comparison of forecasting value by model type
Full size table

In evaluating Global Moran’s Z-score for each of the three input types, the same hierarchy emerges. Once again, it is important to note that the non-fatal collisions had a higher level of clustering as measured by Global Moran’s I. Indeed, non-fatal collisions had a Z-score of 8.53 in comparison to 3.75 for fatal collisions. While this is interesting, it must be noted that the chances that either of these distributions are the result of complete spatial randomness is below 1%. Finally, it is again surprising that randomly generated points yielded a Moran Z-score of 2.24. This indicates that there is a 5% or less chance that the points were completely spatially random. If anything, this demonstrates the need for using only the strictest tolerances for Z-scores.